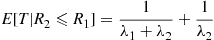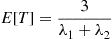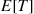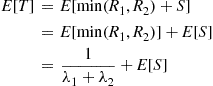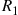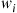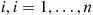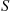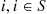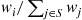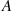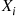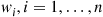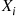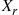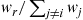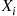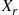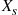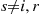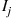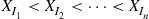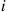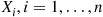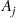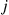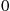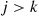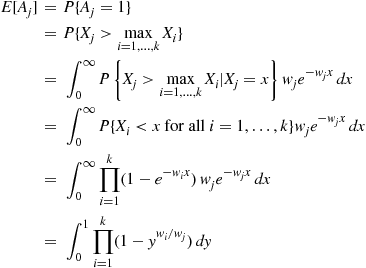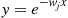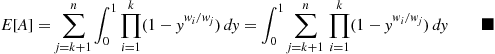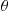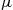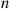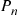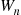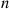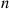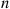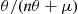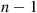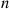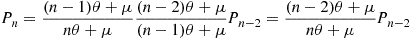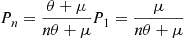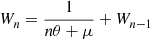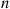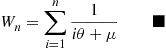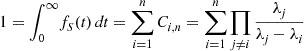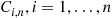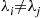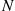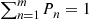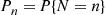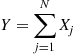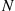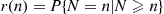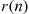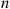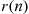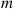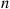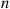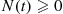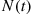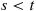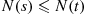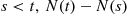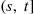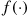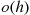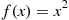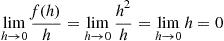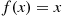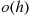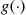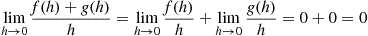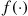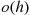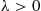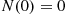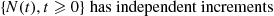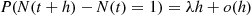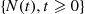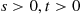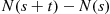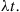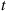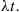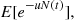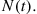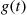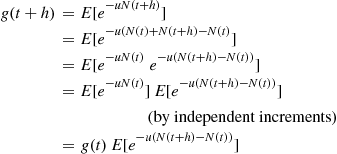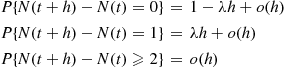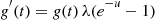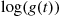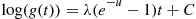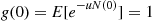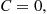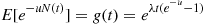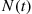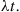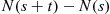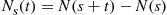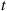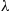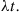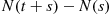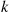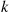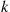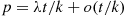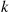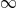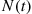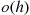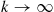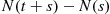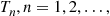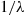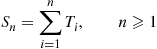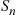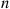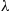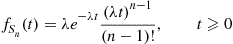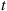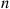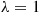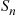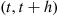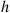5.2.4 Convolutions of Exponential Random Variables
Let 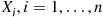 , be independent exponential random variables with respective rates
, be independent exponential random variables with respective rates 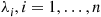 , and suppose that
, and suppose that  for
for 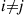 . The random variable
. The random variable 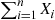 is said to be a hypoexponential random variable. To compute its probability density function, let us start with the case
is said to be a hypoexponential random variable. To compute its probability density function, let us start with the case  . Now,
. Now,

Using the preceding, a similar computation yields, when 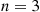 ,
,

which suggests the general result
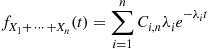
where

We will now prove the preceding formula by induction on 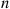 . Since we have already established it for
. Since we have already established it for 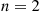 , assume it for
, assume it for 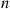 and consider
and consider  arbitrary independent exponentials
arbitrary independent exponentials 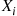 with distinct rates
with distinct rates 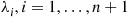 . If necessary, renumber
. If necessary, renumber 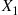 and
and 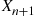 so that
so that  . Now,
. Now,
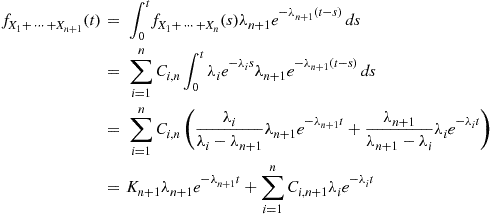 (5.7)
(5.7)where 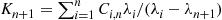 is a constant that does not depend on
is a constant that does not depend on 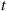 . But, we also have that
. But, we also have that
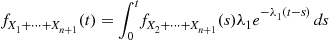
which implies, by the same argument that resulted in Equation (5.7), that for a constant 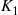
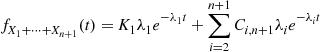
Equating these two expressions for  yields
yields
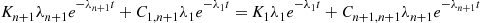
Multiplying both sides of the preceding equation by 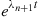 and then letting
and then letting 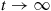 yields [since
yields [since 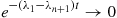 as
as 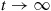 ]
]
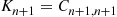
and this, using Equation (5.7), completes the induction proof. Thus, we have shown that if 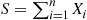 , then
, then
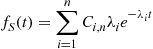 (5.8)
(5.8)
where
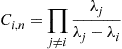
Integrating both sides of the expression for  from
from  to
to  yields that the tail distribution function of
yields that the tail distribution function of  is given by
is given by
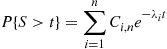 (5.9)
(5.9)
Hence, we obtain from Equations (5.8) and (5.9) that 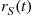 , the failure rate function of
, the failure rate function of 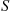 , is as follows:
, is as follows:
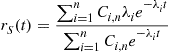
If we let 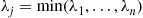 , then it follows, upon multiplying the numerator and denominator of
, then it follows, upon multiplying the numerator and denominator of 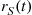 by
by 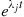 , that
, that

From the preceding, we can conclude that the remaining lifetime of a hypoexponentially distributed item that has survived to age 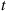 is, for
is, for 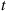 large, approximately that of an exponentially distributed random variable with a rate equal to the minimum of the rates of the random variables whose sums make up the hypoexponential.
large, approximately that of an exponentially distributed random variable with a rate equal to the minimum of the rates of the random variables whose sums make up the hypoexponential.
5.3 The Poisson Process
5.3.1 Counting Processes
A stochastic process 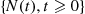 is said to be a counting process if
is said to be a counting process if 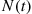 represents the total number of “events” that occur by time
represents the total number of “events” that occur by time 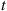 . Some examples of counting processes are the following:
. Some examples of counting processes are the following:
(a) If we let 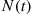 equal the number of persons who enter a particular store at or prior to time
equal the number of persons who enter a particular store at or prior to time 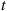 , then
, then 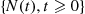 is a counting process in which an event corresponds to a person entering the store. Note that if we had let
is a counting process in which an event corresponds to a person entering the store. Note that if we had let  equal the number of persons in the store at time
equal the number of persons in the store at time 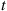 , then
, then 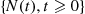 would not be a counting process (why not?).
would not be a counting process (why not?).
(b) If we say that an event occurs whenever a child is born, then 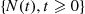 is a counting process when
is a counting process when 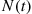 equals the total number of people who were born by time
equals the total number of people who were born by time 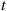 . (Does
. (Does 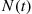 include persons who have died by time
include persons who have died by time 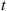 ? Explain why it must.)
? Explain why it must.)
(c) If 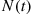 equals the number of goals that a given soccer player scores by time
equals the number of goals that a given soccer player scores by time  , then
, then  is a counting process. An event of this process will occur whenever the soccer player scores a goal.
is a counting process. An event of this process will occur whenever the soccer player scores a goal.
From its definition we see that for a counting process 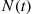 must satisfy:
must satisfy:
A counting process is said to possess independent increments if the numbers of events that occur in disjoint time intervals are independent. For example, this means that the number of events that occur by time 10 (that is, 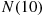 ) must be independent of the number of events that occur between times 10 and 15 (that is,
) must be independent of the number of events that occur between times 10 and 15 (that is, 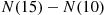 ).
).
The assumption of independent increments might be reasonable for example (a), but it probably would be unreasonable for example (b). The reason for this is that if in example (b) 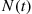 is very large, then it is probable that there are many people alive at time
is very large, then it is probable that there are many people alive at time 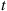 ; this would lead us to believe that the number of new births between time
; this would lead us to believe that the number of new births between time  and time
and time  would also tend to be large (that is, it does not seem reasonable that
would also tend to be large (that is, it does not seem reasonable that 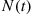 is independent of
is independent of  , and so
, and so  would not have independent increments in example (b)). The assumption of independent increments in example (c) would be justified if we believed that the soccer player’s chances of scoring a goal today do not depend on “how he’s been going.” It would not be justified if we believed in “hot streaks” or “slumps.”
would not have independent increments in example (b)). The assumption of independent increments in example (c) would be justified if we believed that the soccer player’s chances of scoring a goal today do not depend on “how he’s been going.” It would not be justified if we believed in “hot streaks” or “slumps.”
A counting process is said to possess stationary increments if the distribution of the number of events that occur in any interval of time depends only on the length of the time interval. In other words, the process has stationary increments if the number of events in the interval 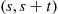 has the same distribution for all
has the same distribution for all  .
.
The assumption of stationary increments would only be reasonable in example (a) if there were no times of day at which people were more likely to enter the store. Thus, for instance, if there was a rush hour (say, between 12 P.M. and 1 P.M.) each day, then the stationarity assumption would not be justified. If we believed that the earth’s population is basically constant (a belief not held at present by most scientists), then the assumption of stationary increments might be reasonable in example (b). Stationary increments do not seem to be a reasonable assumption in example (c) since, for one thing, most people would agree that the soccer player would probably score more goals while in the age bracket 25–30 than he would while in the age bracket 35–40. It may, however, be reasonable over a smaller time horizon, such as one year.
5.3.2 Definition of the Poisson Process
One of the most important types of counting process is the Poisson process. As a prelude to giving its definition, we define the concept of a function 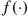 being
being 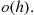
In order for the function 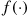 to be
to be  it is necessary that
it is necessary that  go to zero as
go to zero as 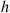 goes to zero. But if
goes to zero. But if 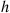 goes to zero, the only way for
goes to zero, the only way for  to go to zero is for
to go to zero is for 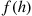 to go to zero faster than
to go to zero faster than 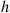 does. That is, for
does. That is, for  small,
small, 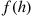 must be small compared with
must be small compared with 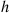 .
.
The  notation can be used to make statements more precise. For instance, if
notation can be used to make statements more precise. For instance, if 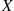 is continuous with density
is continuous with density  and failure rate function
and failure rate function  then the approximate statements
then the approximate statements
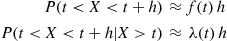
can be precisely expressed as

We are now in position to define the Poisson process.

5.3.3 Interarrival and Waiting Time Distributions
Consider a Poisson process, and let us denote the time of the first event by  . Further, for
. Further, for  , let
, let  denote the elapsed time between the
denote the elapsed time between the 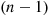 st and the
st and the 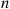 th event. The sequence
th event. The sequence 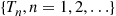 is called the sequence of interarrival times. For instance, if
is called the sequence of interarrival times. For instance, if  and
and 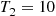 , then the first event of the Poisson process would have occurred at time 5 and the second at time 15.
, then the first event of the Poisson process would have occurred at time 5 and the second at time 15.
We shall now determine the distribution of the 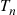 . To do so, we first note that the event
. To do so, we first note that the event 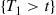 takes place if and only if no events of the Poisson process occur in the interval
takes place if and only if no events of the Poisson process occur in the interval 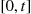 and thus,
and thus,
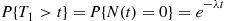
Hence, 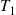 has an exponential distribution with mean
has an exponential distribution with mean 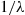 . Now,
. Now,
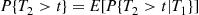
However,
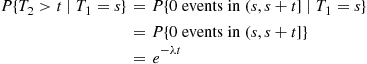 (5.12)
(5.12)where the last two equations followed from independent and stationary increments. Therefore, from Equation (5.12) we conclude that 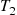 is also an exponential random variable with mean
is also an exponential random variable with mean  and, furthermore, that
and, furthermore, that 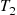 is independent of
is independent of 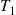 . Repeating the same argument yields the following.
. Repeating the same argument yields the following.
Proposition 5.1 also gives us another way of defining a Poisson process. Suppose we start with a sequence 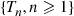 of independent identically distributed exponential random variables each having mean
of independent identically distributed exponential random variables each having mean 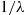 . Now let us define a counting process by saying that the
. Now let us define a counting process by saying that the  th event of this process occurs at time
th event of this process occurs at time
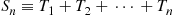
The resultant counting process 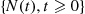 ∗ will be Poisson with rate
∗ will be Poisson with rate 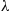 .
.