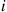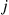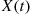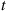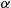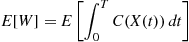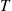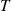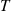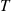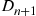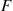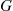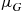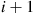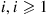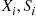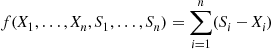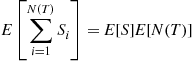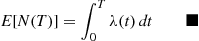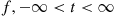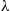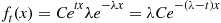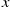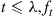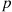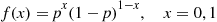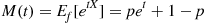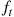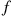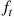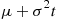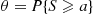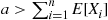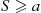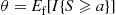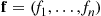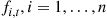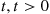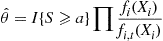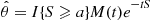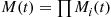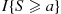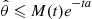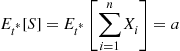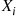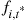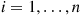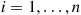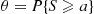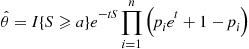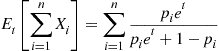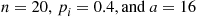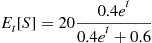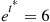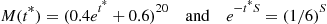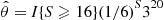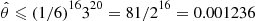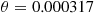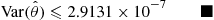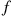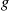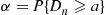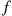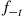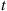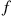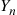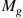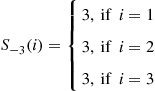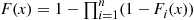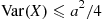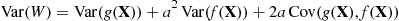
Simple calculus shows that the preceding is minimized when
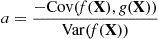
and, for this value of  ,
,
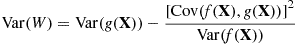
Because  and
and 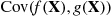 are usually unknown, the simulated data should be used to estimate these quantities.
are usually unknown, the simulated data should be used to estimate these quantities.
Dividing the preceding equation by 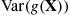 shows that
shows that

where  is the correlation between
is the correlation between  and
and 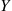 . Consequently, the use of a control variate will greatly reduce the variance of the simulation estimator whenever
. Consequently, the use of a control variate will greatly reduce the variance of the simulation estimator whenever 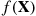 and
and  are strongly correlated.
are strongly correlated.
11.6.4 Importance Sampling
Let 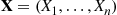 denote a vector of random variables having a joint density function (or joint mass function in the discrete case)
denote a vector of random variables having a joint density function (or joint mass function in the discrete case)  , and suppose that we are interested in estimating
, and suppose that we are interested in estimating

where the preceding is an  -dimensional integral. (If the
-dimensional integral. (If the  are discrete, then interpret the integral as an
are discrete, then interpret the integral as an  -fold summation.)
-fold summation.)
Suppose that a direct simulation of the random vector  , so as to compute values of
, so as to compute values of 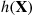 , is inefficient, possibly because (a) it is difficult to simulate a random vector having density function
, is inefficient, possibly because (a) it is difficult to simulate a random vector having density function 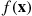 , or (b) the variance of
, or (b) the variance of  is large, or (c) a combination of (a) and (b).
is large, or (c) a combination of (a) and (b).
Another way in which we can use simulation to estimate 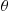 is to note that if
is to note that if  is another probability density such that
is another probability density such that  whenever
whenever  , then we can express
, then we can express  as
as
 (11.14)
(11.14)where we have written  to emphasize that the random vector
to emphasize that the random vector  has joint density
has joint density  .
.
It follows from Equation (11.14) that  can be estimated by successively generating values of a random vector
can be estimated by successively generating values of a random vector  having density function
having density function 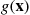 and then using as the estimator the average of the values of
and then using as the estimator the average of the values of  . If a density function
. If a density function  can be chosen so that the random variable
can be chosen so that the random variable 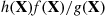 has a small variance then this approach—referred to as importance sampling—can result in an efficient estimator of
has a small variance then this approach—referred to as importance sampling—can result in an efficient estimator of 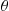 .
.
Let us now try to obtain a feel for why importance sampling can be useful. To begin, note that 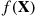 and
and  represent the respective likelihoods of obtaining the vector
represent the respective likelihoods of obtaining the vector  when
when 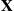 is a random vector with respective densities
is a random vector with respective densities  and
and  . Hence, if
. Hence, if 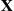 is distributed according to
is distributed according to 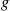 , then it will usually be the case that
, then it will usually be the case that  will be small in relation to
will be small in relation to  and thus when
and thus when  is simulated according to
is simulated according to  the likelihood ratio
the likelihood ratio  will usually be small in comparison to 1. However, it is easy to check that its mean is 1:
will usually be small in comparison to 1. However, it is easy to check that its mean is 1:
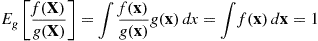
Thus we see that even though  is usually smaller than 1, its mean is equal to 1; thus implying that it is occasionally large and so will tend to have a large variance. So how can
is usually smaller than 1, its mean is equal to 1; thus implying that it is occasionally large and so will tend to have a large variance. So how can 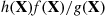 have a small variance? The answer is that we can sometimes arrange to choose a density
have a small variance? The answer is that we can sometimes arrange to choose a density  such that those values of
such that those values of 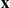 for which
for which  is large are precisely the values for which
is large are precisely the values for which  is exceedingly small, and thus the ratio
is exceedingly small, and thus the ratio 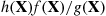 is always small. Since this will require that
is always small. Since this will require that  sometimes be small, importance sampling seems to work best when estimating a small probability; for in this case the function
sometimes be small, importance sampling seems to work best when estimating a small probability; for in this case the function 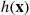 is equal to 1 when
is equal to 1 when  lies in some set and is equal to 0 otherwise.
lies in some set and is equal to 0 otherwise.
We will now consider how to select an appropriate density 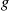 . We will find that the so-called tilted densities are useful. Let
. We will find that the so-called tilted densities are useful. Let  be the moment generating function corresponding to a one-dimensional density
be the moment generating function corresponding to a one-dimensional density  .
.
A random variable with density 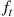 tends to be larger than one with density
tends to be larger than one with density  when
when  and tends to be smaller when
and tends to be smaller when  .
.
In certain cases the tilted distributions  have the same parametric form as does
have the same parametric form as does  .
.
In certain situations the quantity of interest is the sum of the independent random variables  . In this case the joint density
. In this case the joint density 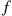 is the product of one-dimensional densities. That is,
is the product of one-dimensional densities. That is,
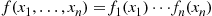
where 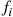 is the density function of
is the density function of  . In this situation it is often useful to generate the
. In this situation it is often useful to generate the 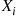 according to their tilted densities, with a common choice of
according to their tilted densities, with a common choice of  employed.
employed.
11.7 Determining the Number of Runs
Suppose that we are going to use simulation to generate  independent and identically distributed random variables
independent and identically distributed random variables  having mean
having mean 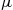 and variance
and variance 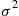 . We are then going to use
. We are then going to use
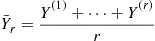
as an estimate of 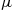 . The precision of this estimate can be measured by its variance
. The precision of this estimate can be measured by its variance

Hence, we would want to choose  , the number of necessary runs, large enough so that
, the number of necessary runs, large enough so that 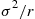 is acceptably small. However, the difficulty is that
is acceptably small. However, the difficulty is that  is not known in advance. To get around this, you should initially simulate
is not known in advance. To get around this, you should initially simulate 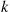 runs (where
runs (where 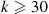 ) and then use the simulated values
) and then use the simulated values  to estimate
to estimate 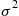 by the sample variance
by the sample variance

Based on this estimate of 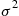 the value of
the value of  that attains the desired level of precision can now be determined and an additional
that attains the desired level of precision can now be determined and an additional 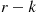 runs can be generated.
runs can be generated.
11.8 Generating from the Stationary Distribution of a Markov Chain
11.8.1 Coupling from the Past
Consider an irreducible Markov chain with states  and transition probabilities
and transition probabilities 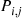 and suppose we want to generate the value of a random variable whose distribution is that of the stationary distribution of this Markov chain. Whereas we could approximately generate such a random variable by arbitrarily choosing an initial state, simulating the resulting Markov chain for a large fixed number of time periods, and then choosing the final state as the value of the random variable, we will now present a procedure that generates a random variable whose distribution is exactly that of the stationary distribution.
and suppose we want to generate the value of a random variable whose distribution is that of the stationary distribution of this Markov chain. Whereas we could approximately generate such a random variable by arbitrarily choosing an initial state, simulating the resulting Markov chain for a large fixed number of time periods, and then choosing the final state as the value of the random variable, we will now present a procedure that generates a random variable whose distribution is exactly that of the stationary distribution.
If, in theory, we generated the Markov chain starting at time  in any arbitrary state, then the state at time
in any arbitrary state, then the state at time 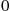 would have the stationary distribution. So imagine that we do this, and suppose that a different person is to generate the next state at each of these times. Thus, if
would have the stationary distribution. So imagine that we do this, and suppose that a different person is to generate the next state at each of these times. Thus, if  , the state at time
, the state at time  , is
, is 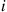 , then person
, then person  would generate a random variable that is equal to
would generate a random variable that is equal to 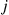 with probability
with probability  , and the value generated would be the state at time
, and the value generated would be the state at time 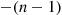 . Now suppose that person
. Now suppose that person 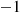 wants to do his random variable generation early. Because he does not know what the state at time
wants to do his random variable generation early. Because he does not know what the state at time  will be, he generates a sequence of random variables
will be, he generates a sequence of random variables  , where
, where  , the next state if
, the next state if 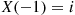 , is equal to
, is equal to  with probability
with probability 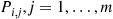 . If it results that
. If it results that 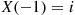 , then person
, then person 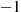 would report that the state at time
would report that the state at time 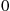 is
is
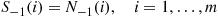
(That is,  is the simulated state at time
is the simulated state at time 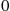 when the simulated state at time
when the simulated state at time 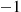 is
is 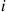 .)
.)
Now suppose that person 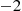 , hearing that person
, hearing that person 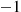 is doing his simulation early, decides to do the same thing. She generates a sequence of random variables
is doing his simulation early, decides to do the same thing. She generates a sequence of random variables  , where
, where 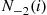 is equal to
is equal to 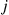 with probability
with probability 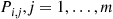 . Consequently, if it is reported to her that
. Consequently, if it is reported to her that 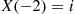 , then she will report that
, then she will report that 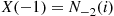 . Combining this with the early generation of person
. Combining this with the early generation of person 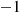 shows that if
shows that if 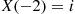 , then the simulated state at time
, then the simulated state at time 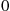 is
is
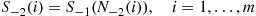
Continuing in the preceding manner, suppose that person 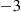 generates a sequence of random variables
generates a sequence of random variables 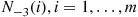 , where
, where  is to be the generated value of the next state when
is to be the generated value of the next state when  . Consequently, if
. Consequently, if  then the simulated state at time
then the simulated state at time 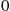 would be
would be
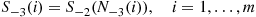
Now suppose we continue the preceding, and so obtain the simulated functions

Going backward in time in this manner, we will at some time, say  , have a simulated function
, have a simulated function 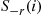 that is a constant function. That is, for some state
that is a constant function. That is, for some state  will equal
will equal 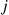 for all states
for all states  . But this means that no matter what the simulated values from time
. But this means that no matter what the simulated values from time  to
to  , we can be certain that the simulated value at time
, we can be certain that the simulated value at time  is
is  . Consequently,
. Consequently, 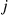 can be taken as the value of a generated random variable whose distribution is exactly that of the stationary distribution of the Markov chain.
can be taken as the value of a generated random variable whose distribution is exactly that of the stationary distribution of the Markov chain.
11.8.2 Another Approach
Consider a Markov chain whose state space is the nonnegative integers. Suppose the chain has stationary probabilities, and denote them by 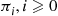 . We now present another way of simulating a random variable whose distribution is given by the
. We now present another way of simulating a random variable whose distribution is given by the 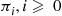 , which can be utilized if the chain satisfies the following property. Namely, that for some state, which we will call state 0, and some positive number
, which can be utilized if the chain satisfies the following property. Namely, that for some state, which we will call state 0, and some positive number 
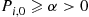
for all states 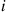 . That is, whatever the current state, the probability that the next state will be 0 is at least some positive value
. That is, whatever the current state, the probability that the next state will be 0 is at least some positive value 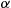 .
.
To simulate a random variable distributed according to the stationary probabilities, start by simulating the Markov chain in the obvious manner. Namely, whenever the chain is in state 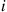 , generate a random variable that is equal to
, generate a random variable that is equal to  with probability
with probability  , and then set the next state equal to the generated value of this random variable. In addition, however, whenever a transition into state 0 occurs a coin, whose probability of coming up heads depends on the state from which the transition occurred, is flipped. Specifically, if the transition into state 0 was from state
, and then set the next state equal to the generated value of this random variable. In addition, however, whenever a transition into state 0 occurs a coin, whose probability of coming up heads depends on the state from which the transition occurred, is flipped. Specifically, if the transition into state 0 was from state 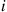 , then the coin flipped has probability
, then the coin flipped has probability  of coming up heads. Call such a coin an
of coming up heads. Call such a coin an  -coin,
-coin, 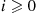 . If the coin comes up heads then we say that an event has occurred. Consequently, each transition of the Markov chain results in an event with probability
. If the coin comes up heads then we say that an event has occurred. Consequently, each transition of the Markov chain results in an event with probability 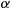 , implying that events occur at rate
, implying that events occur at rate  . Now say that an event is an
. Now say that an event is an 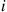 -event if it resulted from a transition out of state
-event if it resulted from a transition out of state  ; that is, an event is an
; that is, an event is an 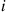 -event if it resulted from the flip of an
-event if it resulted from the flip of an  -coin. Because
-coin. Because 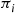 is the proportion of transitions that are out of state
is the proportion of transitions that are out of state  , and each such transition will result in an
, and each such transition will result in an 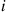 -event with probability
-event with probability  , it follows that the rate at which
, it follows that the rate at which  -events occur is
-events occur is 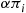 . Therefore, the proportion of all events that are
. Therefore, the proportion of all events that are 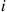 -events is
-events is 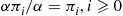 .
.
Now, suppose that  . Fix
. Fix 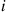 , and let
, and let 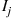 equal 1 if the
equal 1 if the 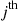 event that occurs is an
event that occurs is an  -event, and let
-event, and let  equal 0 otherwise. Because an event always leaves the chain in state 0 it follows that
equal 0 otherwise. Because an event always leaves the chain in state 0 it follows that  , are independent and identically distributed random variables. Because the proportion of the
, are independent and identically distributed random variables. Because the proportion of the 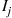 that are equal to 1 is
that are equal to 1 is 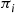 , we see that
, we see that
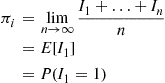
where the second equality follows from the strong law of large numbers. Hence, if we let
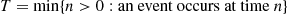
denote the time of the first event, then it follows from the preceding that

As the preceding is true for all states  , it follows that
, it follows that 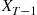 , the state of the Markov chain at time
, the state of the Markov chain at time  , has the stationary distribution.
, has the stationary distribution.
Exercises
*1. Suppose it is relatively easy to simulate from the distributions 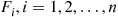 . If
. If 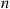 is small, how can we simulate from
is small, how can we simulate from

Give a method for simulating from
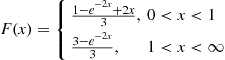
2. Give a method for simulating a negative binomial random variable.
*3. Give a method for simulating a hypergeometric random variable.
4. Suppose we want to simulate a point located at random in a circle of radius  centered at the origin. That is, we want to simulate
centered at the origin. That is, we want to simulate  having joint density
having joint density
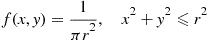
(a) Let 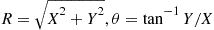 denote the polar coordinates. Compute the joint density of
denote the polar coordinates. Compute the joint density of 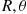 and use this to give a simulation method. Another method for simulating
and use this to give a simulation method. Another method for simulating  is as follows:
is as follows:
Step 1: Generate independent random numbers 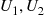 and set
and set 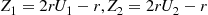 . Then
. Then 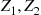 is uniform in the square whose sides are of length
is uniform in the square whose sides are of length 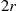 and which encloses, the circle of radius
and which encloses, the circle of radius  (see Figure 11.6).
(see Figure 11.6).
Step 2: If 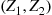 lies in the circle of radius
lies in the circle of radius  —that is, if
—that is, if  —set
—set 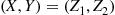 . Otherwise return to step 1.
. Otherwise return to step 1.
(b) Prove that this method works, and compute the distribution of the number of random numbers it requires.
5. Suppose it is relatively easy to simulate from  for each
for each 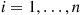 . How can we simulate from
. How can we simulate from
(c) Give two methods for simulating from the distribution 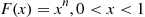 .
.
*6. In Example 11.4 we simulated the absolute value of a standard normal by using the Von Neumann rejection procedure on exponential random variables with rate 1. This raises the question of whether we could obtain a more efficient algorithm by using a different exponential density—that is, we could use the density  . Show that the mean number of iterations needed in the rejection scheme is minimized when
. Show that the mean number of iterations needed in the rejection scheme is minimized when 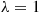 .
.
7. Give an algorithm for simulating a random variable having density function

8. Consider the technique of simulating a gamma  random variable by using the rejection method with
random variable by using the rejection method with 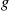 being an exponential density with rate
being an exponential density with rate 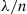 .
.
(a) Show that the average number of iterations of the algorithm needed to generate a gamma is 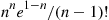 .
.
(b) Use Stirling’s approximation to show that for large  the answer to part (a) is approximately equal to
the answer to part (a) is approximately equal to  .
.
(c) Show that the procedure is equivalent to the following:
Step 1: Generate  and
and 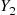 , independent exponentials with rate 1.
, independent exponentials with rate 1.
Step 2: If 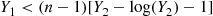 , return to step 1.
, return to step 1.
(d) Explain how to obtain an independent exponential along with a gamma from the preceding algorithm.
9. Set up the alias method for simulating from a binomial random variable with parameters  .
.
10. Explain how we can number the 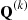 in the alias method so that
in the alias method so that 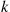 is one of the two points that
is one of the two points that  gives weight.
gives weight.
Hint: Rather than giving the initial 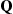 the name
the name  , what else could we call it?
, what else could we call it?
11. Complete the details of Example 11.10.
12. Let  be independent with
be independent with
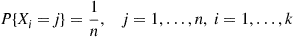
If  is the number of distinct values among
is the number of distinct values among  show that
show that

13. The Discrete Rejection Method: Suppose we want to simulate 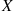 having probability mass function
having probability mass function  and suppose we can easily simulate from the probability mass function
and suppose we can easily simulate from the probability mass function 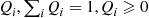 . Let
. Let  be such that
be such that  . Show that the following algorithm generates the desired random variable:
. Show that the following algorithm generates the desired random variable:
Step 1: Generate  having mass function
having mass function  and
and 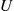 an independent random number.
an independent random number.
Step 2: If 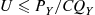 , set
, set 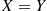 . Otherwise return to step 1.
. Otherwise return to step 1.
14. The Discrete Hazard Rate Method: Let 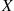 denote a nonnegative integer valued random variable. The function
denote a nonnegative integer valued random variable. The function  , is called the discrete hazard rate function.
, is called the discrete hazard rate function.
(a) Show that 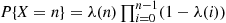 .
.
(b) Show that we can simulate  by generating random numbers
by generating random numbers  stopping at
stopping at

(c) Apply this method to simulating a geometric random variable. Explain, intuitively, why it works.
(d) Suppose that  for all
for all  . Consider the following algorithm for simulating
. Consider the following algorithm for simulating  and explain why it works: Simulate
and explain why it works: Simulate  where
where 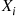 is geometric with mean
is geometric with mean 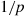 and
and 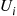 is a random number. Set
is a random number. Set 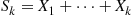 and let
and let
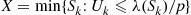
15. Suppose you have just simulated a normal random variable  with mean
with mean 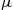 and variance
and variance  . Give an easy way to generate a second normal variable with the same mean and variance that is negatively correlated with
. Give an easy way to generate a second normal variable with the same mean and variance that is negatively correlated with 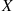 .
.
*16. Suppose  balls having weights
balls having weights  are in an urn. These balls are sequentially removed in the following manner: At each selection, a given ball in the urn is chosen with a probability equal to its weight divided by the sum of the weights of the other balls that are still in the urn. Let
are in an urn. These balls are sequentially removed in the following manner: At each selection, a given ball in the urn is chosen with a probability equal to its weight divided by the sum of the weights of the other balls that are still in the urn. Let  denote the order in which the balls are removed—thus
denote the order in which the balls are removed—thus  is a random permutation with weights.
is a random permutation with weights.
(a) Give a method for simulating  .
.
(b) Let  be independent exponentials with rates
be independent exponentials with rates  . Explain how
. Explain how  can be utilized to simulate
can be utilized to simulate  .
.
17. Order Statistics: Let  be i.i.d. from a continuous distribution
be i.i.d. from a continuous distribution  , and let
, and let  denote the
denote the 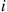 th smallest of
th smallest of 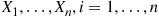 . Suppose we want to simulate
. Suppose we want to simulate 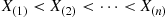 . One approach is to simulate
. One approach is to simulate  values from
values from  , and then order these values. However, this ordering, or sorting, can be time consuming when
, and then order these values. However, this ordering, or sorting, can be time consuming when 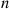 is large.
is large.
(a) Suppose that  , the hazard rate function of
, the hazard rate function of 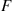 , is bounded. Show how the hazard rate method can be applied to generate the
, is bounded. Show how the hazard rate method can be applied to generate the 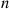 variables in such a manner that no sorting is necessary.
variables in such a manner that no sorting is necessary.
Suppose now that 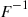 is easily computed.
is easily computed.
(b) Argue that  can be generated by simulating
can be generated by simulating  —the ordered values of
—the ordered values of 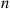 independent random numbers—and then setting
independent random numbers—and then setting 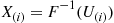 . Explain why this means that
. Explain why this means that 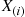 can be generated from
can be generated from 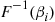 where
where 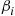 is beta with parameters
is beta with parameters  .
.
(c) Argue that  can be generated, without any need for sorting, by simulating i.i.d. exponentials
can be generated, without any need for sorting, by simulating i.i.d. exponentials  and then setting
and then setting
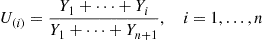
Hint: Given the time of the  st event of a Poisson process, what can be said about the set of times of the first
st event of a Poisson process, what can be said about the set of times of the first  events?
events?
(d) Show that if  then
then  has the same joint distribution as the order statistics of a set of
has the same joint distribution as the order statistics of a set of  uniform
uniform  random variables.
random variables.
(e) Use part (d) to show that  can be generated as follows:
can be generated as follows:
Step 1: Generate random numbers  .
.
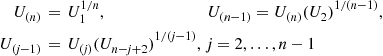
18. Let  be independent exponential random variables each having rate 1. Set
be independent exponential random variables each having rate 1. Set
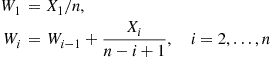
Explain why  has the same joint distribution as the order statistics of a sample of
has the same joint distribution as the order statistics of a sample of 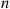 exponentials each having rate 1.
exponentials each having rate 1.
19. Suppose we want to simulate a large number  of independent exponentials with rate 1—call them
of independent exponentials with rate 1—call them  . If we were to employ the inverse transform technique we would require one logarithmic computation for each exponential generated. One way to avoid this is to first simulate
. If we were to employ the inverse transform technique we would require one logarithmic computation for each exponential generated. One way to avoid this is to first simulate  , a gamma random variable with parameters
, a gamma random variable with parameters 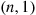 (say, by the method of Section 11.3.3). Now interpret
(say, by the method of Section 11.3.3). Now interpret 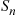 as the time of the
as the time of the 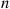 th event of a Poisson process with rate 1 and use the result that given
th event of a Poisson process with rate 1 and use the result that given 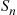 the set of the first
the set of the first 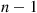 event times is distributed as the set of
event times is distributed as the set of  independent uniform
independent uniform  random variables. Based on this, explain why the following algorithm simulates
random variables. Based on this, explain why the following algorithm simulates 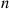 independent exponentials:
independent exponentials:
Step 1: Generate  , a gamma random variable with parameters
, a gamma random variable with parameters  .
.
Step 2: Generate 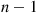 random numbers
random numbers  .
.
Step 3: Order the  to obtain
to obtain 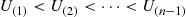 .
.
Step 4: Let  , and set
, and set  .
.
When the ordering (step 3) is performed according to the algorithm described in Section 11.5, the preceding is an efficient method for simulating 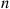 exponentials when all
exponentials when all  are simultaneously required. If memory space is limited, however, and the exponentials can be employed sequentially, discarding each exponential from memory once it has been used, then the preceding may not be appropriate.
are simultaneously required. If memory space is limited, however, and the exponentials can be employed sequentially, discarding each exponential from memory once it has been used, then the preceding may not be appropriate.
20. Consider the following procedure for randomly choosing a subset of size  from the numbers
from the numbers  : Fix
: Fix  and generate the first
and generate the first  time units of a renewal process whose interarrival distribution is geometric with mean
time units of a renewal process whose interarrival distribution is geometric with mean  —that is,
—that is,  . Suppose events occur at times
. Suppose events occur at times  . If
. If  , stop;
, stop;  is the desired set. If
is the desired set. If 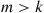 , then randomly choose (by some method) a subset of size
, then randomly choose (by some method) a subset of size 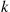 from
from  and then stop. If
and then stop. If  , take
, take  as part of the subset of size
as part of the subset of size 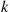 and then select (by some method) a random subset of size
and then select (by some method) a random subset of size  from the set
from the set  . Explain why this algorithm works. As
. Explain why this algorithm works. As 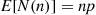 a reasonable choice of
a reasonable choice of 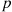 is to take
is to take 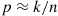 . (This approach is due to Dieter.)
. (This approach is due to Dieter.)
21. Consider the following algorithm for generating a random permutation of the elements  . In this algorithm,
. In this algorithm, 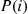 can be interpreted as the element in position
can be interpreted as the element in position 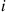 .
.
Step 3: If  , stop. Otherwise, let
, stop. Otherwise, let  .
.
Step 4: Generate a random number 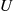 , and let
, and let
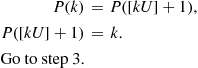
(a) Explain in words what the algorithm is doing.
(b) Show that at iteration 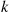 —that is, when the value of
—that is, when the value of 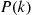 is initially set—that
is initially set—that 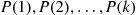 is a random permutation of
is a random permutation of  .
.
Hint: Use induction and argue that
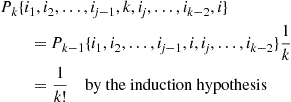
The preceding algorithm can be used even if  is not initially known.
is not initially known.
22. Verify that if we use the hazard rate approach to simulate the event times of a nonhomogeneous Poisson process whose intensity function  is such that
is such that 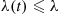 , then we end up with the approach given in method 1 of Section 11.5.
, then we end up with the approach given in method 1 of Section 11.5.
*23. For a nonhomogeneous Poisson process with intensity function  , where
, where  , let
, let  denote the sequence of times at which events occur.
denote the sequence of times at which events occur.
(a) Show that 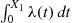 is exponential with rate 1.
is exponential with rate 1.
(b) Show that 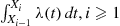 , are independent exponentials with rate 1, where
, are independent exponentials with rate 1, where  .
.
In words, independent of the past, the additional amount of hazard that must be experienced until an event occurs is exponential with rate 1.
24. Give an efficient method for simulating a nonhomogeneous Poisson process with intensity function

25. Let 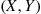 be uniformly distributed in a circle of radius
be uniformly distributed in a circle of radius  about the origin. That is, their joint density is given by
about the origin. That is, their joint density is given by

Let 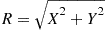 and
and  denote their polar coordinates. Show that
denote their polar coordinates. Show that 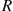 and
and 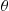 are independent with
are independent with 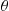 being uniform on
being uniform on 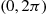 and
and  .
.
26. Let 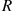 denote a region in the two-dimensional plane. Show that for a two-dimensional Poisson process, given that there are
denote a region in the two-dimensional plane. Show that for a two-dimensional Poisson process, given that there are  points located in
points located in  , the points are independently and uniformly distributed in
, the points are independently and uniformly distributed in  —that is, their density is
—that is, their density is  where
where  is the inverse of the area of
is the inverse of the area of 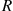 .
.
27. Let  be independent random variables with
be independent random variables with  , and consider estimates of
, and consider estimates of 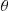 of the form
of the form  where
where 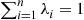 . Show that
. Show that  is minimized when
is minimized when
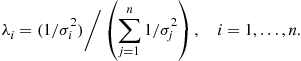
Possible Hint: If you cannot do this for general 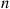 , try it first when
, try it first when 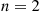 .
.
The following two problems are concerned with the estimation of  where
where  is uniform
is uniform 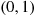 .
.
28. The Hit–Miss Method: Suppose 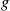 is bounded in [
is bounded in [ ]—for instance, suppose
]—for instance, suppose 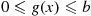 for
for 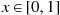 . Let
. Let  be independent random numbers and set
be independent random numbers and set  —so the point
—so the point  is uniformly distributed in a rectangle of length 1 and height
is uniformly distributed in a rectangle of length 1 and height 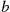 . Now set
. Now set
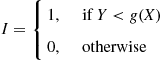
That is, accept 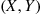 if it falls in the shaded area of Figure 11.7.
if it falls in the shaded area of Figure 11.7.
(a) Show that  .
.
(b) Show that 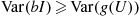 , and so hit–miss has larger variance than simply computing
, and so hit–miss has larger variance than simply computing  of a random number.
of a random number.
29. Stratified Sampling: Let  be independent random numbers and set
be independent random numbers and set 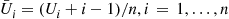 . Hence,
. Hence, 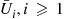 , is uniform on
, is uniform on 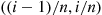 .
.  is called the stratified sampling estimator of
is called the stratified sampling estimator of  .
.
(a) Show that  .
.
(b) Show that  .
.
Hint: Let  be uniform
be uniform  and define
and define  by
by  if
if  . Now use the conditional variance formula to obtain
. Now use the conditional variance formula to obtain

30. If  is the density function of a normal random variable with mean
is the density function of a normal random variable with mean  and variance
and variance 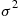 , show that the tilted density
, show that the tilted density  is the density of a normal random variable with mean
is the density of a normal random variable with mean  and variance
and variance  .
.
31. Consider a queueing system in which each service time, independent of the past, has mean 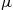 . Let
. Let  and
and  denote, respectively, the amounts of time customer
denote, respectively, the amounts of time customer  spends in the system and in queue. Hence,
spends in the system and in queue. Hence,  where
where  is the service time of customer
is the service time of customer 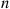 . Therefore,
. Therefore,
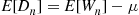
If we use simulation to estimate 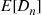 , should we
, should we
(a) use the simulated data to determine  , which is then used as an estimate of
, which is then used as an estimate of  ; or
; or
(b) use the simulated data to determine 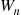 and then use this quantity minus
and then use this quantity minus  as an estimate of
as an estimate of 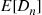 ?
?
Repeat for when we want to estimate  .
.
*32. Show that if  and
and 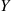 have the same distribution then
have the same distribution then

Hence, conclude that the use of antithetic variables can never increase variance (though it need not be as efficient as generating an independent set of random numbers).
34. Suppose in Example 11.19 that no new customers are allowed in the system after time  . Give an efficient simulation estimator of the expected additional time after
. Give an efficient simulation estimator of the expected additional time after  until the system becomes empty.
until the system becomes empty.
35. Suppose we are able to simulate independent random variables  and
and 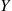 . If we simulate
. If we simulate  independent random variables
independent random variables  and
and  , where the
, where the 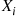 have the same distribution as does
have the same distribution as does 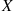 , and the
, and the 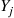 have the same distribution as does
have the same distribution as does  , how would you use them to estimate
, how would you use them to estimate 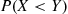 ?
?
36. If  are independent uniform (0, 1) random variables, find
are independent uniform (0, 1) random variables, find 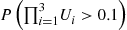 .
.


Hint: Relate the desired probability to one about a Poisson process.