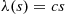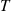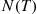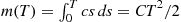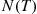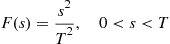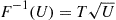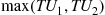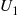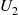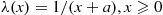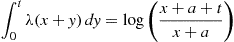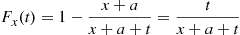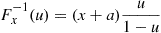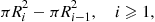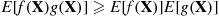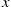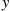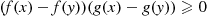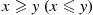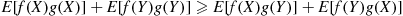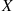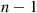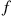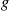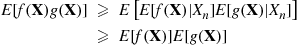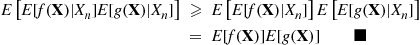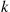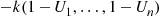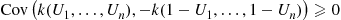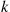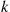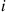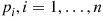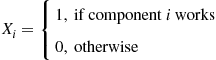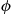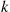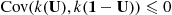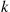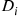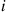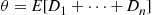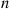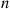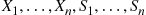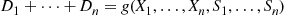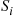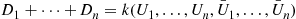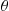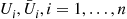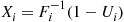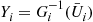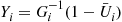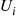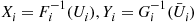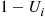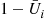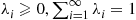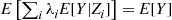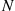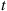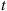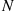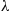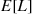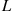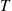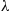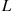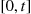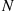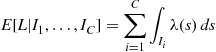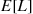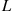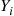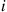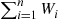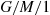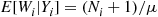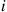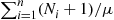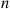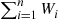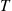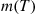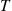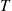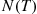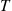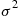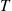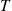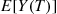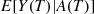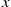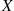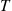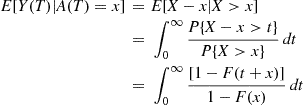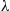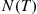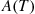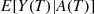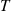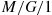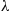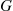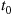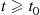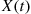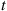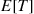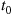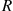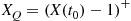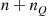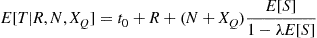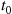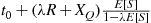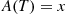Method 2 Conditional Distribution of the Arrival Times
Recall the result for a Poisson process having rate  that given the number of events by time
that given the number of events by time  the set of event times are independent and identically distributed uniform
the set of event times are independent and identically distributed uniform 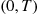 random variables. Now suppose that each of these events is independently counted with a probability that is equal to
random variables. Now suppose that each of these events is independently counted with a probability that is equal to 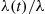 when the event occurred at time
when the event occurred at time 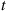 . Hence, given the number of counted events, it follows that the set of times of these counted events are independent with a common distribution given by
. Hence, given the number of counted events, it follows that the set of times of these counted events are independent with a common distribution given by 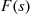 , where
, where

The preceding (somewhat heuristic) argument thus shows that given 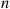 events of a nonhomogeneous Poisson process by time
events of a nonhomogeneous Poisson process by time 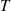 the
the 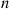 event times are independent with a common density function
event times are independent with a common density function
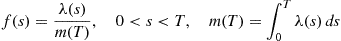 (11.10)
(11.10)Since 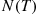 , the number of events by time
, the number of events by time  , is Poisson distributed with mean
, is Poisson distributed with mean 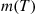 , we can simulate the nonhomogeneous Poisson process by first simulating
, we can simulate the nonhomogeneous Poisson process by first simulating 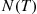 and then simulating
and then simulating 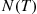 random variables from the density function of (11.10).
random variables from the density function of (11.10).
If the distribution function specified by Equation (11.10) is not easily invertible, we can always simulate from (11.10) by using the rejection method where we either accept or reject simulated values of uniform 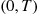 random variables. That is, let
random variables. That is, let 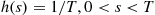 . Then
. Then
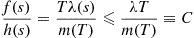
where 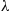 is a bound on
is a bound on 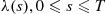 . Hence, the rejection method is to generate random numbers
. Hence, the rejection method is to generate random numbers 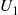 and
and  then accept
then accept 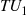 if
if
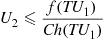
or, equivalently, if
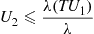
Method 3 Simulating the Event Times
The third method we shall present for simulating a nonhomogeneous Poisson process having intensity function 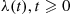 is probably the most basic approach—namely, to simulate the successive event times. So let
is probably the most basic approach—namely, to simulate the successive event times. So let 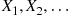 denote the event times of such a process. As these random variables are dependent we will use the conditional distribution approach to simulation. Hence, we need the conditional distribution of
denote the event times of such a process. As these random variables are dependent we will use the conditional distribution approach to simulation. Hence, we need the conditional distribution of 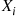 given
given 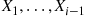 .
.
To start, note that if an event occurs at time 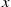 then, independent of what has occurred prior to
then, independent of what has occurred prior to 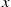 , the time until the next event has the distribution
, the time until the next event has the distribution 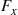 given by
given by
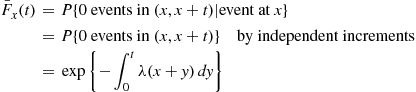
Differentiation yields that the density corresponding to 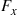 is
is
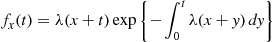
implying that the hazard rate function of 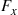 is
is
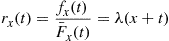
We can now simulate the event times 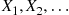 by simulating
by simulating  from
from  ; then if the simulated value of
; then if the simulated value of 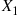 is
is 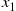 , simulate
, simulate 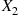 by adding
by adding 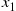 to a value generated from
to a value generated from 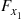 , and if this sum is
, and if this sum is 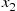 simulate
simulate 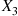 by adding
by adding 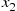 to a value generated from
to a value generated from 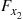 , and so on. The method used to simulate from these distributions should depend, of course, on the form of these distributions. However, it is interesting to note that if we let
, and so on. The method used to simulate from these distributions should depend, of course, on the form of these distributions. However, it is interesting to note that if we let  be such that
be such that 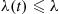 and use the hazard rate method to simulate, then we end up with the approach of Method 1 (we leave the verification of this fact as an exercise). Sometimes, however, the distributions
and use the hazard rate method to simulate, then we end up with the approach of Method 1 (we leave the verification of this fact as an exercise). Sometimes, however, the distributions 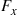 can be easily inverted and so the inverse transform method can be applied.
can be easily inverted and so the inverse transform method can be applied.
11.5.2 Simulating a Two-Dimensional Poisson Process
A point process consisting of randomly occurring points in the plane is said to be a two-dimensional Poisson process having rate 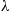 if
if
(a) the number of points in any given region of area 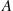 is Poisson distributed with mean
is Poisson distributed with mean 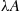 ; and
; and
(b) the numbers of points in disjoint regions are independent.
For a given fixed point O in the plane, we now show how to simulate events occurring according to a two-dimensional Poisson process with rate 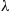 in a circular region of radius
in a circular region of radius  centered about
centered about  . Let
. Let 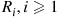 , denote the distance between
, denote the distance between  and its
and its 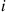 th nearest Poisson point, and let
th nearest Poisson point, and let 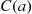 denote the circle of radius
denote the circle of radius  centered at
centered at  . Then
. Then
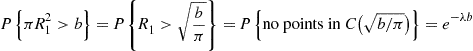
Also, with  denoting the region between
denoting the region between 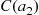 and
and 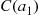 :
:
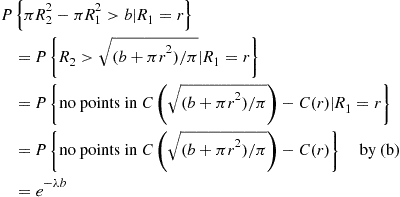
In fact, the same argument can be repeated to obtain the following.
In other words, the amount of area that needs to be traversed to encompass a Poisson point is exponential with rate 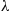 . Since, by symmetry, the respective angles of the Poisson points are independent and uniformly distributed over
. Since, by symmetry, the respective angles of the Poisson points are independent and uniformly distributed over 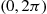 , we thus have the following algorithm for simulating the Poisson process over a circular region of radius
, we thus have the following algorithm for simulating the Poisson process over a circular region of radius  about
about  :
:
Step 1 Generate independent exponentials with rate 1, 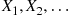 , stopping at
, stopping at

Step 2 If 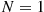 , stop. There are no points in
, stop. There are no points in  . Otherwise, for
. Otherwise, for  , set
, set
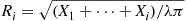
Step 3 Generate independent uniform 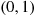 random variables
random variables 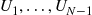 .
.
Step 4 Return the  Poisson points in
Poisson points in  whose polar coordinates are
whose polar coordinates are

The preceding algorithm requires, on average, 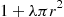 exponentials and an equal number of uniform random numbers. Another approach to simulating points in
exponentials and an equal number of uniform random numbers. Another approach to simulating points in 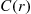 is to first simulate
is to first simulate 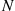 , the number of such points, and then use the fact that, given
, the number of such points, and then use the fact that, given 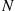 , the points are uniformly distributed in
, the points are uniformly distributed in  . This latter procedure requires the simulation of
. This latter procedure requires the simulation of 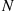 , a Poisson random variable with mean
, a Poisson random variable with mean 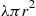 ; we must then simulate
; we must then simulate 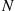 uniform points on
uniform points on 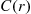 , by simulating
, by simulating  from the distribution
from the distribution 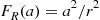 (see Exercise 25) and
(see Exercise 25) and 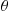 from uniform
from uniform 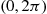 and must then sort these
and must then sort these 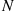 uniform values in increasing order of
uniform values in increasing order of  . The main advantage of the first procedure is that it eliminates the need to sort.
. The main advantage of the first procedure is that it eliminates the need to sort.
The preceding algorithm can be thought of as the fanning out of a circle centered at  with a radius that expands continuously from 0 to
with a radius that expands continuously from 0 to  . The successive radii at which Poisson points are encountered is simulated by noting that the additional area necessary to encompass a Poisson point is always, independent of the past, exponential with rate
. The successive radii at which Poisson points are encountered is simulated by noting that the additional area necessary to encompass a Poisson point is always, independent of the past, exponential with rate  . This technique can be used to simulate the process over noncircular regions. For instance, consider a nonnegative function
. This technique can be used to simulate the process over noncircular regions. For instance, consider a nonnegative function  , and suppose we are interested in simulating the Poisson process in the region between the
, and suppose we are interested in simulating the Poisson process in the region between the  -axis and
-axis and  with
with  going from 0 to
going from 0 to 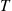 (see Figure 11.4). To do so we can start at the left-hand end and fan vertically to the right by considering the successive areas
(see Figure 11.4). To do so we can start at the left-hand end and fan vertically to the right by considering the successive areas 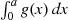 . Now if
. Now if  denote the successive projections of the Poisson points on the
denote the successive projections of the Poisson points on the  -axis, then analogous to Proposition 11.6, it will follow that (with
-axis, then analogous to Proposition 11.6, it will follow that (with 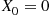 )
) 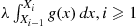 , will be independent exponentials with rate 1. Hence, we should simulate
, will be independent exponentials with rate 1. Hence, we should simulate  , independent exponentials with rate 1, stopping at
, independent exponentials with rate 1, stopping at
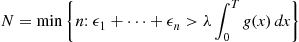
and determine 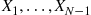 by
by
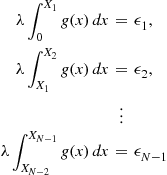
If we now simulate  —independent uniform
—independent uniform 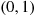 random numbers—then as the projection on the
random numbers—then as the projection on the 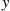 -axis of the Poisson point whose
-axis of the Poisson point whose  -coordinate is
-coordinate is 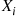 is uniform on (0,
is uniform on (0, 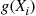 ), it follows that the simulated Poisson points in the interval are
), it follows that the simulated Poisson points in the interval are  .
.

Of course, the preceding technique is most useful when  is regular enough so that the foregoing equations can be solved for the
is regular enough so that the foregoing equations can be solved for the  . For instance, if
. For instance, if  (and so the region of interest is a rectangle), then
(and so the region of interest is a rectangle), then

and the Poisson points are

11.6 Variance Reduction Techniques
Let  have a given joint distribution, and suppose we are interested in computing
have a given joint distribution, and suppose we are interested in computing

where  is some specified function. It is often the case that it is not possible to analytically compute the preceding, and when such is the case we can attempt to use simulation to estimate
is some specified function. It is often the case that it is not possible to analytically compute the preceding, and when such is the case we can attempt to use simulation to estimate  . This is done as follows: Generate
. This is done as follows: Generate  having the same joint distribution as
having the same joint distribution as  and set
and set
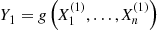
Now, simulate a second set of random variables (independent of the first set)  having the distribution of
having the distribution of  and set
and set
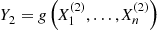
Continue this until you have generated  (some predetermined number) sets, and so have also computed
(some predetermined number) sets, and so have also computed 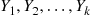 . Now,
. Now,  are independent and identically distributed random variables each having the same distribution of
are independent and identically distributed random variables each having the same distribution of  . Thus, if we let
. Thus, if we let 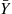 denote the average of these
denote the average of these 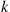 random variables—that is,
random variables—that is,
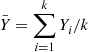
then
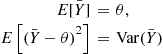
Hence, we can use 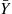 as an estimate of
as an estimate of 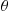 . As the expected square of the difference between
. As the expected square of the difference between  and
and 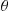 is equal to the variance of
is equal to the variance of 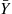 , we would like this quantity to be as small as possible. In the preceding situation,
, we would like this quantity to be as small as possible. In the preceding situation, 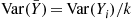 , which is usually not known in advance but must be estimated from the generated values
, which is usually not known in advance but must be estimated from the generated values  . We now present three general techniques for reducing the variance of our estimator.
. We now present three general techniques for reducing the variance of our estimator.
11.6.1 Use of Antithetic Variables
In the preceding situation, suppose that we have generated  and
and  , identically distributed random variables having mean
, identically distributed random variables having mean 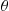 . Now,
. Now,
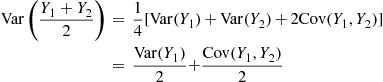
Hence, it would be advantageous (in the sense that the variance would be reduced) if 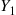 and
and  rather than being independent were negatively correlated. To see how we could arrange this, let us suppose that the random variables
rather than being independent were negatively correlated. To see how we could arrange this, let us suppose that the random variables  are independent and, in addition, that each is simulated via the inverse transform technique. That is,
are independent and, in addition, that each is simulated via the inverse transform technique. That is, 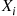 is simulated from
is simulated from 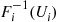 where
where 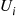 is a random number and
is a random number and 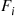 is the distribution of
is the distribution of  . Hence,
. Hence, 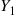 can be expressed as
can be expressed as

Now, since 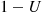 is also uniform over
is also uniform over 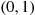 whenever
whenever 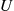 is a random number (and is negatively correlated with
is a random number (and is negatively correlated with  ) it follows that
) it follows that 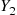 defined by
defined by

will have the same distribution as  . Hence, if
. Hence, if  and
and  were negatively correlated, then generating
were negatively correlated, then generating  by this means would lead to a smaller variance than if it were generated by a new set of random numbers. (In addition, there is a computational savings since rather than having to generate
by this means would lead to a smaller variance than if it were generated by a new set of random numbers. (In addition, there is a computational savings since rather than having to generate  additional random numbers, we need only subtract each of the previous
additional random numbers, we need only subtract each of the previous  from 1.) The following theorem will be the key to showing that this technique—known as the use of antithetic variables—will lead to a reduction in variance whenever
from 1.) The following theorem will be the key to showing that this technique—known as the use of antithetic variables—will lead to a reduction in variance whenever  is a monotone function.
is a monotone function.
Since 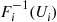 is increasing in
is increasing in  (as
(as 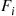 , being a distribution function, is increasing) it follows that
, being a distribution function, is increasing) it follows that  is a monotone function of
is a monotone function of  whenever
whenever  is monotone. Hence, if
is monotone. Hence, if 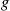 is monotone the antithetic variable approach of twice using each set of random numbers
is monotone the antithetic variable approach of twice using each set of random numbers  by first computing
by first computing  and then
and then  will reduce the variance of the estimate of
will reduce the variance of the estimate of  . That is, rather than generating
. That is, rather than generating 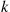 sets of
sets of  random numbers, we should generate
random numbers, we should generate  sets and use each set twice.
sets and use each set twice.
11.6.2 Variance Reduction by Conditioning
Let us start by recalling (see Proposition 3.1) the conditional variance formula
 (11.12)
(11.12)Now suppose we are interested in estimating 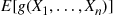 by simulating
by simulating 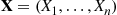 and then computing
and then computing  . Now, if for some random variable
. Now, if for some random variable 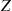 we can compute
we can compute 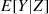 then, as
then, as 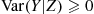 , it follows from the conditional variance formula that
, it follows from the conditional variance formula that

implying, since  , that
, that  is a better estimator of
is a better estimator of 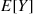 than is
than is 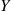 .
.
In many situations, there are a variety of  that can be conditioned on to obtain an improved estimator. Each of these estimators
that can be conditioned on to obtain an improved estimator. Each of these estimators  will have mean
will have mean 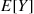 and smaller variance than does the raw estimator
and smaller variance than does the raw estimator 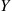 . We now show that for any choice of weights
. We now show that for any choice of weights 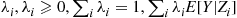 is also an improvement over
is also an improvement over 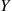 .
.
11.6.3 Control Variates
Again suppose we want to use simulation to estimate 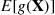 where
where 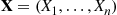 . But now suppose that for some function
. But now suppose that for some function  the expected value of
the expected value of  is known—say,
is known—say,  . Then for any constant
. Then for any constant  we can also use
we can also use

as an estimator of  . Now,
. Now,