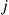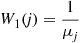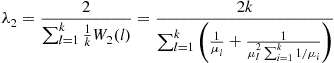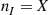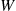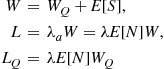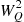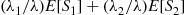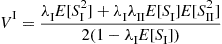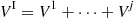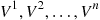(8.27)
(8.27)
Also using the fact that 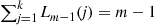 (why?) we obtain, from Equation (8.26), the following:
(why?) we obtain, from Equation (8.26), the following:
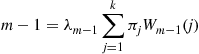
or
 (8.28)
(8.28)
Hence, from Equation (8.27), we obtain the recursion
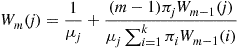 (8.29)
(8.29)
Starting with the stationary probabilities  , and
, and 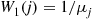 we can now use Equation (8.29) to determine recursively
we can now use Equation (8.29) to determine recursively  . We can then determine the throughput rate
. We can then determine the throughput rate 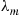 by using Equation (8.28), and this will determine
by using Equation (8.28), and this will determine  by Equation (8.26). This recursive approach is called mean value analysis.
by Equation (8.26). This recursive approach is called mean value analysis.
Another approach to learning about the stationary probabilities specified by Equation (8.22), which finesses the computational difficulties of computing the constant  , is to use the Gibbs sampler of Section 4.9 to generate a Markov chain having these stationary probabilities. To begin, note that since there are always a total of
, is to use the Gibbs sampler of Section 4.9 to generate a Markov chain having these stationary probabilities. To begin, note that since there are always a total of  customers in the system, Equation (8.22) may equivalently be written as a joint mass function of the numbers of customers at each of the servers
customers in the system, Equation (8.22) may equivalently be written as a joint mass function of the numbers of customers at each of the servers  , as follows:
, as follows:

where 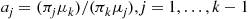 . Now, if
. Now, if  has the preceding joint mass function then
has the preceding joint mass function then

It follows from the preceding that we may use the Gibbs sampler to generate the values of a Markov chain whose limiting probability mass function is  as follows:
as follows:
1. Let  be arbitrary nonnegative integers satisfying
be arbitrary nonnegative integers satisfying  .
.
2. Generate a random variable 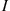 that is equally likely to be any of
that is equally likely to be any of  .
.
3. If 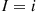 , set
, set 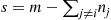 , and generate the value of a random variable
, and generate the value of a random variable  having probability mass function
having probability mass function

The successive values of the state vector 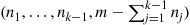 constitute the sequence of states of a Markov chain with the limiting distribution
constitute the sequence of states of a Markov chain with the limiting distribution  . All quantities of interest can be estimated from this sequence. For instance, the average of the values of the
. All quantities of interest can be estimated from this sequence. For instance, the average of the values of the 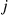 th coordinate of these vectors will converge to the mean number of individuals at station
th coordinate of these vectors will converge to the mean number of individuals at station  , the proportion of vectors whose
, the proportion of vectors whose  th coordinate is less than
th coordinate is less than  will converge to the limiting probability that the number of individuals at station
will converge to the limiting probability that the number of individuals at station 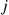 is less than
is less than  , and so on.
, and so on.
Other quantities of interest can also be obtained from the simulation. For instance, suppose we want to estimate  , the average amount of time a customer spends at server
, the average amount of time a customer spends at server  on each visit. Then, as noted in the preceding,
on each visit. Then, as noted in the preceding,  , the average number of customers at server
, the average number of customers at server 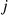 , can be estimated. To estimate
, can be estimated. To estimate 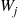 , we use the identity
, we use the identity

where 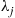 is the rate at which customers arrive at server
is the rate at which customers arrive at server  . Setting
. Setting 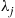 equal to the service completion rate at server
equal to the service completion rate at server 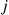 shows that
shows that

Using the Gibbs sampler simulation to estimate  then leads to an estimator of
then leads to an estimator of 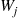 .
.
8.5 The System M / G / 1 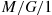
8.5.1 Preliminaries: Work and Another Cost Identity
For an arbitrary queueing system, let us define the work in the system at any time 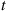 to be the sum of the remaining service times of all customers in the system at time
to be the sum of the remaining service times of all customers in the system at time  . For instance, suppose there are three customers in the system—the one in service having been there for three of his required five units of service time, and both people in queue having service times of six units. Then the work at that time is
. For instance, suppose there are three customers in the system—the one in service having been there for three of his required five units of service time, and both people in queue having service times of six units. Then the work at that time is  . Let
. Let  denote the (time) average work in the system.
denote the (time) average work in the system.
Now recall the fundamental cost Equation (8.1), which states that the
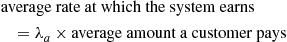
and consider the following cost rule: Each customer pays at a rate of y/unit time when his remaining service time is y, whether he is in queue or in service. Thus, the rate at which the system earns is just the work in the system; so the basic identity yields

Now, let  and
and  denote respectively the service time and the time a given customer spends waiting in queue. Then, since the customer pays at a constant rate of
denote respectively the service time and the time a given customer spends waiting in queue. Then, since the customer pays at a constant rate of 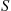 per unit time while he waits in queue and at a rate of
per unit time while he waits in queue and at a rate of  after spending an amount of time
after spending an amount of time 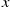 in service, we have
in service, we have
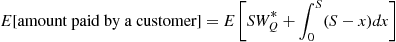
and thus
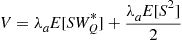 (8.30)
(8.30)
It should be noted that the preceding is a basic queueing identity (like Equations (8.2)– (8.4)) and as such is valid in almost all models. In addition, if a customer’s service time is independent of his wait in queue (as is usually, but not always the case),∗ then we have from Equation (8.30) that
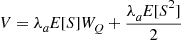 (8.31)
(8.31)
8.5.2 Application of Work to M/G/1
The 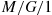 model assumes (i) Poisson arrivals at rate
model assumes (i) Poisson arrivals at rate  ; (ii) a general service distribution; and (iii) a single server. In addition, we will suppose that customers are served in the order of their arrival.
; (ii) a general service distribution; and (iii) a single server. In addition, we will suppose that customers are served in the order of their arrival.
Now, for an arbitrary customer in an  system,
system,
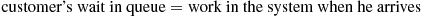 (8.32)
(8.32)This follows since there is only a single server (think about it!). Taking expectations of both sides of Equation (8.32) yields

But, due to Poisson arrivals, the average work as seen by an arrival will equal 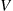 , the time average work in the system. Hence, for the model
, the time average work in the system. Hence, for the model 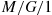 ,
,

The preceding in conjunction with the identity
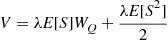
yields the so-called Pollaczek–Khintchine formula,
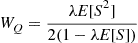 (8.33)
(8.33)
where  and
and  are the first two moments of the service distribution.
are the first two moments of the service distribution.
The quantities 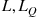 , and
, and  can be obtained from Equation (8.33) as
can be obtained from Equation (8.33) as
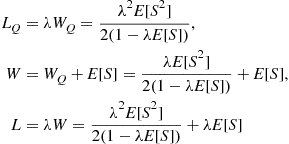 (8.34)
(8.34)
8.5.3 Busy Periods
The system alternates between idle periods (when there are no customers in the system, and so the server is idle) and busy periods (when there is at least one customer in the system, and so the server is busy).
Let  and
and 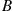 represent, respectively, the length of an idle and of a busy period. Because
represent, respectively, the length of an idle and of a busy period. Because  represents the time from when a customer departs and leaves the system empty until the next arrival, it follows, since arrivals are according to a Poisson process with rate
represents the time from when a customer departs and leaves the system empty until the next arrival, it follows, since arrivals are according to a Poisson process with rate  , that
, that  is exponential with rate
is exponential with rate  and thus
and thus
 (8.35)
(8.35)To determine 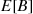 we argue, as in Section 8.3.3, that the long-run proportion of time the system is empty is equal to the ratio of
we argue, as in Section 8.3.3, that the long-run proportion of time the system is empty is equal to the ratio of 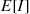 to
to  . That is,
. That is,
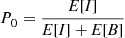 (8.36)
(8.36)
To compute  , we note from Equation (8.4) (obtained from the fundamental cost equation by supposing that a customer pays at a rate of one per unit time while in service) that
, we note from Equation (8.4) (obtained from the fundamental cost equation by supposing that a customer pays at a rate of one per unit time while in service) that
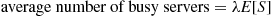
However, as the left-hand side of the preceding equals  (why?), we have
(why?), we have
 (8.37)
(8.37)
and, from Equations (8.35)– (8.37),

or

Another quantity of interest is  , the number of customers served in a busy period. The mean of
, the number of customers served in a busy period. The mean of  can be computed by noting that, on the average, for every
can be computed by noting that, on the average, for every 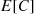 arrivals exactly one will find the system empty (namely, the first customer in the busy period). Hence,
arrivals exactly one will find the system empty (namely, the first customer in the busy period). Hence,

and, as  because of Poisson arrivals, we see that
because of Poisson arrivals, we see that
8.6 Variations on the M / G / 1 
8.6.1 The M/G/1 with Random-Sized Batch Arrivals
Suppose that, as in the  , arrivals occur in accordance with a Poisson process having rate
, arrivals occur in accordance with a Poisson process having rate  . But now suppose that each arrival consists not of a single customer but of a random number of customers. As before there is a single server whose service times have distribution
. But now suppose that each arrival consists not of a single customer but of a random number of customers. As before there is a single server whose service times have distribution  .
.
Let us denote by 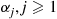 , the probability that an arbitrary batch consists of
, the probability that an arbitrary batch consists of  customers; and let
customers; and let  denote a random variable representing the size of a batch and so
denote a random variable representing the size of a batch and so  . Since
. Since 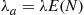 , the basic formula for work (Equation (8.31)) becomes
, the basic formula for work (Equation (8.31)) becomes
 (8.38)
(8.38)
To obtain a second equation relating 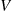 to
to  , consider an average customer. We have that
, consider an average customer. We have that

Taking expectations and using the fact that Poisson arrivals see time averages yields
 (8.39)
(8.39)
Now,  can be computed by conditioning on the number in the batch, but we must be careful because the probability that our average customer comes from a batch of size
can be computed by conditioning on the number in the batch, but we must be careful because the probability that our average customer comes from a batch of size  is not
is not  . For
. For  is the proportion of batches that are of size
is the proportion of batches that are of size 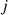 , and if we pick a customer at random, it is more likely that he comes from a larger rather than a smaller batch. (For instance, suppose
, and if we pick a customer at random, it is more likely that he comes from a larger rather than a smaller batch. (For instance, suppose 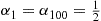 , then half the batches are of size 1 but
, then half the batches are of size 1 but 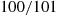 of the customers will come from a batch of size 100!)
of the customers will come from a batch of size 100!)
To determine the probability that our average customer came from a batch of size 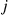 we reason as follows: Let
we reason as follows: Let 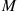 be a large number. Then of the first
be a large number. Then of the first  batches approximately
batches approximately 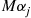 will be of size
will be of size  , and thus there would have been approximately
, and thus there would have been approximately  customers that arrived in a batch of size
customers that arrived in a batch of size  . Hence, the proportion of arrivals in the first
. Hence, the proportion of arrivals in the first  batches that were from batches of size
batches that were from batches of size 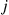 is approximately
is approximately  . This proportion becomes exact as
. This proportion becomes exact as  , and so we see that
, and so we see that

We are now ready to compute  , the expected wait in queue due to others in the batch:
, the expected wait in queue due to others in the batch:
 (8.40)
(8.40)
Now if there are  customers in his batch, then our customer would have to wait for
customers in his batch, then our customer would have to wait for  of them to be served if he was
of them to be served if he was  th in line among his batch members. As he is equally likely to be either 1st, 2nd,
th in line among his batch members. As he is equally likely to be either 1st, 2nd,  , or
, or  th in line we see that
th in line we see that

Substituting this in Equation (8.40) yields

and from Equations (8.38) and (8.39) we obtain
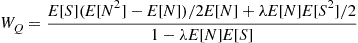
8.6.2 Priority Queues
Priority queueing systems are ones in which customers are classified into types and then given service priority according to their type. Consider the situation where there are two types of customers, which arrive according to independent Poisson processes with respective rates 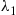 and
and 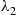 , and have service distributions
, and have service distributions  and
and  . We suppose that type 1 customers are given service priority, in that service will never begin on a type 2 customer if a type 1 is waiting. However, if a type 2 is being served and a type 1 arrives, we assume that the service of the type 2 is continued until completion. That is, there is no preemption once service has begun.
. We suppose that type 1 customers are given service priority, in that service will never begin on a type 2 customer if a type 1 is waiting. However, if a type 2 is being served and a type 1 arrives, we assume that the service of the type 2 is continued until completion. That is, there is no preemption once service has begun.
Let  denote the average wait in queue of a type
denote the average wait in queue of a type  customer,
customer, 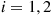 . Our objective is to compute the
. Our objective is to compute the  .
.
First, note that the total work in the system at any time would be exactly the same no matter what priority rule was employed (as long as the server is always busy whenever there are customers in the system). This is so since the work will always decrease at a rate of one per unit time when the server is busy (no matter who is in service) and will always jump by the service time of an arrival. Hence, the work in the system is exactly as it would be if there was no priority rule but rather a first-come, first-served (called FIFO) ordering. However, under FIFO the preceding model is just 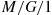 with
with
 (8.41)
(8.41)which follows since the combination of two independent Poisson processes is itself a Poisson process whose rate is the sum of the rates of the component processes. The service distribution  can be obtained by conditioning on which priority class the arrival is from—as is done in Equation (8.41).
can be obtained by conditioning on which priority class the arrival is from—as is done in Equation (8.41).
Hence, from the results of Section 8.5, it follows that  , the average work in the priority queueing system, is given by
, the average work in the priority queueing system, is given by
 (8.42)
(8.42)
where  has distribution
has distribution  , 2.
, 2.
Continuing in our quest for  let us note that
let us note that  and
and  , the service and wait in queue of an arbitrary customer, are not independent in the priority model since knowledge about
, the service and wait in queue of an arbitrary customer, are not independent in the priority model since knowledge about 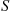 gives us information as to the type of customer, which in turn gives us information about
gives us information as to the type of customer, which in turn gives us information about  . To get around this we will compute separately the average amount of type 1 and type 2 work in the system. Denoting
. To get around this we will compute separately the average amount of type 1 and type 2 work in the system. Denoting 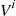 as the average amount of type
as the average amount of type  work we have, exactly as in Section 8.5.1,
work we have, exactly as in Section 8.5.1,
 (8.43)
(8.43)
If we define
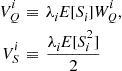
then we may interpret  as the average amount of type
as the average amount of type 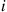 work in queue, and
work in queue, and 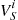 as the average amount of type
as the average amount of type 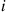 work in service (why?).
work in service (why?).
Now we are ready to compute 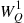 . To do so, consider an arbitrary type 1 arrival. Then
. To do so, consider an arbitrary type 1 arrival. Then
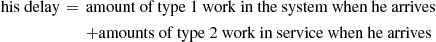
Taking expectations and using the fact that Poisson arrivals see time average yields
 (8.44)
(8.44)
or
 (8.45)
(8.45)
To obtain  we first note that since
we first note that since 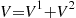 , we have from Equations (8.42) and (8.43) that
, we have from Equations (8.42) and (8.43) that

Now, using Equation (8.45), we obtain

or
 (8.46)
(8.46)
8.6.3 An M/G/1 Optimization Example
Consider a single-server system where customers arrive according to a Poisson process with rate 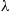 , and where the service times are independent and have distribution function
, and where the service times are independent and have distribution function  . Let
. Let  , where
, where 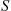 represents a service time random variable, and suppose that
represents a service time random variable, and suppose that 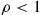 . Suppose that the server departs whenever a busy period ends and does not return until there are
. Suppose that the server departs whenever a busy period ends and does not return until there are 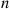 customers waiting. At that time the server returns and continues serving until the system is once again empty. If the system facility incurs costs at a rate of
customers waiting. At that time the server returns and continues serving until the system is once again empty. If the system facility incurs costs at a rate of  per unit time per customer in the system, as well as a cost
per unit time per customer in the system, as well as a cost  each time the server returns, what value of
each time the server returns, what value of  , minimizes the long-run average cost per unit time incurred by the facility, and what is this minimal cost?
, minimizes the long-run average cost per unit time incurred by the facility, and what is this minimal cost?
To answer the preceding, let us first determine 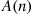 , the average cost per unit time for the policy that returns the server whenever there are
, the average cost per unit time for the policy that returns the server whenever there are  customers waiting. To do so, say that a new cycle begins each time the server returns. As it is easy to see that everything probabilistically starts over when a cycle begins, it follows from the theory of renewal reward processes that if
customers waiting. To do so, say that a new cycle begins each time the server returns. As it is easy to see that everything probabilistically starts over when a cycle begins, it follows from the theory of renewal reward processes that if 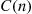 is the cost incurred in a cycle and
is the cost incurred in a cycle and  is the time of a cycle, then
is the time of a cycle, then

To determine 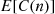 and
and  , consider the time interval of length, say,
, consider the time interval of length, say,  , starting from the first time during a cycle that there are a total of
, starting from the first time during a cycle that there are a total of  customers in the system until the first time afterward that there are only
customers in the system until the first time afterward that there are only  . Therefore,
. Therefore,  is the amount of time that the server is busy during a cycle. Adding the additional mean idle time until
is the amount of time that the server is busy during a cycle. Adding the additional mean idle time until  customers are in the system gives
customers are in the system gives
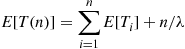
Now, consider the system at the moment when a service is about to begin and there are 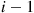 customers waiting in queue. Since service times do not depend on the order in which customers are served, suppose that the order of service is last come first served, implying that service does not begin on the
customers waiting in queue. Since service times do not depend on the order in which customers are served, suppose that the order of service is last come first served, implying that service does not begin on the 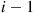 presently in queue until these
presently in queue until these  are the only ones in the system. Thus, we see that the time that it takes to go from
are the only ones in the system. Thus, we see that the time that it takes to go from  customers in the system to
customers in the system to 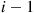 has the same distribution as the time it takes the
has the same distribution as the time it takes the  system to go from a single customer (just beginning service) to empty; that is, its distribution is that of
system to go from a single customer (just beginning service) to empty; that is, its distribution is that of 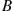 , the length of an
, the length of an  busy period. (Essentially the same argument was made in Example 5.25.) Hence,
busy period. (Essentially the same argument was made in Example 5.25.) Hence,

implying that
 (8.48)
(8.48)
To determine 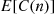 , let
, let  denote the cost incurred during the interval of length
denote the cost incurred during the interval of length  that starts with
that starts with  in queue and a service just beginning and ends when the
in queue and a service just beginning and ends when the  in queue are the only customers in the system. Thus,
in queue are the only customers in the system. Thus,  represents the total cost incurred during the busy part of the cycle. In addition, during the idle part of the cycle there will be
represents the total cost incurred during the busy part of the cycle. In addition, during the idle part of the cycle there will be  customers in the system for an exponential time with rate
customers in the system for an exponential time with rate  , resulting in an expected cost of
, resulting in an expected cost of  . Consequently,
. Consequently,
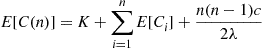 (8.49)
(8.49)
To find  , consider the moment when the interval of length
, consider the moment when the interval of length  begins, and let
begins, and let  be the sum of the initial service time plus the sum of the times spent in the system by all the customers that arrive (and are served) until the moment when the interval ends and there are only
be the sum of the initial service time plus the sum of the times spent in the system by all the customers that arrive (and are served) until the moment when the interval ends and there are only  customers in the system. Then,
customers in the system. Then,

where the first term refers to the cost incurred due to the  customers in queue during the interval of length
customers in queue during the interval of length 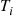 . As it is easy to see that
. As it is easy to see that  has the same distribution as
has the same distribution as  , the sum of the times spent in the system by all arrivals in an
, the sum of the times spent in the system by all arrivals in an  busy period, we obtain
busy period, we obtain
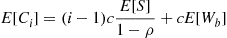 (8.50)
(8.50)
Using Equation (8.49), this yields

Utilizing the preceding in conjunction with Equation (8.48) shows that
 (8.51)
(8.51)
To determine  , we use the result that the average amount of time spent in the system by a customer in the
, we use the result that the average amount of time spent in the system by a customer in the  system is
system is

However, if we imagine that on day 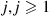 , we earn an amount equal to the total time spent in the system by the
, we earn an amount equal to the total time spent in the system by the  th arrival at the
th arrival at the  system, then it follows from renewal reward processes (since everything probabilistically restarts at the end of a busy period) that
system, then it follows from renewal reward processes (since everything probabilistically restarts at the end of a busy period) that

where 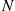 is the number of customers served in an
is the number of customers served in an  busy period. Since
busy period. Since  we see that
we see that
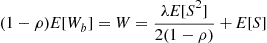
Therefore, using Equation (8.51), we obtain

To determine the optimal value of 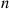 , treat
, treat 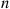 as a continuous variable and differentiate the preceding to obtain
as a continuous variable and differentiate the preceding to obtain
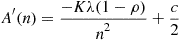
Setting this equal to 0 and solving yields that the optimal value of  is
is

and the minimal average cost per unit time is

It is interesting to see how close we can come to the minimal average cost when we use a simpler policy of the following form: Whenever the server finds the system empty of customers she departs and then returns after a fixed time 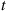 has elapsed. Let us say that a new cycle begins each time the server departs. Both the expected costs incurred during the idle and the busy parts of a cycle are obtained by conditioning on
has elapsed. Let us say that a new cycle begins each time the server departs. Both the expected costs incurred during the idle and the busy parts of a cycle are obtained by conditioning on  , the number of arrivals in the time
, the number of arrivals in the time  that the server is gone. With
that the server is gone. With  being the cost incurred during a cycle, we obtain
being the cost incurred during a cycle, we obtain

The final term of the first equality is the conditional expected cost during the idle time in the cycle and is obtained by using that, given the number of arrivals in the time  , the arrival times are independent and uniformly distributed on
, the arrival times are independent and uniformly distributed on  ; the second equality used Equation (8.50). Since
; the second equality used Equation (8.50). Since 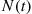 is Poisson with mean
is Poisson with mean  , it follows that
, it follows that  . Thus, taking the expected value of the preceding gives
. Thus, taking the expected value of the preceding gives

Similarly, if  is the time of a cycle, then
is the time of a cycle, then

Hence, the average cost per unit time, call it  , is
, is

Thus, from Equation (8.51), we see that

which shows that allowing the return decision to depend on the number presently in the system can reduce the average cost only by the amount 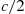 . ■
. ■
8.6.4 The M/G/1 Queue with Server Breakdown
Consider a single server queue in which customers arrive according to a Poisson process with rate  , and where the amount of service time required by each customer has distribution
, and where the amount of service time required by each customer has distribution  . Suppose, however, that when working the server breaks down at an exponential rate
. Suppose, however, that when working the server breaks down at an exponential rate  . That is, the probability a working server will be able to work for an additional time
. That is, the probability a working server will be able to work for an additional time  without breaking down is
without breaking down is  . When the server breaks down, it immediately goes to the repair facility. The repair time is a random variable with distribution
. When the server breaks down, it immediately goes to the repair facility. The repair time is a random variable with distribution  . Suppose that the customer in service when a breakdown occurs has its service continue, when the sever returns, from the point it was at when the breakdown occurred. (Therefore, the total amount of time a customer is actually receiving service from a working server has distribution
. Suppose that the customer in service when a breakdown occurs has its service continue, when the sever returns, from the point it was at when the breakdown occurred. (Therefore, the total amount of time a customer is actually receiving service from a working server has distribution  .)
.)
By letting a customer’s “service time” include the time that the customer is waiting for the server to come back from being repaired, the preceding is an  queue. If we let
queue. If we let  denote the amount of time from when a customer first enters service until it departs the system, then
denote the amount of time from when a customer first enters service until it departs the system, then  is a service time random variable of this
is a service time random variable of this  queue. The average amount of time a customer spends waiting in queue before its service first commences is, thus,
queue. The average amount of time a customer spends waiting in queue before its service first commences is, thus,
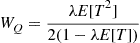
To compute 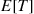 and
and  , let
, let 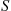 , having distribution
, having distribution 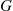 , be the service requirement of the customer; let
, be the service requirement of the customer; let  denote the number of times that the server breaks down while the customer is in service; let
denote the number of times that the server breaks down while the customer is in service; let  be the amounts of time the server spends in the repair facility on its successive visits. Then,
be the amounts of time the server spends in the repair facility on its successive visits. Then,

Conditioning on  yields
yields
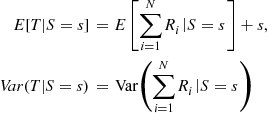
Now, a working server always breaks down at an exponential rate  . Therefore, given that a customer requires
. Therefore, given that a customer requires  units of service time, it follows that the number of server breakdowns while that customer is being served is a Poisson random variable with mean
units of service time, it follows that the number of server breakdowns while that customer is being served is a Poisson random variable with mean  . Consequently, conditional on
. Consequently, conditional on  , the random variable
, the random variable  is a compound Poisson random variable with Poisson mean
is a compound Poisson random variable with Poisson mean 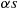 . Using the results from Examples 3.10 and 3.17, we thus obtain
. Using the results from Examples 3.10 and 3.17, we thus obtain

where 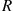 has the repair distribution
has the repair distribution  . Therefore,
. Therefore,
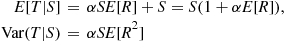
Thus,

and, by the conditional variance formula,

Therefore,

Consequently, assuming that 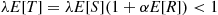 , we obtain
, we obtain

From the preceding, we can now obtain

Some other quantities we might be interested in are
(i) 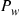 , the proportion of time the server is working;
, the proportion of time the server is working;
(ii) 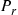 , the proportion of time the server is being repaired;
, the proportion of time the server is being repaired;
These quantities can all be obtained by using the queueing cost identity. For instance, if we suppose that customers pay 1 per unit time while actually being served, then

Therefore, the identity yields

To determine  , suppose a customer whose service is interrupted pays 1 per unit time while the server is being repaired. Then,
, suppose a customer whose service is interrupted pays 1 per unit time while the server is being repaired. Then,