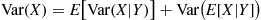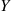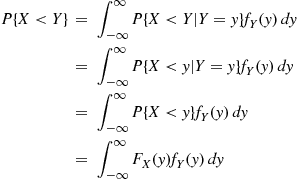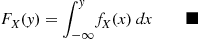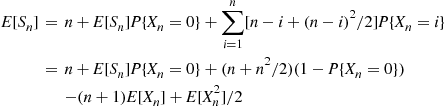
Substituting the identities 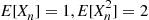 in the preceding shows that
in the preceding shows that
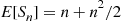
and the induction proof is complete. (c) If we let  denote the number of hats chosen by person
denote the number of hats chosen by person 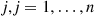 then
then
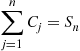
Taking expectations, and using the fact that each 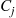 has the same mean, yields the result
has the same mean, yields the result
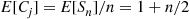
Hence, the expected number of false selections by person 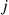 is
is
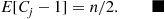
Example 3.15
Independent trials, each of which is a success with probability  , are performed until there are
, are performed until there are  consecutive successes. What is the mean number of necessary trials?
consecutive successes. What is the mean number of necessary trials?
Solution: Let 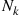 denote the number of necessary trials to obtain
denote the number of necessary trials to obtain 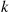 consecutive successes, and let
consecutive successes, and let 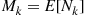 . We will determine
. We will determine 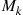 by deriving and then solving a recursive equation that it satisfies. To begin, write
by deriving and then solving a recursive equation that it satisfies. To begin, write
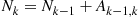
where 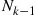 is the number of trials needed for
is the number of trials needed for 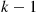 consecutive successes, and
consecutive successes, and 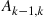 is the number of additional trials needed to go from having
is the number of additional trials needed to go from having 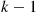 successes in a row to having
successes in a row to having 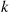 in a row. Taking expectations gives that,
in a row. Taking expectations gives that,
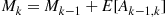
To determine 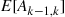 , condition on the next trial after there have been
, condition on the next trial after there have been 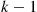 successes in a row. If it is a success then that gives
successes in a row. If it is a success then that gives 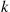 in a row and no additional trials after that are needed; if it is a failure then at that point we are starting all over and so the expected addtional number from then on would be
in a row and no additional trials after that are needed; if it is a failure then at that point we are starting all over and so the expected addtional number from then on would be 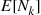 . Thus,
. Thus,
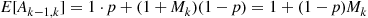
giving that
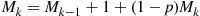
or
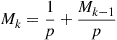
Since  , the time of the first success, is geometric with parameter
, the time of the first success, is geometric with parameter  , we see that
, we see that
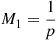
and, recursively
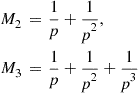
and, in general,
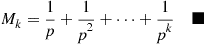
Example 3.16
Analyzing the Quick-Sort Algorithm
Suppose we are given a set of 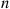 distinct values—
distinct values— —and we desire to put these values in increasing order or, as it is commonly called, to
—and we desire to put these values in increasing order or, as it is commonly called, to 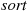 them. An efficient procedure for accomplishing this is the quick-sort algorithm, which is defined recursively as follows: When
them. An efficient procedure for accomplishing this is the quick-sort algorithm, which is defined recursively as follows: When 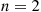 the algorithm compares the two values and puts them in the appropriate order. When
the algorithm compares the two values and puts them in the appropriate order. When 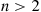 it starts by choosing at random one of the
it starts by choosing at random one of the 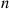 values—say,
values—say, 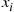 —and then compares each of the other
—and then compares each of the other 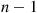 values with
values with 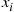 , noting which are smaller and which are larger than
, noting which are smaller and which are larger than 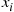 . Letting
. Letting 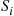 denote the set of elements smaller than
denote the set of elements smaller than 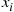 , and
, and 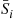 the set of elements greater than
the set of elements greater than 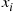 , the algorithm now sorts the set
, the algorithm now sorts the set 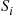 and the set
and the set 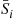 . The final ordering, therefore, consists of the ordered set of the elements in
. The final ordering, therefore, consists of the ordered set of the elements in 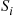 , then
, then 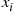 , and then the ordered set of the elements in
, and then the ordered set of the elements in 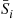 . For instance, suppose that the set of elements is 10, 5, 8, 2, 1, 4, 7. We start by choosing one of these values at random (that is, each of the 7 values has probability of
. For instance, suppose that the set of elements is 10, 5, 8, 2, 1, 4, 7. We start by choosing one of these values at random (that is, each of the 7 values has probability of 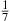 of being chosen). Suppose, for instance, that the value 4 is chosen. We then compare 4 with each of the other six values to obtain
of being chosen). Suppose, for instance, that the value 4 is chosen. We then compare 4 with each of the other six values to obtain
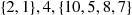
We now sort the set {2, 1} to obtain
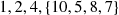
Next we choose a value at random from 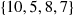 —say 7 is chosen—and compare each of the other three values with 7 to obtain
—say 7 is chosen—and compare each of the other three values with 7 to obtain
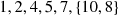
Finally, we sort 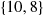 to end up with
to end up with
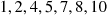
One measure of the effectiveness of this algorithm is the expected number of comparisons that it makes. Let us denote by 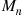 the expected number of comparisons needed by the quick-sort algorithm to sort a set of
the expected number of comparisons needed by the quick-sort algorithm to sort a set of 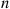 distinct values. To obtain a recursion for
distinct values. To obtain a recursion for 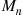 we condition on the rank of the initial value selected to obtain
we condition on the rank of the initial value selected to obtain
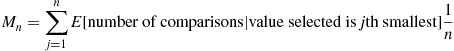
Now, if the initial value selected is the 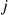 th smallest, then the set of values smaller than it is of size
th smallest, then the set of values smaller than it is of size  , and the set of values greater than it is of size
, and the set of values greater than it is of size 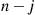 . Hence, as
. Hence, as 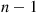 comparisons with the initial value chosen must be made, we see that
comparisons with the initial value chosen must be made, we see that
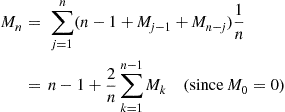
or, equivalently,
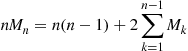
To solve the preceding, note that upon replacing 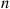 by
by  we obtain
we obtain
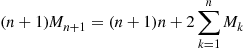
Hence, upon subtraction,
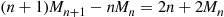
or
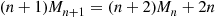
Therefore,

Iterating this gives
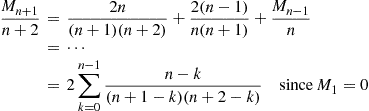
Hence,
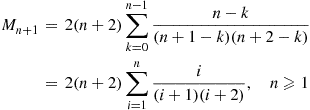
Using the identity 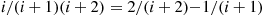 , we can approximate
, we can approximate 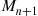 for large
for large 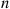 as follows:
as follows:
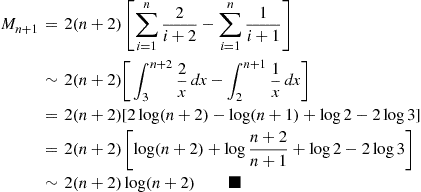
Although we usually employ the conditional expectation identity to more easily enable us to compute an unconditional expectation, in our next example we show how it can sometimes be used to obtain the conditional expectation.
Example 3.17
In the match problem of Example 2.31 involving 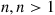 , individuals, find the conditional expected number of matches given that the first person did not have a match.
, individuals, find the conditional expected number of matches given that the first person did not have a match.
Solution: Let  denote the number of matches, and let
denote the number of matches, and let 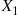 equal
equal 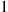 if the first person has a match and
if the first person has a match and 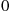 otherwise. Then,
otherwise. Then,
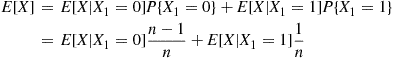
But, from Example 2.31
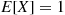
Moreover, given that the first person has a match, the expected number of matches is equal to 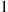 plus the expected number of matches when
plus the expected number of matches when  people select among their own
people select among their own 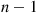 hats, showing that
hats, showing that
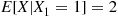
Therefore, we obtain the result
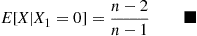
3.4.1 Computing Variances by Conditioning
Conditional expectations can also be used to compute the variance of a random variable. Specifically, we can use
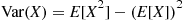
and then use conditioning to obtain both 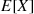 and
and 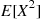 . We illustrate this technique by determining the variance of a geometric random variable.
. We illustrate this technique by determining the variance of a geometric random variable.
Example 3.18
Variance of the Geometric Random Variable
Independent trials, each resulting in a success with probability 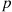 , are performed in sequence. Let
, are performed in sequence. Let 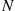 be the trial number of the first success. Find
be the trial number of the first success. Find 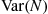 .
.
Solution: Let 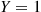 if the first trial results in a success, and
if the first trial results in a success, and 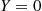 otherwise.
otherwise.
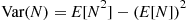
To calculate 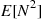 and
and 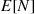 we condition on
we condition on 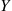 . For instance,
. For instance,
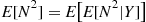
However,
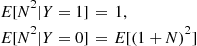
These two equations are true since if the first trial results in a success, then clearly 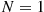 and so
and so 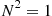 . On the other hand, if the first trial results in a failure, then the total number of trials necessary for the first success will equal one (the first trial that results in failure) plus the necessary number of additional trials. Since this latter quantity has the same distribution as
. On the other hand, if the first trial results in a failure, then the total number of trials necessary for the first success will equal one (the first trial that results in failure) plus the necessary number of additional trials. Since this latter quantity has the same distribution as  , we get that
, we get that 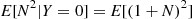 . Hence, we see that
. Hence, we see that

Since, as was shown in Example 3.10,  , this yields
, this yields
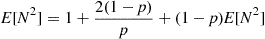
or
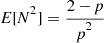
Therefore,
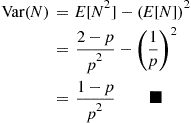
Another way to use conditioning to obtain the variance of a random variable is to apply the conditional variance formula. The conditional variance of 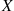 given that
given that 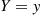 is defined by
is defined by
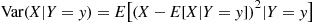
That is, the conditional variance is defined in exactly the same manner as the ordinary variance with the exception that all probabilities are determined conditional on the event that 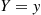 . Expanding the right side of the preceding and taking expectation term by term yields
. Expanding the right side of the preceding and taking expectation term by term yields
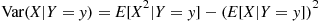
Letting 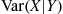 denote that function of
denote that function of 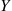 whose value when
whose value when 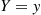 is
is 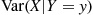 , we have the following result.
, we have the following result.
Proof
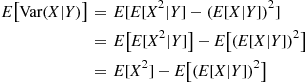
and
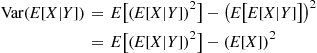
Therefore,
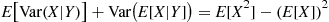
which completes the proof. ■
Example 3.19
The Variance of a Compound Random Variable
Let 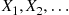 be independent and identically distributed random variables with distribution
be independent and identically distributed random variables with distribution 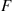 having mean
having mean 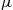 and variance
and variance 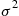 , and assume that they are independent of the nonnegative integer valued random variable
, and assume that they are independent of the nonnegative integer valued random variable 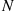 . As noted in Example 3.10, where its expected value was determined, the random variable
. As noted in Example 3.10, where its expected value was determined, the random variable 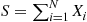 is called a compound random variable. Find its variance.
is called a compound random variable. Find its variance.
Solution: Whereas we could obtain 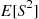 by conditioning on
by conditioning on 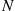 , let us instead use the conditional variance formula. Now,
, let us instead use the conditional variance formula. Now,
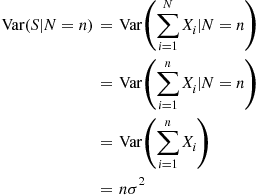
By the same reasoning,
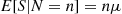
Therefore,
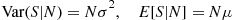
and the conditional variance formula gives
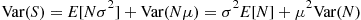
If 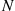 is a Poisson random variable, then
is a Poisson random variable, then 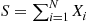 is called a compound Poisson random variable. Because the variance of a Poisson random variable is equal to its mean, it follows that for a compound Poisson random variable having
is called a compound Poisson random variable. Because the variance of a Poisson random variable is equal to its mean, it follows that for a compound Poisson random variable having 
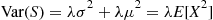
where 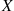 has the distribution
has the distribution  . ■
. ■
Example 3.20
The Variance in the Matching Rounds Problem
Consider the matching rounds problem of Example 3.14, and let 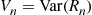 denote the variance of the number of rounds needed when there are initially
denote the variance of the number of rounds needed when there are initially 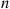 people. Using the conditional variance formula, we will show that
people. Using the conditional variance formula, we will show that

The proof of the preceding is by induction on 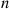 . To begin, note that when
. To begin, note that when  the number of rounds needed is geometric with parameter
the number of rounds needed is geometric with parameter 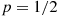 and so
and so
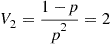
So assume the induction hypothesis that
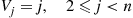
and now consider the case when there are 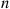 individuals. If
individuals. If 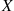 is the number of matches in the first round then, conditional on
is the number of matches in the first round then, conditional on 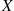 , the number of rounds
, the number of rounds 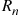 is distributed as 1 plus the number of rounds needed when there are initially
is distributed as 1 plus the number of rounds needed when there are initially  individuals. Consequently,
individuals. Consequently,
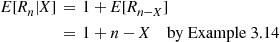
Also, with 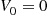 ,
,

Hence, by the conditional variance formula
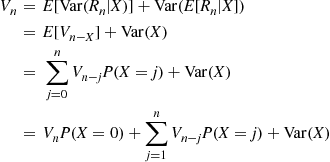
Because 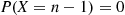 , it follows from the preceding and the induction hypothesis that
, it follows from the preceding and the induction hypothesis that

As it is easily shown (see Example 2.31 and Exercise 72 of Chapter 2) that 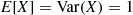 , the preceding gives
, the preceding gives
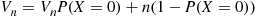
thus proving the result. ■
3.5 Computing Probabilities by Conditioning
Not only can we obtain expectations by first conditioning on an appropriate random variable, but we may also use this approach to compute probabilities. To see this, let  denote an arbitrary event and define the indicator random variable
denote an arbitrary event and define the indicator random variable  by
by
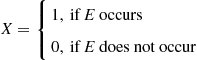
It follows from the definition of 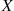 that
that

Therefore, from Equations (3.2a) and (3.2b) we obtain
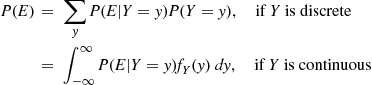
Example 3.21
Suppose that 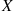 and
and 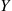 are independent continuous random variables having densities
are independent continuous random variables having densities 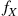 and
and 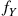 , respectively. Compute
, respectively. Compute 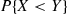 .
.
Example 3.22
An insurance company supposes that the number of accidents that each of its policyholders will have in a year is Poisson distributed, with the mean of the Poisson depending on the policyholder. If the Poisson mean of a randomly chosen policyholder has a gamma distribution with density function
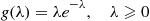
what is the probability that a randomly chosen policyholder has exactly  accidents next year?
accidents next year?
Solution: Let  denote the number of accidents that a randomly chosen policyholder has next year. Letting
denote the number of accidents that a randomly chosen policyholder has next year. Letting 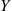 be the Poisson mean number of accidents for this policyholder, then conditioning on
be the Poisson mean number of accidents for this policyholder, then conditioning on 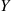 yields
yields
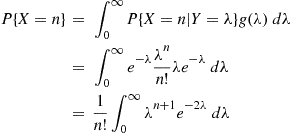
However, because
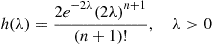
is the density function of a gamma  random variable, its integral is
random variable, its integral is 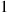 . Therefore,
. Therefore,
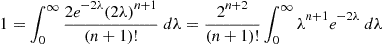
showing that
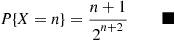
Example 3.23
Suppose that the number of people who visit a yoga studio each day is a Poisson random variable with mean 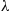 . Suppose further that each person who visits is, independently, female with probability
. Suppose further that each person who visits is, independently, female with probability 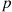 or male with probability
or male with probability  . Find the joint probability that exactly
. Find the joint probability that exactly  women and
women and 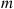 men visit the academy today.
men visit the academy today.
Solution: Let 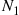 denote the number of women and
denote the number of women and 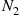 the number of men who visit the academy today. Also, let
the number of men who visit the academy today. Also, let 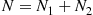 be the total number of people who visit. Conditioning on
be the total number of people who visit. Conditioning on 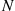 gives
gives
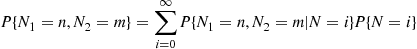
Because 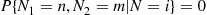 when
when 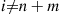 , the preceding equation yields
, the preceding equation yields

Given that  people visit it follows, because each of these
people visit it follows, because each of these  is independently a woman with probability
is independently a woman with probability 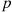 , that the conditional probability that
, that the conditional probability that  of them are women (and
of them are women (and 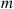 are men) is just the binomial probability of
are men) is just the binomial probability of 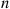 successes in
successes in  trials. Therefore,
trials. Therefore,
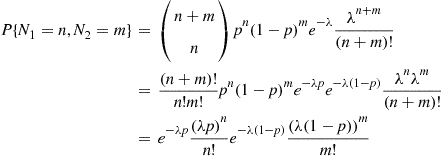
Because the preceding joint probability mass function factors into two products, one of which depends only on 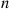 and the other only on
and the other only on 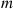 , it follows that
, it follows that 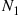 and
and 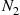 are independent. Moreover, because
are independent. Moreover, because

and, similarly,

we can conclude that 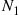 and
and 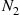 are independent Poisson random variables with respective means
are independent Poisson random variables with respective means 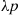 and
and 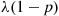 . Therefore, this example establishes the important result that when each of a Poisson number of events is independently classified either as being type
. Therefore, this example establishes the important result that when each of a Poisson number of events is independently classified either as being type 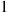 with probability
with probability 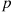 or type
or type 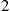 with probability
with probability  , then the numbers of type
, then the numbers of type  and type
and type 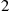 events are independent Poisson random variables. ■
events are independent Poisson random variables. ■
The result of Example 3.23 generalizes to the case where each of a Poisson distributed number of events, 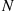 , with mean
, with mean  is independently classified as being one of
is independently classified as being one of 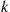 types, with the probability that it is type
types, with the probability that it is type 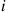 being
being 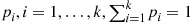 . If
. If 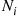 is the number that are classified as type
is the number that are classified as type 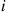 , then
, then  are independent Poisson random variables with respective means
are independent Poisson random variables with respective means  . This follows, since for
. This follows, since for 
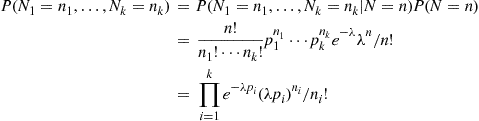
where the second equality used that, given a total of 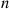 events, the numbers of each type has a multinomial distribution with parameters
events, the numbers of each type has a multinomial distribution with parameters  .
.
Example 3.24
The Distribution of the Sum of Independent Bernoulli Random Variables
Let  be independent Bernoulli random variables, with
be independent Bernoulli random variables, with 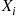 having parameter
having parameter  . That is,
. That is, 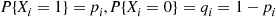 . Suppose we want to compute the probability mass function of their sum,
. Suppose we want to compute the probability mass function of their sum,  . To do so, we will recursively obtain the probability mass function of
. To do so, we will recursively obtain the probability mass function of  , first for
, first for 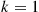 , then
, then 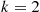 , and on up to
, and on up to 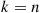 . To begin, let
. To begin, let
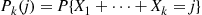
and note that
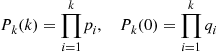
For  , conditioning on
, conditioning on 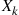 yields the recursion
yields the recursion
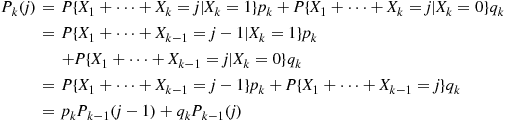
Starting with 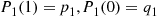 , the preceding equations can be recursively solved to obtain the functions
, the preceding equations can be recursively solved to obtain the functions 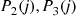 , up to
, up to 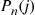 . ■
. ■
Example 3.25
The Best Prize Problem
Suppose that we are to be presented with 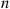 distinct prizes in sequence. After being presented with a prize we must immediately decide whether to accept it or reject it and consider the next prize. The only information we are given when deciding whether to accept a prize is the relative rank of that prize compared to ones already seen. That is, for instance, when the fifth prize is presented we learn how it compares with the first four prizes already seen. Suppose that once a prize is rejected it is lost, and that our objective is to maximize the probability of obtaining the best prize. Assuming that all
distinct prizes in sequence. After being presented with a prize we must immediately decide whether to accept it or reject it and consider the next prize. The only information we are given when deciding whether to accept a prize is the relative rank of that prize compared to ones already seen. That is, for instance, when the fifth prize is presented we learn how it compares with the first four prizes already seen. Suppose that once a prize is rejected it is lost, and that our objective is to maximize the probability of obtaining the best prize. Assuming that all 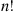 orderings of the prizes are equally likely, how well can we do?
orderings of the prizes are equally likely, how well can we do?
Solution: Rather surprisingly, we can do quite well. To see this, fix a value 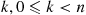 , and consider the strategy that rejects the first
, and consider the strategy that rejects the first 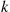 prizes and then accepts the first one that is better than all of those first
prizes and then accepts the first one that is better than all of those first 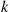 . Let
. Let 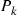 (best) denote the probability that the best prize is selected when this strategy is employed. To compute this probability, condition on
(best) denote the probability that the best prize is selected when this strategy is employed. To compute this probability, condition on 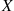 , the position of the best prize. This gives
, the position of the best prize. This gives
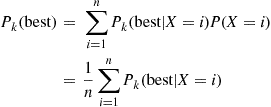
Now, if the overall best prize is among the first 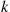 , then no prize is ever selected under the strategy considered. On the other hand, if the best prize is in position
, then no prize is ever selected under the strategy considered. On the other hand, if the best prize is in position 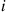 , where
, where 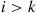 , then the best prize will be selected if the best of the first
, then the best prize will be selected if the best of the first 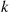 prizes is also the best of the first
prizes is also the best of the first 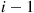 prizes (for then none of the prizes in positions
prizes (for then none of the prizes in positions 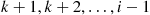 would be selected). Hence, we see that
would be selected). Hence, we see that
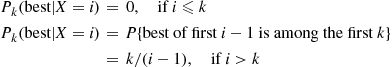
From the preceding, we obtain
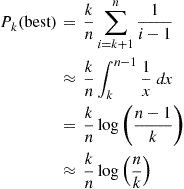
Now, if we consider the function
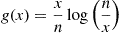
then
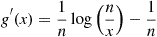
and so