Let’s say your class is doing an art project with googly eyes. There are a bunch of boxes that have 10 googly eyes each, and it’s your job to open the boxes and give some to each of your classmates. In other words, you need to “unbox” the googly eyes.

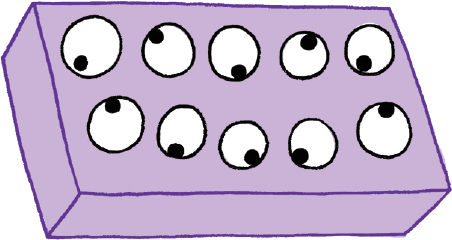
But now there’s only one classmate left, and the box you’ve been using just became empty, so you have to open a whole new box just to give her two googly eyes! I mean, there’s a stack of boxes next to you, but it’s still kind of annoying to have to open a whole new box, right?

Oh well, things like this happen sometimes, even in math! Maybe we should try to be grateful that the boxes are there in the first place….

Unbox Those Googly Eyes: Subtracting Two-Digit Numbers with Ungrouping

Let’s do 83 – 64. Just like with addition, we want to keep everyone in their freeway lanes, so let’s write it that way:

Great. So first we look at just the ones column, and we need to subtract: 3 − 4. Wait, what? We can’t do that, because 3 isn’t big enough to subtract 4 from it…but that’s okay! After all, we have 8 boxes of googly eyes right next to us—sort of! We have 8 tens sitting right there. We can take 1 full ten, which is like a box of 10 googly eyes, “open the box,” and put the 10 googly eyes in the ones column! This “unboxing” in math is called ungrouping. Check it out:

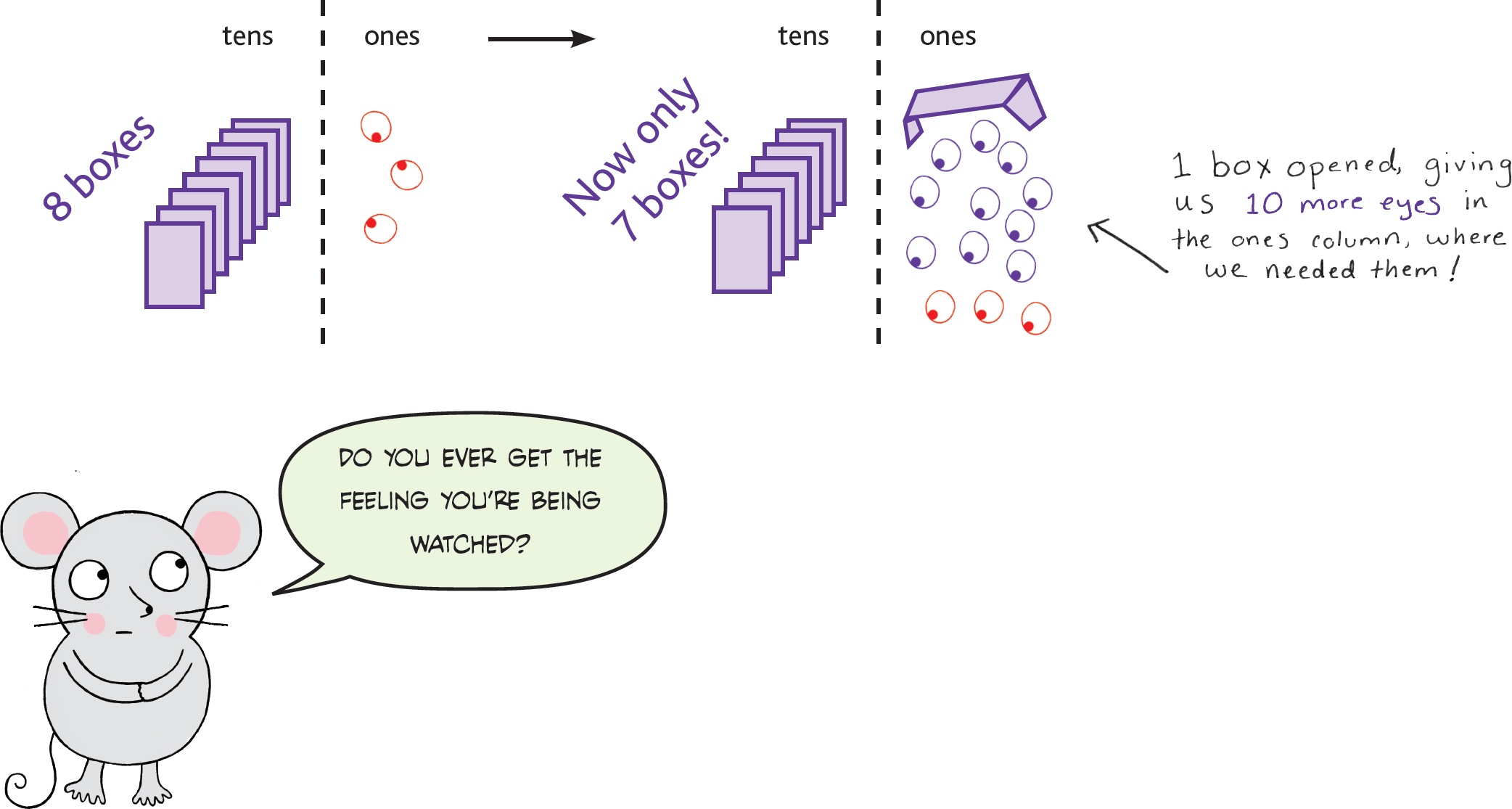
Let’s see what this looks like with our numbers! We took 10 from the tens column and gave it to the ones column, right? So the 8 becomes 7 (there are only 7 boxes left) and the 3 becomes 13 (we got 10 new googly eyes from that box)!

And now we have a total of 10 + 3 = 13 ones in the ones column, which is more than enough to do our subtraction in the ones column, yay!

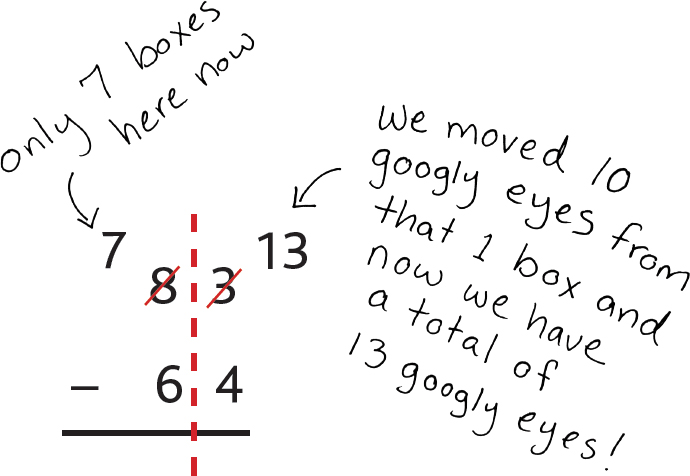
So, for the ones column, we do: 13 – 4 = 9, and then for the tens column, we do: 7 – 6 = 1.

We end up with 1 ten and 9 ones—in other words, 19! And we’ve just shown that 83 – 64 = 19. Nice work!

Two-Digit Subtraction: When Do We Ungroup?

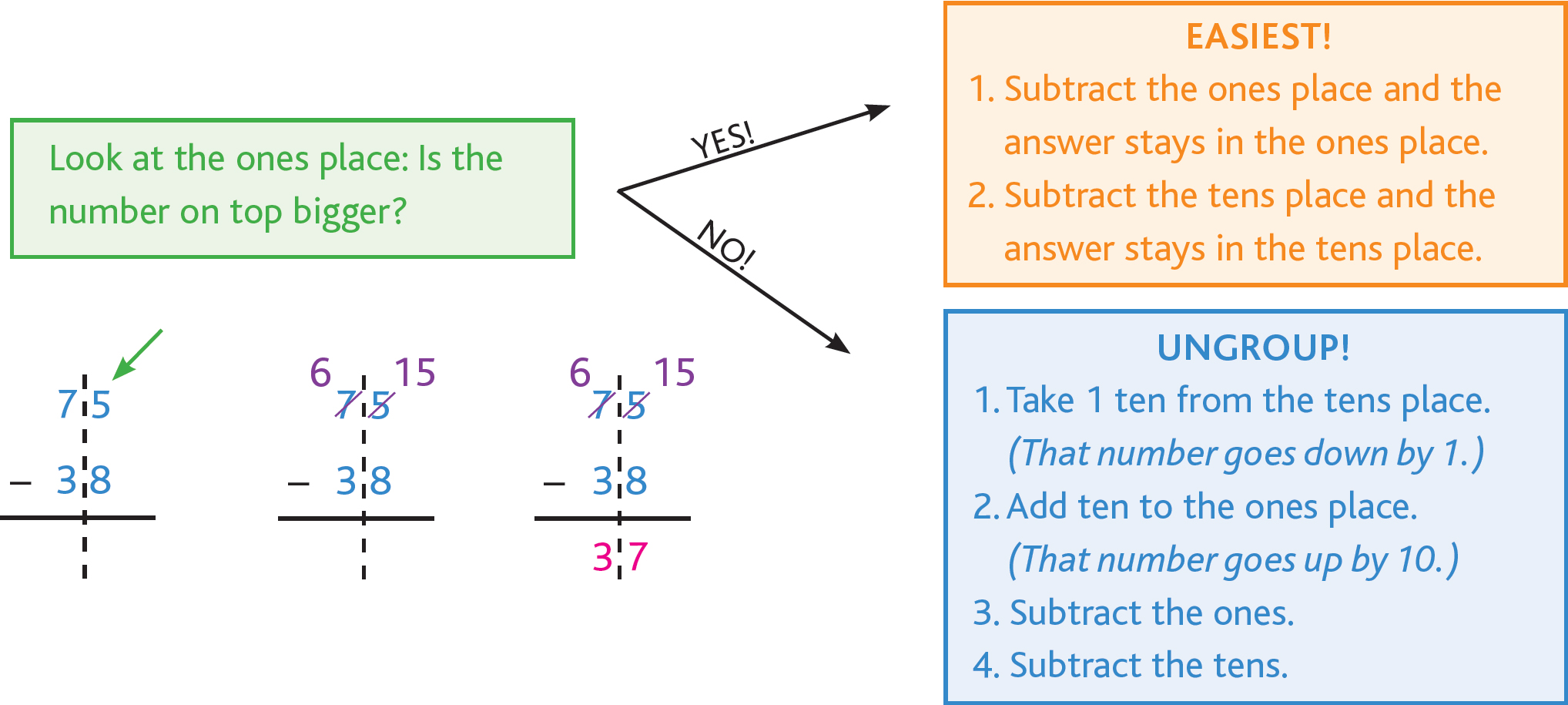
Instead of “ungrouping,” some people call this “regrouping” or even “borrowing.” But of course it’s not really borrowing, because it’s not like we’re going to ever give those 10 ones back to the tens column.

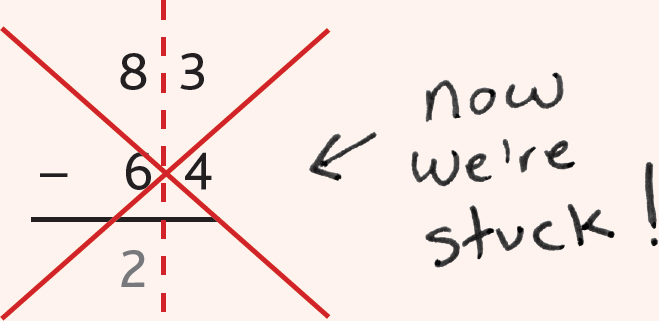
Always, always ungroup first, and then subtract the ones column. If we had started with the tens column for 83 – 64 without ungrouping, look at the trouble we would have gotten into!

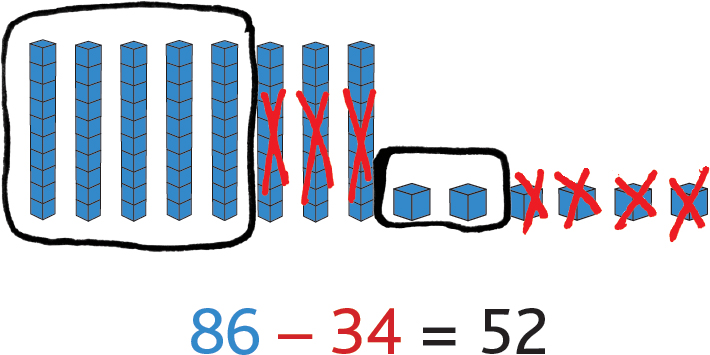
Remember back in Chapter 5 when we used models for subtraction? We’d first model the bigger number, and then cross off the parts we’re subtracting. For example, on pages 73 and 74, for 86 – 34, first we modeled 86, then crossed off 34 and circled what was left over: 52!

Now let’s subtract 56 – 39. Okay, first we’ll model 56 with 5 tens and 6 ones, right? Next we want to cross off 39, but wait—there aren’t 9 ones to cross off, are there? I guess it’s time to open a box of googly eyes—I mean, ungroup one of those ten sticks into 10 little ones!

Here’s what it looks like when we “ungroup” the ten, and now we’re ready to cross stuff off.

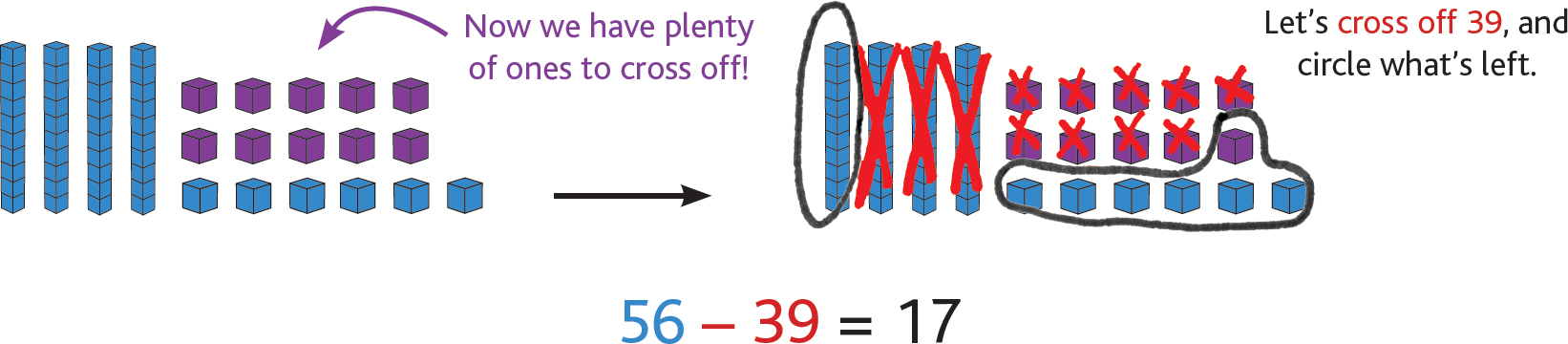
We just showed with models that 56 – 39 = 17! Ta-da!

 

Choices!

When you do these subtraction problems with ungrouping, you can choose to think about (and draw!) the models like we just did, or think about boxes of googly eyes, or not! You can also simply draw the freeway lanes and make the numbers change. It’s your brain—so do what you like most!

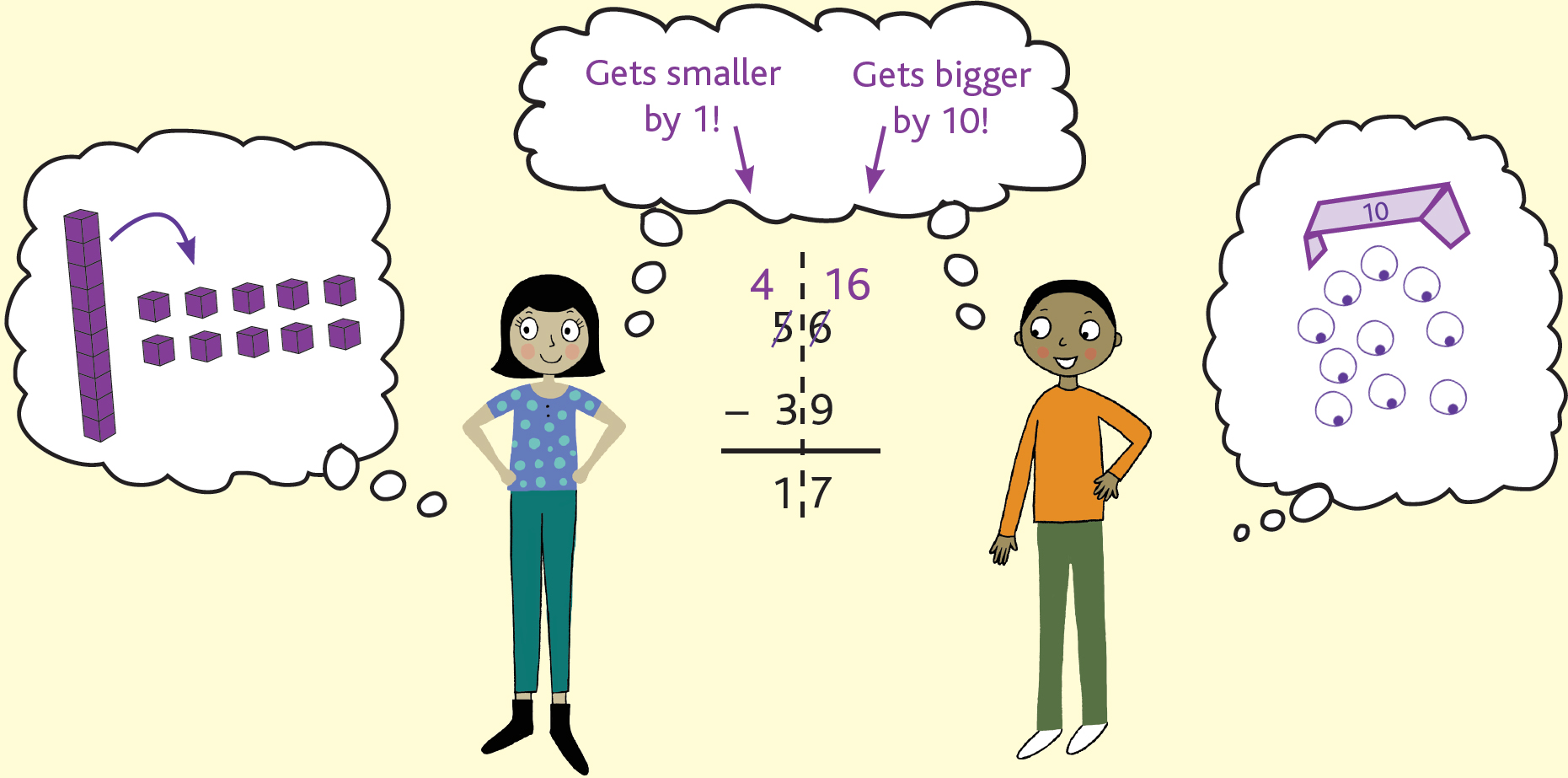
PUT YOUR THINKING CAP ON!

Whenever things feel extra challenging, remember to put your thinking cap on, like we talked about on page 39. You got this!

It’s nice to have choices, don’t you think? But no matter how we choose to think about ungrouping, it’s very important to check our answers, because it’s so easy to make mistakes along the way, especially with subtraction!

Return of the Turkey Sandwich: Checking Our Answers with Addition!

Remember the “turkey sandwich” fact families we talked about in Chapter 2? Well, every time we do any addition or subtraction problem, we are discovering a new turkey sandwich—a new fact family! And because of that, we can use addition to check our subtraction answers.

On page 128 we did the subtraction problem 83 − 64 = 19, which is like destroying the sandwich, remember? And the “sandwich” is the biggest number: 83! So if we made the sandwich, we could do: 64 + 19 = 83 or 19 + 64 = 83—it doesn’t matter which we choose. Let’s try it:

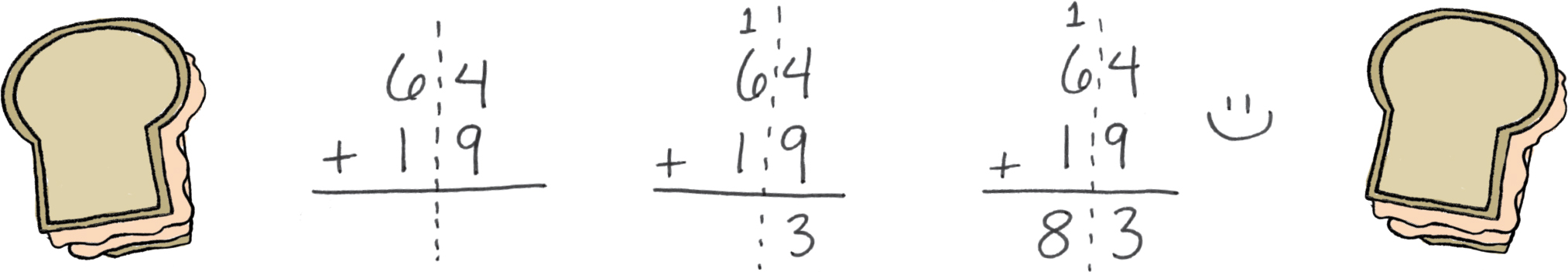
Yep, we got 83! Since making and destroying turkey sandwiches is all part of the same fact family (shown below in a box), we know we did our subtraction problem correctly. Yay!