2
Light
To see we need light. This may seem too obvious to mention but it has not always been recognized. Greek philosophers, including Plato and Euclid, thought of vision as due not to light entering but rather to particles shooting out of the eyes, as fingers touching surrounding objects. It is hard to imagine now why they did not try to settle the matter with a few simple experiments. Although to philosophers the problem of how we see has always been a favourite topic of speculation, only in the last hundred and fifty years or so has it been subjected to systematic experiments. This is odd, for all observations in science depend upon the human senses, especially sight.
How are images produced? The simplest way an image can be formed is by a pinhole. Figure 2.1 shows how this comes about. A ray from a point of the object reaches a point on the screen by the straight line passing through the pinhole, so an upside-down and right–left reversed picture of the object is formed. The pinhole image will be dim, for the hole must be small for the image to be sharp. (Though if too small it will be blurred, because the wave structure of the light is upset.)
A lens may be thought of as a pair of curved prisms (Figure 2.2). It directs a lot of light from each point of the object to a corresponding point on the screen, thus giving a bright image. Lenses only work well when suitable and adjusted correctly.
What is light?
In the last three hundred years there have been two rival accounts of the nature of light. Sir Isaac Newton (1642–1727) thought of light as a shower of particles. The Dutch physicist Christiaan Huygens (1629–95; Figure 2.3) proposed that it is pulses travelling through an all-pervading medium—the aether—which he thought of as small elastic balls in contact with each other. Any disturbance, he suggested, would be carried in all directions through the packed spheres as a wave, and this wave is light.
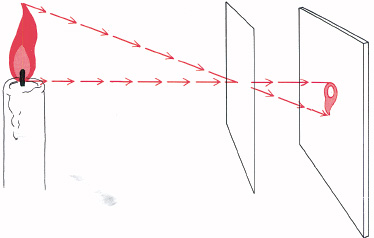
2.1 Forming an image with a pinhole. A ray from a given region of the source reaches only a single region of the screen by passing through the hole. Thus an inverted and sideways reversed image is built up from rays passing through the hole. The image is free of distortion, but it is dim and not very sharp. A very small hole gives a still dimmer image, with increased blurring through diffraction effects due to the wave nature of light.
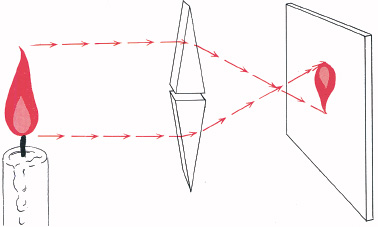
2.2 A focusing lens can be thought of as a pair of converging prisms. The image is far brighter than from a pinhole, but it is generally distorted in some degree, and the range of sharp focus is limited. (This figure should not be taken too literally—image-forming lenses have curved surfaces.)

2.3 Christiaan Huygens (1629–95) by an unknown artist. As well as being a highly creative scientist, Huygens had an unusually active life, as secretary to the Prince of Orange. He invented the pendulum clock (suggested by Galileo on his death bed) and showed how to make a strictly isochronous (equal time for any amplitude) pendulum. He correctly described Saturn’s ring, and discovered (at the same time as Christopher Wren) the laws of elastic bodies. He argued that light travels as waves through an all-pervading aether of tightly packed balls.
The controversy over the nature of light is one of the most interesting in the history of science. A crucial question in the early stages of the discussion was whether light travels at a finite speed or whether it arrives instantaneously. This was answered in an entirely unexpected way by a Danish astronomer, Olaus Roemer (1644–1710). He was engaged in recording eclipses of the four bright satellites orbiting Jupiter, and found that the times he observed were not regular, but depended on the distance of Jupiter from the earth. He came to the conclusion (in 1675) that this was due to the changing time light took to reach him from Jupiter’s satellites—the time increasing when the distance increased—because of the finite speed of light. The distance of Jupiter varies by about 300 000 000 km (twice the distance of the Sun from Earth), and the greatest time difference he observed was 16 minutes 36 seconds earlier or later than the calculated time of the eclipses of the satellites. From his somewhat faulty estimate of the distance of the Sun, he calculated the speed of light at 309 000 km per second. With our modern knowledge of the diameter of the Earth’s orbit we correct this to about 300 000 km per second, or 3 × 1010 cm/s. The speed of light has since been measured very accurately over short distances on earth and is now regarded as a primary constant of the universe.
Because of the finite speed of light and, more important for terrestrial objects, the considerable delay while nervous messages reach the brain, we always sense the past. Our perception of the Sun is eight minutes late, and all we know of the furthest object visible to the unaided eye (the Andromeda nebula) is from before humans appeared on earth. For nearby objects, there is the neural delay of several hundredths of a second, which is significant for fast action.
The value of 3 × 1010 cm/s for the speed of light strictly holds only for a perfect vacuum. When light travels through glass, or water, or any other transparent substance, it is slowed down to a velocity which depends on the refractive index (roughly the density) of the medium through which it passes. This slowing down of light is extremely important. It is this that causes prisms to bend light and lenses to form images. The principle of refraction (the bending of light when passing through changes of refractive index) was first understood in 1621 by a Dutch mathematician at Leyden, Willebrod von Roijen Snell (1591–1626). Snell died at thirty-five, leaving his results unpublished. The French philosopher-mathematician René Descartes (1596–1650) published the law of refraction, or sine law, 11 years later, (Figure 2.4).
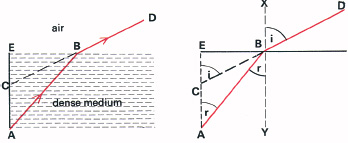
2.4 The sine law of refraction. When light passes from a medium A into a medium B, the sine of the angle of incidence bears to the sine of the angle of refraction a constant ratio.
We can see what happens with a simple diagram: if AB is a ray passing from a dense medium (glass) into a vacuum (or air) the ray will emerge into the air at some angle i along BD. The law states that sin i = u/sin r. The constant u is the refractive index of the glass, or other refracting substance.
Newton (Figure 2.5) thought of his corpuscles of light as being attracted to the surface of the denser medium, while Huygens thought that the bending was due to the light travelling more slowly. It was many years before the French physicist Jean Bernard Léon Foucault (1819–68) showed by direct measurement that light does indeed travel more slowly in a denser medium. It seemed for a time that Newton’s corpuscle theory of light was entirely wrong—that light is purely a series of waves radiating through the aether—but at the beginning of the twentieth century it was shown that the wave account is not adequate for all the phenomena of light. It now seems that light is both particles and waves.
When light is bent by a prism, each wavelength (or frequency) is deviated through a slightly different angle, so the beam comes out as a fan of light, with the spectral colours spread out. Newton discovered that white light is a compound of the spectral colours by splitting a beam of sunlight into a spectrum in this way (Figure 2.6); then found that he could recombine the colours back into white light, by passing the spectrum through a second similar prism held the other way up. Newton named seven spectral colours: red, orange, yellow, green, blue, indigo, violet. One does not really see indigo as a separate colour, and orange is a bit doubtful; but Newton liked seven, as a magical number, and he thought of the spectrum in terms of the notes of a musical stave, so he added the names orange and indigo to make up seven.
We know now, though Newton did not, that each spectral colour or hue is light of a different frequency. We also know that all electro-magnetic radiation is essentially the same; the physical differences between radio waves, infrared, visible light, ultraviolet, X-rays, and so on are only their frequencies. A very narrow band of this huge range of frequencies, less than an octave in width, stimulates the eye to give vision. Figure 2.7 shows how this narrow window of the total spectrum fits into the physical picture. Looked at in this way we are almost blind!

2.5 Sir Isaac Newton (1642–1727), by Charles Jervas. On the whole Newton held that light consists of particles, but he anticipated many of the difficulties which have been faced by the modern theory that light has dual properties of particles and waves. Newton devised the first experiments to show that white light is a mixture of the spectral colours, which paved the way to an understanding of colour vision. He realized that light itself is not coloured—but elicits colours—created as we now know by specialized cells of the brain.
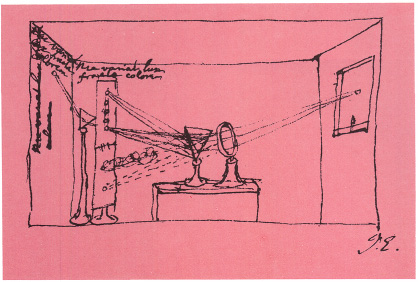
2.6 Newton’s drawing of one of his experiments on colour. He first split light into a spectrum (with the large prism), then allowed light of a single colour to pass through a hole in a screen to a second prism. This did not produce more colours. He also found that a second prism placed in the spectrum would recombine the colours into white. Thus white light (sunlight) is made up of all the colours of the spectrum.
From the speed of light (λ) it is a simple matter to calculate wavelength from frequency, or vice versa, as F λ = 3 × 108 metres/second. In fact frequency is difficult to measure directly: it is easier to measure visible wavelengths, though this is not so for the much lower-frequency radio waves. The wavelength of light is measured by splitting it up with a grating of finely ruled lines, which also produces the colours of the spectrum. (This can be seen by holding a compact disc at an oblique angle to a source of light, when the reflection will be brilliantly coloured.) From the spacing of the lines of an optical grating, and the angle reflecting light of a given colour, wavelength may be determined very accurately. Blue light has a wavelength of about 4 × 10−7 m. Red light is about 7 × 10−7 m.
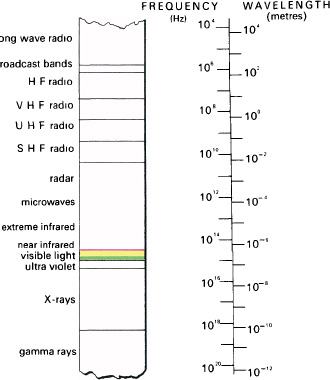
2.7 Visible light is but a narrow band of the total electromagnetic spectrum. The different properties of various frequencies are due to how electromagnetic radiations react with matter.
The range of wavelengths which is accepted for vision is important, for it sets the limit to the eyes’ resolution, just as for optical instruments such as microscopes and cameras. Resolution increases with the frequency of the light and with the size (optical aperture) of an eye or instrument. Eyes are adapted to accept wavelengths of maximum energy of sunlight, without undue damage to the biological materials of which they are made. Compound eyes of insects work in the ultraviolet, no doubt because they are so small.
The present wave account of light is more complicated than ripples on a pond, for light is electromagnetic—meaning it is waves of both electrical and magnetic fields. These are at right angles to each other, and displaced by half a wave length, so that as one increases the other decreases (Figure 2.8).
Light is also thought of as consisting of particles of energy, called photons for visible light. Quanta is the general term used for all wavelengths or frequencies of radiation. These combine the characteristics of particles and of waves. Photons are sometimes thought of as packets of waves. The shorter the wavelength, the more waves in each photon. This is expressed by saying that the energy of a single photon (or quantum), is a function of frequency, such that E = hv, where E is the energy in ergs, h is a small constant (Planck’s constant) and v is the frequency of the radiation.
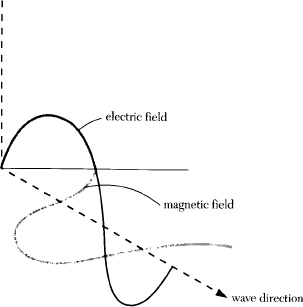
2.8 Light is waves of electrical and magnetic fields, at right angles to each other, one increasing as the other decreases.
We cannot, with the unaided eye, see individual quanta of light—known as ‘photons’; but the receptors in the retina are so sensitive that they can be stimulated by a single photon, though something like five to eight are required for experience of a short dim flash. The individual receptors of the retina are as sensitive as it is possible for any light detector to be, since a quantum is the smallest amount of energy which can exist. It is rather sad that the transparent media of the eye do not quite match this development, as less than half the quanta reach the receptors, the rest being lost by absorption and scattering within the eye. In spite of this loss it would be possible, under ideal conditions, to see a single candle placed nearly twenty miles away.
The first experiment for measuring the number of quanta required for the eye to detect light was undertaken in 1942 by three physiologists, S. Hecht, S. Schlaer, and M. H. Pirenne. Realizing that the eye must be almost as sensitive as theoretically possible, they devised an ingenious experiment depending on probabilities, based on a function, the Poisson distribution. This gives the expected distribution of hits on a target. The idea is that at least part of the moment-to-moment variation in the effective sensitivity of the eye is not due to anything in the eye, or the nervous system, but to the moment-to-moment variation of energy of a weak light source when there are only a few quanta arriving. Imagine a desultory rain of bullets: they will not arrive at a constant rate, but will fluctuate. Similarly there is fluctuation in the number of light quanta arriving at the eye. So a given dim flash may contain a small or large number of quanta, and is more likely to be detected if there happen to be more than the average number in the flash. From lengthy experiments to build up ‘frequency-of-seeing’ curves, the number of quanta can be deduced from the steepness of the curves. So basic physics is important for vision.
The quantal nature of light is important for detecting fine detail. One of the reasons why it is possible to read only the largest newspaper headlines by moonlight is that too few photons fall on the retina to build up a complete image (within the time-span over which the eye can integrate energy, which is about a tenth of a second.) This is pure physics. Sometimes it is hard to establish whether a visual effect should be thought of as belonging to psychology, to physiology, or to the physics of light.







