5

Seeing brightness

There is supposed to be a tribe of cattle breeders who have no word for green in their language but have six words for different shades of red. Specialists in all fields adopt special meanings for their own use, and generally name more distinctions than are usually seen or at least noticed. Before embarking on a discussion of brightness and colour we should stop for a moment to sharpen some words—as a carpenter might stop to sharpen his chisel before attempting delicate work.

We speak of physical intensity of light entering the eye giving rise to apparent or seen brightness. Physical intensity of light may be measured by various kinds of photometer, including the familiar photographer’s exposure meter; but brightness is an experience, which is very hard and perhaps impossible to measure. We believe we know what another person means when he says: ‘What a bright day!’ He means, not only that he could take photographs with a slow film in his camera, but also that he experiences a dazzling sensation. This sensation is roughly, but only roughly, related to the intensity (also called ‘luminance’) of the light entering the eye.

When talking technically about colour vision we do not generally talk of ‘colours’ but rather of ‘hues’. This is simply to avoid the difficulty that ‘colours’ are apt to mean sensations to which we can give a specific name such as ‘red’ or ‘blue’. We thus speak technically of ‘spectral hues’ rather than ‘spectral colours’, but this is not always necessary. The distinction between physical intensity and seen brightness is more important.

Another important distinction to be made is between colour as a sensation and colour as a wavelength (or set of wavelengths) of light. Strictly speaking light itself is not coloured: it gives rise to sensations of brightness and colour, but only in conjunction with a suitable eye and nervous system. Although Sir Isaac Newton was quite clear on this in his Optics of 1704, the technical language is somewhat confused on this matter. We do speak sometimes of ‘coloured light’, such as ‘yellow light’, but it should be taken to mean light which generally gives rise to a sensation described by most people as ‘coloured’ or specifically ‘yellow’.

Without attempting to explain how physical intensities and wavelengths of radiation give rise to different sensations (and ultimately we do not know the answer), we should realize quite clearly that without life there would be no brightness and no colour. Before life came, especially higher forms of life, all was invisible and silent though the sun shone and the mountains toppled.

The simplest of the visual sensations is brightness. It is impossible to describe the sensation. A blind man knows nothing of it; yet to the rest of us, reality is made up of brightness and of colour. The opposed sensation of blackness is as powerful—we speak of a ‘solid wall of blackness pressing in on us’—but to the blind this also means nothing. The sensation given to us by absence of light is blackness; but to the blind it, it is nothingness. We come nearest to picturing the world of the blind, who have no brightness and no black, by thinking of the region behind our heads. We do not experience blackness behind us: we experience nothing, and this is very different from blackness.

Brightness is not just a simple matter of the intensity of light striking the retinas. The brightness seen by a given intensity depends upon the state of adaptation of the eyes, and also upon various complicated conditions determining the contrast of objects or of patches of light. In other words, brightness is a function not only of the intensity of light falling on a given region of the retina at a certain time, but also of the intensity of the light that the retina has been subject to in the recent past, and of the intensities of light falling on other regions of the retina.

Dark–light adaptation

If the eyes are kept in a low light level for some time they grow more sensitive, and a given light will look brighter. This ‘dark adaptation’ is rapid for the first few seconds, then slows down. The rod and cone receptor cells adapt at different rates: cone adaptation is completed in about seven minutes, while rod adaptation continues for an hour or even more. This is shown in Figure 5.1 which shows the two adaptation curves—one for the rods, the other for the cones. It is as if we have not one but two retinas, lying intermingled in the eye.

The mechanisms of dark adaptation are beginning to be understood in detail, largely through the ingenious and technically brilliant experiments of the British physiologist W. A. H. Rushton at Cambridge. It was suggested many years ago that adaptation is due to regeneration of the visual pigments of the eye bleached by light—this bleaching in some unknown way stimulating the receptors to transmit electrical signals to the optic nerve. The photochemical rhodopsin was extracted from the frog’s eye, and its density to light measured during bleaching and regeneration, and compared with human dark adaptation curves. The two curves are shown together in Figure 5.2, and indeed they do correspond very closely, suggesting a strong connection between the photochemistry of rhodopsin and the changing sensitivity of the rod eye. It would also seem that brightness must be related to the amount of photochemical present to be bleached. What Rushton has done is to measure the density of the photochemical in the living eye, during adaptation to darkness. The technique is, essentially, to shine a brief flash of light into the eye and to measure the amount of light reflected from it with a very sensitive photocell. At first it seemed impossible to do this for the human eye because so little light remains to be reflected after the almost complete absorption by the photochemicals and the black pigment lying behind the receptors. So a cat’s eye was used, the reflecting layer at the back, the tapetum, serving as a mirror to reflect light to the photocell. The method worked with the cat’s eye and Rushton then succeeded in making it sufficiently sensitive to detect and measure the very feeble light reflected from the human eye. He found that there is bleaching of the photochemicals with adaptation, though this was much less than expected. He then detected the three colour-sensitive pigments in this way, obtaining results broadly confirmed by microscopic spectral absorption measurements of individual cone cells.

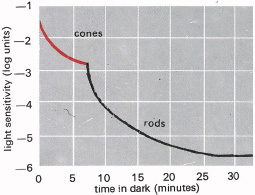
5.1 Increase in sensitivity of the eye in the dark, known as dark adaptation. The red curve shows how the cone cells adapt, while the black curve shows rod adaptation, which is slower and proceeds to greater sensitivity. In dim light only the rods are functional, while they are probably inhibited in brighter light by the active cones.

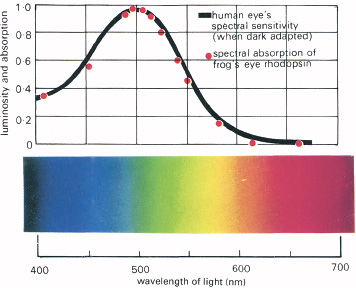
5.2 The chemical basis of vision. The curve in black shows the sensitivity of the dark adapted human eye to various wavelengths of light. The red dots show the amount of light over the same range of wavelengths absorbed by the photochemical rhodopsin in the frog’s eye. The curves are substantially the same, indicating that the human eye (when dark adapted) functions by absorption of light by the same photochemical.

Contrast

Another factor which affects brightness is the intensity of surrounding areas. A given region generally looks brighter if its surroundings are dark, and a given colour looks more intense if it is surrounded by its complementary colour. This is no doubt related to the cross-connections between the retinal receptors. Contrast enhancement seems to be tied up with the general importance of borders in perception. It seems that it is primarily the existence of borders which is signalled to the brain. Little information is needed on regions of constant intensity, and the visual system extrapolates information between borders, which no doubt saves a lot of information-handling. Although the phenomena of contrast and enhancement of borders are no doubt mainly because of retinal mechanisms that are due to cross connections between cones, which effectively sharpen the signalling of borders (by lateral inhibition), there also seem to be more central contributions. This is brought out in Figure 5.3. There is more brightness difference in the grey ring when a fine thread is placed across it, marking the division of the background. The contrast is greater when the figure is interpreted as two separate halves than when it is regarded as all one figure, which perhaps suggests that ‘central’ processing is occurring.

Something of the subtlety of the human brightness system is shown by Fechner’s paradox. This is as follows. Present the eye with a small fairly bright source: it will look a certain brightness, and the pupil will close to a certain size when the light is switched on. Now add a second, dimmer light. This is placed some way from the first, so that a different region of retina is stimulated. What happens? Although the total intensity has increased, with the addition of the second light, the pupil does not close further as one might expect. Rather, it opens—to correspond to an intensity between the first and the second light. It is evidently set not by the total, but by the average illumination.

5.3 Simultaneous contrast. The part of the grey ring against the black appears somewhat lighter than the rest of the ring against the white background. This effect is enhanced when a thread is placed across the ring, along the black–white junction.

Try shutting one eye, and note any change in brightness. There is practically no difference, whether one or two eyes receive the light. This is not so, however, when small dim lights are viewed in surrounding darkness: they do look considerably brighter, with two eyes than with one. This phenomenon is not understood.

Brightness is a function of colour. If we shine lights of different colours, but the same intensity, into the eyes, the colours at the middle of the spectrum will look brighter than those at the ends. This is shown in Figure 5.4, the curve being known as the spectral luminosity curve. This is of some practical importance, for if a distress signal light is to be clearly visible it should be of a colour for which the eye is maximally sensitive—in the middle of the spectrum. It is complicated by the fact that, although the sensitivity curves for rods and cones are similar in general shape, the cones are most sensitive to yellow, while the rods are most sensitive to green. The change with increasing intensity is known as the Purkinje shift, after the Austrian physiologist Johannes Evangelista Purkinje (1787–1869), who was an extremely good observer of ‘entoptic’ (within the eye) phenomena.

The luminosity curve tells us nothing much about colour vision. It is sensitivity to light plotted against wavelength of light, but with no reference to the colours seen at each wavelength. Animals without colour vision show a similar luminosity curve.

It seems that, although there are photochemical changes associated with adaptation to light, there are also several additional mechanisms at work, these being not photochemical but neural. In particular, as the eye becomes dark adapted, it trades its acuity in space and time for increase in sensitivity. With decrease of intensity, and the compensating dark adaptation, ability to make out fine detail is lost. This is no simple matter, but it is in part due to the retina integrating over a greater area and so a greater number of receptors. There is also an increase in the time over which photic energy is integrated as the eye adapts to dim light, much as photographers use longer exposures to compensate for low light levels.

The trading of temporal discrimination for sensitivity with dark adaptation is elegantly (if somewhat indirectly) observed in a curious and dramatic phenomenon known as the Pulfrich pendulum effect (Figure 5.5). One remarkable feature of this is the way it was discovered, because it cannot be seen without two functional eyes and yet its discoverer was blind in one eye! The experiment is well worth trying. Take a length of string and a weight for a bob, to make a pendulum about one metre long. Swing the pendulum in a straight arc at right angles to the line of sight. View the oscillating bob with both eyes, but cover one with a dark, though not opaque, glass such as one filter of a pair of sunglasses.

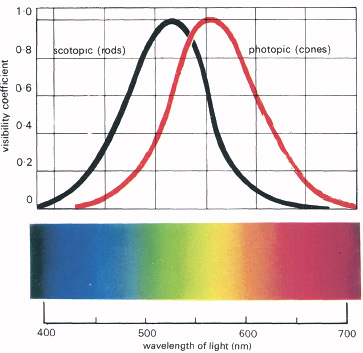
5.4 The spectral luminosity curve. This shows how the sensitivity of the eye to various wavelengths is different when the eye is light adapted. The black curve shows that the maximum sensitivity shifts along the spectrum when the eye is dark adapted. The red curve shows sensitivity when the eye is light adapted. This is the Purkinje shift, and is presumably due to changing relative contributions from the rod and cone receptors.

You will see that the bob does not appear to swing in a straight arc, but to describe an ellipse. The ellipse may be extremely eccentric—indeed the longer axis can lie along the line of sight, though the bob is actually swinging straight across the line of sight. What causes this strange effect? By reducing the light, the dark glass delays signals from this eye. These receptors take longer to respond, and the dark adaptation produces a delay in the message reaching the brain from this eye. The delay causes the affected eye to see the bob slightly in the past. As the bob speeds up in the middle of its swing the delay becomes more important, for the eye with the filter sees it in a position further and further behind the position signalled to the brain by the unaffected eye. This gives an effective horizontal shift of the moving image—as signalled—generating stereo depth. To the brain, it is as though the bob is swinging elliptically. It seems that increased delay with dark adaptation is associated with increase in temporal integrating time: as when a photographer uses a longer exposure in dim light. We see this also, and more directly, from the ‘comet’s tail’ following a moving firework at night, as dark adaptation increases the effective exposure-time of the eye to increase its sensitivity.

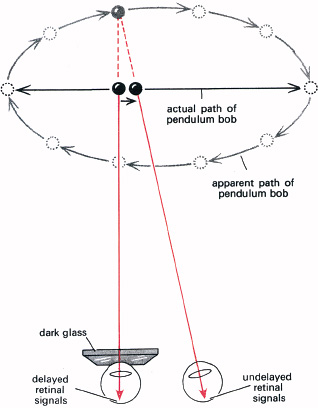
5.5 The Pulfrich pendulum. When a pendulum swinging in a straight arc across the line of sight is viewed with a dark glass (such as one filter of a pair of sunglasses) over one eye, both eyes being open, it appears to swing in an ellipse. This is due to signals from the eye which is dark-adapted by the dark glass being delayed. The bob’s increasing velocity towards the centre of its swing gives an increasingly signalled disparity, accepted as stereo signals corresponding to an elliptical path.

Both the increase in the delay of messages from the retina to the brain, and the increase in the integrating time which this allows, have some practical significance. The retinal delay produces a lengthening of reaction time in drivers in dim light, and the increased integrating time makes precise localization of moving objects more difficult. Games cannot be played so well: the umpire calls ‘Cease play for poor light’ long before the spectators think it right to bow before the setting sun.

The eye’s sensitivity to light

As intensity of light is increased, the rate of firing of the receptors increases, intensity being signalled by the rate of firing. Unfortunately it is not possible to record the electrical activity in the receptors of a vertebrate eye because the retina is ‘inside out’ so an electrode cannot be attached to receptors without doing extensive damage. By the time signals reach the optic nerve, they have been complicated by the cross-connections of the layers of nerve cells in the retina. There is however one type of eye—that of a living fossil, the horseshoe crab, Limulus, found on the eastern seaboard of the United States—in which the receptors are connected directly to separate nerve fibres. Figure 5.6 shows the electrical activity in a nerve fibre of a Limulus eye. The rate of firing of its receptors is logarithmically related to intensity.

Figure 5.6a shows a rate of firing after the eye has been in the dark for one minute. Figure 5.6b shows the firing rate increasing as the eye has been in the dark a longer time. This corresponds to our own experience of increasing brightness after being in the dark.

What happens when we look at a very faint light in an otherwise dark room? One might imagine that in the absence of light there is no activity reaching the brain, and when there is any light at all the retina signals its presence and we see the light. But it is not quite so simple. In the total absence of light, the retina and optic nerve are not entirely free of activity. There is some residual neural activity reaching the brain even when there is no stimulation of the eye by light. This is known from direct recording from the optic nerve in the fully dark-adapted cat’s eye, and we have strong reasons for believing that the same is true for the human and all other eyes. This continuous background of random activity is of great importance: it sets a continuous problem.

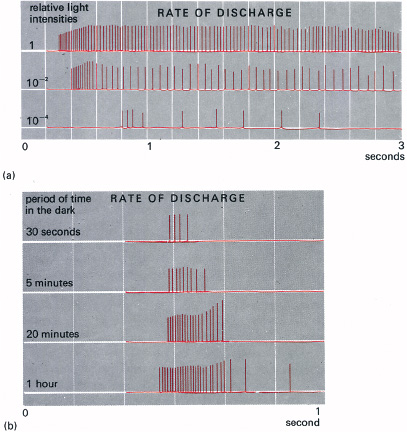
5.6 (a) Electrical activity, recorded on an oscilloscope, of a single fibre of the optic nerve of Limulus at three intensities of light. The rate of firing increases roughly logarithmically to the intensity. (b) The rate of firing after various durations of darkness. With increasing dark adaptation the firing rate increases, leading to an increase in apparent brightness, though the actual intensity of the light remains the same.

Imagine some neural pulses arriving at the brain: are they due to light entering the eye, or are they merely spontaneous noise in the system? The brain’s problem is to ‘decide’ whether neural activity is representing outside events, or whether it is mere noise, which should be ignored. This is a situation familiar to a communications engineer, because all sensitive detectors are subject to random noise, which degenerates signals, and limits the sensitivity of detectors. There are ways of reducing harmful effects of noise, which are applied with good effect by radio astronomers (noise masks the radio sources in space just as it masks and confuses weak visual signals). The eye adopts certain measures to reduce the effects of noise, notably by increasing the duration over which signals are integrated (which we saw reflected in the Pulfrich pendulum effect) and by demanding several confirming signals from neighbouring receptors serving as independent witnesses.

One of the oldest laws in experimental psychology is Weber’s Law (Figure 5.7). This states that the smallest difference in intensity which can be detected is directly proportional to the background intensity. For example, if we light a candle in a brightly lit room, its effect is scarcely noticeable; but if the room is dim to start with (lit by just a few other candles) then the added candle makes a marked difference. In fact we can detect a change in intensity of about one per cent of the background illumination. This is written ΔI/I = C, where C is a constant, and ΔI is the small incremental intensity over the background intensity, I. This law holds fairly well over a wide range of background intensity but it breaks down for low intensities. If Weber’s Law did hold for all values down to zero intensity, Figure 5.7a would show a horizontal straight line, indicating invariance of the just detectable differential intensity (ΔI/I) over all values of I. In fact, there is a marked rise in ΔI/I as the background intensity becomes small. This breakdown is largely explained if we take into account the residual firing of the retinal cells in the absence of light. To the brain, this residual activity is exactly equivalent to a more-or-less constant dim light added to the background. We may estimate its value by plotting ΔI against I, extrapolating back past the origin and reading off the y-axis of the graph (Figure 5.7b). This gives a value for residual activity (or noise) in terms of an equivalent light intensity, which we may call k. There is evidence that this internal noise of the visual system increases with age, and is partly responsible for the gradual loss of all visual discriminations with ageing. Increased neural noise may also affect motor control and memory.

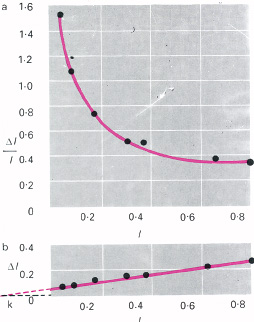
5.7 Weber’s law (ΔI/I = C). (a) Plotting ΔI/I (Incremental Intensity/Intensity) against I gives a horizontal straight line over a wide range of I. But the law breaks down at low intensities (as shown here), when ΔI must be raised to be detected because of the residual neural activity, or ‘noise’, which is present in all communication channels. (b) The breakdown is roughly represented by adding a small constant, k, in the denominator of Weber’s law (ΔI/I + k = C). See text for more details.

The idea that discrimination is limited by noise in the nervous system has far-reaching consequences. It suggests that the old idea of a threshold intensity, above which stimuli need to be if they are to have any effect on the nervous system, is wrong. We now think of any stimulus as having an effect on the nervous system, but only being accepted as a signal of an event when the neural activity is unlikely to be merely a chance increase in the noise level (Figure 5.8). This shows a patch of light serving as a background (I) on which is an added light (ΔI). These two intensities of light give rise to statistically distributed neural impulse rates. The problem for the brain is to ‘decide’ when a given increase is merely noise, and when it is due to the increased intensity of the signal. If the brain accepted any increase from the average activity, then we would often ‘see’ flashes of light that are not in fact present. We thus reach the idea that a statistically significant difference is demanded before neural activity is accepted as representing a signal. The smallest difference (ΔI) we can see is determined not simply by the sensitivity of the receptors of the retina, but also by the difference in neural pulse rates demanded for acceptance as a genuine signal.

When we do see flashes which are not there, these are due to the noise exceeding the demanded significance level.

The brain’s ‘choice’ of the level above which activity is accepted is a matter of trading reliability for sensitivity. There is evidence that this level is to some extent variable, and depends on our ‘set’ to mobilize physiological and psychological resources for a given situation, task, or skill. When we are particularly careful, more information is demanded and sensitivity suffers.

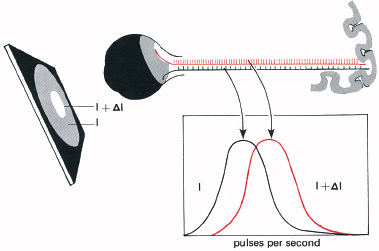
5.8 The statistical problem presented to the brain by the random firing of nerves. When the signal field (I + ΔI) is being discriminated from its dimmer background (I), the pulse rates are not always different, but are distributed as in the graph. So we may ‘see’ a light due to noise, or miss seeing a genuine light when the rate happens to be lower than average. The brain demands a significant difference before accepting neural activity as a signal.

Intensity discrimination applies in this way throughout the nervous system. It applies not only to differences between intensities but also to the absolute limit of detection against darkness, because the absolute threshold is determined by the smallest signal which can be detected reliably against the random background of the neural noise, which is present in the visual brain even when no light enters the eye.

Implications of randomness

Randomness—events occurring unpredictably without apparent cause—has been seized on to rescue the nervous system (or rather our view of it) from being a machine without volition or free will. But this leads us to puzzling questions: How can we be responsible for actions, whether the nervous system is precisely determined, or if it is partly random? It is sometimes argued that randomness allows free will, but how can we be responsible, or take credit, for actions set off by chance events? Here neurology meets philosophy and ethics. The debate continues.

What can nerves signal?—only specific qualities

The founding father of modern physiology, Johannes Muller (1801–58), propounded a fundamental law of nerves: that a nerve fibre can only signal one kind of quality. Known as the Law of Specific Energies (or better, Law of Qualities), it is the key to how sensory systems, such as eyes and ears, are designed through Natural Selection to respond to complex characteristics of objects, including movements and colours.

All sensory nerves are essentially the same, signalling with just the same action potentials—yet they may give very different sensations—of brightness, pain, weight, tickle, sound, … and far more. What we experience depends on which region of brain a nerve is connected to. So if optic nerves were connected to the auditory cortex we would hear lights! The nerves signalling colours are identical, so how can we see different colours? This works because long, medium, and short wavelengths of light stimulate different nerves in the brain. How this works is described in Chapter 7 (shown in Figure 7.3).

For seeing movement, there are circuits which convert complex movements at the eyes to the usual simple electrical pulses of action potentials, which—coming from the movement-detecting circuits—can signal directions and speeds of motion of objects or of the observer. It may need higher and sometimes cognitive (knowledge-based) brain processes to make sense of movement, or any other sensory signals. Let’s look at this in more detail: first for movement, then for colour.