14.6 Dynamisch erzeugte Ausdrücke
Das Einfügen von mathematischen Ausdrücken, die Eingabedaten des Benutzers beinhalten, in bereits geladene Dokumente ist sehr aufwendig. Daher arbeite ich in diesem Abschnitt mit zwei getrennten Dokumenten, dem Objekt location und der Übergabe einer Suchzeichenkette, siehe auch Abschnitt 7.3.2. Im ersten Dokument gibt der Benutzer seine Daten ein und sendet sie mithilfe von JavaScript zum zweiten Dokument. Dort sind sie dann zum Ladezeitpunkt des Dokuments bereits vorhanden und können, wiederum mithilfe von JavaScript, in die mathematischen Ausdrücke eingefügt werden.
Im vorliegenden Beispiel wird das Skalarprodukt von zwei Vektoren mit jeweils drei Komponenten berechnet. Das Skalarprodukt entspricht der Summe der Produkte der zusammengehörenden Komponenten. Im vorliegenden Beispiel ergibt sich:
sp = 3.2 * (-2.6) + (-2.7) * 0.6 + 1.9 * 3.4 = -3.48
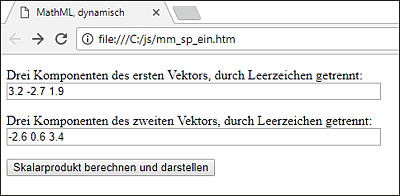
Der Benutzer gibt die Komponenten durch Leerzeichen getrennt ein, siehe Abbildung 14.7. Nach dem Absenden wird das Ergebnis berechnet und der gesamte Ausdruck wird ausgegeben, siehe Abbildung 14.8. Die gezeigte Technik lässt sich natürlich auch auf komplexere Beispiel anwenden. Das könnte ein Skalarprodukt von zwei Vektoren mit einer beliebigen Anzahl von Komponenten sein oder die Multiplikation von zwei Matrizen.
Abbildung 14.7 Eingabe der Komponenten
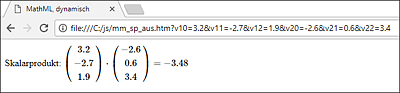
Abbildung 14.8 Berechnung des Ergebnisses und Darstellung
Zunächst das Programm zur Eingabe:
...
<script>
function rechnen()
{
var tx1 = document.getElementById("idVektor1").value;
var v1 = tx1.split(" ");
var tx2 = document.getElementById("idVektor2").value;
var v2 = tx2.split(" ");
if(v1.length != 3 || v2.length != 3)
{
alert("Es müssen jeweils drei Komponenten sein");
return;
}
location.href = "mm_sp_aus.htm"
+ "?v10=" + v1[0] + "&v11=" + v1[1] + "&v12=" + v1[2]
+ "&v20=" + v2[0] + "&v21=" + v2[1] + "&v22=" + v2[2];
}
</script>
</head>
<body>
<p>Drei Komponenten des ersten Vektors, durch Leerzeichen
getrennt:<br><input size="60" id="idVektor1"></p>
<p>Drei Komponenten des zweiten Vektors, durch Leerzeichen
getrennt:<br><input size="60" id="idVektor2"></p>
<p><input type="button" id="idRechnen"
value="Skalarprodukt berechnen und darstellen"></p>
<script>
document.getElementById("idRechnen")
.addEventListener("click", rechnen);
</script>
</body></html>
Listing 14.7 Datei »mm_sp_ein.htm«
Nach der Eingabe und der Betätigung der Schaltfläche werden beide Eingabezeichenketten jeweils anhand des Leerzeichens getrennt und in einem Feld gespeichert. Falls eines der Felder nicht genau drei Elemente beinhaltet, wird das Programm verlassen. Mithilfe der erforderlichen Sonderzeichen ?, & und = sowie der Inhalte der beiden Felder wird die Suchzeichenkette zusammengesetzt und es wird das zweite Dokument aufgerufen.
Es folgt das Programm zur Auswertung:
...
<body>
<script>
var v = new Array();
var suchfeld = location.search.split("&");
for(let i=0; i<suchfeld.length; i++)
{
if(i==0)
suchfeld[0] = suchfeld[0].substr(1);
let teile = suchfeld[i].split("=");
v.push(teile[1]);
}
document.write("Skalarprodukt: <math>");
document.write("<mfenced separators=''> <mtable>");
for(let i=0; i<3; i++)
document.write("<mtr> <mtd> <mn>" + v[i] + "</mn> </mtd> </mtr>");
document.write("</mtable> </mfenced>");
document.write("<mo>⋅</mo>");
document.write("<mfenced separators=''> <mtable>");
for(let i=0; i<3; i++)
document.write("<mtr> <mtd> <mn>" + v[i+3] + "</mn> </mtd> </mtr>");
document.write("</mtable> </mfenced>");
var sp = 0;
for(let i=0; i<3; i++)
sp += v[i] * v[i+3];
document.write("<mo>=</mo> <mn>" + sp.toFixed(2) + "</mn>");
document.write("</math>");
</script>
</body></html>
Listing 14.8 Datei »mm_sp_aus.htm«
Die Suchzeichenkette wird anhand der Sonderzeichen wieder zerlegt. Die insgesamt sechs Komponenten der beiden Vektoren werden in einem Feld gespeichert. Mithilfe der Container <mfenced> und <mtable> werden jeweils die Werte der beiden Vektoren dargestellt. Das Skalarprodukt wird berechnet und ebenfalls dargestellt.