17Bildbearbeitung mit Mathematica
Mit Mathematica erzeugte Grafiken, siehe insbesondere Kapitel 6, sind im Regelfall sog. Vektorgrafiken, welche sich aus grafischen Primitiven (einfachen geometrischen Formen wie Linien, Kreise etc., die sich durch Formeln beschreiben lassen) zusammensetzen und deshalb beliebig in ihrer Größe verändert (skaliert) werden können. Mit den in Abschnitt 6.3 vorgestellten Werkzeugen kann man die Bestandteile einer solchen Vektorgrafik einzeln bearbeiten und anpassen. Gängige Dateiformate für Vektorgrafiken, in die man eine fertige Mathematica-Grafik verlustfrei exportieren kann, vgl. Abschnitt 4.3, sind beispielsweise EPS, PDF und SVG.
Bei sehr komplexen Grafiken wie z. B. Fotografien ist es jedoch schwierig, diese aus einfachen geometrischen Formen zusammenzusetzen. Stattdessen ist es üblich, das fertige Bild als sog. Rastergrafik abzuspeichern (z. B. im Dateiformat BMP, GIF, JPG, PNG, TIF etc.), d. h. über die Grafik wird ein Gitter bestimmter Feinheit gelegt und jeder Gitterzelle (Pixel) wird ein Farbwert zugeordnet. Wenn der Leser eine ihm vorliegende digitale Fotografie sehr stark vergrößert, so wird er recht deutlich diese Rasterung erkennen und es wird offensichtlich, dass Rastergrafiken nicht beliebig vergrößerbar sind. Und genau mit derartigen Rastergrafiken befasst sich die mit Version 7 bei Mathematica eingeführte, und seither mit jeder neuen Version weiter ausgebaute Werkzeugsammlung zur (digitalen) Bildbearbeitung. Auf den ersten Blick mag es überraschend wirken, dass sich gerade eine Mathematik-Software der Bearbeitung von Rastergrafiken (in der Praxis vor allem Fotografien) annimmt. Da aber eine Rastergrafik, wie eben beschrieben, letztlich nichts anderes als eine zweidimensionale Tabelle von Farbwerten ist und diese Farbwerte durch Zahlen oder Zahlenvektoren beschrieben werden, erscheint das Ganze auf den zweiten Blick wesentlich plausibler, vor allem im Hinblick auf die vielen bei Mathematica implementierten Befehle zur Manipulation von Listen, siehe Abschnitt 4.2. Und tatsächlich werden wir in Abschnitt 17.1 erfahren, dass Mathematica eine Rastergrafik intern als mehrdimensionale Liste abspeichert und Bildbearbeitung letztlich heißt, die Listenwerte nach einer bestimmten Vorschrift zu verändern. Die damit erzielbaren Effekte wie die Anpassung von Farben, das Drehen von Bildern oder die Anwendung von Filtern werden wir in den Abschnitten 17.2 bis 17.4 besprechen. Abschnitt 17.5 schließlich zeigt, wie Mathematica beispielsweise zur Texterkennung eingesetzt werden kann.
17.1Das Image-Objekt für Rastergrafiken
Mit Version 7 wurde bei Mathematica das Image-Objekt eingeführt, welches der Speicherung von Rastergrafiken wie etwa digitalen Fotografien dient. Um das Image-Objekt zu verstehen, muss man sich verdeutlichen, dass sich eine Rastergrafik vollständig durch eine zweidimensionale Tabelle von Zahlen oder Zahlenvektoren repräsentieren lässt, welche auf geeignete Weise die Farben der einzelnen Pixel codieren, siehe die Einleitung zu Kapitel 17. Entsprechend besteht ein Image-Objekt auch nur aus drei Bestandteilen:
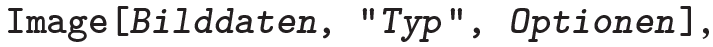
wobei die Bilddaten die genannte Liste von Farbwerten sind. Beginnen wir mit dem einfachsten Fall, der Repräsentation eines Graustufenbildes. In diesem Fall nimmt die Option ColorSpace (Farbraum) den Wert "Grayscale" an und jeder Grauton lässt sich durch eine einzelne Zahl (also ein Farbkanal) des Intervalls [0; 1] beschreiben, siehe das GrayLevel-Kommando in Tab. 6.4. Da nur ein Farbkanal vorliegt, erhält Interleaving („Verschränkung“) den Wert "None" und die zweidimensionale Liste Bilddaten umfasst Zahlen. Betrachten wir ein simples Beispiel:

Ausgegeben wird die grafische Darstellung des Image-Objektes graubild, die Werte der 2 ×3-Liste liste werden als Graustufen interpretiert und in eine Rastergrafik mit 2 Zeilen und 3 Spalten übersetzt. Durch graubild //InputForm erhält der Leser die vollständige, oben beschriebene, interne Repräsentation des Image-Objektes graubild, wogegen man die drei Bestandteile einzeln durch die Kommandos ImageData[graubild], ImageType[graubild] bzw. Options[graubild] abfragt. Speziell ergibt

da wir liste mit Dezimalbrüchen gefüllt hatten, was als Zahl vom Typ Real interpretiert wird, siehe Abschnitt 5.1. Alternativ hätten wir liste auch mit Ganzzahlen n zwischen 0 und 255 (Typ "Byte") oder gar zwischen 0 und 65 535 (Typ "Bit16") füllen können, dann würden die Graustufen n/ 255 bzw. n /65 535 angezeigt. Der Leser führe z. B.

aus. Für den Spezialfall des Schwarzweißbildes gibt es den Typ "Bit", die Bilddatenliste füllt man nur mit Nullen (schwarz) und Einsen (weiß).
Die Bildgröße ist durch die Dimensionierung der Bilddatenliste festgelegt, kann also mit Hilfe von Dimensions erfragt werden. Speziell für Image-Objekte gibt es aber auch den Befehl ImageDimensions:

Im zweiten Fall wird zuerst die Breite (=Spaltenzahl) und dann die Höhe (=Zeilenzahl) ausgegeben. Die Anzahl der Farbkanäle (im momentanen Beispiel also 1) erfragt man mit ImageChannels. Das Seitenverhältnis muss man seit Version 8 nicht mehr manuell aus obigen Abmessungen berechnen, sondern kann es direkt via ImageAspectRatio abfragen:
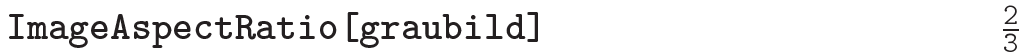
Analog fragt man den Farbraum via ImageColorSpace ab. Auch muss man seit Version 8 nicht mehr die Eigenschaften einzelner Pixel über den Umweg mit ImageData abfragen, sondern verwendet direkt PixelValue oder ImageValue:

Der Unterschied erklärt sich aus einer unterschiedlichen Indizierung der Pixel: Beide Befehle starten mit dem Pixel unten links, aber ImageValue beginnt die Zählung mit (0.5, 0.5) im Zentrum dieses Pixels, PixelValue dagegen mit (1, 1).
Wenden wir uns nun Farbbildern zu. Hier stehen uns die drei Farbräume "RGB" mit 3 Farbkanälen, "CMYK" mit 4 Farbkanälen und "HSB" mit 3 Farbkanälen zur Verfügung, siehe auch Tabelle 6.4. Entsprechend sind hier nun die Farbwerte durch drei- oder vierdimensionale Zahlenvektoren festzulegen. Tatsächlich kann man optional bei allen Farbräumen (auch "Grayscale") optional noch einen weiteren Farbkanal hinzufügen (entsprechend erhöht sich die Dimensionalität der Zahlenvektoren um 1), nämlich einen Transparenzwert zwischen 0 und 1, siehe die Beschreibung des Opacity-Kommandos und die Diskussion der AlphaChannel-Befehle in Abschnitt 17.4.
Exemplarisch betrachten wir den Fall des weit verbreiteten Farbraums " RGB", ein Beispiel für "HSB" zeigt Bemerkung 20.4.1. Hier geben die drei Farbkanäle r, g, b ϵ [0; 1] den Anteil der drei Farben Rot, Grün und Blau bei der (additiven) Farbmischung wieder, z. B. ergibt (r, g, b) = (1, 0, 0) die Farbe Rot, (0, 0, 0) Schwarz, (0.5, 0.5, 0.5) Grau, (1, 1, 1) Weiß und (1, 1, 0) Gelb. Als Beispiel führe der Leser folgende Zeilen aus, wobei die Bilddatenliste nun lauter dreidimensionale Vektoren umfasst:

Die Ausführung von ImageChannels[farbbild] ergibt 3, die Anzahl der Farbkanäle und somit Dimension der Farbvektoren, ferner hat nun Interleaving den Wert "True". Auch ohne explizite Angabe des Typs "Real"wäre dieser wieder automatisch erkannt worden; alternativ hätten wir die Farben auch wieder durch Ganzzahlwerte (Typen "Byte" oder "Bit16") codieren können.
Bevor wir uns einem praxisnäheren Beispiel zuwenden, sollen noch kurz zwei weitere Optionen des Image-Objekts vorgestellt werden, die nur die grafische Ausgabe im Notebook beeinflussen. Durch ImageSize -> n wird festgelegt, dass das Bild mit einer Breite von n Bildpunkten dargestellt wird, durch Magnification -> m, dass das Bild um den Faktor m gegenüber der eigentlichen Dimension vergrößert wird. Der Leser probiere
In der Praxis wird man Mathematicas Fähigkeiten zur Bildbearbeitung wohl meist auf digitale Fotografien anwenden wollen. Prinzipiell sind dann also die folgenden Schritte zu durchlaufen:
- Import der Bilddatei in ein Image-Objekt mit Hilfe des Import-Befehls aus Abschnitt 4.3 (ggf. unter Angabe des vorliegenden Bildformats);
- Bearbeitung des Image-Objekts;
- Export des Image-Objekts in eine Bilddatei mit Hilfe des Export-Befehls aus Abschnitt 4.3 (ggf. unter Angabe des gewünschten Bildformats).
Betrachten wir als Beispiel ein sehr bekanntes Testbild, „Lena“, welches bei Mathematica im Unterordner \Documentation\English\System\ExampleData mitausgeliefert wird:

Seit Version 7 werden Bilddateien automatisch in ein Image-Objekt importiert (nachprüfbar via ImageQ). Prinzipiell betrifft dies auch Beispiel 4.3.1, wenn auch nach außen nicht unmittelbar sichtbar. Fragt der Leser nun, wie oben beschrieben, die Eigenschaften von lena ab, zeigt sich, dass ein RGB-Bild vorliegt (mit 3 Farbkanälen) und die Farben via "Byte" codiert sind (Konsequenz: Es gibt maximal 256·256·256 = 224 Farben, also ein 24 Bit-Bild.). Ferner ist das Bild 150 Pixel breit und 116 Pixel hoch – durch starke Vergrößerung wird dieses Raster deutlich sichtbar, der Leser probiere etwa Image[lena, Magnification -> 5].
In den folgenden Abschnitten 17.2 bis 17.4 werden wir lernen, wie man das Bild lena bearbeiten kann; nach Abschluss dieser Bildkorrekturen können wir das fertige Bild z. B. ins JPG-Format wie folgt exportieren: Export["C:\\...\\lena_korr.jpg", lena].
Tatsächlich besteht seit Version 11 auch die Möglichkeit, mittels ImageGraphics aus der Image-Grafik eine Vektorgrafik (Typ Graphics) zu erzeugen. Beispielsweise reduziert ImageGraphics[lena,4] lena auf vier Farben und rekonstruiert anschließend Flächen gleicher Farbe durch Umrandung mit Linien.
Bemerkung 17.1.1. Zu Beginn des Abschnitts 17.1 hatten wir die Bilddatenliste des Image-Objekts direkt eingegeben, bei lena wurde sie durch den Import-Befehl erzeugt. Tatsächlich kann man aus nahezu jedem Mathematica-Kommando heraus ein Image-Objekt erzeugen, indem man das Kommando mit Image[·] oder gleich Rasterize[·] umschließt (im ersten Fall wird im Hintergrund Rasterize zur Erzeugung des Image-Objekts ausgeführt). So können wir z. B. eine mit Plot erzeugte Grafik oder selbst eine Formel in eine Rastergrafik vom Typ Image umwandeln, wobei wir via RasterSize -> {b,h} die Breite und Höhe des Punktrasters bestimmen. Der Leser teste

Abschließend sei erwähnt, dass Mathematica seit Version 9 sogar die Möglichkeit bietet, dreidimensionale Bilder darzustellen bzw. zu bearbeiten. Grundlage dazu stellt der Befehl Image3D dar, der als Argument entsprechend eine dreidimensionale Bilddatenliste erwartet.
17.2Farben korrigieren
In diesem und den folgenden Abschnitten wollen wir uns mit lena beschäftigen, einem RGB-Bild mit den Abmessungen 150×116 Pixel, und verschiedene Möglichkeiten der Bildbearbeitung vorführen. Zu Beginn stehen dabei Eingriffe in die Farben des Bildes auf dem Programm, siehe die Zusammenfassung in Tab. 17.1. Alle vorgeführten Änderungen führen wir dabei nicht dauerhaft durch; wenn der Leser später seine privaten Urlaubsfotos wirklich dauerhaft korrigieren will, müsste er alle Programmzeilen nach folgendem Schema ändern: Statt Korrektur[bild] ist bild=Korrektur[bild] auszuführen, d. h. das vorherige Image-Objekt wird überschrieben.
Bemerkung 17.2.1. Gleich mit der Einführung von Version 7 wurden einige der im Folgenden zu besprechenden Funktionen zur Bildbearbeitung auch über jenes PopUp-Menü zur Verfügung gestellt, welches erscheint, wenn man mit der rechten Maustaste direkt auf das zu bearbeitende Bild klickt. Führt der Leser dies bei lena aus, so gibt es beispielsweise den Eintrag Adjust Image, nach dessen Aufruf der in Abb. 17.1 gezeigte Dialog erscheint, mit dessen Hilfe man u. a. die Helligkeit des Bildes ändern kann.
Mit Version 9 wurden dann eine weitere Assistenzfunktion eingeführt, welche an die aus Abschnitt 3.3 bekannte Vorschlagsleiste erinnert. Diese erscheint durch Anklicken des Bildes mit der linken Maustaste und lässt sich durch Klick auf more noch erweitern, siehe Abb. 17.2. Durch das verfügbare „Crop Tool“ lässt sich beispielsweise das Bild einfach mit Hilfe der Maus zuschneiden. •
Der einfachste Eingriff in das Farbsystem besteht darin, den Farbraum zu ändern. Dies leistet der Befehl ColorConvert, bei dem man als zweites Argument den Zielraum angibt, also z. B. ColorConvert[lena, "Grayscale"], wodurch wir ein Graustufenbild erhalten. Noch extremer wirkt sich Binarize aus,
Abb. 17.1. Dialog zur Bearbeitung von Farbeigenschaften eines Bildes.
Abb. 17.2. Der mit Version 9 eingeführte Assistent zur Bildbearbeitung.

es resultiert ein reines Schwarzweißbild (Typ "Bit"), was man mit Hilfe von Binary-ImageQ prüft. Ein anderer, elementarer Eingriff, der zur Reduzierung des Speicherplatzes eingesetzt werden kann, besteht darin, die Anzahl der verschiedenen Farben oder Graustufen zu reduzieren. Dazu gibt man als zweites Argument bei ColorQuantize einfach die gewünschte Farbzahl an, etwa

Tab. 17.1. Farbkorrektur beim Image-Objekt bild (seit Version 7).
| Befehl | Beschreibung | |
ColorConvert[bild, "Farbraum_neu] |
Wandelt alten Farbraum von bild in den neuen um. | |
Binarize[bild] |
Erzeugt Schwarzweiß-Variante von bild. | |
ColorQuantize[bild, n] |
Reduziert Anzahl der Farben/Grauwerte auf n. | |
ColorNegate[bild] |
Invertiert Farben von bild. | |
Lighter[bild, h] |
Hellt Bild um h · 100% auf. | |
Darker[bild, h] |
Dunkelt Bild um h · 100% ab. | |
ImageAdjust[bild, {k,h,g}] |
Änderung von Kontrast und Helligkeit um k·100%bzw. h ·100% sowie eine Gamma-Korrektur mit Exponent g. Keinerlei Änderung bei k = h = 0 und g = 1. | |
Bei nur acht verschiedenen Farben ist ein deutlicher Qualitätsverlust sichtbar. Um die Auswirkungen interaktiv studieren zu können, führe der Leser folgende Zeile aus, siehe auch Abschnitt 16.5:

Die Farben invertiert man (d. h. aus Positiv wird Negativ u. u.) via ColorNegate:

Dies ist letztlich nur ein spezieller Fall von Anwendung einer Funktion f : [0; 1] → [0; 1] auf die einzelnen Farbwerte (nämlich der Funktion f (x) = 1 −x). Ganz allgemeine Funktionen kann man auf die Farbwerte via ImageApply anwenden, und seit Version 8 auf die Pixelkoordinaten via ImageTransformation. Ein simples Beispiel wäre etwa:

Man beachte die umgekehrte Reihenfolge der Argumente. Neben vorgefertigten Funktionen kann man hierbei auch selbst definierte reine Funktionen, siehe Abschnitt 7.1.1, einsetzen. Seit Version 11 ist ImageApply fast schon wieder hinfällig, denn nun kann man derartige Funktionen direkt auf das Image-Objekt anwenden, z. B. Sqrt[lena]. Bei einer Helligkeitskorrektur mit Lighter oder Darker, siehe Tabelle 17.1, werden die RGB-Farbwerte einfach mit 1 + h bzw. 1 − h multipliziert, bei einer Gamma-Korrektur via ImageAdjust mit g potenziert. Im letztgenannten Fall ändern sich Helligkeit und Kontrast simultan. Eine alleinige Gamma-Korrektur mit Exponent 1.8 führt zu deutlich satteren Farben:

Seit Version 8 kann man mittels ImageClip pro Farbkanal Werte jenseits vorgebbarer Schranken durch die jeweilige Schranke ersetzen lassen, z. B. ImageClip[lena, {0.1,0.9}].

Ausblick: Für fortgeschrittene Bildbearbeiter bietet Mathematica an, mittels ImageHistogram ein Histogramm der Farb- bzw. Grauwerte eines Image-Objekts zu erstellen, oder die zugehörige Häufigkeitstabelle mit Hilfe von ImageLevels einzusehen. Detaillierte Informationen hierzu und zu weiteren Farbkorrekturen bietet der Hilfeeintrag guide/ColorProcessing.
17.3Bilder zuschneiden und justieren
Im Gegensatz zu den Optionen ImageSize und Magnification eines Image-Objekts wird durch Anwendung des Befehls ImageResize das Bild nicht nur in der neuen Größe angezeigt, sondern tatsächlich auch die Zahl der Pixel angepasst. Deutlich wird dies durch folgendes Beispiel, bei dem sich die Pixelzahlen in beiden Richtungen verdreifachen:

Um lena um 30 Grad im Uhrzeigersinn zu drehen, führen wir aus:

Um lena dagegen so zu spiegeln, dass die obere Seite des Bildes nach links zeigt, führen wir aus:
Tab. 17.2. Eingriffe in die Bildgeometrie des Image-Objekts bild (seit Version 7).
| Befehl | Beschreibung |
ImageResize[bild,b] |
Ändert Bildbreite verzerrungsfrei zu b Pixeln. Um ein verkleinertes Vorschaubild der Breite b zu erzeugen, kann man auch verwenden: Thumbnail[bild,b]. |
ImageRotate[bild, x Degree] |
Dreht bild um x Grad im Gegenuhrzeigersinn. |
ImageReflect[bild, Seite1 -> Seite2] |
Spiegelt bild so, dass Seite1 bei Seite2 landet. Mögliche Spezifikationen: Top, Bottom, Left, Right. |
ImageCrop[bild, {b,h}] |
Schneidet gleichmäßig Punkte von links und rechts sowie von oben und unten ab, so dass Bildgröße b × h Pixel resultiert. Durch optionale Seitenangaben einseitiges Abschneiden. |
ImageTake[bild, {y1,y2}, {x1,x2}] |
Entnimmt Ausschnitt von x1 nach x2 in X-Richtung und y1 bis y2 in Y-Richtung. |
ImagePad[bild, Breite, Farbe] |
Erzeugt Rand um bild in vorgegebener Breite und Farbe. |

Zum Zuschneiden von Bildern bietet Mathematica die Befehle ImageCrop und Image-Take, siehe Tab. 17.2. Soll lena etwa auf 120 × 80 Pixel gestutzt werden, wobei nur von rechts und von oben weggeschnitten werden darf, so führt man aus:

Ist man dagegen gezielt am Ausschnitt mit der linken, unteren Ecke (x1, y1) = (70, 50) und der rechten, oberen Ecke (x2, y2) = (100, 100) interessiert, verwendet man folgenden Code:
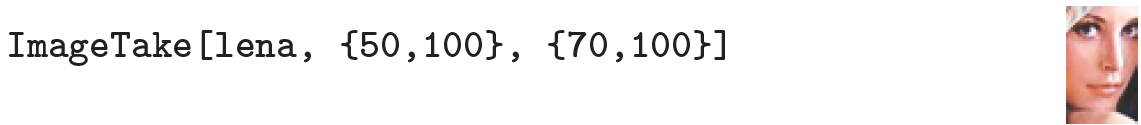
Seit Version 8 kann man den Ausschnitt auch mit den Pixelkoordinaten der Ecken spezifizieren (links unten ist (0, 0)), wenn man stattdessen ImageTrim verwendet, im konkreten Beispiel also ImageTrim[lena, {{69,16}, {100,67}}] bzgl. der linken, unteren Ecke (x1, y1) = (69, 16).
Einen schwarzen Rand mit 5 Pixeln Breite erzeugt man dagegen folgendermaßen:

Seit Version 8 kann man die Ausmaße eines Randes mit BorderDimensions abfragen:

Die gezeigten Transformationen wie Drehungen, Spiegelungen, Randerzeugungen, etc. kann man auch mit Hilfe des viel mächtigeren, seit Version 8 verfügbaren Befehls ImageTransformation realisieren, vgl. Abschnitt 17.2.

Ausblick: Der eben besprochene Befehl ImagePad ist noch weitaus mächtiger und erlaubt es beispielsweise, den erzeugten Rand aus Bildern zusammenzusetzen. Detaillierte Informationen hierzu und zu verwandten Befehlen bietet der Hilfeeintrag guide/BasicImageManipulation.