CHAPTER 8
Quantitative Comparison Strategies
Study this chapter to learn about:
Quantitative Comparison Format
Though the choices on the test do not state it explicitly, your concern is whether there is a constant relationship between the quantities. Specifically, if you can determine that in some instances, Quantity A is greater, but in other instances, Quantity B is greater, then the answer is Choice D: the relationship cannot be determined. To choose A, B, or C, you need to show that the given relationship is always true. Let’s look at a sample question:
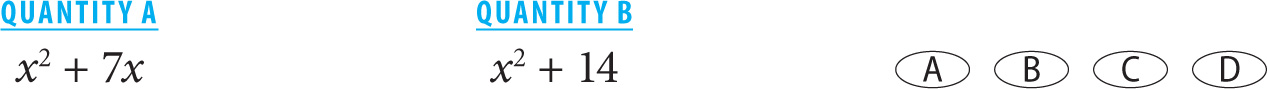
Choose:
 if Quantity A is greater
if Quantity A is greater
 if Quantity B is greater
if Quantity B is greater
 if the two quantities are equal
if the two quantities are equal
 if the relationship between the two quantities cannot be determined
if the relationship between the two quantities cannot be determined
SOLUTION: If x is greater than 2, then Quantity A is always greater. For example, if x = 3, then the value of Quantity A is 30, and the value of Quantity B is 23. Thus you can eliminate choices B and C. Why? Because if Quantity A is greater in this instance, then it is not possible for Quantity B to always be greater or for the two quantities to always be equal. Now that the choice is between A and D, determine whether Quantity A will always be greater. Substitute 1 for x. Quantity A = 8, and Quantity B = 15. In this case, Quantity B is greater. Since different values yield different relationships, the relationship cannot be determined, so the correct answer is Choice D.
Strategy: Play Devil’s Advocate
The example question illustrates the type of reasoning fundamental to Quantitative Comparison questions. The best way to think about the quantities is to ask yourself: “Will this relationship always be true?” Often, it will turn out that the value in one column is sometimes larger than the value in the other column, and sometimes smaller than the value in the other column. In such cases, the answer will be D, not A or B. For the answer on Quantitative Comparison to be A, B, or C, that relationship must always be true. If you find contradictory relationships between the columns, then the answer is Choice D.
As you might expect, many tougher Quantitative Comparison questions will expect you to identify situations in which there is an indeterminate relationship between the columns. To identify that this is the case, your ultimate goal should be to arrive at Choice D! For example, if you determine that Quantity A is greater in one situation, your next step should be to determine whether there are other situations in which the relationship between the two quantities is different. Look at the following examples:

Choose:
 if Quantity A is greater
if Quantity A is greater
 if Quantity B is greater
if Quantity B is greater
 if the two quantities are equal
if the two quantities are equal
 if the relationship between the two quantities cannot be determined
if the relationship between the two quantities cannot be determined
SOLUTION: When x = 1, the value of Quantity A = 3(26) = 78. In this case, the value of Quantity A is greater. Since it is not possible for Quantity B to always be greater or for the two quantities to always be equal, you can eliminate choices B and C.
Now that you have determined that Quantity A is sometimes greater, the next step is to see whether any values will provide a counterexample to that relationship. For reasons that will be further explained in the next chapter, a good number to choose is 0.
When x = 0, the value of Quantity A will equal 3(25) = 75. In this case, the values in the two columns are equal. You have now found a counterexample to the relationship that was obtained when x = 1. Since different values for x give different relationships for the columns, the relationship cannot be determined. The answer is Choice D.

Choose:
 if Quantity A is greater
if Quantity A is greater
 if Quantity B is greater
if Quantity B is greater
 if the two quantities are equal
if the two quantities are equal
 if the relationship between the two quantities cannot be determined
if the relationship between the two quantities cannot be determined
When y = 1, the value of Quantity A = 17, and the value of Quantity B = 20. Thus in this case, Quantity B is greater, and the answer must be Choice B or D. When y = 0, Quantity A = 0, and Quantity B = 0. In this case, the columns are equal. You have found contradictory relationships, so the answer is D.
Strategy: Plug In Numbers with Interesting Properties
When plugging in numbers for variables in Quantitative Comparison questions, it might be difficult to determine where to start. After all, there are literally infinite possibilities! However, because your ultimate goal is to prove Choice D, you should choose numbers that will most likely give you contradictory relationships. The best numbers to choose will therefore be numbers that have interesting properties. Of all numbers, the best to choose are 0,1, and –1.
However, the test-makers will throw nuances at you that will force you to test other types of numbers. The following is a list of other types of numbers you should consider when plugging in numbers in Quantitative Comparisons:
 Numbers less than –1
Numbers less than –1
 Numbers between –1 and 0 (i.e., negative proper fractions)
Numbers between –1 and 0 (i.e., negative proper fractions)
 Numbers between 0 and 1 (i.e., positive proper fractions)
Numbers between 0 and 1 (i.e., positive proper fractions)
 Numbers greater than 1
Numbers greater than 1
Though it might seem like plugging in so many different values will be time-consuming, it’s important to remember the following:
 You only need to find one contradictory relationship to prove Choice D.
You only need to find one contradictory relationship to prove Choice D.
 Many Quantitative Comparison questions provide constraints on the variables that will eliminate some of the types of numbers mentioned previously.
Many Quantitative Comparison questions provide constraints on the variables that will eliminate some of the types of numbers mentioned previously.
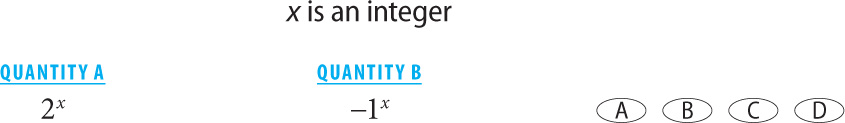
SOLUTION: Let x = 1. When x = 1, the value of Quantity A will be 21 = 2, and the value of Quantity B will be –11 = –1. In this case, the value of Quantity A is greater, so the answer must be A or D. Now plug in a new value for x. Since x is an integer, you cannot choose a fraction. A smart number here would be the strangest-behaving integer: 0. When x = 0, the value of Quantity A will be 20 = 1, and the value of Quantity B will be –10 = 1. In this case, the values of the two quantities are equal. Since different values give different relationships between the quantities, the relationship cannot be determined. The answer is Choice D.
Strategy: Make Comparisons, Not Calculations
When doing Quantitative Comparison questions, it is essential to step out of the problem-solving mind-set that you’re accustomed to. Quantitative Comparison questions are designed to test mathematical intuition and quick, efficient mathematical reasoning, and this fact should dictate your approach. One key consequence of this fact is that you should always look at both columns before you begin any calculations. In many situations, doing so will help you reduce or even completely avoid any calculations. Look at the following examples:

SOLUTION: You want to not only get this question right, but to do so quickly. With your calculator, you can of course get a value for both columns. But before diving into the calculations, look to see whether you can make a quick comparison. You should notice that 0.98 > 0.92 and that 576 > 574. Since both values in Quantity A are greater than both values in Quantity B, the product of the two values in Quantity A must be greater. Thus the answer is A.
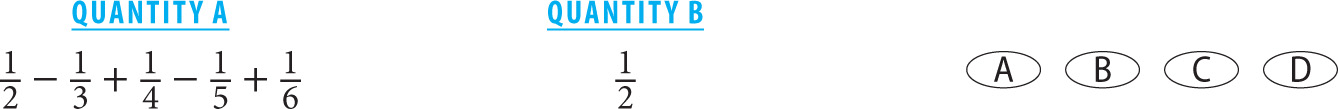
SOLUTION: Your first step should be to look at both columns. Since Quantity B is  , you should look to see whether adding and subtracting the fractions in Column A will make the ultimate value greater than or less than
, you should look to see whether adding and subtracting the fractions in Column A will make the ultimate value greater than or less than  . Again, you can do the calculations here, but a better use of time is to look at the different fractions being added in pairs.
. Again, you can do the calculations here, but a better use of time is to look at the different fractions being added in pairs.  is greater than
is greater than  , so subtracting
, so subtracting  from a number and then adding
from a number and then adding  will result in a value smaller than the original number.
will result in a value smaller than the original number.  is greater than
is greater than 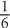 , so subtracting
, so subtracting  from a number and then adding
from a number and then adding 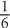 will also result in a number smaller than the original value. Thus the cumulative result of the operations in Quantity A will be a value less than
will also result in a number smaller than the original value. Thus the cumulative result of the operations in Quantity A will be a value less than  , and the correct answer is Choice B.
, and the correct answer is Choice B.
Strategy: Make the Columns Comparable
An extension of the preceding principle is the following: if the columns do not appear comparable, manipulate one or both columns to make the comparison simpler. Look at the following question:
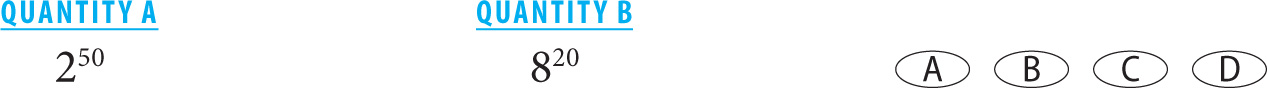
As it stands, it would not be possible to draw a comparison between the two quantities in a reasonable amount of time. So instead of attempting to calculate, you should attempt to manipulate one or both columns to make the comparison easier. It is important to keep in mind that when manipulating the columns, you are not changing their values. You are simply rewriting them to make the question simpler. In this case, you should manipulate the value in Quantity B to have a base of 2:
(23)20 = 260
Now the values in both quantities are expressed with a base of 2. To determine which quantity is greater, you simply need to determine which quantity has the larger exponent. In this case, the exponent in Quantity B is greater, and the correct answer is thus Choice B.
Strategy: Use the Implied Relationship Between the Quantities
The nature of Quantitative Comparisons is that there exists an implied algebraic relationship between the two quantities. Because of this fact, when you are working with Quantitative Comparisons, you can perform the same operations to both columns, as long as the operation satisfies one of the following conditions:
 Add or subtract the same value or variable to both columns.
Add or subtract the same value or variable to both columns.
 Divide or multiply both columns by a positive value or variable.
Divide or multiply both columns by a positive value or variable.
 Square or square root both columns, as long as you know that all the values in the columns are positive.
Square or square root both columns, as long as you know that all the values in the columns are positive.
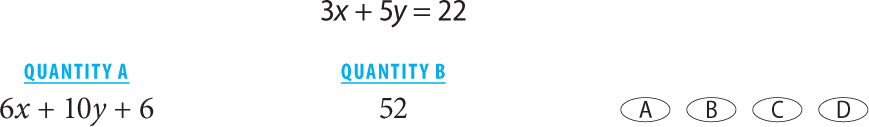
SOLUTION: Since the given information concerns the sum 3x + 5y, you should manipulate the two columns to isolate 3x + 5y. First, subtract 6 from both columns:
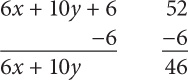
Next divide both columns by 2:
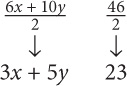
Since you are told that 3x + 5y = 22, Quantity B is greater.
Strategy: Work Backward
In some Quantitative Comparison questions, you will be asked to compare an unknown to a given value. In these situations, it is often helpful to use the given value as a baseline for comparison. Look at the following examples:
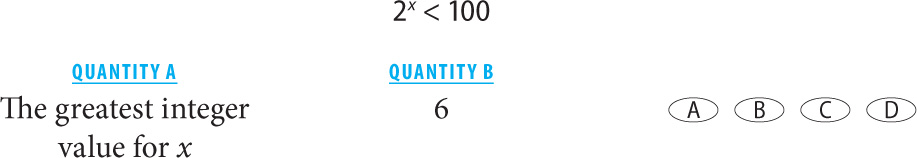
SOLUTION: Instead of solving for x, you should see whether the value in Column B will satisfy the given information, and make inferences about x from that relationship. If x = 6, then 26 = 64. Since 64 < 100, you know that 6 is a possible value for x. The correct answer is Choice C or D. Now to determine whether you can identify a counterexample, plug in an integer value larger than 6 for x. If x = 7, then 2x = 27 = 128. 128 > 100, so 7 is too large of a value for x. Thus the greatest integer value for x must be 6. The answer is Choice C.

SOLUTION: Doing this question algebraically is certainly an option, but an alternative approach is to plug the value in Quantity B into the original equation and see how it compares to the given information. If the original price of the shirt was $120, then after a 20% reduction, the price of the shirt would be 0.8(120) = $96. Since the reduced price of the shirt must be more than $100, the original price of the shirt must be more than $120. Thus the value in Quantity A is greater.
Exercise: Quantitative Comparison Questions
1. 
2. 
3. 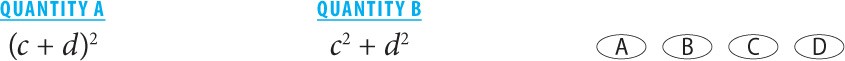
4. 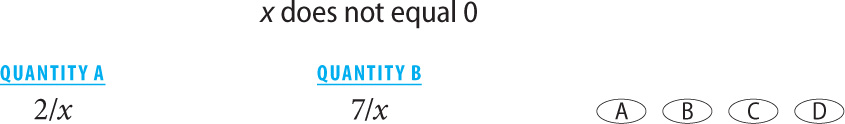
5. 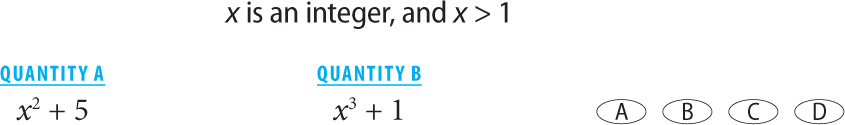
6. 
7. 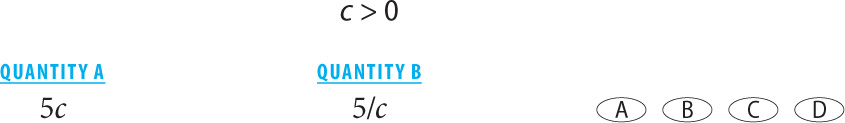
8. 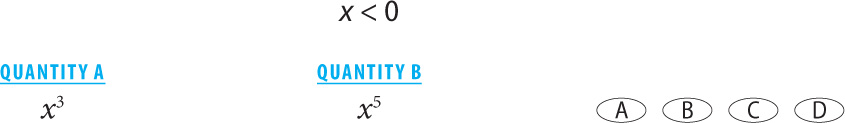
9. 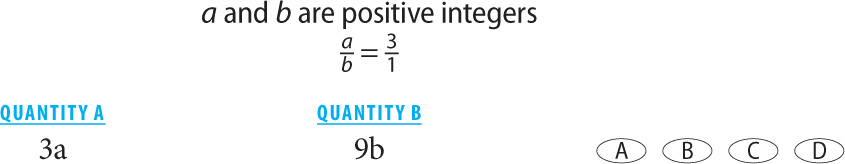
10. 
Set A contains all the integers from 1–1,000, inclusive.
11. 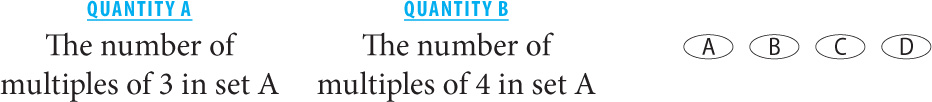
The radius of Circle O is greater than 2.
12. 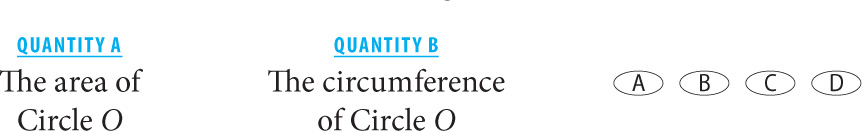
x and y are integers such that x > y > 0 and x + y is even
13. 
14. 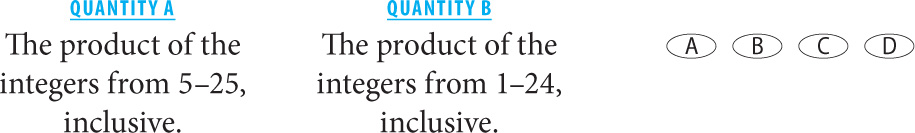
15. 
A merchant paid $200 for a coat. His profit on the coat was more than 20%.
16. 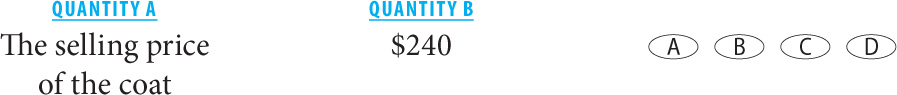
Exercise Answers
1. D Plug in numbers:

Since there are contradictory relationships between the columns, a relationship cannot be determined.
2. A Subtract a from both quantities. Quantity A thus equals: (a + 7) – a = 7. Quantity B thus equals: (a – 12) – a = –12. 7 > –12, so Quantity A is greater.
3. D Substitute values for c and d.

Since a relationship cannot be determined, the correct answer is D.
4. D Substitute values.
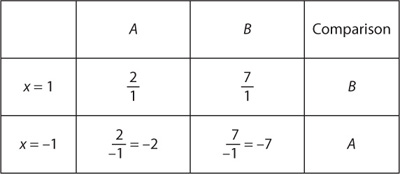
When x is positive, Quantity B is greater. When x is negative, Quantity A is greater. The relationship cannot be determined.
5. D Since you are given a range for x, you should choose extremes. Let x = 2, and then let x = 10.

Since different values yield different relationships between the quantities, the correct answer is D.
6. C Make the columns comparable by manipulating Quantity A to be a fraction. 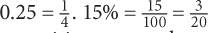 . The value in Quantity A is thus
. The value in Quantity A is thus 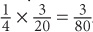 . The two quantities are equal.
. The two quantities are equal.
7. D Manipulate the quantities:
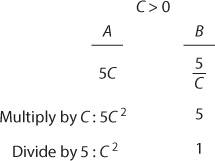
Note that you were able to multiply by c because you were told that c > 0.
The comparison is c2 versus 1. If c > 1, then Quantity A is greater. If c is a fraction, then Quantity B is greater.
8. D Choose values for x. If x = –1, then the two quantities are equal. If x = –2, then Quantity A = –8, and Quantity B = –32, in which case Quantity A is greater. Since a relationship cannot be determined, the correct answer is D.
9. C First, cross-multiply the given proportion: 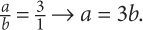 Next, to make the quantities comparable, substitute 3b for a in Quantity A. Thus Quantity A = 3(3b) = 9b. The values in the quantities are equal.
Next, to make the quantities comparable, substitute 3b for a in Quantity A. Thus Quantity A = 3(3b) = 9b. The values in the quantities are equal.
10. B Don’t calculate! If the diameter of the circle in Quantity B is 40, then the radius of that circle is  (40) = 20. Since the radius of the circle in Quantity B is greater than the radius of the circle in Quantity A, the area of the circle in Quantity B must be greater.
(40) = 20. Since the radius of the circle in Quantity B is greater than the radius of the circle in Quantity A, the area of the circle in Quantity B must be greater.
11. A Both quantities concern the same set. Within any finite set of numbers, there are fewer multiples of 4 than there are multiples of 3. For example, from 1–12, inclusive, there are four multiples of 3 (3, 6, 9, 12), but only three multiples of 4 (4, 8, 12). Thus Quantity A is greater.
12. A Since you are not given a value for the radius, assign a variable. Let the radius = r. In terms of r, Quantity A = πr2. In terms of r, Quantity B = 2πr. Now manipulate the columns to simplify the comparison:
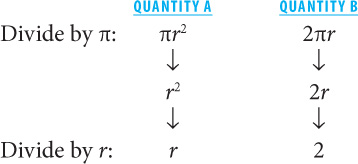
Since you are told that the radius is greater than 2, Quantity A must be greater.
13. A Substitute values for x and y that satisfy the given information. Let x = 13 and y = 1. In this case, both are integers, x > y > 0, and their sum is even. Now, substitute these values into Quantity A: 13 – 1 = 12. In this case, Quantity A is greater. Choose new values for x and y that satisfy the given information. To prove Choice D, you want to make the difference between x and y as small as possible. Let x = 3 and y = 1. In this case, all the restrictions are satisfied. 3 – 1 = 2. Thus Quantity A is still greater.
14. A Don’t calculate! Identify what the quantities have in common. Since both quantities share the product (5 × 6 × 7 × … 24), you can divide both quantities by the product of the integers from 5–24, inclusive. After doing so, the real comparison becomes:
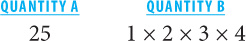
1 × 2 × 3 × 4 = 24. Thus Quantity A is greater.
15. B Since the comparison is between a value and a variable, you can work backward. If x = 7, then x2 = 49 < 36. Thus to satisfy the given inequality, x must be less than 7.
16. A Since the quantities compare a value to an unknown, work backward with Quantity B. If the selling price of the coat were $240, then the profit on the coat would be 240 – 200 = 40. Now determine 40 as a percentage of 200. 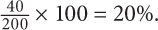 Since you know that the profit must be greater than 20%, the selling price must have been greater than $240.
Since you know that the profit must be greater than 20%, the selling price must have been greater than $240.
 Quantitative Comparison format
Quantitative Comparison format Strategy: Play devil’s advocate
Strategy: Play devil’s advocate Strategy: Plug in numbers with interesting properties
Strategy: Plug in numbers with interesting properties Strategy: Make comparisons, not calculations
Strategy: Make comparisons, not calculations Strategy: Make the columns comparable
Strategy: Make the columns comparable Strategy: Use the implied relationship between the quantities
Strategy: Use the implied relationship between the quantities Strategy: Work backward
Strategy: Work backward if Quantity A is greater
if Quantity A is greater if Quantity B is greater
if Quantity B is greater if the two quantities are equal
if the two quantities are equal if the relationship between the two quantities cannot be determined
if the relationship between the two quantities cannot be determined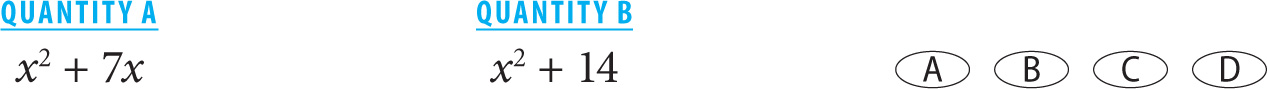
 if Quantity A is greater
if Quantity A is greater if Quantity B is greater
if Quantity B is greater if the two quantities are equal
if the two quantities are equal if the relationship between the two quantities cannot be determined
if the relationship between the two quantities cannot be determined

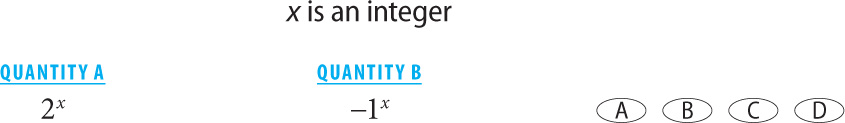

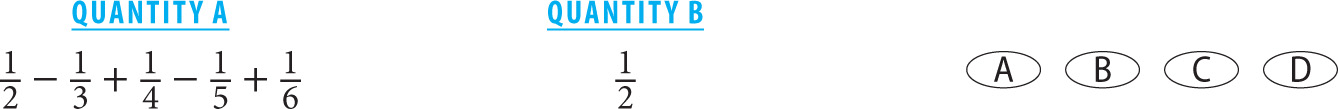
 , you should look to see whether adding and subtracting the fractions in Column A will make the ultimate value greater than or less than
, you should look to see whether adding and subtracting the fractions in Column A will make the ultimate value greater than or less than  is greater than
is greater than  , so subtracting
, so subtracting  is greater than
is greater than 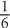 , so subtracting
, so subtracting 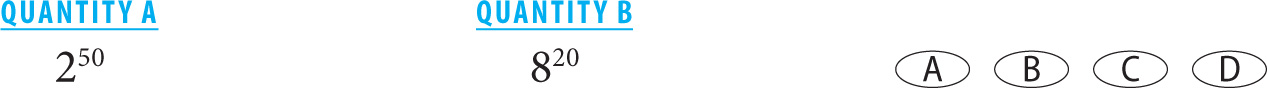
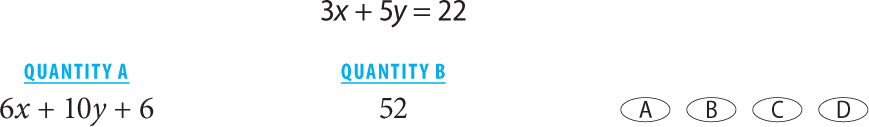
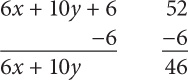
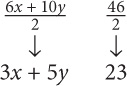
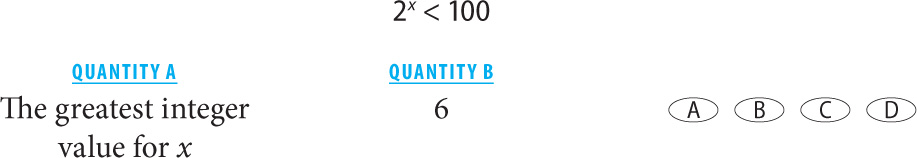



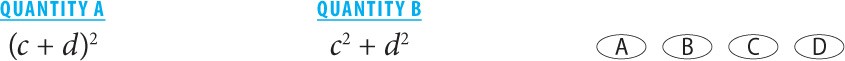
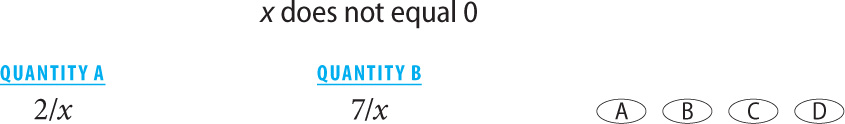
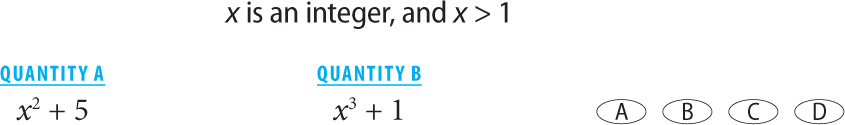

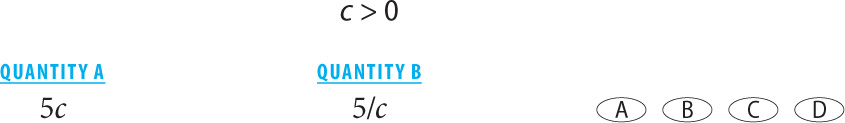
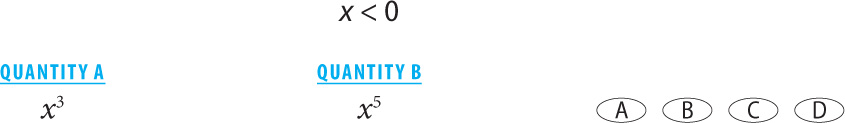
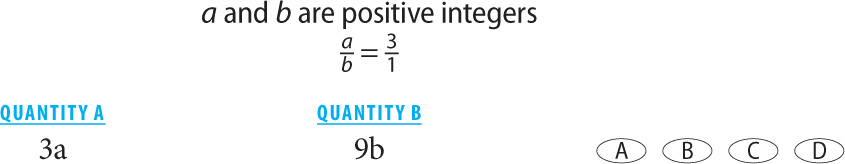

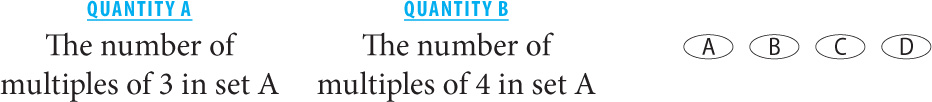
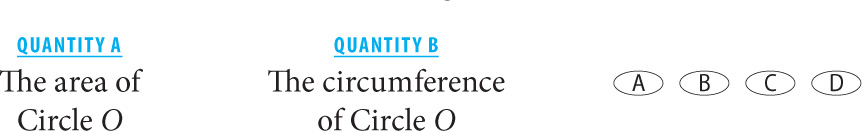

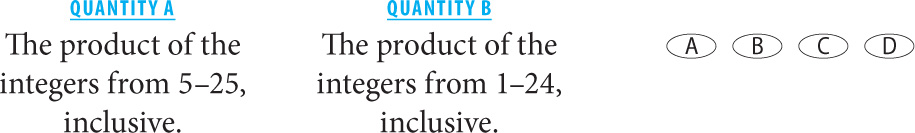

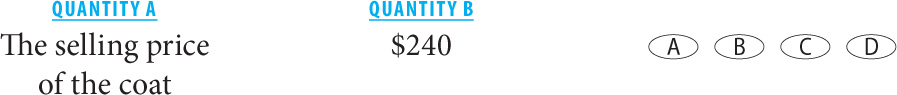




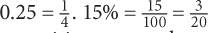 . The value in Quantity A is thus
. The value in Quantity A is thus 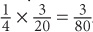 . The two quantities are equal.
. The two quantities are equal.
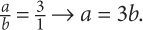 Next, to make the quantities comparable, substitute 3b for a in Quantity A. Thus Quantity A = 3(3b) = 9b. The values in the quantities are equal.
Next, to make the quantities comparable, substitute 3b for a in Quantity A. Thus Quantity A = 3(3b) = 9b. The values in the quantities are equal.
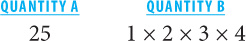
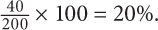 Since you know that the profit must be greater than 20%, the selling price must have been greater than $240.
Since you know that the profit must be greater than 20%, the selling price must have been greater than $240.