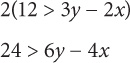Linear equations
Linear equations
 Exponents and roots
Exponents and roots
 Quadratic equations
Quadratic equations
 Formulas, functions, and sequences
Formulas, functions, and sequences
 Inequalities and absolute value
Inequalities and absolute value
Study this chapter to learn about:
In broad terms, you can think of algebra as any situation where you manipulate an equation or inequality to solve for one or more unknown values. An unknown value is a variable (such as x or y) or an expression (such as a + b or  Before diving into manipulating equations and inequalities, you will first look at the basic mathematical operations.
Before diving into manipulating equations and inequalities, you will first look at the basic mathematical operations.
PEMDAS is a helpful acronym for remembering the proper order of operations. When working with an expression that contains only values (no variables), you must perform the operations in the order dictated by PEMDAS. The following question would require proficiency with PEMDAS:
(8 + 1)2 divided by 3 × (5 + 2) = ?
Before answering this question, let’s review what each letter in PEMDAS stands for. The acronym PEMDAS represents Parentheses, Exponents, Multiplication/Division, Addition/Subtraction.
When evaluating an expression, you must use the order as dictated by PEMDAS. However, note that there is no priority between multiplication and division, and no priority between addition and subtraction. When choosing between these operations, always move from left to right. The following list outlines what each operation represents:
 Parentheses ( ) or [ ]: parentheses are used to bracket off part of an expression from the rest of the expression. For example: (3 + 5) × 2.
Parentheses ( ) or [ ]: parentheses are used to bracket off part of an expression from the rest of the expression. For example: (3 + 5) × 2.
 Exponents 43, 35, and so on: exponents tell you how many times you multiply the base by itself. 43 is the same as 4 × 4 × 4. 35 is the same as 3 × 3 × 3 × 3 × 3.
Exponents 43, 35, and so on: exponents tell you how many times you multiply the base by itself. 43 is the same as 4 × 4 × 4. 35 is the same as 3 × 3 × 3 × 3 × 3.
 Roots
Roots 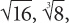 and so on: roots are the opposite of exponents. In terms of PEMDAS, roots take the same priority as exponents. To get the square root of a number, you need to determine which value, when multiplied by itself, will yield the number under the square root.
and so on: roots are the opposite of exponents. In terms of PEMDAS, roots take the same priority as exponents. To get the square root of a number, you need to determine which value, when multiplied by itself, will yield the number under the square root.
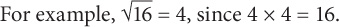
 Multiplication 3 × 4; (3)(4); xy: Note that multiplication is the opposite of division. If you multiply 3 times 4 and then divide that result by 4, the result is 3.
Multiplication 3 × 4; (3)(4); xy: Note that multiplication is the opposite of division. If you multiply 3 times 4 and then divide that result by 4, the result is 3.
 Division,
Division, 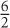 : Next, you will evaluate any expressions that require multiplication or division. Note: There is no hierarchy between multiplication and division! When presented with these two operations, always work from left to right:
: Next, you will evaluate any expressions that require multiplication or division. Note: There is no hierarchy between multiplication and division! When presented with these two operations, always work from left to right:
6 divided by 3 × 9 → First do 6 ÷ 3 = 2, then 2 × 9 = 18.
 Addition/Subtraction 4 + 7 + 11; 8 – 3 = 5: Next, you will evaluate any expressions that require addition or subtraction. Note: Just as with multiplication and division, there is no priority between addition and subtraction! When presented with these two operations, always work from left to right:
Addition/Subtraction 4 + 7 + 11; 8 – 3 = 5: Next, you will evaluate any expressions that require addition or subtraction. Note: Just as with multiplication and division, there is no priority between addition and subtraction! When presented with these two operations, always work from left to right:
7 – 9 + 5 → First, do 7 – 9 = –2, then do –2 + 5 = 3.
Now that you’ve reviewed PEMDAS, let’s work through the question at the beginning of this section:
(8 + 1)2 divided by 3 × (5 + 2)
You see two expressions within parentheses, so first evaluate those expressions:
92 divided by 3 × 7
Next, you see a term raised to an exponent, so evaluate that term:
81 divided by 3 × 7
Now you are left with division and multiplication. Remember, there’s no priority between these two operations. Just work from left to right.
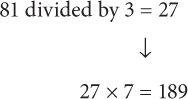
Before you dive into the process for solving for a variable, let’s review ways to simplify expressions. An expression is some combination of variables, values, or both. Examples of expressions are 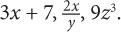
When presented with an expression, either by itself or as part of an equation, your first step should always be to simplify the expression. Generally, there are three ways to do so:
Simplify: 3x + 5z + 9x – 2z.
SOLUTION: Combine the xs and arrive at 12x. Combine the zs and arrive at 3z. The expression simplifies to 12x + 3z.
Simplify: 2(x+3) + 3(x + 3).
SOLUTION: Think of (x +3) as a variable, such as z. 2z + 3z = 5z. Therefore, 2(x + 3) + 3(x + 3) = 5(x + 3).
Simplify: 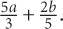
SOLUTION: Find a common denominator of 15 for both terms.

Simplify: 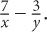
SOLUTION: Find a common denominator of xy for both terms.
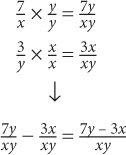
To factor an expression, take out the factors common to all terms in the expression.
Simplify: 6ab + 3a
SOLUTION: Each term has 3a as a factor. To see this, rewrite the expression as 3a × 2b + 3a × 1. Take 3a out of each term and arrive at 3a(2b + 1).
Simplify: 4x2 + 3x
SOLUTION: Each term shares a factor of x. Take x out of each term and arrive at x(4x + 3)
Whenever two expressions are set equal to each other, you have an equation:
7 × 6 = 14 × 3
The fundamental rule for all equations is the following: you can perform any operation on an equation as long as you perform that operation on both sides.
In the preceding example, if you divide both sides by 3, you will end up with 7 × 2 = 14. While the values on both sides of the equation changed, the equation itself is still true.
In algebra, equations will have variables, which are letters used to represent some unknown quantity in an equation.
If 3x + 2 = 14, then x = ?
When asked to solve for a variable, your goal will be isolate the variable by undoing the operations done to that variable. To do so, you are going to use PEMDAS, but in reverse!

Let’s look at another example:
If 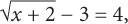 what is the value of x?
what is the value of x?
SOLUTION:
Step 1: Isolate 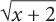 by adding 3 to both sides of the equation.
by adding 3 to both sides of the equation.

Step 2: (x + 2) is within parentheses, so you should manipulate the equation to isolate the expression within the parentheses. To do so, square both sides of the equation.
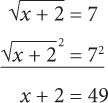
Often, the GRE will present you with two or more equations with multiple variables and will ask you to solve for the value of one or more of the variables in those equations. This is called a system of equations. When working with a system of equations, your ultimate goal is to arrive at a situation similar to what you saw in the previous section: one equation with one variable. To accomplish this, you can take two approaches: substitution or combination.
Let’s say you are given the following question:
3x + 2y = 18
2x + y = 9
What is x?
Step 1: Express one variable in terms of the other variable.
3x + 2y = 18
y = 9 – 2x
Step 2: Take the expression for y and substitute it for y in the first equation: 3x + 2(9 – 2x) = 18.
3x + 18 – 4x = 18
–x + 18 = 18
–x = 0
x = 0
Most systems of equations on the GRE can be solved with substitution, but you will sometimes need to use combination. Let’s look at an example:
3a + 2z = 12
4a + 3z = 18
Solve for a and z.
Step 1: When solving by combination, your ultimate goal is to arrive at the same coefficient for one of the variables. To do so, you will have to multiply each equation by a factor that will yield you a common coefficient for one of the variables. In this case, let’s make the coefficients on z equal to 6:
3(3a + 2z = 12) → 9a + 6z = 36
2(4a + 3z = 18) → 8a + 6z = 36
Step 2: Multiply across one equation by negative 1.
–1(9a + 6z = 36) = –9a – 6z = –36
8a + 6z = 36
Step 3: Add the equations to arrive at one equation and one variable (your ultimate goal!).
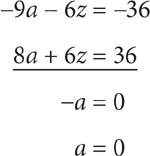
Substitute 0 for a into either equation to solve for x:
3(0) + 2z = 12
2z = 12
z = 6
1. If x + 7 = 14, what is the value of (x – 5)2?
 2
2
 4
4
 25
25
 49
49
 196
196
For this question, write your answer in the box.
2. If 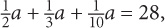 what is the value of a?
what is the value of a?

3. If 2x + 3y = 2y + 3, what is y in terms of x?
 3 – 2x
3 – 2x
 3 + 2x
3 + 2x


 x
x
 x + 6
x + 6
4. If 2a + 3b = 4, and x = 4a + 6b, what is the value of x?
 4
4
 8
8
 12
12
 16
16
 It cannot be determined from the given information.
It cannot be determined from the given information.
5. If  what is
what is  , in terms of x?
, in terms of x?
 3 – x
3 – x

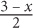



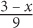

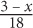
6. If 3p + 5q = 27, and p + 2q = 15, then q equals.
 –21
–21
 –3
–3
 9
9
 12
12
 18
18
For this question, write your answer in the box.
7. If 1.5a + 3b = 20 and 6a + 9b = 60, what is the value of b?

8. If x2 + 5x + 6 = 32, what is the value of x2 + 5x – 12?
 14
14
 18
18
 20
20
 22
22
 24
24
For this question, write your answer in the box.
9. What is the value of –2(3 – 5) ÷ 122?

10. If 2a + 2b = 13, 2b + 2c = 19, and 2a + 2c = 8, then a + b + c =
 5
5
 10
10
 15
15
 20
20
 40
40
11. If 3(x + b) + 5(x + b) = 72, then x + b =
 8
8
 9
9
 15
15
 24
24
 36
36
12. If a + 3b + 5c = 30, and 6b + 10c = 20, what is the value of 4a?
 10
10
 20
20
 40
40
 60
60
 80
80
13. If = x, what is y in terms of x?
 x2 + 3
x2 + 3
 2x2 + 3
2x2 + 3
 2x2 – 3
2x2 – 3

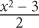

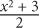
For this question, write your answer in the box.
14. If 3x = 12y – 7, what is the value of x – 4y?

1. B To solve for (x – 5), subtract 12 from both sides of the equation: x – 5 = 2. Substitute 2 for (x – 5): 22 = 4.
2. 28 To get rid of the denominators, multiply across the equation by 30 (which is a multiple of the values in all the denominators):

Combine like terms:
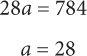
3. A To express y in terms of x, you need to isolate y. Subtract 2y and 2x from both sides of the equation and arrive at y = 3 – 2x.
4. B Notice that 4a + 6b = 2(2a + 3b). Therefore, to combine the equations, multiply the first equation by 2 and arrive at 4a + 6b = 8. Substitute 4a + 6b into the second equation and arrive at x = 8.
5. D To express  in terms of x, you need to isolate
in terms of x, you need to isolate  . To do so, first subtract x from both sides:
. To do so, first subtract x from both sides: 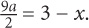 To go from
To go from 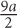 to
to  , divide both sides by 9 and arrive at
, divide both sides by 9 and arrive at 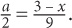
6. E Since you have two linear equations, you have to decide between combination and substitution. Since the coefficient in front of p in the second equation is 1, substitution is the preferred method. Write p in terms of q: p = 15 – 2q. Substitute (15 – 2q) for p in the first equation and arrive at 3(15 – 2q) + 5q = 27. Distribute: 45 – 6q + 5q = 27. Solve for q. q = 18.
7. 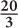 Since none of the variables has a coefficient of 1, use combination. You want to solve for b, so multiply across the first equation by –4:
Since none of the variables has a coefficient of 1, use combination. You want to solve for b, so multiply across the first equation by –4:
–4(1.5a + 3b = 20)
–6a – 12b = –80
Now the equations are:
–6a – 12b = –80
6a + 9b = 60
Add the equations and arrive at –3b = –20. Solve for b: b = 20/3.
8. A What is the relationship between x2 + 5x + 6 and x2 + 5x – 12? x2 + 5x + 6 is 18 more than x2 + 5x – 12. Since x2 + 5x + 6 = 32, x2 + 5x – 12 = 32 – 18 = 14.
9. 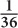 Use PEMDAS: First evaluate the expression within the parentheses: 3 – 5 = –2:
Use PEMDAS: First evaluate the expression within the parentheses: 3 – 5 = –2:
–2(–2) ÷ 122
Next, evaluate the exponential term: 122 = 144
–2(–2) ÷ 144
Since multiplication is to the left of division, multiply –2 × –2 = 4.
4 ÷ 144
Next, do the division: 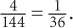
10. B Solution: Add up the equations:
4a + 4b + 4c = 40
4(a + b + c) = 40
a + b + c = 10
11. B Solution: note that the two expressions share the common term of (x + b). Combine like terms and arrive at 8(x + b) = 72. Divide both sides of the equation by 8: x + b = 9.
12. E You should always attempt to simplify equations, if possible. In the second equation, you can factor 2 from all the terms: 2(3b + 5c) = 20. Divide both sides by 2: 3b + 5c = 10. Substitute 10 for 3b + 5c in the first equation: a + 10 = 30. Solve for a: a = 20. Therefore, 4a = 80.
13. C To solve for y in terms of x, you must isolate y. First, get rid of the square root by squaring both sides of the equation: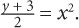 Next, multiply both sides by 2: y + 3 = 2x2. Then subtract 3 from both sides: y = 2x2 – 3. The correct answer is C.
Next, multiply both sides by 2: y + 3 = 2x2. Then subtract 3 from both sides: y = 2x2 – 3. The correct answer is C.
14. 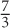 Since you are trying to solve for an expression that has y and x, manipulate the equation to get the xs and ys on the same side: 3x – 12y = –7. Factor 3 from both terms on the right side of the equation: 3(x – 4y) = 7. Solve for x – 4y: x – 4y =
Since you are trying to solve for an expression that has y and x, manipulate the equation to get the xs and ys on the same side: 3x – 12y = –7. Factor 3 from both terms on the right side of the equation: 3(x – 4y) = 7. Solve for x – 4y: x – 4y = 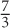 .
.
1. C
Step 1: To make the columns look similar, try to factor the expression in Quantity A:
pr + qr = r(p + q) and qs + ps = s(q + p).
Step 2: Combine like terms: r(p + q) + s(q + p) = (r + s)(p + q).
The two quantities are equal.
2. C
Step 1: To avoid working with a fraction, multiply both sides of the given equation by 7: xz = 7y
Step 2: To make the columns look similar, substitute 7y for xz in Quantity B: 7(7y) = 49y
The two quantities are equal.
3. B To avoid working with fractions, cross-multiply and arrive at: 3a = bc. To make the columns look similar, substitute 3a for bc in Quantity B: 4(3a) = 12a. The comparison is 9a versus 12a. Since you are told that a is positive, you can divide both quantities by a. The comparison is thus:

Quantity B is greater.
4. C
Step 1: To simplify the comparison, add 8 to both quantities: Quantity A = 6x + 9y and Quantity B = 36.
Step 2: To arrive at a value for Quantity A, manipulate the equation in the prompt to look similar to the expression in Quantity A:
3(2x + 3y = 12)
6x + 9y = 36
Step 3: Substitute 36 for 6x + 9y in Quantity A
The two quantities are equal.
5. A
Step 1: To make the two quantities look similar, factor the expression in Quantity A: ax + ay = a(x + y).
Step 2: Divide both quantities by (x + y). Quantity A = a and Quantity B = b. Since you are told that a > b, the value in Quantity A is greater.
In the term 53, five is the base and 3 is the exponent. The exponent represents the number of times you multiply the base by itself. So 53 comes out to 5 × 5 × 5. Both the exponent and base can be any real number (not just positive integers).
Most GRE questions dealing with exponents will require you to use a few simple rules and manipulate them in unorthodox situations. But before getting to these rules, let’s look at some other properties of exponents:
An even exponent always yields a positive result.
The base of an exponential expression can be positive or negative, but when the base is raised to an even exponent, the result will always be positive. Consider:
x2 = 16
The most obvious solution to the preceding equation is 4. If you substitute 4 for x, you arrive at 42 = 16, which is a true statement. But notice that –4 is also a solution for x! If you substitute –4 back into the equation, you arrive at (–4)2 = (–4)(–4) = 16, which is also true.
The previous example illustrates the following general principle: An even exponent will hide the sign of the base.
In other words, whether the base is positive or negative, when it is raised to an even power, the result will be positive. This is because an even number of negative factors will always cancel out to create a positive product.
The flip-side of this fact concerns odd exponents. An odd exponent will preserve the sign of the base.
For example, if x3 = –8, then there is just one solution for x: –2. Notice that 2 is not a solution for x because if you plug it back into the equation, you arrive at (2)3 = 8, not –8.
Base of 0, 1, and –1
 When a base of zero is raised to any power, the result is zero: 02 = 0
When a base of zero is raised to any power, the result is zero: 02 = 0
 When 1 is raised to any power, the result is 1: 110 = 1; 1–300 = 1
When 1 is raised to any power, the result is 1: 110 = 1; 1–300 = 1
 When –1 is raised to an even power, the result is 1. When –1 is raised to an odd power, the result will be –1: –110 = 1; –1–303 = –1
When –1 is raised to an even power, the result is 1. When –1 is raised to an odd power, the result will be –1: –110 = 1; –1–303 = –1
Fractional Base
 When a positive proper fraction (a number between 0 and 1) is raised to a power, an interesting property results: the resulting value is less than the original base:
When a positive proper fraction (a number between 0 and 1) is raised to a power, an interesting property results: the resulting value is less than the original base:
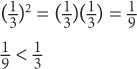
Compare the preceding to what happens when you raise an integer base to a power:
52 = (5)(5) = 25
25 > 5
 When a fraction is raised to a power, the exponent distributes to the numerator and denominator of that fraction:
When a fraction is raised to a power, the exponent distributes to the numerator and denominator of that fraction: 
Most situations with exponents will require knowledge of basic exponent rules. A good rule of thumb is that most exponent rules concern situations where either the base or the exponent is the same and where you’re either multiplying or dividing.
Multiplying Exponents with the Same Base: Add the Exponents
 When multiplying exponential terms with the same base, keep the base and add the exponents: (35)(33) = 3(5+3). To understand why you are adding the exponents, write out 35 and 33. Notice that you arrive at: (3 × 3 × 3 × 3 × 3) (3 × 3 × 3). This leaves you with 3 multiplied by itself 8 times. Thus 38.
When multiplying exponential terms with the same base, keep the base and add the exponents: (35)(33) = 3(5+3). To understand why you are adding the exponents, write out 35 and 33. Notice that you arrive at: (3 × 3 × 3 × 3 × 3) (3 × 3 × 3). This leaves you with 3 multiplied by itself 8 times. Thus 38.
Dividing Exponents with the Same Base: Subtract the Exponents
 When dividing exponential terms with the same base, keep the base and subtract the exponents:
When dividing exponential terms with the same base, keep the base and subtract the exponents:  To understand why you are subtracting the exponents, write out 57 and 53. Notice that you arrive at
To understand why you are subtracting the exponents, write out 57 and 53. Notice that you arrive at  When you cancel out the common factors, you are left with four 5s in the numerator. Thus 54.
When you cancel out the common factors, you are left with four 5s in the numerator. Thus 54.
Raising a Power to a Power: Multiply the Exponents
 When raising an exponential term to a power, to simplify the term, you should multiply the exponents: (54)3 = 5(4×3) = 512. Why? (54)3 = (54)(54)(54). This takes you back to the first scenario in which you were multiplying exponential terms with the same base. Recall that in such a situation, you should add the exponents. This will yield 5(4+4+4) = 512.
When raising an exponential term to a power, to simplify the term, you should multiply the exponents: (54)3 = 5(4×3) = 512. Why? (54)3 = (54)(54)(54). This takes you back to the first scenario in which you were multiplying exponential terms with the same base. Recall that in such a situation, you should add the exponents. This will yield 5(4+4+4) = 512.
Multiplying and Dividing Exponents with Different Bases but the Same Exponent: Multiply or Divide the Bases
 When multiplying exponential terms with different bases but the same exponent, keep the exponent and multiply the bases. Thus far, you have looked only at situations in which the base is the same. What about when the bases are different? You can still manipulate the expression if the exponents are the same!
When multiplying exponential terms with different bases but the same exponent, keep the exponent and multiply the bases. Thus far, you have looked only at situations in which the base is the same. What about when the bases are different? You can still manipulate the expression if the exponents are the same!
54 × 34 = (5 × 3)4 = 154
Why are you allowed to combine the bases? Again, write them out.
54 = 5 × 5 × 5 × 5
34 = 3 × 3 × 3 × 3
Notice that when you multiply these two terms, you will end up with 4 combinations of (5 × 3), giving you (5 × 3)4.
It is also important to notice that this rule works in reverse. If a product is raised to an exponent, then the exponent will distribute to all the factors in the product:
(23 × 35)4 = [(23)4] × [(35)4] = 212 × 320
When dividing exponential terms with different bases but the same exponent, keep the exponent and divide the bases: 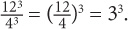 To understand why, once again expand the numerator and denominator. You arrive at:
To understand why, once again expand the numerator and denominator. You arrive at:
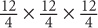
You thus have 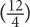 three times, giving you
three times, giving you 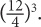
When raising a number to a negative exponent, to get rid of the negative exponent, you simply flip the base:

Knowing the preceding rules is essential for success on exponent questions, but the GRE will make such questions difficult by forcing you to evaluate expressions where it seems that none of these rules apply. To get past these difficulties, you should always be concerned with manipulating what’s given to you to get to the same base. By doing so, you can then use the rules that were just covered. Look at the following:
(84)(325) =
 29
29
 220
220
 237
237
 820
820
 25620
25620
To simplify the expression, rewrite the exponential terms to have the same base. By doing so, you will be able to use the exponent rule that says you can add the exponents when multiplying exponential terms with the same base:
8 = 23, so 84 = (23)4. Using your exponent rules, you know this comes out to 212.
32 = 25, so 325 = (25)5. Using your exponent rules, you know this comes out to 225.
Now you can use your rules! The expression now reads: (212)(225). Since you are multiplying exponential terms with the same base, you keep the base and add the exponents: (212)(225) = 2(12+25) = 237. The correct answer is C.
Let’s look at another example:
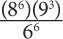
 7212
7212
 123
123
 212
212
 92
92
 123
123
Again, your focus should be to manipulate the numerator and denominator so that all the terms are in their prime forms.
86 = (23)6 = 218
93 = (32)3 = 36
66 = (3 × 2)6 = 36 × 26
So your new fraction is:
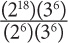
Use your exponent rules for division and you get 2(18–6) × 30. And this comes out to 212. The correct answer is C.
Table 1 Exponent Rules Table

Table 2 lists common powers and roots that appear on the GRE. Committing these rules to memory will help you save precious time on the exam.
Table 2 Common Powers & Roots
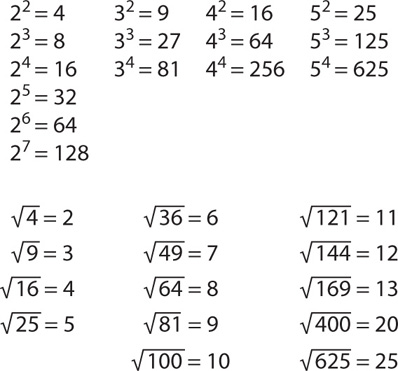
So far, most of the questions that you have looked at have concerned shortcuts for evaluating exponential expressions. Sometimes, however, you will be asked to solve for a variable that is in the place of an exponent. Look at the following example:
If 2x = 8, then what is the value of x?
No exponent rule will work here. Instead, you must recognize the following property: If two values are equal, then they must have the same prime factorization. To solve for x, you should thus rewrite 8 as the product of its prime factors. 8 = 23, so the equation now reads: 2x = 23. Now that the bases are equal, you know the exponents are equal, so x = 3.
If x and y are integers, and (3x)(2y) = 324, what is the value of x + y?
SOLUTION: Rewrite 324 as the product of its prime factors:
324 = 9 × 36 = 3 × 3 × 6 × 6 = 3 × 3 × 3 × 2 × 3 × 2 = (34)(22).
Thus (3x)(2y) = (34)(22). Now that both sides of the equation are expressed in terms of the same bases, you know that x = 4 and y = 2.
Sometimes you will be given an exponent question that concerns the addition or subtraction of exponential terms. Since exponent rules only apply to the multiplication or division of exponents, you should almost always factor when two exponential terms are added or subtracted. How will you do so? Look at the following example:
232 – 230 is equivalent to which of the following?
 22
22
 223
223
 210
210
 230
230
 2303
2303
SOLUTION: 232 can be rewritten as (230)(22). You can thus rewrite the expression as (230)(22) – (230)(1). Since both terms share a factor of 230, the expression can be written as: 230(22 – 1) = 230(3). The correct answer is Choice E.
Roots are the opposite of exponents. Generally, a root will be denoted using the following symbol:
If  then what is x?
then what is x?
SOLUTION: x is the positive number that when squared yields 16. 42 = 16, so the answer is 4.
In the preceding example, 16 is a perfect square. A perfect square is any number whose square root is an integer. For example, 9 is a perfect square because its square root is 3, but 15 is not a perfect square, since its square root is 3.87….
If you are asked to simply evaluate a square root, you can of course use your on-screen calculator. But many root questions will require you to instead manipulate the root. For example: 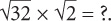
When multiplying square roots, you can combine all the terms underneath one square root. Thus
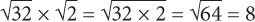
When dividing square roots, you can combine all the terms underneath one square root:
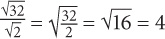
Note that these rules also work in reverse:
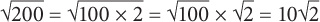
Simplifying a perfect square root is straightforward and can always be done on your calculator. But what if, after going through a question, you arrived at an answer of  If you looked at the choices,
If you looked at the choices,  would not appear in any of them. Why? Because
would not appear in any of them. Why? Because  is not simplified. To simplify it, you have to take any perfect squares out of the radical. You would simplify
is not simplified. To simplify it, you have to take any perfect squares out of the radical. You would simplify  in the following way:
in the following way:
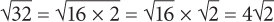
4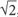 is the simplified form of
is the simplified form of  . Generally, when you are trying to simplify a square root, you should break it up into any known perfect squares and remove those perfect squares from the square root.
. Generally, when you are trying to simplify a square root, you should break it up into any known perfect squares and remove those perfect squares from the square root.
Simplify. 
SOLUTION: First, rewrite 150 as 25 × 6. Thus 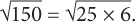 Now, break up the square root:
Now, break up the square root: 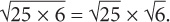 Finally, simplify any perfect squares.
Finally, simplify any perfect squares. 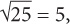 so the answer is
so the answer is 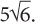
When solving Quantitative Comparison questions that test exponents, it is essential to recall both the rules discussed previously, and just as importantly, the exceptions to these rules. Remember that success on Quantitative Comparison questions often requires testing for Choice D, which requires challenging your assumptions.
When solving a Quantitative Comparison question where either the exponent or the base is a variable, always test 0, 1, and –1. For example:

If x is positive, then Column B will always be greater. But remember that the exponents 0, 1, and –1 have interesting properties, so make sure to test those cases to see whether Column B is always greater.
 If x = 0, then the two quantities are equal.
If x = 0, then the two quantities are equal.
 If x = 1, then Column B is greater.
If x = 1, then Column B is greater.
 If x = –1, then Column A becomes
If x = –1, then Column A becomes  and Column B becomes
and Column B becomes  meaning that Column A is greater.
meaning that Column A is greater.
These different values give you contradictory relationships, and the answer is therefore D. When comparing numbers expressed as exponents, make sure to express each column using the same base:

Rewrite 1,000 using a base of 10: 1,000 = 103. Substitute 103 for 1,000 in Column A, and compare the new expressions:

Use your exponent rules for Column A: (103)600 = 101,800. The two columns are equal, and the answer is therefore Choice C.
Discrete Quantitative Questions
1. 42165 = 2x. What is x?
 7
7
 9
9
 10
10
 20
20
 24
24
For this question, write your answer in the box.
2. 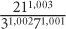 equals
equals

3. If 5x + 5x + 5x + 5x + 5x = 56, then x equals
 1
1

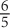
 5
5
 6
6
 30
30
4. If 2x+2 × 3Y+3 = 576, where x and y are integers, what is x + y?
 2
2
 3
3
 5
5
 6
6
 8
8
5. If a = 0.729, which of the following must be true?
 a > a2 >
a > a2 > 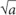
 a >
a > 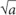 > a2
> a2
 a2 > a >
a2 > a > 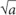

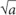 > a2 > a
> a2 > a

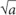 > a > a2
> a > a2
6. Which of the following equals 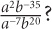
 a9b–23
a9b–23
 a17b–35
a17b–35
 a17b5
a17b5
 a45b–115
a45b–115
 b–22
b–22
7.  equals
equals
 3
3
 4
4
 6
6
 15
15
 30
30
8. If 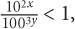 1, which of the following must be true?
1, which of the following must be true?
 x < 3y
x < 3y
 2x < 3y
2x < 3y
 2x < y
2x < y
 2x + 3y < 1
2x + 3y < 1
 2x + 3y < 0
2x + 3y < 0
9.  =
=
 3
3
 6
6
 9
9
 12
12
 18
18
10. If  = 8 and
= 8 and 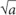 –
– 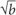 = 0, what is a?
= 0, what is a?
 0
0
 2
2
 4
4
 8
8
 32
32
11. If 37 – 35 = (2x)(3y), where x and y are integers, what is x + y?
 2
2
 3
3
 8
8
 15
15
 243
243
12. 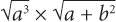 is equivalent to which of the following?
is equivalent to which of the following?
 ab
ab
 ab
ab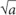
 (a2)(b)
(a2)(b)
 (a2)(b2)
(a2)(b2)
 (a4)(b2)
(a4)(b2)
1. E To solve for x, you should express all the terms with a base of 2: 42 = (22)2 = 24. 165 = (24)5 = 220. Thus:

2. 5 When simplifying exponential expressions, you should express all bases in their prime forms. Express 21 in terms of base 7 and 3: 211,003 = (7 × 3)1,003 = (71,003)(31,003). The fraction now reads:
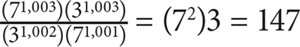
3. C Note that you are adding the same term (5x) five times. Thus:
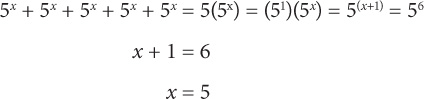
4. B Since the two sides of this equation are equal, they must have the same prime factorization. Thus the exponent on the 2 on the left side of the equation represents the number of times 2 appears in the prime factorization of 576, and the exponent on the 3 on the left side of the equation represents the number of times that 3 appears in the prime factorization of 576. To solve for these exponents, you should express 576 in terms of base 2 and 3:


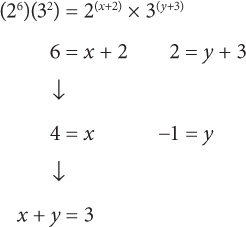
5. E If the base of an exponential term is between 0 and 1, then as the exponent increases, the result decreases. Thus a2 < a. Eliminate A, C, and D. Now compare B and E. What happens when you take the square root of a fraction? The opposite of when you square it! Squaring a positive fraction results in a value smaller than the original fraction, so taking the square root of a fraction results in a value larger than the original fraction. Thus the answer is E. For illustration:  Note that the result (0.7) is larger than the original value whose square root was taken.
Note that the result (0.7) is larger than the original value whose square root was taken.
6. B The numerator has a compound base, so you should distribute the exponent to both terms:
a2b–35 = a2×5b–3×5 = a10b–15
The fraction now reads:
a10b–15/a–7b20 = a10–(–7) × b–15–20 = a17b–35
7. B Split the numerator:  The first term can be reduced:
The first term can be reduced: 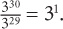 The second term can be reduced:
The second term can be reduced: 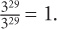 Thus the fraction reduces to 3 + 1 = 4.
Thus the fraction reduces to 3 + 1 = 4.
8. A To simplify exponential expressions, it is generally a good idea to make the bases similar. In this case, express the denominator as base 10: 1003y = (102)3y = 106y.
The inequality now reads: (102x)/(106y) < 1. Multiply both sides by 106y:
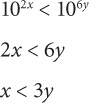
9. D First, simplify the values inside the radical: 12 – 4 = 8. Next, multiply the terms underneath the radical: 2 × 8 × 9 = 144. The square root of 144 is 12.
10. E A good rule of thumb is to eliminate radicals where possible. In the first equation, you can do so by squaring both sides: 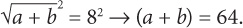 In the second equation, you should first add
In the second equation, you should first add 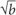 to both sides:
to both sides: 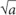 =
= 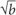 . Now square both sides:
. Now square both sides:
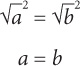
Now substitute a for b in the first equation:
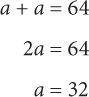
11. C When a question adds or subtracts exponential terms, a good rule of thumb is to factor out what the terms have in common. 37 and 35 share 35 as a factor, so the left side of the equation can be rewritten as 35(32 – 1) = 35(8) = (35)(23). Thus
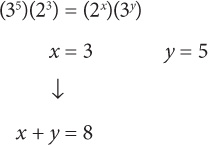
12. C When multiplying square roots, combine the terms underneath one radical. Thus 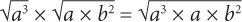

1. A To make the columns comparable, rewrite 258 with a base of 5: 258 = (52)8 = 516. Now that both columns are expressed in base 5, the column with the larger exponent will have the greater value. The exponent in Quantity A is greater, so the answer is A.
2. C Simplify Quantity A: 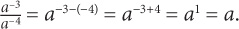 The two quantities are equal.
The two quantities are equal.
3. C Simplify Quantity A by expressing the numerator with base 2:
 Substitute 2v for w: 2–2v+2v = 20 = 1. The two quantities are equal.
Substitute 2v for w: 2–2v+2v = 20 = 1. The two quantities are equal.
4. D Although b > a, b is raised to a smaller exponent than a is. Thus a relationship cannot be determined. For illustration, plug in numbers: if b = 2 and a = 1, then b2 = 4 and a3 = 1. In this case, Quantity A is greater. But if b = 4 and a = 3, b2 = 16, and a3 = 27. In this case, Quantity B is greater. The relationship cannot be determined.
5. D First, rewrite all the terms in the given equation to have base 2: (2a)(22b) = 26 => a + 2b = 6. Now you can plug in numbers: if a = 0, then b = 3. In this case, a + b = 3, and the two quantities are equal. If b = 0, then a = 6. In this case, a + b = 6, and Quantity A is greater. A relationship cannot be determined.
6. B When a fraction is raised to a power, the result gets closer to zero as the exponent increases. Since x is a negative fraction, the result will become less negative as the exponent increases. Thus when –1 < x < 0, x5 is less negative than x3, meaning that x5 > x3. Quantity B is greater.
7. A Your initial goal should be to manipulate the columns to make the bases comparable. However, it is not possible to express base 20 using base 2. Thus a different approach is required. Instead of making the bases comparable, make the exponents comparable. Note that 120 = (3)(40). Therefore, 2120 = 2(3×40) = (23)40 = 840. Now the two quantities have the same exponent. The quantity with the greater base will have the greater value.
8. D If xa = 1, it is possible that a = 0 and that x equals any number (since any number raised to the power of zero = 1). However, that possibility is eliminated by the information that a > 0. So what can x be? It would appear that x must equal 1, since 1 raised to any power equals 1. However, what if a is an even integer? In that case, x can equal –1, since a negative raised to an even power yields a positive result. If x = 1, the two quantities are equal. If x = –1, Quantity B is greater. Thus the relationship cannot be determined.
9. C Since the quantities compare c to an expression that contains a and b, you should manipulate the given equation to isolate c. First, cross-multiply: 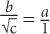
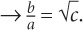 Next, square both sides:
Next, square both sides:  The quantities are equal.
The quantities are equal.
So far, you have looked only at linear equations. In linear equations, there will always be one solution for a given variable. In contrast, in quadratic equations, a variable will usually have more than one solution. How do you know you have a quadratic equation?
You have a quadratic equation whenever at least one of the variables in the equation is raised to an even exponent.
Let’s say you are asked to evaluate (–4)2. Using PEMDAS, you know that the result is (–4) × (–4) = 16. Now let’s say that you are asked to evaluate 42. You get 4 × 4 = 16. Note that both 4 and –4 gave the same result. Why? Because raising a variable to an even exponent will always produce a positive result.
Now let’s flip it:
If x2 = 16, what are the possible values of x?
You may be tempted to calculate the square root of 16 and say that x = 4. But watch out for the even exponent! Since the exponent on x is even, there will be a positive and a negative solution for x. Thus the two solutions are x = 4 or –4.
Other forms of quadratic equations are:

On the GRE, quadratic equations will take a few common forms. The most common form is
ax2 + bx + c = 0
When presented with a quadratic equation in the preceding form, you will usually be asked to find the solutions of that equation. To do so, you will need to factor. Let’s look at an example:
If x2 + 7x + 5 = –7, what are the possible values for x?
Step 1: Manipulate the equation to match the preceding template. In this example, you would need to set the equation equal to zero.

Step 2: Rewrite the equation in factored form: x2 + 7x + 12 = (x + __)(x + __).
Step 3: Determine the values for the slots. To get the factors of the equation, you need to find two integer values that add to yield your b and that multiply to yield your c. In the preceding equation, 7 is your b and 12 is your c. What two values multiply to 12 and add to 7? 3 and 4.
In the slots, you will put the two integer values that you arrived at in Step 2. Thus in its factored form, the equation is (x + 3)(x + 4) = 0.
Step 4: Solve for x. To solve for x, you must recognize an essential fact: any time a product of two or more factors is zero, at least one of those factors must have a value of zero.
In the preceding example, if (x + 3)(x + 4) = 0, then either:

So the roots of this equation are –3 and –4. Note that if you plug either of these values into the original equation, you will arrive at a true statement.
Oftentimes, you will be presented with a quadratic equation that does not appear to match the preceding template.
For example, if 4x2 = x, then x = ?
Seeing x on both sides of the equation, many students are tempted to divide both sides of the equation by x to arrive at:
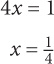
Though  is certainly a solution to the equation, the hypothetical student committed an error here when dividing by x. Why? Because the student essentially eliminated one of the solutions for x! Instead of arriving at two solutions, the student arrived at only one.
is certainly a solution to the equation, the hypothetical student committed an error here when dividing by x. Why? Because the student essentially eliminated one of the solutions for x! Instead of arriving at two solutions, the student arrived at only one.
So stick to the following rule: Set quadratic equations equal to zero. Let’s redo the preceding example:
4x2 = x
Step 1: Subtract x from both sides: 4x2 – x = 0.
Step 2: Factor x from both terms: x(4x – 1) = 0.
Step 3: Solve for x.
Since you have a product set equal to zero, either:

So far, you have looked at situations where you have taken quadratic equations in their expanded form and put them into factored form. Sometimes, you will be expected to go in the opposite direction: from factored form to expanded form. To do so, you will want to use an acronym that you may remember from high school: FOIL.
FOIL stands for:
First
Outer
Inner
Last
To expand the expression (x + 3)(x – 5), do the following:
First: Multiply the first term in each parentheses together: (x)(x) = x2
Outer: Multiply the first term in the first parentheses by the last term in the second parentheses: x(–5) = –5x
Inner: Multiply the inner terms of the product together: 3(x) = 3x
Last: Multiply the last term in each set of parentheses together: 3(5) = 15
Now you have an expression with four terms: x2 – 5x + 3x + 15. Group like terms, and you will arrive at the quadratic: x2 – 2x + 15.
Three quadratic expressions appear so frequently on the GRE that it is worth memorizing their structure instead of factoring or using FOIL each time you encounter them:
1. (x + y)(x – y) = x2 – y2
2. (x + y)(x + y) = (x + y)2 = x2 + 2xy + y2
3. (x – y)(x – y) = (x – y)2 = x2 – 2xy + y2
Memorizing the preceding formulas is useful for a couple of reasons:
 If you know the forms of these expressions after applying FOIL and after factoring, you will be able to save time when you encounter their general form on the GRE.
If you know the forms of these expressions after applying FOIL and after factoring, you will be able to save time when you encounter their general form on the GRE.
 Often, the GRE will put these expressions in an unorthodox form. In these cases, you will need to recognize that an unusual-seeming expression is actually one of the common quadratics.
Often, the GRE will put these expressions in an unorthodox form. In these cases, you will need to recognize that an unusual-seeming expression is actually one of the common quadratics.
For example, (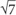 +
+ 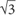 )(
)(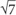 –
– 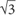 )= ?
)= ?
Since you are multiplying two binomials, you might be tempted to distribute, but notice that (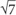 +
+ 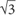 )(
)(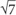 –
– 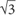 ) is in the same form as (x + y)(x – y), where
) is in the same form as (x + y)(x – y), where 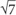 is x and
is x and 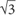 is y. From the first special product, you know that (x + y)(x – y) = (x2 – y2). Therefore,
is y. From the first special product, you know that (x + y)(x – y) = (x2 – y2). Therefore,
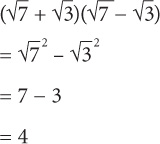
1. If 2x2 + 20x = –48, then x could equal which of the following values?
 –12
–12
 –8
–8
 –7
–7
 –4
–4
 0
0
2. If a – b = 4, then a2 – 2ab + b2 =
 2
2
 8
8
 12
12
 16
16
 20
20
3. If (x + 3)2 = 81, then x could equal which of the following?
 –15
–15
 –12
–12
 –9
–9
 3
3
 9
9
For this question, write your answer in the box.
4. If x2 – y2 = 12, and x + y = 4, then what is the value of x?

5. If (a + b)2 = 36, and ab = 4, then a2 + b2 =
 3
3
 6
6
 9
9
 28
28
 32
32
6. If  then x2 – y2 =
then x2 – y2 =






 1
1
 2
2
For this question, write your answer in the box.
7. If a2 + 8a + k = (a – 10)(a + 18), then what is the value of k?

8. If y2 + ky + b = (y – z)(y + q), then what is b, in terms of q and z?
 q + z
q + z
 q – z
q – z
 qz
qz
 –qz
–qz
 q/z
q/z
9. If (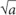 –
– 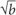 )(
)(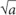 +
+ 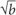 ) = 12, then what is a in terms of b?
) = 12, then what is a in terms of b?
 b + 12
b + 12
 b2 + 12
b2 + 12




1. D Simplify the equation by dividing both sides by 2: x2 + 10x = –24. Since you have a quadratic, you should set it equal to zero: x2 + 10x + 24 = 0. Now factor the quadratic: (x + 6)(x + 4) = 0. Either factor can equal zero, so:
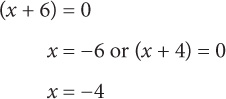
2. D Notice that a2 – 2ab + b2 is one of the special products. The expression factors to (a – b)2. If (a – b) = 4, then (a – b)2 = 16.
3. B Note that the given equation is quadratic. There will thus be two solutions for (x + 3): the positive square root of 81 and the negative square root of 81. Thus (x + 3) = 9 → x = 6 or (x + 3) = –9 → x = –12.
4. 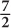 Since x2 – y2 is a difference of squares, you can factor the original equation to (x + y)(x – y) = 12. Substitute 4 for (x + y) in the original equation: 4(x – y) = 12. Divide both sides of the equation by 4: (x – y) = 3. So you know that x – y = 3 and that x + y = 4. To solve for x, you will add the equations:
Since x2 – y2 is a difference of squares, you can factor the original equation to (x + y)(x – y) = 12. Substitute 4 for (x + y) in the original equation: 4(x – y) = 12. Divide both sides of the equation by 4: (x – y) = 3. So you know that x – y = 3 and that x + y = 4. To solve for x, you will add the equations:
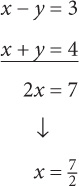
5. D Expand the expression on the left side of the first equation: a2 + 2ab + b2 = 36. Substitute 4 for ab: a2 + 8 + b2 = 36. Subtract 8 from both sides to solve for (a2 + b2): a2 + b2 = 28.
6. B To isolate the variables, multiply both sides of the equation by (2x –2y): (2x + 2y)(2x – 2y) = 1. Notice that (2x + 2y)(2x – 2y) is in the form of (a + b)(a – b). Since (a + b)(a – b) becomes a2 – b2 after applying FOIL, (2x + 2y)(2x – 2y) becomes (2x)2 – (2y)2 = 4x2 – 4y2 after applying FOIL. The equation is now 4x2 – 4y2 = 1. Factor 4 from both terms on the left side: 4(x2 – y2) = 1. Divide by 4: x2 – y2 
7. –180 Notice that the right side of the equation is the factored form of the left side. How do you factor a common quadratic? Think of a simpler situation: x2 + 5x + 6 = (x + 3)(x +2). Why? Because 3 and 2 multiply to yield 6 and add to yield 5. So in the original equation, –10 and 18 multiply to yield k. k = –180.
8. D Notice that the right side of the equation is the factored form of the left side. How do you factor a common quadratic? Think of a simpler situation: x2 + 5x + 6 = (x + 3)(x +2). Why? Because 3 and 2 multiply to yield 6 and add to yield 5. So in the original equation, –z and q multiply to yield b. Thus b = –qz.
9. A Note that the expression on the left side of the equation is the factored form of a difference of squares: (x + y)(x – y) = x2 – y2, so (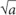 –
– 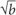 )(
)(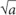 +
+ 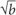 ) =
) = 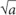 2 –
2 – 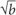 2 = a – b. Thus a – b = 12. Isolate a: a = b + 12.
2 = a – b. Thus a – b = 12. Isolate a: a = b + 12.
1. D Since the exponent on the variable is even, 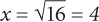 or
or  The relationship cannot be determined. The correct answer is D.
The relationship cannot be determined. The correct answer is D.
2. C If ab = 0, then a = 0 and/or b = 0. If bc = 3, then neither b nor c = 0. Since b does not equal zero, a must equal zero. The two quantities are equal. The correct answer is C.
3. A Add the given equations to solve for x: 2x + 14 → x = 7. Substitute x for 7 in the first equation to solve for y:
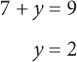
The value of Quantity A is 72 – 22 = 45. The value of Quantity B is 22 – 72 = 4 – 49 = –45. Quantity A is greater.
4. B Set the quadratic equal to zero: x2 + 7x + 12 = 0. Factor: (x + 3)(x + 4) = 0. There are two solutions:

Since both solutions are negative, x < 0 and –x > 0. Quantity B is greater.
5. A First, solve for x by setting the first equation equal to zero:
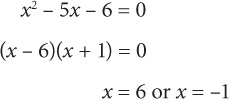
Next, solve for y by setting the second equation equal to zero:
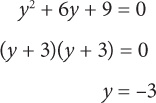
If x = 6, then Quantity A is greater. If x = –1, then Quantity A is greater.
The next type of algebra question concerns situations where the question gives you a formula to determine some value.
In formula questions, the question will define a formula for you and will ask you to substitute values or variables into the formula to arrive at an answer. A typical question would be:
A company estimates the number of potential customers, P, in a day by using the following formula: 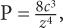 where c = the number of customers the company had the previous day and z = the number of competitors for that month. If the company had 10 customers yesterday and has 2 competitors this month, how many customers will the company have today?
where c = the number of customers the company had the previous day and z = the number of competitors for that month. If the company had 10 customers yesterday and has 2 competitors this month, how many customers will the company have today?
SOLUTION: Substitute the given values into the formula. Substitute 10 for c and 2 for 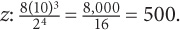
Sometimes, formula questions will not give you values for the variables. Instead, they will ask you to determine how changes in certain variables affect the output of the formula. In these cases, you should always plug in numbers! For example:
The formula for the volume of a sphere is  πr3. If the radius of a sphere is doubled, the volume of the resulting sphere will be how many times the volume of the original sphere?
πr3. If the radius of a sphere is doubled, the volume of the resulting sphere will be how many times the volume of the original sphere?
 2
2
 4
4
 8
8
 16
16
 32
32
SOLUTION: Let the original radius = 2. The original volume is thus (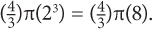 After the radius doubles, the new volume is
After the radius doubles, the new volume is 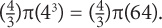
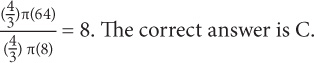
You can think of a function as a recipe. Recipes specify certain steps you need to take to achieve a desired dish; in the same way, functions specify certain operations you need to perform to achieve a given outcome. Because of their strange notation, functions tend to intimidate a lot of people, but it is important to remember that fundamentally functions are just substitution!
A simple function question would be the following:
If, for all numbers, x, f(x) is defined by f(x) = 3x + 5, then f(7) =
It is important to note that “f(x)” does not mean f × x. f is the name of the function, and the term in the parentheses represents the input of the function. Using the recipe analogy, this formula tells you that to get the value (also known as “output”) of the function, f, you must multiply what is inside of the parentheses by 3 and then add 5. So in the preceding example, to get the value of f(7), you must multiply 7 by 3 and then add 5. 3(7) + 5 = 22.
In the preceding example, you were given the formula for the function and its input, and you were asked to arrive at the output. Sometimes you will be given the formula for the function and its output, and you will be asked to arrive at the input. Look at the following example:
For all positive numbers, x, the function f is defined as f(x) = (x + 3)2 – 5.
If f(a) = 59, then a = ?
First, note that the function only applies to positive inputs, so you know your answer will be positive. To solve for a, you go through a similar substitution process as presented earlier.
Step 1: Plug a into the function and arrive at f(a) = (a + 3)2 – 5
Step 2: Set the second expression equal to 59: (a + 3)2 – 5 = 59
Step 3: Solve for a: (a + 3)2 = 64 → (a + 3) = 8 → a = 5
Certain function questions will give you two functions and ask you to use the output of one function as the input for the other function. Look at the following example:
For all numbers, x, f(x) is defined by f(x) = x2 + 12, and g(x) is defined by 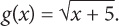 What is the value of f(g4)?
What is the value of f(g4)?
This question wants you to use the output of g(4) as your input for the function f. When working with a compound function, always go inside-out:
Step 1: Solve for 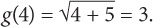
Step 2: Substitute the output of g(4) into the function f: f(3) = 32 + 12 = 21.
A different type of function question will define a formula using symbols rather than the notation covered in the previous section. Such questions are often a source of intimidation for students, but the process for these questions is almost identical to the process for normal function questions.
If the operation * is defined for all numbers, a, by a* = 2a3, and (b + 3)* = 54, then b = ?
Step 1: Understand the formula: you should substitute whatever is in front of the multiplication sign for a in the formula 2a3.
Step 2: Substitute (b +3) for a: 2(b + 3)3 = 54.
Step 3: Solve for b:
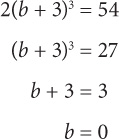
Let’s do another symbolism question with two symbols:
If the operation # is defined for all numbers, a and b, by 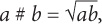 then 60 # (25 # 9) = ?
then 60 # (25 # 9) = ?
Step 1: Understand the formula: multiply the terms before and after the symbol and then take their square root.
Step 2: Since 60 # (25 # 9) is a compound function, you should first find the value of (25 # 9) and then input that value into the original function: 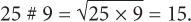
Step 3: Solve for 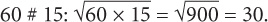
The last type of formula question you will see are sequences. A sequence is any group of numbers whose order is determined by a rule. Consecutive integers are an example of a sequence: for example, the rule for the set of consecutive integers 3, 4, 5, 6, 7 is that any given term in the set is one more than the term before it. Mathematically, the previous sequence would be defined in the following way:
an = an–1 + 1, where n > 1
The subnotation refers to the position of a term in the sequence. So a1 is the first term of the sequence, a2 is the second term, and so on. The rule tells you that the nth term of the sequence equals the value of previous term plus 1. Why does it specify “where n > 1”? Because this rule cannot apply to the first term, since there is no number preceding that term. Thus starting with the second term, any term will have a value one greater than the term before it.
Generally, sequence questions will ask you to determine one of three things:
1. The rule for a series of numbers
2. The value of a specific term in the sequence
3. The sum or difference of two or more terms in the sequence
Example 1: The sequence a1, a2, a3, …, an, … is such that an = 2an–1 for all n > 1. If a2 = 7, what is a5?
SOLUTION: The rule is that any given term is double the term before it. a5 is 3 places after a2, so
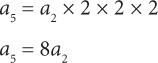
Since a2 = 7, you know that a5 = 8 × 7 = 56.
Example 2: The sequence a1, a2, a3, …, an, … is such that 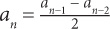 for all n > 2. If a3 = 12 and a4 = 5, what is a2?
for all n > 2. If a3 = 12 and a4 = 5, what is a2?
SOLUTION: Substitute the value of a4 for an, the value of a3 for an–1 and a2 for an–2:
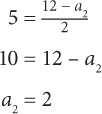
Example 3: In the sequence S, s1 = 4, s2 = 11, and s3 = 18. Which of the following could be the definition of the sequence?
 sn = sn–1 + 4
sn = sn–1 + 4
 sn = 2sn–1 + 3
sn = 2sn–1 + 3
 sn = sn–1 + 7
sn = sn–1 + 7
 sn = 2sn–1 – 4
sn = 2sn–1 – 4
 sn = sn–1 – 7
sn = sn–1 – 7
SOLUTION: Substitute the three values into each of the choices, and determine which choice maintains the values for all three terms:
A: 11 = 4 + 4? No → Eliminate Choice A.


D: 11 = 24 – 4? No → Eliminate Choice D.
E: 11 = 4 – 7 No → Eliminate Choice E.
For this question, write your answer in the box.
1. If all the edges of a cube are doubled, the new volume of the cube will be how many times the original volume? (Volume of a cube = e3)

2. A student’s efficiency, E, is measured by the following formula: 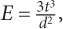 where t = hours spent studying and d = hours spent browsing the Internet. Yesterday, Gerald and Harry spent the same amount of time studying, but Gerald spent twice as much time browsing the Internet. Yesterday, Gerald’s efficiency was how many times greater than Harry’s?
where t = hours spent studying and d = hours spent browsing the Internet. Yesterday, Gerald and Harry spent the same amount of time studying, but Gerald spent twice as much time browsing the Internet. Yesterday, Gerald’s efficiency was how many times greater than Harry’s?
 2
2
 3
3
 4
4
 7
7
 8
8
For this question, write your answer in the box.
3. For all numbers, a and b, if the operation * is defined by a * b = 3a + 2b, then 5 * 3 =

4. For all numbers x where x ≠ 0, if f(x) is defined by 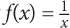 and g(x) is defined by
and g(x) is defined by 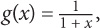 then f(g2) =
then f(g2) =




 1
1
 2
2
 3
3
5. For all numbers, x, the function f is defined by 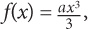 where a is a constant. If f(3) = 45, then a =
where a is a constant. If f(3) = 45, then a =
 3
3
 5
5
 15
15
 30
30
 35
35
6. For all numbers a and b, if the operation $ is defined by 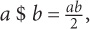 then 3 $ (5 $ 8) =
then 3 $ (5 $ 8) =
 10
10
 20
20
 30
30
 40
40
 60
60
7. For all numbers, x, if f(x) is defined by f(x) = 3x2, and f(x – 3) = 12, then x could equal which of the following?
 2
2
 4
4
 5
5
 7
7
 8
8
For this question, indicate all of the answer choices that apply.
8. For which of the following does a × b = b × a?
 a × b = b(a – b)
a × b = b(a – b)
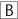 a × b = 3(a + b)
a × b = 3(a + b)
 a × b = (ab)3
a × b = (ab)3
9. The sequence a1, a2, a3, …, an, … is such that an = 3an–1 + 2an–2 for all n > 2. If a3 = 7 and a4 = 35, what is a2?
 7
7
 14
14
 17
17
 19
19
 21
21
10. In a certain sequence, each term is 7 greater than the term before it. If the third term of the sequence is 39, what is the 13th term?
 102
102
 109
109
 116
116
 123
123
 130
130
In a certain body fat measurement, a 1-unit increase represents a 5-pound increase in body fat
1. 8 Plug in values: Let the original edge of the cube = 2. The original volume of the cube is thus 23 = 8. If the original edge = 2, then the new edge = 4. The new volume of the cube is thus (43) = 64. The new volume is thus 8 times the original volume.
2. C Plug in values: Let t = 1 for Gerald and Harry. Let d = 2 for Harry and let d = 4 for Gerald. Harry’s efficiency is thus  Gerald’s efficiency is
Gerald’s efficiency is 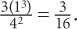
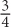 is 4 times greater than
is 4 times greater than 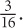
3. 21 The formula specifies to triple the value in front of the star, double the value after the star, and then add the resulting terms. Substitute 5 for a in the original formula and substitute 3 for b to arrive at 3(5) + 2(3) = 21.
4. E Solution: When working with compound functions, solve for the inside value first: 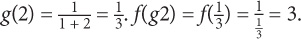
5. B Substitute 3 for x in the original function:

6. C When working with compound functions, first obtain the value of the function within the parentheses. 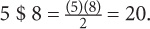 Substitute 20 for (5 $ 8) and arrive at a value for: 3 $ 20. Repeat the formula:
Substitute 20 for (5 $ 8) and arrive at a value for: 3 $ 20. Repeat the formula: 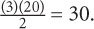
7. C Substitute (x – 3) for x:
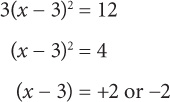
If (x – 3) = 2, then x = 5. If (x – 3) = –2, then x = 1. Only 5 appears in the choices.
8. B and C Substitute values for a and b. Let a = 2 and b = 3. Now identify for which of the choices 2 * 3 = 3 * 2.
A: 3 * 2 = 2(3 – 2) = 2; 2 * 3 = 3(2 – 3) = –3. → Eliminate Choice A.
B: 3 * 2 = 3(3 + 2) = 3(5) = 15; 2 * 3 = 3(2 + 3) = 3(5) = 15. The outputs are equal. → B is an answer.
C: 3 * 2 = (3 × 2)3 = 63 = 216; 2 * 3 = (2 × 3)3 = 63 = 216. The outputs are equal. → C is an answer.
9. A Solution: a4 = 3a3 + 2a2. Thus:
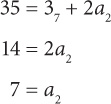
10. B To determine the 13th term, you will have to add 7 a certain number of times to the third term. How many times? To go from the 3rd to the 4th term, you add 7 once. To go from the 3rd to the 5th term, you add 7 twice. Thus to go from the 3rd to the 13th term, you should add 7 ten times. The 13th term thus equals 3rd term + 7(10) = 39 + 7(10) = 109.
1. C Substitute the values in the quantities into the given formula:  The two quantities are equal.
The two quantities are equal.
2. C Because of the even exponent, (x – 3)2 > 0. Thus the minimum value for 2(x – 3)2 = 0. The value of the function will be minimized when 2(x – 3)2 = 0. 7 + 0 = 7. The two quantities are equal.
3. B Since each unit represents a 5-pound increase, the difference in pounds between three units is 3(5) = 15.
4. D Without knowing the value of any of the terms in the sequence, you cannot determine anything about the value of a4.
5. B a3 = a2 + 7. a2 = a1 + 7. Substitute a1 + 7 for a2 in the first equation: a3 = (a1 + 7) + 7 = a1 + 14. Quantity B is greater.
Inequalities look like the following:

The following list translates inequalities:
Types of Inequalities
 a > b means “a is greater than b”
a > b means “a is greater than b”
 a < b means “a is less than b”
a < b means “a is less than b”
 a ≥ b means “the value of a is at least equal to the value of b”
a ≥ b means “the value of a is at least equal to the value of b”
 a ≤ b means “the value of a is at most equal to the value of b”
a ≤ b means “the value of a is at most equal to the value of b”
 3 < a < 5 means “the value of a is between 3 and 5” (This is called a compound inequality.)
3 < a < 5 means “the value of a is between 3 and 5” (This is called a compound inequality.)
The fundamental difference between equations and inequalities is the following: Whereas an equation will give you a concrete value for a variable, an inequality will only give you a range.
Compare:

If you plot these on the number line, you will see that the equation x = 7 provides one and only one value for x. On the other hand, the inequality x > 7 does not provide a specific value; instead, it restricts the possible values that x can be. Since x > 7, it can only be any number to the right of 7 on the number line.
As is the case with equations, your initial goal with inequalities will usually be to simplify what’s given to you. Fortunately, most of the rules you have learned for manipulating equations will also apply to inequalities.
Addition and Subtraction with Inequalities
x + 3 > 12. Solve for x.
SOLUTION:

Here is another example:
If –x + 2y > y – 2x, then which of the following must be true? (Indicate all that apply.)
 x > 0
x > 0
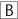 y > 0
y > 0
 x + y > 0
x + y > 0
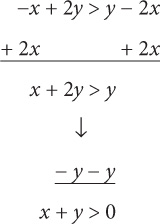
The correct answer is C.
When multiplying or dividing across an inequality, keep in mind the following rules:
If you multiply or divide across an inequality by a positive value, the inequality arrow does not change.
If 2x > 6, what is the range for x?
SOLUTION: To isolate x, divide both sides of the inequality by 2.
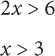
Note that the sign does not change, since you are dividing by a positive.
If you multiply or divide across an inequality by a negative value, the inequality arrow flips.
–2x < 6. Solve for x.
SOLUTION: Divide both sides by –2:
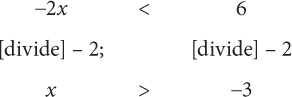
But remember to flip the sign: x > –3.
You cannot multiply or divide across an inequality by an unknown.
For example, if you are told that 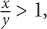 you may be tempted to multiply both sides by y and arrive at x > y. However, this would be incorrect. Why? Because you do not know the sign of y. Since you don’t know the sign of y, you do not know whether the inequality arrow will flip when you multiply. Thus you need to keep the inequality in its original form.
you may be tempted to multiply both sides by y and arrive at x > y. However, this would be incorrect. Why? Because you do not know the sign of y. Since you don’t know the sign of y, you do not know whether the inequality arrow will flip when you multiply. Thus you need to keep the inequality in its original form.
From the introduction to this section, recall that a compound inequality looks like the following: –7 < a + 3 < 12.
The rules for manipulating compound inequalities are the exact same ones as those for normal inequalities. Just make sure that you perform the same operation on all three parts of the inequality.
Let’s solve for a in the preceding example:
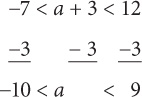
In some inequality questions, you will be presented with multiple inequalities, or with an inequality and an equation, and will be asked to draw inferences about their products. In these examples, choosing extreme values for the variables is often the optimal approach.
If a = 3 and –6 < b < 12, which of the following can equal ab? Indicate all that apply:
 –18
–18
 0
0
 18
18
 24
24
 36
36
SOLUTION: Since you are trying to figure out possible values of ab, you should consider the greatest value that ab could be and the smallest value that ab could be. Since you know a = 3, the product will be smallest when b is smallest. So choose the extreme value for b: in this case, –6. If b = –6, then ab = –18. However, you know b > –6. Therefore, ab > –18. Now try the upper bound. If b = 12, then ab = 36. However, you know that b < 12, meaning that ab < 36. You arrive at the compound inequality: –18 < ab < 36. The answer is B, C, and D.
Another common type of inequality question will give you two inequalities and ask you for the maximum or minimum value of their product. In these cases, it is essential to consider the extremes for all variables.
If –7 ≤ a ≤ 12 and –11 ≤ b ≤ 5, what is the maximum value of ab?
SOLUTION: The trap here is to multiply the maximum value for a and the maximum value for b and arrive at 60. However, note that if a and b are both negative, their product will be positive! Thus it is possible that the product of the smallest values of a and b will yield a larger value than the product of the largest values of a and b. And that is exactly what happens here: take the minimum value for a, –7; and the minimum value for b, –11; and the product is 77, which is greater than 60.
Let’s look at an example with minimization:
If –12 ≤ q ≤ 9 and 8 ≤ r ≤ 12, then the minimum value of qr = ?
SOLUTION: As in the preceding example, it might be tempting to multiply the smallest value for q and r and arrive at –96. However, note that when you multiply a negative and positive value, the result becomes smaller as the positive number becomes larger—for example, –3(9) < –3(7). Thus you will minimize qr when you multiply the minimum value of q by the maximum value of r: –12 × 12 = –144.
In its simplest form, absolute value refers to the distance between a number, variable, or expression and zero. Absolute value is denoted using brackets, for example, |(x + y)| or |–3|.
Since absolute value refers to distance, the absolute value of a number or expression will always be positive. For example, |–8| = 8 since –8 is 8 units away from zero.
When an unknown term or expression is within an absolute value, there will be two possible values for the unknown. For example, if |x| = 2, then x = 2 or x = –2. Why are there two values for x? Because absolute value refers to distance! Both 2 and –2 are two units away from zero, so x can equal either of those values. When solving for an unknown within an absolute value, use the following process:
If 9 + |x + 4| = 28, what are the possible values for x?
Step 1: Isolate the absolute value:

Step 2: Create two equations. In one equation, the expression inside the absolute value will equal the positive value on the right. In the other equation, the expression inside the absolute value will equal the negative version of the value on the right:
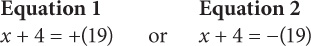
Step 3: Solve for the unknown in both equations:

In tougher absolute value questions, you will be given a range for the absolute value instead of a concrete value. For example:

To solve these questions, take the following approach:
If |x + 3| < 7, what of the following describes the range for x?
Step 1: Set up two solutions:
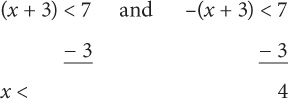
Step 2: Multiply by –1 (flip the sign!):
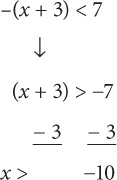
Step 3: Combine the inequalities:
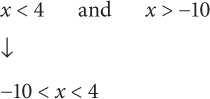
When answering a “must be true” question or Quantitative Comparison question with absolute values, it is helpful to test positive and negative cases.
For this question, indicate all of the answer choices that apply.
If x ≠ 0, then which of the following must be true? (Indicate all that apply).
 |x| = x
|x| = x
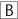
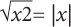

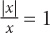


 |x| × |x| = x2
|x| × |x| = x2
SOLUTION: Choose a positive and a negative value for x, and see which choices are true for both cases. Let’s use –2 and 2 for x. Note that you will start with the negative case, since this is the case most likely to contradict the given equations.
A: 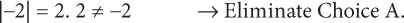
B: 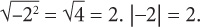 The equation is true when x = –2. Now try 2:
The equation is true when x = –2. Now try 2: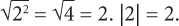 The equation is true when x = –2. → Keep Choice B.
The equation is true when x = –2. → Keep Choice B.
C: 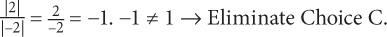
D: 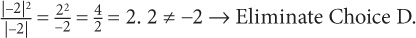
E: |–2| × |–2| = 2 × 2 = 4. (–2)2 = 4. The equation is true when x = –2. Now try 2: |2| × |2| = 2 × 2 = 4. (2)2 = 4. The equation is true when x = 2. → Keep Choice E.
The correct answer is C and E.
1. If –x + y > y + 2x, which of the following must be true?
 x < 0
x < 0
 y > 0
y > 0
 x + y > 0
x + y > 0
 x + y < 0
x + y < 0
 xy > 0
xy > 0
2. If |x + 3| = 12 and |y +2| = 9, the maximum value of xy =
 63
63
 84
84
 99
99
 132
132
 165
165
For this question, indicate all of the answer choices that apply.
3. If 3 + 9|x + 3| = 48, then x could equal which of the following?
 –8
–8
 –5
–5
 2
2
 3
3
 5
5
4. If x2 > 16, then x could equal which of the following?
 –3
–3
 –2
–2
 0
0
 3
3
 5
5
5. If a, b, and c are positive integers, a > b > c, and a + b + c < 27, what is the maximum value for a?
 23
23
 24
24
 25
25
 26
26
 27
27
For this question, indicate all of the answer choices that apply.
6. If x < y < 0, which of the following must be true?
 xy < y
xy < y
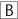 x + y < 0
x + y < 0

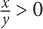
 |x| > |y|
|x| > |y|


7. If x > 8, y > 2x, and z > x, then y + z can equal all of the following EXCEPT
 56
56
 48
48
 40
40
 32
32
 24
24
For this question, write your answer in the box.
8. If |a + 3)| ≤ 6 and |(b + 4)| ≤ 12, what is the maximum value of ab?

9. If b, c, x, and y are positive and  which of the following must be true?
which of the following must be true?
 x > b
x > b
 x > c
x > c
 b > y
b > y
 b < y
b < y
 b > c
b > c
10. For how many integers, a, is it true that 2 < |a| < 9?
 4
4
 5
5
 6
6
 10
10
 12
12
1. A To simplify the inequality, combine like terms. Add x to both sides: y > y + 3x. Subtract y from both sides: 0 > 3x. Divide both sides by 3: 0 > x.
2. E To determine the maximum value of xy, you should first find the solutions for x and y. Solve for x:
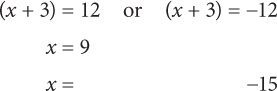
Solve for y:

The maximum value for xy will be (–15)(–11) = 165.
3. A and C When solving for an absolute value, you must isolate the term or expression inside the absolute value. Here, subtract 3 from both sides: 9|x + 3| = 45. Divide both sides by 9: |x + 3| = 5. Thus
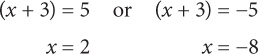
4. E Back-solving is a good approach here. Start with B: (–2)2 = 4. 4 is not greater than 16, so eliminate B. Since B is too small, any choice with an absolute value smaller than 2 will be too small. Thus C is also too small. Now look at 3: 32 = 9. 9 < 16. So you can eliminate D. 32 and (–3)2 have the same value, so A is also out.
5. A To maximize the value of a, you should first maximize the value of a + b + c. Since a + b + c < 27 and all the variables are integers, the maximum value of a + b + c = 26. Next, you should minimize the values of b and c. Since they are both positive integers and b > c, the minimum value for c = 1 and the minimum value for b = 2. Plug these values into the equation: a + 2 + 1 = 26. Solve for a: a = 23.
6. B, C, D, and E Use properties of positives and negatives to manipulate the choices:
A: Divide both sides by y: x > 1 (remember to flip the sign!). You know that x < 0, so x cannot be greater than 1. → Eliminate Choice A.
B: The sum of two negatives is negative. → Choice B is true.
C: negative/negative > 0. → Choice C is true.
D: If x is more negative than y, then x is further from zero than y is. → Choice D is true.
E: Multiply both sides by y: x < y (remember to flip the sign!). → Choice E is true.
7. E You have a range for x, and you have ranges for y and z in terms of x. Manipulate to get ranges for y and z. If x > 8, then 2x > 16. If y > 2x, then y > 16. If z > x and x > 8, then z > 8. Choosing extremes, you know that if y > 16 and z > 8, then y + z > 24. All of the values in the choices are greater than 24 except for E.
8. 192 To solve for the maximum value of ab, first get the ranges of a and b individually. If |a + 3| ≤ 6, then a + 3 must be at most 6 units away from zero. Expressed algebraically, this means that –6 ≤ a + 3 ≤ 6. Solve for a: –9 ≤ a ≤ 3. Go through the same process to determine a range for b. Using this reasoning, you can determine that –12 ≤ b + 4 ≤ 12. Solve for b: –16 ≤ b ≤ 8. It might be tempting to choose 24 as the maximum value of ab, but notice that (–16)(–9) will yield 192.
9. C Solution: Rewrite the inequality as (x/c)(b/y) > x/c. Divide both sides by (x/c): b/y > 1. Multiply both sides by y: b > y. Note that you were able to divide by these variables because you are told that all the variables are positive.
10. E Think of absolute value as distance from zero. If |a| is between 2 and 9, then a is between 2 and 9 units away from zero. Looking to the right of zero, this means that a can be any integer from 3 through 8, inclusive. Looking to the left of zero, this means that a can be any integer from –8 through –3, inclusive. There are 6 integers from 3 through 8, inclusive, and 6 integers from –8 through –3, inclusive. Thus there are 12 possible values for a. The correct answer is E.
1. A Since you are comparing an unknown to a value, let’s determine how the possible values of that unknown relate to 1. You have ranges for x and y, so choose extremes. If  and
and  then sum will be
then sum will be 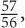 which is greater than 1. If you choose larger values for x and y, the sum will only get larger. Therefore, x + y will always be greater than 1.
which is greater than 1. If you choose larger values for x and y, the sum will only get larger. Therefore, x + y will always be greater than 1.
2. D The best approach here is to choose values. Since the columns deal with absolute values, you should consider positive and negative cases that satisfy x > y.
Case 1: x = 3 and y = 2. In this case, |3| is greater than |2| and Column A is greater.
Case 2: x = 3 and y = –5. In this case, |3| is less than |–5|, and Column B is greater. A relationship cannot be determined.
3. B It might be tempting to multiply the minimum value for a and the minimum value for b to arrive at –6. However, note that when you multiply a negative by a positive, the larger the positive number is, the more negative the product is. Thus to minimize ab, you should multiply –2 by the largest value for b: 5. –2(5) = –10, which is less than –6.
4. A When comparing an unknown to zero, your concern should be the sign of that unknown. You want to know the sign of a + b, so you should manipulate the given information to isolate a + b. Add 3b to both sides and arrive at 3a + 3b > 0. Factor: 3(a + b) > 0. Divide both sides by 3: a + b > 0.
5. B Since you want to compare 6y – 4x to a value, you should manipulate the given information to see if you can arrive at a range for 6y – 4x. First, isolate the terms with y and x by subtracting 2x from both sides of the given inequality: 12 > 3y – 2x. Since 6y – 4x is double 3y – 2x, you should multiply both sides of the inequality by 2: