 Lines and angles
Lines and angles
 Triangles
Triangles
 Polygons
Polygons
 Circles
Circles
 Solids and cylinders
Solids and cylinders
 The coordinate plane
The coordinate plane
Study this chapter to learn about:
About 20 percent of the questions on the GRE will deal with geometry. These questions will address your knowledge of geometric properties and formulas and your ability to use these formulas to construct algebraic relationships. When answering geometry questions, you should generally follow these steps:
1. Draw the diagram and input all given information.
2. Infer all properties and relationships implied by the diagram.
3. Use these relationships to create algebraic relationships.
4. Solve for what the question is asking for.
Notice that the approach for geometry questions is in many ways similar to the approach for word problems. In both cases, your ultimate goal is to use the information given to construct algebraic relationships. The distinguishing element of geometry questions is that you will use geometric principles instead of words to create these algebraic relationships. This chapter focuses on these principles and how they are tested on the exam.
An angle is formed at the intersection of two rays or lines. The measurement of an angle can be between 0 degrees and 360 degrees. The angle below has a measure of 45 degrees.
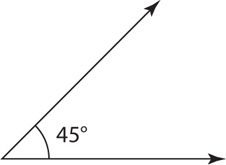
One type of angle that occurs throughout geometry questions is a right angle. A right angle has a measure of 90 degrees and is denoted by the square at the intersection of the two lines or rays. When two lines intersect to form a right angle, those lines are said to be perpendicular.

A straight line will always have an angle measure of 180 degrees. From this, you can infer Property 1: the angles on a line must add up to 180. Angles whose measures sum to 180 are termed supplementary angles.

What is the value of (a + b) in the figure above?
SOLUTION: Since these four angles lie on line CD:

The intersection of two lines will always create four angles.
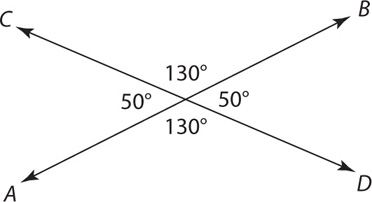
These angles have two properties:
1. They will add up to 360.
2. The angles opposite each other will be equal. These angles are termed vertical angles.

What is the value of x in the figure above?
SOLUTION: Since x and 2y lie on the same line, x + 2y = 180. The angle vertical to 2y = 80, so you can substitute 80 for 2y in the equation and solve: x + 80 = 180 → x = 100.
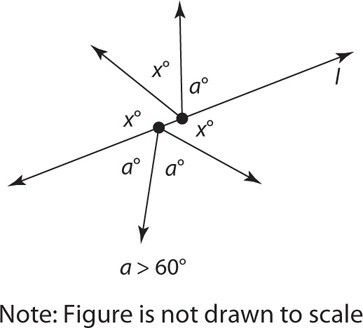
Note that the two preceding properties can apply to situations in which more than two lines intersect. Here is the more general form of Property 1: the angles around a point must add up to 360.
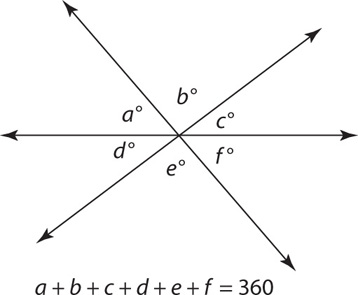
Since these angles are all around a point, a + b + c + d + e + f = 360. In addition, a = f, b = e, c = d. Finally, a, b, and c are supplementary, and d, e, and f are supplementary.
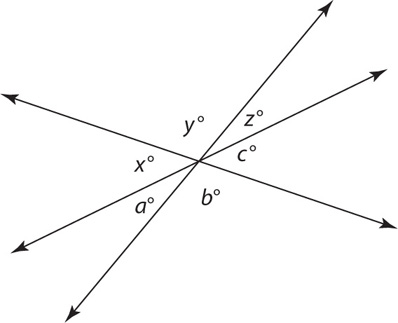
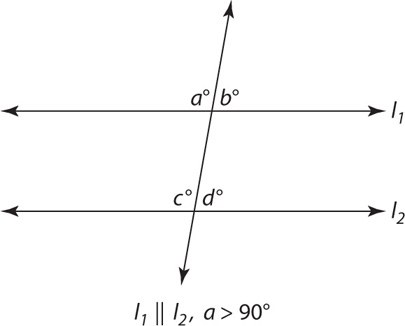
Parallel lines by definition will never intersect. On the GRE, you will be expected to understand the relationships among the angles of parallel lines cut by a transversal.
The best way to think about the relationship among the angles is in terms of the small angles and the large angles. All of the smaller angles will be acute (less than 90 degrees), and all of the larger angles will be obtuse (greater than 90 degrees). All the smaller angles will have the same measure, and all of the larger angles will have the same measure. Thus in the preceding diagram, x < 90, and y > 90. Finally, the sum of any small angle and any large angle will always be 180. Thus x + y = 180. Understanding and implementing these properties will equip you well on most questions that test parallel lines and transversals.
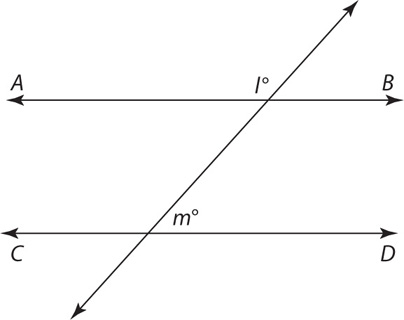
In the diagram above, lines AB and CD are parallel. If the ratio of l to m is 3 to 2, what is l?
SOLUTION: When two parallel lines are cut by a transversal, the sum of the small and large angles is 180. Thus l + m = 180. Since  =
= 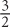 , you can let l = 3x and let m = 2x. Substitute these terms into the first equation:
, you can let l = 3x and let m = 2x. Substitute these terms into the first equation:

1. If y = 3x in the diagram above, then what is x?
 45
45
 60
60
 90
90
 115
115
 135
135
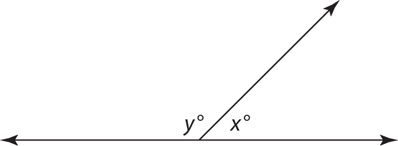
Questions 2–4 refer to the figure above.
2. If a + b = 100, what is y + z?
 60
60
 80
80
 100
100
 140
140
 It cannot be determined from the given information.
It cannot be determined from the given information.
3. If a > b > c, then which of the following must be true?
 a > 60
a > 60
 b < 60
b < 60
 z < 60
z < 60
 x = a
x = a
 x + a > 120
x + a > 120
4. In this figure, x + y = 75. What is the value of q – y?
 95
95
 100
100
 105
105
 110
110
 145
145
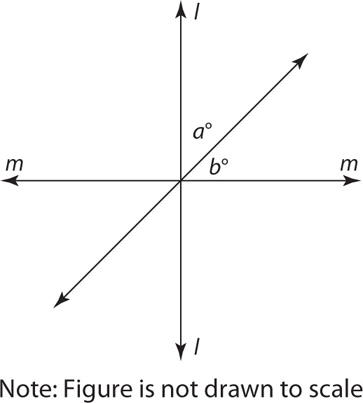
5. In the figure, lines l and m are perpendicular. If a = 3b, then a – b = ?
 22.5
22.5
 35
35
 45
45
 67.5
67.5
 75
75

Questions 6–8 refer to the figure above.
6. If b = 100, then c = ?
 50
50
 60
60
 70
70
 80
80
 100
100
7. If a = d + 30, then d = ?
 75
75
 80
80
 85
85
 90
90
 95
95
8. If a – c = 20, then what is the value of b?
 60
60
 80
80
 100
100
 110
110
 120
120
For this question, write your answer in the box.

9. In the figure above, d = 100. If a + b = 40, then a = ?



1. A Since y and x form the angles on a line, they must be supplementary. Thus y + x = 180. Substitute 3x for y:
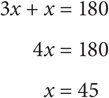
2. C Angles a, b, and x lie on a line, so a + b + x = 180. Substitute 100 for (a + b):
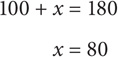
Since x, y, and z lie on a line, they are supplementary: x + y + z = 180. Substitute 80 for x:
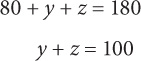
3. A Since angles a, b, and c lie on a line, a + b + c = 180. If a is the largest of the three values, then a must be greater than 60. To understand why, think of what would happen when a = 60. If a = 60 and b and c are smaller than a, then the sum of the three angles cannot be 180. Thus a > 60.
4. C Since b is a straight line, the five angles above a must add to 180: 4x + y = 180. Since x + y = 75, you can use substitution to solve for x: y = 75 – x. Substitute (75 – x) for y in the first equation:

If x = 35, then y = 40. Now solve for q. Since a is a straight line, x + q = 180. x = 35, so q = 180 – 35 = 145. q – y = 145 – 40 = 105.
5. C Since l and m are perpendicular, all the angles formed at the intersection of l and m must equal 90 degrees. Thus a + b = 90. Substitute 3b for a to solve for b:
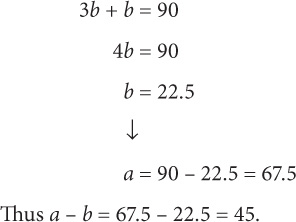
6. D Since b is a large angle created by the transversal and c is the small angle created by the transversal, b + c = 180. Substitute 100 for b:
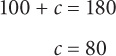
7. A Since l and k are parallel lines cut by a transversal, the sum of the smaller and larger angles must equal 180. Thus a + d = 180. Substitute d + 30 for a:
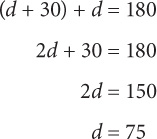
8. C Since a and c are the two angles above l, their sum must equal 180: a + c = 180. Add the two equations to solve for a:
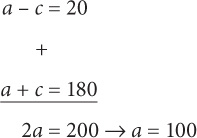
Since a and b are the larger angles formed by the transversal, they must be equal. Thus b = 100.
9. 30 Since (3a + b) and d are the larger angles formed by the transversal, 3a + b = 100. Combine this equation with a + b = 40:
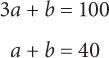
To solve for a, express b in terms of a: b = 40 – a. Substitute 40 – a for b in the first equation:
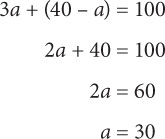
1. B Since a > 90, a must be the larger angle created by the transversal. Thus b and d must be the smaller angles created by the transversal. The smaller angles created by the transversal are always less than 90 degrees. Thus Quantity B is greater.
2. B Since a and b create line l, they must be supplementary. If a > 90, then b < 90.
3. A The angles above line l must add to 180. Thus 2x + a = 180. The angles below line l must add to 180. Thus 2a + x = 180. Add these equations:

Divide both sides by 3: x + a = 120. Since x > 60, a < 60.
4. D Although a and z are the larger angles formed by a transversal, the transversals forming these angles are different. Thus you can only infer that a and x are each greater than 90. No information can be deduced about their relationship. The correct answer is D.
5. A Since lines 1 and 2 intersect to the left of the diagram, they are not parallel. As they converge, the angles closer to them become smaller. Thus a > c, and b > d. Since a and c are supplementary and b and d are supplementary, a and c must each be greater than 90. Thus their sum must be greater than 180.
Triangles are the GRE’s favorite shape. They appear not only in questions that explicitly ask you about triangles, but also in disguised form on questions addressing other polygons, such as squares or rectangles. As you may recall from high school, there are numerous properties associated with triangles. Let’s look below at the properties you need to master for the GRE.

Basic Properties of Triangles
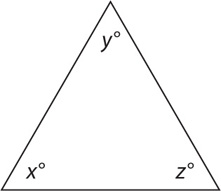
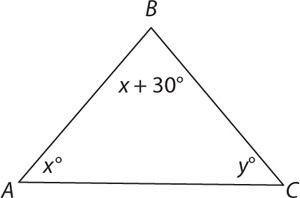
Basic Property 1: The sum of the internal angles in a triangle equals 180. Thus in the preceding diagram, a + b + c = 180.
In the figure above, x = y = 2z. What is x?
SOLUTION: Since x, y, and z are the interior angles of a triangle, x + y + z = 180. Use the given information to express all variables in terms of z:
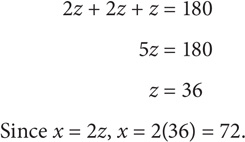
Basic Property 2: The length of any given side of a triangle must be greater than the difference of the other two side lengths and less than the sum of the other two side lengths.
For this question, indicate all the answer choices that apply.
If a triangle has side lengths of 4 and 7, which of the following could be the length of the third side of the triangle?
 3
3
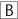 4
4
 5
5
 9
9
 11
11
 13
13
SOLUTION: The third side of the triangle must be greater than (7 – 4) and less than (7 + 4). Thus the length of the third side must be between 3 and 11. Of the choices, the length could be 4, 5, or 9.
Basic Property 3: The greater the measurement of a triangle’s angle, the greater the length of the corresponding side. An angle’s corresponding side is the side opposite that angle. In the following triangle, each angle’s corresponding side is indicated by the arrows. Note that this relationship also works in reverse: the greater the length of a side, the greater the measurement of the corresponding angle. It is also important to note that this information only provides a relationship between the corresponding sides and angles of a triangle. Without additional information, you cannot infer how much greater one side or angle is than another side or angle.
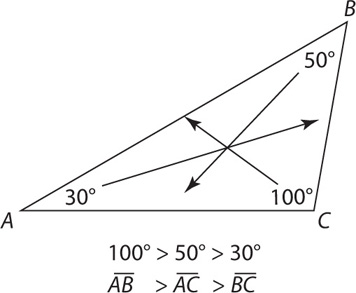
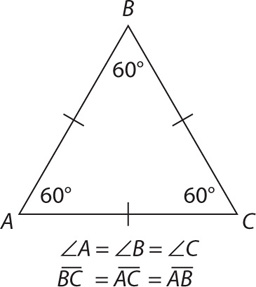
An isosceles triangle is any triangle that has two equal angles. Since the two angles are equal, the corresponding sides will also be equal. Thus as you saw with the Basic Property 3, the relationship works in reverse. If a triangle has two equal sides, it will be isosceles, and the angles opposite those sides will be equal.
This information is helpful because when you are working with an isosceles triangle, you can assign the same variable to different angles or sides.
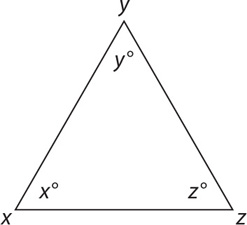
In the figure above, side XZ = side XY. If x = 2y, then y = ?
SOLUTION: Since YZ and XY are equal, their corresponding angles must be equal. Thus x = z. The sum of the interior angles of a triangle is 180, so x + x + y = 180. Substitute 2y for x:
However, from the fact that a triangle is isosceles, you cannot necessarily infer which sides or angles are equal.
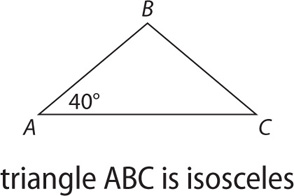
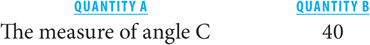
SOLUTION: Since triangle ABC is isosceles, it is possible that angle C = 40, in which case the two quantities are equal. However, it can also be the case that angle B = 40 and angle C = 100, in which case angle C > 40. Thus, the relationship cannot be determined. The answer is D.
An equilateral triangle is a triangle in which all angles are equal and all sides are equal. Since the angle measurements are the same and their sum is 180, each angle in an equilateral triangle measures 60 degrees.
The perimeter of a triangle is the sum of all the side lengths.
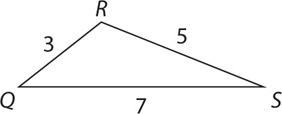
The perimeter of the preceding triangle is 3 + 5 + 7 = 15.
The area of a triangle refers to the amount of space within the triangle. Area is expressed in square units, such as cm2 (square centimeters), in.2 (square inches), and so on. The formula for the area of a triangle is ( ) × b × h.
) × b × h.
Note that the base (b) and height (h) must be perpendicular to each other. Look at the following figure:

In this example, the base is 8 and the height is 7. You know that the height is 7 because the line segment drawn from angle C creates a perpendicular angle when it intersects the base, AB. The area of this triangle will thus be  × 8 × 7 = 28.
× 8 × 7 = 28.
In the example, AB was the base of the triangle. However, any side can be the base of a triangle. The height will be defined as the perpendicular line from the angle opposite the base. Next, you will see the same triangle as earlier, but now BC is the base.

Now, to calculate the area:  × 4 × 14 = 28.
× 4 × 14 = 28.
Sometimes you will have to extend the base to determine the corresponding height:
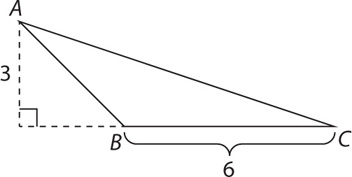
In this example, the base is 6. To draw the height, it was necessary to extend base BC until it intersected the height. The area of this triangle is  × 6 × 3 = 9.
× 6 × 3 = 9.
The GRE’s favorite shape is a right triangle. A right triangle is any triangle that has a 90-degree angle. The 90-degree angle is formed at the intersection of the two shorter sides, which are called the legs. The side opposite the 90-degree angle is the longest side of a right triangle. It is called the hypotenuse.

The formula for the area of any triangle applies to right triangles, but in right triangles, determining the area is easier than with other triangles. Why? Because the base and height will simply be the two sides that form the 90-degree angle. This is so because these two sides are perpendicular, meaning that one leg can be considered the base and the other leg can be considered the height (it doesn’t matter which leg you call the base and which leg you call the height).
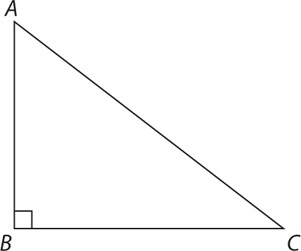
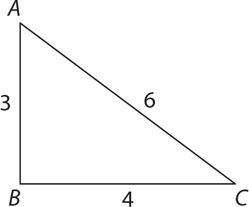
The area of the preceding triangle is 48. If the length of AB = 8, then what is the length of BC?
SOLUTION: The area of a right triangle is  × (leg 1) × (leg 2). Substitute 8 for (leg 1) and BC for leg 2:
× (leg 1) × (leg 2). Substitute 8 for (leg 1) and BC for leg 2:
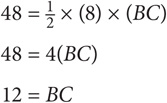
Recall from Basic Property 3 that the greater the angle of a triangle, the longer the corresponding side. Since the 90 degree angle in a triangle must be the largest angle of the triangle, its corresponding side must be the longest side of the triangle. This side is called the hypotenuse. The two sides forming the 90 degree angle are called the legs.
The Pythagorean theorem provides a relationship that always holds true between the sides of a right triangle. If a = the length of one leg, b = the length of the other leg, and c = the length of the hypotenuse, then:
a2 + b2 = c2
What is the perimeter of the triangle above?
 13
13
 17
17
 25
25
 30
30
 42
42
SOLUTION: To determine the perimeter, solve for side BC, which is the hypotenuse. You can use the Pythagorean theorem to solve for the hypotenuse:
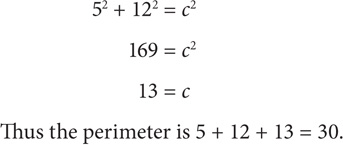
There are certain combinations of right-triangle side lengths that occur throughout the GRE. Though you can always use the Pythagorean theorem in these situations, you will save precious time by memorizing these triplets and their multiples:
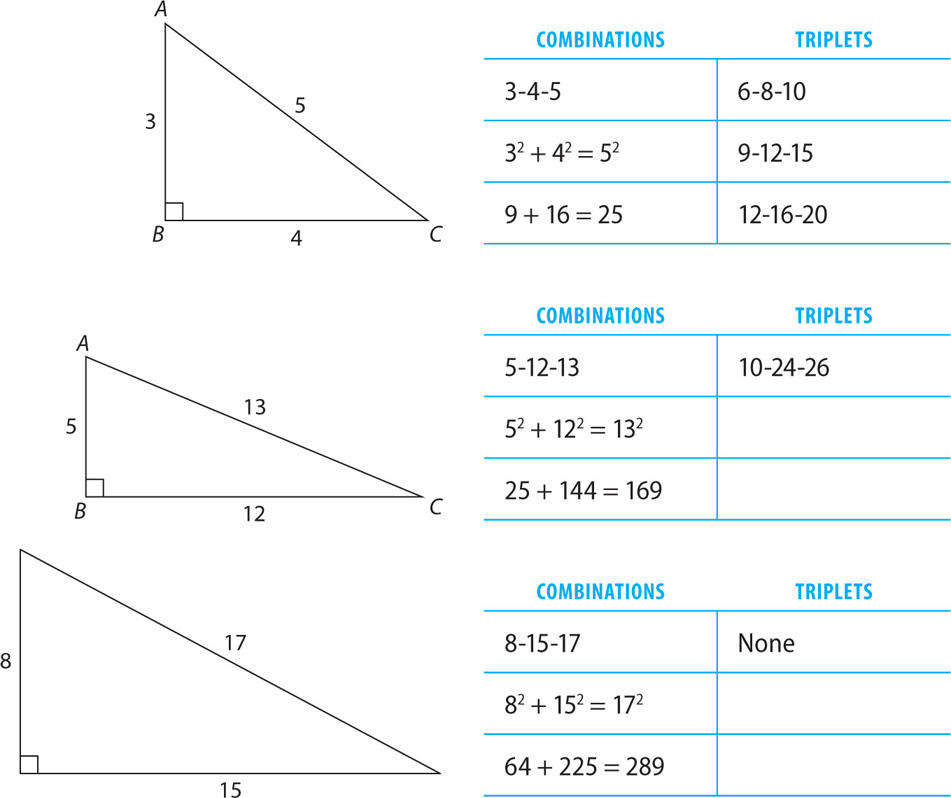
What is the perimeter of the figure above?
SOLUTION: To determine the perimeter, you need to add up all the sides. You know all the side-lengths except CD. To solve for CD, first solve for AC. The legs of right triangle ABC have lengths of 3 and 4, so AC = 5. If AC = 5 and AD = 12, then CD = 13. The perimeter of the figure is thus 3 + 4 + 12 + 15 = 34.
However, be careful about assuming that any right triangle with two side lengths from the Pythagorean triplets will necessarily conform to the preceding list. The triplets only apply in situations where the largest value of the triplet is the length of the hypotenuse:


SOLUTION: Even though ABC is a right triangle with two sides of 3 and 4, it is not a Pythagorean triplet. The side with length 4 is the hypotenuse, which means that the length of AC must be less than 4. Thus Quantity B is greater.
In addition to the Pythagorean triplets, there are two other triangle combinations that you will need to know for the GRE: isosceles right triangles and 30-60-90 triangles.
An isosceles right triangle is any right triangle in which the lengths of the legs are equal. Since the lengths of the legs are equal, their corresponding angles will also be equal, with each having a measurement of 45 degrees. Thus another term for an isosceles right triangle is a 45-45-90 triangle.
The legs of every isosceles right triangle will have a specific ratio that you should memorize:

It is important to note that the preceding combination only specifies a ratio, and not actual values. For example, if you are told that the leg length of an isosceles triangle is 5, then the hypotenuse is 5 . Or if the leg length is 7. 3
. Or if the leg length is 7. 3 , then the hypotenuse is 7.3. The best way to think about the relationships of the leg lengths is that the hypotenuse will be
, then the hypotenuse is 7.3. The best way to think about the relationships of the leg lengths is that the hypotenuse will be  × the leg.
× the leg.
One commonly tested fact about 45-45-90 triangles is that the diagonal of a square will form two 45-45-90 triangles. This is helpful because you can use the diagonal of the square to solve for the side lengths of the square and vice versa.
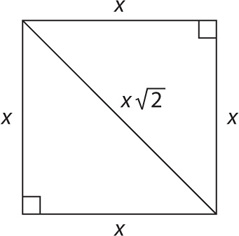
What is the area of a square with a diagonal of length 20?
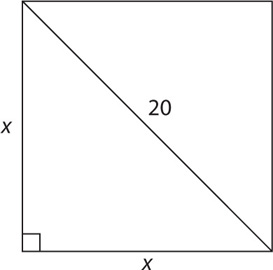
Solution: To solve for the area, you need the length of a side. The length of the side will be the leg of an isosceles right triangle with a hypotenuse of 20. Let x = leg length:
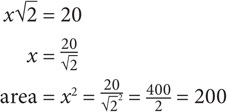
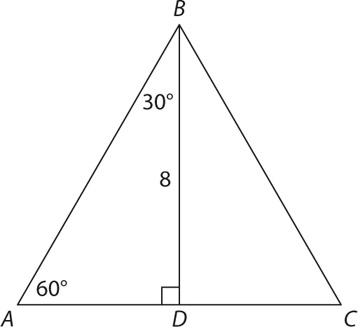
The other type of special right triangle you need to master is the 30-60-90 triangle. To understand the properties of a 30-60-90 triangle, look at what happens when you draw the height of an equilateral triangle:
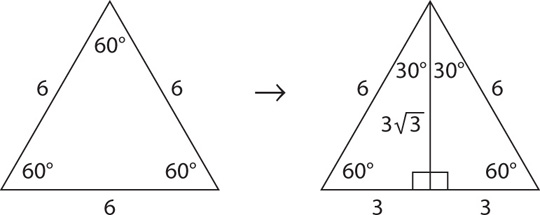
Fact 1: The height of an equilateral triangle will cut the base in half.
Fact 2: The resulting smaller triangles will have degree measurements of 30-60-90.
Fact 3: The sides of the 30-60-90 triangle will be in the following ratio, which you must memorize:
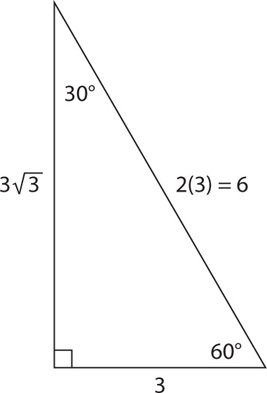
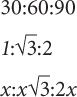
Finally, as was the case with 45-45-90 triangles, with 30-60-90 triangles, the side relationships only specify ratios, not values.

What is the perimeter of triangle BCD in the figure above?
SOLUTION: To determine the perimeter, you must determine the side lengths of BCD. Note that side BC is the hypotenuse of the 45-45-90 triangle ABC. Thus BC = 5 ×
×  = 5 × 2 = 10. Since BC is the shorter leg of 30-60-90 triangle BCD, the longer leg, CD, will equal 10
= 5 × 2 = 10. Since BC is the shorter leg of 30-60-90 triangle BCD, the longer leg, CD, will equal 10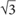 , and the hypotenuse, BD, will equal 10 × 2 = 20. The perimeter of BCD is thus 10 + 20 + 10
, and the hypotenuse, BD, will equal 10 × 2 = 20. The perimeter of BCD is thus 10 + 20 + 10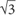 = 30 +
= 30 + 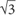 .
.
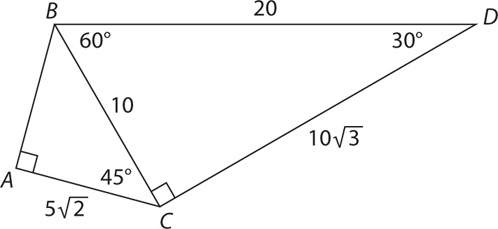

1. In the figure above, what is the value of a?
 30
30
 35
35
 140
140
 145
145
 150
150
2. In triangle ABC, side AB = 3 and side BC = 8. Which of the following CANNOT be the perimeter of triangle ABC?
 18
18
 19
19
 20
20
 21
21
 22
22
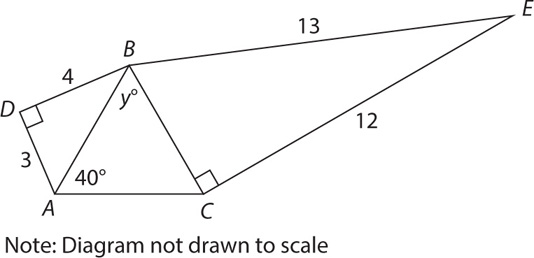
3. What is the value of y in the figure above?
 30
30
 40
40
 45
45
 60
60
 100
100
For this question, write your answer in the box.
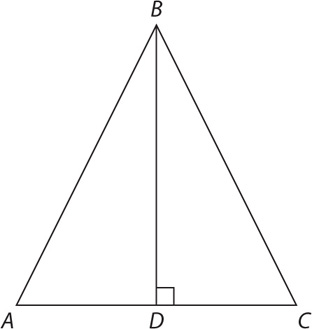
4. In the figure shown, the length of altitude BD is  . What is the area of equilateral triangle ABC?
. What is the area of equilateral triangle ABC?

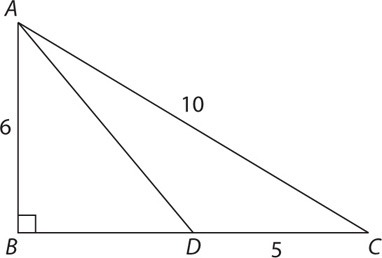
5. What is the length of AD in the figure above?

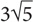


 8
8

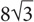


6. In the figure above, angle BAD = angle ABD. What is the area of triangle ABD?
 30
30
 60
60
 72
72
 102
102
 144
144
7. The base of a 20-foot rope is 8 feet above the ground. If the rope is extended at a 60-degree angle, the top of the rope will be how many feet above the ground?
 18
18
 28
28
 10
10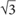
 10
10 + 8
+ 8
 10
10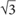 + 8
+ 8
For this question, write your answer in the box.
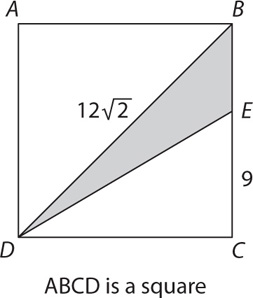
8. In the figure above, what is the area of triangle BDE?

9. In the figure above, BD = DC. If AD = 6, what is BD?
 4
4
 6
6
 8
8
 10
10
 12
12

10. What is the perimeter of triangle ABC?
 44
44
 45
45
 54
54
 60
60
 96
96
For this question, write your answer in the box.
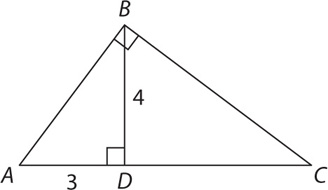
11. If the perimeter of triangle ABC is 20, what is the length of DC?

12. The area of the triangle above is 24. If a is 2 more than b, what is c?
 6
6
 8
8
 10
10

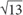
 2
2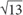
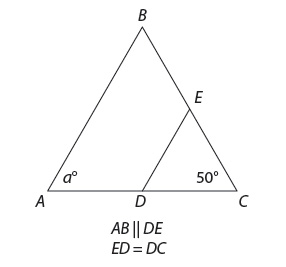
13. If XZ is double AC, then the area of triangle XYZ is how many times greater than the area of triangle ABC?


 2
2
 4
4
 8
8
 16
16
14. What is the value of a?
 30
30
 50
50
 80
80
 130
130
 150
150
15. If the angles of a triangle are in the ratio 3:4:5, what is the measurement of the smallest angle?
 45
45
 60
60
 75
75
 90
90
 100
100
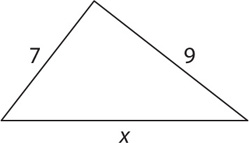
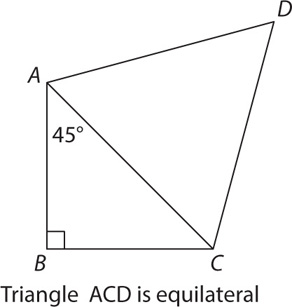
Two sides of an isosceles triangle have lengths of 7 and 12.


The area of triangle XYQ < the area of triangle YQZ

1. D Since the interior angles of a triangle add up to 180,

Since a and x are supplementary, a + x = 180. Substitute 35 for x:
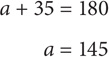
2. E The length of AC must be greater than (8 – 3) and less than (8 + 3). Thus 5 < AC < 11. The perimeter of the triangle will be AB + BC + AC = 8 + 3 + AC = 11 + AC. Since 5 < AC < 11, the perimeter must be less than (11 + 11) = 22 and greater than (5 + 11) = 16. The only value in the choices that is not between 16 and 22 is E.
3. E Triangle ABD is a 3-4-5 triangle, so AB = 5. Triangle BCE is a 5-12-13 triangle, so BC = 5. Since AB and BC are equal, their corresponding angles must be equal: angle BAC = angle BCA. You are told that angle BAC = 40, so you can infer that angle BCA = 40. Since the interior angles of a triangle sum to 180, y + 40 + 40 = 180 → y = 100.
4. 9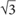 To get the area of ABC, you will need to determine the length of the base. Since BD is the altitude of an equilateral triangle, BCD is a 30-60-90 triangle. The altitude is opposite the 60-degree angle, and DC is opposite the 30-degree angle. Since BD = 3
To get the area of ABC, you will need to determine the length of the base. Since BD is the altitude of an equilateral triangle, BCD is a 30-60-90 triangle. The altitude is opposite the 60-degree angle, and DC is opposite the 30-degree angle. Since BD = 3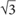
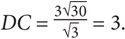 If DC = 3, then AC = 3 (since triangles ABD and BDC are identical). Thus AC = 6. The area of triangle ABC is:
If DC = 3, then AC = 3 (since triangles ABD and BDC are identical). Thus AC = 6. The area of triangle ABC is:
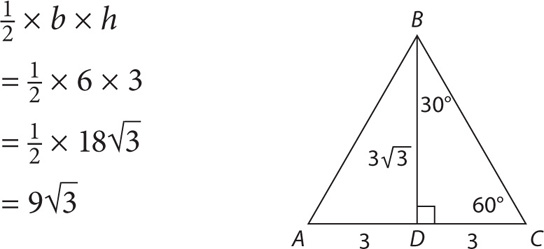
5. A Since triangle ABC has a leg of 6 and a hypotenuse of 10, side BC = 8 (this is a 6-8-10 triangle). If BC = 8, then BD = 8 – 5 = 3. AB2 + BD2 = AD2. Substitute:

6. C Since angle BAD = angle ABD, triangle ABD is an isosceles right triangle. Let x = the length of each leg of triangle ABD. The area will be  Solve for x. Triangle BDC is a right triangle with a leg of 5 and hypotenuse of 13. It is thus a 5-12-13 triangle. Side BD = 12. Substitute 12 for x to solve for the area of triangle ABD:
Solve for x. Triangle BDC is a right triangle with a leg of 5 and hypotenuse of 13. It is thus a 5-12-13 triangle. Side BD = 12. Substitute 12 for x to solve for the area of triangle ABD: 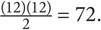
7. E First, draw the diagram:

The rope starts off 8 feet above the ground. To determine its total height from the ground, solve for the side opposite the 60-degree angle and add 8. Since the triangle in the diagram is a 30-60-90 triangle, the side opposite the 60-degree angle will be 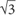 × the side opposite the 30-degree angle. The side opposite the 30-degree angle is half of the hypotenuse:
× the side opposite the 30-degree angle. The side opposite the 30-degree angle is half of the hypotenuse:  The side opposite the 60-degree angle is thus 10
The side opposite the 60-degree angle is thus 10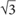 The rope is thus 8 + 10
The rope is thus 8 + 10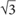 feet off the ground.
feet off the ground.
8. 6 Since triangles BDC and EDC are right triangles, calculate the area of triangle BDC and subtract that from the area of triangle EDC. Calculate the area of triangle BDC: since ABCD is a square, the diagonal is times the base. Thus DC = 12. If DC = 12, the area of triangle BDC = 12 × 12 ×  = 72.
= 72.
Calculate the area of triangle EDC: Since ABCD is a square, the diagonal is  times the base. Thus DC = 12. If DC = 12, the area of triangle EDC = 12 × 9 ×
times the base. Thus DC = 12. If DC = 12, the area of triangle EDC = 12 × 9 ×  = 54. The difference of the areas of triangles BDC and EDC is 72 − 54 = 18.
= 54. The difference of the areas of triangles BDC and EDC is 72 − 54 = 18.
9. B Since ∠BDC is the exterior angle of triangle BAD,
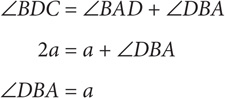
If ∠DBA = a, then triangle BAD is isosceles, and BD = AD. Since AD = 6, BD = 6. Since BD = DC, DC = 6.
10. D To solve for the perimeter, you need to solve for AB and DC. Triangle ABD is a 9-12-15 triangle (one of the multiples of a 3-4-5 triangle), so AB = 15. Triangle BDC is a 12-16-20 triangle (one of the multiples of a 3-4-5 triangle), so DC = 16. The perimeter is thus 15 + 20 + 9 + 16 = 60.
11. 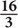 This is a challenging question! First, identify that AB = 5, since AB is the hypotenuse of a 3-4-5 triangle. Next, let DC = x. Since triangle BDC is a right triangle, you can use the Pythagorean theorem to express BC in terms of x:
This is a challenging question! First, identify that AB = 5, since AB is the hypotenuse of a 3-4-5 triangle. Next, let DC = x. Since triangle BDC is a right triangle, you can use the Pythagorean theorem to express BC in terms of x:
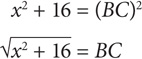
Square both sides:

12. C Since c is the hypotenuse of the right triangle, solve for a and b, and use the Pythagorean theorem to solve for c. Since the area is 24,

Since b represents the length of a side, it must be positive. Thus b = 6. If b = 6, then a = 8. The triangle is thus a 6-8-10 triangle. c = 10.
13. C Plug in values: Let XZ = 2 . In this case, XY and XZ will each equal 2. The area of triangle XYZ will be 2 × 2 ×
. In this case, XY and XZ will each equal 2. The area of triangle XYZ will be 2 × 2 ×  = 2. If XZ = 2
= 2. If XZ = 2 , then AC =
, then AC =  . If AC = 2
. If AC = 2 , then AB and BC = 1. The area of triangle ABC is thus 1 × 1 ×
, then AB and BC = 1. The area of triangle ABC is thus 1 × 1 ×  =
=  2 is 4 times as great as
2 is 4 times as great as  .
.
14. C Since AB and ED are parallel lines cut by a transversal, the measure of angle BAD = the measure of angle EDC. Solve for EDC. Since ED = DC, angle ECD = angle DEC. Thus angle DEC = 50. Thus 50 + 50 + EDC = 180 → EDC = 80. Since EDC = 80, BAD = 80.
15. A Use the unknown multiplier:
3x = smallest angle
4x = middle angle
5x = largest angle
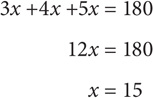
The measurement of the smallest angle is 3(15) = 45.
1. B Based on the triangle inequality theorem,
(9 − 7) < x < (7 + 9)
2 < x < 16
Since x < 16, Quantity B is greater. The correct answer is B.
2. D Since the triangle is isosceles, the third side can have a length of 7 or 12. If the length of the third side is 7, then the perimeter is 7 + 7 + 12 = 26. In this case, the two quantities are equal. If the third side is 12, then the perimeter is 7 + 12 + 12 = 31. In this case, Quantity A is greater. The relationship cannot be determined.
3. A Recall that the relationship of the sides in an obtuse triangle is a2 + b2 < c2. In the triangle, this inequality is satisfied: 32 + 42 < 62. Thus triangle ABC is obtuse and the measure of angle ABC > 90.
4. A To determine a relationship between the areas, determine the relationship between the side lengths. If the altitude in the triangle in Quantity A is 8, then the side length must be more than 8. To understand why, see the following figure.
Side AB is the hypotenuse of triangle ABD, which means that AB > 8. Thus the side length of the triangle in Quantity A is greater than the side length of the triangle in Quantity B. Therefore, the area of the triangle in Quantity A is greater.
5. D From the diagram, you can infer that
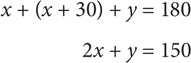
However, without any other relationships, the relationship between x and y cannot be determined.
6. C Recall that the diagonal of a square splits the square into two right triangles. Since leg BC of 45-45-90 triangle ABE = the side of BCDE, the hypotenuse of ABE = the diagonal of BCDE. Thus ABE  = of BCDE. The two quantities are equal.
= of BCDE. The two quantities are equal.
7. B The shared side of the two triangles is AC. The perimeter of triangle ACD = 3(AC). Since AC is the hypotenuse of a right triangle, the legs must be less than AC. Thus the perimeter of ABC will be less than 3(AC) and therefore less than the perimeter of ACD.
8. B The area of XYQ =  × XQ × YQ. The area of YQZ = × QZ × YQ. Thus
× XQ × YQ. The area of YQZ = × QZ × YQ. Thus
 × XQ × YQ <
× XQ × YQ <  × QZ × YQ → XQ < QZ
× QZ × YQ → XQ < QZ
To solve for XY, use the Pythagorean theorem: (XQ)2 + (YQ)2 = (XY)2. To solve for YZ, use the Pythagorean theorem: (QZ)2 + (YQ)2 = (YZ)2. Since both triangles share side YQ and XQ < QZ, XY must be less than YZ.
9. C Since AB = BC, angle BAC = angle BCA.
BAC + BCA = 110
BAC = 55 and BCA = 55
If ∠BAC = 55, then ∠BAD = 55 − 30 = 25. Since AD = DC, angle ∠DCA = 30. If ∠DCA = 30 and ∠BCA = 55, then ∠BCD = 55 − 30 = 25. The two quantities are equal.
A polygon is any two-dimensional shape. Familiar examples of polygons are squares, triangles, and rectangles. Here are some definitions that you will find useful in working with polygons:
 The Sum of the Angles: The sum of the angles of any polygon can be determined by using the following formula: sum of the angles = (n − 2)180, where n = the number of sides.
The Sum of the Angles: The sum of the angles of any polygon can be determined by using the following formula: sum of the angles = (n − 2)180, where n = the number of sides.
 The Perimeter of a Polygon: The perimeter of any polygon will be the sum of its side lengths.
The Perimeter of a Polygon: The perimeter of any polygon will be the sum of its side lengths.
 Quadrilaterals: A quadrilateral is any four-sided polygon. The sum of the angles of any quadrilateral is 360. The quadrilaterals most commonly tested on the GRE are parallelograms.
Quadrilaterals: A quadrilateral is any four-sided polygon. The sum of the angles of any quadrilateral is 360. The quadrilaterals most commonly tested on the GRE are parallelograms.
 Parallelograms: A parallelogram is a quadrilateral in which opposite sides are parallel.
Parallelograms: A parallelogram is a quadrilateral in which opposite sides are parallel.
A parallelogram has the following properties:
1. Opposite sides are equal.
2. Opposite angles are equal.
3. The area = base × height.
4. The diagonal of a parallelogram creates two equivalent triangles.
5. Adjacent angles add up to 180.
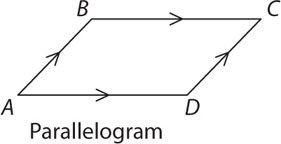
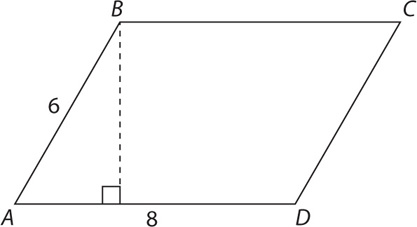
In the parallelogram above, a = 2b. What is c?
SOLUTION: From Property 4, you know that a + b = 180. Substitute 2b for a:

From Property 2, you know that a = c. Thus c = 120.
A rectangle is a special type of parallelogram in which all angles equal 90 degrees. The area of a rectangle is l × w. The perimeter of a rectangle is 2(l + w).
A square is a special type of rectangle in which all sides are equal. The area of a square = s2 (where s = the length of a side). The perimeter of a square is 4s (where s = the length of a side).
What is the area of a square that has a perimeter of 20?
SOLUTION: Let s = the length of a side of the square. Thus
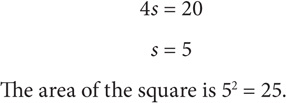
In a certain rectangle, the length is double the width. If the area of the rectangle is 72, what is the length of the rectangle?
SOLUTION: Let w = the width of the rectangle. The length therefore equals 2w. The area of the rectangle is lw = 2w × w = 2w2 = 72. Thus
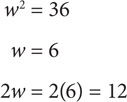
Some tougher GRE questions will give you the perimeter of a parallelogram or triangle and ask you for the maximum area. Given a fixed perimeter, the maximum area of any polygon will be reached when all sides are equal.
To maximize the area of a rectangle, you should make the side lengths equal. Notice that when you do so, you create a square!
What is the maximum area of a rectangle with a perimeter of 28?
SOLUTION: To maximize the area of the rectangle, make all the sides equal. Let x = the length of one side. The perimeter is thus
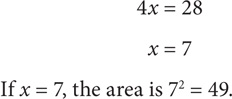
In the preceding examples, you used the perimeter of the shapes to determine the side lengths that would maximize the area. Sometimes you will be given the lengths of the two sides of a parallelogram or triangle and asked to determine the maximum area from this information. In these situations, use the following rule: Given the lengths of two sides of a triangle or parallelogram, you can maximize the area by making the two sides perpendicular. In the case of a parallelogram, this means creating a rectangle. In the case of a triangle, this means creating a right triangle.

SOLUTION: To maximize the area of the triangle, make it a right triangle. Assume that the legs are AB and BC. In this case, the area of the triangle is  × 3 × 4 = 6. Quantity B is greater.
× 3 × 4 = 6. Quantity B is greater.

1. The area of rectangle ABCD is equal to the area of rectangle MNOP. What is the length of MN?
 30
30
 40
40
 50
50
 60
60
 70
70
For this question, write your answer in the box.
2. The angles in a six-sided polygon are in the ratio 2:3:4:4:5:6. What is the measure of the smallest angle?

3. A certain rectangle has an area of 36 and a perimeter of 26. If the length of the rectangle is greater than the width, what is the rectangle’s length?
 4
4
 6
6
 9
9
 10
10
 13
13
4. The area of the rectangle above is 36. What is the length of diagonal AC?
 6
6
 12
12
 18
18
 24
24
 30
30

5. In the figure above, the area of square ABCD is half the area of rectangle AEFC. What is the ratio of AC to BE?









6. In the figure above, ABCD is a square with an area of 64. If E is the midpoint of BC and F is the midpoint of DC, what is the area of the shaded region?
 24
24
 32
32
 48
48
 56
56
 60
60
For this question, write your answer in the box.
7. What is the maximum possible area of a rectangle with a perimeter of 24?


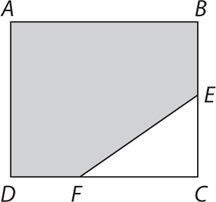
8. What is the area of the figure above?
 18
18
 24
24
 26
26
 32
32
 40
40
For Questions 9 and 10, write your answer in the box.
9. What is the maximum possible area of a triangle with a side of length 7 and another side of length 10?

10. A rectangle has an area of 48 and a diagonal of 10. What is the perimeter of the rectangle?

The area of square A is double the area of square B
Quadrilateral ABCD is a parallelogram Angle ACD is less than 60
1. D ADC is a right triangle with sides 30, 40, and 50 (this is a multiple of the 3-4-5 triangle). Thus AD = 30. If AD = 30, the area of ABCD = lw = 30(40) = 1,200. Since the area of MNOP = 1,200:
0 × (MN) = 1,200
MN = 60
2. 60 Recall that the sum of the angles of a polygon = (n − 2)180, where n = number of sides. Thus the sum of the angles in a six-sided polygon is (6 − 2)180 = 4(180) = 720. Use the unknown multiplier to represent the quantities of the angles as 2x, 3x, 4x, 4x, 5x, and 6x. The sum of these quantities = 720:
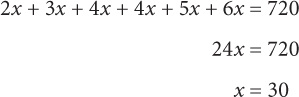
The smallest angle = 2x = 2(30) = 60.
3. C Let l = length of the rectangle and w = width of the rectangle:
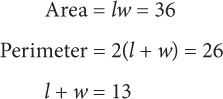
Use substitution to solve for l: w = 13 − l. Substitute (13 − l) for w in the first equation:
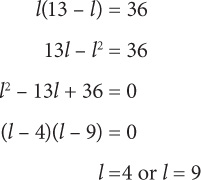
If l = 4, then w = 9. If l = 9, then w = 4. Since you are told that l > w, l = 9. The correct answer is C.
4. B The length and width of the rectangle are the legs of the 30-60-90 triangle ABC. Let the length of AB = x. The length of BC is thus x 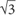 . Thus:
. Thus:

The hypotenuse of a 30-60-90 triangle is double the shorter leg. Thus AC = 12.
5. D Since this question only provides relationships and no values, plugging in is a good strategy. First, choose a value for the area of the square. If AB = 2, then the area of the square = 22 = 4. If the area of the square is 4, then the area of the rectangle must be 8. Since lw = AC × AE = 8, AE = 4. If AB = 2, then BE = 2. The ratio of AC to BE is 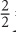 =
=  .
.
6. D To determine the area of the shaded region, subtract the area of the triangle from the area of the square. You are told that the area of the square is 64, so you must solve for the area of the triangle. Since the area of the square is 64, the length of each side must be 8. If the length of each side is 8, then FC = 4 and EC = 4. Since ECF is a right triangle, its area is  × 4 × 4 = 8. The area of the shaded region is thus 64 − 8 = 56.
× 4 × 4 = 8. The area of the shaded region is thus 64 − 8 = 56.
7. 36 To maximize the area of a rectangle, make the length and width as close as possible. You are told that
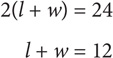
Let l = w = 6. The resulting shape will be a square. The area of the square is 62 = 36.
8. C Identify shapes within the figure that you are familiar with. The shape can be redrawn as a rectangle and right triangle, as indicated in the figure below:
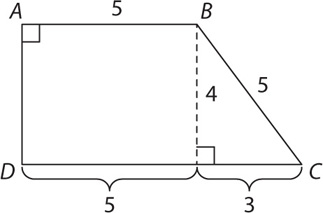
To find the area of the figure, add the area of the resulting rectangle and triangle. The area of the rectangle is l × w = 5 × 4 = 20. The area of the triangle is  × b × h =
× b × h =  × 3 × 4 = 6. The area of the figure is 20 + 6 = 26. The correct answer is C.
× 3 × 4 = 6. The area of the figure is 20 + 6 = 26. The correct answer is C.
9. 35 To maximize the area of a triangle, make the given sides perpendicular. When you do so, you will have a right triangle. Since 7 and 10 are the leg lengths of this right triangle, the area of the triangle is  × 7 × 10 = 35.
× 7 × 10 = 35.
10. 48 You are asked to solve for 2(l + w), where l = length of the rectangle and w = width of the rectangle: area = lw = 48. The diagonal of a rectangle cuts the rectangle into two equivalent right triangles in which the legs are the length and width of the rectangle.
1. A Plug in numbers. Let the area of square A = 16. In this case, the area of square B = 8. Each side of square A has a length of 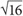 = 4. Each side of square B has a length of
= 4. Each side of square B has a length of 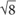 = 2
= 2 . The ratio of 4 to 2
. The ratio of 4 to 2 is less than 2.
is less than 2.
2. A Interior angles of a parallelogram must add up to 180. Thus the sum of the measures of angles ACD and CAB is 180. If the measure of angle ACD is less than 60, then the measure of angle CAB must be greater than 120.
3. A Recall that the sum of the interior angles of a regular polygon can be arrived at with the following formula: (n − 2)180, where n = number of sides. Since an octagon has 8 sides, the sum of its angles is (8 − 2)180 = 1,080. The measure of each angle is  Quantity A is greater.
Quantity A is greater.
4. A The area of a parallelogram can be determined by using the formula base × height. The base of the parallelogram is 8. To determine the relationship between the quantities, you must determine the relationship between the height and 6. Note that when you drop the height, a right triangle is formed in which the height of the parallelogram is one of the legs, and side AB is the hypotenuse.
Since each leg of a right triangle must be smaller than the hypotenuse, the height of the parallelogram must be less than 6. The area of the parallelogram is thus less than 48.
5. B Instead of calculating, recognize that if BC were extended to have a length of 10, the area of the resulting rectangle would be 40. Since BC is less than 10, the area of the trapezoid must be less than 40.
A circle is a group of points that are all equidistant from a central point, known as the center. Any line segment that connects the center to a point on the circle is called the radius. Any circle has infinite radii, and all radii for a given circle are equal.
A chord is any line that connects two points on a circle. The diameter of a circle is any chord that passes through the center of the circle. The diameter is the longest possible chord.
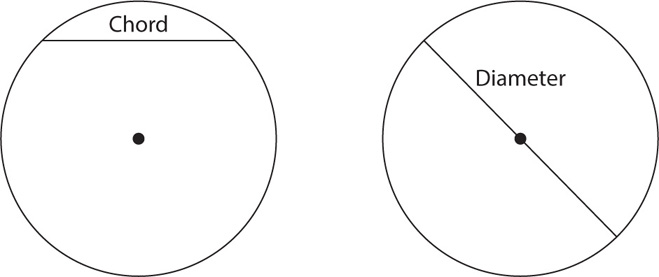
Note that for any given circle, the diameter is twice the radius. Thus when you are provided with the diameter of a circle, you can determine its radius and vice versa. A diameter is one type of chord.
Let’s now look at calculations that involve the diameter and radius. The circumference of a circle is the perimeter of the circle. Think of it in the following way: If you flattened the circle to be a straight line, the length of that straight line would be the circle’s circumference.
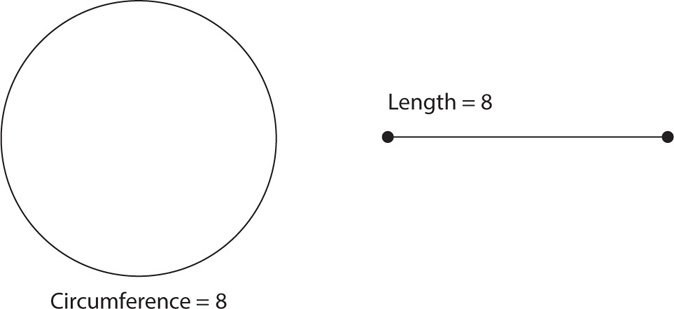
There is a constant relationship between circumference and diameter:

From this, you can derive the formula for circumference:
circumference = π × diameter (d)
Pi (π) might appear intimidating, but it’s simply a constant. Its value is roughly 3.14. For the GRE, though, almost any question that involves π will expect you to represent your answer using π instead of a decimal. For example, if you are asked to solve for the circumference of a circle with a diameter of 8, the answer would be 8π instead of 8 × 3.14 = 25.12.
What is the radius of a circle whose circumference is 24π?
 6
6
 12
12
 18
18
 24
24
 30
30
SOLUTION: Use the circumference formula:
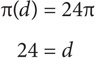
Since the radius is half of the diameter, the radius of the circle is 12. The correct answer is B.
The next element of a circle that you can calculate using radius and diameter is the area. The area of a circle represents the amount of space within that circle.

The formula for area of a circle is πr2.
If a circle has a circumference of 16π, what is its area?
 4π
4π
 8π
8π
 16π
16π
 64π
64π
 256π
256π
SOLUTION: To solve for the circle’s area, you need to determine the radius. Use the formula for circumference to determine the radius:

Since d = 2r, r = 8. Substitute 8 for r in the area formula: area = π82 = 64π. The answer is D.
Sector area represents the area of a piece of a circle. Arc length represents the length of a piece of a circle’s circumference.

 To determine sector area, you will need to know the area of the circle and what fraction the given piece is of the entire circle’s area.
To determine sector area, you will need to know the area of the circle and what fraction the given piece is of the entire circle’s area.
 To determine arc length, you will need to know the circumference of the circle and what fraction the arc length is of the entire circumference.
To determine arc length, you will need to know the circumference of the circle and what fraction the arc length is of the entire circumference.
If you are told what fraction the arc length or sector area is of a given circle, the question is pretty straightforward. Let’s say a circle has an area of 16π. If you are asked to determine the area of  of this circle, just divide the area by 4 and arrive at 4π. Likewise, let’s say a circle has a circumference of 8π. If you are asked to calculate
of this circle, just divide the area by 4 and arrive at 4π. Likewise, let’s say a circle has a circumference of 8π. If you are asked to calculate  of the circumference, just divide the circumference by 4, and arrive at 2π.
of the circumference, just divide the circumference by 4, and arrive at 2π.
Unfortunately, a real GRE question will not make things so simple. Instead of telling you what fraction the sector is of the entire circle, a typical question will expect you to infer this information from the central angle of the sector or arc. The central angle is simply the angle formed by two intersecting radii. For example, when you formed a quarter circle in the preceding example, the central angle was 90 degrees:
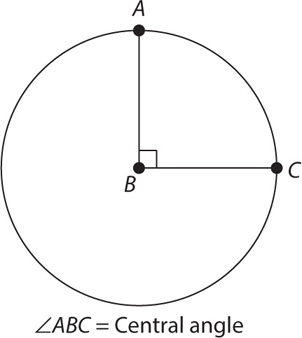
From the preceding example, you can infer the following two relationships:

Why do these relationships hold? Because the central angle is simply a fraction of the entire circle’s angle measurement. Since the angles around a circle’s center measure 360, a central angle of 60 degrees means the sector area is  of the circle’s area. Similarly, if the central angle is 40, then the arc length is simply
of the circle’s area. Similarly, if the central angle is 40, then the arc length is simply 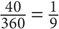 of the circumference. So how will you use the central angle to determine sector area? Let’s look at an example.
of the circumference. So how will you use the central angle to determine sector area? Let’s look at an example.
If a circle has an area of 90π, what is the area of a sector with a central angle of 60 degrees?
1. Determine what fraction the sector is of the entire circle. Use the formula:
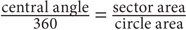
In this case,  Thus the sector area is
Thus the sector area is 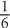 of the circle’s entire area.
of the circle’s entire area.
2. Multiply the area of the circle by 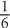 : 90π ×
: 90π × 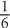 = 15π.
= 15π.
In the example, you used the central angle to determine the sector area, but you can also use sector area or arc length to determine the central angle.
A sector has an arc length of 9π and an area of 100π. What is the central angle of the sector?
SOLUTION: Use the formula central angle/360 = arc length/circumference. You know the arc length, so to determine the central angle, you need to determine the circumference, and then solve the proportion. You can use the area to determine the radius: 100π= πr2. Thus r = 10. If r = 10, then the diameter = 20, and the circumference = 20π. Now you can plug these values into the original formula: substitute 20π for the circumference and 9π for the arc-length:
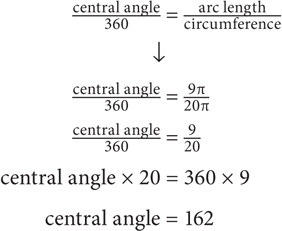
If a triangle is inscribed in a semicircle, two properties follow:
1. The triangle is a right triangle.
2. The diameter of the circle = the triangle’s hypotenuse.
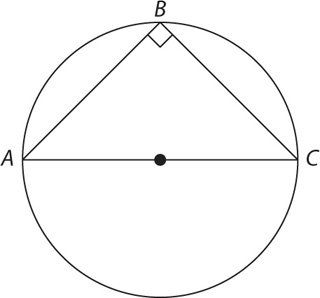
1. What is the circumference of a circle whose area is 49π?
 7π
7π
 14π
14π
 24.5π
24.5π
 35π
35π
 49π
49π
2. What is the area of a circle whose circumference is π?

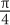

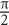
 π
π
 2π
2π
 4π
4π

3. In the figure above, a circle is inscribed in a square with an area of 16. What is the area of the circle?
 π
π
 2π
2π
 4π
4π
 8π
8π
 16π
16π
For the following question, write your answer in the box.
4. In the figure above, a square is inscribed in a circle whose area is 200π. What is the area of the square?


5. In the figure above, a circular pond is bordered by a garden with a uniform width of 2, represented by the shaded region. If the area of the circular pond is 81π, what is the area of the shaded region?
 16π
16π
 20π
20π
 36π
36π
 40π
40π
 169π
169π
Questions 6 and 7 refer to the figure below.

6. In the circle above, central angle AOB measures 120 degrees. If the radius of the circle is 3, what is the area of sector AOB?

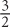 π
π
 3π
3π
 6π
6π
 9π
9π
 18π
18π
7. In the circle above, the length of arc AB is 3π. If the circle has an area of 16π, what is the measure of central angle AOB?
 45
45
 67.5
67.5
 95
95
 115
115
 135
135
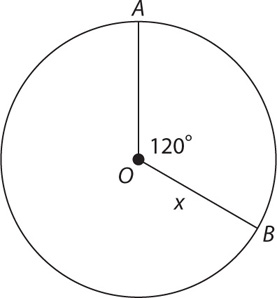
8. In the figure above, the measure of angle AOB is 120 degrees. If the radius of OB is x, then arc AB is what fraction of the area of sector AOB, in terms of x?





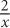



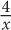
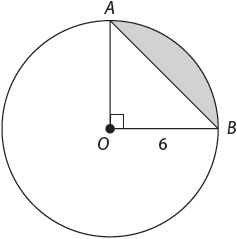
9. If the radius of the circle above is 6, then what is the area of the shaded region?
 18
18
 36
36
 9π − 18
9π − 18
 18π − 18
18π − 18
 18π − 36
18π − 36

10. If the radius of the circle above is 4, what is the length of side AB?

11. In the figure above, radius OB has a length of 4. What is the area of triangle ABC?
 4
4
 8
8
 12
12
 16
16
 20
20
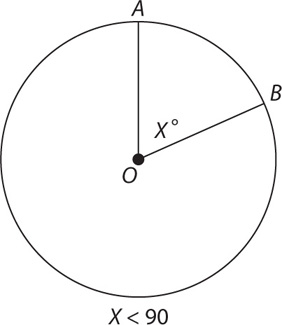
Point O is the center of the circle above.

Point O is the center of the circle on the left;
Point P is the center of the circle on the right
The circumference of a certain circle is less than 40π
A circular wheel with a diameter of 3 feet rotates at a constant speed of 2 revolutions per second.

Equilateral triangle ABC is inscribed in the circle above. The length of arc ABC is 36.
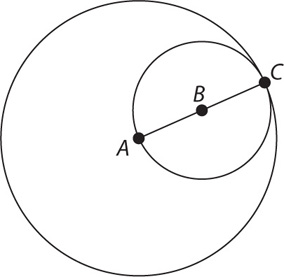
Point A is the center of the larger circle above. Point B is the center of the smaller circle above.
1. B Use the area formula:
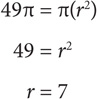
The diameter is thus 14. The circumference = 14π
2. A Use the circumference formula:
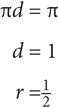
Now substitute  for r in the area formula: area =
for r in the area formula: area = 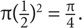
3. C If the area of the square is 16, then each of its sides = 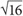 = 4. The side of the square represents the diameter of the circle, so the circle’s diameter is also 4. Thus the radius of the circle is 2. Substitute 2 for the radius in the area formula: area = π(r2) = π(22) = 4π
= 4. The side of the square represents the diameter of the circle, so the circle’s diameter is also 4. Thus the radius of the circle is 2. Substitute 2 for the radius in the area formula: area = π(r2) = π(22) = 4π
4. 100 The key to solving this question is to recognize that the diameter of the circle is the diagonal of the square:
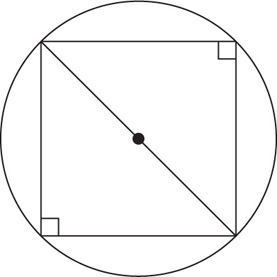
To solve for the area of the square, first solve for the diagonal: if area of the circle = 200π, then
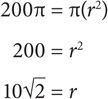
If r = 10 , then the diameter = 20
, then the diameter = 20 . The diagonal of the square is thus 20
. The diagonal of the square is thus 20 . Recall that the diagonal of a square forms two 45-45-90 triangles. The side length of the square will be the leg of one of the 45-45-90 triangles. Since the hypotenuse of one of the resulting 45-45-90 triangles is 10
. Recall that the diagonal of a square forms two 45-45-90 triangles. The side length of the square will be the leg of one of the 45-45-90 triangles. Since the hypotenuse of one of the resulting 45-45-90 triangles is 10 , the length of the leg will be 10. Thus the side of the square = 10. The area of the square is 102 = 100.
, the length of the leg will be 10. Thus the side of the square = 10. The area of the square is 102 = 100.
5. D The area of the shaded region = area of the larger circle − area of the pond. You are told that the area of the pond is 81π, so solve for the area of the larger circle. The radius of the larger circle = the radius of the pond + width of the garden. Use the area formula to solve for the radius of the pond:

Add 9 to the width of the garden: 9 + 2 = 11. The radius of the larger circle is thus 11, and its area is π(112) = 121π. The area of the shaded region is thus: 121π − 81π = 40π.
6. B Since the central angle measures 120, the sector area = 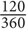 × the circle area
× the circle area 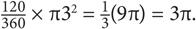
7. E Use the formula: central angle/360 = arc length/circumference. Plug in what you are told: 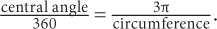 To solve for the central angle, you must solve for the circumference.
To solve for the central angle, you must solve for the circumference.
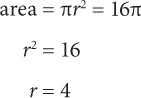
The diameter = 2r = 8. The circumference = 8π. Substitute 8π for the circumference in the preceding proportion:
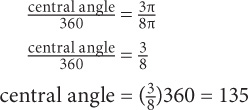
8. C Since the central angle is 120 degrees, the arc length = 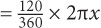 and the sector area
and the sector area 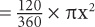 . Thus
. Thus
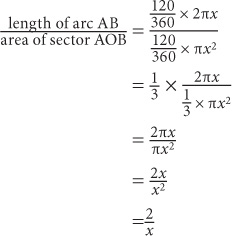
9. C To determine the area of the shaded region, calculate the area of sector AOB and subtract the area of triangle AOB. Since the central angle of sector AOB is 90, the area of sector  The area of right triangle AOB =
The area of right triangle AOB =  × leg1 × leg2 =
× leg1 × leg2 =  × 6 × 6 = 18. The area of the shaded region is thus 9π − 18.
× 6 × 6 = 18. The area of the shaded region is thus 9π − 18.
10. 4 Since AO and AB are radii of the circle, they must be equal. Thus, corresponding angles BAO and ABO must be equal. Since angle ABO = 60, angle BO = 60. Thus angle AOB + 60 + 60 = 180 → angle AOB = 60. All three angles of the triangle are equal, which means all three sides are equal. Thus the length of AB is 4.
11. D When a right angle is inscribed in a semicircle, its hypotenuse = the diameter of the circle. Thus AB = 8. Since ABC is a 45-45-90 triangle, each of the legs 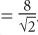 The area of triangle ABC is thus
The area of triangle ABC is thus 
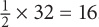 .
.
1. B Since x < 90, the sector area will be less than  the area of the circle. Thus the sector area will be less than 25% of the area of the circle.
the area of the circle. Thus the sector area will be less than 25% of the area of the circle.
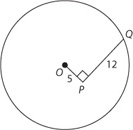
2. C Since point Q is on the circle, the circle’s radius is equivalent to OQ. Note that OQ is the hypotenuse of right triangle OPQ. Since the legs of the right triangle are 5 and 12, the hypotenuse OPQ and thus the radius of the circle must be 13.
3. C Instead of solving for the respective arc lengths, look at the relationships between the two. Central angle AOB is double central angle CPD, but the radius of circle P is double the radius of circle O. Thus the differences between the two circles offset each other. The arc lengths are equal.
4. D Test Choice B against the conditions in the prompt. If the radius of the circle is 19, then the circumference of the circle is 38π. Since you are told that the circumference is less than 40π, a radius greater than 19 or smaller than 19 would satisfy the given conditions. Thus the relationship between the two quantities cannot be determined.
5. A Since circumference = π × diameter, Quantity A can be expressed as  is approximately 3.14, which is greater than 3. Thus Quantity A is greater.
is approximately 3.14, which is greater than 3. Thus Quantity A is greater.
6. A Each time the wheel revolves, it travels the equivalent of its circumference. Thus the wheel travels 3π × 2 = 6π feet per second. Set up a proportion: 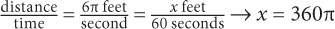 . Quantity A is greater.
. Quantity A is greater.
7. B Since triangle ABC is equilateral, the rays of each angle intersect  of the circle’s circumference. Thus, arc ABC represents
of the circle’s circumference. Thus, arc ABC represents  of the circle’s circumference. If arc ABC
of the circle’s circumference. If arc ABC  is of the circle’s circumference, it follows that 36 =
is of the circle’s circumference, it follows that 36 =  y, where y = the circle’s circumference. Thus y = 36
y, where y = the circle’s circumference. Thus y = 36 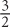 = 54. Quantity B is greater.
= 54. Quantity B is greater.
8. B Since AC is the radius of the larger circle and the diameter of the smaller circle, it follows that the diameter of the larger circle is double the diameter of the smaller circle. To determine the ratio, plug in numbers. Let AC = 4 and BC = 2. If AC = 4, the area of the larger circle is π42 = 16π and the area of the smaller circle is π22 = 4π. The ratio of the area of the smaller circle to the area of the larger circle is thus  . Quantity B is greater.
. Quantity B is greater.
So far, you have only looked at two-dimensional shapes. The GRE will occasionally test your knowledge of three-dimensional shapes. You will need to know how to calculate the surface area and volume of rectangular solids, cubes, and cylinders. A cube is a type of rectangular solid, so let’s consider cubes and rectangular solids together.
The following figure is a rectangular solid:
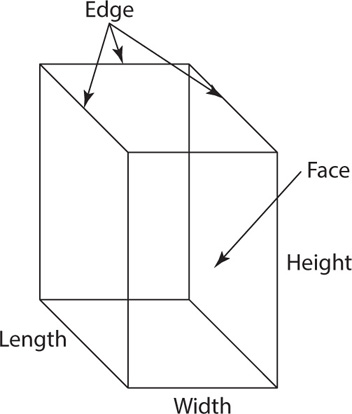
The edge of a rectangular solid refers to any line that joins two vertices, and the face of a rectangular solid refers to any of the rectangles formed by four edges. All rectangular solids have six faces, and opposite faces have the same dimensions.
It may seem tedious to calculate surface area of a rectangular solid, since you would presumably need to calculate the area of each face. But remember that opposite faces have the same dimensions. So instead of calculating the area of each face, just calculate the area of each unique face and double that.
The formula for calculating surface area of a rectangular solid is therefore:
SArectangular solid = 2lw + 2lh + 2wh
What is the surface area of a rectangular solid with dimensions 3 × 4 × 5?
SOLUTION: Use the preceding formula. Let l = 3, w = 4, and h = 5. Substitute: 2(3)(4) + 2(3)(5) + 2(4)(5) = 94.
A cube is a type of rectangular solid in which all edges are equal. Since all edges of a cube are equal, all faces will have an equal area.
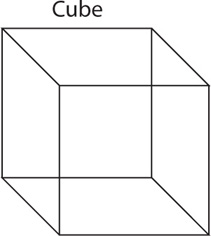
Thus to calculate the surface area of a cube, just calculate the area of one face and multiply that by six (since the cube has six sides). The formula for the surface area of a cube is
SAcube= 6e2, where e = the length of an edge
If the area of one face of a cube is 81, what is the surface area of the cube?
SOLUTION: Since all faces have the same area, the surface area of the cube = 81 × 6 = 486.
The volume of a rectangular solid refers to the amount of space within that shape. Volume is measured in cubic units, such as 2 cubic meters or 3.7 cubic inches. To calculate the volume of a rectangular solid, just multiply all the dimensions:
Vrectangular solid= l × w × h
The same rule applies to a cube. But since all the edges of a cube are equal, you just need one side of the cube to calculate a cube’s volume:
Vcube= e3
If the volume of a rectangular solid with a length of 4, a width of 2, and a height of x equals the volume of a cube with an edge of 4, what is x?
 1
1
 2
2
 4
4
 8
8
 16
16
SOLUTION: Since the volumes are equal,
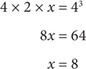
The correct answer is D.
The diagonal of a rectangular solid is the straight line distance from one vertex to the opposite vertex.
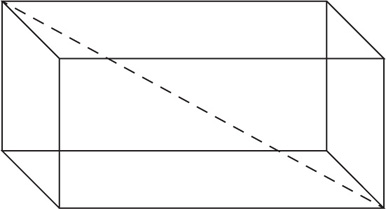
To determine the diagonal of a rectangular solid, use the following formula:

If a rectangular solid has dimensions of 5, 5, and 10, what is the greatest straight-line distance from one vertex to another vertex?
 10
10
 20
20
 25
25
 5
5
 5
5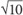
SOLUTION: Use the formula: Let l = 5, w = 5, and h = 10. The diagonal = 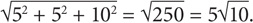 The correct answer is E.
The correct answer is E.
A cylinder is rectangular solid whose base is a circle.

To determine the volume of a cylinder, multiply the area of the base by the height. In the case of a cylinder, the area of the base is πr2 since the base is a circle. The formula for the volume of a cylinder is
Vcylinder= πr2h
For this question, write your answer in the box.
How many cubic feet of water are needed to fill a cylinder with a radius of 10 feet and a height of 6 feet?

SOLUTION: Use the volume formula: volume = πr2h = π102(6) = 600π
1. If the volume of a cube equals its surface area, what is the length of an edge of the cube?
 3
3
 6
6
 9
9
 12
12
 18
18
2. What is the surface area of a cube whose volume is 125?
 100
100
 125
125
 150
150
 175
175
 200
200
For this question, write your answer in the box.
3. What is the volume, in cubic inches, of a cube whose edges each measure 2 feet?

4. A certain cylinder with radius, r, and height, h, has the same volume as a cube with edge, e. If the radius of the cylinder equals the edge of the cube, what is h, in terms of e?
 eπ
eπ
 e2π
e2π
 e5π
e5π
 e/π
e/π
 e2/π
e2/π
5. What is the length of the diagonal of a cube whose surface area is 216?
 6
6
 9
9
 12
12
 6
6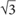
 9
9
6. An empty cylindrical tank with a radius of 5 inches and a height of 10 inches is filled with water at a rate of 75 cubic feet per second. Approximately how many seconds will it take for the tank to be full?
 8
8
 9
9
 11
11
 13
13
 15
15
For this question, write your answer in the box.
7. The edge of Cube X is half the length of the edge of Cube Y. What is the ratio of the volume of Cube X to the volume of Cube Y?
8. The length of a certain rectangular solid is doubled, its width is tripled, and its height is quadrupled. The volume of the resulting rectangular solid will be what percent greater than the volume of the original rectangular solid?
 1,100%
1,100%
 1,200%
1,200%
 2,200%
2,200%
 2,300%
2,300%
 2,400%
2,400%
For this question, write your answer in the box.
9. What is the maximum number of cubes with an edge of length 5 that can fit into a box whose dimensions are 10 × 15 × 20?

10. Three metal cubes with edges of two will be dropped into an empty cylindrical tank with a base of 3 and a height of 8. The three cubes will take up what fraction of the volume of the tank?





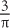

 π
π

 π
π
1. B Let e = the edge of the cube. Using the formulas for surface area and volume, divide both sides by 
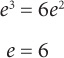
2. C To solve for surface area, use the formula surface area of a cube = 6e2, where e = edge length. If the volume is 125, then

Substitute e into the formula for surface area: 6(5)2 = 150.
3. 13,824 cubic inches First, convert from feet to inches. 2 feet = 24 inches. The volume of the cube, in cubic inches, is thus 243 = 13,824 cubic inches.
4. D Let e = the length of the cube’s edge. Thus the radius of the cylinder also = e. Now create an equation: π(e2)h = e3. Isolate 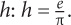
5. A Use the formula for surface area:

The formula for the diagonal of a cube is e. Thus the length of the diagonal is 6.
6. C The volume of the tank is π(r2)h = π(52)10 = 250π. To solve for time, use the r × t = w formula, where the rate is 75 cubic feet/second, and the work is 250π:
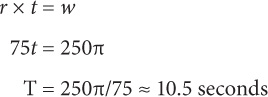
The closest answer is C.
7.  Plug in numbers. Let the edge of cube y = 4. The edge of Cube X is thus 2. In this case, the volume of Cube Y is 43 = 64, and the volume of Cube X is 23 = 8.
Plug in numbers. Let the edge of cube y = 4. The edge of Cube X is thus 2. In this case, the volume of Cube Y is 43 = 64, and the volume of Cube X is 23 = 8. 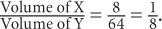
8. D Plug in numbers. Let the original length = 2, the original width = 3, and the original height = 4. The original volume is thus 2 × 3 × 4 = 24. The new length will be 2 × 2 = 4. The new width will be 3 × 3 = 9. The new height will be 4 × 4 = 16. The new volume is thus 4 × 9 × 16 = 576. Now use the percent greater formula: Percent of − 100%:  − 100 = 2,300%.
− 100 = 2,300%.
9. 24 The volume of the box is 10 × 15 × 20 = 3,000. Each of the small cubes being placed into the box has a volume of 53 = 125. The number of cubes that can fit into the box 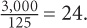
10. D Each metal cube has a volume of 23 = 8. Since there are three metal cubes, their combined volume is 8 × 3 = 24. The volume of the cylinder is π(r2)h = π(32)(8) = 72π. 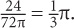
1. B The formula for the diagonal of a cube is e. The value in Quantity A is thus 3. The formula for the diagonal of a rectangular solid is  The value in Quantity B is thus
The value in Quantity B is thus 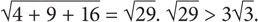 Thus Quantity B is greater.
Thus Quantity B is greater.
2. B The value in Quantity A is 4 × 5 × 6 = 120. The value in Quantity B is π(62)3= 108π. 108π > 120. Quantity B is greater.
3. A Let e = the edge of the cube. You are thus comparing e3 to 6e2. To simplify the comparison, divide both sides by e2 (you can do this since e2 is positive). The new comparison is thus:

Since you are told that e > 6, Quantity A is greater.
The coordinate plane is used to designate points in a two-dimensional plane. It is created by two perpendicular lines that meet at the origin. The horizontal line is called the x-axis and the vertical line is called the y-axis. These lines split the plane into four quadrants: I, II, III, and IV.
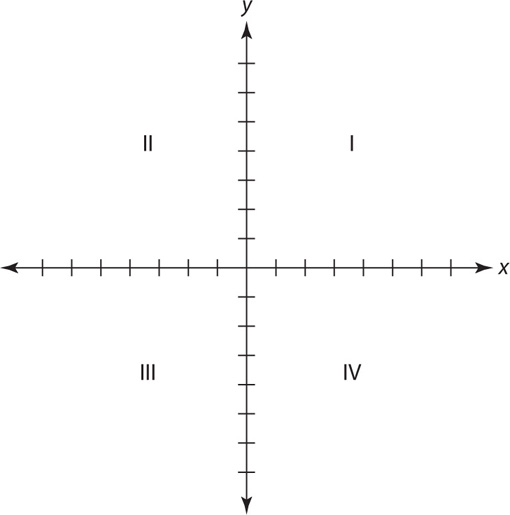
Points on the coordinate plane are designated by assigning two numbers: an x-coordinate and a y-coordinate. A point is written in the form (x,y).
The x-coordinate designates the horizontal position of a point. If a point is to the right of the origin, then its x-coordinate is positive. If a point is to the left of the origin, then its x-coordinate is negative. If a point is on the y-axis, then its x-coordinate is zero.
The y-coordinate designates the vertical position of a point. If a point is above the origin, then its y-coordinate is positive. If a point is below the origin, then its y-coordinate is negative. If a point is on the x-axis, then its y-coordinate is zero.

On the coordinate plane, a line is formed by joining two points. Any line on the coordinate plane will be defined by the following equation:
y = mx + b
x and y can refer to any point on the line, but m and b are constants—they define properties of a line.
In the equation y = mx + b, m refers to the slope of the line. The slope of a line indicates its steepness and whether it is rising or falling.
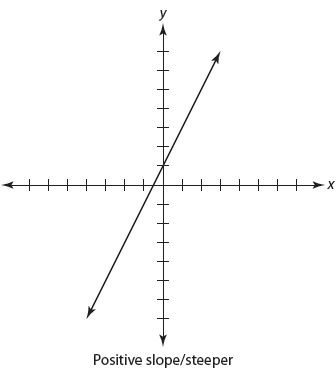
To determine the slope of a line, you are looking for the ratio of how much the line rises vertically to how much the line moves horizontally.
What is the slope of a line that contains the points (2,3) and (5,7)?
SOLUTION: Use the preceding formula: 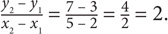
Line k passes through the points (2,3) and (4,6).

SOLUTION: Plug the above values into the slope formula: 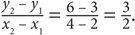 2 >
2 > 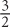 , so Quantity B is greater.
, so Quantity B is greater.
In the equation y = mx + b, b refers to the y-intercept of the line. The y-intercept of a line refers to where a line crosses the y-axis. Since this point is on the y-axis, the x-coordinate will always be zero.
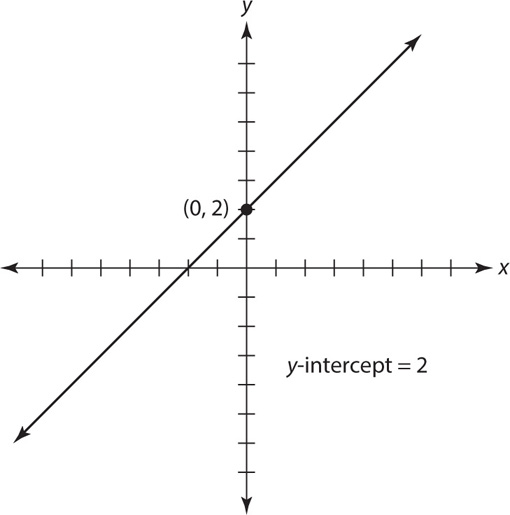
Once you know the slope and y-intercept of a line, you can substitute those values into the equation for the line. For example, if you are told that a line has a y-intercept of 3 and a slope of 7, plug in 3 for b and 7 for m: y = 7x + 3.
Sometimes, the GRE will define a line using a different form than the previous one. Always manipulate the equation to be in y = mx + b form.
If the equation for line k is 2x + 3y = 6, what is the slope of line k?
SOLUTION: Isolate y so that the equation is in y = mx + b form. Subtract 2x:
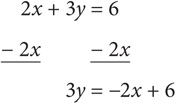
Divide both sides by 3:
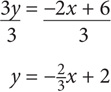
The slope of the line is − .
.
Generally, if the GRE asks you to determine the equation for a line, it will do so by providing you with two points. Let’s look at how to do so:
What is the equation for the line that passes through (2,11) and (5,20)?
Step 1: Use the slope formula to determine m:

Step 2: Substitute the value for m in the equation for the line:
y = 3x + b
Step 3: Solve for b: Since (2,11) and (5,20) lie on the line, both points will satisfy the equation for the line. Thus you can plug in the coordinates for either point to solve for b. Use the point (2,11):
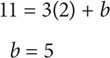
Step 4: Substitute b into the equation:
y = 3x + 5
In the previous example, you used two points on a line to determine its equation. In other situations, you will be given the equation for a line and will be asked to find a point that lies on the line. Let’s look at an example:
If line k is defined by the equation y = 7x + 3, then which of the following points must lie on the line?
 (3,7)
(3,7)
 (7,3)
(7,3)
 (3,0)
(3,0)
 (2,17)
(2,17)
 (17,2)
(17,2)
SOLUTION: Plug each point into the equation. Whichever point keeps the equation true will be your answer.
A: 7 = 7(3) + 3? → False
B: 3 = 7(7) + 3? → False
C: 0 = 7(3) + 3? → False
D: 17 = 7(2) + 3? → True
E: 2 = 7(17) + 3? → False
The correct answer is D.
Any horizontal line will have a slope of zero. Because such lines have no slope, they will always be written in the form: y= b. For example, the equation for the line below is y = 7.

Any vertical line will have an undefined slope. Such lines will be written in the form: x = a, where a represents the x-intercept of the line. For example, the equation for the line below is x = 4.

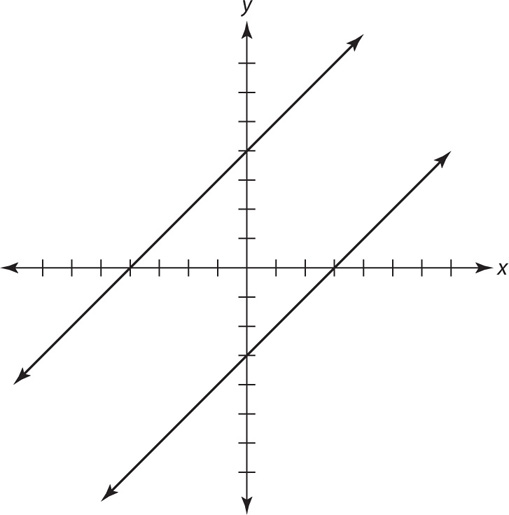
If two lines are parallel, then their slopes are equal and the lines never intersect. (See figure.)
If two lines are perpendicular, then the product of their slopes is −1. Another way to say this is that their slopes are negative reciprocals. (See figure.)

Line k is defined by the equation y = 2x − 3. Lines l and m are each perpendicular to line k.

SOLUTION: Since the equation for line k is y = 2x − 3, you know that the slope of line k is 2. Since lines l and m are perpendicular to line k, each of their slopes is the negative reciprocal of 2: − . −
. − + −
+ − = −1. Quantity A is greater.
= −1. Quantity A is greater.
You can use the Pythagorean theorem to calculate the distance between two points on the coordinate plane. For example:
What is the distance between (1,3) and (4,7)?
Step 1: Plot the two points.

Step 2: Connect the two points to create a right triangle.
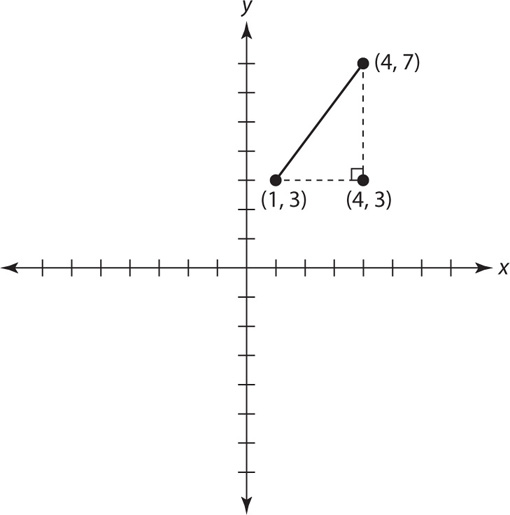
Step 3: Calculate the lengths of each side of the resulting triangle:
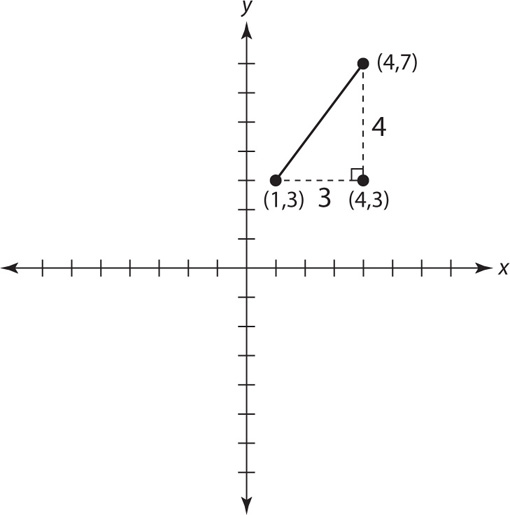
The length of the horizontal leg will be the difference between the x-coordinates of the given points: 4 − 1 = 3. The length of the vertical leg will be the difference between the y-coordinates of the two points: 7 − 3 = 4. Now that you have two legs of a right triangle, you can determine the distance between the two points by calculating the hypotenuse:
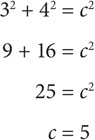
The distance between the two points is 5.
For this question, write your answer in the box.
1. What is the slope of a line whose equation is 2x + 5y − 3= 12?

2. If line p is defined by the equation 3x − 2y = −12, then which of the following points must lie on line p?
 (0,12)
(0,12)
 (12,18)
(12,18)
 (12,24)
(12,24)
 (2,3)
(2,3)
 (3,2)
(3,2)
3. What is the x-intercept of line k, if line k has a slope of  and contains the point (6,14)?
and contains the point (6,14)?
 −15
−15
 −14
−14
 0
0
 10
10
 15
15
4. In the xy-plane, the center of circle C is at point (0,0). If the point (−5,5) is on the circumference of the circle, what is the radius of the circle?
 5
5
 10
10
 7.5
7.5
 5
5
 10
10
For this question, indicate all answers that apply.
5. If the slope of a line on the coordinate plane is negative, which of the following must be true?
 The line passes through Quadrant I.
The line passes through Quadrant I.
 The line passes through Quadrant II.
The line passes through Quadrant II.
 The line passes through Quadrant III.
The line passes through Quadrant III.
 The line passes through Quadrant IV.
The line passes through Quadrant IV.
 The line passes through the origin.
The line passes through the origin.
6. If line l is perpendicular to line k, which of the following must be true?
 The slopes of l and k are equal.
The slopes of l and k are equal.
 The product of the slopes of l and k is 1.
The product of the slopes of l and k is 1.
 The product of the slopes of l and k is −1.
The product of the slopes of l and k is −1.
 The y-intercepts l and k are equal.
The y-intercepts l and k are equal.
 The x-intercepts of l and k are equal.
The x-intercepts of l and k are equal.
7. Point (2,3) is the vertex of a square, and point (−2,7) is the opposite vertex of the same square. What is the area of the square?
 8
8
 9
9
 16
16
 25
25
 16
16
8. Line k is defined by the equation y = 4x − b. If the x-intercept of line k is 3, what is b?
 0
0



 4
4
 12
12
9. Line l is defined by the equation y = 3x + 10. If lines l and k intersect to form a right angle at the point (3,4), which of the following is the equation of line k?
 y = −3x + 6
y = −3x + 6
 y = −3x + 10
y = −3x + 10
 y = 3x + 10
y = 3x + 10
 y = −
y = − + 5
+ 5
 y = −
y = − + 6
+ 6
10. Line k is defined by the equation ax + by = c. If the slope of line k is positive, which of the following must be true?

 > 0
> 0

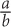 < 0
< 0
 a > 0
a > 0
 b > 0
b > 0
 a + b > 0
a + b > 0
Lines l and m intersect at the point (3,5)
Line q passes through the origin and contains the point (a,b).

The line above is defined by the equation y = mx + b.
Line p is defined by the equation 2y − 3x + 7 = 12.
In the xy-plane, the circumference of Circle C contains the points (x, 0) and (0,y).
Line l is defined by the equation y = 3x − 7.
Line l intersects line k at the point (5,8).

The equation of the line graphed above is y = − x + 3.
x + 3.
1. − Isolate y to put the equation into slope-intercept form:
Isolate y to put the equation into slope-intercept form:
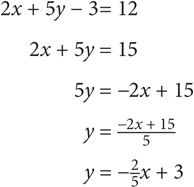
The slope is − .
.
2. C Substitute the coordinates into the equation for the line. The coordinates that satisfy the equation will be the answer. Of the choices, only (12, 24) satisfies the equation. For illustration: 3(12) − 2(24) = 36 − 48 = −12.
3. A First, determine the equation for the line. Since the slope is  , the equation initially reads: y =
, the equation initially reads: y =  x + b. To solve for b, substitute the coordinates (6,14) into the equation:
x + b. To solve for b, substitute the coordinates (6,14) into the equation:

The equation for the line is thus y =  x + 10. Since the x-intercept represents the point at which the line intersects the x-axis, the y-coordinate of that point will be zero. Thus substitute 0 for y into the equation to determine the x-intercept:
x + 10. Since the x-intercept represents the point at which the line intersects the x-axis, the y-coordinate of that point will be zero. Thus substitute 0 for y into the equation to determine the x-intercept:

4. D Draw the diagram and connect the points (0,0) and (−5,5). The resulting line will be the hypotenuse of a right triangle whose legs each have a length of 5.
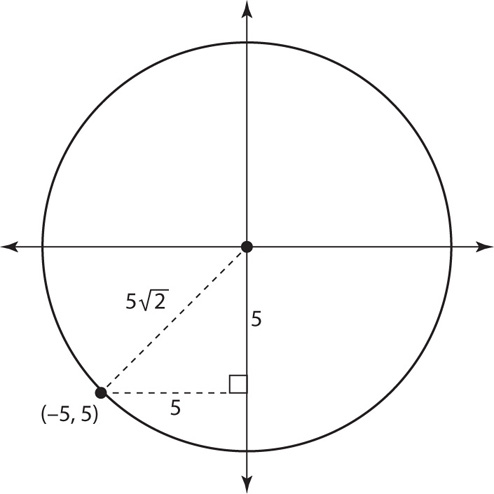
Since this is an isosceles right triangle, the hypotenuse will be 5 .
.
5. B and D Any line with a negative slope will intercept quadrants II and IV. Whether the line intercepts Quadrant I or III depends on the line’s y-intercept. Since you are not given information about the line’s y-intercept, you cannot determine whether it will pass through the other quadrants or the origin. The correct answer is II and IV. For illustration, see the following figure:
All three lines have negative slopes and pass through Quadrants II and IV. Whether the lines pass through the other quadrants depends on their y-intercepts.
6. C If two lines are perpendicular, then the slope of one line is the negative reciprocal of the slope of the other line. The product of reciprocals is 1. The product of negative reciprocals is thus −1.
7. C To determine the area, you need to determine the length of a side. To determine the length of a side, connect the two points to create a right angle:
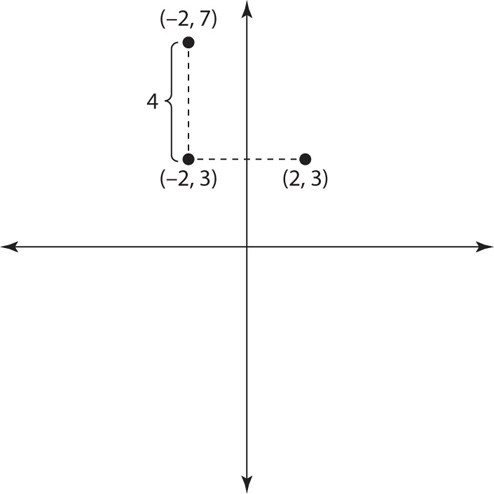
The right angle is formed at the point (−2,3). To determine the length of a side of the square, subtract the y-coordinate of the upper point from the y-coordinate of the point below it: 7 − 3 = 4. The length of a side of the square is 4. The area is thus 42 = 16.
8. E Since the x-intercept represents the point at which the line intersects the x-axis, the coordinates of the x-intercept are (3,0). Substitute 3 for x and 0 for y to solve for b: 0 = 4(3) − b → 0 = 12 − b → 12 = b.
9. D Since lines l and k are perpendicular, their slopes are negative reciprocals. Since the slope of line l is − , the slope of line k is −. The equation for line k now reads: y = −
, the slope of line k is −. The equation for line k now reads: y = − x + b. Since the lines intersect at the point (3,4), those coordinates must satisfy the equation for line k. To solve for b, plug those coordinates into the equation:
x + b. Since the lines intersect at the point (3,4), those coordinates must satisfy the equation for line k. To solve for b, plug those coordinates into the equation:
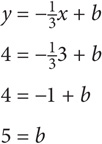
The equation for line k is thus y = − x + 5.
x + 5.
10. A Isolate y so that the equation is in y = mx + b form:
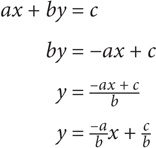
The slope of the line is thus − . Since the slope of the line is negative, −
. Since the slope of the line is negative, −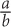 0. Thus
0. Thus 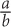 > 0.
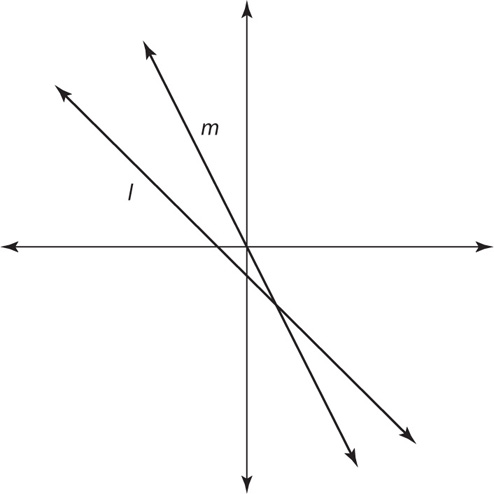
> 0.
1. A Since the lines go downward, both slopes are negative. Line m is steeper, meaning its slope is more negative than the slope of l. Thus the slope of l is greater. The correct answer is A.
2. B Since line m contains the points (0,0) and (3,5), its slope is (5 − 0)/(3 – 0) = 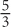 . Line m is steeper than line l, so the slope of line l must be less than
. Line m is steeper than line l, so the slope of line l must be less than 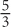 , meaning its slope is less than 2. The correct answer is B.
, meaning its slope is less than 2. The correct answer is B.
3. C Since line q passes through the origin, it must contain the point (0,0). The slope of line q is thus 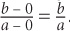 The two quantities are equal. The answer is C.
The two quantities are equal. The answer is C.
4. B The slope of the line is 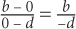 . Since the line points downward, its slope must be negative. Thus
. Since the line points downward, its slope must be negative. Thus 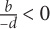 . Multiply both sides by −1 (remember to flip the inequality!):
. Multiply both sides by −1 (remember to flip the inequality!):  > 0. Since m < 0 and
> 0. Since m < 0 and 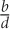 > 0, Quantity B is greater.
> 0, Quantity B is greater.
5. B Manipulate the equation to be in y = mx + b form:
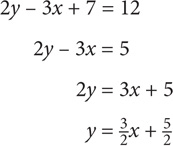
The slope is 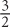 and the y-intercept is
and the y-intercept is 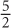 . Quantity B is greater.
. Quantity B is greater.
6. C Since the circle touches the axes at these points, the distance between the center of the circle and (0,y) must equal the distance between the center of the circle and (x, 0).

Thus |y| = the radius of the circle, as does |x|. Thus the sum of |x| and |y| = the circle’s diameter. The two quantities are equal.
7. D The only information given about line k is that it contains the point (5,8). One point on a line is not sufficient to infer any information about that line’s slope.
8. B OA is the distance between the origin and the y-intercept of the line. Since the y-intercept of the line is 3, OA is 3. OB is the distance between the origin and the x-intercept of the line. To determine the x-intercept of the line, set y equal to zero:
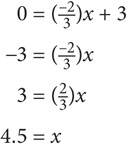
OB is thus 4.5. Quantity B is greater.