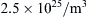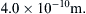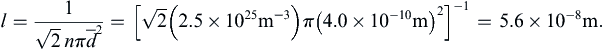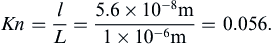1.4. Continuum Hypothesis
A fluid is composed of a large number of molecules in constant motion undergoing collisions with each other, and is therefore discontinuous or discrete at the most microscopic scales. In principle, it is possible to study the mechanics of a fluid by studying the motion of the molecules themselves, as is done in kinetic theory or statistical mechanics. However, the average manifestation of molecular motions is more important for macroscopic fluid mechanics. For example, forces are exerted on the boundaries of a fluid’s container due to the constant bombardment of the fluid molecules; the statistical average of these collision forces per unit area is called pressure, a macroscopic property. So long as we are not interested in the molecular mechanics of the origin of pressure, we can ignore the molecular motion and think of pressure as simply the average force per unit area exerted by the fluid.
When the molecular density of the fluid and the size of the region of interest are large enough, such average properties are sufficient for the explanation of macroscopic phenomena and the discrete molecular structure of matter may be ignored and replaced with a continuous distribution, called a continuum. In a continuum, fluid properties like temperature, density, or velocity are defined at every point in space, and these properties are known to be appropriate averages of molecular characteristics in a small region surrounding the point of interest.
The simplest way to quantitatively assess the extent of molecular velocity variation in pure gases and the applicability limits of the continuum approximation is through use of the Maxwell distribution of molecular velocity v = (v1, v2, v3). Here, v is random vector variable that represents possible molecular velocities. When the gas at the point of interest has average velocity u, the Maxwell distribution is:
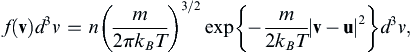 (1.1)
(1.1)
[Chapman and Cowling, 1970] where n is the number of molecules per unit volume, m is the molecular mass, kB is Boltzmann’s constant, T is the absolute temperature, and d3v = dv1dv2dv3 is a small volume in velocity space centered on v. The distribution (1.1) specifies the number of molecules at the point of interest with velocities near v. When (1.1) is integrated over all possible molecular velocities, the molecular number density n is recovered,
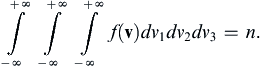
Thus, f(v)/n is the probability density function for molecular velocity and the average gas velocity, v ¯ 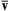 , and the variances of molecular velocity components,
, and the variances of molecular velocity components, σ i 2 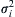 , can be determined similarly from appropriate integrations:
, can be determined similarly from appropriate integrations:
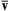 , and the variances of molecular velocity components,
, and the variances of molecular velocity components, 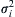 , can be determined similarly from appropriate integrations:
, can be determined similarly from appropriate integrations: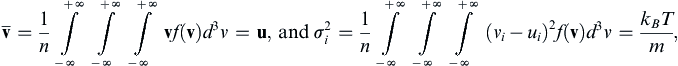 (1.2, 1.3)
(1.2, 1.3)
(see Exercise 1.3). When u = 0, (1.1) specifies the distribution of purely random molecular velocities in the gas and can be simplified by integrating over velocity directions to obtain the distribution of molecular speed, v = | v | 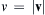 :
:
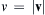 :
: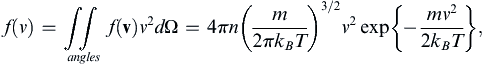 (1.4)
(1.4)
where dΩ is the differential solid-angle element. Using (1.4), the mean molecular speed can be found:
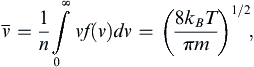 (1.5)
(1.5)
(see Exercise 1.4). The results (1.2), (1.3), and (1.5) specify the average gas velocity, the variance of its components, and the average molecular speed. Interestingly, σ i 2 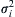 and
and v ¯ 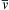 only depend on the temperature and molecular mass, and
only depend on the temperature and molecular mass, and v ¯ 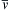 (= 464 m/s for air at room temperature) may be large compared to u. Thus, averaging over a significant number of gas molecules is necessary for the accuracy of the continuum approximation.
(= 464 m/s for air at room temperature) may be large compared to u. Thus, averaging over a significant number of gas molecules is necessary for the accuracy of the continuum approximation.
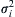 and
and 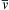 only depend on the temperature and molecular mass, and
only depend on the temperature and molecular mass, and 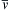 (= 464 m/s for air at room temperature) may be large compared to u. Thus, averaging over a significant number of gas molecules is necessary for the accuracy of the continuum approximation.
(= 464 m/s for air at room temperature) may be large compared to u. Thus, averaging over a significant number of gas molecules is necessary for the accuracy of the continuum approximation.The continuum approximation is valid at the length scale L (a body length, a pore diameter, a turning radius, etc.) when the Knudsen number, Kn = l/L where l is the molecular mean free path, is much less than unity. The molecular mean free path, l, is the average distance a gas molecule travels between collisions. It depends on the average molecular velocity v ¯ 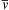 , the number density of molecules n, the collision cross section of two molecules
, the number density of molecules n, the collision cross section of two molecules π d ¯ 2 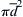 (
(d ¯ 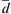 is the molecular collision diameter), and the average relative velocity between molecules,
is the molecular collision diameter), and the average relative velocity between molecules, v ¯ r = 2 v ¯ 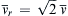 (see Exercises 1.5, and 1.6):
(see Exercises 1.5, and 1.6):
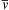 , the number density of molecules n, the collision cross section of two molecules
, the number density of molecules n, the collision cross section of two molecules 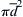 (
(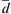 is the molecular collision diameter), and the average relative velocity between molecules,
is the molecular collision diameter), and the average relative velocity between molecules, 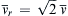 (see Exercises 1.5, and 1.6):
(see Exercises 1.5, and 1.6): (1.6)
(1.6)
The mean free path specifies the average distance that a molecule travels before it communicates its presence, temperature, or momentum to other molecules. The mean free path is a random-molecular-motion concept that leads to the macroscopically observed phenomena of species, heat, and momentum diffusion in fluids.
For most terrestrial situations, the requirement Kn << 1 is not a great restriction since l ≈ 60 nm for air at room temperature and pressure. Furthermore, l is more than two orders of magnitude smaller for water under the same conditions. However, a molecular-kinetic-theory approach may be necessary for analyzing flows over very small objects or in very narrow passages (where L is small), or in the tenuous gases at the upper reaches of the atmosphere (where l is large).