2.8. Vector Dot and Cross Products
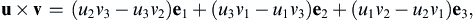 (2.20)
(2.20)
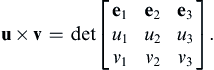
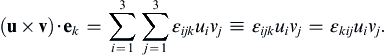 (2.21)
(2.21)
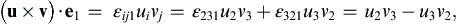
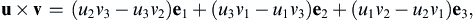 (2.20)
(2.20)
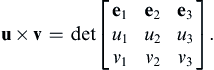
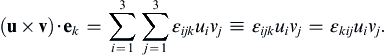 (2.21)
(2.21)
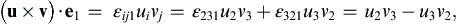
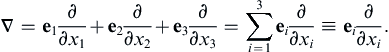 (2.22)
(2.22)
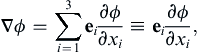
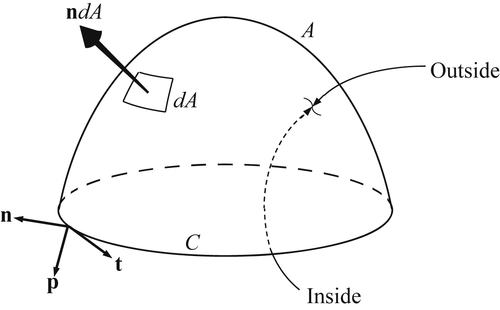
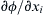 . The vector ∇ϕ is called the gradient of ϕ, and ∇ϕ is perpendicular to surfaces defined by ϕ = constant. In addition, it specifies the magnitude and direction of the maximum spatial rate of change of ϕ (Figure 2.7). The spatial rate of change of ϕ in any other direction n is given by:
. The vector ∇ϕ is called the gradient of ϕ, and ∇ϕ is perpendicular to surfaces defined by ϕ = constant. In addition, it specifies the magnitude and direction of the maximum spatial rate of change of ϕ (Figure 2.7). The spatial rate of change of ϕ in any other direction n is given by: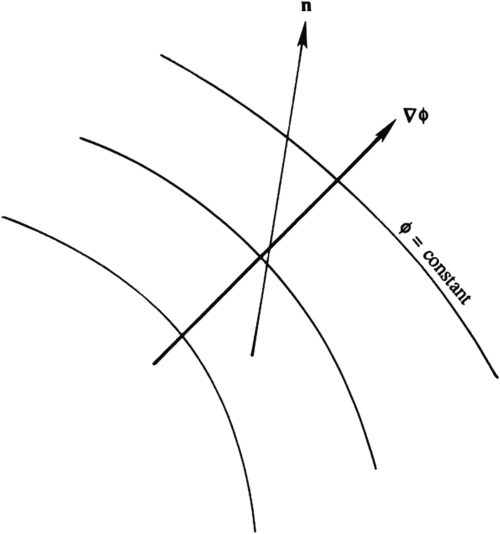
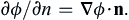
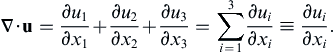 (2.23)
(2.23)
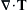 , of a second-order tensor T can be defined as the vector whose j-component is:
, of a second-order tensor T can be defined as the vector whose j-component is: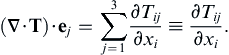
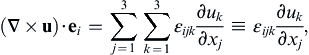 (2.24)
(2.24)
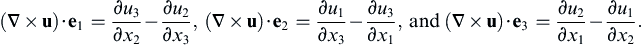 (2.25)
(2.25)
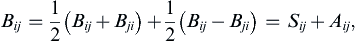
 (2.26)
(2.26)
 (2.27)
(2.27)
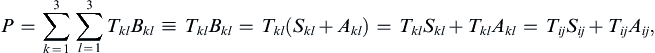 (2.28)
(2.28)
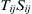 –
–  , but this can also be written
, but this can also be written 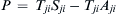 because Sij and
because Sij and 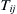 are symmetric. Now, replace the index j by k and the index i by l to find:
are symmetric. Now, replace the index j by k and the index i by l to find: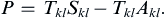 (2.29)
(2.29)
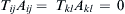 , and:
, and: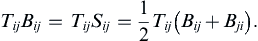
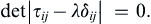
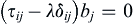
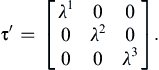
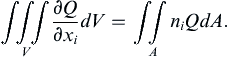 (2.30)
(2.30)
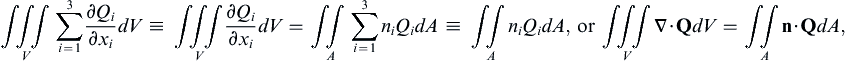
 , of Q when considered in its limiting form for a vanishingly small volume:
, of Q when considered in its limiting form for a vanishingly small volume: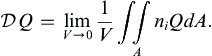 (2.31)
(2.31)
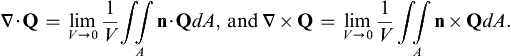 (2.32, 2.33)
(2.32, 2.33)
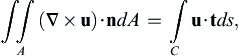 (2.34)
(2.34)
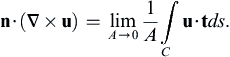 (2.35)
(2.35)
 where b = (1, 4, 17) and c = (–4, –3, 1).
where b = (1, 4, 17) and c = (–4, –3, 1).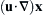 where u a vector with components ui.
where u a vector with components ui.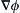 , where
, where  and h is a constant vector with components hi.
and h is a constant vector with components hi. , where u = Ω × x and Ω is a constant vector with components Ωi.
, where u = Ω × x and Ω is a constant vector with components Ωi.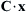 , where
, where
 .
.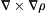 to indicial notation and show that it is zero in Cartesian coordinates for any twice-differentiable scalar function ρ.
to indicial notation and show that it is zero in Cartesian coordinates for any twice-differentiable scalar function ρ.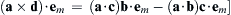 .]
.]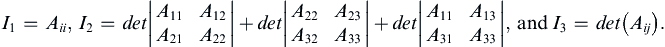
 . Then show that AijAji and AijAjkAki are also invariants. In fact, all contracted scalars of the form AijAjk ċċċ Ami are invariants. Finally, verify that
. Then show that AijAji and AijAjkAki are also invariants. In fact, all contracted scalars of the form AijAjk ċċċ Ami are invariants. Finally, verify that 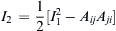 , and
, and 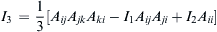 . Because the right-hand sides are invariant, so are I2 and I3.]
. Because the right-hand sides are invariant, so are I2 and I3.] , and the Pythagorean theorem to show that u·v = 0 when u and v are perpendicular.
, and the Pythagorean theorem to show that u·v = 0 when u and v are perpendicular.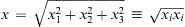 is the length of x.
is the length of x.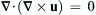 for any twice-differentiable vector function u regardless of the coordinate system.
for any twice-differentiable vector function u regardless of the coordinate system.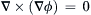 for any single-valued twice-differentiable scalar ϕ regardless of the coordinate system.
for any single-valued twice-differentiable scalar ϕ regardless of the coordinate system.