 Counting
Counting
 Counting Principle
Counting Principle
 Permutations and Combinations
Permutations and Combinations
 Venn Diagrams
Venn Diagrams
 Probability
Probability
 Practice Exercises
Practice Exercises
 Answer Explanations
Answer Explanations
12-O. COUNTING AND PROBABILITY
 Counting
Counting
 Counting Principle
Counting Principle
 Permutations and Combinations
Permutations and Combinations
 Venn Diagrams
Venn Diagrams
 Probability
Probability
 Practice Exercises
Practice Exercises
 Answer Explanations
Answer Explanations
Some questions on the GRE begin, “How many ... .” In these problems you are being asked to count something: how many apples can she buy, how many dollars did he spend, how many pages did she read, how many numbers satisfy a certain property, or how many ways are there to complete a particular task. Sometimes these problems can be handled by simple arithmetic. Other times it helps to use TACTIC 8 from Chapter 8 and systematically make a list. Occasionally it helps to know the counting principle and other strategies that we will review in this section.
Counting
USING ARITHMETIC TO COUNT
The following three examples require only arithmetic. But be careful; they are not the same.
EXAMPLE 1
Brian bought some apples. If he entered the store with $113 and left with $109, how much, in dollars, did the apples cost?

EXAMPLE 2
Scott was selling tickets for the school play. One day he sold tickets numbered 109 through 113. How many tickets did he sell that day?

EXAMPLE 3
Brian is the 109th person in a line and Scott is the 113th person. How many people are there between Brian and Scott?

SOLUTIONS 1–3.
 It may seem that each of these examples requires a simple subtraction: 113 – 109 = 4. In Example 1, Brian did spend $4 on apples; in Example 2, however, Scott sold 5 tickets; and in Example 3, only 3 people are on line between Brian and Scott!
It may seem that each of these examples requires a simple subtraction: 113 – 109 = 4. In Example 1, Brian did spend $4 on apples; in Example 2, however, Scott sold 5 tickets; and in Example 3, only 3 people are on line between Brian and Scott!
 Assume that Brian went into the store with 113 one-dollar bills, numbered 1 through 113; he spent the 4 dollars numbered 113, 112, 111, and 110, and still had the dollars numbered 1 through 109; Scott sold the 5 tickets numbered 109, 110, 111, 112, and 113; and between Brian and Scott the 110th, 111th, and 112th persons—3 people—were on line.
Assume that Brian went into the store with 113 one-dollar bills, numbered 1 through 113; he spent the 4 dollars numbered 113, 112, 111, and 110, and still had the dollars numbered 1 through 109; Scott sold the 5 tickets numbered 109, 110, 111, 112, and 113; and between Brian and Scott the 110th, 111th, and 112th persons—3 people—were on line.
In Example 1, you just needed to subtract: 113 – 109 = 4. In Example 2, you need to subtract and then add 1: 113 – 109 + 1 = 4 + 1 = 5. And in Example 3, you need to subtract and then subtract 1 more: 113 – 109 – 1 = 3. Although Example 1 is too easy for the GRE, questions such as Examples 2 and 3 do appear, because they’re not as obvious and they require that little extra thought. When do you have to add or subtract 1?
The issue is whether or not the first and last numbers are included. In Example 1, Brian spent dollar number 113, but he still had dollar number 109 when he left the store. In Example 2, Scott sold both ticket number 109 and ticket 113. In Example 3, neither Scott (the 113th person) nor Brian (the 109th person) was to be counted.
KEY FACT O1
To count how many integers there are between two integers, follow these rules:
 If exactly one of the endpoints is included, subtract.
If exactly one of the endpoints is included, subtract.
 If both endpoints are included, subtract and add 1.
If both endpoints are included, subtract and add 1.
 If neither endpoint is included, subtract and subtract 1 more.
If neither endpoint is included, subtract and subtract 1 more.
EXAMPLE 4
From 1:09 to 1:13, Adam read pages 109 through 113 in his English book. What was his rate of reading, in pages per minute?
SOLUTION.
Since Adam read both pages 109 and 113, he read 113 – 109 + 1 = 5 pages. He started reading during the minute that started at 1:09 (and ended at 1:10). Since he stopped reading at 1:13, he did not read during the minute that began at 1:13 (and ended at 1:14). So he read for 1:13 – 1:09 = 4 minutes. He read at the rate of 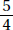 pages per minute.
pages per minute.
TACTIC |
Systematically Making a List |
When a question asks “How many ... ?” and the numbers in the problem are small, just systematically list all of the possibilities.
Proper use of TACTIC O1 eliminates the risk of making an error in arithmetic. In Example 4, rather than even thinking about whether or not to add 1 or subtract 1 after subtracting the number of pages, you could have just quickly jotted down the numbers of the pages Adam read (109, 110, 111, 112, 113), and then counted them.
EXAMPLE 5
Ariel has 4 paintings in the basement. She is going to bring up 2 of them and hang 1 in her den and 1 in her bedroom. In how many ways can she choose which paintings go in each room?

SOLUTION.
Label the paintings 1, 2, 3, and 4, write B for bedroom and D for den, and make a list.
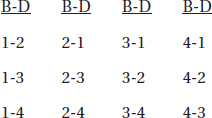
There are 12 ways to choose which paintings go in each room.
In Example 5, making a list was feasible, but if Ariel had 10 paintings and needed to hang 4 of them, it would be impossible to list all the different ways of hanging them. In such cases, we need the counting principle.
The Counting Principle
KEY FACT O2
If two jobs need to be completed and there are m ways to do the first job and n ways to do the second job, then there are m × n ways to do one job followed by the other. This principle can be extended to any number of jobs.
In Example 5, the first job was to pick 1 of the 4 paintings and hang it in the bedroom. That could be done in 4 ways. The second job was to pick a second painting to hang in the den. That job could be accomplished by choosing any of the remaining 3 paintings. So there are 4 × 3 = 12 ways to hang 2 of the paintings.
Now, assume that there are 10 paintings to be hung in 4 rooms. The first job is to choose one of the 10 paintings for the bedroom. The second job is to choose one of the 9 remaining paintings to hang in the den. The third job is to choose one of the 8 remaining paintings for the living room. Finally, the fourth job is to pick one of the 7 remaining paintings for the dining room. These 4 jobs can be completed in 10 × 9 × 8 × 7 = 5,040 ways.
EXAMPLE 6
How many integers are there between 100 and 1,000 all of whose digits are odd?

SOLUTION.
We’re looking for three-digit numbers, such as 135, 711, 353, and 999, in which all three digits are odd. Note that we are not required to use three different digits. Although you certainly wouldn’t want to list all of them, you could count them by listing some of them and seeing if a pattern develops.
 In the 100s there are 5 numbers that begin with 11: 111, 113, 115, 117, 119.
In the 100s there are 5 numbers that begin with 11: 111, 113, 115, 117, 119.
 Similarly, there are 5 numbers that begin with 13: 131, 133, 135, 137, 139.
Similarly, there are 5 numbers that begin with 13: 131, 133, 135, 137, 139.
 There are 5 that begin with 15; 5 that begin with 17; and 5 that begin with 19.
There are 5 that begin with 15; 5 that begin with 17; and 5 that begin with 19.
 A total of 5 × 5 = 25 in the 100s.
A total of 5 × 5 = 25 in the 100s.
 In the same way there are 25 in the 300s, 25 in the 500s, 25 in the 700s, and 25 in the 900s, for a grand total of 5 × 25 = 125.
In the same way there are 25 in the 300s, 25 in the 500s, 25 in the 700s, and 25 in the 900s, for a grand total of 5 × 25 = 125.
You can actually do this in less time than it takes to read this paragraph.
The best way to solve Example 6, however, is to use the counting principle. Think of writing a three-digit number as three jobs that need to be done. The first job is to select one of the five odd digits and use it as the digit in the hundreds place. The second job is to select one of the five odd digits to be the digit that goes in the tens place. Finally, the third job is to select one of the five odd digits to be the digit in the units place. Each of these jobs can be done in 5 ways. So the total number of ways is 5 × 5 ×5 = 125.
EXAMPLE 7
How many different arrangements are there of the letters A, B, C, and D?
 4
4  6
6  8
8  12
12  24
24
Since from the choices given, we know that the answer is a relatively small number, we could just use TACTIC O1 and systematically list them: ABCD, ABDC, ACBD, ... . However, this method would not be suitable if you had to arrange as few as 5 or 6 letters and would be essentially impossible if you had to arrange 10 or 20 letters.
SOLUTION.
Think of the act of arranging the four letters as four jobs that need to be done, and use the counting principle. The first job is to choose one of the four letters to write in the first position; there are 4 ways to complete that job. The second job is to choose one of the remaining three letters to write in the second position; there are 3 ways to complete that job. The third job is to choose one of the two remaining letters to write in the third position; there are 2 ways to complete that job. Finally, the fourth job is to choose the one remaining letter and to write it; that can be done in 1 way. So, the total number of arrangements of the letters A, B, C, and D is: 4 × 3 × 2 × 1 = 24.
Permutations and Combinations
PERMUTATIONS
Example 7 is a special case of a more general situation. Any order or arrangement of a set of objects is called a permutation of those objects. So what Example 7 asks is, “How many permutations are there of the letters A, B, C, and D?” The answer is (4)(3)(2)(1) = 24. More generally, the number of permutations of a set of n objects is:
n(n – 1)(n – 2)···(3)(2)(1)
This product occurs so frequently in mathematics that it has been given a special name and symbol. It is called n factorial and is written n!.
By special convention 0! = 1, 1! = 1; and for all positive integers greater than 1:
n! = n(n – 1)(n – 2)···(3)(2)(1)
For example:
2! = (2)(1) = 2
3! = (3)(2)(1) = 6
4! = (4)(3)(2)(1) = 24
5! = (5)(4)(3)(2)(1) = 120
10! = (10)(9)(8)(7)(6)(5)(4)(3)(2)(1) = 3,628,800
As you can see, factorials get big very quickly. When written out, 20! is a 19-digit number, and 50! is 65 digits long. Sometimes we want to know how many ways there are to order only some of the objects of a given set.
EXAMPLE 8
How many different 4-letter arrangements are there of the letters A, B, C, D, E, F, and G?

SOLUTION.
Proceed exactly as we did in Example 7. There are 7 choices for the first letter, 6 for the second letter, 5 for the third letter, and 4 for the fourth letter. So, there are 7 × 6 × 5 × 4 = 840 ways to arrange 4 of the 7 letters.
Example 8 is also a special case of a more general situation. What Example 8 asks is, “How many permutations of 7 letters are there, if we take only 4 of them?” In general, nPk represents the number of permutations of n objects taken k at a time. Note that in Example 8,

In general,
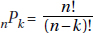
Note that

COMBINATIONS
Sometimes the order of the objects doesn’t matter. If there are 10 students in a club and one is chosen to be president, a second to be secretary, and a third to be treasurer, the order matters. President Amy, secretary Bob, and treasurer Chris is a different scenario from president Bob, secretary Chris, and treasurer Amy. But if the club needs to choose three members to serve on a committee, the order in which they are chosen doesn’t matter. The committee consisting of Amy, Bob, and Chris is exactly the same as the committee consisting of Bob, Chris, and Amy. When order doesn’t matter, we talk about the number of combinations of n objects taken k at a time, for which the symbol is nCk. The number of ways of choosing a president, secretary, and treasurer from a 10-person club is 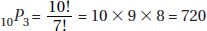 . The number of 3-person committees that can be chosen from a 10-person club is much smaller. The 3! permutations of A, B, and C (representing Amy, Bob, and Chris):
. The number of 3-person committees that can be chosen from a 10-person club is much smaller. The 3! permutations of A, B, and C (representing Amy, Bob, and Chris):
ABC, ACB, BAC, BCA, CAB, CBA
all represent the same committee. So to get the value of 10C3, we have to divide 10P3 by 3!. In general,

Note: Choosing a committee of 3 people from a group of 10 people could be accomplished by choosing the other 7 people not to be on the committee. So, 10C3 = 10C7, and more generally, nCk = nCn–k.
Venn Diagrams
A Venn diagram is a figure with two or three overlapping circles, usually enclosed in a rectangle, which is used to solve certain counting problems. To illustrate this, assume that a school has 100 seniors. The following Venn diagram, which divides the rectangle into four regions, shows the distribution of those students in the band and the orchestra.
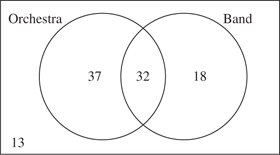
The 32 written in the part of the diagram where the two circles overlap represents the 32 seniors who are in both band and orchestra. The 18 written in the circle on the right represents the 18 seniors who are in band but not in orchestra, while the 37 written in the left circle represents the 37 seniors who are in orchestra but not in band. Finally, the 13 written in the rectangle outside of the circles represents the 13 seniors who are in neither band nor orchestra. The numbers in all four regions must add up to the total number of seniors: 32 + 18 + 37 + 13 = 100. Note that there are 50 seniors in the band—32 who are also in the orchestra and 18 who are not in the orchestra. Similarly, there are 32 + 37 = 69 seniors in the orchestra. Be careful: the 50 names on the band roster and the 69 names on the orchestra roster add up to 119 names—more than the number of seniors. That’s because 32 names are on both lists and so have been counted twice. The number of seniors who are in band or orchestra is only 119 – 32 = 87. Those 87 together with the 13 seniors who are in neither make up the total of 100.
On the GRE, Venn diagrams are used in two ways. It is possible to be given a Venn diagram and asked a question about it, as in Example 8. More often, you will come across a problem, such as Example 9, that you will be able to solve more easily if you think to draw a Venn diagram.
EXAMPLE 9
If the integers from 1 through 15 are each placed in the diagram at the right, which regions are empty?
Indicate all such regions.
 A
A
 B
B
 C
C
 D
D
 E
E
 F
F
 G
G
 H
H
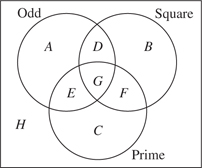
SOLUTION.
The easiest way is just to put each of the numbers from 1 through 15 in the appropriate region.

The empty regions are F and G.
EXAMPLE 10
Of the 410 students at H. S Truman High School, 240 study Spanish and 180 study French. If 25 students study neither language, how many study both?

SOLUTION.
Draw a Venn diagram.

Let x represent the number of students who study both languages, and write x in the part of the diagram where the two circles overlap. Then the number who study only Spanish is 240 – x, and the number who study only French is 180 – x. The number who study at least one of the languages is 410 – 25 = 385, so we have
385 = (240 – x) + x + (180 – x) = 420 – x ⇒ x = 420 – 385 = 35
students who study both.
NOTE: No problem requires the use of a Venn diagram. On some problems you might even find it easier not to use one. In Example 9, you could have reasoned that if there were 410 students in the school and 25 didn’t study either language, then there were 410 – 25 = 385 students who studied at least one language. There are 240 names on the Spanish class lists and 180 on the French class lists, a total of 240 + 180 = 420 names. But those 420 names belong to only 385 students. It must be that 420 – 385 = 35 names were repeated. In other words, 35 students are in both French and Spanish classes.
Probability
The probability that an event will occur is a number between 0 and 1, usually written as a fraction, which indicates how likely it is that the event will happen. For example, if you spin the spinner in the diagram, there are 4 possible outcomes. It is equally likely that the spinner will stop in any of the 4 regions. There is 1 chance in 4 that it will stop in the region marked 2. So we say that the probability of spinning a 2 is one-fourth and write P(2) = 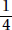 . Since 2 is the only even number on the spinner we could also say P(even) =
. Since 2 is the only even number on the spinner we could also say P(even) = 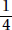 . There are 3 chances in 4 that the spinner will land in a region with an odd number in it, so P(odd) =
. There are 3 chances in 4 that the spinner will land in a region with an odd number in it, so P(odd) =  .
.

KEY FACT O3
If E is any event, the probability that E will occur is given by

assuming that the possible outcomes are all equally likely.
In the preceding example, each of the 4 regions is the same size, so it is equally likely that the spinner will land on the 2, 3, 5, or 7. Therefore,

Note that the probability of not getting an odd number is 1 minus the probability of getting an odd number:  . Let’s look at some other probabilities associated with spinning this spinner once.
. Let’s look at some other probabilities associated with spinning this spinner once.

KEY FACT O4
Let E be an event, and P(E) the probability it will occur.
 If E is impossible (such as getting a number greater than 10), P(E) = 0.
If E is impossible (such as getting a number greater than 10), P(E) = 0.
 If it is certain that E will occur (such as getting a prime number), P(E) = 1.
If it is certain that E will occur (such as getting a prime number), P(E) = 1.
 In all cases 0 ≤ P(E) ≤ 1.
In all cases 0 ≤ P(E) ≤ 1.
 The probability that event E will not occur is 1 – P(E).
The probability that event E will not occur is 1 – P(E).
 If 2 or more events are mutually exclusive and constitute all the outcomes, the sum of their probabilities is 1.
If 2 or more events are mutually exclusive and constitute all the outcomes, the sum of their probabilities is 1.
[For example, P(even) + P(odd) =  .]
.]
 The more likely it is that an event will occur, the higher its probability (the closer to 1 it is); the less likely it is that an event will occur, the lower its probability (the closer to 0 it is).
The more likely it is that an event will occur, the higher its probability (the closer to 1 it is); the less likely it is that an event will occur, the lower its probability (the closer to 0 it is).
Even though probability is defined as a fraction, we can write probabilities as decimals or percents, as well.
Instead of writing P(E) = 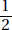 , we write P(E) = .50 or P(E) = 50%.
, we write P(E) = .50 or P(E) = 50%.
EXAMPLE 11
An integer between 100 and 999, inclusive, is chosen at random.
What is the probability that all the digits of the number are odd?

SOLUTION.
By KEY FACT O1, since both endpoints are included, there are 999 – 100 + 1 = 900 integers between 100 and 999. In Example 6, we saw that there are 125 three-digit numbers all of whose digits are odd. So the probability is
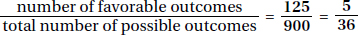
NOTE: On a numeric entry question it is not necessary to reduce fractions, so 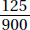 is perfectly acceptable.
is perfectly acceptable.
KEY FACT O5
If an experiment is done two (or more) times, the probability that first one event will occur and then a second event will occur is the product of the probabilities.
EXAMPLE 12
A fair coin is flipped three times. What is the probability that the coin lands heads each time?

SOLUTION.
When a fair coin is flipped:

By KEY FACT O5, P(3 heads) =
P(head 1st time) × P(head 2nd time) × P(head 3rd time) = 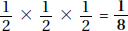
Another way to handle problems such as Example 12 is to make a list of all the possible outcomes. For example, if a coin is tossed three times, the possible outcomes are
|
head, head, head |
head, head, tail |
|
|
head, tail, head |
head, tail, tail |
|
|
tail, head, head |
tail, head, tail |
|
|
tail, tail, head |
tail, tail, tail |
|
On the GRE, of course, if you choose to list the outcomes on your scrap paper, you should abbreviate and just write HHH, HHT, and so on. In any event, there are eight possible outcomes, and only one of them (HHH) is favorable. So the probability is 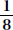 .
.
EXAMPLE 13
Three fair coins are flipped.

SOLUTION.
From the list of the 8 possible outcomes mentioned, you can see that in 4 of them (HHH, HHT, HTH, THH) there are more heads than tails, and that in 4 of them (TTT, TTH, THT, HTT) there are more tails than heads. Each probability is 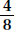 . The answer is C.
. The answer is C.
In Example 12, it wasn’t even necessary to calculate the two probabilities. Since heads and tails are equally likely, when several coins are flipped, it is just as likely to have more heads as it is to have more tails. This is typical of quantitative comparison questions on probability; you usually can tell which of the two probabilities is greater without having to calculate either one. This is another instance where you can use TACTIC 5 from Chapter 10: don’t calculate, compare.
EXAMPLE 14
The numbers from 1 to 1,000 are each written on a slip of paper and placed in a box. Then 1 slip is removed.

SOLUTION.
Since there are many more multiples of 5 than there are of 7, it is more likely that a multiple of 5 will be drawn. Quantity A is greater.
PRACTICE EXERCISES—COUNTING AND PROBABILITY
Discrete Quantitative Questions
1.Alyssa completed exercises 6–20 on her math review sheet in 30 minutes. At this rate, how long, in minutes, will it take her to complete exercises 29–57?
 56
56
 57
57
 58
58
 60
60
 65
65
2.A diner serves a lunch special, consisting of soup or salad, a sandwich, coffee or tea, and a dessert. If the menu lists 3 soups, 2 salads, 7 sandwiches, and 8 desserts, how many different lunches can you choose? (Note: Two lunches are different if they differ in any aspect.)
 22
22
 280
280
 336
336
 560
560
 672
672
3.Dwight Eisenhower was born on October 14, 1890 and died on March 28, 1969. What was his age, in years, at the time of his death?
 77
77
 78
78
 79
79
 80
80
 81
81
4.How many four-digit numbers have only even digits?

5.There are 27 students on the college debate team. What is the probability that at least 3 of them have their birthdays in the same month?
 0
0
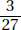

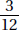
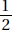
 1
1
6.Let A be the set of primes less than 6, and B be the set of positive odd numbers less than 6. How many different sums of the form a + b are possible, if a is in A and b is in B?
 6
6
 7
7
 8
8
 9
9
 10
10
7.There are 100 people on a line. Aviva is the 37th person and Naomi is the 67th person. If a person on line is chosen at random, what is the probability that the person is standing between Aviva and Naomi?

8.A jar has 5 marbles, 1 of each of the colors red, white, blue, green, and yellow. If 4 marbles are removed from the jar, what is the probability that the yellow one was removed?


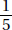




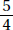
9.Josh works on the second floor of a building. There are 10 doors to the building and 8 staircases from the first to the second floor. Josh decided that each day he would enter by one door and leave by a different one, and go up one staircase and down another. How many days could Josh do this before he had to repeat a path he had previously taken?
 80
80
 640
640
 800
800
 5040
5040
 6400
6400
10.A jar contains 20 marbles: 4 red, 6 white, and 10 blue. If you remove marbles one at a time, randomly, what is the minimum number that must be removed to be certain that you have at least 2 marbles of each color?
 6
6
 10
10
 12
12
 16
16
 18
18
11.At the audition for the school play, n people tried out. If k people went before Judy, who went before Liz, and m people went after Liz, how many people tried out between Judy and Liz?
 n – m – k – 2
n – m – k – 2
 n – m – k – 1
n – m – k – 1
 n – m – k
n – m – k
 n – m – k + 1
n – m – k + 1
 n – m – k + 2
n – m – k + 2
12.In a group of 100 students, more students are on the fencing team than are members of the French club. If 70 are in the club and 20 are neither on the team nor in the club, what is the minimum number of students who could be both on the team and in the club?
 10
10
 49
49
 50
50
 60
60
 61
61
13.From a group of four boys and six girls, how many ways are there to choose five of the children, if you must choose at least two boys and two girls?

QUESTIONS 14–15 REFER TO THE FOLLOWING DIAGRAM.
A is the set of positive integers less than 20; B is the set of positive integers that contain the digit 7; and C is the set of primes.
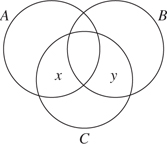
14.How many numbers are in the region labeled x?
 4
4
 5
5
 6
6
 7
7
 8
8
15.What is the sum of all the numbers less than 50 that are in the region labeled y?

Quantitative Comparison Questions
 Quantity A is greater.
Quantity A is greater.
 Quantity B is greater.
Quantity B is greater.
 The two quantities are equal.
The two quantities are equal.
 It is impossible to determine which quantity is greater.
It is impossible to determine which quantity is greater.

A jar contains 4 marbles: 2 red and 2 white.
2 marbles are chosen at random.


A congressional committee consisting of 10 Democrats and 10 Republicans is to choose a subcommittee consisting of 4 Democrats and 6 Republicans.


 Repeating Sequences
Repeating Sequences
 Arithmetic Sequences
Arithmetic Sequences
 Geometric Sequences
Geometric Sequences
 Practice Exercises
Practice Exercises
 Answer Explanations
Answer Explanations
On a typical GRE math test, there are often one or two questions about sequences. In this section, you will read about the different types of sequences that could be the source of a GRE question.
A sequence is a list of objects separated by commas. Most often, the objects are numbers, but they don’t have to be. A sequence can be finite, such as 2, 5, 10, 17, 26, or can be infinite, such as 2, 4, 6, 8, 10, ... . The numbers in the list are called the terms of the sequence.
The terms of a sequence don’t have to follow any regular pattern or rule. Suppose John tossed a die 100 times and recorded the outcomes. If you saw the first 10 terms of that sequence—4, 6, 6, 2, 5, 3, 5, 4, 4, 2—you would have no way of knowing what the 11th term is.
On the GRE, however, there is always a definite rule that determines the terms of a sequence. If Mary creates a sequence of 100 terms by writing down the number 5 and then continually adding 3 to each term, the first 10 terms would be 5, 8, 11, 14, 17, 20, 23, 26, 29, 32. Not only do you know what the eleventh term of her sequence is, as you will see, you can easily calculate the 88th, or any other, term.
On the GRE, the most common type of question concerning sequences gives you a rule and asks you to find a particular term. The three types of sequences that occur most often are repeating sequences, arithmetic sequences, and geometric sequences.
Repeating Sequences
A sequence whose terms repeat in a cyclical pattern is called a repeating sequence. For example, the following three sequences are repeating sequences:
a, b, c, a, b, c, a, b, c, a, b, c, ...
0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, ...
7, 1, 4, 2, 8, 5, 7, 1, 4, 2, 8, 5, ...
Sometimes we use the notation {an} for a squence. Here an represents the n-th term of the sequence: a1 is the first term, a2 is the second term, and so on.
KEY FACT P1
When a sequence consists of a group of k terms that repeat in the same order indefinitely, to find the nth term, find the remainder, r, when n is divided by k. The rth term and the nth term are equal.
The fraction  is equivalent to the repeating decimal 0.714285714285... in which the six digits, 7, 1, 4, 2, 8, 5, repeat indefinitely. Examples 1 and 2 refer to this sequence of digits.
is equivalent to the repeating decimal 0.714285714285... in which the six digits, 7, 1, 4, 2, 8, 5, repeat indefinitely. Examples 1 and 2 refer to this sequence of digits.
EXAMPLE 1
What is the 1,000th digit to the right of the decimal point in the expansion of  ?
?
 1
1  2
2  4
4  7
7  8
8
SOLUTION.
Use KEY FACT P1. Since the repeating portion consists of 6 digits, divide 1,000 by 6.
1,000 ÷ 6 = 166.666... ⇒ the quotient is 166
166 × 6 = 996 ⇒ the remainder is 1,000 – 996 = 4
Therefore, the 1,000th term is the same as the 4th term, namely 2 (B).
EXAMPLE 2
What is the sum of the 101st through the 106th digits in the decimal expression  ?
?

SOLUTION.
You could repeat what was done in Example 1 six times, but, of course, you shouldn’t. Any six consecutive terms of this sequence consist, in some order, of the same six digits—7, 1, 4, 2, 8, 5—whose sum is 27. In this case, the order is 8, 5, 7, 1, 4, 2, but you do not need to know that.
Consider the following sequence, called the Fibonacci sequence, after the 13th century Italian mathematician: a1 = 1, a2 = 1, and for all n > 2, an = an–1 + an–2. Then a3 = a2 + a1 = 1 + 1 = 2; a4 = 2 + 1 = 3; a5 = 3 + 2 = 5; a6 = 5 + 3 = 8, and so on. Clearly this is not a repeating sequence, and it would be totally unreasonable to ask you to find the 100th term. However, there are some questions, such as the one in Example 3, that you could be asked.
EXAMPLE 3
Of the first 100 terms of the Fibonacci sequence, how many are odd?

SOLUTION.
The sequence itself does not form a repeating sequence, but its pattern of odd (O) and even (E) terms does:
1 1 2 3 5 8 13 21 34
O O E O O E O O E
Note that the Os and Es form a repeating sequence:

The first 99 terms consist of 33 sets of  . Since each set contains two Os and one E, of the first 99 terms, 66 are odd and 33 are even. The 100th term is the first term in the next set and so is O. In all, there are 67 odd terms.
. Since each set contains two Os and one E, of the first 99 terms, 66 are odd and 33 are even. The 100th term is the first term in the next set and so is O. In all, there are 67 odd terms.
Arithmetic Sequences
An arithmetic sequence is a sequence such as 5, 8, 11, 14, 17, ... in which the difference between any two consecutive terms is the same. In this sequence, the difference is 3 (8 – 5 = 3; 11 – 8 = 3; 14 – 11 = 3, ...). An easy way to find the nth term of such a sequence is to start with the first term and add the common difference n – 1 times. Here, the 5th term is 17, which can be obtained by taking the first term, 5, and adding the common difference, 3, four times: 5 + 4(3) = 17. In the same way, the 100th term is 5 + 99(3) = 5 + 297 = 302.
KEY FACT P2
If a1, a2, a3, ... is an arithmetic sequence whose common difference is d, then an = a1 + (n – 1)d.
EXAMPLE 4
If the 8th term of an arithmetic sequence is 10 and the 20th term is 58, what is the first term?

SOLUTION.
Use KEY FACT P2 twice and subtract:

Then
10 = a1 + 7d = a1 + 7(4) = a1 + 28 ⇒ a1 = –18
Geometric Sequences
A geometric sequence is a sequence such as 3, 6, 12, 24, 48, ... in which the ratio between any two consecutive terms is the same. In this sequence, the ratio is
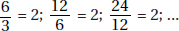
An easy way to find the nth term of a geometric sequence is to start with the first term and multiply it by the common ratio n – 1 times. Here the 5th term is 48, which can be obtained by taking the first term, 3, and multiplying it by the common ratio, 2, four times: 3 × 2 × 2 × 2 × 2 = 3 × 24 = 3 × 16 = 48. In the same way, the 100th term is 3 × 299.
KEY FACT P3
If a1, a2, a3, ... is a geometric sequence whose common ratio is r, then  .
.
EXAMPLE 5
What is the 12th term of the sequence 3, –6, 12, –24, 48, –96, . . . ?

SOLUTION.
This is a geometric sequence whose common ratio is –2. By KEY FACT P3,
a12 = a1(–2)11 = 3(–2)11 = 3(–2,048) = –6,144
1.{an} and {bn} are two sequences defined as follows: a1 = 10 and for n > 1, an = an–1 + 3; b1 = 100 and for all n > 1, bn = bn–1 – 3. What is a16 + b16?
 45
45
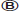 55
55
 90
90
 110
110
 200
200
2.What is the 500th digit to the right of the decimal point when 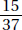 is expressed as a decimal?
is expressed as a decimal?
 0
0
 3
3
 4
4
 5
5
 7
7
3.July 4, 2009 was a Saturday. What day of the week was July 4, 2011? (Note: 2009, 2010, and 2011 were all regular years with 365 days.)
 Sunday
Sunday
 Monday
Monday
 Tuesday
Tuesday
 Friday
Friday
 Saturday
Saturday
4.The number of bacteria in a culture increases by 20% every 20 minutes. If there are 1,000 bacteria present at noon on a given day, to the nearest thousand, how many will be present at midnight of the same day?
 9,000
9,000
 43,000
43,000
 174,000
174,000
 591,000
591,000
 709,000
709,000
5.A gum ball dispenser is filled with exactly 1,000 pieces of gum. The gum balls always come out in the following order: 1 red, 2 blue, 3 green, 4 yellow, and 5 white. After the fifth white, the pattern repeats, starting with 1 red, and so on. What is the color of the last gum ball to come out of the machine?
 red
red
 blue
blue
 green
green
 yellow
yellow
 white
white
6.{an} is an arithmetic sequence. If a21 = 57 and a89 = 227, what is a333?
 367
367
 417
417
 587
587
 793
793
 837
837