ANSWER EXPLANATIONS

Section 1—Analytical Writing: Issue Essay

Though there are no right or wrong answers to the essay questions, you can get an idea of the level of writing required to achieve a particular score by reviewing the sample essays that follow. We have included a sample essay for each score from 6 (the best) through 1 (the poorest). Each sample essay also includes a short explanation of how the score was derived by using the rubric. In evaluating your own essays you should apply the rubric in a similar fashion.

PROMPT #1

“Question authority. Only by questioning accepted wisdom can we advance our understanding of the world.”

Compose an essay that identifies how greatly you concur (or differ) with the recommendation provided and describe the rationale for your argument. As you build and provide evidence for your argument, include examples that demonstrate circumstances in which implementing the recommendation might (or might not) be beneficial. Be sure to explain the impact these examples have on your argument.

SCORE 6 ISSUE ESSAY

In their infamous 1984 ad campaign for Macintosh computers, Apple, Inc. showed a mass of gray, unblinking faces entranced by a droning voice emanating from a massive screen—suddenly, a beautiful blonde woman in a brightly-colored jumpsuit appears and smashes the screen with a hammer. The video was followed by an imprint of Apple’s fluorescent logo and a command: “Think Differently.” The call to “question authority” is certainly a convenient catch-phrase for corporations; however, the circumstances of an individual’s relationship to authority are often much more complex than walking to an Apple Store and buying a smartphone. “Question authority” is a blunt command that fails to account for the potentially grave consequences of defiance.

It is undeniable that challenging conventional wisdom is necessary to advance our understanding of the mysterious universe in which we find ourselves. A classic example is the case of Galileo Galilei, the Italian astronomer. In the 17th century, Galileo used a telescope to map the celestial bodies, using methods of logical inference that today most children are taught as “the scientific method.” His profound insight led him to the conclusion that the Earth revolved around the Sun—this was not an entirely “new” idea, but it was a highly controversial one at the time. During the Roman Inquisition, the Catholic Church attempted to root out those who promulgated views contradicting the religious doctrine; this, of course, included Galileo’s writings on the “heliocentric” theory, and he was eventually imprisoned, and his works censored.

Galileo’s case illustrates that questioning authority is a rare privilege, with often serious consequences. We can find more humble examples in our own society: for example, a single mother in a major metropolitan area who works several jobs to support her children—one week into a new job as cashier at a fast food restaurant, she asks for overtime in order to make an upcoming rent payment. Her employer not only refuses, but berates her for having the audacity to ask for overtime, the right to which belongs to more established employees. Of course, she may have the instinct to challenge this arbitrary rule; but, more likely, she would lose her job for lack of obedience. After all, there is no shortage of people who could fill her position.

In both examples—a philosopher in a theocratic society, or a laborer in a situation of exploitation—the desire to openly challenge authority comes up against a pragmatic need to keep quiet in the interest of one’s welfare. Although there is something quite powerful about adopting an ethos of “Thinking Differently” (and perhaps this explains its success as a marketing slogan), the circumstances in which we have opportunities to challenge authority figures are contingent and complex. Rather than an inflexible command, perhaps we should understand the call to “question authority” as an ethical guide—encouraging us to have the courage to say what we feel is true, when the cost of failing to speak outweighs the reprisals we may invite. This way, “Think Differently” might become, more than a corporate platitude, a meaningful motto for a progressive society.

ARGUMENT The essay presents a clear and perceptive argument that the command to question authority is too simplistic and that the cost of complying with it may be too high for some to pay. The writer does an especially good job responding to the task instruction to describe situations in which adopting the recommendation could be disadvantageous. One shortcoming is that the author accepts without examination the second half of the quotation, which asserts that questioning authority is the only way to advance knowledge.

SUPPORT The essay includes two strong examples of situations in which questioning authority was dangerous to the questioner. It also provides an example in the introductory paragraph that demonstrates how the command to question authority is an oversimplified catch-phrase, much like those used in advertising.

STRUCTURE The essay is well focused and does not stray from the task of proving its thesis. The transitions, especially those from the second to third paragraph and from the third to fourth paragraph, are graceful and clearly link one topic to the next.

FLUENCY The essay displays sophisticated vocabulary and varied sentence structure throughout.

CONVENTIONS Outstanding. The essay includes no noticeable errors in grammar, usage, or mechanics.

SCORE 5 ISSUE ESSAY

Recently, a friend of mine posted the following status on Facebook: “Those who are obedient will be blessed.” Although it sounds like perhaps it is scripture, it may just have been a simple moment of alleged wisdom in her own words. Whatever the case, I reflected on this post for quite some time. Am I obedient? Do I aspire to follow in the footsteps of other obedient people? And I am blessed?

The post brought to mind another favorite quote, one I am sure can be attributed to an actual person, although the original speaker escapes me: “Well behaved women rarely make history.” This is true of women, and it is true of the people of all oppressed groups in the history of the United States. An overview of American history shows us pretty clearly that the questioning of authority has shaped the entire destiny of this country and its inhabitants. Obedience has guaranteed rights to no one. Women following the rules and expectations for them were not simply granted the right to vote out of the kindness of men’s hearts. They suffered for suffrage, toiling, protesting, marching, and lobbying the public and the political leaders in order to gain this right. If the women of the Seneca Falls convention accepted the wisdom of the day—that politics was the work of men—millions of Americans would still be disenfranchised.

Similarly, the Voting Rights Act created a pathway to civic participation that had been blocked to African-Americans simply because of race. While Black men were granted the right to vote in theory long before women of any race were, prohibitive laws and customs prevented African-American voting from reconstruction until the middle of the 20th century. (Indeed, there is good reason to believe that the suppression of Black voting is still active and accepted de facto law in some parts of the country despite the Voting Rights Act). While constitutionally originally 3/5 of a person, Black people have been a backbone of this country, but accepting authority never ensured political representation or even political consideration. African-Americans living under Jim Crow laws during reconstruction and beyond were not rewarded for good behavior with equal rights socially, politically, or economically. Those rights had to be demanded. Our present political landscape, including the Black Lives Matter movement, shows us that Black people questioning authority is an ongoing need. Without vocal and strategic demands that authority be interrogated, we see that authority does what it does best— uphold its own interest at the risk of the well-being of those being governed by its power.

Voting rights, of course, are not the only rights that have been prevented by maintaining the status quo. Japanese-Americans needed only be Japanese (and, in fact, often needed only be any Asian group) to be interned as possible traitors whether they had obeyed all US laws or not. Their heritage made them suspect, and obeying authority did not protect them from internment. Until recently, LGBTQ people law-abidingly living without marriage rights were able to vote but missed out on minor perks and major life-changing powers that heterosexual couples enjoyed via custom and via the law. In today’s headlines, we see abuse or neglect of authority everywhere from the Flint, Michigan, water scandal to the current standoff at Standing Rock in protest of the Dakota Pipeline.

ARGUMENT The essay presents a clear argument that authority must be questioned in order for social progress to be made. While the thesis is clear, it does not consider the possibility that there may be instances in which questioning authority may be disadvantageous. A more perceptive and complex argument would take potential disadvantages into account (while still concluding that those disadvantages are outweighed).

SUPPORT The essay includes compelling and detailed examples that provide strong support for its thesis that progress cannot be made without questioning authority.

STRUCTURE The essay is generally well focused, though the introduction is a bit of a diversion. Transitions between paragraphs are logical. The conclusion is abrupt, and reads as if the writer was unable to finish their thought.

FLUENCY The ideas in the essay are clear, and its vocabulary use is appropriate and effective, if a bit colloquial at times. Sentence structure is varied.

CONVENTIONS The essay demonstrates solid command of the grammar, usage, and mechanics of standard written English. There are few, if any, obvious errors.

SCORE 4 ISSUE ESSAY

There is a great thrill from questioning authority. Young children question the authority of their parents by testing boundaries and pushing them. Students question the authority of their teachers with disrespect or refusing to submit their assignments. When confronted with progress, knowledge itself is challenged. In this essay, I will argue that questioning authority is a critical part of changing human knowledge. This can be observed in both historical and modern times.

Questioning authority does create greater understanding of the world, as we can see from the historical example of Galileo. This historical era scientist questioned common knowledge of astronomy and the earth’s place in the universe. His research made him think that the sun was the center, and that planets like Earth revolve around it. This is why Galileo is a founding father of modern science. His questioning of the common knowledge of his time was a challenge to authority that changed many things we know about the universe today.

Questioning authority is not just part of history, but is also a modern day occurrence. LGBT marriage is an example of this, which ended in several court cases and laws being changed. Until recently, the common knowledge of most Americans was that marriage is between a man and a woman, but now the United States Supreme Court has ruled that same-sex marriage is legal in all 50 states. But someone had to question that common knowledge before the law could be changed.

As you can see, this quotation can be proven true with historical examples and current events. But there is still one flaw. The “Only by” in the quotation says that there is a single way to change understanding of the world, and that is to question authority. This is too simple a solution to resolve all of the questions about progress and advancement of knowledge. Galileo’s work was destroyed when he questioned the authority that said earth was the center of the universe. He was punished and placed under house arrest for the rest of his life. Today the movement for LGBT marriage has caused some backlash. This has magnified homophobia and increased violence against LGBT people. Questioning authority may be a good way to challenge conventional wisdom, but it cannot be considered the only option.

ARGUMENT The essay presents a reasonably clear argument on the statement, agreeing that questioning authority is needed for progress in human understanding. The argument grows muddled, however, at the end of the essay, when the writer, in describing possible risks to questioning authority, posits that there are other options for promoting change.

SUPPORT The essay includes relevant examples to support its thesis, though with less detail than is provided in higher scoring essays.

STRUCTURE The essay is adequately focused and organized to support its thesis, though the final paragraph appears to undermine, or at least moderate, its primary argument.

FLUENCY The essay demonstrates adequate control of the conventions of standard written English, though it is at times repetitive or awkward.

CONVENTIONS There are minor errors in grammar and mechanics, but they do not undermine the meaning.

SCORE 3 ISSUE ESSAY

I think it is imperative that authority be questioned. In fact, I would go as far to say that it is immoral for anything to not be questioned. Only when statements and authority are protected against criticism is when our freedom is truly encroached.

In the United States, the first amendment of the Bill of Rights protects the right to free speech. Under this, theoretically Americans have the ability to speak out against not only the authority of the government, but against other forms of authority as well. For example, without protected free speech in the political realm, the authority of the government upholding racist laws in the Jim Crow era of America might not have been questioned as people might have been too scared to stand up to the abhorrent laws.

Furthermore, authority should be questioned not just on the governmental level, but on all levels of academia and media as well. A common misconception that permeates today (whether in newspapers or television shows) is the danger difference, or lack thereof, between powder cocaine and crack cocaine. In truth, pharmacologically, the two are very similar—the main difference is that crack cocaine has a methylated branch while the powder does not. This structural difference has no pharmacological difference in the biochemical effects the drug has, but the media and the majority of academia reject to see this. Only a few researcher, Dr. Carl Hart, for example, are advocates against the majority. These advocates have no fear in standing up and questioning the larger authority, and I think that this is greatly beneficial for society. Without their work, it still could be a reality that crack offenders would be punished more harshly by a ratio of 100:1 than powder offenders. Because of their work, crack possessors are punished instead 18:1 more harshly. Even though there is an improvement made, things still have a ways to go.

I do see that the constant barrage of questioning of authority can prove problematic. In fact, it can be likened to herding cats sometimes when authority is always being questioned. When there is no faith in a system, then it is near impossible to enact any meaningful change. However, only by questioning a government can it be ensured that its power is kept in check and that the people’s rights are protected.

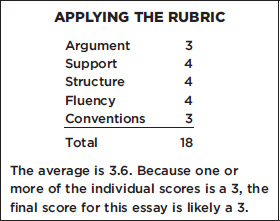
ARGUMENT The essay presents a reasonably clear argument, but it does not respond to the topic. Instead of addressing the topic, that questioning authority is necessary in order to advance understanding of the world, the essay focuses on questioning authority as a necessary check on government power.

SUPPORT The essay includes two examples in which questioning authority has been beneficial. The second example provides greater detail than needed, so much detail that it obscures the point the example is attempting to demonstrate.

STRUCTURE The essay is reasonably well focused and organized, though its transitions are awkward or minimal. Additionally, the length and level of detail in the third paragraph is out of proportion with the rest of the essay.

FLUENCY The essay is reasonably effective in expressing its ideas, and its word choice is generally appropriate.

CONVENTIONS The essay includes frequent minor errors in grammar and usage, some of which obscure meaning.

SCORE 2 ISSUE ESSAY

“Question authority” is a famous saying in the United States. It is popular but it is the wrong thing to do.

Example 1 is American children are very disrespectful to there parents. They do not listen to advise from them, sometimes they even call them a disrespectful name. Children in other cultures show much more respect, that is the proper way.

Example 2 is students. In the United States they do not respect teachers. If they talk when the teacher is talking you visit school to see it. Sometimes they attack even the teacher and vandalize the class room. Teacher in the United States also is receive poor pay checks. Why would any one be teacher when the student “question authority”?

Example 3 is police. They do the very dangerous job to keep safe from preventing crime. Today people do not follow there order when they tell them stop. They make a high speed chase that is very dangerous for the community. Inoccent peoples are killed in high speed chase.

In conclusion, the United States saying “Question authority” is a bad idea.

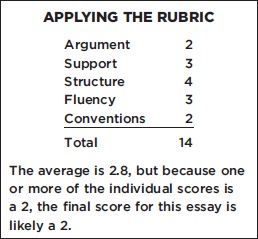
ARGUMENT The essay presents an argument that is clear, but fails to address the full topic or the specific task instructions. No mention is made of advancing understanding of the world, though this is the topic’s justification for questioning authority.

SUPPORT The essay includes three examples to support its thesis, but they are rather limited in this role.

STRUCTURE The essay appears to be organized, as a result of its explicit numerical structure. At the same time, transitions are abrupt, signaled by nothing more than numbering.

FLUENCY The essay is somewhat unclear due to incorrect word choice or sentence structure.

CONVENTIONS The essay includes major errors in grammar and mechanics, some of which obscure meaning.

SCORE 1 ISSUE ESSAY

People should question authority because authority might be wrong and not understanding the real issue very well.

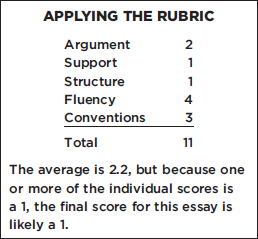
ARGUMENT The essay presents an argument that is on topic, but fails to address the specific requirement in the task instructions.

SUPPORT The essay includes no examples and very limited reasoning to support its thesis.

STRUCTURE The essay is excessively short.

FLUENCY The essay is reasonably clear in making its argument.

CONVENTIONS The essay includes an error in grammar. A single error would not be significant in a longer piece, but it is glaring in an essay this brief.

Section 1—Analytical Writing: Argument Essay

Though there are no right or wrong answers to the essay questions, you can get an idea of the level of writing required to achieve a particular score by reviewing the sample essays that follow. We have included a sample essay for each score from 6 (the best) through 1 (the poorest). Each sample essay also includes a short explanation of how the score was derived by using the rubric. In evaluating your own essays you should apply the rubric in a similar fashion.

PROMPT #2:

The following appeared in an editorial in the Bayside Sentinel.

“Bayside citizens need to consider raising local taxes if they want to see improvements in the Bayside School District. Test scores, graduation and college admission rates, and a number of other indicators have long made it clear that the Bayside School District is doing a poor job educating our youth. Our schools look run down. Windows are broken, bathrooms unusable, and classroom equipment hopelessly out of date. Yet just across the Bay, in New Harbor, school facilities are up-to-date and in good condition. The difference is money; New Harbor spends twenty-seven percent more per student than Bayside does, and test scores and other indicators of student performance are stronger in New Harbor as well.”

Compose an essay that identifies and considers the assumptions (implicit and/or explicit) on which the argument is based. The essay must clarify the importance of these assumptions to the argument and explain the impact on the argument’s validity should the assumptions be faulty.

SCORE 6 ARGUMENT ESSAY

Though conservative pundits have long claimed that there is no link between education spending and student outcomes, the editors of the Bayside Sentinel disagree, arguing that higher taxes and education spending are needed to improve the academic performance of Bayside students. While I am a staunch advocate of increased funding for public education, the argument presented by the Bayside Sentinel is disappointingly weak because it makes fundamental errors in causation, assuming the existence of a causal link without adequate evidence. Though poor funding may, in fact, lead to poor educational outcomes, this editorial has not demonstrated this to be the case. As a result, it has failed to make a strong argument for Bayside voters to increase their taxes.

The first error in causation made by the Bayside Sentinel’s editors involves their focus on the condition of Bayside school facilities when compared to those in New Harbor. Though it is possible that poor facilities cause poor student outcomes, the editorial only implies this by observing that Bayside schools have both poor facilities and poor results, while New Harbor schools have both new facilities and better student performance. The editorial makes no direct claim of causation, simply assuming that a causal relationship exists and providing no evidence that there is more afoot in this case than a simple correlation.

Due to this lack of evidence, it is entirely possible that the editors have even gotten the causal relationship between Bayside students’ academic performance and the condition of their school facilities reversed. One alternate explanation for the relationship might be that students who are alienated from and perform poorly in school are more likely to vandalize school facilities. It is also possible that the academic challenges faced by Bayside students, unlike those faced by their counterparts in New Harbor, are so great that the Bayside district is forced to spend so much on remediation that it cannot adequately fund facilities maintenance. In other words, the academic challenges Bayside students face may be the cause of the poor condition of their school facilities, rather than their result.

The editorial commits an additional error in causation by failing to consider alternate causes for the poor performance of Bayside schools. It is quite possible that the real cause of the disparity in performance between the schools in Bayside and New Harbor is not their per pupil spending, but the wealth of members of the respective communities. If high test scores, graduation rates, and college admission rates are, as many studies suggest, products of high socio-economic status, it is possible that disparities in wealth between the two communities are the real cause of Bayside’s poor results. Ironically, this disparity may also explain the difference in per pupil spending between the two districts, as the residents of Bayside may be less able to spend on education than are their neighbors in New Harbor.

If the editors of the Bayside Sentinel want to provide a strong justification to Baysiders for increasing their taxes, they need to provide evidence that poor funding is causing poor student outcomes in Bayside schools. They also need to identify how new funds would be spent and demonstrate that those changes are likely to improve student performance. Without this information, Baysiders can be forgiven for their reluctance to spend more on their schools.

ARGUMENT The essay displays significant insight in pinpointing two ways in which the argument presented fails to prove its thesis. It does this first by observing that the argument assumes causation, while only demonstrating correlation, and second by proposing several alternate theories that might explain both why Bayside schools are in poor condition and why Bayside students do not perform as well as New Harbor students.

SUPPORT The essay offers detailed and persuasive support by means of multiple examples of factors that might also (or even better) explain the relationship between school funding and student results in Bayside and New Harbor.

STRUCTURE The essay expresses its ideas in a well-organized and clear manner. Transitions between ideas are clear and logical.

FLUENCY The essay expresses its ideas clearly and utilizes sophisticated vocabulary and varied sentence structure throughout.

CONVENTIONS Impressive. The essay includes no noticeable errors in grammar, usage, or mechanics.

SCORE 5 ARGUMENT ESSAY

The opinion piece in the Bayside Sentinel regarding raising taxes to improve our schools makes several arguments. There are three pieces of evidence the author considers valuable for comparison: metrics like standardized test scores, equipment and facilities, and revenue stream. In this piece he compares these three metrics between two different school districts. These comparisons are designed to convince the reader that an increase in revenue stream will create an increase in standardized test scores and equipment and facilities. However, there are several hidden assumptions within this opinion piece that undercut the strength of the argument as presented.

The most glaring of these assumptions is the author’s claim that raising local taxes will mean an increase in funding for the school district. While the author lays out a careful argument about what an increase in revenue stream could provide for the community, they do not provide a piece of evidence that an increase in local taxes would benefit the school district. They argue that New Harbor is spending more money per student, but do not indicate from where New Harbor received that funding. There is a logical leap that more taxes would mean more funding for Bayside schools, without a warrant to prove that is true.

An additional problem with this opinion piece is that it wholly omits a discussion of teachers and the differences between the two school districts in terms of teachers. It is possible that New Harbor has twice as many teachers as Bayside, or that the teachers in New Harbor have more current training than the teachers in Bayside. The author here argues that by improving facilities and equipment with increased tax revenue, test scores would increase. However, teachers are a crucial component to educational success. No one writes a thank you letter to their favorite computer station upon graduating from high school. Without a discussion of teachers, it is impossible to know if increased revenue stream will actually improve performance.

The final problem I will highlight here is that there is no causal relationship between increased revenue and increases in other metrics such as test scores. The proposed revenue stream may not be allocated to the school, or may be allocated in such a way that it does not resolve the problems laid out in the original letter. It is easy to assume that an increase in taxes would return to the community, but unless specially earmarked for improving facilities or increasing test scores, it is questionable whether or not the funding would reach its intended target. There is no interrogation of why New Harbor spends more per student; it is possible that other problems in Bayside are affecting students, such as political corruption or mismanagement of existing tax dollars.

While this opinion piece attempts to locate a problem and suggest a solution for that problem, it falls short of making a complete argument. Too many questions are unanswered about the comparison between Bayside and New Harbor in terms of existing socio-economic status, the current revenue streams and expenses, and teachers. Absent these and other comparisons, this argument is severely weakened. While increases in measurable success such as standardized test scores and college admission ratings is an admirable community goal, the steps to get there are much more complicated than simply raising local taxes.

ARGUMENT The essay pinpoints the elements of the argument at issue and evaluates them with great insight, focusing primarily on the questions of whether funds from a tax increase will be allocated to the schools and whether funds allocated to the schools will be spent in a manner that will improve test scores. It also, though less clearly, questions whether the differences in academic performance between Bayside and New Harbor may result from differences in the number or quality of teachers in the two districts.

SUPPORT The essay provides thoughtful and persuasive support for its main points by pointing out that the proposed increase in tax revenue may not be spent on the schools, or that it may be misspent. It also includes teacher quality as another variable that is unexamined in the original argument.

STRUCTURE The essay expresses ideas clearly and is generally well organized, with suitable transitions between ideas. Two exceptions are the abrupt and incomplete ending of the third paragraph (almost certainly accidental) and the odd placement of that paragraph. It seems out of place between two paragraphs on funding, and would have been more logically placed before or after them.

FLUENCY The essay expresses ideas effectively, with appropriate word choice and varied sentence structure, though the abrupt ending of the third paragraph is a bit confusing.

CONVENTIONS The essay displays solid command of the grammar, usage, and mechanics of standard written English, though it includes a few careless errors.

SCORE 4 ARGUMENT ESSAY

Although I am generally for increased school spending, I want to examine the argument that additional funding would automatically improve the state of Bayside schools. This is an unproven assumption. While spending in New Harbor is higher per student than in Bayside, this does not mean that higher spending is the only factor in higher test scores for New Harbor students.

First, let us note that standardized testing can be a flawed way of measuring student learning. There are numerous critiques of this system, and many of those critiques are based on examining whether standardized testing actually measures knowledge or simply measures testing ability. That said, standardized testing, while it is flawed, is the system we use. It would be useful to know which scores are differnet and how different they are.

If cultural factors such as parent education or language (especially ESL) play a factor in standardized test scores, this may be as much an influence on those scores as much as spending. Thus raising per student spending in Bayside might not have as much impact as one would hope on helping those students match New Harbor scores.

Still, I lean toward agreeing with the argument that more spending per student would help. When schools are in disarray, not only is it distracting for students, its demoralizing. A student who has seen New Harbor schools in comparison with their own is likely to see the community’s acceptance of subpar schools as an issue of pride and faith—if my community believed in me as much as New Harbor believes in their kids, they would invest in me the same way, but they must not, so I must not be worth it.

However, an increase in spending doesn’t automatically equal improved facilities. The editorial would be stronger if it said how taxes would be used. How much would go into facilities and how much would go into things like professional development for teachers, after school programs, tutoring, and so on? And is there evidence that this spending will turn things around for students in Bayside?

In other words, I’m all for spending more on schools. Of all the things my tax dollars could be going towards, schools are actually my favorite. However, the editorial arguing for more school fudning leaves me with questions because it does not say what the money will be spent on. I’m willing to spend the money, but I’d be more convinced by an editorial that laid out more of a plan. The premise—more money will fix it—is probably true, but I want to know how more money will fix it.

ARGUMENT The essay identifies the elements of the argument at issue and evaluates them, but may include less relevant points.

SUPPORT The essay provides sufficient, though possibly uneven, support for its main points.

STRUCTURE The essay expresses ideas reasonably clearly and is organized, but transitions between ideas are inadequate or absent.

FLUENCY The essay expresses ideas effectively, with appropriate word choice.

CONVENTIONS Despite some obvious typographical errors, the essay displays command of the grammar, usage, and mechanics of standard written English.

SCORE 3 ARGUMENT ESSAY

The Bayside Sentinel editorial places the blame for Bayside School District’s low levels of academic achievement squarely on lack of funds. Certainly, there is hardly a public school system in the world that could not use more money—however, the editorial’s proposal of increased local taxation, specifically toward funding infrastructural improvement (e.g., repairing and remodeling old buildings and purchasing new equipment), is wasteful when those funds could be better spent. While I might support increasing taxes to improve education in Bayside, I do not agree that this new revenue should be spent on infrastructure.

The most important factor in student academic success is the relationship between teachers and students, the social environment in which students are learning. If teachers are not well-prepared and well-trained, and not well-attuned to the particular needs of students in that specific cohort, they will not be able to make their students engaged or interested in their schoolwork. Because teachers play such an important role in student academic success, the proposed new tax revenue should be spent on teacher training rather than improved facilities.

Even if Bayside can afford to take on the burden of additional taxation, improved infrastructure is not the best use of those funds. Given the importance of culture and academic climate to student achievement, it might be better to increase funding for programs that more directly influence those factors. For example, an after school program offering one-on-one tutoring is more likely to improve student performance than is a new coat of paint, and an academic activity like a debate or mock trial team is more likely to drive student engagement than is a new globe in the History classroom. Additionally, providing greater opportunity for students to work closely with college counselors is a proven method of increasing student engagement and improving academic outcomes. If Bayside taxes are to be raised, it should be done to support programs like these, rather than for updating infrastructure.

The editorial’s author clearly has good intentions, but their investment proposal leaves much to be desired. If the Bayside community can afford to spend more on its schools, those monies should be utilized in the areas that will have the greatest impacts on student academic performance.

ARGUMENT While the essay presents a clear response to the argument presented in the prompt, it fails to meet the demands of the specific task instructions. The task instructions require the writer to examine the stated and unstated assumptions in the argument. The essay’s focus on its author’s disagreement with the argument, rather than on the assumptions made in the argument, is not relevant to the task instructions. This essay is a classic example of an otherwise satisfactory effort’s being brought down by its failure to meet the requirements stated in the task instructions.

SUPPORT The essay provides sufficient but uneven support for its main argument, sometimes making assertions without evidence. Examples of this tendency are the claims that after school tutoring and increased college counseling are likely to have a greater impact on student performance than are facilities improvements.

STRUCTURE The essay expresses its ideas in a reasonably organized and clear manner, but the transitions between ideas are somewhat jarring.

FLUENCY The essay expresses its ideas clearly and utilizes appropriate vocabulary and varied sentence structure throughout.

CONVENTIONS The essay displays solid command of the grammar, usage, and mechanics of standard written English.

SCORE 2 ARGUMENT ESSAY

First and foremost, in this statement that appeared in the editorial, the writer clearly by mistake believes that external and internal have a direct relationship. This is false. The vast majority of the editorial is the physical appearances and differences between the two schools. There is only one sentence regarding the good of the school—test scores, graduation, and college admissions.

In my opinion, the purpose of school is to prepare someone for life, and this involves learning life skills. These skills can be proper socialization according to society, communication skills, accountability, honesty, and many other positive personality traits can be fostered by mentors like teachers at a young age. The test score does not make the kind of person a child is.

Different socio economic status can have a extremely massive impact on education that is completely separate from schooling but can effect education. For example, a child from a lower socio economic class might have a partime job to add income while those in a more rich neighborhood would be ignorant of struggles like these.

A different solution instead of raising local taxes in which might already be a less affluent area would to look into a different allocation of resources.

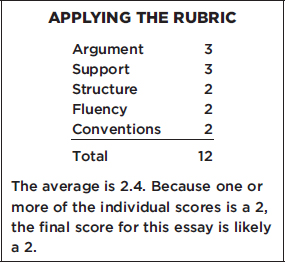
ARGUMENT The essay fails to distinguish or evaluate the most relevant elements of the argument, though it does lightly examine the relationship of money to educational outcomes. It does not, however, explicitly examine the assumptions made in the argument, which was the charge in the specific task instructions.

SUPPORT The essay provides support that is sometimes irrelevant to its point, when that point can be identified. For example, the discussion of students of lower socioeconomic status does not appear to be offered in support of any particular idea.

STRUCTURE The essay’s purpose is unclear because it expresses its ideas inadequately. Additionally, although the author uses language to signal the beginning of the essay, there is no logic to its organization.

FLUENCY The essay’s point is unclear due to its frequent use of faulty sentence structure.

CONVENTIONS The essay includes frequent errors in grammar that render its meaning unclear.

SCORE 1 ARGUMENT ESSAY

Bayside citizens should increase taxes for the education of better test scores and colleges rates. Money is difference of broken windows and out of date bathrooms. Good conditions is the difference for New Harbor. 27% more student gets test scores and indicators stronger in New Harbor. Bayside needs 27% more indicators of student performance to. Bayside increase taxes fixes the hopelessly of the students. Then there indicators of student performance is in good condition.

ARGUMENT The essay fails to evaluate the argument using logic, though it is on topic. Generally, the essay parrots back terms from the essay prompt in a manner that demonstrates some limited grasp of the argument.

SUPPORT The essay provides no support for its main point.

STRUCTURE The essay’s organization is unclear and it is excessively short.

FLUENCY The essay is unclear due to frequent incorrect word choice and poor sentence structure.

CONVENTIONS The essay includes significant errors in grammar, usage, and mechanics that render its meaning unclear.

Section 2—Verbal Reasoning

1. (C, D) Both apt and prone have several meanings. Apt, for example, can mean appropriate, as in an apt remark, or it can mean unusually quick and intelligent, as in an apt pupil. Prone can mean prostrate; it can also mean having a downward slope. Here both apt and prone are used in the sense of inclined or liable.

Note the use of indeed to both confirm and emphasize the preceding statement. Not only do many of us try to rewrite our lives, but we are almost universally inclined to do so.

2. (D, F) Far from is a contrast signal. It indicates that you are looking for an antonym for condemn. The critics do not condemn Warhol for what seems to be superficiality and commercialism. Instead, they extol or hail him for having captured the superficial, commercial nature of American culture during the 1970s.

Note that hail in this context is synonymous with acclaim or approve enthusiastically (secondary meaning).

3. (B, F) By definition, embezzlers are inclined to fraud. By definition, tricksters are inclined to trickery, that is, to chicanery or artifice. Here artifice means subtle but base deception, not skill or ingenuity.

4. (B, E) Paradoxically inherently signals a contrast. It indicates that something unexpected and unwanted has occurred. An admonition or warning intended to reform a spendthrift failed to have the desired result. Instead, it reinforced his profligate behavior, confirming or strengthening him in his wasteful habits.

5. (A, B) You are looking for an antonym for outspoken (frank and unreserved in speech). To be reserved is to be restrained or reticent in manner. To be discreet is to be judicious in conduct or speech.

6. (D, F) The key word here is circuitousness. The writer here is developing an analogy between the way lawyers drive their cars and the way they build or construct their legal arguments. Thus, someone known for choosing circuitous (roundabout; twisty) routes might also be known for coming up with devious (tricky; oblique) or indirect (roundabout; not direct) arguments.

7. (C) The author states that the later novels of James play down prominent action. Thus, they lack overtly dramatic incident. However, the author goes on to state that James’s novels do possess interest; they carry the reader through “a rich analysis of the mental adjustments of the characters to the realities of their personal situations.” It is this implicitly dramatic psychological revelation that sustains the reader’s interest.

Question A is unanswerable on the basis of the passage. It is evident that James wrote psychological novels; it is nowhere stated that he originated the genre.

Question B is unanswerable on the basis of the passage. Although conventional narrative technique relates “events in distinctly phased sequences,” clearly separating them, it does not necessarily recount action in strictly chronological order.

Question D is unanswerable on the basis of the passage. The passage does not deal with the general public’s reaction to James.

Question E is unanswerable on the basis of the passage. The passage talks of qualities in James as a novelist in terms of their being characteristic, not in terms of their making him unique.

8. (C) In the third sentence the author describes James’s later novel as offering “slow piecemeal additions of perception.” To clarify the process, he goes on in sentence four to paint a picture in words, using figurative language. No literal curtain is drawn away here; however, the image of a curtain being slowly drawn away helps the reader develop a feeling for James’s method of psychological revelation.

9. (D) The word “attend” here is used in the sense of “to accompany or go with as a concurrent circumstance or result.” People’s actions inevitably involve moral and psychological realizations and consequences; they go with the territory, so to speak.

10. (C) The subduction zone is the site of the destruction or consumption of existing lithospheric material. In contrast, the mid-ocean ridge is the site of the creation or emergence of new lithospheric material.

Choice A is incorrect. Both mid-ocean ridges and subduction zones are boundaries between plates.

Choice B is incorrect. Both are located on the ocean floor.

Choice D is incorrect. It is unsupported by the passage.

Choice E is incorrect. The reverse is true.

11. (B) Choice B is correct. You are told that the new lithospheric material is injected into a mid-ocean ridge, a suboceanic mountain range. This new material does not disappear; it is added to the material already there. Thus, it is incorporated into the existing mid-ocean ridge.

Choice A is incorrect. “In general the plates are in motion with respect to one another.” Nothing suggests that they become immobilized; indeed, they are said to diverge from the ridge, sliding as they diverge.

Choice C is incorrect. The passage specifically denies it. (“The size of the earth is essentially constant.”)

Choice D is incorrect. It is the earth itself whose magnetic field reverses. Nothing in the passage suggests the new lithospheric material has any such potential.

Choice E is incorrect. At a mid-ocean ridge, the site at which new lithospheric material is injected from below, the plates diverge; they do not sink. (They sink, one plate diving under another, at a subduction zone.)

12. (B) How did Semmelweis save women from dying of childbed fever? He did so by establishing or instituting strict rules of hygiene.

13. (B, F) Given the ubiquity of light, it is unsurprising that creatures have developed the biologically helpful ability to make use of light energy.

Note the use of therefore indicating that the omitted portion of the sentence supports or continues a thought developed elsewhere in the sentence.

14. (A, E) Here the author is contrasting appropriate clerical behavior with inappropriate clerical behavior. The Austen brothers behave appropriately: they are properly deferential to their social superiors, paying them proper respect. The fictional Mr. Collins, however, behaves inappropriately: he is sycophantic (obsequious, fawning) to his social superiors.

15. (B, D) To contest an action is to dispute it or call it in question. The reclassification of Pluto did not go uncontested, for a large number of astronomers asked the International Astronomical Union to reconsider or rethink its decision, calling the union’s action in question.

Note the use of for, indicating a relationship of cause and effect.

16. (A, F) The politicians are unwilling to forsake or abandon center stage. However, if they did leave center stage once in a while, the public might like them better for their self-effacement (withdrawal from attention).

17. (D) The opening sentence describes the shattering of the Iroquois leadership’s pro-British policy. The remainder of the passage describes how Iroquois policy changed to reflect changes in European military goals.

Choice A is incorrect. The passage is expository, not accusatory.

Choice B is incorrect. Nothing in the passage suggests that such charges were made against the Iroquois.

Choice C is incorrect. It is unsupported by the passage.

Choice E is incorrect. The passage demonstrates the Iroquois were able to play European power politics.

Remember, when asked to find the main idea, be sure to check the opening and summary sentences of each paragraph.

18. (E) Lines 22–34 indicate that in the early 1700s and through most of the eighteenth century the Iroquois did receive concessions from the European powers. Therefore, Choice E is the correct answer.

Choice A is incorrect. The raid on Lachine was an effective response to French aggression, as was the Iroquois-enforced policy of aggressive neutrality.

Choice B is incorrect. James II’s overthrow was followed by colonial uprisings.

Choice C is incorrect. In response to the Iroquois leaders’ supposed favoring of the British, the French initiated attacks on the Iroquois (lines 7–13).

Choice D is incorrect. This sums up the policy of aggressive neutrality.

19. (A, C) Choice A is supported by the passage: the opening sentence of the passage discusses a “recent assessment” of the status of global amphibian populations. Likewise, Choice C is supported by the passage: habit degradation, which negatively affects amphibians, can be caused by “the introduction of exotic invasive species,” that is, non-native species. Note that to receive credit for this question you must have chosen both correct answers, not just one.

20. (B) The author never cites or quotes an authority.

Choice A is incorrect. The author defines the term habit fragmentation.

Choice C is incorrect. The author states a probability. He asserts, “Outright habitat loss probably has the greatest effect on amphibians.”

Choice D is incorrect. The author qualifies a statement. He first states, “Outright habitat loss probably has the greatest effect on amphibians.” He then qualifies what he has said by stating that habitat degradation similarly affects amphibians.

Choice E is incorrect. The author makes several assertions.

Section 3—Quantitative Ability

1. (D) Use the laws of exponents. (See KEY FACT A17 on page 337.)

Quantity A is a⁴a⁵ = a⁴⁺⁵ = a⁹.

Quantity B is (a³)² = a^3×2 = a⁶.

If a = 1, the quantities are equal; but if a = 2, Quantity A is much greater. Neither quantity is always greater, and the two quantities are not always equal (D).

2. (C) Since the measure of an exterior angle of a triangle is equal to the sum of the measures of the two opposite interior angles. (See KEY FACT J2 on page 457.)

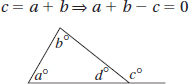
The quantities are equal (C).

Alternative Solution. Plug in easy-to-use numbers. If a = 60 and b = 70, then d = 50 ⇒ c = 130, and 60 + 70 − 130 = 0.

3. (B)

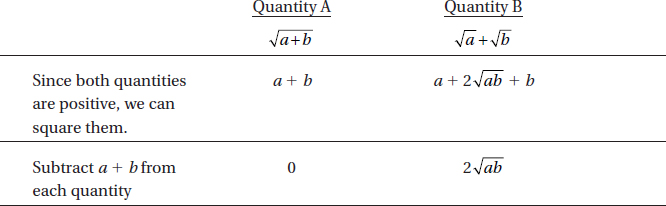
Since a and b are positive, 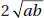is positive. Quantity B is greater.

4. (B) From the 124 people in front of Jill, remove Jack plus the 24 people in front of Jack: 124 − 25 = 99. Quantity B is greater.

5. (A) Since OA and OB are radii, they are each equal to 5. With no restrictions on x, chord AB could be any positive number less than 10 (the length of a diameter). If x were 90, by the Pythagorean theorem (page 459), AB² = 5² + 5² = 50. So, AB would be 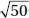; since x > 90, AB > 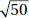> 7. Therefore, the perimeter of AOB is greater than 5 + 5 + 7 = 17. Quantity A is greater.

6. (A) Do not waste time calculating any standard deviations.

• Quantity A: Every number in Set 2 is three times the corresponding number in Set 1, so the standard deviation of the numbers in Set 2 is three times greater than the standard deviation of the numbers in Set 1.

• Quantity B: Every number in Set 3 is 50 more than the corresponding number in Set 1, so the standard deviation of the numbers in Set 3 is equal to the standard deviation of the numbers in Set 1.

• Quantity A is greater.

7. (C) Since the sum of the measures of the three angles of any triangle is 180°, the average of the three measures is 180° ÷ 3 = 60°. The quantities are equal (C).

8. (C) By KEY FACT L8 (page 491), the area of a circle whose radius, r, is πr². The area of the shaded region is the area of the large circle, 25π, minus the area of the middle circle, 16π: 25π – 16π = 9π. The striped region is just a circle of radius 3. Its area is also 9π. The quantities are equal (C).

9. (B) By KEY FACT I4 (page 447), the unmarked angle opposite the 60° angle also measures 60°, and by KEY FACT I3 (page 447), the sum of the measures of all six angles in the diagram is 360°. So,

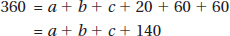
Subtracting 140 from each side, we get that a + b + c = 220.

10. (C) 4¹⁰ × 64² = 4¹⁰ × (4³)² = 4¹⁰ × 4⁶ = 4¹⁶.

Also, 16² × 4ⁿ = (4²)² × 4ⁿ = 4⁴ × 4ⁿ = 4⁴⁺ⁿ.

So, 4¹⁶ = 4⁴⁺ⁿ and 16 = 4 + n. Then n = 12.

11. (D) Let x be the amount in dollars that each of the 20 children were going to contribute; then 20x represents the cost of the present. When 4 children dropped out, the remaining 16 each had to pay (x + 1.50) dollars. So, 16(x + 1.5) = 20x ⇒ 16x + 24 = 20x ⇒ 24 = 4x ⇒ x = 6, and so the cost of the present was 20 × 6 = 120 dollars.

Alternative Solution. Since each of the 16 remaining children had to pay an extra $1.50, the extra payments totaled 16 × $1.50 = $24. This is the amount that would have been paid by the 4 children who dropped out, so each of the 4 would have paid $6. The cost of the gift was 20 × $6 = $120.

12. 110 Draw a Venn diagram (see page 530). Since 10 seniors are in both band and orchestra, 30 are in band only and 50 are in orchestra only.

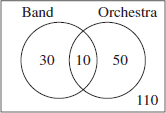
Therefore, 10 + 30 + 50 = 90 seniors are in at least one group, and the remaining 110 are in neither.

13. (C, D, E, F, G) On the six tests, Benjamin earned a total of 6 × 89 = 534 points. On his first five tests, he earned at least 5 × 90 = 450 points, but no more than 5 × 100 = 500 points. So his grade on the sixth test was at least 534 – 500 = 34 and at most 534 – 450 = 84.

Only answer Choices C, D, E, F, and G are between 34 and 84.

14. (E) Exports to Eastern Europe from other Eastern European countries increased from $9.8 billion (10% of $98 billion) to $20.88 billion (12% of $174 billion)—an increase of slightly more than 100%.

15. (C) If France’s exports to Eastern Europe were four times those of the United States, then France accounted for 8% of the total exports. Since 8% is 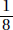of 64%, France accounted for 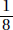or 12.5% of the exports from the European Union.

16. 198 The percent increase in total exports to Eastern Europe from 1993 to 1996 was

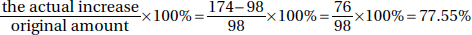
So, in billions of dollars, the increase in total exports to Eastern Europe from 1996 to 2000 was 0.7755 × 174 = 134.94, making total exports 174 + 135 = 309 billion dollars. The value of exports from the European Union was 64% of 309 = 197.76 billion dollars. To the nearest billion, the figure was 198.

17. (C) Set up the equation:

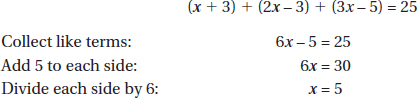
Plugging in 5 for x, we get that the lengths of the sides are 8, 7, and 10.

The length of the shortest side is 7.

18. (D) A nice way to answer this question is to pick easy-to-use numbers. Assume that in 1990 there were 200 boys and 100 girls who earned varsity letters. Then in 2000, there were 150 boys and 125 girls. So, the ratio of girls to boys was 125:150 = 5:6 or .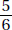

19. (E) The easiest way to solve this is to plug in numbers. Let x = 2 and y = 1. Then xy = 2, a = 4, and b = 0. Now, plug in 4 for a and 0 for b and see which of the five choices is equal to 2. Only Choices C and E work:

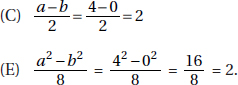
To determine whether Choice C or E is the correct answer, plug in different numbers. If x = 3 and y = 1, then xy = 3, a = 5, and b = 1. Now Choice C doesn’t work:

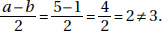
This is the type of algebra you want to avoid.

20. (D) Since you need a ratio, the length of the side is irrelevant. The area of a square whose sides are s is s² (KEY FACT K9, page 479), and the area of an equilateral triangle whose sides are s is 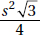(KEY FACT J15, page 466).

Then the ratio is .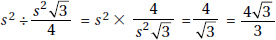

Of course, you could have used 5 (or any number) instead of s, and if you forgot (or didn’t know) the formula for the area of an equilateral triangle, you could have used the formula 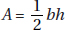(KEY FACT J14, page 465).

Exercise A

1. (C, D) If, rather than ending in 45 minutes, a storm lasts for four hours, then clearly it persists or endures.

2. (A, C) A reader who distrusts fluency (eloquence, articulateness) in authors might well regard the fluent author John Updike with wariness or suspicion.

3. (C, E) What made people lose confidence in this person? He made promises, but failed to carry them out or deliver on them.

4. (A, D) What amazed people? The speaker had made an electrifying, exciting speech. Why were they amazed? They were amazed because he was known to be a prosaic, pedestrian (unimaginative, dull) public speaker.

5. (C, F) The mixture had a tendency to vaporize or evaporate. Therefore, its nature was volatile (easily evaporated) or unstable.

6. (E, F) By definition, biodegradable means capable of being decomposed by bacteria or other living organisms. The plastic trash bags decompose or disintegrate in the sunlight.

7. (D, E) The European nations are attempting to seize territory in the Americas. For this reason, the Americans regard them as rapacious (aggressively greedy) and predatory (seeking to exploit others).

8. (A, D) If few plants can grow under the canopy of the sycamore tree, the sycamore must be doing something to inhibit or suppress the growth of other plants. In fact, sycamore leaves and pods produce a natural herbicide, a substance that is toxic to plants.

9. (D, F) To pout is to push one’s lips forward to express annoyance. The spoiled child is annoyed because she is not getting all her parents’ attention. For this reason, she is sullen (bad-tempered and sulky) and grumpy.

10. (A, F) The speaker is being critical of the reasoning in the editorial, which is flawed: it can’t fool anyone. The missing words must be negative. Check the answer choices for their positive and negative connotations. Only two answers, unsound (not based on reliable reasoning or evidence) and specious (plausible on the surface, but actually wrong), are negative. They are the correct answers.

11. (D, E) Someone who cannot contain his scorn for his boss is likely to make negative comments about his superior. Again, check the answers for their positive and negative connotations. Only two answers, contemptuous (scornful) and scathing (severely critical) are negative. They are the correct answers.

12. (D, F) “Though” signals a contrast, in this case a contrast between the Congressman’s supposed position (a “friend of labor” would in theory have a voting record that was favorable to labor unions) and his actual position (his voting record is anti-labor). His voting record thus belies or contradicts the impression that he is pro-labor.

13. (A, B) The simple lines of modern buildings are neither flamboyant (elaborate) nor ornate (highly decorated).

14. (B, D) Employers would most likely promote someone for his positive qualities, not his negative ones. The missing words must be positive. Check the answer choices for their positive and negative connotations. Only two answers, assiduous (careful and diligent) and industrious (hard-working) are positive. They are the correct answers.

15. (C, D) What is most significant about the career paths chosen by the three young doctors? Although they are all possible careers for graduates of medical schools, they are very different in nature. In other words, these paths are divergent (developing in different directions) or dissimilar. While lucrative (financially rewarding) and traditional may describe a career in medicine, these terms do not emphasize how greatly these three careers vary in nature. Likewise, while unrealistic and quixotic are alike in meaning, they do not work in the context, for all three career paths are quite practical.

Exercise B

1. (C, F) The key word here is truculent, quick to argue or fight. The states are quick to take action to defend their rights from outside interference. Thus, they bicker and squabble (quarrel, often about trivial things).

2. (A, B) Watch out for words that have uncommon secondary meanings. At first glance none of the answer choices appear to be alike in meaning. However, nice, which commonly means enjoyable or good, as in having a nice time, has the secondary meaning of very slight or subtle. In using one script for Latin texts and a different script for Old English texts, the scribes subtly distinguished the texts from one another.

3. (A, C) The book is described in positive terms: it is “(w)ritten in an amiable (agreeable; pleasing) style;” it “provides a comprehensive (broad, wide-ranging) overview.” Therefore, it should be engaging or inviting to anyone with an interest in wine. However, it would not necessarily be inspirational (soul-stirring; emotionally moving) to such a person.

4. (B, E) Would you expect someone shy and uncomfortable at public gatherings to be a natural politician? No, he would be an unlikely, improbable politician.

5. (C, D) As an actor, Guinness is described in highly positive terms: he “has few equals among … actors.” His writing is described in similarly positive terms: it is “uncommonly felicitous (well expressed) or happy (apt, as in “a happy turn of phrase”). Again, check words for possible secondary meanings. Happy, commonly means joyful or merry, as in “Have a happy birthday!,” which has the secondary meaning of fitting or apt.

6. (D, F) An objective, impartial scientist would trust solid evidence, even when that evidence contradicted his cherished beliefs. Pauling stuck to his beliefs despite the evidence. Therefore, his colleagues feared he had lost his scientific objectivity or impartiality.

7. (B, E) The adverb even is used here to emphasize something surprising. Not only didn’t these dumb Westerners fail to appreciate what made African music distinctive (special and noteworthy), they didn’t even discern (recognize, spot) it or remark (show they noticed by commenting) on it. While ignored and neglected are alike in meaning, they do not work in the context.

8. (B, E) The student welcomes a change from a verbose (wordy) and rambling (aimlessly wandering) prose style. This suggests that the student wants prose that is the opposite of wordy. In other words, she would like prose that is terse (effectively concise) and pithy (brief).

9. (B, C) A pragmatist is a practical person, one who is concerned whether a particular course of action will work. Such a person would be unwilling to try to build a castle (which needs a solid foundation) on sands that moved or shifted. Likewise, the woman described here is disinclined or loath (reluctant, averse) to base her future on impractical dreams. Watch out for words that look alike. The verb loathe means hate. Sue loathes beets. The adjective loath means unwilling. Because her boyfriend loved beets, Sue was loath to tell him that she loathed his favorite vegetable.

10. (A, C) The key word here is illogically. If eighteenth-century English society did not encourage women to get an education, then it was clearly illogical for society to decry (denounce, condemn) or criticize women’s lack of education.

11. (C, E) Someone who shuns or avoids society may well be described as reclusive (avoiding other people’s company) and withdrawn (unsociable; remote). While infamous and notorious are alike in meaning, they do not work in the context.

12. (B, F) If the studded surface is able to protect the starfish from external threats, then it is unlikely to be brittle (easily broken) or vulnerable (an easy target for attack). The surface is far more likely to be described as armored (protected by armor) or rugged (tough).

13. (A, F) What sort of speed is dangerous? Inordinate (extreme, unreasonable), excessive speed.

14. (C, D) What sort of response would a brilliant, passionate, eloquent book most likely inspire? Probably some sort of positive response. However, Baldwin’s book is described as “penetrating (piercing or sharp) in its candor (directness, outspokenness).” It is also likely that the book’s frankness may be more than its readers can comfortably handle. Thus, the conclusion that the book is bound to disquiet (agitate, alarm) or unsettle (disturb) any reader. None of the other choices are likely responses to a brilliant, eloquent book.

15. (C, E) The key phrase here is “a dark underside.” According to Glendon, there is something fundamentally wrong with the American adherence to rugged individualism (the belief that individuals should be independent and self-reliant). If you take this adherence too far, it can degenerate (go bad and fall) into or regress (deteriorate) to atomism. (Social atomism looks on all individuals as interchangeable units; it ignores the idea that each individual is unique, formed by individual circumstances and having individual needs.)

Exercise C

1. (B) The key word here is “mourn.” By definition, examples of elegiac verse (verse expressing grief or lamentation) mourn. Milton’s Lycidas differs from other examples of elegiac verse because in addition to mourning King’s death, the poem condemns wickedness and depravity in the church.

2. (B, D) By definition, cowardice is the mark of the craven (person lacking in courage).

3. (C, D) The key word here is “surprised.” We would expect someone with a reputation for petulance (sulkiness, bad temper) to greet people in an irritable, grumpy way. It would be surprising for someone petulant to greet people affably (in a good-natured, friendly way).

4. (C, D, H) The key phrase here is “cared deeply.” Someone who cared deeply about his art would be unlikely to work at it ambivalently (with mixed feelings about what he was doing). Likewise, someone who cared deeply about his art would be unlikely to work at it only intermittently (sporadically; at odd moments). No. We would expect someone with such deep feelings to work at his art diligently (carefully, conscientiously). “Despite” signals a contrast. The contrast is between Warhol’s deep feelings for his art and the appearance he affected or shammed. He tries to appear nonchalant (unconcerned), and his affected nonchalance makes people who don’t look closely think he is indifferent (uncaring) about his paintings.

5. (B, F) “Although” signals a contrast. The contrast here is between how the basic facts about the Milky Way were regarded a few years ago and how they are regarded now. Back then, folks thought they understood the Milky Way; they regarded the basic facts about it as established (generally accepted). Now, even its dimensions and mass are no longer generally accepted; they have come into question.

6. (B, E, I) What sort of educator would call the New York City’s public school system a “rotten barrel”? Dr. Shalala was clearly an outspoken educator, one who frankly stated her opinions, especially if they were shocking or controversial, and the opinion she stated was shocking enough to ignite (trigger, spark) controversy. Finally, if the school system was rotten through and through, what kind of reform was needed to mend it? The answer is systemic reform, reform that would affect the entire organization, not just one particular classroom or school.

7. (E) If a piece of glass cable 100 miles thick is clearer than an ordinary windowpane, then the glass that makes up the cable must be extraordinarily transparent.

8. (C, F) The Christians considered the ancient religion of the Celts to be heathen (pagan; non-Christian, and therefore heretical). They were proud of their Celtic ancestors, but had a hard time thinking of these ancestors as wicked pagans. So Christian texts either muddied (obscured or made unclear) any references to the Celts’ ancient religion or completely suppressed (concealed; hid) such references.

9. (C) The key words here are “alleviate” and “cursory.” A problem exists: “contaminated chicken” is making people sick. A study panel hopes to alleviate this problem, making it less severe. They recommend changing inspections from cursory (hasty, and therefore not thorough) checks to rigorous (extremely thorough and careful) random sampling.

10. (C, D) The structure “so . . . that” signals cause and effect. The orator’s voice was soporific (sleep-inducing). By definition, it caused people to become drowsy (sleepy). That was its effect.

11. (C, E) The key words here are “sarcastic” and “revealed.” What trait would be revealed in sarcastic (scornful, contemptuous) asides (sidecomments; remarks not meant to be heard by everyone)? Certainly not charm or anxiety (unease, worry). Clearly, the sarcastic asides reveal the woman’s bitterness. Because she is bitter and resentful, her true feelings manifest (show) themselves in her snarky comments.

12. (A, E) By definition, “finally” means after a long time, typically when there has been some delay. In this case, it has taken a long time for the sugar to dissolve; it dissolved only gradually (slowly, by degrees). What was left? An almost imperceptible (unnoticeable, impossible to detect) leftover small amount on the bottom of the glass.

13. (C, D) The Japanese-Americans were neither acquitted (found innocent) of spying nor reminded of (caused to remember) spying for Japan. Instead they were suspected (believed guilty) of spying even though no proof existed to back up (support) that belief.

14. (A, F) How would victims of pointed (unambiguously critical; biting) satire most likely react to being the targets of such sharp criticism? Most likely they would wince (flinch or make a face indicating their distress). However, Mencken’s readers who were not the targets of his satire might well have enjoyed his cutting wit.

15. (B, D) “Given” here means considering something or taking it into account. If you take into account that the current mood in government circles is anti-regulatory (against controlling something, especially a business activity, by means of rules and regulations), what would you expect regulators and law enforcement agencies to do about the activities of predatory (greedy, exploitative) for-profit schools? Sadly, not much. That’s what critics of for-profit colleges think: they question whether the regulators and law enforcement agencies would ever rein in (check, control) the greedy schools that fool underqualified students into wasting their money signing up for worthless or inappropriate classes. How do the colleges fool these students into signing up? The for-profit colleges misrepresent their programs, giving a false impression of their nature.

Exercise D

1. (B) The key word here is “conception,” which here means the forming or devising of an idea. Kelly is a painter. The ideas behind his paintings may be chaotic (messy, disorganized), but the paintings themselves are neat as a pin. So, the paintings are messy in conception, but neat in execution (the way a plan or course of action is carried out). Note that the writer is using a secondary meaning of the noun execution here.

2. (C, E) By definition, the rococo style in furniture was characterized by elaborate scrollwork and excessive ornamentation. It was over the top.

3. (A, F) The missing words are explained by the parentheses following each blank.

Go through the answer choices, testing each one to see whether it makes sense. Eliminate any choices that you can. If you don’t know the meaning of an answer choice, go on to the next one to see whether you can eliminate that. If you can eliminate two answer choices, the third choice must be the correct answer. If you swear an oath of loyalty in order to keep your job, are you being opportunistic? The word is unfamiliar; go on to the next answer choice.

If you swear an oath of loyalty in order to keep your job, are you being selfless (unselfish, altruistic)? No, you are thinking of yourself. You can eliminate choice B. If you swear an oath of loyalty in order to keep your job, are you being theoretical (conceptual, not practical)? No, you are being practical. You can eliminate Choice C. The correct answer must be Choice A, opportunistically. To be opportunistic is to be ready to exploit immediate opportunities, regardless of principle. Toqueville decided to swear an oath that he was loyal because that was his chance to keep his job.

Now, go through the answer choices for the second blank. If you swear an oath of loyalty because you believe that the new government’s policies inevitably will win, are you being altruistic (unselfish)? No, you are simply accepting the inevitable. You can eliminate Choice D. Are you being irresolute (indecisive or uncertain)? No, you are certain that the democratization of politics will inevitably occur. You can eliminate Choice E. Are you being pragmatic (practical)? Yes, it was practical for Toqueville to go along with the regime whose success he believed was inevitable. Choice F is correct.

4. (B, E) The key words here are “rediscover” and “curio status.” Someone who needs to be rediscovered is someone who has been forgotten. Once, Hurston was respected as a writer: she enjoyed or possessed the “high regard” of literary society. Then, aesthetic values shifted. Her writing was no longer valued. The change in aesthetic values relegated (downgraded or consigned) her to curio status, the status of a no longer fashionable literary curiosity.

5. (C, E) Use the process of elimination to fill in the first blank. A tapeworm is an organism that lives within or on another creature. By definition it is not autonomous (independent, self-sufficient). You can eliminate Choice A. A tapeworm is an organism that depends on a host (an animal or plant that provides nutrition for an organism living within or on it). It is not hospitable in any sense of the word. You can eliminate Choice B. A tapeworm, however, by definition is parasitic, deriving (obtaining) some or all of its nutrients from its host.

6. (A, F) The key words here are “helpful” and “warnings.” “Warnings” is your clue to the correct answer choice for the first blank. Why would consumers need to be warned about certain wines? Not because those wines were superior (higher in quality) or vintage (of high quality), but because they were overpriced (too highly priced). Likewise, the fact that her wine notes are helpful is your clue that these notes provide a trusty (reliable) guide to the wines of Burgundy.

7. (B, F) To be subject to something is to be likely to be affected by it, especially if it is unwelcome or unpleasant. In this case, measurement is a complex activity that is subject to error. What is more, even when no actual errors of measurement occur, measurement can be misinterpreted and misunderstood.

8. (C, F) Use the process of elimination to fill in the first blank. A zealot is a fanatic who refuses to make any compromises about his or her religious, political, or other ideals. Zealots are marked by fanaticism, not by insincerity. You can eliminate Choice A. A skeptic is a person inclined to question or doubt that something is true. Skeptics are marked by a lack of belief, not by a lack of sincerity. You can eliminate Choice B. Insincerity, however, is the mark of a hypocrite: “a person who feigns some desirable or publicly approved attitude, especially one whose private life, opinions, or statements belie his or her public statements.” Such a person by definition is insincere. Tackle the second blank the same way. Is boastfulness the mark of the glutton (overly greedy eater)? No, greed marks the glutton. You can eliminate Choice D. Is boastfulness the mark of the autocrat (person who insists on absolute obedience from others)? No, domineering arrogance marks the autocrat. You can eliminate Choice E. Only Choice F is left. Boastfulness is the mark of the braggart.

9. (C, E) The key words here are “ritual,” “holy,” and “rite .” They reinforce the idea that, in Miro’s view, to create art is to perform a sacred (holy) ritual or religious ceremony.

10. (C, D, H) More than a century after the supposedly “unsinkable” R.M.S. Titanic went down in the North Atlantic, the sinking of the Titanic still fascinates people. Look at the “If . . . then” structure of the opening portion of the sentence. If the ship had hit the iceberg head on, then the ship might have been saved from ________. What words come to mind? Sinking, disaster, destruction. Clearly, the first missing word must be negative. Adversity (misfortune, ill luck, hardship) is a negative term; however, it may not be a negative enough term to describe the Titanic’s fate. Check the other answer choices before settling on Choice A. A denouement is the outcome of a situation, the time when things are made clear. The word makes no sense in this context; you can eliminate Choice B. To founder is to fill with water and sink. Clearly, Choice C, foundering, is the best choice for the first missing word.

Now, examine the context for the second missing word. The key word here is “swerved” (changed direction abruptly). Why would the Titanic swerve? To avoid the iceberg. Neither contract (decrease in size) nor mollify (pacify, soften) makes sense in the context. Finally, what effect would opening the watertight compartments to the sea have on the vessel’s fate? It would neither avert (prevent) nor limit the disaster. Instead, it would make the disaster inevitable (unavoidable).

11. (B, E) The key word here is “democratic.” To be democratic in one’s habits of thought is to believe that whether something is true or not can be settled by voting. In other words, that truth can be determined (established) by a plebiscite (the direct vote of all the members of an electorate on an important public question) of facts.

12. (B, D) The phrase “usually uninspiring” signals a contrast between the way economics is usually presented and the way the so-called dismal science is presented by this writer. “Uninspiring” and “dismal” are negative terms. The missing words must be positive. Neither choice A, pedestrian (dull; unexciting), nor Choice C, grandiloquent (pompous, overdone), is positive. Choice B, felicitous (apt, well-chosen), however, is decidedly positive. Similarly, Choice D, engaging (appealing) is positive as well.

13. (A, E) What do we know about Crimond and his group? Crimond is the leader; he is passionately committed to a political cause. He is neither indifferent to (uninterested in) politics nor in retreat from politics. Instead, he is deeply engaged (involved) in politics.

Crimond’s disciples or followers, however, are far less committed than their leader; their political faith has lapsed. Thus, it is fair to say that Crimond’s passionate engagement in politics is inversely proportional to his followers’ lack of engagement. Their reactions are opposite.

14. (C, E) To suffer something is to experience or be subjected to (something bad or unpleasant). Therefore, the first missing word must be negative. Also, it must be something negative that can happen to the economy. Contradictions (refutations, denials) may be bad or unpleasant. However, “contradictions” is not a term used in economic circles: it has no specific application to economics. You can eliminate choice A. Digressions (departures from the topic, ramblings) may be positive or negative; in addition, the term has no specific economic definition. You can eliminate Choice B. A downturn, however, by definition, is a decline in economic, business, or other activity. The economy frequently suffers downturns.

Although signals a contrast. Despite the downturns, the economy can recover: it has strong recuperative and self-correcting tendencies.

15. (C) To keep one’s own counsel is to say nothing about what one thinks or plans. Thus, a government that keeps its own counsel can be described figuratively as a reticent (tight-lipped, uncommunicative) regime.

1. (B) Take a close look at the sentences that immediately precede and follow the boldfaced sentence. What do they discuss? They talk about changes in business, in the facilities for production, in investments in “machinery or ‘heavy’ industry.” These changes reflect business owners’ optimism about the future of economic growth. If the owners of industrial firms were not optimistic that their businesses were going to grow, they would be unwilling to invest money in purchasing new equipment. The correct answer is Choice B.

2. (B) To the author, it is no big deal that an end comes to the business cycle’s expansion phase. He describes the end of the prosperity cycle in a matter-of-fact manner: “a time comes when this phase reaches a peak and stops spiraling upwards.” To him, cyclical ends to business expansion are normal.

Use the process of elimination to make sure you have come up with the correct answer. Does the author believe that when consumers lose their confidence in the market, a recession follows? There is no evidence to support this statement: the passage never even mentions recessions or consumer loss of confidence. You can eliminate Choice A. Does the author believe that luxury goods such as jewelry are unaffected by industrial expansion? While the author discusses industrial expansion, he never mentions luxury goods. You can eliminate Choice C. Does the author believe that with sound economic policies, prosperity can become a fixed pattern? Definitely not. He states that a time comes when the prosperity period stops spiraling upwards; rather than becoming a fixed pattern, prosperity comes to an end. You can eliminate Choice D. Does the author believe that the creation of new products is essential for prosperity? Most likely not. He doesn’t talk about new products; he certainly never asserts that their creation is essential for prosperity. You can eliminate Choice E. Only Choice B is left. It is the correct answer.

3. (E) What is the topic of this passage? It is the business cycle’s expansion phase. From the passage’s opening sentence (“One phase of the business cycle is the expansion phase.”) to its concluding sentence (“This is the end of the expansion phase.”), the author has been describing this one phase. By definition, a phase is one stage in a process of change or development. The business cycle therefore must consist of more than one phase. Thus, it is likely that the paragraph immediately following a description of the business cycle’s expansion phase would describe a different phase of the business cycle. Choice E, The other phase of the business cycle is called the recession phase, is a likely introductory sentence for such a paragraph.

4. (A, C) The passage’s opening sentence lists factors that may cause plants and animals to change or adapt. These factors include changes in the climate or in the sort of food supply available. Thus, the author provides information to answer the question “What factors can cause change in organisms?” Choice A is correct.

Although the passage mentions the word evolution, it fails to provide information that would serve to answer the question “What is the theory of evolution?” Choice B is incorrect.

The passage also answers the question of how horses’ legs are related to seals’ flippers. Although adaptive divergence has caused them to look very different and to serve very different functions, they are definitely related as “equivalent elements of the mammalian limb.” Choice C also is correct.

Pay particular attention to the instruction “Select all that apply.” One, two, or three answers may be correct.

5. (C) The term homologous, as used in biology, means similar in position, structure, and evolutionary origin but not necessarily in function. In spite of great alterations, the structures or organs are equivalent elements; they correspond to one another.

6. (A) We are not told why the Bilge Islanders perceive fewer colors than most persons in the United States do. We are told only that the Bilge Islanders do perceive fewer colors than most Americans do, and that there are no physical differences between the islanders’ visual organs and the visual organs of most Americans. From this information we can conclude only that (h)uman color perception is at least partly determined by factors other than the physical structure of the visual organs.

7. (B) If the jet streams move from west to east at high velocities, then this suggests that jet planes flying from the west (Los Angeles) to the east (New York) will enjoy a better rate of speed than jet planes flying from the east to the west.

8. (B) Lines 14–16 state that “[t]emperatures within the troposphere decrease about 3.5° per 1,000-foot increase in altitude.” The question specifies that the top of Jungfrau is 12,000 feet above the town of Interlaken. If you multiply 3.5° by 12, your answer is 42°. This suggests that the temperature on the mountaintop should be about 42° colder than on the ground.

9. (E) Scan the passage looking for the key phrase “warmest part.” You will find the phrase, and the answer to this question, in lines 5–9: “It is the warmest part of the atmosphere because most of the solar radiation is absorbed by the earth’s surface, which warms the air immediately surrounding it.” The warmth or heat of the earth’s surface makes the troposphere the warmest part of the atmosphere.

10. (B) Scan the passage looking for the key phrase “literary criticism.” You will find the phrase, and the answer to this question in lines 18–20, and the sentences immediately following. Women are interpreting literature from their own perspective; thus, they are changing literary criticism by seeing literature from their own fresh points of view.

11. (E) The passage’s opening paragraph uses quotes from Joyce, Woolf, and Lawrence to establish the point that the interest in feminist issues is not new. Indeed, the passage states that Woolf claimed the shift took place early in the 20th century.

12. (D) We are told that the African sculptor was highly trained and followed the rules without thinking about them. Analogously, a veteran fiddler can expertly improvise variations on a traditional tune without giving the process much thought. Both creative artists have over the course of time developed a mastery of their chosen medium. They need neither to follow recipes nor to impose rules on others.

13. (A) The passage argues that, because America’s recycling efforts are so successful, we no longer need “to ban logging in national parks” and other environmentally sensitive areas. Choice A, however, points out that our recycling efforts have been far less successful than the passage attempts to show. Thus, Choice A seriously undermines the argument’s conclusion.

 

Two asterisks (**) indicate an alternative method of solving.

1.(C) This is a relatively simple ratio problem, but use TACTIC 7 and make sure you get the units right. To do this you need to know that there are 100 cents in a dollar and 12 inches in a foot.

Now cross-multiply and solve:

96x = 4,800 ⇒ x = 50

2.(C) Use TACTICS 2 and 4. On your scrap paper, extend line segments OP and OR.

Square OPQR, whose area is 8, takes up most of quarter-circle OXY. So the area of the quarter-circle is certainly between 11 and 13. The area of the whole circle is 4 times as great: between 44 and 52. Check the five choices: they are approximately 25, 36, 50, 100, 200. The answer is clearly C.

**Another way to use TACTIC 4 is to draw in line segment OQ.

Since the area of the square is 8, each side is , and diagonal OQ is × = = 4.

But OQ is also a radius, so the area of the circle is π(4)² =16π.

3.(E) Use TACTIC 1: draw a picture representing a pile of books or a bookshelf.

In the two years the number of French books Diana read was 7 + 2x and the total number of books was 17 + 3x. Then 60% or 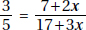. To solve, cross-multiply:

5(7 + 2x) = 3(17 + 3x) ⇒ 35 + 10x = 51 + 9x ⇒ x = 16

In 2000, Diana read 16 English books and 32 French books, a total of 48 books.

4.160 Use TACTIC 8. Systematically list the numbers that contain the digit 1, writing as many as you need to see the pattern. Between 1 and 99 the digit 1 is used 10 times as the units digit (1, 11, 21, . . ., 91) and 10 times as the tens digit (10, 11, 12, . . ., 19) for a total of 20 times. From 200 to 299, there are 20 more (the same 20 preceded by a 2). From 100 to 199 there are 20 more plus 100 numbers where the digit 1 is used in the hundreds place. So the total is 20 + 20 + 20 + 100 = 160.

5.(D) Use TACTIC 2. Trust the diagram: AC, which is clearly longer than OC, is approximately as long as radius OE.

Therefore, AC must be about 10. Check the choices. They are approximately 1.4, 3.1, 7, 10, and 14. The answer must be 10.

**The answer is 10. Use TACTIC 4: copy the diagram on your scrap paper and draw in diagonal OB.

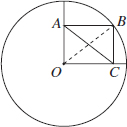
Since the two diagonals of a rectangle are equal, and diagonal OB is a radius, AC = OB = 10.

6.(E) Use TACTIC 5: subtract to find the shaded area. The area of the square is 4. The area of the equilateral triangle (see Section 12-J) is 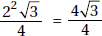= . So the area of the shaded region is 4 – .

7.(C) Use TACTIC 6: don’t do more than you have to. In particular, don’t solve for x.

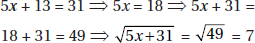
8.2.5 Use TACTIC 6: don’t do more than is necessary. We don’t need to know the values of a and b, only their average. Adding the two equations, we get

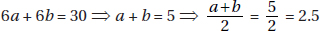
9.(C) Use TACTIC 5: to get DE, subtract OD from radius OE, which is 4. Draw AO (TACTIC 4).

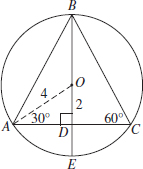
Since AOD is a 30-60-90 right triangle, OD is 2 (one half of OA). So, DE = 4 – 2 = 2.

10.(D) Use TACTIC 4 and add some lines: connect the centers of the three circles to form an equilateral triangle whose sides are 2.

Now use TACTIC 5 and find the shaded area by subtracting the area of the three sectors from the area of the triangle. The area of the triangle is 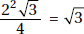(see Section 12-J).

Each sector is one sixth of a circle of radius 1. Together they form one half of such a circle, so their total area is 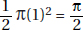. Finally, subtract: the shaded area is .

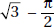11.(B) If you don’t see how to answer this, use TACTIC 2: trust the diagram. Estimate the measure of each angle: for example, a = 45, b = 70, c = 30, and d = 120. So c + d (150) is considerably greater than a + b (115). Choose B.

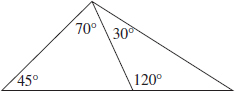
**In fact, d by itself is equal to a + b (an exterior angle of a triangle is equal to the sum of the opposite two interior angles). So c + d > a + b.

12.(B) From the figure, it appears that x and y are equal, or nearly so. However, the given information states that BC > CD, but this is not clear from the diagram. Use TACTIC 3: when you draw the figure on your scrap paper, exaggerate it. Draw it with BC much greater than CD. Now it is clear that y is greater.

13.(C) Use TACTIC 8 (page 259). Systematically list all the factors of 30, either individually or in pairs: 1, 30; 2, 15; 3, 10; 5, 6. Of the 8 factors, 4 are even and 4 are odd.

14.(A) Quantity A: When 10³ (1,000) is divided by 3, the quotient is 333 and the remainder is 1. Quantity B: 10⁵ is divisible by 5, so the remainder is 0.

   Quantity A is greater.

15.(A) Quantity A: since c < d, the quotient when c is divided by d is 0, and the remainder is c. Quantity B: when d is divided by c the remainder must be less than c.

   So Quantity A is greater.

 

Two asterisks (**) indicate an alternative method of solving.

1.(D) Test the answer choices starting with the smallest value. If Evan had 200 books, Jason would have 40. But Jason has more than 40, so 200 is too small. Trying 205 and 210, we see that neither is a multiple of 4, so David wouldn’t have a whole number of books. Finally, 220 works. (So does 240, but we shouldn’t even test it since we want the least value.)

**Since Jason has at least 41 books, Evan has at least 41 × 5 = 205. But Evan’s total must be a multiple of 4 and 5, hence of 20. The smallest multiple of 20 greater than 205 is 220.

2.49.50 Judy intends to go to the Gallery 16 times during the year. Buying a single admission each time would cost 16 × $3.50 = $56, which is less than the annual pass. If she bought a 3-month pass for June, July, and August, she would pay $18 plus $31.50 for 9 single admissions (9 × $3.50), for a total expense of $49.50, which is the least expensive option.

3.(D) Use TACTIC 1: backsolve starting with C. If Alison is now 24, Jeremy is 8, and 5 years ago, they would have been 19 and 3, which is more than 5 times as much. Eliminate A, B, and C, and try a bigger value. If Alison is now 30, Jeremy is 10, and 5 years ago, they would have been 25 and 5. That’s it; 25 is 5 times 5.

**If Jeremy is now x, Alison is 3x, and 5 years ago they were x – 5 and 3x – 5, respectively. Now, solve:

3x – 5 = 5(x – 5) ⇒ 3x – 5 = 5x – 25 ⇒ 2x = 20 ⇒ x = 10 ⇒ 3x = 30

4.(C) Test the choices starting with C: 255 is divisible by 17 (255 = 17 × 15), so this is a possible answer. Does 255 have a larger prime factor? Neither Choice D nor E is prime, so the answer must be Choice C.

5.(B) Use TACTIC 2. Pick simple values for a, b, and c. Let a = 3, b = 2, and c = 6. Then a ÷ b = 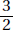. Without these values of a, b, and c, only B is equal to .

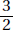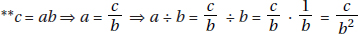
6.(A) Use TACTIC 2. If 2 widgets cost 10 cents, then widgets cost 5 cents each, and for 3 dollars, you can get 60. Which of the choices equals 60 when w = 2, c = 10, and d = 3? Only A.

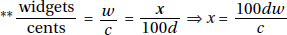
7.(C) Since 120% of 80 = 80% of 120, let a = 80 and b = 120. Then a + b = 200, and 200 ÷ 80 = 2.5.

8.(C) If you don’t know how to solve this, you must use TACTIC 4 and guess after eliminating the absurd choices. Which choices are absurd? Certainly, A and B, both of which are negative. Also, since Choice D is about 94, which is much more than half the area of the square, it is much too big. Guess between Choice C (about 43) and Choice E (about 50). If you remember that the way to find shaded areas is to subtract, guess C.

**The area of the square is 12² = 144. The area of each semicircle is 8π, one-half the area of a circle of radius 4. So together the areas of the semicircles is 32π.

9.(D, E) Test each choice until you find all the correct answers.

(A)Could y = –1? Is there an integer x such that x³ = (–1)² = 1? Yes, x = 1.

(B)Similarly, if y = 1, x = 1.

(C)Could y = 8? Is there an integer x such that x³ = (8)² = 64? Yes, x = 4.

(D)Could y = 12? Is there an integer such that x³ = 12² = 144? No, 5³ = 125, which is too small; and 6³ = 216, which is too big.

(E)Could y = 16? Is there an integer x such that x³ = 16² = 256? No, 6³ = 216, which is too small, and 7³ = 343, which is too big.

(F)Could y = 27? Is there an integer x such that x³ = 27² = 729? Yes, 9³ = 729.

The answer is D and E.

10.(B)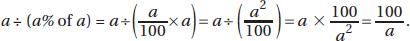

**Use TACTICS 2 and 3: replace a by a number, and use 100 since the problem involves percents. 100 ÷ (100% of 100) = 100 ÷ 100 = 1.

Test each choice; which ones equal 1 when a = 100. Both A and B: 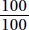= 1.

Eliminate Choices C, D, and E, and test A and B with another value for a.

50 ÷ (50% of 50) = 50 ÷ (25) = 2

Now, only B works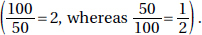

11.10 Set up a ratio:

    **Use TACTIC 1 (page 268): Test choices starting with C:

100 meters/second = 6,000 meters/minute = 360,000 meters/hour = 360 kilometers/hour

    Not only is that too big, it is too big by a factor of 10. The answer is 10.

12.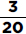 Use TACTIC 3. The LCM of all the denominators is 120, so assume that the committee has 120 members. Then there are 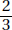× 120 = 80 men and 40 women. Of the 80 men 30 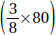are American. Since there are 72 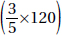French members, there are 120 – 72 = 48 Americans, of whom 30 are men, so the other 18 are women. Finally, the fraction of American women is .

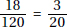This is illustrated in the Venn diagram below.

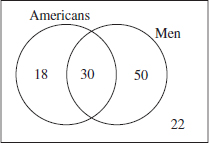
13.(D) Use the laws of exponents to simplify the equation, and then solve it:

8^2x–4 = 16^x ⇒ (2³)^2x–4 = (2⁴)^x ⇒ 3(2x – 4) = 4x ⇒ 6x – 12 = 4x ⇒ 2x = 12 ⇒ x = 6

14.(B) Add the two equations:

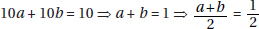
Do not waste time solving for a and b.

15.(C) Pick easy-to-use numbers. Since 100% of 10 is 10, let x = 100 and y = 10. When x = 100, Choices C and E are each 10. Eliminate Choices A, B, and D, and try some other numbers: 50% of 20 is 10. Of Choices C and E, only C = 20 when x = 50.

 

The direct mathematical solution to a problem is almost always the preferable one, so it is given first. It is often followed by one or more alternative solutions, indicated by a double asterisk (**), based on the various tactics discussed in this chapter. Occasionally, a solution based on one of the tactics is much easier than the straightforward one. In that case, it is given first.

1.(B) Using the onscreen calculator, this can easily be solved in 20 or 30 seconds by adding, but in only 5 seconds by thinking! Use TACTIC 5: don’t calculate; compare. Each of the three numbers in Quantity B is greater than the corresponding numbers in Quantity A.

2.(D) Use TACTIC 1. When x = 1, the quantities are equal; when x = 2, they aren’t.
**Use TACTIC 3

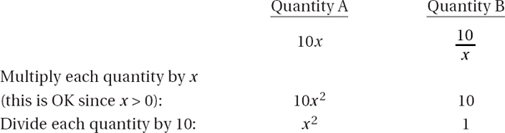
This is a much easier comparison. x² could equal 1, but doesn’t have to. The answer is Choice D.

3.(A) You can easily calculate each of the times—divide 7 by 6 to evaluate Quantity A, and 6 by 7 in Quantity B. However, it is easier to just observe that Quantity A is more than one hour, whereas Quantity B is less than one hour.

4.(B) Use TACTIC 3

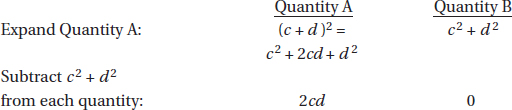
Since it is given that cd < 0, so is 2cd.

**If you can’t expand (c + d)², then use TACTIC 1. Replace c and d with numbers satisfying cd < 0.

Both times Quantity B was greater: choose B.

5.(C) The average of 3 numbers is their sum divided by 3. Since in any triangle the sum of the measures of the 3 angles is 180°, the average in each quantity is equal to 180 ÷ 3 = 60.

**Use TACTIC 1. Pick values for the measures of the angles. For example, in isosceles ABC choose 70, 70, 40; in right XYZ, choose 30, 60, 90. Each average is 60. Choose C.

6.(B) Since b < 0, 6b is negative, whereas b⁶ is positive.

**Use TACTIC 1 (page 285). Replace b with numbers satisfying b < 0.

Both times Quantity B was greater: choose B.

7.(B) Use TACTIC 5: don’t calculate the two areas; compare them. The circle in Quantity A is the area of a circle whose radius is 17 and whose diameter is 34. Quantity B is the area of a circle whose diameter is 35, and so is clearly greater.

8.(A) Use TACTIC 5: don’t calculate either slope. Quickly, make a rough sketch of line k, going through (1,1) and (5,2), and draw line m perpendicular to it.

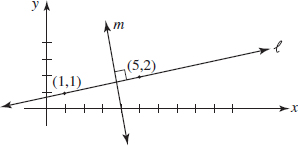
Line k has a positive slope (it slopes upward), whereas line m has a negative slope (it slopes downward). Quantity A is greater.

[Note: The slope of k is and the slope of m is –4, but you don’t need to calculate either one. See Section 12-N for all the facts you need to know about slopes.]

**If you don’t know this fact about slopes, use TACTIC 6. The answer cannot be Choice D, and if two lines intersect, their slopes cannot be equal, so eliminate Choice C. Guess Choice A or B.

9.(D) Every sixth integer is a multiple of 6 and every ninth integer is a multiple of 9, so in a large interval there will be many more multiples of 6. But in a very small interval, there might be none or possibly just one of each.

**Use TACTIC 1. Let x = 1. Between 100 and 101 there are no multiples of 6 and no multiples of 9. Eliminate Choices A and B. Choose a large number for x: 100, for example. Between 100 and 200 there are many more multiples of 6 than there are multiples of 9. Eliminate Choice C.

10.(C) Add the equations.

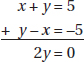
Since 2y = 0, y = 0.

**Use TACTIC 4. Could y = 0? In each equation, if y = 0, then x = –5. So, y can equal 0. Eliminate Choices A and B, and either guess between Choices C and D or continue. Must y = 0? Yes, when you have two linear equations in two variables, there is only one solution, so nothing else is possible.

11.(A) With a calculator, you can multiply 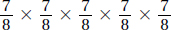, but it is annoying and time-consuming. However, you can avoid the arithmetic, if you know KEY FACT A24:

If 0 < x < 1 and n > 1, then xⁿ < x.

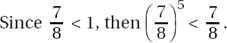
12.(B) The area of the shaded region is the area of quarter-circle AOB minus the area of the square. Since r = OA = 6, the area of the quarter-circle is 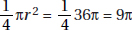. OY, the diagonal of the square, is 6 (since it is a radius of the circle), so OZ, the side of the square, is 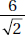(see KEY FACT J8, page 461). So the area of the square is Finally, the area of the shaded region is 9π – 18, which is approximately 10.

**The solution above requires several steps. (See Sections 12-J, K, L, to review any of the facts used.) If you can’t reason through this, you still should be able to answer this question correctly. Use TACTIC 6. The shaded region has a definite area, which is either 12, more than 12, or less than 12. Eliminate D. Also, the area of a curved region almost always involves π, so assume the area isn’t exactly 12. Eliminate Choice C. You can now guess between Choices A and B, but if you trust the diagram and know a little bit you can improve your guess. If you know that the area of the circle is 36π, so that the area of the quarter-circle is 9π or about 28, you can estimate the shaded region. It’s well less than half of the quarter-circle, so less than 14 and probably less than 12. Guess Choice B.

13.(C) Use TACTIC 4. Could the edge be 6? Test it. If each edge is 6, the area of each face is 6 × 6 = 36, and since a cube has 6 faces, the total surface area is 6 × 36 = 216. The volume is 6³ = 216. So the quantities could be equal. Eliminate Choices A and B. If you have a sense that this is the only cube with this property, choose C. In fact, if you had no idea how to do this, you might use TACTIC 6, assume that there is only one way, eliminate Choice D, and then guess C. The direct solution is simple enough if you know the formulas. If e is the length of an edge of the cube, then the area is 6e² and the volume is e³: 6e² = e³ ⇒ 6 = e.

14.(D) There are several ways to answer this question. Use TACTIC 1: plug in a number for x. If x = 2, Quantity A is 2π, which is slightly more than 6, and Quantity B is 2² = 4. Quantity A is greater: eliminate Choices B and C. Must Quantity A be greater? If the only other number you try is x = 3, you’ll think so, because 3² = 9, but 3π > 9. But remember, x does not have to be an integer: 3.9² > 15, whereas 3.9π < 4π, which is a little over 12.

**Use TACTIC 4. Could πx = x²? Yes, if x = π. Must x = π? No.

**Use TACTIC 3. Divide each quantity by x: Now Quantity A is π and Quantity B is x. Which is bigger, π or x? We cannot tell.

15.(D) Use TACTIC 4. Could the area of ABC = 3? Since the height is 6, the area would be 3 only if the base were 1: 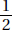(1)(6) = 3. Could BC = 1? Sure (see the figure). Must the base be 1? Of course not.

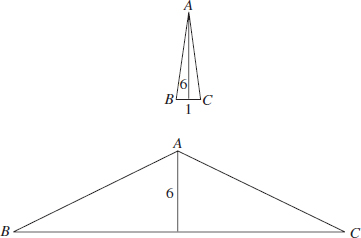
1.(C) According to the graph, there are approximately 70 milligrams of vitamin C in 100 grams of orange and 40 milligrams in the same amount of orange juice. This is a ratio of 70:40 = 7:4. Since the question refers to the same amount of orange and orange juice (500 grams), the ratio is unchanged.

2.(E) From the graph, you can see that by eating 100 grams of raw broccoli, you could receive as much as 165 milligrams of vitamin C. Since 100 grams of tomato could have as little as 10 milligrams of vitamin C, you would have to eat 1,650 grams of tomato to be sure of getting 165 milligrams of vitamin C.

3.(B) From the top graph, we see that among fourth-graders in 1996:

25% did no homework;

55% did less than 1 hour;

  5% did more than 2 hours.

This accounts for 85% of the fourth-graders; the other 15% did between 1 and 2 hours of homework per day.

4.(E) In 1984, approximately 540,000 eleventh-graders watched television 1 hour or less per day (27% of 2,000,000). By 1996, the number of eleventh-graders had increased by 10% to 2,200,000, but the percent of them who watched television 1 hour or less per day decreased to about 18%: 18% of 2,200,000 is 396,000. This is a decrease of 144,000, or approximately 150,000.

5.(C) The central angle of the sector representing Brand C is 12% of 360°:

(0.12) × 360° = 43.2°

The central angle of the sector representing Brand D is 7% of 360°:

(0.7) × 360° = 25.2°

Finally, 43.2° – 25.2° = 18°

**Note this can be done in one step by noticing that the percentage difference between Brands C and D is 5% and 5% of 360 is (0.05) × 360 = 18.

6.(C) Since total sales in 2000 were $1,000,000, in 2005 sales were $1,500,000 (a 50% increase).

In 2000, sales of Brand A were $400,000 (40% of $1,000,000).

In 2005 sales of Brand A were $500,000 (25% or more than in 2000).

Finally, $500,000 is 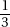or 33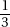% of $1,500,000.

7.(B) Reading from the top graph, we get the following enrollment figures:

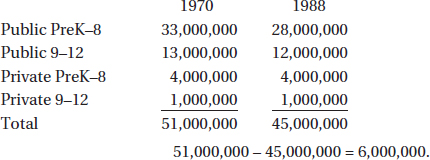
8.(B) In 1988, 8,800,000 (22% of 40,000,000) students lived in the West. From 1988–1998 this figure increased by 27%—for simplicity use 25%: an additional 2,200,000 students; so the total was then 11,000,000. The projected increase from 1998–2008 is about 10%, so the number will grow by 1,100,000 to 12,100,000.

9.25 The bar representing underweight adult females who perceive themselves to be underweight extends from about 70% to about 95%, a range of approximately 25%.

10.(A) Almost all overweight females correctly considered themselves to be overweight; and more than half of all females of normal weight correctly considered themselves “about right.” But nearly 70% of underweight adult females inaccurately considered themselves “about right.”

11.970 Referring only to the New York State table, we see that the amount of tax on a taxable income between $15,000 and $17,000 was $860 plus 10% of the excess over $15,000. Therefore, the tax on $16,100 is $860 plus 10% of $1,100 = $860 + $110 = $970.

12.(D) According to the tables, each additional dollar of taxable income over $25,000 was subject to a New York State tax of 14% and a New York City tax of 4.3%, for a total tax of 18.3%. Therefore, an additional $500 in taxable income would have incurred an additional tax of 0.183 × 500 = $91.50.

13.(B) In Norway, the life expectancy of a female born in 1955 was 75 years, which is greater than the life expectancy of a male born in 1990. In Hungary, the life expectancy of a female born in 1955 was 66 years, whereas the life expectancy of a male born in 1990 was greater than 67. In the other two countries, the life expectancy of a female born in 1955 was less than 65 years, and the life expectancy of a male born in 1990 was greater than 65.

14.(A) The life expectancy of a Korean female born in 1955 was about 51 and in 1990 it was about 74, an increase of 23 years. This is greater than any other nationality and sex.

15.(C) Since there were 10,000 bias-motivated offenses based on ethnicity, and that represents 10% of the total, there were 100,000 bias-motivated offenses in total. Of these, 16,000 (16% of 100,000) were based on religion, and 15,600 (15.6% of 100,000) were based on sexual orientation. The difference is 400.

16.(C, D, E) Since this is a question about percentages, assume that the total number of bias-motivated offenses in 1998 was 100, of which 16 were based on religion and 58 were based on race.

•If 8 of the religion-based offenses (50% of 16) were deleted, then there would have been 92 offenses in all, of which 58 were based on race.

•If 4 of the religion-based offenses (25% of 16) were deleted, then there would have been 96 offenses in all, of which 58 were based on race.

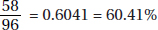
Only Choices C, D, and E lie between 60.41% and 63.04%.

1.(C) Since a is positive, we can divide both sides of the given inequality by a: a² ≤ 2a ⇒ a ≤ 2 ⇒ a = 1 or 2.

2.(A, B) Since a < b, a – b is negative (A is true). Since a and b are positive, so is their product, ab; and the reciprocal of a positive number is positive (B is true).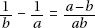
, and we have just seen that the numerator is negative and the denominator positive; so the value of the fraction is negative (C is false).

3.3 If all four integers were negative, their product would be positive, and so could not equal one of them. If all of the integers were positive, their product would be much greater than any of them (even 1 × 2 × 3 × 4 = 24). So, the integers must include 0, in which case their product is 0. The largest set of four consecutive integers that includes 0 is 0, 1, 2, 3.

4.(C) In the 9 hours from 3:00 to 12:00, the temperature rose 32 – (–13) = 32 + 13 = 45 degrees. So, the average hourly increase was 45° ÷ 9 = 5°.

5.(B, C) Since b is negative and c is positive, b < c ⇒ –b > –c ⇒ a – b > a – c (A is false). Since c is positive, dividing by c preserves the inequality. (B is true.) Since b is negative, 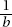is negative, and so is less than , which is positive (C is true).

6.(E) To make y – x as large as possible, let y be as big as possible (12), and subtract the smallest amount possible (x = –7): 12 – (–7) = 19.

7.(B) (7^a)(7^b) = 7^a+b, and 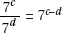. Therefore,

a + b = c – d ⇒ a + b + d = c ⇒ d = c – a – b

8.4 Just list the 9 possible outcomes of replacing and by +, –, and ×, and see that there are 4 different values: –2, 2, 6, 8.

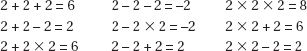
9.(D) There are 15 “terrific” numbers: 2, 3, 4, 6, 8, 9, 10, their opposites, and 0.

10.(D) There are 5 integers (1, 0, –1, –2, –3) that are greater than –3.14 (–π) and less than .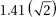

11.(A, B) Since 5 and 7 have two positive factors each, τ(5) = τ(7). (A is true.) Since 35 has 4 divisors (1, 5, 7, and 35) and τ(5) · τ(7) = 2 × 2 = 4. (B is true.) Since the positive divisors of 12 are 1, 2, 3, 4, 6, and 12, τ(12) is 6, which is not equal to 2 + 2. (C is false.)

12.(C) τ(τ(τ(12))) = τ(τ(6)) = τ(4) = 3

13.(A, B, C) All primes greater than 2 are odd, so p and q are odd, and p + q, the sum of two odd numbers, is even (A is true). The product of two odd numbers is odd (B is true). Since p and q are odd, so are their squares, and so the difference of their squares is even (C is true).

14.(B) For any number, x, between 0 and 1: x² < x and .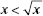

15.(C) First, multiply inside the parentheses: 7⁸ × 7⁹ = 7¹⁷; then, raise to the 10th power: (7¹⁷)¹⁰ = 7¹⁷⁰.

16.(A) Quantity B is the product of nine factors (–8, –6, –4, –2, 0, 2, 4, 6, 8). Since one of the factors is 0, Quantity B is equal to 0. Quantity A is the product of eight factors (–7, –5, –3, –1, 1, 3, 5, 7). The product of the four negative factors is positive, as is the product of the four positive factors. So Quantity A is positive, and, therefore, greater than Quantity B.

17.(D) If a and b are each 1, then a + b = 2, and ab = 1; so, Quantity A is greater. But, if a and b are each 3, a + b = 6, and ab = 9, then Quantity B is greater.

18.(B) The remainder is always less than the divisor.

19.(A) According to PEMDAS, you divide and multiply from left to right (do not do the multiplication first): 24 ÷ 6 × 4 = 4 × 4 = 16.

20.(A) By the distributive law, 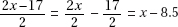, which is greater than x – 17 (the larger the number you subtract, the smaller the difference).

21.(A) The LCM of 2, 3, 4, 5, 6 is 60; and all multiples of 60 are divisible by each of them. So, n could be 61 or 1 more than any multiple of 60.

22.(C) The only prime divisible by 2 is 2, and the only prime divisible by 3 is 3. Quantity A and Quantity B are each 1.

23.(C) If you make a factor tree for n², the first branches should be n and n. Now, when you factor each n, you get exactly the same prime factors. (See the example below.)

24.(C) Just list the factors of 30: 1, 2, 3, 5, 6, 10, 15, 30. Four of them are odd and four are even.

25.(D) If n is even, then n + 1 is odd, and consequently (–10)ⁿ is positive, whereas (–10)ⁿ⁺¹ is negative. If n is odd, exactly the opposite is true.

1.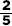 The class has 30 students, of whom 12 are boys. So, the boys make up of the class.

2.(C) If a is even, then 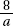is not in lowest terms, since both a and 8 are divisible by 2. Therefore, the only possibilities are 31, 33, 35, 37, and 39; but and 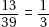, so only 3 integers—31, 33, and 37—satisfy the given condition.

3. There are 24 hours in a day and 7 days in a week, so there are 24 × 7 = 168 hours in a week: .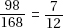

4.(A) Reduce each fraction and multiply:

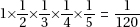
5.(E) Don’t bother writing an equation for this one; just think. We know that 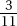of the number is 22, and 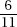of a number is twice as much as 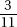of it: 2 × 22 = 44.

6.(C) The algebra way is to let x = the number of goldfish Jason won. During the first week 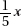died, so were still alive. During week two, 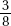of them died and 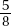of them survived:

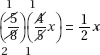
On the GRE, the best way is to assume that the original number of goldfish was 40, the LCM of the denominators (see TACTIC 3, Chapter 9).

Then, 8 died the first week (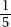 of 40), and 12 of the 32 survivors ( 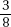of 32) died the second week. In all, 8 + 12 = 20 died; the other 20 ( the original number) were still alive.

7.(A) If x is the number, then 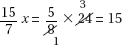. So, 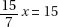, which means (dividing by 15) that 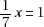, and so x = 7.

8.(A) 7a = 3 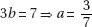and and .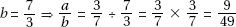

9.(A) Don’t start by doing the arithmetic. This is just 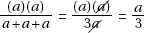. Now, replacing a with 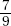gives .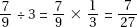

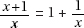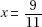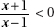10.(A, B) The reciprocal of a positive number less than 1 is greater than 1 (A is true). , which is greater than 1 (B is true). Since is positive and is negative, when , and, therefore, less than x (C is false).

11.960 If s is the number of students enrolled, is the number who were absent, and is the number who were present. Since 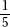of them went on a field trip, 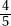of them stayed in school. Therefore,

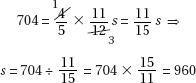
12.(B) Since a < 1, 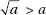(A is false). Since a < 1, a² < a (B is true). The reciprocal of a positive number less than 1 is greater than 1 (C is false).

13.(D) There are two easy ways to do this. The first is to see that (34.56)(7.89) has 4 decimal places, whereas (.3456)(78.9) has 5, so the numerator has to be divided by 10. The second is to round off and calculate mentally: since 30 × 8 = 240, and .3 × 80 = 24, we must divide by 10.

14.(A) Nine fractions are formed:

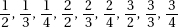
Note that although some of these fractions are equivalent, we do have nine distinct fractions.

When you multiply, the three 2s and the three 3s in the numerators cancel with the three 2s and three 3s in the denominators. So, the numerator is 1 and the denominator is 4 × 4 × 4 = 64.

15.(C) Multiplying Ezra’s incorrect answer by 1,000 would undo the final division he made. At that point he should have multiplied by 1,000. So, to correct his error, he should multiply again by 1,000. In all, Ezra should multiply his incorrect answer by 1,000 × 1,000 = 1,000,000.

16.(C) Each quantity equals .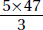

17.(A) Quantity A: .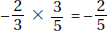

Quantity B: –.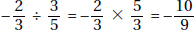

Finally, .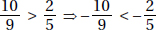

18.(A) Quantity A: .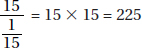

19.(C) 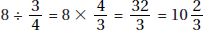. Since 10 packages wouldn’t be enough, she had to buy 11. (10 packages would weigh only 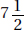pounds.)

20.(B) You don’t need to multiply on this one: since , of is less than , which is already less than .

21.(C) Quantity B is the sum of 2 complex fractions:

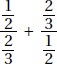
Simplifying each complex fraction, by multiplying numerator and denominator by 6, or treating these as the quotient of 2 fractions, we get 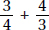, which is exactly the value of Quantity A.

22.(A) When two fractions have the same numerator, the one with the smaller denominator is bigger, and 2¹⁰⁰ < 3¹⁰⁰.

23.(A) Since Quantity A is the product of 4 negative numbers, it is positive, and so is greater than Quantity B, which, being the product of 3 negative numbers, is negative.

24.(A) Quantity A: .

Since Quantity B is the reciprocal of Quantity A, Quantity B = .

25.(B) If 0 < x < 1, then 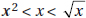. In this question, .

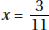1.(D) If 4 students failed, then the other 25 – 4 = 21 students passed, and .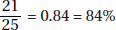

2.(D) Since 5% of 60 is 3, Amanda saved $3, and thus paid $57 for the sweater. She then had to pay 5% sales tax on the $57: .05 × 57 = 2.85, so the total cost was $57 + $2.85 = $59.85.

3.(B) 10% of 20% of 30% = .10 × .20 × .30 = .006 = .6%.

4.(C) 500% of c = 5c, which is 1% of 500c.

5.(E)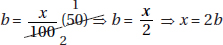

6.

7.(C) To find Mario’s earnings during his first week, divide his earnings from the second week by 1.25: 110 ÷ 1.25 = 88.

8.(D) Since 20% of 80 is 16, Bernie wants to get $96 for each radio he sells. What price should the radios be marked so that after a 20% discount, the customer will pay $96? If x represents the marked price, then .80x = 96 ⇒ x = 96 ÷ .80 = 120.

9.(B) Assume that Mrs. Fisher usually contributed $100 each month, for an annual total of $1200. Having decided not to contribute for 2 months, the $1200 will have to be paid in 10 monthly deposits of $120 each. This is an increase of $20, and a percent increase of .

10.(B) Assume that a loaf of bread used to cost $1 and that now it costs $1.20 (20% more). Then 300 loaves of bread used to cost $300. How many loaves costing $1.20 each can be bought for $300? 300 ÷ 1.20 = 250.

11.(D) 1 micron = 10,000 angstroms ⇒ 10 microns = 100,000 angstroms; dividing both sides by 1,000, we get 100 angstroms = 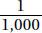(10 microns); and .

12.65 Assume that there are 100 boys and 200 girls in the class. Then, 45 boys and 60 girls have handed in their reports. So 105 students have handed them in, and 300 – 105 = 195 have not handed them in. What percent of 300 is 195?

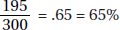
13.(D) The increase in the value of the vase was $9,000. So the percent increase is

14.150 If p represents the original price, the jacket was priced at 1.15p instead of .85p. Since this was a $45 difference, 45 = 1.15p – .85p = .30p ⇒ p = 45 ÷ .30 = $150.

15.(D) To earn a grade of 80% on the entire exam, Eve needs to correctly answer 64 questions (80% of 80). So far, she has answered 45 questions correctly (75% of 60). Therefore, on the last 20 questions she needs 64 – 45 = 19 correct answers; and .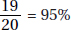

16.(C) Quantity A: 400% of 3 = 4 × 3 = 12.
Quantity B: 300% of 4 = 3 × 4 = 12.

17.(A) Since n% of 25 is 50, then 25% of n is also 50, and 50% of n is twice as much: 100. If you don’t see that, just solve for n:

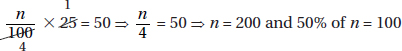
18.(D) A 25% discount on a $10 television is much less than $25, whereas a 25% discount on a $1,000 television is much more than $25. (They would be equal only if the regular price of the television were $100.)

19.(B) Assume that the list price of cellular phone 2 is $100; then the list price of cellular phone 1 is $120, and on sale at 20% off it costs $24 less: $96.

20.(C) For any numbers a and b: a% of b is equal to b% of a.

21.(D)

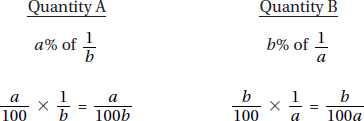
Multiply by 100:

The quantities are equal if a and b are equal, and unequal otherwise.

22.(A) Bank B would have to increase its rate from 4% to 5%, an actual increase of 1%. This represents a percent increase of .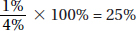

23.(B) Assume that the original mixture consists of 20 grams of sugar and 80 grams of cinnamon. If the amount of sugar is doubled, there would be 40 grams of sugar and 80 grams of cinnamon.

The sugar will then comprise 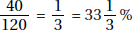of the mixture.

24.(D) If b = 2, then b² = 4, and 2 = 50% of 4; in this case, the quantities are equal. If b = 4, b² = 16, and 4 is not 50% of 16; in this case, the quantities are not equal.

25.(C) Avoid the algebra and just assume Ali started with $100. After giving Lior $50, she had $50 left, which was 20% or one-fifth of what he had. So, Lior had 5 × $50 = $250, which means that originally he had $200.

Quantity A: 75% of $200 = $150.

Quantity B: 150% of $100 = $150.

The quantities are equal.

1.(A) Of every 4 employees, 3 are not college graduates, and 1 is a college graduate. So the ratio of graduates to nongraduates is 1:3.

2.(D) Cross-multiplying, we get: 2a² = 90 ⇒ a² = 45.

3.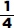 If 80% were rejected, 20% were accepted, and the ratio of accepted to rejected is 20:80 = 1:4.

4.(B) Set up a proportion: , and cross-multiply: .

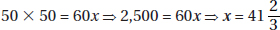5.(D) Out of every 8 team members, 3 are juniors and 5 are seniors. Seniors, therefore, make up 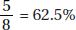of the team.

6.(A, B) It is worth remembering that if the ratio of the measures of the angles of a triangle is 1:1:2, the angles are 45-45-90 (see Section 12-J). Otherwise, the first step is to write x + x + 2x = 180 ⇒ 4x = 180 ⇒ x = 45.

Since two of the angles have the same measure, the triangle is isosceles, and since one of the angles measures 90°, it is a right triangle. I and II are true, and, of course, III is false.

7.(E) By definition, π is the ratio of the circumference to the diameter of a circle (see Section 12-L). Therefore, .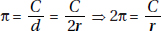

8.(D) The fraction of the team that is sophomores is 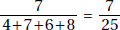, and .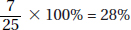

9.490 Let the number of students taking Spanish be 7x, and the number taking French be 2x. Then, 2x = 140 ⇒ x = 70 ⇒ 7x = 490.

10.(D) Since , 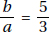. So, 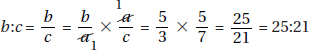. Alternatively, we could write equivalent ratios with the same value for a:

a:b = 3:5 = 15:25 and a:c = 5:7 = 15:21

So, when a = 15, b = 25, and c = 21.

11.(C) To solve a proportion, cross-multiply: .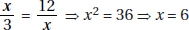

12.(C) Let b = 7x and a = 2x. Then, 7x + 2x = 180 ⇒ 9x = 180 ⇒ x = 20 ⇒ b = 140 and a = 40 ⇒ b – a = 140 – 40 = 100.

13.(A) Set up the proportion, keeping track of units:

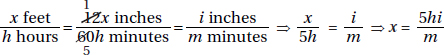
14.(B) Gilda grades at the rate of .

Since she can grade tx tests each hour, in x hours she can grade x(tx) = tx² tests.

15.(B) Suppose that x boys and x girls joined the club. Then, the new ratio of boys to girls would be (3 + x):(5 + x), which we are told is 3:4.

So, .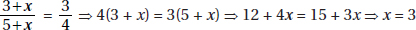

Therefore, 3 boys and 3 girls joined the other 3 boys and 5 girls: a total of 14.

16.(D) Cross-multiplying, we get:

11(3x – 1) = 25(x + 5) ⇒ 33x – 11 = 25x +125 ⇒ 8x = 136 ⇒ x = 17

17.(C) Since 4 boys can shovel the driveway in 2 hours, or 2 × 60 = 120 minutes, the job takes 4 × 120 = 480 boy-minutes; and so 5 boys would need

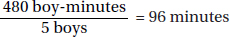
18.4 Since 500 pounds will last for 20 pig-weeks = 140 pig-days, 200 pounds will last for pig-days = 56 pig-days, and .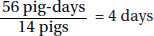

19.(A) Assume that to start there were 3x red marbles and 5x blue ones and that y of each color were added.

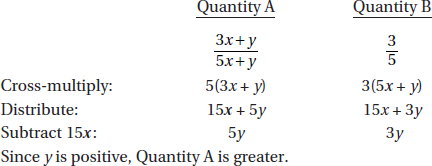
20.(C) The shares are 2x, 5x, and 8x, and their sum is 3,000:

2x + 5x + 8x = 3,000 ⇒ 15x = 3,000 ⇒ x = 200, and so 8x – 2x = 6x = 1,200

21.(D) Ratios alone can’t answer the question, “How many?” There could be 5 boys in the chess club or 500. We can’t tell.

22.(C) Assume that Sally invited x boys and x girls. When she wound up with x girls and x + 5 boys, the girl:boy ratio was 4:5. So,

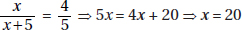
Sally invited 40 people (20 boys and 20 girls).

23.(A) If the probability of drawing a red marble is 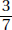, 3 out of every 7 marbles are red, and 4 out of every 7 are non-red. So the ratio of red:non-red = 3:4, which is greater than .

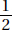24.(A) Multiplying the first equation by 3 and the second by 2 to get the same coefficient of b, we have: 9a = 6b and 6b = 10c. So, 9a = 10c and .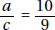

25.(B) Assume the radius of circle I is 1 and the radius of circle II is 3. Then the areas are π and 9π, respectively. So, the area of circle II is 9 times the area of circle I, and 3π > 9.

1.(E) Use TACTIC E1. For Michael’s average on five tests to be an 84, he needs a total of 5 × 84 = 420 points. So far, he has earned 4 × 80 = 320 points. Therefore, he needs 100 points more.

2.(C) Use TACTIC E1. So far, Maryline has earned 320 points. She can survive a low grade on test five if she gets the maximum possible on both the sixth and seventh tests. So, assume she gets two 100s. Then her total for tests 1, 2, 3, 4, 6, and 7 would be 520. For her seven-test average to be 85, she needs a total of 7 × 85 = 595 points. Therefore, she needs at least 595 – 520 = 75 points.

3.(D) Since Sandrine’s 4-test average is 80, she earned a total of 4 × 80 = 320 points. Could Sandrine have earned a total of 320 points with:

0 grades of 80?	Easily; for example, 20, 100, 100, 100 or 60, 70, 90, 100.
1 grade of 80?	Lots of ways; 80, 40, 100, 100, for instance.
2 grades of 80?	Yes; 80, 80, 60, 100.
4 grades of 80?	Sure: 80, 80, 80, 80.
3 grades of 80?	NO! 80 + 80 + 80 + x = 320 ⇒ x = 80, as well.

4.(D) Clearly, the sequence of integers from 1 to 100 has 100 terms, and so by KEY FACT E4, we know that the average of all the numbers is the average of the two middle ones: 50 and 51. The average, therefore, is 50.5.

5.1.75 Since 10a + 10b = 35, dividing both sides of the equation by 10, we get that a + b = 3.5. Therefore, the average of a and b is 3.5 ÷ 2 = 1.75.

6.(A) Whenever a question involves three equations, add them:

7.(C) Use TACTIC E1: the sum of the 4 numbers is 4 times their average:

5 + 6 + 7 + w = 4 × 8 = 32 ⇒ 18 + w = 32 ⇒ w = 14

8.108 The average of the measures of the five angles is the sum of their measures divided by 5. The sum is (5 – 2) × 180 = 3 × 180 = 540 (see Section 12-K). So, the average is 540 ÷ 5 = 108.

9.(E) Calculate the average:

10.(C) Since a + b + c + d = 360, and e + f + g + h = 360 (see Section 12-I), the sum of the measures of all 8 angles is 360 + 360 = 720, and their average is 720 ÷ 8 = 90.

11.(C) The average of 2¹⁰ and 2²⁰ is .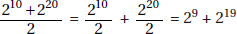

12.(D) Arrange the numbers in increasing order: 10, 20, 40, 70, 70, 90. M, the median, is the average of the middle two numbers: 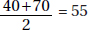; the mode, m, is 70, the number that appears most frequently. The average of M and m, therefore, is the average of 55 and 70, which is 62.5.

13.(C) In any triangle, the sum of the measures of the three angles is 180°, and the average of their measures is 180 ÷ 3 = 60.

14.(D) From KEY FACT E1, we know only that at least one grade was above 80. In fact, there may have been only one (9 grades of 79 and 1 grade of 89, for example). But there could have been five or even nine (for example, 9 grades of 85 and 1 grade of 35).

Alternative solution. The ten students scored exactly 800 points. Ask, “Could they be equal?” Could there be exactly five grades above 80? Sure, five grades of 100 for 500 points and five grades of 60 for 300 points. Must they be equal? No, eight grades of 100 and two grades of 0 also total 800.

15.(C) The average of 2x and 2y is , which equals 180.

16.(D) It is possible that no boy weighs over 150 (if every single boy weighs exactly 150); on the other hand, it is possible that almost every boy weighs over 150. The same is true for the girls.

17.(B) Use TACTIC E1: 22 + 38 + x + y = 4(15) = 60 ⇒ 60 + x + y = 60 ⇒ x + y = 0. Since it is given that x is positive, y must be negative.

18.(C) Do not calculate either standard deviation. Clearly, the mean of List 1 is 5, and the differences between each number and the mean are –4, –2, 0, 2, 4. In List 2, the mean is 15, and again the differences between each number and the mean are –4, –2, 0, 2, 4. Since the differences are the same, the average of the squares of the differences will be the same. The two standard deviations are equal.

19.(A) You don’t have to calculate the averages. Quantity A is clearly greater than 17, so by KEY FACT E3, adding 17 to the set of numbers being averaged must lower the average.

20.(D) Use KEY FACT E3: If x < y, then the average of x and y is less than y, and surely less than 2y. So, 2y has to raise the average. On the other hand, if x is much larger than y, then 2y would lower the average.

1.235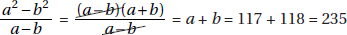

2.(A, C) Adding the two equations, we get that 2a² = 50 ⇒ a² = 25 ⇒ b² = 4. So, a = 5 or –5 and b = 2 or –2. The only possibilities for their product are 10 and –10. (Only A and C are true.)

3.(E) To find the average, take the sum of the three polynomials and then divide by 3.

Their sum is (x² + 2x – 3) + (3x² – 2x – 3) + (30 – 4x²) = 24, and 24 ÷ 3 = 8.

4.(E) You can avoid messy, time-consuming arithmetic if you recognize that x² + 12x + 36 = (x + 6)². The value is (994 + 6)² = 1,000² = 1,000,000.

5.(A) Start by squaring c – d: 2 = (c – d)² = c² – 2cd + d² = c² + d² – 2cd = 4 – 2cd.

So, 2 = 4 – 2cd ⇒ 2cd = 2 ⇒ cd = 1.

6.(C) First multiply out both pairs of binomials: (2x + 3)(x + 6) = 2x² + 15x + 18 and (2x – 5)(x + 10) = 2x² + 15x – 50.

Now subtract: (2x² + 15x + 18) – (2x² + 15x – 50) = 18 – (–50) = 68.

7.(B)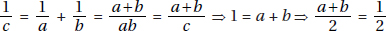

8.(A) x² – y² = (x – y)(x + y) ⇒ 28 = 8(x + y) ⇒ x + y = 28 ÷ 8 = 3.5

Finally, the average of x and y is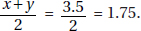

9.(B) Expand each square:

Similarly,

Subtract: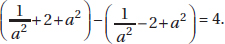

10.(C) 100 =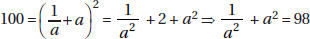

11.(B) Since n is negative, n² is positive, and so –2n² is negative. Therefore, Quantity A is negative, whereas Quantity B is positive.

12.(D) c > d ⇒ c – d is positive, so divide each side by c – d:

Subtract c from each quantity:

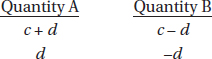
If d = 0 the quantities are equal; if d = 1, they aren’t.

13.(B) Quantity A: –(–3)²2³ = – (9)(8) = –72.

14.(C) Quantity B: r(s + r) – s(r + s) = rs + r² – sr – s² = r² – s²

Quantity A: (r + s)(r – s) = r² – s².

15.(D) Quantity A: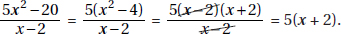

Quantity B: 4x + 8 = 4(x + 2). If x = –2, both quantities are 0; for any other value of x the quantities are unequal.

1.(C) The easiest method is to recognize that x + 3 is 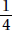of 4x + 12 and, therefore, equals 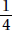of 36, which is 9. If you don’t see that, solve normally:

4x + 12 = 36 ⇒ 4x = 24 ⇒ x = 6 and so x + 3 = 9

2.(D) Subtracting 20 from each side of 7x + 10 = 44 gives 7x – 10 = 24. If you don’t see that, subtract 10 from each side, getting 7x = 34. Then subtract 10 to get 7x – 10 = 24.

The worst alternative is to divide both sides of 7x = 34 by 7 to get 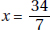; then you have to multiply by 7 to get back to 34, and then subtract 10.

3.(C) Add 2x to each side: 6x + 13 = 7. Subtract 13 from each side: 6x = –6. Divide by 6: x = –1.

4.165 x – 4 = 9 ⇒ x = 13 ⇒ x² = 169 and so x² – 4 = 165

5.(A) Treat a, b, c, and d as constants, and use the six-step method to solve for x:

ax – b = c – dx ⇒ ax – b + dx = c ⇒ ax + dx = c + b ⇒ x(a + d) = b + c ⇒ x =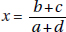

6.(D) Multiply both sides by 18, the LCD:

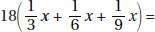18(33) ⇒ 6x + 3x + 2x = 594 ⇒ 11x = 594 ⇒ x = 54

It’s actually easier not to multiply out 18 × 33; leave it in that form, and then divide by 11: .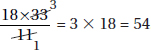

7.(D) Be alert. Since you are given the value of 3x – 4, and want the value of (3x – 4)², just square both sides: 11² = 121. If you don’t see that, you’ll waste time solving the equation 3x – 4 = 11(getting that x = 5), only to use that value to calculate that 3x – 4 is equal to 11, which you aready knew.

8.(E) 2^{a – 3} = 64¹² = (2⁶)¹² = 2⁷² ⇒ a – 3 = 72, and so a = 75.

9.(D) Since a = 2b, 2a = 4b. Therefore, the average of 3a and 4b is the average of 3a and 2a, which is 2.5a. Therefore, 2.5a < 50 ⇒ a < 20. So the largest integer value of a is 19.

10.(C) Taking the reciprocal of each side, we get a – b = 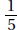. So a = b + .

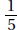11.(A) x = 3a + 7 ⇒ x – 7 = 3a ⇒ a = .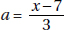

Therefore, .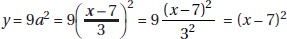

12.132 Solving for y yields .

Then, since .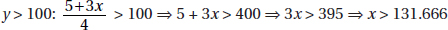

The smallest integer value of x is 132.

13.(B) Adding the two equations, we get that 2a = 26. Therefore, a = 13 and b = 0.

14.(A) Express each side of 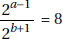as a power of 2:

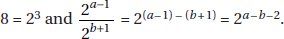
Therefore, a – b – 2 = 3 ⇒ a = b + 5, and so a is greater.

15.(B) 4x² = 3x ⇒ 4x² – 3x = 0 ⇒ x(4x – 3) = 0.

So,

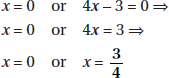
There are two possible values of x, both of which are less than 1.

16.(C) When we add all three equations, we get

2a + 2b + 2c = 6 ⇒ a + b + c = 3, and so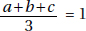

17.(A) Use substitution. Replace y in the first equation with 2x:

3x – 4(2x) = 5 ⇒ 3x – 8x = 5 ⇒ –5x = 5 ⇒ x = –1 ⇒ y = –2

18.(A) Multiply both sides by 6, the LCD:

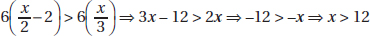
19.(B) The first thing to try is to add the equations. That yields 5r – 11s = 24, which does not appear to be useful. So now try to subtract the equations. That yields r + s = 10.

So the average of r and s is .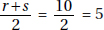

20.(B) Multiply both sides of the given equation by cd, the LCD of the fractions:

Since d is positive, d + 1 > 1, and so So c < d.

1.100

After the gift, Ronald will have 3 times as much money as Howard: x + 50 = 3(3x – 50) ⇒ x + 50 = 9x – 150 ⇒ 8x = 200, and so x = 25.
So Ronald has $25 and Howard has $75, for a total of $100.

2.(B) Beth’s average rate of reading is determined by dividing the total number of pages she read (200) by the total amount of time she spent reading. In the afternoon she read for 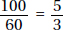hours, and in the evening for 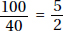hours, for a total time of 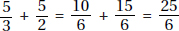hours. So, her average rate was 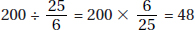pages per hour.

3.(E) Let the 5 consecutive integers be n, n + 1, n + 2, n + 3, n + 4. Then, S = n + n + 1 + n + 2 + n + 3 + n + 4 = 5n + 10 ⇒ 5n = S – 10 ⇒ n = . Choice A, therefore, is the smallest of the integers; the largest is

4.(D) Let x represent the number of chocolate bars sold; then 150 – x is the number of lollipops sold. We must use the same units, so we could write 75 cents as .75 dollars or 74 dollars as 7400 cents. Let’s avoid the decimals: x chocolates sold for 75x cents and (150 – x) lollipops sold for 40(150 – x) cents. So,

7,400 = 75x + 40(150 – x) = 75x + 6,000 – 40x = 6,000 + 35x ⇒ 1,400 = 35x ⇒ x = 40 and 150 – 40 = 110

5.(E) If b is the number of blue marbles, then there are 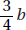white ones, and 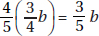red ones.

Therefore,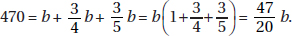

So,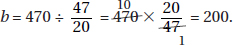

6.720 If x is the number of shells in Justin’s collection, then Judy has .80x. Since Justin has 80 more shells than Judy,

x = .80x + 80 ⇒ .20x = 80 ⇒ x = 80 ÷ .20 = 400

So Justin has 400 and Judy has 320: a total of 720.

7.(B) If x represents the greater and y the smaller of the two numbers, then (x + y) = 30 + (x – y) ⇒ y = 30 – y ⇒ 2y = 30, and so y = 15. Since xy = 900, x = 900 ÷ 15 = 60.

8.(D) If x represents the number of students earning 100, then 10 – x is the number of students earning 80. So

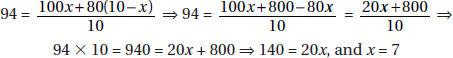
9.(D) Since 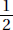x years ago, Adam was 12, he is now 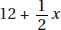. So 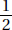x years from now, he will be . But, we are told that at that time he will be 2x years old. So, 12 + x = 2x ⇒ x = 12.

Thus, he is now 12 + 6 = 18, and 3x or 36 years from now he will be 18 + 36 = 54.

10.(C) Let x be Barry’s weight in 1950. By 1980, he had gained 60 pounds (2 pounds per year for 30 years) and was 40% heavier: 60 = .40x ⇒ x = 60 ÷ .4 = 150. So in 1980, he weighed 210. Fifteen years later, in 1995, he weighed .

11.(A) You can do the simple algebra, but you might realize that if in the past 10 years Lindsay’s age doubled, she was 10 and is now 20. Similarly, Kimberly is now 10 and in 10 years will be 20.
Here is the algebra: if x represents Lindsay’s age now,

x = 2(x – 10) ⇒ x = 2x – 20 ⇒ x = 20

Similarly, Kimberly is now 10 and will be 20 in 10 years.

12.(C) Let x represent the amount of Boris’s take-home pay. On Saturday, he spent 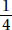x and still had 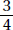x; but on Sunday, he spent 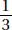of that: 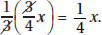. Therefore, he spent 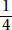of his take-home pay each day.
So, he spent 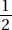of his pay and saved 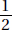of his pay.

13.(A) If x represents Tiffany’s age now, then in 8 years she will be x + 8, and so x + 8 = 3x ⇒ 8 = 2x ⇒ x = 4.

Tiffany will be 6 times as old 20 years from now, when she will be 24.

14.(D) If x and y represent the number of 4-cent stamps and 7-cent stamps that Rachel used, respectively, then 4x + 7y = 50. This equation has infinitely many solutions but only 2 in which x and y are both positive integers: y = 2 and x = 9 or y = 6 and x = 2.

15.(C) Draw a diagram. In 9 hours Car A drove 360 miles north and Car B drove 270 miles east. These are the legs of a right triangle, whose hypotenuse is the distance between them. Use the Pythagorean theorem if you don’t recognize that this is just a 3x–4x–5x right triangle: the legs are 90 × 3 and 90 × 4, and the hypotenuse is 90 × 5 = 450.

1.(D) The markings in the five angles are irrelevant. The sum of the measures of the five angles is 360°, and 360 ÷ 5 = 72. If you calculated the measure of each angle you should have gotten 36, 54, 72, 90, and 108; but you would have wasted time.

2.(C) From the diagram, we see that 6a = 180, which implies that a = 30, and that 5b = 180, which implies that b = 36. So, .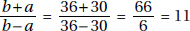

3.36 Since vertical angles are equal, the two unmarked angles are 2b and 4a. Since the sum of all six angles is 360°, 360 = 4a +2b + 2a + 4a + 2b + b = 10a + 5b.

However, since vertical angles are equal, b = 2a ⇒ 5b = 10a. Hence,

360 = 10a + 5b = 10a + 10a = 20a, so a = 18 and b = 36.

4.(C) Since x + y + 90 = 180, x + y = 90. Also, since y:x = 3:2, y = 3t and x = 2t. Therefore, 3t + 2t = 90 ⇒ 5t = 90. So t = 18, and x = 2(18) = 36.

5.115 For problems such as this, always draw a diagram. The measure of each of the 12 central angles from one number to the next on the clock is 30°. At 1:50 the minute hand is pointing at 10, and the hour hand has gone 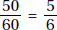the way from 1 to 2. So from 10 to 1 on the clock is 90°, and from 1 to the hour hand is , for a total of 90° + 25° = 115°.

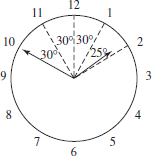
6.(A) No conclusions can be made about the lines; they could form any angles whatsoever. (B and C are both false.) Since a = b,

c = 180 – a = 180 – b = d

(A is true.)

7.(E) Since a:b = 3:5, then a = 3x and b = 5x. c:b = c:5x = 2:1 ⇒ c = 10x. Then, 3x + 5x + 10x = 180 ⇒ 18x = 180. So, x = 10 and c = 10x = 100.

8.(E) If a diagram is not provided on a geometry question, draw one on your scrap paper. From the figure below, you can see that MN:BC = 2:1.

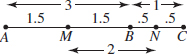
9.(C) Since the lines are parallel, the angle marked y and the sum of the angles marked x and 45 are equal: y = x + 45 ⇒ y – x = 45.

10.(B) Let x = 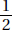m∠AOC, and y = 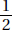m∠AOB.

Then, x + y = 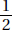m∠AOC + 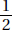m∠AOB = (180) = 90.

11.(D) No conclusion can be made: x could equal 50 or be more or less.

12.(B) Since m∠A + 32 + 75 = 180, m∠A = 73; and since AB is parallel to CD, a = 73, whereas, because vertical angles are equal, b = 75.

13.(D)

There is no way to determine whether a is less than, greater than, or equal to c.

14.(C) Whether the lines are parallel or not, a + b = c + d = e + f = g + h = 180.

Each quantity is equal to 360.

15.(C) Extend line segment AB to form a transversal. Since w + z = 180 and w + (x + y) = 180, it follows that z = x + y.

1.(D) x + 2x + 30 = 180 ⇒ 3x + 30 = 180 ⇒ 3x = 150 ⇒ x = 50

2.(B) Draw a diagram and label it.

Then write the equations: x + y = 90 and x – y = 8.

So x = 49 and y = 90 – 49 = 41.

3.(B) Draw altitude AD in equilateral ABC.

By KEY FACT J11, 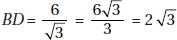, and BD is one half the base. So, the area is 2 × 6 = 12.

4.(B, E) If the triangle were not required to be a right triangle, by KEY FACTS J11 and J12 any number greater than 1 and less than 25 could be the length of the third side, and the answer would be A, B, C, D, E. But for a right triangle, there are only two possibilities:

If 13 is the hypotenuse, then the legs are 12 and 5. (B is true.) (If you didn’t recognize the 5-12-13 triangle, use the Pythagorean theorem: 12² + x² = 13², and solve.)

If 12 and 13 are the two legs, then use the Pythagorean theorem to find the hypotenuse: 12² + 13² = c² ⇒ c² = 144 + 169 = 313 ⇒ c = 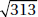. (E is true.)

5.(D) Use the Pythagorean theorem twice, unless you recognize the common right triangles in this figure (which you should). Since PR = 20 and QR = 16, PQR is a 3x-4x-5x right triangle with x = 4. So PQ = 12, and PQS is a right triangle whose legs are 5 and 12. The hypotenuse, PS, therefore, is 13.

6.(D) If the measures of the angles are in the ratio of 1:2:3,

x + 2x + 3x = 180 ⇒ 6x = 180 ⇒ x = 30

So the triangle is a 30-60-90 right triangle, and the sides are a, 2a, and a. Since a = 10, then 2a, the length of the longest side, is 20.

7.115 Label the other angles in the triangle.

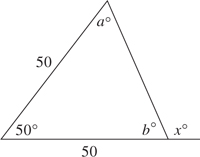
50 + a + b = 180 ⇒ a + b = 130, and since the triangle is isosceles, a = b. Therefore, a and b are each 65, and x = 180 – 65 = 115.

8.110 Here, 50 + 90 + a = 180 ⇒ a = 40, and since vertical angles are equal, b = 40. Then, 40 + 30 + w = 180 ⇒ w = 110.

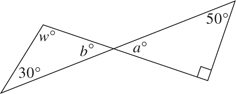
9.(B) You could calculate the area of the rectangle and subtract the area of the two white right triangles, but you shouldn’t. It is easier to solve this problem if you realize that the shaded area is a triangle whose base is 4 and whose height is 12. The area is 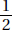(4)(12) = 24.

10.(D) Since both BD and ED are the hypotenuses of right triangles, their lengths can be calculated by the Pythagorean theorem, but these are triangles you should recognize: the sides of DCE are 5-12-13, and those of BAD are 9-12-15 (3x-4x-5x, with x = 3). So the perimeter of BED is 4 + 13 + 15 = 32.

11.(B) Since DGH is a right triangle whose hypotenuse is 5 and one of whose legs is 3, the other leg, GH, is 4. Since GF = DE is 7, HF is 3. Now, DFH has a base of 3 (HF) and a height of 3 (DG), and its area is 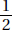(3)(3) = 4.5.

12.(B) In DFH, we already have that DH = 5 and HF = 3; we need only find DF, which is the hypotenuse of DEF. By the Pythagorean theorem, (DF)² = 3² + 7² = 9 + 49 = 58 ⇒ DF = .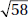

So the perimeter is .

13.(A) x + 2x + 3y = 180 ⇒ 3x + 3y = 180. So x + y = 60, and y = 60 – x.

14.(C) ABD is a right triangle whose hypotenuse is 15 and one of whose legs is 9, so this is a 3x-4x-5x triangle with x = 3; so AD = 12. Now ADC is a 30-60-90 triangle, whose shorter leg is 12. Hypotenuse AC is 24, and leg CD is 12. So the perimeter is 24 + 15 + 9 + 12 = 48 + 12.

15.(C) From the solution to 14, we have the base (9 + 12) the height (12) of ABC.

Then, the area is (12)(9 + 12) = 54 + 72.

16.(A) Any side of a triangle must be greater than the difference of the other two sides (KEY FACT J13), so the third side is greater than 11 – 7 = 4.

17.(C) Draw a diagram. A diagonal of a square is the hypotenuse of each of the two 45-45-90 right triangles formed. The ratio of the length of the hypotenuse to the length of the leg in such a triangle is :1, so the quantities are equal.

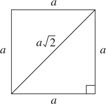
18.(D) BC can be any positive number less than 20 (by KEY FACTS J12 and J13), BC > 10 – 10 = 0 and BC < 10 + 10 = 20). So the perimeter can be any number greater than 20 and less than 40.

19.(A) Since OA and OB are radii, they are each equal to 5. With no restrictions on x, AB could be any positive number less than 10, and the bigger x is, the bigger AB is. If x were 90, AB would be 5, but we are told that x > 90, so AB > 5 > 7.

20.(B) Since AB must be less than 10, the perimeter is less than 20.

21.(B) Don’t calculate either area. The length of a side of an equilateral triangle is greater than the length of an altitude. So Quantity B is larger since it is the area of a triangle whose sides are greater.

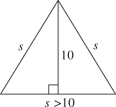
22.(A) Quantity A: The perimeter of the shaded region consists of 12 line segments, each of which is the hypotenuse of a 45-45-90 right triangle whose legs are 1. So each line segment is , and the perimeter is 12. Quantity B: The perimeter of the square is 16.

To compare 12 and 16, square them: (12)² = 144 × 2 = 288; 16² = 256.

23.(A) The white region consists of 12 right triangles, each of which has an area of 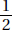, for a total area of 6. Since the area of the large square is 16, the area of the shaded region is 16 – 6 = 10.

24.(C) Since a = 180 – 145 = 35 and b = 180 – 125 = 55, a + b = 35 + 55 = 90. Therefore, 180 = a + b + c = 90 + c ⇒ c = 90.

25.(B) Since 65 + 45 = 110, m∠P = 70. Since ∠P is the largest angle, QR, the side opposite it, is the largest side.

1.60 Draw a diagram and label it.

Since the area is 144, then 144 = (4x)(x) = 4x² ⇒ x² = 36 ⇒ x = 6.

So the width is 6, the length is 24, and the perimeter is 60.

2.(B) The area of the square is 2² = 4, and each triangle is one-fourth of the square. So the area of DEC is 1.

3.(D) DEC is a 45-45-90 right triangle whose hypotenuse, DC, is 2.

Therefore, each of the legs is . So the perimeter is 2 + 2.

4.(C) The sum of the angles of a five-sided polygon is (5 – 2) × 180 = 3 × 180 = 540. Therefore, 540 = 2x + 3x + 3x + 5x + 5x = 18x.

So, x = 540 ÷ 18 = 30.

The measure of the smallest angle is 2x = 2 × 30 = 60.

5.(C) The area of rectangle ABCD is (x + 1)(x + 4) = x² + 5x + 4.

The area of rectangle EFGH is (x + 2)(x + 3) = x² + 5x + 6, which is exactly 2 more than the area of rectangle ABCD: 100 + 2 = 102.

6.(D) Draw a picture and label it.

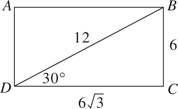
Since BCD is a 30-60-90 right triangle, BC is 6 (half the hypotenuse) and CD is 6.

So the area is w = 6(6) = 36.

7.(C) The perimeter of the rectangle is 2( + w) = 2(6 + 6) = 12 + 12.

8.(E) The sum of the degree measures of an interior and exterior angle is 180, so 180 = 8x + x = 9x ⇒ x = 20.

Since the sum of the measures of all the exterior angles is 360, there are 360 ÷ 20 = 18 angles and 18 sides.

9.(A) Let x represent the side of the square. Then the dimensions of the rectangle are (x + 5) and (x – 5), and its area is (x + 5)(x – 5) = x² – 25. Since the area of the square is 45, x² = 45 ⇒ x² – 25 = 45 – 25 = 20.

10.(C) Each triangle surrounding quadrilateral MNOP is a 6-8-10 right triangle. So each side of MNOP is 10, and its perimeter is 40.

11.96 The area of each of the triangles is 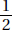(6)(8) = 24, so together the four triangles have an area of 96. The area of the rectangle is 16 × 12 = 192. Therefore, the area of quadrilateral MNOP is 192 – 96 = 96.
Note: Joining the midpoints of the four sides of any quadrilateral creates a parallelogram whose area is one-half the area of the original quadrilateral.

12.(C) Each of the 10 marked angles is an exterior angle of the pentagon. If we take one angle at each vertex, the sum of those five angles is 360; the sum of the other five is also 360: 360 + 360 = 720.

13.150 Let W, X, Y, and Z represent the measures of the four angles. Since W + X + Y + Z = 360, W + X + Y = 360 – Z. Also,

So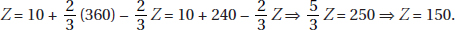

14.(B) Since M and N are midpoints of sides of length 2, AM, MB, AN, and ND are all 1. MN = , since it’s the hypotenuse of an isosceles right triangle whose legs are 1; and BD = 2, since it’s the hypotenuse of an isosceles right triangle whose legs are 2. So the perimeter of the shaded region is 1 + + 1 + 2 = 2 + 3.

15.(A) The area of ABD = 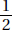(2)(2) = 2, and the area of AMN is (1)(1) = 0.5.

So the area of the shaded region is 2 – 0.5 = 1.5.

16.(C) The area of AED is .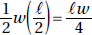

The area of EDC is .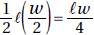

Note: Each of the four small triangles has the same area.

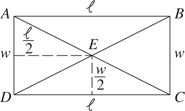
17.(B) By KEY FACT J5, since ∠Z is acute and ∠Y is obtuse, (WY)² < a² + b², whereas (XZ)² > a² + b².

18.(A) Since an octagon has eight sides, Quantity B is 8x.

Quantity A: By KEY FACT J10, the hypotenuse of the triangle is 4x, and the longer leg is 2x. So the perimeter is 2x + 4x + 2x. Since > 1, then

2x + 4x + 2x > 2x + 4x + 2x = 8x.

19.(A) The perimeter of a rectangle of area 50 can be as large as we like, but the least it can be is when the rectangle is a square. In that case, each side is 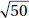, which is greater than 7, and so the perimeter is greater than 28.

20.(C) TR is a transversal cutting the parallel sides PQ and RS. So b = x and 2b = 2x. But since the opposite angles of a parallelogram are equal, a = 2x. So a = 2b.

1.(D) A = πr² = 100π ⇒ r² = 100 ⇒ r = 10 ⇒ C = 2πr = 2π(10) = 20π

2.(A)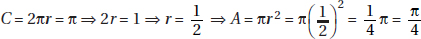

3.(B) Draw a diagram.

Since the area of square ABCD is 2, AD = .

Then diameter EF = and radius 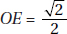. Then the area of the circle is .

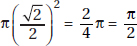4.(C) Draw a diagram.

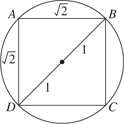
Since the area of square ABCD is 2, AD = . Then, since ABD is an isosceles right triangle, diagonal BD = × = 2.

But BD is also a diameter of the circle. So the diameter is 2 and the radius is 1. Therefore, the area is π(1)² = π.

5.6.5 Draw a diagram.

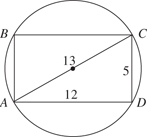
By the Pythagorean theorem (or by recognizing a 5-12-13 triangle), we see that diagonal AC is 13. But AC is also a diameter of the circle, so the diameter is 13 and the radius is 6.5.

6.(D) Since the shaded area is 85% of the circle, the white area is 15% of the circle. So, w is 15% of 360°: 0.15 × 360 = 54.

7.(B) Since C = aπ = bπ = A, we have 2πr = πr² ⇒ 2r = r² ⇒ r = 2.

8.(C) The length of arc RS is 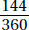of the circumference:

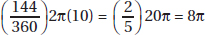
9.(E) The area of the shaded sector is 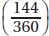of the area of the circle:

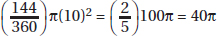
10.54 Since two of the sides are radii of the circles, the triangle is isosceles. So the unmarked angle is also x:

180 = 72 + 2x ⇒ 2x = 108 ⇒ x = 54

11.(A)

12.(D) If the area of the square is 4, each side is 2, and the length of a diagonal is 2. The area of a circle whose radius is 2 is π(2)² = 8π.

13.(B) There’s nothing to calculate here. Each arc of the circle is clearly longer than the corresponding chord, which is a side of the pentagon. So the circumference, which is the sum of all the arcs, is greater than the perimeter, which is the sum of all the chords.

14.(D)

If r = 2, the quantities are equal; otherwise, they’re not.

15.(B) Quantity A: A = π(2)² = 4π.

Quantity B: The area of a semicircle of radius 3 is 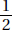π(3)² = 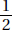(9π) = 4.5π.

16.(A) By KEY FACT L4, 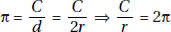, which is greater than 6.

17.(B) The area of sector A is .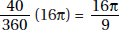

The area of sector B is .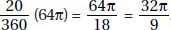

So sector B is twice as big as sector A.

18.(C) Since the triangles are equilateral, the two white central angles each measure 60°, and their sum is 120°. So the white area is 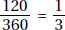of the circle, and the shaded area is 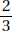of the circle. The area of the circle is π(3)² = 9π, so the shaded area is .

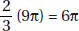19.(C) Since BC = 12, the diameter of each circle in Figure 1 is 6, and so the radius of each circle is 3. So the area of each circle is 9π, and the total area of the 4 circles is 36π. Since FG = 12, the diameter of each circle in Figure 2 is 4, and so the radius of each circle is 2. So the area of each circle is 4π, and the total area of the 9 circles is 36π. Since both squares have sides of 12, their areas are equal, and since their white areas are equal, so are their shaded areas.

20.(A) Let A represent the area of the square and the circle.

1.(A) Since a cube has 12 edges, we have . Therefore, .

2.125 Since the surface area is 150, each of the 6 faces is a square whose area is 150 ÷ 6 = 25. So the edges are all 5, and the volume is 5³ = 125.

3.(C) Since the volume of the cube is 64, we have e³ = 64 ⇒ e = 4. The surface area is 6e² = 6 × 16 = 96.

4.(E) The volume of a cube whose edges are 1 foot can be expressed in either of two ways:

5.(C) The volume of the tank is 3 × 4 × 5 = 60 cubic units, but the solid cube is taking up 3³ = 27 cubic units. Therefore, the tank can hold 60 – 27 = 33 cubic units of water.

6.(E) Draw a diagram and label it.

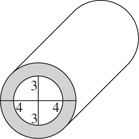
Since the surface of a cylinder is given by A = 2πrh, the area of the exterior is 2π(4)(5) = 40π, and the area of the interior is 2π(3)(5) = 30π. The area of each shaded end is the area of the outer circle minus the area of the inner circle: 16π – 9π = 7π, so the total surface area is

40π + 30π + 7π + 7π = 84π ⇒ k = 84

7.(A) Since the volumes are equal, πr²h = e³ = h³.

Therefore, .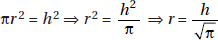

8.(B) Draw a diagram.

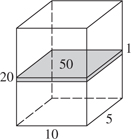
Since the area of the base is 5 × 10 = 50 square centimeters, each 1 centimeter of depth has a volume of 50 cubic centimeters. Therefore, 325 cubic centimeters will raise the water level 325 ÷ 50 = 6.5 centimeters.

(Note that we didn’t use the fact that the tank was half full, except to be sure that the tank didn’t overflow. Since the tank was half full, the water was 10 centimeters deep, and the water level could rise by 6.5 centimeters. Had the tank been three-fourths full, the water would have been 15 centimeters deep and the extra water would have caused the level to rise 5 centimeters, filling the tank; the rest of the water would have spilled out.)

9.(A) Since V = πr²h, we need to express r and h in terms of C. It is given that h = 4C and since C = 2πr, then 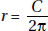. Therefore, .

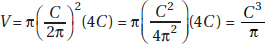10.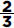 To avoid using r, assume that the radii of the spheres and the can are 1. Then the volume of each ball is 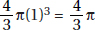, and the total volume of the 3 balls is 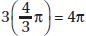. Since the height of the can is 6 (the diameter of each sphere is 2), the volume of the can is π(1)²(6) = 6π. So the balls take up of the can.

11.(A) Drawing a diagram makes it easier to visualize the problem. The volume of a cylinder is πr²h. In each case, we know the height but have to determine the radius in order to calculate the volume.

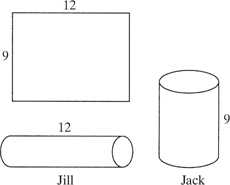
Jack’s cylinder has a circumference of 12:

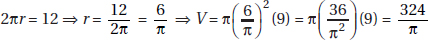
Jill’s cylinder has a circumference of 9:

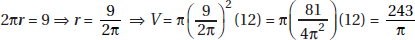
12.(A) Quantity A: V = 6³ = 216. Quantity B: V = 5 × 6 × 7 = 210.

13.(D) There is no relationship between the two quantities. If the box is a cube of edge 1, A = 6 and V = 1. If the box is a cube of edge 10, A = 600 and V = 1,000.

14.(B) The base, AB, of ABP is 1. Since the diagonal is the longest line segment in the cube, the height, h, of the triangle is definitely less than the diagonal, which is .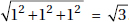

So the area of the triangle is less than 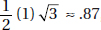, which is less than 1.

(You could also have just calculated the area: 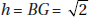, so the area is .)

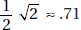15.(A) You probably don’t know how to find the volume of a sphere; fortunately, you don’t need to. You should be able to visualize that the sphere is much bigger than the cube. (In fact, it is more than 4 times the size.)

1. If you sketch the line, you see immediately that the slope of the line is positive. Without even knowing the slope formula, therefore, you can eliminate Choices A, B, and C. To determine the actual slope, use the formula: .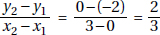

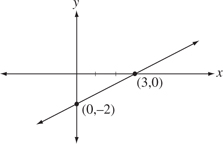
2.(C) Sketch the triangle, and then calculate the slopes.

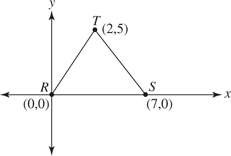
Since RS is horizontal, its slope is 0.

The slope of RT = 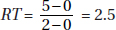. The slope of .

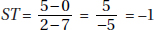Now add: 0 + 2.5 + (–1) = 1.5

3.(C) Draw a diagram and label it. The area of square ABCD is s², where s = AB, the length of a side. By the Pythagorean theorem:

s² = 2² + 4² = 4 + 16 = 20

4.(D) Since the line segment joining (3, 3) and (0, 0) is a radius of the circle, r² = 3² + 3² = 18. Therefore, area = πr² = 18π ⇒ k = 18. Note that you do not actually have to find that the value of r is .

5.(D) Draw a diagram. Any point whose x-coordinate is 2 or 8 could be another vertex. Of the choices, only (–2, 8) is not possible.

6.(D) Draw a diagram. The radius of the circle is 10 (since it’s the hypotenuse of a 6-8-10 right triangle). Which of the choices are 10 units from (6, 8)? First, check the easy ones: (–4, 8) and (16, 8) are 10 units to the left and right of (6, 8), and (6, –2) is 10 units below. What remains is to check (12, 0), which works, and (–2, 12), which doesn’t.

Here is the diagram for solutions 7 and 8.

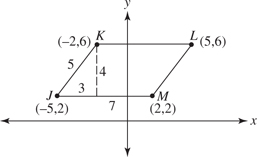
7.(B) The base is 7 and the height is 4. So, the area is 7 × 4 = 28.

8.24 Sides JM and KL are each 7, and sides JK and LM are each the hypotenuse of a 3-4-5 right triangle, so they are 5. The perimeter is 2(7 + 5) = 24.

9.(A) The formula for the slope is , but before using it, look.

Since the y-coordinates are equal and the x-coordinates are not equal, the numerator is 0 and the denominator is not 0. So the value of the fraction is 0.

10.(E) The slope is equal to .

So a – c = 4c and a = 5c.

11.(D) If the sides of the square are horizontal and vertical, then m is 1 or –1, and m² is 1. But the square could be positioned any place, and the slope of a diagonal could be any number.

12.(A) Line , which goes through (0, 0) and (1, 1), also goes through (a, a), and since (a, b) is below (a, a), b < a. Therefore, a – b is positive. Quantity A is greater.

13.(A) The line going through (–3, 3) and (0, 0) has slope –1. Since l is steeper, its slope is a number such as –2 or –3; since k is less steep, its slope is a number such as –0.5 or –0.3. Therefore, the slope of k is greater.

14.(A) Since (a, b) is on the y-axis, a = 0; and since (c, d) is on the x-axis, d = 0.

Then by the slope formula, .

Since b and c are both positive, b < c.

15.(C) Draw a diagram.

Since the distance between the two points is 10, by the distance formula:

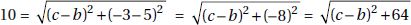
Squaring both sides gives 100 = (c – b)² + 64 ⇒ (c – b)² = 36. So c – b = 6.

Notice that the equation 100 = (c – b)² + 64 is exactly what you could have gotten immediately by using the Pythagorean theorem: 10² = (c – b)² + 8².

1.(C) Alyssa completed 20 – 6 + 1 = 15 exercises in 30 minutes, which is a rate of 1 exercise every 2 minutes. Therefore, to complete 57 – 29 + 1 = 29 exercises would take her 58 minutes.

2.(D) You can choose your soup or salad in any of 5 ways, your beverage in any of 2 ways, your sandwich in 7 ways, and your dessert in 8 ways. The counting principle says to multiply: 5 × 2 × 7 × 8 = 560. (Note that if you got soup and a salad, then instead of 5 choices for the first course there would have been 2 × 3 = 6 choices for the first two courses.)

3.(B) His last birthday was in October 1968, when he turned 78: 1968 – 1890 = 78.

4.500 The easiest way to solve this problem is to use the counting principle. The first digit can be chosen in any of 4 ways (2, 4, 6, 8), whereas the second, third, and fourth digits can be chosen in any of 5 ways (0, 2, 4, 6, 8). Therefore, the total number of four-digit numbers all of whose digits are even is 4 × 5 × 5 × 5 = 500.

5.(E) If there were no month in which at least 3 students had a birthday, then each month would have the birthdays of at most 2 students. But that’s not possible. Even if there were 2 birthdays in January, 2 in February, ..., and 2 in December, that would account for only 24 students. It is guaranteed that with more than 24 students, at least one month will have 3 or more birthdays. The probability is 1.

6.(B) A = {2, 3, 5} and B = {1, 3, 5}. Any of the 3 numbers in A could be added to any of the 3 numbers in B, so there are 9 sums that could be formed. However, there could be some duplication. List the sums systematically; first add 1 to each number in A, then 3, and then 5: 3, 4, 6; 5, 6, 10; 7, 8, 10. There are 7 different sums.

7.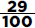 There are 67 – 37 – 1 = 29 people between Aviva and Naomi, so, the probability that one of them is chosen is .

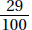8.(D) It is equally likely that any one of the 5 marbles will be the one that is not removed. So, the probability that the yellow one is left is 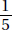and the probability that it is removed is .

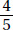9.(D) This is the counting principle at work. Each day Josh has four jobs to do: choose 1 of the 10 doors to enter and 1 of the 9 other doors to exit; choose 1 of the 8 staircases to go up and 1 of the other 7 to come down. This can be done in 10 × 9 × 8 × 7 = 5,040 ways. So on each of 5,040 days Josh could choose a different path.

10.(E) In a problem like this the easiest thing to do is to see what could go wrong in your attempt to get 2 marbles of each color. If you were really unlucky, you might remove 10 blue ones in a row, followed by all 6 white ones. At that point you would have 16 marbles, and you still wouldn’t have even 1 red one. The next 2 marbles, however, must both be red. The answer is 18.

11.(A) It may help to draw a line and label it:

From the n people who tried out, subtract the k people who went before Judy and the m people who went after Liz, and then subtract 2 more (for Judy and Liz). The number of people to try out between Judy and Liz was n – k – m – 2 = n – m – k – 2.

12.(E) Draw a Venn diagram, letting x be the number of students who are on the team and in the club.

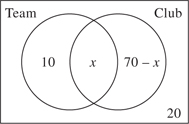
Of the 100 students, 70 are in the club, so 30 are not in the club. Of these 30, 20 are also not on the team, so 10 are on the team but not in the club.

Since more students are on the team than in the club, 10 + x > 70 ⇒ x > 60. Since x must be an integer, the least it can be is 61.

13.180 There are two possibilities: we can choose two boys and three girls or three boys and two girls.

By the counting principle, the number of ways of choosing two boys and three girls is

(the number of ways of choosing 2 of the 4 boys) times
(the number of ways of choosing 3 of the 6 girls):

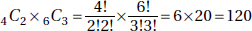
Similarly, the number of ways of choosing three boys and two girls is

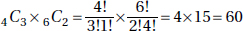
The total number of ways to choose the five children is 120 + 60 = 180.

14.(C) The region labeled x contains all of the primes less than 20 that do not contain the digit 7. They are 2, 3, 5, 11, 13, 19.

15.84 Region y consists of primes that contain the digit 7 and are greater than 20. There are two of them that are less than 50: 37 and 47. Their sum is 84.

16.(C) Don’t calculate the probabilities. The probability of no heads is equal to the probability of no tails; but no tails means all heads.

17.(B) The simplest solution is to notice that whatever color the first marble is, there is only 1 more marble of that color, but there are 2 of the other color, so it is twice as likely that the marbles will be of different colors.

18.(C) By the counting principle, Quantity A is 5·4·3·2 and Quantity B is 5·4·3·2·1. Clearly, the quantities are equal.

19.(C) Quantity A is ₁₀C₄ and Quantity B is ₁₀C₆. Since ₁₀C₄ = ₁₀C₆, the quantities are equal.

20.(A) Every prime between 100 and 199 is odd (the only even prime is 2). So Quantity A is 1, which is greater than .99.

1.(D) {a_n} and {b_n} are arithmetic sequences whose common differences are 3 and –3, respectively. Sequence II is an arithmetic sequence whose common difference is –3.

a₁₆ = 10 + 15(3) = 10 + 45 = 55

b₁₆ = 100 + 15(–3) = 100 – 45 = 55

a₁₆ + b₁₆ = 55 + 55 = 110.

2.(A) Use your calculator to divide: 15 ÷ 37 = 0.405405405. So the question is equivalent to asking, “What is the 500th term in the repeating sequence 4, 0, 5, 4, 0, 5, 4, 0, 5, ... ?” Since there are 3 terms in the repeating portion, divide 500 by 3:

500 ÷ 3 = 166.66 ⇒ the quotient is 166

166 × 3 = 498 ⇒ the remainder is 500 – 498 = 2

So the 500th term was the same as the second term: 0.

3.(B) July 4, 2011 was exactly 2 years = 2 × 365 = 730 days after July 4, 2009. The days of the week form a repeating sequence in which 7 terms repeat.

730 ÷ 7 = 104.2857... ⇒ the quotient is 104

104 × 7 = 728 ⇒ the remainder is 730 – 728 = 2

So 730 days after a Saturday will always be the same day as 2 days after a Saturday, namely Monday.

4.(E) Every 20 minutes, the number of bacteria present is muliplied by a factor of 1.2. This creates a geometric sequence whose first term is 1,000 and whose common ratio is 1.2:

1,000, 1,200, 1,440, 1,728, ...

The 12 hours from noon to midnight consist of 36 20-minute intervals. So the number of bacteria at midnight is

1,000 × (1.2)³⁶ = 1,000(708.8) = 708,800 ≈ 709,000

5.(D) Since the pattern repeats itself after every 15 gum balls, divide 1,000 by 15. The quotient is 66, and the remainder is 10. Therefore, the 1,000th gum ball is the same color as the 10th gum ball, which is yellow.

6.(E) Since a_n = a₁ + (n – 1)d, we have

57 = a₂₁ = a₁ + 20d

227 = a₈₉ = a₁ + 88d

Subtracting the first equation from the second yields

170 = 68d ⇒ d = 2.5

So 57 = a₁ + 20(2.5) = a₁ + 50 ⇒ a₁ = 7.

Finally, a₃₃₃, the 333rd term, is

7 + 332(2.5) = 7 + 830 = 837

Section 1—Analytical Writing

PROMPT #1

“We venerate loyalty—to our schools, employers, institutions, friends—as a virtue. Loyalty, however, can be at least as detrimental an influence as it can be a beneficial one.”

Compose an essay that identifies how greatly you concur (or differ) with the statement provided, describing in detail the rationale for your argument. As you build and provide evidence for your argument, include examples that demonstrate circumstances in which the statement could (or could not) be valid. Be sure to explain the impact these examples have on your argument.

SCORE 6 ISSUE ESSAY

In press coverage of the epidemic of violence in some urban area like Chicago, there is frequent reference to a “Code of the Streets” that counsels residents, “don’t be a snitch.” Law enforcement officials decry this loyalty as misguided and ultimately harmful, agreeing with those who argue that loyalty “can be as detrimental an influence as it can be a beneficial one.” They are, of course, correct. Loyalty can be detrimental. Their error comes in failing to recognize that this observation applies to themselves as much as it does to the members of the community whose silence they criticize.

The “Code of the Streets” has an analog in the “Blue Code of Silence” that places loyalty to fellow police officers, right or wrong, above the interests and safety of the community. News stories abound with examples of incidents in which police officers describe events one way, only to have their stories contradicted by video evidence. It is not surprising that police officers who have behaved improperly might stretch the truth, or even concoct stories out of whole cloth, in order to avoid being held responsible for their actions. The actions of lawless police officers are a serious problem, but the loyalty of their brothers and sisters in blue is even more detrimental. The inability of the majority of law-abiding police officers to speak out against the misconduct of so-called bad apples undermines the legitimacy of law enforcement as a whole in many of the communities that need its help the most.

Though the “Code of the Streets” and the “Blue Code of Silence” demonstrate that loyalty can be detrimental, the solution is not to embrace disloyalty. It is, after all, difficult to imagine how valuing betrayal could lead to better consequences. The problem in these instances is not really loyalty per se, but a mistaken understanding of community. So long as police officers and members of the public feel that they are not members of one community, their loyalty will be misguided, focused on protecting their own (be they police officers or civilians) from threatening and lawless others (be they police officers or civilians). If we could break down this divide and accept that we are all members of the same community, our loyalty to that greater community would shatter both the “Code of the Streets” and the “Blue Code of Silence.” When we learn to embrace our historic enemies as members of a single human community, rather than combatants from warring factions, loyalty will be a venerable virtue. Until that distant day, it will remain, as often as not, an abhorrent vice.

ARGUMENT The essay presents a clear and perceptive argument that loyalty can be as detrimental as it is beneficial. The writer does an especially good job of presenting instances in which loyalty can have consequences that fracture communities and threaten public safety. The argument is also quite sophisticated, proposing an additional factor that may cause loyalty to be harmful and suggesting that, absent that reason, loyalty might be a virtue.

SUPPORT The essay includes two strong examples of groups whose loyalty to their members does great harm to the larger community, though it focuses more deeply on a single group—police officers.

STRUCTURE The essay is well focused and does not stray from the task of proving its thesis. Its organization is clear, and transitions between paragraphs are logical.

FLUENCY The essay displays sophisticated and powerful vocabulary. Its sentence structure is varied throughout.

CONVENTIONS Outstanding. The essay includes no noticeable errors in grammar, usage, or mechanics.

SCORE 5 ISSUE ESSAY

Loyalty is considered a virtue in our culture, but where is the breaking point at which one decides that loyalty does more damage than good? Can loyalty be more detrimental than beneficial?

Recently, professional football player Colin Kaepernick came under fire from patriotic Americans for his decision to “take a knee” when the national anthem is played at NFL football games. Kaepernick cited the number of African-Americans killed by police as one of many examples that the United States does not value the lives of its African-American citizens. He questioned why he should demonstrate loyalty or patriotism to a country that treats some people as second-class citizens. Across America—especially on the internet—pundits, both professional and amateur, weighed in on the subject. Even among those who claimed to agree with his motivation, many took the stance that he was somehow still protesting in the “wrong” way. “He can be upset,” they said, “but he’s being unpatriotic, disrespectful, disloyal.” Loyalty to country was seen as a virtue, and criticism, as un-American.

Interestingly enough, loyalty as a fan also became part of the debate around Kaepernick’s protest. If Kaep’s team, the 49ers, is “your” team, are you allowed to break ranks with them in protest of his disloyalty? Does that make you a fair-weather fan? Is it fair to the other players on the team if you, as a fan, jump ship because one player is doing something you don’t like? Of course, if loyalty is hierarchical, loyalty to country must outweigh loyalty to team. The order of importance is God, country, family, and football (though some fans disagree with the order of the last two). This is the American way.

Or is it?

If a hallmark of American citizenship is freedom, is loyalty in the form of patriotism a virtue? Loyalty to our country, especially post-September 11, can be seen as a form of collective strength. But does blind allegiance to an ideal vision of what America could and should be require that we turn a blind eye to what America is? In other areas of life, we know that pretending that toxic behavior and attitudes are acceptable simply because we are loyal to those who engage in such behaviors cannot only be harmful to ourselves, but also to the perpetrator. Why isn’t the same true of loyalty to country? If your child’s school was harming children, would you allow it to continue out of loyalty to the institution? Or would your loyalty to the school end the second someone’s child was in danger? Why, then, do we not have the same standard for the ill treatment of adults? If an institution is abusive, must we remain loyal despite the abuse because it could be worse elsewhere? Is “America—love it or leave it” the only acceptable response when our country fails to live up to its lofty goals? Is this a standard of loyalty we would live by when it came to any subject other than patriotism?

The answer to this question is clearly no. Loyalty can clearly be detrimental in so many circumstances. We would never stand by and let a teacher abuse students because of loyalty to the school. When Penn State was found guilty of covering up an employee’s sexual abuse of children, the public was rightly horrified at the behavior of the individuals who knew about the abuse but remained silent as a result of their loyalty to the institution. Similarly, we do not expect victims of spousal abuse to remain with their abusers. We counsel them that their abusers do not deserve their loyalty, and that they must inform the authorities of their situation. We encourage them to testify against their abusers in court so that justice can be done. It is high time that we recognize that our country too can do wrong, and that it must be corrected and held accountable when it does so. Turning a blind eye to our nation’s failures out of loyalty is harmful and wrong. When we see our nation behave unjustly, we should “take a knee” with Colin Kaepernick.

ARGUMENT The essay presents a clear and thoughtful argument that loyalty, even loyalty to country, can be detrimental.

SUPPORT The essay includes compelling examples that provide strong support for its thesis. The Penn State example is especially persuasive, demonstrating terrible consequences of remaining silent out of loyalty to an institution. The Colin Kaepernick example is engaging, while also demonstrating the complexity of choosing to criticize one’s country.

STRUCTURE The essay is generally well focused, though the Kaepernick/49ers story at the start runs a bit long, slightly obscuring the essay’s thesis. Transitions between paragraphs are logical, and the thesis becomes crystal clear in the final paragraph.

FLUENCY The ideas in the essay are clear, and its vocabulary use is appropriate and effective, if a bit colloquial at times. Sentence structure is varied.

CONVENTIONS The essay demonstrates solid command of the grammar, usage, and mechanics of standard written English. There are few, if any, obvious errors.

SCORE 4 ISSUE ESSAY

I agree that loyalty is detrimental, especially blind loyalty.  Loyalty should be conditional upon the other institution or person meeting certain standards.  Loyalty is a virtue in that it is indicative of the faith that one person holds in the other.  However, this faith should not be given without inhibition, but should be given on a merit basis.

I think blindly pledging loyalty to a political party can be detrimental. In pre-World War II Germany, Adolf Hitler’s militant Nazism and charisma gained him a large following—large enough to place him at the head of Germany at the time and allowed him to lead the country to commit atrocious horrors upon Jews, homosexuals, the disabled, and other minorities not fitting into his vision for what Germany should look like. If people weren’t so ready to blindly pledge loyalty but were more autonomous, perhaps concentration camps wouldn’t have occurred, or perhaps not on the scale that they did.

Blindly giving loyalty to an employer can also have a dangerous outcome. Say, for example, there is a factory and the company running the factory knows of safety hazards, but doesn’t report them to avoid the cost of fixing the safety hazards.  The employees see the safety hazards too, but don’t report them because of company loyalty.  Worst-case scenario is that there could be a serious injury or worse if the danger goes unreported. This would all be because people were too loyal to go over the company’s head and do something about the concern.

There are nevertheless benefits of loyalty. It can be good to feel as if you can rely on someone, and likewise for them be able to rely on you. It makes things predictable in that you know how things will run, assuming conditions run their course. However, that is not how it always is—sometimes events blindside us. For these unplanned and uncharacteristic events, loyalty not only can be, but should be, questioned. If a large enough and horrendous enough crime were committed by my friend, I definitely would question my loyalty to him or her.  If I, however, decided instead to protect my guilty friend and hide this person, not only would I be obstructing justice (a crime unto itself) but I would also be hurting society by allowing a crime like this to go unpunished.

Loyalty is detrimental when it is blind and its continual questioning is beneficial to society.

ARGUMENT The essay presents a clear argument that misplaced loyalty can lead to devastating consequences. Though the analysis could be more sophisticated, it admits some complexity to the issue, granting that loyalty can provide comfort and reliability.

SUPPORT The essay includes two strong examples that provide strong support for its thesis. The third, contrasting example (the friend who commits a crime) is a bit muddled and underdeveloped.

STRUCTURE The essay is reasonably well focused, though the transitions between paragraphs are abrupt. The conclusion is too short, and fails to adequately summarize the essay’s arguments.

FLUENCY The ideas in the essay are clear, and its vocabulary use is generally appropriate, with a few distracting errors. The essay sounds awkward in places, but it is generally effective despite this.

CONVENTIONS The essay demonstrates adequate command of the grammar, usage, and mechanics of standard written English. There are several minor errors, but not enough to obscure meaning.

PROMPT #2

The following appeared in a petition presented by Classen University students to the school’s administration.

“The purpose of higher education is to prepare students for the future, but Classen students are at a serious disadvantage in the competition for post-college employment due to the University’s burdensome breadth requirements. Classen’s job placement rate is substantially lower than placement rates of many top-ranked schools. Classen students would be more attractive to employers if they had more time to take advanced courses in their specialty, rather than being required to spend fifteen percent of their time at Classen taking courses outside of their subject area. We demand, therefore, that the University abandon or drastically cut back on its breadth requirements.”

Compose an essay that identifies the questions that must be answered before reaching a conclusion about whether the prediction and the argument supporting it make sense. In writing your essay you should describe the impact that the answers to these questions would have on your assessment of the prediction.

SCORE 6 ARGUMENT ESSAY

As the technology sector of the US economy has burgeoned, the argument for increasing education in STEM subjects (Science, Technology, Engineering, and Math) and consequently decreasing time spent on the Humanities has grown popular. The students at Classen University echo this argument (that education should focus on preparing workers to meet the needs of the economy) in their petition demanding a decrease in the University’s breadth requirements. Though their argument is a popular one, it is grounded on a number of questionable premises that bear further examination.

The Classen students start off on the wrong foot by making the unsubstantiated claim that “the purpose of higher education is to prepare students for the future.” But is preparing students for the future truly higher education’s sole purpose? If Classen’s petitioning students are wrong about the answer to this question, their claim is flawed from the outset. While it is unarguable that preparing students for the future is a purpose of higher education, there is no consensus on a single, overriding purpose. Additionally, even if the students are correct that preparation for the future is the primary purpose of higher education, their focus on career preparation and employment is based on a very narrow view of that future. During the course of their lives these students will be citizens, community members, parents, and friends, not just workers. Perhaps a university education could and should prepare students for these roles as well.

Granting, for the sake of argument, that the purpose of higher education is to prepare students for employment, the students’ case for decreasing breadth requirements is still weak because it fails to answer several additional important questions. The first among these is whether the top-ranked schools to which they compare Classen actually have fewer breadth requirements than Classen. If they do not, there is little reason to believe that decreasing Classen’s breadth requirements will, in fact, improve the job placement rate of its graduates.

Another crucial question that remains unanswered by the students’ petition is whether the demographics of the student body at Classen are similar to those of the student population of the top-ranked schools to which Classen is being compared. Are Classen’s students as academically strong as those at these unnamed schools? Does Classen have a greater number of students for whom English is not their first language? Does Classen serve a student population with an unusually high percentage of students who are the first in their families to attend college? Do the students at the top-ranked schools come from wealthier families than do those at Classen? Because these factors all influence student success both in school and after graduation, answering the aforementioned questions is essential to evaluating whether Classen is indeed doing a poor job of preparing its graduates for employment.

Finally, even if the students are correct that Classen is doing a poor job of preparing its graduates for employment, it is not clear that decreasing breadth requirements is the solution to this problem. The students assert that graduates “would be more attractive to employers if they had more time to take advanced courses in their specialty,” but they offer no evidence for this claim. What are employers looking for in potential employees? This question must be answered before an effective solution to the low job placement rate of Classen graduates can be crafted. If employers want to hire graduates with work experience, the solution may lie in a summer internship program. If they want employees with substantial advanced coursework in their specialty, the students’ proposal may be sound. But if they require employees with a broad range of knowledge and the ability to attack problems flexibly and take different perspectives into account, more, rather than fewer, breadth requirements may be in order.

ARGUMENT The essay successfully pinpoints a number of problematic elements in the provided argument, explaining how its strength depends on the answers to several unanswered questions. The essay explicitly and thoughtfully describes the impact that these answers would have on the reliability of the students’ argument.

SUPPORT The essay provides detailed and persuasive support for its main points, introducing a number of rival factors that might explain the poor job placement rate of Classen University students.

STRUCTURE The essay is well organized, expressing its position clearly and in a logicalprogression. Transitions between ideas are well executed, and the essay builds to a strong conclusion, suggesting that the best solution to Classen students’ poor employment results may be the inverse of the plan advocated by the students.

FLUENCY The essay reads smoothly and uses sophisticated vocabulary. Sentence structure is varied.

CONVENTIONS Outstanding. The essay includes no noticeable errors in grammar, usage, or mechanics.

SCORE 5 ARGUMENT ESSAY

Classen students have presented a demand to their administration that breadth requirements be either drastically reduced or eliminated. In considering this demand, the University must evaluate two main points. First, do the students demonstrate an understanding of the purpose of a University education and know where breadth requirements fit into this purpose? Second, do the students make a clear case that the disadvantages that they attribute to the breadth requirements are in fact the sole reason for their lower job placement rates, and upon what do they base this case? Only with this information can the administration make a reasoned decision about whether to reduce or remove breadth requirements.

The students’ assertion that “higher education is to prepare students for the future” is arguably a given. However, their definition of preparation for the future seems to be limited solely to job placement. However, while the university has a role to play in preparing for the work force, career preparation is not the sole purpose of higher education, and I suspect that nowhere in the mission statement of the school does the University state that its main focus is job training. Scholarship is important, both to individuals and to the greater culture. If it were not so, we could simply send students to various trade schools. While undergraduates should have opportunities to take advanced coursework in their fields, as the students assert, graduate school is the place to focus more intently on a particular field. While it may be frustrating for students to wade through other requirements before getting to that point, their frustration does not warrant scrapping the entire system.

Furthermore, the students have not considered or addressed the reality that breadth requirements are often instituted by schools because of feedback from employers—directly and culturally—that students are not socially or intellectually prepared for adult life. In other words, just as colleges admit students not solely on the basis of one skill or talent, so too do employers want employees with life skills, critical thinking skills, and other analytical skills in addition to the practical skills in their fields. Breadth requirements actually prepare students to do advanced work in their fields, by helping them learn how to learn, learn how to negotiate subjects with which they may be less familiar, and learn how to work with others whose strengths and interests lie in different areas than their own.

Even assuming that it’s true that job placement is the sole goal of a college education (it isn’t), the students have shown no evidence that Classen’s lower job placement rate is the fault of breadth requirements. They are vague about “many top-ranked schools,” without citing those schools, their course requirements, or their job placement rates. Perhaps the schools are top-ranked for other reasons, and those reasons are part of employers’ motivation for hiring the students. In fact, what if some of the schools with higher job placement rates actually have more broad requirements? What if the very reason their graduates do better in the workforce is precisely because they experienced varied subject matter, teaching styles, and skills practice than do students who focus more exclusively within their own fields?

The simplicity of the Classen students’ demands is actually exemplary of precisely why they need breadth requirements in the first place. Correlation is not causation (science classes teach that); their thesis is flawed (English classes teach that); the market needs varied skills (economics classes teach that); and their lack of understanding of greater socio-cultural influences on education means they are not considering the full extent of their demands (sociology classes teach that). Their demand statement is Freshman 101 level; they cannot use it to argue against the existence of Freshman 101 when they haven’t passed the course yet.

ARGUMENT The essay successfully pinpoints two questions that must be answered in order to assess the argument in the Classen students’ petition, and it evaluates their impact thoughtfully. If there is any weakness here it is only that the essay focuses somewhat more on the views of its author than it does on how different answers to the questions posed might lead to different conclusions about the strength of the students’ argument.

SUPPORT The essay provides detailed support for its main points, especially in its exploration of other factors that might be driving Classen students’ low job placement rate.

STRUCTURE The essay is well organized, with effective transitions between ideas. It could, however, be a bit clearer about which of the two questions it is addressing in each paragraph.

FLUENCY The essay expresses its ideas clearly, using appropriate vocabulary and varied sentence structure.

CONVENTIONS The essay displays solid command of the conventions of standard written English.

SCORE 4 ARGUMENT ESSAY

I disagree with this petition. I think that a well-rounded education is a beneficial one. When young, it is difficult to know what you want to do and having a requirement to take different classes in different disciplines can be good to allow students the opportunity to explore different disciplines. Furthermore, there are many factors at play for job placement and classes don’t necessarily play that large of a part in that measurement. In addition, job placement isn’t necessarily the only reason that people go to college.

First of all, taking different classes allows students to explore different topics of interest, all while fulfilling degree requirements. This is very beneficial to ensure that they truly do like what they plan to study for four years in the process of obtaining a bachelor’s degree. Also, it is only fifteen percent of the classes, and that is less than a fifth so it is a very small percentage of classes that this petition is referring to.

Moreover, there are plenty of factors at play for getting jobs—classes just being one. We need to ask what factors are important in getting jobs to understand whether decreasing breadth requirements can help. There is a saying that “life isn’t what you know but who you know,” and there is definitely some truth to that. Networking is a very important skill that can’t be learned in a class but is more taught through life. Furthermore, the petition is comparing job placements to other, larger and more prestigious universities where there are presumably larger budgets, more resources, and a more competitive student pool. All of these factors can change job placement rates. For example, larger and more prestigious companies might tend to prefer to higher from more prestigious universities. Though it’s obviously not impossible to get positions at these firms, attending certain universities can arguably provide “leg up” to some individual students applying for certain positions at certain firms, thus affecting the job placement rates.

In addition, the petition begins with, “[the] purpose of higher education is to prepare students for the future,” and I completely agree with this statement, but I measure future preparation in a different way. Preparedness for the future can’t be quantitately measured through percentage of students landing jobs, or even how long these students last at these companies. Instead, being prepared for the future has more of a qualitative essence—it can’t be measured through numerical evidence but is demonstrated by happiness and ability for students to meet any problems and struggles that life throws at them.

ARGUMENT The essay identifies and evaluates many elements of the argument provided, but its examination of questions that would need to be answered in order to evaluate the argument could be better. Only one of the essay’s four paragraphs examines these questions, which are the main requirement of the task instructions.

SUPPORT The essay provides thoughtful and persuasive support for its main points.

STRUCTURE The essay expresses its ideas clearly and has adequate transitions (using words like “first of all” and “in addition.” Despite this, the order in which the essay presents its points appears somewhat random, and the conclusion is abrupt.

FLUENCY The essay generally uses vocabulary effectively to express its ideas.

CONVENTIONS The essay generally displays command of the conventions of standard written English, despite the presence of a few minor errors that do not interfere with meaning.

Section 2—Verbal Reasoning

1. (B, F) The verbs estrange and disaffect are synonyms; both mean to make unfriendly or to distance. The two words can be used interchangeably here. Think of “estranged couples” getting a divorce and “disaffected voters” leaving a political party.

2. (C, F) Baseball metaphors are examples of Americanisms, American idioms enthusiastically embraced by Britons despite the British lack of understanding of the original context of these terms. The Britons are hooked on or enamored of them.

3. (A, D) A contrarian is someone who takes a contrary view or action, one who makes decisions that contradict prevailing wisdom. Because he is a contrarian, the general is resolved to fight to the bitter end; clearly, the wise or sane course would be to capitulate or submit. Note that submit here is a synonym for yielding or giving in, not for asserting or proposing something.

4. (C, E) If the plan, though tough, is not loving, then it certainly would not be accurate for the White House to describe it as tough love. It would not be particularly witty or salient (strikingly conspicuous) for the White House to do so. It might indeed have been diplomatic (tactful) for the White House to describe the plan as tough love. However, critics of the administration would be unlikely to put such a positive spin on the administration’s description. Also, none of the other choices are synonyms for diplomatic. Only two choices remain: disingenuous and mendacious. To be disingenuous is to be insincere or untruthful. Likewise, to be mendacious is to be untruthful.

5. (A, D) Perfectionists expect perfection of themselves. Therefore, when they make even tiny errors, they feel vexation (annoyance with themselves) and chagrin (annoyance mixed with humiliation).

6. (C) The fact that the writers were more involved with fighting problems in the system than with attacking the system itself suggests that fundamentally they were not opposed to the democratic system of government.

Choice A is incorrect. The fact that the writers did not revolt against the system does not necessarily imply that they played a minor role in fighting abuses of the system.

Choice B is incorrect. There is nothing in the statement that would imply that, left to itself, the system was certain to function efficiently.

Choice D is incorrect. There is nothing in the statement that would imply that in order for the system to operate efficiently, blacks must seize the reins of power in America.

Choice E is incorrect. There is nothing in the statement that would imply that Black writers were too caught up in aesthetic questions to identify the true nature of the conflict.

7. (C) In lines 6–12, the author mentions the growing interest in social and economic problems among the writers of the Harlem Renaissance. They used poetry, prose, and song to cry out against social and economic wrongs. Thus, they transformed their increasing social and political consciousness into art.

Choice A is incorrect. The author distrusts the foreign ideologies (lines 28–34) with their commitment to international solidarity.

Choice B is incorrect. The author states that the writers wished to contribute to American culture; they did not totally reject American society, but wished to improve it.

Choices D and E are incorrect. Neither is implied by the author.

8. (A) The author’s evident concern to distinguish Negro writers from those who “embraced” socialist and communist propaganda (lines 28–34) suggest that he is a historian concerned with presenting these writers as loyal Americans.

Choice B is incorrect. The author touches on literature only in relationship to historical events.

Choices C, D, and E are incorrect. There is nothing in the passage to suggest any of these interpretations.

9. (B) The author makes the point that the writers essentially ignored socialist and communist propaganda. This point is apparently contradicted by the Messenger quote asserting that the same forces that produced socialism and communism produced the New Negro (and thus the new black writer). The author then limits the application of his original assertion by giving only qualified assent to that assertion. (“Such forces may have produced the New Negro.”)

10. (E) Choice E is answerable on the basis of this passage.

The passage cites the battles for better working conditions, desegregation, and social and political equality in which the black writers of the period were engaged. These were specific socioeconomic causes with which the writers associated themselves.

Choice A is unanswerable on the basis of this passage. The passage mentions an “improvement in the capacity for expression” in the period, but cites no factors leading to this stylistic improvement.

Choice B is unanswerable on the basis of this passage. The passage mentions no specific names.

Choice C is unanswerable on the basis of this passage. The passage states the writers did not “embrace the several foreign ideologies that sought to sink their roots” in America. However, it nowhere suggests that the writers were in rebellion against these foreign ideologies.

Choice D is unanswerable on the basis of this passage. No such information is supplied by the passage.

11. (A, D) The author concedes that the big-bang theory has been changed somewhat: it has undergone refinement or polishing. However, he denies that its validity has been threatened seriously by any rival theories: it has resisted or defied all challenges.

The use of the support signal and indicates that the first missing word is similar in meaning to “modification.” The use of the contrast signal but indicates that the second missing word is contrary in meaning to “undergone modification.”

12. (C, D) Someone described as “rigid and conventional” would lack both the flexibility (adaptability) to adjust to changes and the creativity (inventiveness; imagination) to come up with new, innovative ideas.

13. (B, D, H) The phrases “some years after having been lauded” and “his reputation having suffered a decline” provide the key to unlocking this sentence. The subject here is the change in Perugino’s reputation. In the beginning, he received wealth and status, but his fame did not last: he did not win enduring glory. Instead, Michaelangelo derided (ridiculed; mocked) him as an artistic bumpkin (clod; oaf).

14. (B, F) The play Amadeus portrays Joseph II as “wedded to orthodox theories of musical composition.” Thus, it depicts him as a doctrinaire thinker, dogmatic about which theories or doctrines he accepts. This view of Emperor Joseph is in contrast with his image as a reformer whose reign was impressively enlightened (liberal; civilized) for the period. The best way to attack this sentence is to complete the second blank first. Note that the second blank immediately precedes a long descriptive phrase that clarifies what kind of thinker Joseph II was.

15. (B, D, I) The adverb even (indeed) is used here as an intensive to stress something. Not only do fixed poetic forms invite wordiness, they may even encourage it. Because these fixed forms require the poet to write a specific number of lines or syllables, they place a constraint (limitation; restriction) on the poet. Without that constraint, the poet might have an easier time spotting and eliminating unnecessary syllables and words.

16. (E) One would have to disentangle a skein or coiled and twisted bundle of yarn. Note how the presence of the verb disentangle, which may be used both figuratively and literally, influences the writer’s choice of words. In this case, while line is a possible choice, the word does not possess the connotations of twistings and tangled contortions that make skein a more suitable choice.

17. (D) The author opens the paragraph by stating that many literary critics have begun reinterpreting the study of women’s literature. She then goes on to cite individual comments that support her assertion. Clearly, she is receptive or open to the ideas of these writers, for they and she share a common sense of the need to reinterpret their common field.

Choices A and B are incorrect. The author cites the literary critics straightforwardly, presenting their statements as evidence supporting her thesis.

Choice C is incorrect. The author does not disparage or belittle these critics. By quoting them respectfully she implicitly acknowledges their competence.

Choice E is incorrect. The author quotes the critics as acknowledged experts in the field. However, she does not look on these critics with awe (an overwhelming feeling of reverence, admiration, or fear).

18. (B, E) Question B is answerable on the basis of the passage. According to lines 19–20, Ellen Moers “sees women’s literature as an international movement,” in other words, as a movement that transcends national boundaries.

Likewise, Question E is answerable on the basis of the passage. According to lines 9–10, Mill disbelieved in the idea that women “have had a literature of their own all along.”

19. (B) The writer neither lists (enumerates) nor sorts (classifies) anything in the opening paragraph.

Choice A is incorrect. The writer likens the female tradition to a lost continent and develops the metaphor by describing the continent “rising . . . from the sea of English literature.”

Choice C is incorrect. The author refers or alludes to the classical legend of Atlantis.

Choice D is incorrect. The author quotes Colby and Thompson.

Choice E is incorrect. The author contrasts the revised view of women’s literature with Mill’s view.

20. (A, C) The statement that “The rate of population increase has begun to decline in Northern Europe, but the food supply has not diminished” weakens Malthus’s postulate that food supply cannot keep pace with the rate of increase of human population. Likewise, if “[h]uman population growth may be limited by the use of contraception,” then it is possible that increasing the supply of food might not necessarily be followed by an increase in human population.

Section 3—Quantitative Ability

Two asterisks (**) indicate an alternative method of solving.

1. (A) The only positive divisors of 19 are 1 and 19. So, Quantity A equals 1 + 19 = 20, and Quantity B equals 1 × 19 = 19. Quantity A is greater.

2. (A) Since (a, b) is on the positive portion of the x-axis, a is positive and b = 0; so a + b is positive. Also, since (c, d) is on the negative portion of the y-axis, c = 0 and d is negative; so c + d is negative. Quantity A is greater.

3. (D) By the distributive law (KEY FACT A21), Quantity A is 5r + 5t. Subtracting 5r from each of Quantity A and Quantity B, we are left with 5t and t, respectively. So quantities A and B are equal if t = 0 and unequal otherwise. Neither quantity is always greater, and the two quantities are not always equal (D).

4. (A) Quantity A: there are 5 positive multiples of 5 less than 26: 5, 10, 15, 20, 25; their average is 15, the middle one [KEY FACT E5].

Quantity B: there are 3 positive multiples of 7 less than 26: 7, 14, 21; their average is 14.

Quantity A is greater.

5. (B) Since .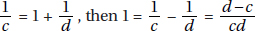

Therefore, d – c = cd, which is positive, since both c and d are. Then, d – c is positive, and so d > c.

Quantity B is greater.

6. (C) The simplest solution is to realize that there is one palindrome between 100 and 109 (101), one between 390 and 399 (393), one between 880 and 889 (888), and in general, one out of every 10 numbers. So the probability is . The answer is (C).

**The more direct solution is to count the number of 3-digit palindromes. Either systematically make a list and notice that there are 10 of them between 100 and 199, and 10 in each of the hundreds from the 100s to the 900s, for a total of 90; or use the counting principle (KEY FACT O2): the hundreds digit can be chosen in any of 9 ways (any of the digits from 1 through 9), the tens digit in any of 10 ways (any of the digits from 0 through 9), and the units digit, since it must match the hundreds digit, can be chosen in only 1 way (9 × 10 × 1 = 90). Since there are 900 three-digit numbers, the probability is .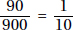

7. (C) Let P = the price of the TV set. Then Jack paid 1.085(.90P), whereas Jill paid .90(1.085P). The quantities are equal (C).

**Use TACTIC 2 in Chapter 10, and choose a convenient number: assume the TV cost $100. Jack paid $90 plus $7.65 tax (8.5% of $90) for a total of $97.65. Jill’s cashier rang up $100 plus $8.50 tax and then deducted $10.85 (10% of $108.50) for a final cost of $97.65.

8. (A) Quantity A: Since ABC is a 45-45-90 right triangle whose hypotenuse is 2, by KEY FACT J8, the length of each leg is , and the area is .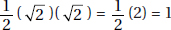

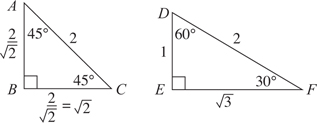
Quantity B: Since DEF is a 30-60-90 right triangle whose hypotenuse is 2, by KEY FACT J11 the shorter leg is 1, the longer leg is , and the area is 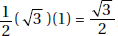, which is less than 1 because is less than 2.

Quantity A is greater.

9. (D) Since 400 = 12 × 33 + 4, 100 months is 4 months more than 33 years. 33 years from June it will again be June, and 4 months later it will be October.

**Look for a pattern. Since there are 12 months in a year, after every 12 months it will again be June; i.e., it will be June after 12, 24, 36, 48, ..., 120, ..., 360 months. So, 396 (33 × 12) months from now, it will again be June. Count 4 more months to October.

10. 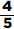Use TACTIC 3 in Chapter 9: pick an easy-to-use number for the number of members of the chorus. Since 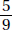of the members are boys, assume there are 9 members, 5 of whom are boys. Then the other 4 are girls, and the ratio of girls to boys is 4 to 5, or .

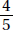11. 27 Since the surface area of the cube is 54, the area of each of the six square faces is: 54 ÷ 6 = 9. Therefore, each edge is 3, and by KEY FACT M1, the volume is 3³ = 27.

12. (A) Use TACTIC 1 in Chapter 8: draw a diagram. See the figure below on the left. Then form rectangle BCDE by drawing DE ⊥ AB, yielding the figure on the right

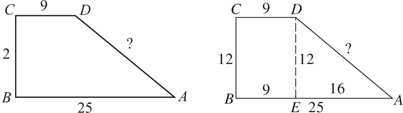
Then, BE = 9, AE = 16, and DE = 12. Finally, DA = 20, because right triangle AED is a 3-4-5 triangle in which each side is multiplied by 4. If you don’t realize that, use the Pythagorean theorem to get DA:

(DA)² = (AE)² + (DE)² = 256 + 144 = 400 ⇒ DA = 20

13. (A, B, C, D)

• In a normal distribution, 5% of the data lie outside of two standard deviations from the mean, in this case less than 300 and greater than 700. That 5% is equally divided: 2.5% below 300 and 2.5% above 700. Statement A is true.

• About 13.5% of the scores lie between one and two standard deviations above the mean (here, between 600 and 700). Of the 34% of the scores that are between one and two standard deviations above the mean (between 500 and 600), well more than half (about 19%) are below 550. Statement B is true.

• About 16% of the scores are below 400. The other 84% are above 400. Statement C is true.

• This is essentially the same as Statement C. About 84% of the scores are below 600.

Since 84% is greater than 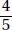, Statement D is true.

14. (D) From the bottom graph, we can estimate the percentage distribution of total enrollment to be:

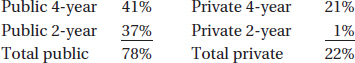
78 ÷ 22 ≈ 3.5, so there were 3.5 times as many students enrolled in public institutions as private ones.

15. (E) In 1972, enrollment in private 4-year institutions was approximately 1,100,000 (22% of the total enrollment of 5,000,000). By 1995, the index for private 4-year institutions had increased from 80 to 120, a 50% increase. Therefore, the number of private 4-year students enrolled in 1995 was approximately 1,650,000 (50% more than the 1,100,000 students enrolled in 1972).

16. (A, B, C)

• From the top graph, we see that for every 100 students enrolled in private 2-year institutions in 1981, the number increased to about 110 in 1983, stayed between 105 and 110 until 1986, and then dropped back to 100 in 1987. Statement A is true.

• From the bottom graph, we see that the percentage of students enrolled in 2-year private institutions remained constant at about 2% from 1981 to 1987. Statement B is true.

•

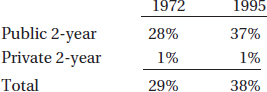
The percent increase from 29 to 38 is 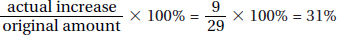, well more than 25%. Statement C is true.

17. (A) Since by KEY FACT L4, C = 2πr, then 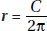, and by KEY FACT L8, the area of the circle is .

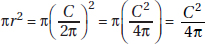18. (B) By the triangle inequality (KEY FACTS J12 and J13),

• The third side must be less than 9 + 10 = 19. (C is false.)

• The third side must be greater than 10 – 9 = 1. (A is false.)

• Any number between 1 and 19 could be the length of the third side. (B is true.)

19. (E) Since p pencils cost c cents, each pencil costs 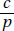cents. By dividing the number of cents we have by 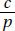, we find out how many pencils we can buy. Since d dollars equals 100d cents, we divide 100d by 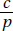, which is equivalent to multiplying 100d by :

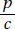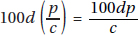
You will probably prefer the alternative solution below.

**Use TACTIC 2 in Chapter 10: replace variables with numbers. Assume 2 pencils cost 10 cents. So, pencils cost 5 cents each or 20 for one dollar. So, for 3 dollars, we can buy 60 pencils. Which of the choices equals 60 when p = 2, c = 10, and d = 3?

Only .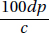

20. (B) The probability that an event will occur is

Here, the number of favorable outcomes is the number of ways of choosing 3 of the 5 boys:

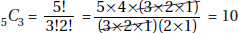
The total number of outcomes is the number of ways of choosing 3 of the 10 children:

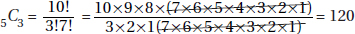
The probability that the 3 children chosen are all boys is .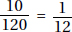

Section 4—Verbal Reasoning

1. (B, D) The spread of genetically engineered matter has become “a significant practical problem.” Thus, it is no longer merely a theoretical (hypothetical; lacking practical application) or abstract worry.

2. (A, E) Under certain circumstances scientists attack each other with ad hominem arguments (personal attacks) and shameless appeals to authority. When is this likely to occur? When facts are established or demonstrable or ineluctable (unavoidable) or relevant? Hardly. Under such circumstances they would rely on the facts to establish their case. It is when facts prove elusive (hard to pin down) or uncertain that they lose control and, in doing so, abandon their pretense of objectivity.

3. (C, E) If “you may wonder” how the expert reaches his conclusions, it appears that it is questionable to rely on teeth for guidance in interpreting fossils. Choices C and E, flimsy and inadequate, create the element of doubt that the clause tries to develop. Choice D, specious, also creates an element of doubt; however, nothing in the context justifies the idea that the reasoning is specious or false.

Note that here you are dealing with an extended metaphor. Picture yourself hanging a heavy winter coat on a slim wooden peg. Wouldn’t you worry that the peg might prove inadequate or flimsy?

4. (A, D) If armed forces take over a country’s administration, then that country is under military law rather than constitutional law. However, in this military takeover, the constitution has not been abolished or stamped out. Instead, some of its provisions merely have been suspended (rendered inoperative for a time) or put in abeyance (temporarily set aside).

5. (C, D) The second clause presents an example of literary mockery or sarcastic jesting. The abstract idea of preserving a nugget of pure truth is appealing; the concrete example of setting it up on the mantelpiece makes light of or mocks the whole idea.

6. (C, E) The passage asserts that literary scholars now reject the idea that Elizabethan drama has it roots in classical Greek and Roman drama. Therefore, it would be inconsistent with the passage to assert Statement C (“Although Elizabethan drama deals with English subject matter, it derives its form and method solely from classical Greek and Roman theater”). Likewise, it would be inconsistent with the passage to assert Statement E (“Modern theater scholars view Elizabethan drama as a direct offshoot of Greek and Roman dramatic traditions”).

7. (E) Choice E does not weaken the argument, because the argument specifically calls for “a truly broad, liberal education.” Choice E, however, merely refers to “the traditional liberal education,” which is not necessarily the truly broad and liberal education the author has in mind.

Choice A weakens the argument: it exposes the argument’s failure to acknowledge that many specific problems may be solved by persons who don’t understand the broad picture.

Choice B weakens the argument: it exposes the assumption that because generalists are needed, all persons should be educated as generalists.

Choice C weakens the argument: it exposes the false dichotomy between specialization and seeing the broad picture.

Choice D weakens the argument: it attacks the implicit assumption that fewer specialists are needed.

8. (E) The last sentence points out that Du Bois originally agreed with Washington’s program.

Choice A is incorrect. Nothing in the passage suggests that Du Bois sacrificed effective strategies out of a desire to try something new.

Choice B is incorrect. Du Bois gained in influence, effectively winning away large numbers of blacks from Washington’s policies.

Choice C is incorrect. Du Bois’s quickness to depart from conventional black wisdom when it proved inadequate to the task of advancing the race shows him to be well able to change with the times.

Choice D is incorrect. Washington, not Du Bois, is described as seeking the good will of powerful whites.

9. (C) The author does not portray Washington as versatile. Instead, he portrays Du Bois as versatile.

Choice A is incorrect. The author portrays Washington as submissive to the majority; he shows him teaching blacks not to protest.

Choice B is incorrect. The author portrays Washington as concerned with financial success; he shows him advocating property accumulation.

Choice D is incorrect. The author portrays Washington as traditional in preaching industry; he shows him advocating hard work.

Choice E is incorrect. The author portrays Washington as respectful of authority; he shows him deferring to powerful whites.

10. (D) Although the author points out that Du Bois’s methods led him into conflicts, he describes Du Bois as “often . . . well in advance of his contemporaries” and stresses that his motives for departing from the mainstream were admirable. Thus, his attitude can best be described as approving.

11. (B) The fact that Monet’s home was filled to overflowing with works by Japanese artists would be sufficient reason for someone to attest (declare; bear witness) that Japanese prints were Monet’s passion.

12. (C, E) The key phrase here is “Breaking with established musical traditions.” Someone who breaks with traditions is by definition iconoclastic (unorthodox; radical; irreverent of tradition). The musical creations of an iconoclastic composer would most likely be heterodox or unorthodox as well.

13. (B, F) A disease in a latent state has yet to manifest itself and emerge into view. Therefore it is almost impossible to determine its existence by observation.

The key phrase here is “almost impossible to determine its existence.” By its very nature, it would not be almost impossible to determine the existence of a disease in its critical (acute) or overt (apparent; unconcealed) state.

14. (A, E) The key phrase here is “his more conventional colleagues.” The paleontologist described here is less conventional than his colleagues. What then is his relationship to orthodoxy (conventionality)? He has departed from conventional ways, has made a break with orthodoxy. Therefore, his more conventional colleagues would contest (challenge) the evidence he has gathered.

15. (A, F) Here the task is to determine the communal reaction to crime. The writer maintains that the criminal justice system of punishments allows the community to purge itself of its anger, its sense of outrage at the criminal’s acts. Thus, it provides a catharsis or purgation for the community.

It is unlikely that an essential purpose of the criminal justice system would be the provision of either a disclaimer (denial or disavowal, as in disavowing responsibility for a legal claim) or a prototype (model; exemplar).

16. (B, E) The key word here is assailed. Housman is attacking his rival. Thus he is in the tradition of scholarly invective (vehement verbal attack), criticizing his foe for turning to manuscripts merely for confirmation or support of old theories and not for enlightenment or illumination. Again, note the use of figurative language, in this case the simile of the drunkard.

17. (A) The capacity of polar bears to scent prey at a great distance is their faculty or ability to do so. Note that faculty here is being used with a secondary meaning.

18. (E) The author first states that the reason for bioluminescence in underwater microorganisms is obscure and then proceeds to enumerate various hypotheses.

19. (B) The author does not deny that predators make use of bioluminescence in locating their prey. Instead, he gives an example of human predators (fishers) who are drawn to their prey (the fish that prey on plankton) by the luminescence of the plankton.

20. (B) As the previous answer makes clear, the phenomenon of plankton bioluminescence does have practical applications. It is a valuable tool for fisheries interested in increasing their catch of fish that prey on plankton.

Section 5—Quantitative Ability

Two asterisks (**) indicate an alternative method of solving.

1. (A) π ≈ 3.14 and 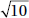≈ 3.16. So π < .

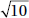By KEY FACT A24, for any positive numbers a and b, if a < b, then 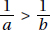. So .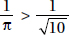

2. (B) It is irrelevant that 700 < n < 800. Every factor of n is a factor of 2n, but 2 is a prime factor of 2n, which is not a factor of n (since n is odd). 2n has one more prime factor than n. Quantity B is greater.

3. (B) Since x < y, the average of x and y is less than y, so having another y raises the average. Quantity B is greater.

** Plug in the numbers: say x = 2 and y = 4.

Quantity A: the average of 2 and 4 is 3.

Quantity B: the average of 2, 4, and 4 is 10 ÷ 3 = 3.333, which is more than 3; the second 4 raised the average.

4. (A) By KEY FACT J3, in any triangle, if one side is longer than a second side, the angle opposite the longer side is greater than the angle opposite the shorter side, so c > d. Quantity A is greater. (It is irrelevant that the third angle is 135°.)

5. (B)

Quantity A: a% of

Quantity B: a% of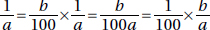

Since a and b are positive and b > a, 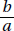> 1, and 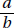< 1.

So Quantity B is greater.

6. (D) Could x and y be equal? Yes, the two small triangles could be right triangles, and x and y could each be 40. Must they be equal? No. On the GRE, diagrams are not necessarily drawn to scale. See the figure below, in which clearly x < y. Neither quantity is always greater, and the quantities are not always equal.

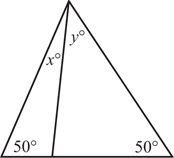
7. (B) Don’t waste time using the slope formula; just make a quick sketch.

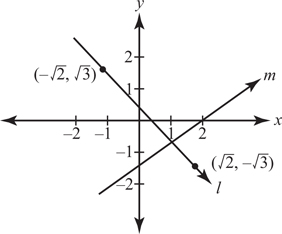
Note that slopes downward, so its slope is negative, whereas m slopes upward, so its slope is positive. (See KEY FACT N4.) Quantity B is greater.

8. (D) The markings in the five angles are irrelevant. The sum of the five angles is 360°, and 360 ÷ 5 = 72.

**If you solve the equation a + 2a + 3a + 3a + 3a = 360, you get that 12a = 360 ⇒ a = 30, and so the degree measures of the five angles are 30, 60, 90, 90, and 90. You would then find that the average of those five numbers is 72; but all of that is a waste of time.

9. (B) By Tactic E1, on her six tests combined, Camille earned a total of 6 × 75 = 450 points. The total of her five best grades is 5 × 85 = 425 points, so her lowest grade was 450 – 425 = 25.

**Since Camille’s average on her 5 best tests is 85, assume that those grades were each 85. Then each one has a deviation of 10 points above the average of 75, and the total deviation above 75 is 5 × 10 = 50 points. Therefore, by KEY FACT E2, her one bad grade must have been 50 points below 75.

10. (B, C, D, E, F) The perimeter of a rectangle whose area is 40 can be as large as we like (for example, if the length is 4,000 and the width is 0.01, the perimeter is 8,000.02). However, the perimeter is the smallest when the rectangle is a square, in which case each side is and the perimeter is . Since 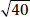> 6, the perimeter is greater than 4 × 6 = 24.

So Choice A, 20, is not possible. All of the other choices are possible.

11. (B, D) Rewriting the equation of the given line, 2x + 3y = 4, in slope-intercept form, we get that y = 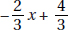. So by KEY FACT N7, the slope of the given line is .

By KEY FACT N6, the slope of any line perpendicular to that line must have a slope of 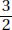, the negative reciprocal of .

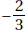Rewrite each of the answer choices in slope-intercept form, and see which ones also have a slope of .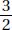

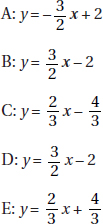
Only Choices B and D are the equations of lines whose slope is .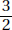

12. (E) Since the diameter of the circle is 20, the radius is 10 and the area is 100π. Since the area of the shaded region is 80π, it is 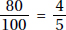of the circle, and the white area is 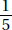of the circle. So the sum of the measures of the two white central angles is 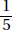of 360°, or 72°. The sum of the measures of all six angles in the two triangles is 360°, so

a + b + c + d + 72 = 360 ⇒ a + b + c + d = 288.

13. 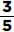The five numbers are 3, 13, 23, 33, and 43, four of which are prime (all except 33).

So the probability that the first number drawn is prime is .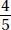

If the first number is prime, then three of the remaining four numbers are prime, and the probability is 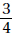that the second number will be prime.

P(both numbers are prime) =

P(1st number is prime) × P(2nd number is prime) = .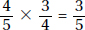

14. (B) From 1994 to 1996 there was a 9.4% decrease in the number of vehicles stolen. Since 9.4% of 1,000,000 = 94,000, the number of vehicles stolen in 1996 was 1,000,000 – 94,000 = 906,000. If you can’t solve problems such as this, you have to guess. But since the number of stolen vehicles is clearly decreasing, be sure to eliminate Choices D and E first.

15. (C) For simplicity, assume that 1,000 vehicles were stolen in 1994. By 1997, the number had decreased by 12.0% to 880 (12% of 1,000 = 120, and 1,000 – 120 = 880); by 1998, the number had decreased 19.4% to 806 (19.4% of 1,000 = 194 and 1,000 – 194 = 806). So from 1997 to 1998, the number of vehicles stolen decreased by 74 from 880 to 806.

This represents a decrease of 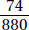= .084 = 8.4%.

16. (D) Simplify the situation by assuming that in 1994 the population was 100,000 and there were 1,000 vehicles stolen. As in the solution to question 15, in 1998 the number of stolen vehicles was 806. At the same time, the number of thefts per 100,000 inhabitants decreased 22.4% from 1,000 to 776. So if there were 776 vehicles stolen for every 100,000 inhabitants, and 806 cars were stolen, the number of inhabitants must have increased.

To know by how much, solve the proportion: 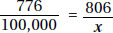. Cross-multiplying, we get 776x = 80,600,000.

So, x = 103,800. Then for every 100,000 inhabitants in 1994, there were 103,800 in 1998, an increase of 3.8%.

17. –9.9

• Since the average of the 5 numbers v, w, x, y, and z is 12.3, their sum is 5 × 12.3 = 61.5.

• Since the average of v and w is 45.6, their sum is 2 × 45.6 = 91.2.

• Then x + y + z = 61.5 – 91.2 = –29.7, and .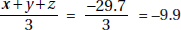

18. (A) Even if you can do the algebra, this type of problem is easier if you use TACTIC 3 in Chapter 9: plug in some easy-to-use numbers; assume that there are 100 girls and 50 boys on staff and that 20% of the girls and 10% of the boys attended the meeting. Then, 20 girls and 5 boys were there, and 5 is 20% of 25, the total number attending.

Of course, you can do this algebraically. If x represents the number of boys on staff, then 2x is the number of girls. If y% of the boys attended the meeting, then 2y% of the girls did. So, the number of boys attending was 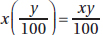, whereas the number of girls attending was .

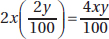Therefore, there were 4 times as many girls in attendance as boys: 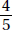of those at the meeting were girls and 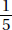or 20% were boys.

19. 96 Since 4 boys can shovel the driveway in 2 hours or 2 × 60 = 120 minutes, the job takes 4 × 120 = 480 boy-minutes to complete. Therefore, 5 boys will need

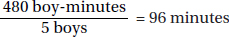
20. (D) Make a table to determine Roberto’s and Juan’s ages. Let x represent Juan’s age in 1950, and fill in the table as shown.

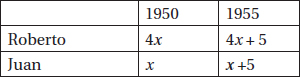
In 1955, Roberto was 3 times as old as Juan, so 4x + 5 = 3(x + 5) = 3x + 15, and so x = 10. Therefore, in 1950, Juan was 10 and Roberto was 40. Because Roberto is 30 years older than Juan, Roberto was 30 when Juan was born.

Section 1—Analytical Writing

PROMPT #1

“Public secondary school students should be required to pass a standardized national exit exam in order to receive a high school diploma.”

Compose an essay that presents your opinion on the policy presented, explicating your rationale for this opinion. As you build and provide evidence for your argument, you must take into account the likely effects of applying the policy and describe the impact these potential effects have on your argument.

SCORE 6 ISSUE ESSAY

Since the publication of the report, “A Nation at Risk,” in the early 1980s, policy makers and pundits have decried the poor quality of American education. They argue that our public schools, once the envy of the world, have lost their way. Business leaders complain that many high school graduates lack basic skills, creating a shortage of qualified workers. Critics also lament the significant achievement gap between students in wealthy suburban communities and their peers in many of the nation’s largest urban school systems. This frustration has led many to support the implementation of a standardized national high school exit exam in order to set high standards for all students. Unfortunately, there is no simple answer to the challenges facing the American system of public education, and the consequences of implementing a standardized national high school exit exam are likely to be both counterproductive and discriminatory.

A standardized national high school exit exam is more likely to harm the quality of American education than it is to improve it. Standardized tests are ideal for measuring subject matter knowledge, but they are inadequate instruments for measuring skills like writing and problem solving. If a standardized national high school exit exam is implemented, schools will be evaluated and ranked based on the scores their students achieve. This ranking will create pressure on administrators and teachers to improve student test scores, and “teaching to the test” will be an inevitable consequence. Tragically, because these tests privilege recall of facts over demonstration of skills, school districts will alter their curricula in order to maximize their students’ performance on the national test. Class time that was once dedicated to writing and hands-on problem solving will be given over to rote memorization and drill, creating students who are less skilled and prepared than their predecessors.

Not only will a national standardized high school exit exam fail to improve the quality of education in the United States, but it will also exacerbate the inequality for which some propose it as a remedy. Standardized testing cannot shrink the achievement gap between wealthy suburban students and their less fortunate urban counterparts. Without improved resources to address the systemic causes of the achievement gap, students in failing districts will continue to struggle. Only now, with a standardized national test, all students will be held to the same standards, regardless of the advantages or disadvantages they face. The upshot of this is that high school graduation will become a more distant goal for the very students who struggle the most. The dropout rate in large urban districts will rise, and the unfortunate products of these schools will find themselves less employable. As businesses abandon these communities due to a shortage of qualified workers, unemployment will increase. As local economies decline, so too will property values, which are the basis of the taxes that support public education in most areas of the country. Finally, with even fewer resources available, the students in these struggling school districts will fall ever further behind their more fortunate peers.

Adopting a standardized national high school exit exam is a simplistic response to a complicated problem. If we want to improve the quality of education for all students in the United States, we need to recognize that one size does not fit all. We need to develop instruments and methods that better evaluate student skills, and we need to provide resources to address the wealth and opportunity gap that drives the achievement gap. We cannot improve the quality of education if we focus on measuring outputs without doing anything to change inputs.

ARGUMENT The essay presents a clear and perceptive argument that a standardized national high school exit exam will be harmful. The essay is especially good at meeting the requirement to examine the consequences of implementing this policy, doing so by describing the chain of events that could be expected to follow its implementation.

SUPPORT The likely consequences of implementing the policy are well supported by strong reasoning. One excellent example of this is the description of how decreases in the number of high school graduates will harm the economy, affecting tax revenues, ultimately resulting in reduced resources for schools and even poorer educational results.

STRUCTURE The essay is well focused and organized, with logical transitions between ideas.

FLUENCY The essay displays sophisticated and powerful vocabulary. Its sentence structure is varied throughout.

CONVENTIONS Outstanding. The essay includes no noticeable errors in grammar, usage, or mechanics.

SCORE 5 ISSUE ESSAY

High school graduation is a rite of passage, a ritual through which young people show that they have completed one stage of their development and are ready for their next. But what does it actually represent about the education of those young people? What does it certify that they are skilled enough to do, that they are learned enough to understand? In theory, a high school diploma indicates that certain basic skills have been attained. In reality, however, the only thing we know for sure about a person who graduated from high school is that they that completed four years of high school. Even a student who has met state requirements for graduation may have met very different requirements from a student with the same amount of schooling from another state.

Assessment of student success varies dramatically from state to state, district to district, school to school, and even teacher to teacher. Some schools do not even have a common standard for what a passing grade is. Teacher A might consider 55% a D. Teacher B might consider 55% an F. One student with a 55% passes the class, even if just barely. Another does not. Standardization is necessary in that school. But it’s easier to manage at a school level than on a national level. We are not willing to put the kind of time and money into standardization that it would take for schools to even educate their faculty about common grading rubrics (even schools that have such rubrics often have no “grade norming” in which teachers undergo professional development training to ensure that they are applying the rubric in similar ways). If we are not willing to fund more professional development for teachers to do something on as small of a scale as their own school, what on earth would demonstrate that we are willing to fund the development of a national standardized test?

While a national standardized test might seem like an obvious solution to ensure that students across the country demonstrate the same knowledge, the actual implementation of such testing would further shift the focus of education toward quantifiable outcomes. The consequence of this is turning students into information regurgitators rather than scholars. The purpose of public education is not just to prepare students for the workforce, but also to prepare them to become responsible citizens.

Completion of high school as a rite of passage is so culturally ingrained that students, and their families, expect that any student who put in their time should be prepared for the world. If a student puts four years into high school and still cannot pass a standardized test, has the student failed or has the system failed? I’m not suggesting we just ignore any possibility of standards in favor of allowing students to bide their time until graduation. I am, however, suggesting that smaller educational communities struggle enough with figuring out how to help students learn; adding to the burdens of overburdened, underfunded schools would mean even fewer graduations for those schools. This would affect already-disadvantaged communities more than it would affect privileged communities. The de facto national exams that exist—the SAT and ACT—are already more accessible to students from better resourced schools, both logistically and in terms of test content. Implementing a standardized national high school exit exam would duplicate this unfairness.

Without standardization, assessment is something of a wildcard. With it, schools become beuracracies in which teachers must focus on delivering measurable results rather than helping young people learn.

ARGUMENT The essay presents a clear and thoughtful argument that the implementation of the proposed policy will negatively change the focus of teaching and present an unfair burden to some schools.

SUPPORT The essay includes concrete examples of how implementing a standardized national high school exit exam will change what schools teach and present a special burden to some schools.

STRUCTURE The essay is generally well focused and organized, though the discussion of the lack of will to fund the teacher training needed to implement standardization at a national level is less clearly a description of the writer’s views on the policy than it is an indictment of the likelihood of its being adopted. Transitions between ideas are logical.

FLUENCY The ideas in the essay are clear, and its vocabulary use is appropriate and effective. Sentence structure is varied.

CONVENTIONS The essay demonstrates solid command of the grammar, usage, and mechanics of standard written English, despite the presence of a few minor errors that do not obscure meaning.

SCORE 4 ISSUE ESSAY

It is no secret in America that we have an education crisis. Our students no longer rank at the top of the charts in terms of meeting standardized educational goals. Other countries have surpassed us and now boast better education systems than the one here in the United States. While there are many solutions to this problem, including an increase in funding and a national standard of higher compensation for teachers, this essay will focus on one possible solution. By requiring public secondary school students to pass a standardized national exit exam in order to receive a high school diploma, schools can set an achievable standard that can help return America to the top of the educational charts.

Though they are controversial, there is great need to create a national standard that will strengthen our national education system. Limiting the curriculum a teacher can present may be a good thing. Too often teachers complain about the heavy amount of preparation time that is needed for them to do their jobs. Moving to a strict and standardized testing system could help alleviate this stress. Though the tests do teach a narrow set of skills, they do not have to focus on rote memorization. Many exams also require a critical thinking or analytical section that is not about memorization of facts. A standardized testing still allows students to take elective courses which supplement their test preparation. While these exams can create anxiety, it can also open the door to a conversation about how to manage the this stress and prepare them for the real world. This creates a learning experience that would not otherwise happen. Setting achievable goals is an important part of passage from being a high school student into adult life.

It is clear that the debate about standardized tests will continue. They can be used to determine a standard of education that must be achieved in order to continue with education or enter the workplace. The set of skills taught can be wide and varied, and do not have to exclude other forms of creative education. Finally, since standardized tests are often the metric of entrance into higher education, this type of testing creates an opportunity for learning good test taking skills early on in one’s educational career, which is a skill that cannot be underestimated.

ARGUMENT The essay presents a clear argument that adequately responds to the task instructions. In answering common fears about standardized testing, it describes ways in which these concerns could be worked around. The argument would be stronger, however, if it examined the likelihood of these scenarios.

SUPPORT The essay includes adequate reasoning and some specific descriptions of how a number of the feared consequences of a standardized national exit exam could be avoided.

STRUCTURE The essay is reasonably well focused and organized, though the introduction is a bit misleading. It focuses more on the need for improved education than it does on the ultimate subject of the essay, the possibility of avoiding some of the negative consequences of standardized testing.

FLUENCY The ideas in the essay are clear, and its vocabulary use is generally appropriate.

CONVENTIONS The essay demonstrates adequate command of the grammar, usage, and mechanics of standard written English. There are a few minor errors, but not enough to obscure meaning.

PROMPT #2

The following appeared in a letter to the editor in the journal Health Matters.

“Statistics gathered over the past three decades show that the death rate is higher among those who do not have jobs than among those with regular employment. Unemployment, just like heart disease and cancer, is a significant health issue. While many health care advocates promote increased government funding for medical research and public health care, it would be folly to increase government spending if doing so were to affect the nation’s economy adversely and ultimately cause a rise in unemployment. A healthy economy means healthy citizens. Reining in government spending is, therefore, the best medicine.”

Compose an essay that identifies the questions that must be answered before deciding whether the conclusion and the argument supporting it make sense. In writing your essay you should describe the impact that the answers to these questions would have on your assessment of the conclusion.

SCORE 6 ARGUMENT ESSAY

According to a letter to the editor of Health Matters, three decades of research shows that people without jobs have a higher death rate than those who work. Thus, argues the writer, any public policy that increases spending on healthcare and medical research is misguided if that spending would destabilize the economy and thereby increase unemployment. The writer concludes, therefore, that decreased government spending will create a healthier population. This conclusion seems, on its face, both simplistic and unlikely. To test it, there are two questions that must be answered.

The first and most fundamental question raised by the letter’s conclusion is whether unemployment does, in fact, cause death. Correlation is not causation. In other words, the fact that two conditions exist in proximity to one another does not mean one is the cause of the other. Higher mortality among people without jobs does not necessarily mean that unemployment causes higher mortality. For one thing, the writer does not specify whether people without regular employment are the same as “unemployed” people. Elderly people do not have regular employment because they are retired, and they have a high mortality rate because they are elderly. Their lack of employment does not cause their high mortality rate. The same is true of people who suffer from serious illnesses like cancer and heart disease. They lack regular employment because they are sick, and they suffer from high mortality for the same reason. The correlation between lack of regular employment and high mortality does not prove that the former causes the latter.

The second question that must be answered in order to evaluate the claim that reducing government spending saves lives is whether that spending would be great enough to cause harm to the economy. The writer makes this broad claim about government spending in the context of spending on healthcare and medical research, thus the question is properly whether this spending in particular would harm the economy. There are several reasons to think that it would not. First, government spending on healthcare keeps people in good health so that they can work. Without that spending more people will be too ill to work, and they, as a result, depend on government programs for their support. In this way, government spending on healthcare may strengthen the economy and, in the long run, reduce or stabilize government spending overall.

An additional way in which government spending on healthcare and medical research may strengthen the economy is by providing jobs. When the government funds healthcare and research, it doesn’t just pour money into a hole to nowhere. Those monies enter the economy as wages for doctors, nurses, and researchers. They pay construction workers who build hospitals, custodians, and cafeteria workers. This in turn increases overall employment, raising revenue from income taxes and decreasing spending on social welfare programs. There are logical reasons to conclude that government spending on healthcare and medical research would strengthen the economy, while the claim that it would harm the economy is an unwarranted assertion.

“Reining in government spending” sounds like an admirable goal. Curtailing financial crisis through fiscal responsibility is, by definition, a good idea. But the claim that increased government spending on healthcare and medical research will have the paradoxical effect of increasing the death rate is supported by neither evidence nor reasoning.

ARGUMENT The essay successfully identifies two questions that must be answered in order to evaluate the argument presented. The essay explicitly and thoroughly answers these questions, providing well-reasoned explanations that support the essay’s thesis on the relationship between government health spending and mortality rates.

SUPPORT The essay provides detailed and persuasive support for its main points, in one case describing how the argument’s author has likely confused correlation for causation, and in the other case outlining theories for how government health spending might logically strengthen, rather than weaken, the economy.

STRUCTURE The essay is well organized, expressing its position clearly and in a logical progression. Transitions between the main ideas in the essay are clear, and the concluding paragraph summarizes the essay’s argument well.

FLUENCY The essay expresses ideas effectively, with appropriate word choice and varied sentence structure.

CONVENTIONS The essay displays impressive command of the conventions of standard written English, with no noticeable errors in grammar, usage, or mechanics.

SCORE 5 ISSUE ESSAY

In this letter to the editor of Health Matters, there are many questions that stand to be answered and little to no proof to hold up its conclusion. There are three main assumptions underlying its conclusion that the government should not spend more money on healthcare: 1. unemployment causes death in citizens, 2. government spending is a problem that outweighs the benefits of government-funded medical research, and 3. government spending creates unemployment. No evidence exists to substantiate any of the claims made.

First and foremost is the question of whether unemployment causes death. It is important to remember correlation does not mean causation. In other words, just because two things might happen at the same time doesn’t mean that one causes the other. In this instance, the author clearly thinks that unemployment causes an earlier death, but doesn’t think that they are merely correlated. But there are many other reasons for the correlation between unemployment and death. If an individual is unemployed, chances are their stress levels are higher. Furthermore, there might be a reason they don’t have a job. For example, they could be sick and that sickness might be the reason they both don’t have a job and they die earlier. In another instance, they could have a substance use disorder that would prevent them from being a productive worker without receiving help first.

The second assumption is that government spending is a problem that outweighs the government funding medical research. But does it? I think not. For example, the US government funds over 90% of the world’s research on substance use disorders through NIDA (National Institute on Drug Abuse). Without the government, a lot of major medical breakthroughs wouldn’t happen because there is no way at this point in time that the private sector would pitch in enough to fund as many innovations as the government helps create.

The final question is whether government spending on medical research causes unemployment. Once again, no data is provided for this. No economic theory is stated or quantitative data is presented to solidify this claim. Based on history, I would think that government spending actually creates jobs. During World War II, the American economy was booming and the government was spending lots of money on the war effort.

In sum, there are many assumptions made in this letter to the editor, with very limited evidence offered in support. A little data would go a long way toward supporting the author’s case. Without it, the argument has no merit.

ARGUMENT The essay successfully pinpoints and responds thoughtfully to three questions that must be answered in order to assess the conclusion that government health spending is counterproductive.

SUPPORT The essay provides thoughtful and reasonably persuasive support for its main points. It is strong in its discussion of alternate causality, but weaker in its use of World War II as proof that government spending strengthens the economy (the scale of spending in these two instances does not seem comparable).

STRUCTURE The essay is well organized, with suitable (though not always smooth) transitions between ideas.

FLUENCY The essay generally uses vocabulary effectively to express its ideas, though it reads awkwardly in places.

CONVENTIONS The essay displays solid command of the conventions of standard written English.

SCORE 4 ARGUMENT ESSAY

There is no way to accept at face value the letter to the editor in Health Matters. The author of the letter makes several logical leaps that require further examination. While the analogy of the healthy economy draws up images of prosperity for everyone, the conclusions this author makes are fundamentally flawed.

There are any number of reasons for the correlation between death rate and employment; this author examines none of them. To accept this premise I would need to know if “regular employment” included retired people, older people, veterans or others on permanent disability, and children. Unless the statistical data of death rate was limited to eligible workers of working age, then the statistics presented are skewed in favor of the author’s ultimate point. They use this shocking claim to draw in the reader and the analogy of health to appeal to the broadest set of people. Health is not a politicized issue; everyone, conceivably, wants to be healthy. However, this analogy is still just an assertion used to support an argument for reducing government spending.

To create a healthy society and cure diseases like cancer, heart disease, and, per the author, unemployment, government spending will likely have to increase. Another question I would need to answer to evaluate the conclusion is where the author thinks money to combat unemployment is going to come from. Other than a thinly veiled jab at healthcare professionals for seeking increased funding, the author has no identifiable solution. I would also need to know whether healthcare spending was going to “affect the nation’s economy adversely” and lead to the spike in unemployment promised by the author. It would seem likely that more funding for “medical research and public health care” would create more jobs rather than less of them.

Ultimately, this author uses their health metaphor to assert that “Reining in government spending is . . . the best medicine.” This health metaphor has come full circle; earlier in the letter, the author argues that increased spending for medical research would lead to a rise in unemployment, but has no problem touting his solution as the best medicine.

ARGUMENT The essay identifies and responds to questions that must be answered in order to evaluate the argument presented. The essay’s discussion of the argument’s use of health as a metaphor is, however, somewhat tangential to the task at hand.

SUPPORT The essay provides sufficient support for its main points, though it does a better job of identifying where the argument provided lacks support than it does in offering counterexamples or reasoning.

STRUCTURE The essay expresses its ideas reasonably clearly, and but could benefit from more graceful transitions. The internal organization of the second and third paragraph, could be stronger.

FLUENCY The essay generally uses vocabulary appropriately to express its ideas.

CONVENTIONS The essay generally displays command of the conventions of standard written English, despite the presence of a few minor errors that do not interfere with meaning.

Section 2—Verbal Reasoning

1. (D, E) Note the two key phrases “Given the human tendency to suspect and disbelieve in” and “it is unsurprising that.” People who view the unconscious with suspicion or disbelieve in it are as a consequence likely to deny or gainsay (contradict) its effect on human interactions.

2. (B, E) In contrast to his reputation, the author is not markedly taciturn (uncommunicative; disinclined to talk). In fact, he seems inclined to talk. In other words, he is not at all averse from or opposed to conversation.

3. (A, C) To call a country “the land of the free” while allowing the institution of slavery to exist struck Mrs. Trollope as evidence of hypocrisy or sanctimoniousness (the act of making a false display of righteousness or piety).

4. (B, D) The key word here is “passionate.” Paul finds himself attracted to a woman who is ardent (fervent; keen) and wholehearted (fully enthusiastic) about her likes and dislikes.

5. (C, E) Soap operas and situation comedies are derivative of contemporary culture: they take their elements from that culture. Therefore, they serve as evidence or indices (signs, indications) of what is going on in that culture; they both point to and point up the social attitudes and values they portray.

Note that the soap operas and comedies here cannot be determinants of our society’s attitudes and values: they derive from these attitudes and values; they do not determine them.

6. (D, E) Whatever word or phrase you choose here must apply equally well both to slander and to counterfeit money. People who would not make up a slanderous statement circulate or spread slander by passing it on. So too people who would not coin or make counterfeit money circulate or spread around counterfeit money by passing it on.

Note how the extended metaphor here influences the writer’s choice of words.

7. (D) The author cites Meredith’s intelligence (brilliance) and his splendor of language (linguistic grandeur).

8. (E) Rather than refuting the claim, the author clearly acknowledges Meredith’s inability to evoke the reader’s sympathy.

Choice A is incorrect. From the start the author points out how Meredith leaves readers cold.

Choice B is incorrect. The author reiterates Meredith’s virtues, citing muscular intelligence and literary merit.

Choice C is incorrect. The author quotes several such imagined criticisms.

Choice D is incorrect. The author indicates that if readers choose to avoid dealing with Meredith they shall be doing a disservice to the cause of criticism.

Only Choice E remains. It is the correct answer.

9. (E) Speaking of the “challenge and excitement of the critical problem as such,” the author clearly finds the prospect of appraising Meredith critically to be stirring and invigorating.

10. (C) The author wishes us to be able to recognize the good qualities of Meredith’s work while at the same time we continue to find it personally unsympathetic. Thus, she would agree that criticism should enable us to appreciate the virtues of works we dislike.

Choices A, B, and E are unsupported by the passage.

Choice D is incorrect. While the author wishes the reader to be aware of Meredith’s excellences, she does not suggest that the reader should ignore those qualities in Meredith that make his work unsympathetic. Rather, she wishes the reader to come to appreciate the very ambivalence of his critical response.

11. (A, E) The off-Broadway and Broadway theatres are contrasted here. The former has manifested or shown a talent for improvisation, extemporaneous or spontaneous performance. The latter has manifested no such talent for spontaneity.

Note the use of whereas to establish the contrast.

12. (C, D) People had complimented her for her fluency or eloquence; it was therefore surprising that she proved inarticulate or tongue-tied at her inauguration.

Note the use of although and surprisingly to signal the contrast.

13. (B, F) The filmmakers wish neither to reject nor to vitiate (impair; weaken) a strong sense of place. Instead, they take pains to impart (communicate; convey) a strong sense of the places they film as well as of the characters they film. Thus, their films become portraits of the spaces their characters inhabit.

14. (B, D) The key phrase here is “they remained the dominant viol size.” The text is discussing changes over time in the popularity of different sizes of bass viols. Before 1600, larger consort bass viols were in fashion. After 1600, the larger consort bass viols were displaced by the smaller division viols. The division viols continued to be popular until some time in the 1700s, when they went out of fashion.

15. (A, E, G) Particles have no need to be wound up because the property of spinning (rotation) is built into their makeup: it is intrinsic. That is the significant difference between the spinning of particles and the spinning of tops.

16. (C) To the author the concept is both simple and traditional, dating as it does from Newton’s time.

17. (A, C) Question A is answerable on the basis of the passage. As the area’s density increases, its gravitational field increases in strength. Likewise, Question C is answerable on the basis of the passage. The end result of the process is the formation of a gravitationally bound object, a newborn star. Remember, you must have selected both A and C to receive credit for this question.

Question B is not answerable on the basis of the passage. The passage nowhere states what disturbs the gas.

18. (E) The passage compares the Quechua empire to a mandala because “it was divided into four parts.” Thus, a mandala is most likely a “figure composed of four divisions.”

19. (B) The author refers to the Quechua as existing in “a state of unremitting anxiety, which could not be resolved by action” and which the Quechua could only deal with by looking into himself and struggling with the depths of his own psyche. This suggests that the Quechua world was highly introspective.

20. (D) Both the unremitting anxiety of Quechua life and the recurring harvest failures that brought starvation to millions illustrate the harshness and frustration of Quechua existence.

Section 3—Quantitative Ability

Two asterisks (**) indicate an alternative method of solving.

1. (D) Use TACTIC 4, Chapter 10. Could m and n be equal? Sure, if each is 5. Eliminate Choices A and B. Must they be equal? No, not if m = 1 and n = 25. Eliminate Choice C, as well. Neither quantity is always greater, and the two quantities are not always equal (D).

2. (D) Since 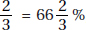, which is clearly more than 65%, it appears that Quantity B is greater. Be carefu! That would be true if a were positive, but no restrictions are placed on a. If a = 0, the columns are equal; if a is negative, Quantity A is greater. Neither quantity is always greater, and the two quantities are not always equal (D).

**Use TACTIC 1, Chapter 10. Just let a = 0, and then let a = 1.

3. (D) Use TACTIC 4, Chapter 10. Could the quantities be equal? Could c = 5? Sure, if this is a 3-4-5 right triangle. Must c = 5? No; if the triangle is not a right triangle, c could be less than or more than 5.

Neither quantity is always greater, and the quantities are not always equal (D). (Note: Since the figure may not be drawn to scale, do not assume that the triangle has a right angle.)

4. (B) You don’t have to solve for a and b. If a – b > a + b, then –b > b, and so b is negative and Quantity B is greater.

**You could solve. Adding the two equations yields 2a = 49 ⇒ a = 24.5 ⇒ b = –0.5.

5. (A) Since in the given figure OA and OB are radii, each is equal to 5. With no restrictions on x, AB could be any positive number less than 10; and the larger x is, the larger AB is.

If x were 90, AB would be , but we are told that x > 90, so AB > > 7.

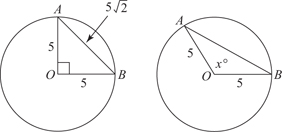
6. (C) The distribution consists of 20 numbers: four 1’s, five 2’s, two 3’s, three 4’s, and six 5’s:

1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 4, 4, 4, 5, 5, 5, 5, 5, 5

• The median is the average of the two middle numbers, which are both 3, so the median is 3.

• The mode is 5, since there are more 5’s than any other number.

• So the quantity in Column A is 4, the average of 3 and 5.

• Since the range of a set of data is the difference between the largest and smallest values, the range is 5 – 1 = 4.

• So, the quantity in Column B is also 4.

• The quantities are equal.

7. (B) Do not waste any time evaluating the two standard deviations. We don’t need the values of the two quantities, we only need to know which quantity is greater. The standard deviation is a measure of how far, on average, the pieces of data are from the mean. The closer the data are to the mean, the smaller the standard deviation; the farther the data are from the mean, the greater the standard deviation. In List 1, the mean is 75, and the five data points are 50, 25, 0, 25, and 50, respectively, away from the mean. In List 2, the mean is 150, and the five data points are 100, 50, 0, 50, and 100, respectively, away from the mean. The data in List 2 are farther from its mean than the data in List 1 are from its mean, so the standard deviation of List 2 is greater.

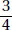8. (C) If there are x seats on each bus, then the group is using seats. After of them get off, of them, or 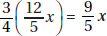remain.

What fraction of the 2x seats on the two buses are now being used?

.

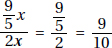**To avoid the algebra, use TACTIC 2 in Chapter 10: choose appropriate numbers. Assume there are 20 seats on each bus. At the beginning, the group is using 48 of the 60 seats on the three buses. When 12 people left, the 36 remaining people used 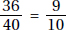of the 40 seats on two buses.

9. (B) Since d divisions each have t teams, multiply to get dt teams; and since each team has p players, multiply the number of teams (dt) by p to get the total number of players: dtp.

**Use TACTIC 2, Chapter 9. Pick three easy-to-use numbers for t, d, and p. Assume that there are 2 divisions, each consisting of 4 teams, so, there are 2 × 4 = 8 teams. Then assume that each team has 10 players, for a total of 8 × 10 = 80 players. Now check the choices. Which one is equal to 80 when d = 2, t = 4, and p = 10? Only dtp.

10. (C) Since, in 1990, 2p pounds of potatoes cost 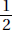d dollars, p pounds cost half as much: 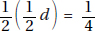d. This is , or 25%, as much as the cost in 1980, which represents a decrease of 75%.

**In this type of problem it is often easier to use TACTIC 2, Chapter 9: replace the variables with numbers. Assume that 1 pound of potatoes cost $100 in 1980. Then in 1990, 2 pounds cost $50, so 1 pound cost $25. This is a decrease of $75 in the cost of 1 pound of potatoes, and

11. 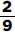There are nine positive integers less than 10: 1, 2, ..., 9. For which of them is 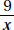> x?

Only 1 and 2: 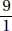> 1 and 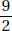> 2. When x = 3, 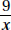= x, and for all the others 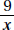< x.

The probability is .

12. (D) If Jason were really unlucky, what could go wrong in his attempt to get one marble of each color? Well, his first nine picks might yield five blue marbles and four white ones. But then the tenth marble would be red, and now he would have at least one of each color. The answer is 10.

13. 94 If a represents Jordan’s average after 5 tests, then he has earned a total of 5a points (see TACTIC E1). A grade of 70 on the sixth test will lower his average 4 points to a – 4. Therefore,

a – 4 = 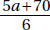⇒ 6(a – 4) = 5a + 70 ⇒ 6a – 24 = 5a + 70 ⇒ 6a = 5a + 94 ⇒ a = 94

**Assume Jordan’s average is a because he earned a on each of his first 5 tests. Since after getting a 70 on his sixth test his average will be a – 4, the deviation on each of the first 5 tests is 4, for a total deviation above the average of 20 points. So, the total deviation below must also be 20 [KEY FACT E3]. Therefore, 70 is 20 less than the new average of a – 4:

70 = (a – 4) – 20 ⇒ a = 94

**Use TACTIC 1, Chapter 9: backsolve. Start with Choice C, 86. If his 5-test average was 90, he had 450 points and a 70 on the sixth test would give him a total of 520 points, and an average of 520 ÷ 6 = 86.666. So, the 70 lowered his average 3.333 points. That’s not enough. Eliminate Choices A, B, and C. Try Choices D or E. Choice E, 94, works.

14. (A, B, C, D)

(A) In 1991, more than 50% of the adults whose highest degree was at least a bachelor’s degree participated in adult education, whereas those whose highest educational attainment was a high school diploma or GED (high school equivalency diploma) fewer than 25% participated. (A is true.)

(B) From 1991 to 1995, among those adults whose highest educational attainment was grades 9–12, without earning a high school diploma, the rate of participation in adult education increased from about 15% to 23%, an increase of about 50%. None of the other groups had nearly that great an increase. (B is true.)

(C) Since the population of the country grew between 1991 and 1995, and the rate of participation in adult education programs increased in every category, the total number of people participating had to increase. (C is true.)

(D) From 1991 to 1995 the rate of participation in adult education for those who had attained at least a bachelor’s degree increased from about 52% to 58%, the least increase of any group on both an absolute and percent basis. (D is true.)

(E) Without knowing how many adults have earned a college degree and how many have attended some college without earning a college degree, it is impossible to make this conclusion. For example, 50% of 100,000,000 is much more than 58% of 50,000,000. (E is false.)

15. (E) 50% of 100,000,000 = 50,000,000; 20% of 40,000,000 = 8,000,000.

50,000,000:8,000,000 = 50:8 = 6.25:1, which is closest to choice E, 6:1.

16. (49) Assume that there were 1,000 adults in the workforce. Then 80 were unemployed and 920 were employed. Since 50% of the employed adults and 40% of the unemployed adults participated in adult education, the number of participants was 50% of 920 + 40% of 80 = 460 + 32 = 492.

So, the rate of participation was .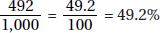

Rounded to the nearest whole percent, the answer is 49.

17. (D)

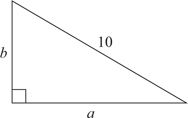
By the Pythagorean theorem,

a² + b² = 10² = 100

and since the area is 20, 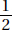ab = 20 ⇒ ab = 40.

Expand:

(a + b)² = a² + 2ab + b² = (a² + b²) + 2ab

Then

(a² + b²) + 2ab = 100 + 2(40) = 180

18. (E) To find the average of three numbers, divide their sum by 3: .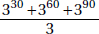

Now use the distributive law (see KEY FACT A21) and divide each term in the numerator by 3: .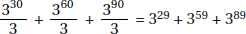

19. (B) Since the radii of the four small semicircles in the figure are 1, 2, 3, and 4, their diameters are 2, 4, 6, and 8; so the diameter of the large semicircle is 2 + 4 + 6 + 8 = 20, and its radius is 10. The perimeter of the shaded region is the sum of the circumferences of all five semicircles. Since the circumference of a circle is πd or 2πr, the circumference of a semicircle is πr, so the perimeter is π + 2π + 3π + 4π + 10π = 20π.

20. 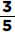a + 25%(a) = 1.25a, and b – 25%(b) = 0.75b.

So, 1.25a = .75b, and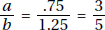

Section 4—Verbal Reasoning

1. (C, D) The key phrase here is “his extravagance and his free-spending lifestyle.” Ironically is an implicit contrast signal: it indicates that you are looking for an antonym or near-antonym to extravagance. The mayor practices extravagance but preaches thrift, that is, economy (financial prudence) or austerity (strict economy; restraint).

2. (A, D) Working on commission, the portrait painter seeks proper recompense or remuneration (payment or reward for services) for undertaking the job.

3. (B, F) Stripped of descriptive phrases, the sentence simply states that jazz would spawn or generate (give rise to) an industry. Note that the verb spawn occurs here with a secondary meaning.

4. (A, C) Several clues suggest that this brief essay is an abridgment or synopsis of more extensive critiques (“arguments rehearsed in much more detail elsewhere”). Thus, it can be described as a condensed (shortened) or synoptic (concise; summary) version.

5. (A, E) If Mrs. Woolf combines both radical and non-radical elements in her fictions, then she presents an anomalous (unusual; not fitting into a common or familiar pattern) or curious (highly unusual) image. Here curious occurs with its secondary meaning (arousing interest or curiosity) rather than with its primary meaning (inquisitive).

6. (C, D) The key phrase here is “move on.” If editors have to travel from firm to firm to succeed in their field, then publishing can be classified as an itinerant or mobile profession, a profession marked by traveling.

7. (D) Immediately before quoting Praz, the author states that the general view of Shelley depicts her as “a transparent medium through which passed the ideas of those around her.” The quotation from Praz provides an excellent example of this particular point of view.

To answer this question correctly, you do not need to read the passage in its entirety. Quickly scroll through the passage, scanning for the name Praz; read only the context in which it appears.

8. (C) The opening sentence points out that Shelley herself acknowledged the influence of her unplanned immersion in the scientific and literary revolutions of her time. Clearly, the author of the passage concedes this as true of Shelley.

9. (B) The concluding paragraph distinguishes Frankenstein from the other overreachers in his desire not to extend his own life but to impart life to another (by creating his monster). Thus, his purpose is atypical of the traditional overreacher.

To say that someone parts from the traditional figure of the overreacher is to say that he differs from it. Thus, to answer this question quickly, scan the passage looking for overreacher and different (or their synonyms).

10. (A) Clearly religious ideas and concepts do not obviate (hinder), preclude (rule out), or deny the practice of medicine and delivery of health care. Neither do they reiterate (repeat) the practice of medicine. However, religious ideas and concepts do inform (pervade; permeate, with obvious effect) medical practices.

11. (B, E) The embittered benefactor thinks of them as ingrates (ungrateful persons) because they do not thank him sufficiently for his generosity. He does not think of them as misers (hoarders of wealth): although they are stingy in expressing thanks, they are extravagant in spending money, that is, being “wasteful of his largesse.” He certainly does not think of them as prigs (self-righteous fuss-budgets): the specific attribute he resents in them is ingratitude, not self-righteousness, or exaggerated propriety.

12. (B, D) The physicists have had good reason to believe in the principle because it has survived rigorous or strict tests. These tests have established (proved) that the principle is accurate.

Note how the second clause supports the first, explaining why the physicists have had reason to be confident in the principle.

13. (A, D) The actress had a knack or talent for getting people to do things for her and was delighted that her new friends were assiduous (diligent) in finding new ways to meet her needs.

Note that it is useful to focus first on the second blank as you answer this question. The key phrase here is “to her delight.” The actress would have no particular cause for delight if her new friends proved dilatory (tardy; slow) or stoical (impassive; unemotional) in finding new ways to meet her needs.

14. (B, F) The presence of inconsistencies (discrepancies; contradictions) in someone’s story would warrant (justify) some incredulity (disbelief) on anyone’s part. Even someone who was not a skeptic (person who maintains a doubting attitude) would be justified in doubting such a tale.

15. (D) The author takes the reader through Wegener’s reasoning step by step, describing what led Wegener to reach his conclusions.

16. (A) Since the existence of the correspondences between the various coastal contours was used by Wegener as a basis for formulating his theory of continental drift, it can be inferred that the correspondences provide evidence for the theory.

Choice B is incorrect. The passage does not indicate that Pangaea’s existence has been proved.

Choice C is incorrect. It is the relative heaviness of sima, not the level or depth of sima, that suggested the possibility of the lighter continents drifting.

Choice D is incorrect. Mobility rather than immobility would provide evidence for continental drift.

Choice E is incorrect. The continents are lighter than the underlying sima.

17. (D) Choice D is answerable on the basis of the passage. The next-to-the-last sentence of the second paragraph states that the Americas “apparently drifted toward the west.”

18. (D) Houston believed that the battle had to begin at the graduate level “to mitigate fear” (relieve apprehension) of race-mixing and miscegenation that might otherwise have caused the judges to rule against the NAACP-sponsored complaints.

19. (B) The separate-but-equal doctrine established by Plessy v. Ferguson allows the existence of racially segregated schools.

20. (A) In assessing the possible effects on judges of race-mixing in the lower grades, Houston was psychologically canny, shrewd in seeing potential dangers and in figuring strategies to avoid these dangers.

Section 5—Quantitative Ability

Two asterisks (**) indicate an alternative method of solving.

1. (A) By KEY FACT A5, the product of 8 negative numbers is positive and the product of 9 negative numbers is negative. Therefore, Quantity A is positive and Quantity B is negative. So, Quantity A is greater.

2. (C)

Quantity A: Since (a⁹)(a⁹) = (a¹⁸), and since a > 0, .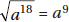

Quantity B: (a²)(a³)(a⁴) = a²⁺³⁺⁴ = a⁹.

The quantities are equal.

3. (B) Assume that the price of a small pizza is $10; then the price of a large pizza is $10 + 0.30($10) = $10 + $3 = $13.

On sale at 30% off, a large pizza costs 30% less than $13.

$13 − 0.30($13) = $13 − $3.90 = $9.10

So, Quantity B is $10 and Quantity A is $9.10.

4. (A) There is not enough information provided to determine the values of a, b, c, d, e, f, and g, but they are irrelevant. By the note following KEY FACT L7, the sum of the measures of the seven angles is 360°, and so their average is 360° ÷ 7 ≈ 51.4°. Quantity A is greater.

5. (C) There are 9 ways to choose the first digit of a 5-digit palindrome (any of the digits from 1 to 9); there are 10 ways to choose the second digit and 10 ways to choose the third digit (any of the digits from 0 to 9). Since the fourth digit must be the same as the second digit, there is only 1 way to choose it. Finally, the fifth digit must be the same as the first digit, so again, there is only 1 choice.

Therefore, the number of 5-digit palindromes is 9 × 10 × 10 × 1 × 1 = 900. In exactly the same way, the number of 6-digit palindromes is 9 × 10 × 10 × 1 × 1 × 1 = 900.

The quantities are equal.

**There is a 1-1 correspondence between the set of 5-digit palindromes and the set of 6-digit palindromes: abcba corresponds to abccba. So the two sets have the same number of members.

6. (B)

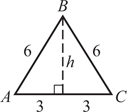
Quantity A: If h is the height of equilateral triangle ABC, then by the Pythagorean theorem 3² + h² = 6² ⇒ h² = 27 ⇒ h = 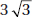. So the area of triangle ABC is

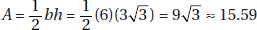
   Alternatively, if you know the special formula for the area of an equilateral triangle (KEY FACT J15), you don’t have to find h:

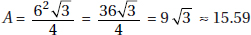
Quantity B:

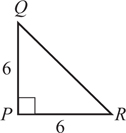
The area of isosceles triangle PQR is 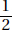(6)(6) = 18.

7. (A) The simplest solution is to notice that if a 1 is chosen first, of the remaining three slips, two of them have –1 on them and one of them has 1 on it. So there are 2 chances in 3 that the second number will be –1 and the product will be –1. Similarly, if a –1 is chosen first, there are 2 chances in 3 that the second number will be 1 and, again, the product will be –1.

Quantity A is 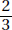and Quantity B is .

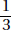**Given 4 numbers a, b, c, and d, there are 6 possible products: ab, ac, ad, bc, bd, and cd. If a = b = 1 and c = d = –1, then 4 of these products equal –1 and two of them equal 1.

So Quantity A is and Quantity B is .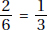

8. (D) Since 8% of 100 is 8, John saved $8, and thus paid $92 for the DVD player. He then had to pay 8% sales tax on the $92: 0.08 × 92 = 7.36, so the total cost was $92 + $7.36 = $99.36.

9. (A)

A cube has 12 edges. (In the diagram, each shaded square base has 4 edges, and there are 4 edges connecting the two bases.) So if e represents the length of each edge, we have that 12e = 3 ⇒ e = 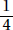. Since by KEY FACT M1 V = e³, we have

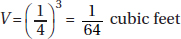
10. 52 How many pages did Mary read in 30 minutes? Since Mary started on page 10, she read the first 24 pages, except pages 1–9: She read 24 − 9 = 15 pages. So she read at the rate of 15 pages every 30 minutes, or 1 page every 2 minutes. Similarly, if Mary reads pages 25 through 50, she will read 50 − 24 = 26 pages. At the rate of 1 page every 2 minutes it will take her 52 minutes to read 26 pages.

11. (D)

• If (m – 5)(m – 45) is positive, either both factors are positive or both factors are negative.

• If both factors are negative, m must be less than 5, so m could be 1, 2, 3, or 4 (4 values).

• If both factors are positive, m must be greater than 45, so m could be 46, 47, … . 100 (55 values).

• The answer is 4 + 55 = 59.

12. (A) Since the diameters of the two mosaics are 30 and 20, the radii are 15 and 10, respectively. So the area of the larger mosaic is π(15)² = 225π, whereas the area of the smaller mosaic is π(10)² = 100π. So the area of the larger mosaic is 2.25 times the area of the smaller mosaic, and hence will require 2.25 times as many tiles.

**The ratio of the diameters is 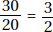. So the ratio of the area is .

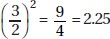13. (B, C, D) Let S = the number of students at Central High School that year.

If 70% of the students attended the rally, then 0.70S = 1,435, and so S = 1,435 ÷ 0.70 = 2,050.

If 85% of the students attended the rally, then 0.85S = 1,435, and so S = 1,435 ÷ 0.85 = 1,688.

So, S must satisfy the inequality 1,688 < S < 2,050.

Only Choices B, C, and D are in this range.

14. 800,000 From the top graph, we see that in 1975, 54% (35% + 19%) of all college students were male, and the other 46% were female. So there were 5,400,000 males and 4,600,000 females—a difference of 800,000.

15. (B) In 1975, of every 100 college students, 46 were female—32 of whom were less than 25 years old, and 14 of whom were 25 years old and over. So, 14 of every 46 female students were at least 25 years old. Finally, 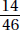= .30 = 30%.

16. (C) From the two graphs, we see that in 1975 54% (35% + 19%) of all college students were male, whereas in 1995 the corresponding figure was 45% (28% + 17%). For simplicity, assume that there were 100 college students in 1975, 54 of whom were male. Then in 1995, there were 140 college students, 63 of whom were male (45% of 140 = 63). So the ratio of the number of male students in 1995 to the number of male students in 1975 is 63:54 = 7:6.

17. 66 Let x represent the number of envelopes Eric can address in 99 minutes and set up a proportion:

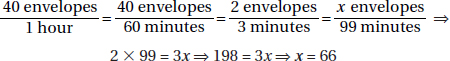
18. (A, C, D, E, F) Start with the least expensive option: 2 regular slices and 2 small sodas.

• This option costs $5.00. (A is true.)

• Changing anything would add at least 50 cents to the cost so $5.25 is not possible. (B is false.)

• Increasing two items by 50 cents each—say, buying 2 medium sodas instead of 2 small sodas—brings the cost to $6.00. (C is true.)

• Now replacing a medium soda with a large soda adds 25 cents, so $6.25 is also possible. (D is true.)

• 2 pepperoni slices and 2 medium sodas cost $7.00. (E is true.)

• Replacing one of those medium sodas with a large soda adds 25 cents, so $7.25 is possible, too. (F is true.)

19. (B) Since a normal distribution is symmetric about the mean, and since in a normal distribution 68% of the scores are within one standard deviation of the mean, 34% are within one standard deviation below the mean, and 34% are within one standard deviation above the mean. The other 32% are more than one standard deviation from the mean, 16% are more than one standard deviation below the mean, and 16% are more than one standard deviation above the mean.

So 16% score below 400, 34% between 400 and 500, 34% between 500 and 600, and 16% above 600. Set up a proportion.

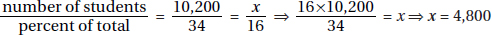
20. (D)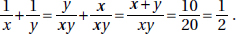

**Estimate. If x = 7 and y = 3, then x + y = 10 and xy = 21. That’s not exactly right; we are told that xy = 20. But it’s close. Then 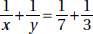≈ .476. So guess .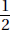