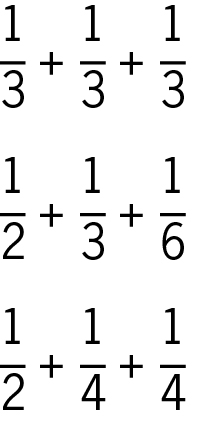
Abgesehen von den möglichen Vertauschungen bei x, y, z gibt es drei verschiedene Lösungen:
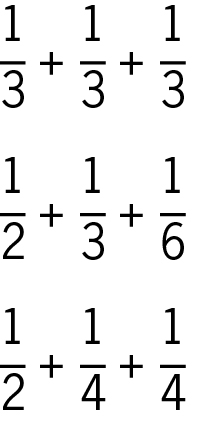
Warum existieren keine weiteren Lösungen? Wenn wir uns die Gleichung

genauer anschauen, wird schnell klar, dass mindestens eine der gesuchten Zahlen kleiner als 4 sein muss. Sind nämlich alle drei Zahlen x, y, z größer oder gleich 4, ist die Summe 1/x+1/y+1/z höchstens 3/4 und damit zu klein.
Nehmen wir an, dass x die kleinste der drei gesuchten natürlichen Zahlen ist. Weil x kleiner als 4 ist, kommen als mögliche Lösungen nur 1, 2 oder 3 infrage. Wir schauen uns die drei Fälle einzeln an:
a) x=1
In diesem Fall wäre die Summe 1/x+1/y+1/z auf jeden Fall größer als 1, denn 1/1 ist ja schon 1. Es gibt deshalb hier keine Lösung!
b) x=2
Die Zahlen y und z müssen dann beide größer sein als 2. Sonst wäre 1/x+1/y+1/z ja größer als 1 (denn 1/2+1/2=1). Nehmen wir an, y ist die zweitkleinste Zahl, also größer oder gleich z. Für y=3 gibt es eine Lösung: z=6, denn 1/2+1/3+1/6=1.
Für y=4 existiert ebenfalls eine Lösung: z=4, denn 1/2+1/4 +1/4=1.
Wenn y größer als 4 ist (und damit auch z größer als 4), kann es keine Lösung mehr geben, denn 1/y+1/z ist dann kleiner oder gleich 2/5. Die Summe 1/y+1/z muss aber 1/2 sein, damit die Gleichung 1/2+1/y+1/z=1 stimmt.
c) x=3
Weil y und z mindestens so groß sind wie x, gibt es nur eine Lösung – nämlich y=3 und z=3. Sobald eine der beiden Zahlen y, z oder beide größer als 3 sind, ist die Summe 1/x+1/y+1/z kleiner als 1 und es kann keine Lösung geben.