
Die Höhe der Pyramide beträgt 1/3.
Man könnte die Höhe auf relativ komplizierte Weise ausrechnen, indem man beispielsweise den Satz des Pythagoras benutzt. Mit einem Trick geht es aber auch viel einfacher. Dabei hilft uns die Volumenformel für Pyramiden:

Die Grundfläche unserer Pyramide ist die gesamte Quadratfläche, von der zweimal ein Viertel dieser Fläche und einmal ein Achtel dieser Fläche abgezogen wird. Sie beträgt deshalb 3/8. Die Höhe kennen wir nicht – und deshalb auch noch nicht das Volumen.
Doch wir könnten das Volumen leicht berechnen, wenn wir die Pyramide auf ihre kleinste Seitenfläche stellen – das graue Dreieck rechts oben. Dieses hat eine Größe von 1/8. Und wir kennen auch die Höhe der auf dieser Seitenfläche stehenden Pyramide. Sie beträgt 1, denn alle drei Winkel der drei Seitenflächen an der rechten oberen Ecke der Pyramide haben eine Größe von 90 Grad. Die Höhe ist damit identisch mit der Seitenlänge des Quadrats. Das Volumen der Pyramide beträgt deshalb 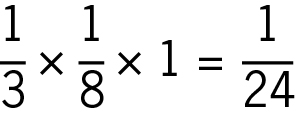 .
.
Nun können wir leicht die Höhe der Pyramide ausrechnen, wenn sie auf ihrer größten Seitenfläche steht. Diese muss 1/3 betragen, denn nur dann ergibt sich als Volumen  .
.