Punkte, Linien, Kreise:
Geometrie ist alles
Mathematik gilt als abstrakte Kunst. Doch das stimmt nicht. Denn Geometrie macht sie sehr anschaulich. Das zeigen die Rätsel dieses Kapitels.
46) Die dreieckige Pyramide
Wir wollen aus einem quadratischen Stück Papier eine Pyramide bauen. Auf dem Blatt sind drei Linien gezeichnet. Benutzen Sie diese drei Linien als Kanten, um die drei hellgrauenEcken des Quadrats nach oben zu falten. Dabei entsteht eine Pyramide mit dreieckiger Grundfläche. Welche Höhe hat diese Pyramide?
Hinweis: Die Seitenlänge des Quadrats beträgt 1. Zwei Faltkanten führen von der linken Ecke zu den Mittelpunkten der rechten und der oberen Quadratseite. Die dritte Faltkante verbindet die Mittelpunkte von rechter und der oberer Quadratseite.
Die Lösung finden Sie hier
Die folgende Knobelei ist schon mehr als 200 Jahre alt und geht auf den Berliner Spielzeughändler Peter Friedrich Catel zurück. Der Feinmechaniker veröffentlichte 1790 einen illustrierten Warenkatalog mit Hunderten Puzzles und mathematischen Spielereien.
Ein Produkt darin war ein aus Pflaumenbaumholz gefertigtes Brett mit drei Öffnungen. Es hieß »Die mathematischen Löcher« und kostete acht Pfennige.
Im Holz befanden sich ein quadratisches, ein dreieckiges und ein rundes Loch, wobei der Durchmesser des Kreises, die Seitenlänge des Quadrats und die Basis des Dreiecks gleich groß waren – siehe Bild oben.
Die Aufgabe formulierte Catel wie folgt: Man solle die dreidimensionale »Figur« angeben, »welche durch alle drei Löcher gehen könne« und diese dabei »vollkommen verstopfe oder ausfülle«. Man könne den gesuchten Körper aus Brot, Kork oder Käse schneiden, empfahl der Spielwarenerfinder.
Gibt es einen Körper, der durch alle drei Löcher passt und diese beim Durchschieben vollkommen verschließt?
Die Lösung finden Sie hier
48) Die eng umschlungene Erde
Mathematische Intuition ist ein faszinierendes Phänomen. Wir ahnen die richtige Lösung eines Problems, ohne es genau durchdacht zu haben. Dabei hilft uns unter anderem Erfahrung – manchmal ist es aber auch einfach nur ein Gefühl.
Wie ist es um Ihre mathematische Intuition bestellt? Die folgende Aufgabe ist ein guter Test dafür. Versuchen Sie die Frage bitte zuerst aus dem Bauch heraus zu beantworten. Und erst danach eine genaue Analyse vorzunehmen. Kommen Sie in beiden Fällen auf dasselbe Ergebnis?
Hier die Aufgabe:
Um unseren Planeten ist entlang des Äquators ein Stoffband geschlungen. Der Einfachheit halber nehmen wir an, dass die Erdoberfläche exakt kugelförmig ist. Es gibt also weder Berge noch Täler und auch der Meeresspiegel hat die gleiche Höhe wie das Land. Das Band ist exakt genauso lang wie der Äquator – und zwar 40.000 Kilometer. Es ist exakt kreisförmig und liegt ohne Falten – sowohl an Land als auch auf dem Wasser.
Im Norden Brasiliens schneidet jemand das Band durch, fügt ein ein Meter langes Zusatzstück ein und näht das Band wieder zusammen. Es ist damit einen Meter länger.
Nun wird das verlängerte Band gleichmäßig um die Erde gespannt, sodass es wieder einen Kreis bildet, dessen Mittelpunkt mit dem Erdmittelpunkt zusammenfällt.
Wie groß ist dann der Abstand des Bandes von der Erdoberfläche?
Die Lösung finden Sie hier
49) Zehn Bäume in fünf Reihen
Schon im alten Ägypten legten Menschen prachtvolle Gärten an. Zu einer eigenen Kunstform entwickelte sich der Gartenbau aber erst viel später – in der Renaissance und im Barock. Wer heute durch den Schlosspark von Versailles wandelt, staunt über die Vielfalt geometrischer Formen, derer sich die Landschaftsarchitekten damals bedienten.
Ein gutes Verständnis der Geometrie benötigt auch der Held des folgenden Rätsels – ein Gärtner. Er soll zehn kleine Bäume, die in kleinen Töpfen geliefert wurden, auf eine Wiese gleich neben dem gepflasterten Weg pflanzen. Aber nicht einfach so. Die zehn Bäume sollen vielmehr fünf gerade Reihen bilden, die aus je vier Bäumen bestehen. So wünscht sich das zumindest die Besitzerin des Grundstücks.
Kann der Gärtner diesen Wunsch erfüllen? Falls ja – wie?
Die Lösung finden Sie hier
50) Wie groß ist das innere Quadrat?
Matroschkas sind eine faszinierende Erfindung: In einer Figur steckt eine kleinere Version davon, und darin eine noch kleinere – und so weiter. Im folgenden Rätsel geht es um eine geometrische Variante dieser aus Russland bekannten Holzfiguren.
In einem Quadrat befindet sich ein Kreis, der so groß ist, dass er alle vier Seiten des Quadrats berührt. In dem Kreis wiederum steckt ein weiteres Quadrat, dessen vier Ecken den Kreis von innen berühren.
Der Einfachheit halber gehen wir davon aus, dass die Liniendicke null beträgt. Also liegen die Eckpunkte des inneren Quadrats auf dem Kreis.
Wenn Sie die Fläche des großen hellgrauen Quadrats kennen – wie groß ist im Verhältnis dazu die Fläche des inneren dunkelgrauen Quadrats?
Die Lösung finden Sie hier
Seit fast 20 Jahren gibt es den Euro. Viele können sich nur noch dunkel an die Geldscheine und Münzen erinnern, die davor in Deutschland galten. Zu den auffälligsten Neuerungen bei den Münzen gehörten das Ein- und das Zweieurostück.
Beide bestehen aus zwei Teilen – dem Ring und dem Kern. Um diese beiden Elemente dreht sich das neue Rätsel – und zwar im buchstäblichen Sinn!
Das Eurostück wird auf einer Ebene genau eine Umdrehung gerollt. Die Strecke A1–A2 ist dann genauso lang wie der Umfang der Münze – siehe folgende Skizze:
Der kreisrunde Kern der Münze rollt die Strecke B1–B2 ab. Wie die Skizze zeigt, sind die Strecken A1–A2 und B1–B2 gleich lang. Wenn das aber zutrifft, dann müssten die Euromünze und der kleinere runde Kern darin den gleich großen Durchmesser haben.
Was stimmt hier nicht?
Die Lösung finden Sie hier
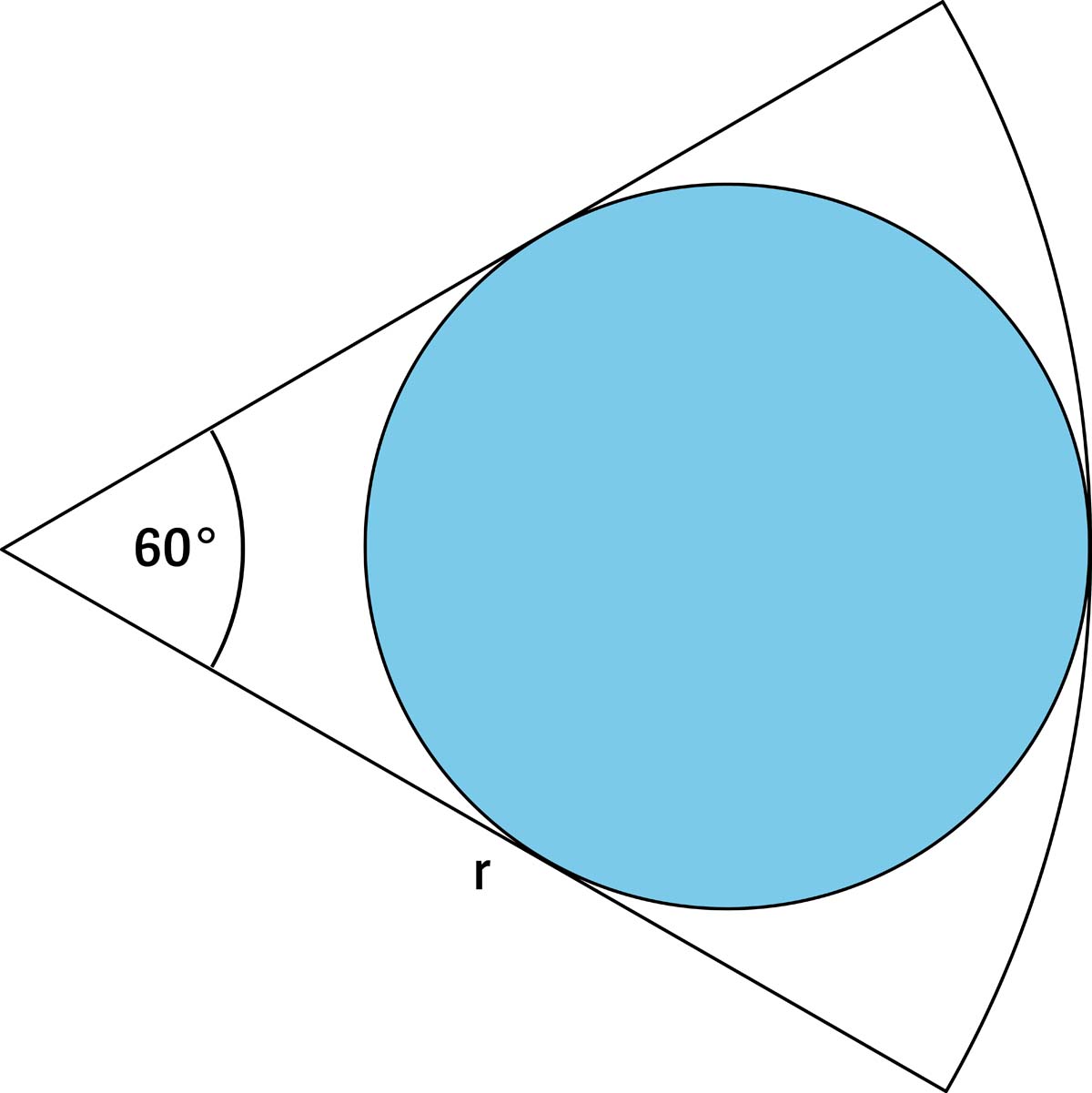
52) Der Kreis im Pizzastück
Wenn Sie eine kreisrunde Pizza in sechs gleich große Stücke zerschneiden, entstehen sogenannte Kreissektoren mit einem Winkel von 60 Grad an der Spitze.
In einen solchen Kreissektor ist ein Kreis gezeichnet, der die Außenkanten des Sektors berührt – siehe Zeichnung.
Wie groß ist der Radius R dieses Innenkreises im Vergleich zum Radius r der Pizza?
Die Lösung finden Sie hier
»Das ist das Haus vom Ni-ko-laus« – jedes Kind kennt dieses Zeichenspiel. Es geht darum, die Linien eines Hauses zu ziehen, wobei jede Silbe des Reims für einen Strich steht. Jede Linie wird nur einmal gezeichnet – und der Stift darf dabei nicht abgesetzt werden.
Die folgende Aufgabe ist von ganz ähnlicher Natur: Sie sollen sechs gerade Striche ziehen – und dürfen dabei ebenfalls nicht neu ansetzen. Doch im Unterschied zum Nikolaus-Haus sind nicht die Striche selbst vorgegeben, sondern 16 Punkte.
Jeder dieser 16 Punkte muss von einem Strich mindestens einmal berührt werden. Nicht irgendwo am Rand, sondern genau in der Mitte.
Bekommen Sie das hin?
Die Lösung finden Sie hier
Ihr räumliches Denken ist gefragt, wenn Sie die folgende Aufgabe lösen möchten. Wir wollen einen Würfel mit einem geraden Schnitt zerteilen. Dabei entstehen zwei kleinere Körper – die Schnittfläche ist eben. Welche geometrischen Formen kann die Schnittfläche bilden?
Ein Quadrat – das klappt auf jeden Fall. Dazu legen wir die Schnittebene einfach parallel zu einer Seitenfläche des Würfels.
Wie aber sieht es mit folgenden Formen für die Schnittfläche aus?
- –
gleichseitiges Dreieck,
- –
regelmäßiges Fünfeck,
- –
regelmäßiges Sechseck?
Können diese entstehen, wenn man einen Würfel mit einem geraden Schnitt zerteilt? Falls ja, wo muss die Schnittebene liegen?
Die Lösung finden Sie hier
55) Umschlossen von sechs Kreisen
Sechs gleich große Kreise sind so aneinandergelegt, dass ihre Mittelpunkte ein regelmäßiges Sechseck bilden. Wie groß ist die von den Kreisen umschlossene Fläche, die in der Zeichnung schwarz gefärbt ist?
Hinweis: Der Radius der sechs Kreise soll 1 betragen.
Die Lösung finden Sie hier
In einem Würfel steckt viel mehr, als man glaubt. Man kann ihn zum Beispiel mit einem geraden Schnitt in zwei Hälften teilen, sodass die Schnittfläche ein gleichseitiges Dreieck ist. Als Schnittfläche ist auch ein regelmäßiges Sechseck möglich.
Die folgende Aufgabe wird Ihr räumliches Denkvermögen womöglich an seine Grenzen bringen. Wieder soll ein Würfel so zerschnitten werden, dass die Schnittfläche ein regelmäßiges Sechseck ist.
Doch es handelt sich nicht um einen normalen Würfel. Vielmehr hat er drei durchgehende Öffnungen mit quadratischem Querschnitt. Die Seitenlänge dieser Querschnittsquadrate beträgt genau ein Drittel der Kantenlänge des Würfels – siehe Zeichnung oben.
Dieser mit Öffnungen versehene Würfel soll nun so zerschnitten werden, dass eine Schnittfläche entsteht, die als äußere Begrenzung ein regelmäßiges Sechseck hat. Doch die Schnittfläche ist keine geschlossene Fläche – in der Mitte hat sie offensichtlich eine Öffnung.
Wie genau sieht die sechseckige Schnittfläche aus?
Die Lösung finden Sie hier