
Die Fläche beträgt 
Wenn wir die Mittelpunkte der sechs Kreise verbinden, entsteht ein regelmäßiges Sechseck. Die eingeschlossene Fläche entspricht dann genau der Fläche des Sechsecks, von der wir noch die sechs Kreissektoren abziehen müssen.

Die Fläche des Sechsecks entspricht der sechsfachen Fläche eines regelmäßigen Dreiecks mit der Kantenlänge 2. Ein solches Dreieck hat eine Höhe von  , was man leicht mit dem Satz des Pythagoras ausrechnen kann (Länge Hypotenuse=2, Länge kurze Kathete=1, Höhe=
, was man leicht mit dem Satz des Pythagoras ausrechnen kann (Länge Hypotenuse=2, Länge kurze Kathete=1, Höhe=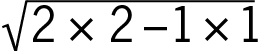 =
= ). Die Dreiecksfläche beträgt damit 2×
). Die Dreiecksfläche beträgt damit 2× /2=
/2= . Für das Sechseck erhalten wir daher als Fläche 6×
. Für das Sechseck erhalten wir daher als Fläche 6× .
.
Jeder der sechs Kreissektoren entspricht einem Drittel der Kreisfläche – insgesamt müssen wir deshalb die doppelte Kreisfläche abziehen – also 2×π.
Für die umschlossene Fläche erhalten wir deshalb:
6× – 2×π
– 2×π