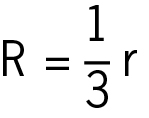Es gilt: 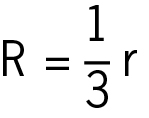 .
.

Es gilt: 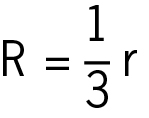 .
.

Wenn wir ein paar zusätzliche Linien in den Kreissektor einzeichnen, ist die Lösung nicht allzu kompliziert. Die Strecke, welche den 60-Grad-Sektor in zwei 30-Grad-Sektoren zerlegt, hat die Länge r. In der folgenden Skizze besteht sie aus zwei Segmenten: Das Stück links hat die Länge s, das Stück rechts die Länge R.
R ist der Radius des Innenkreises und s die Strecke von der Segmentspitze bis zum Mittelpunkt des Innenkreises – siehe Zeichnung. Also ist r=s+R.
Zugleich sehen wir, dass s doppelt so lang sein muss wie R, denn s und R bilden Hypotenuse und Kathete eines rechtwinkligen Dreiecks mit den Winkeln von 30, 60 und 90 Grad.
In einem solchen Dreieck ist die Hypotenuse genau doppelt so lang wie die kurze Kathete. Denn wir können das Dreieck an der längeren Kathete spiegeln und erhalten ein gleichseitiges Dreieck, dessen Innenwinkel alle 60 Grad groß sind.
Also gilt:
s=r–R=2R
Woraus folgt: