
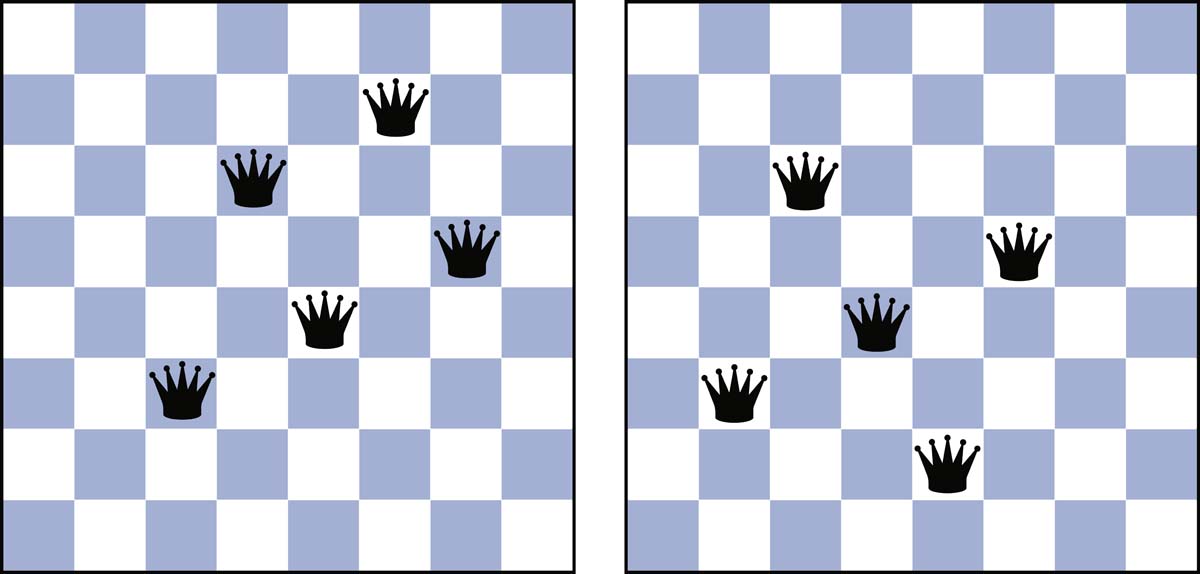
Es gibt ganz offensichtlich mehrere Lösungen – zwei sehen Sie hier. Die Lösung links hat eine überraschende Symmetrie:

Auch die Lösung rechts nutzt eine gewisse Ordnung bei der Positionierung – man muss hier aber etwas genauer hinschauen.
Wie habe ich diese beiden Lösungen gefunden?
Ich bin davon ausgegangen, dass die fünf Damen in einem 5×5 Felder großen Quadrat stehen – jede auf einer anderen Reihe und auf einer anderen Linie. Dieses 5×5-Quadrat soll oben rechts auf dem Brett liegen. Dadurch sind durch waagerechte und senkrechte Züge alle Felder des Schachbretts abgedeckt – bis auf das 3×3 Felder große Quadrat links unten.
Die Felder dieses 3×3-Quadrats werden dann über diagonale Züge der fünf Damen erreicht. Ich habe einfach sämtliche Diagonalen von links unten nach rechts oben gezogen – und dabei genau fünf Diagonalen erhalten.
Wenn nun jede der fünf Damen auf einer dieser fünf Diagonalen steht, sodass alle fünf Diagonalen besetzt sind, sind alle Felder des Schachbretts abgedeckt.
Es gibt übrigens noch Dutzende weitere Konstellationen, die mir Leser geschickt haben. Insgesamt sind wohl 4860 verschiedene Lösungen möglich. So lautet zumindest das Ergebnis von drei Lesern, die jeweils mit einem selbst geschriebenen Computerprogramm nach den Lösungen gefahndet haben. Dabei haben sie alle Stellungen von fünf Damen auf dem Brett systematisch durchprobiert und jeweils (per Code) geschaut, ob alle Felder bedroht sind.
In der wohl kuriosesten Lösung stehen alle fünf Damen in einer Reihe. Trotzdem werden von ihnen sämtliche Felder abgedeckt – natürlich teils über die Diagonalen.

Hübsch sind auch die beiden folgenden Lösungen, bei denen vier Damen auf einer Diagonalen stehen.

Bei vielen der eingesandten Lösungen bilden vier Damen die Eckpunkte eines Quadrats, das in Relation zum Schachbrett leicht gedreht ist. Eine Auswahl solcher Lösungen finden Sie hier:
Zwei weitere Lösungen verblüffen mit ihrer Symmetrie:

Es gibt jedoch auch Lösungen ohne offensichtliche Symmetrie:
