80) Spieglein, Spieglein an der Wand
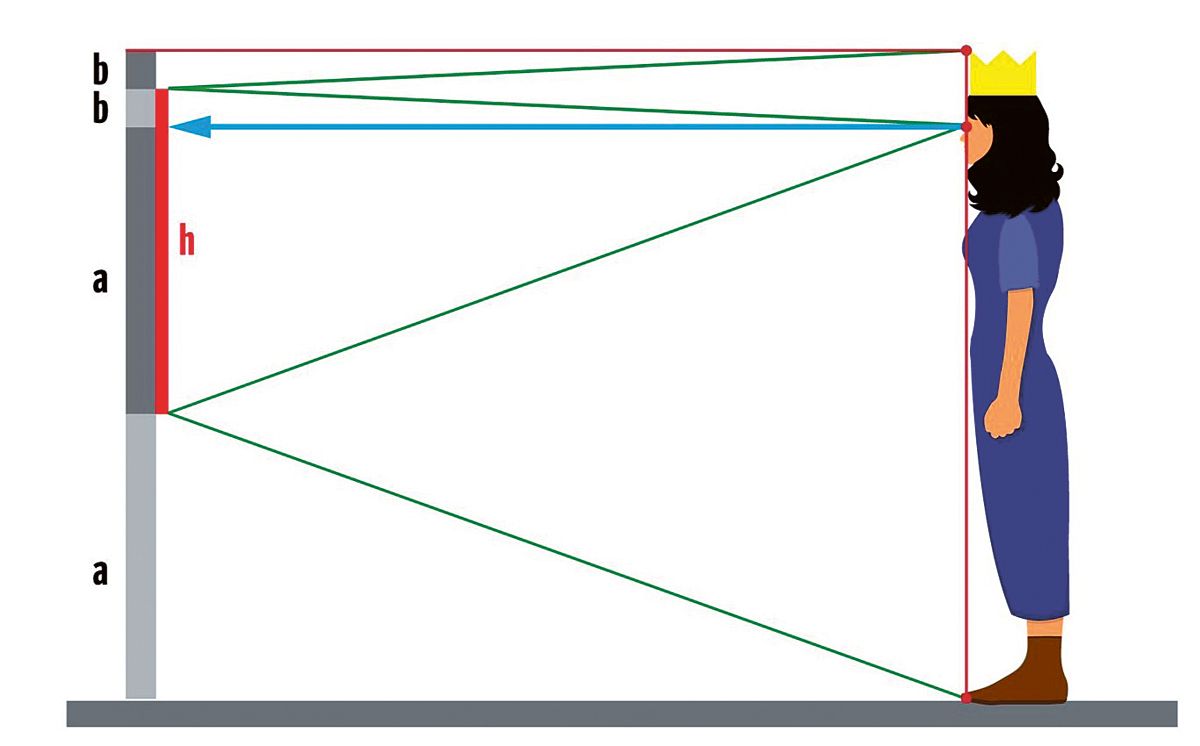
Der Spiegel muss halb so hoch sein wie die Königin samt Krone. Eine kleine Skizze hilft dabei, auf die Lösung zu kommen – und auch die Zusatzfragen zu beantworten:
Der Spiegel ist als schmaler, mit "h" bezeichneter senkrechter Strich gezeichnet.
Wenn die Königin ihre Schuhe im Spiegel sehen kann, treffen Lichtstrahlen auf ihre Augen, die an den Schuhen starten und vom Spiegel reflektiert werden. An einem ebenen Spiegel gilt dabei die Regel: Einfallswinkel der Strahlen ist gleich Ausfallswinkel.
Der tiefste Punkt der Schuhe, der unterste Punkt des Spiegels und die Augen der Königin bilden deshalb ein gleichschenkliges Dreieck. (Wir gehen bei dieser Betrachtung der Einfachheit halber davon aus, dass Schuhspitze und Augen genau senkrecht übereinander liegen.)
Die Höhe a über dem Boden, in der sich die Unterkannte des Spiegels befinden muss, ist deshalb halb so groß wie der senkrechte Abstand zwischen Schuhsohle und Augen.
Damit die Königin die Spitze ihrer Krone sehen kann, muss die Oberkante des Spiegels ein Stückchen oberhalb der Augen liegen. Diese Distanz b entspricht genau der halben senkrechten Strecke zwischen Augen und der höchsten Stelle der Krone.
Rechnet man a und b zusammen, kommt man auf die Höhe des Spiegels: Er muss mindestens halb so hoch sein wie die Königin – Schuhe und Krone inklusive.
Der Spiegel muss in der Höhe a+h über dem Boden hängen.
Der Abstand der Frau zum Spiegel hat übrigens keinen Einfluss auf dessen Mindesthöhe – und auch nicht auf den Abstand des Spiegels über dem Boden. Das liegt daran, dass die Spitzen der gleichschenkligen Dreiecke immer an derselben Stelle bleiben, egal, wie nah die Königin vor dem Spiegel steht.