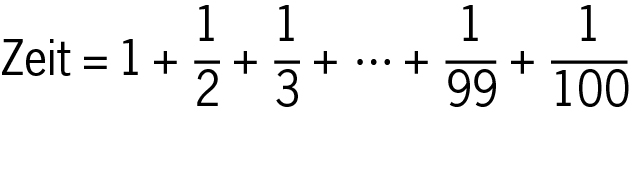
Schauen wir uns die Fahrt einfach in umgekehrter Reihenfolge an. Den letzten Kilometer schleicht das Auto mit nur noch 1 km/h über die Straße. Für diesen Kilometer braucht der harmoniesüchtige Fahrer dann eine Stunde. Beim vorletzten Kilometer, der 2 Kilometer vorm Ziel beginnt, sind es 2 km/h, was eine Fahrzeit von 1/2 Stunde ergibt.
Beim drittletzten Kilometer (3 km/h) erhält man die Fahrzeit von 1/3 Stunde. Beim viertletzten Kilometer ist es 1/4 Stunde und so weiter bis zum allerersten Kilometer (100 km/h) mit 1/100 Stunde Fahrzeit.
Wir sehen, dass die Fahrzeit in Stunden als Summe von hundert Brüchen geschrieben werden kann:
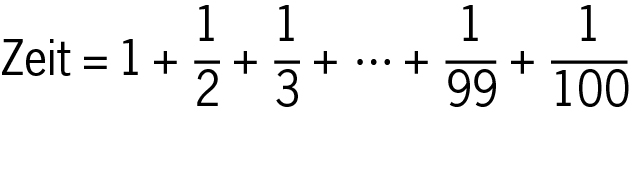
Die Zahlen 1; 1/2; 1/3; 1/4 bezeichnen Mathematiker als harmonische Folge. Summiert man die Zahlen so wie bei der Berechnung der Fahrzeit oben, erhält man eine sogenannte Partialsumme der harmonischen Reihe.
Es gibt übrigens keine allgemeingültige Formel, um diese Summe zu berechnen. Wer mit einer Tabellenkalkulation wie Excel gut umgehen kann, hat das Ergebnis im Nu berechnet: 5,19 Stunden, was rund 5 Stunden und 11 Minuten entspricht.
Es existiert jedoch immerhin eine Näherungsformel für die Partialsumme der harmonischen Reihe. Dabei addiert man den natürlichen Logarithmus der Zahl 100 und die Zahl 0,57721, genannt Euler-Mascheroni-Konstante.
Mit dieser Näherungsformel erhält man als Ergebnis 5,18 Stunden, was sehr nah am tatsächlichen Wert liegt.