© Springer International Publishing AG, part of Springer Nature 2019
Héctor Benítez-Pérez, Jorge L. Ortega-Arjona, Paul E. Méndez-Monroy, Ernesto Rubio-Acosta and Oscar A. Esquivel-FloresControl Strategies and Co-Design of Networked Control Systems Modeling and Optimization in Science and Technologies13https://doi.org/10.1007/978-3-319-97044-8_2

2. Modelling of Networked Control Systems

Héctor Benítez-Pérez1  , Jorge L. Ortega-Arjona2, Paul E. Méndez-Monroy3, Ernesto Rubio-Acosta1 and Oscar A. Esquivel-Flores1
(1)
Departamento de Ingeniería de Sistemas Computacionales y Automatización, IIMAS—National Autonomous University of Mexico, Mexico City, Mexico
(2)
Departamento de Matemáticas Facultad de Ciencias, National Autonomous University of Mexico, Mexico City, Mexico
(3)
Departamento de Ciencias de la Computación, IIMAS Mérida—National Autonomous University of Mexico, Mérida, Yucatán, Mexico
 
 
Héctor Benítez-Pérez
Email: hector.benitez@iimas.unam.mx

Abstract

This chapter shows models for time delays and others network imperfections generated into NCS and how they are integrated into control, scheduling or codesign algorithms. First, a time delay model is presented using a generalized exponential distribution based function with data collect from non-deterministic networks. After, three NCS models are presented, each incorporates information about the network imperfections with the ultimate aim of generating a corrective action. We present models based on control, communication and codesign methodologies. Finally, a neuro-fuzzy identification is presented to model the system states and estimate the parameters of the NCS based on multi-sampling periods.

2.1 Time Delay Model

Most of the nature of time delays has not been completely defined, therefore, it is a possibility to define these as uncertainties for several applications. Since there is not a unique nature of time delays, novel approaches become an affordable and competitive issue on course.

Generally, in common configurations of a NCS (Fig. 2.1), the Round Trip Time (RTT) is defined as the time it takes a package to go from a sensor node to an actuator node. The sensor node sends an information package to the controller node, and then, the controller node computes the control signal and sends it to the actuator node. Thus, the RTT is divided into two kinds of time delays: from the sensor node to controller node ($$\tau _{sc}$$), and from controller node to actuator node ($$\tau _{ca}$$).
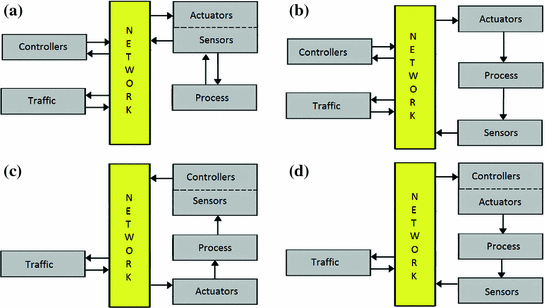
../images/321711_1_En_2_Chapter/321711_1_En_2_Fig1_HTML.gif
Fig. 2.1

NCS common configurations

If the sensor and actuator nodes are the same as case A or all the nodes are completely distributed as case B, the controller node normally is able to measure the $$\tau _{sc}$$, and estimate $$\tau _{ca}$$. In case C, if the sensor and controller nodes are the same, $$\tau _{sc} = 0$$, and $$\tau _{ca}$$ is estimated. Finally, the case D if the controller and actuator nodes are the same, the RTT is simply computed since $$\tau _{sc}$$ can be directly measured and $$\tau _{ca} = 0$$.

From previous configurations, the first two cases present both time delays $$\tau _{sc}$$ and $$\tau _{ca}$$, and thus, the case B is the one to be used to apply the methodologies proposed in this book. As stated before, only this configuration allows to measure $$\tau _{sc}$$, but it is necessary to estimate $$\tau _{ca}$$.

The occurrence of time delays on the nondeterministic networks are generally unknown and time varying and sometimes modelled as a random process with independent distribution. In real NCS implemented over IP networks exhibit time-varying time delays depending on the propagation distance, querying and congestion conditions, etc. This variability may be evaluated and taken into account in the modelling. Figure 2.2 illustrates real RTT delays measured between two x86 PCs interconected with an Ethernet network in the distributed control lab at National Autonomous University of Mexico (UNAM) campus Ciudad Universitaria. It shows the random behaviour in a short time [1].
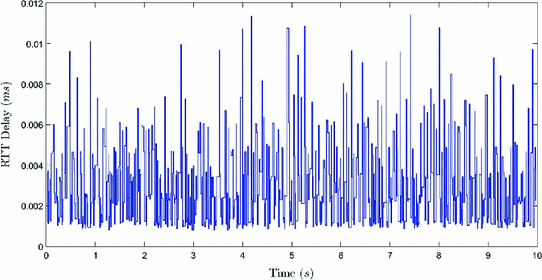
../images/321711_1_En_2_Chapter/321711_1_En_2_Fig2_HTML.gif
Fig. 2.2

RTT delay measured from an Ethernet network at UNAM

Figure 2.3 shows a histogram of the RTT time delays from an Ethernet network at UNAM, the histogram is skew to the left indicating a higher probability to have delays shorter than the mean and with a much lower probability to have delays much longer than the mean. This shape of the histogram can be modelled by a random probability distribution.
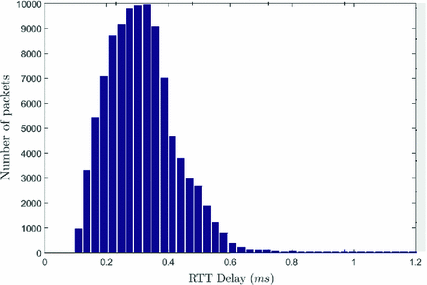
../images/321711_1_En_2_Chapter/321711_1_En_2_Fig3_HTML.gif
Fig. 2.3

Histogram of RTT delays measured into an Ethernet network at UNAM

We use the generalized exponential distribution to describe the RTT delays, this statistical model has the advantage of being simple to compute and easy to implement for real-time prediction. Besides, the parameters can be dynamically adapted, depending on the kind of network and different traffic conditions, significantly reducing the prediction error [2]. These are sufficient reasons to use the generalised exponential distribution as follow:
$$\begin{aligned} P( {\tau } ) = \left\{ {\begin{array}{*{20}c} \frac{1}{\varphi }e^{ - ( \tau - \eta ) \varphi } &{} \tau \ge \eta \\ 0 &{} \tau < \eta \end{array}} \right. \end{aligned}$$
(2.1)
where $$\eta $$ is a location parameter defining by the median of the time delay and $$\varphi $$ is a scale parameter defining by the standard deviation. The sample space is defined by the minimum RTT delay and the maximum allowable time delay bound (MATI) [3].

This distribution is computed for a time window with w previous measurements of time delay ($$\tau _{k-w+1},\ldots , \tau _{k-1}, \tau _k$$), where a expected time delay value for RTT is $$E[\tau _{k|w}] = \varphi + \eta $$ with variance $$Var[\tau _{k|w}]=\varphi ^2$$ [4].

The design of the model starts by choosing $$\eta $$. The median of the window is a feasible election, since it represents an expected time delay within the window. The distribution is obtained for each one of the values in the time window ($$\tau _{k-w+1}, \ldots , \tau _{k-1}, \tau _k$$). $$P[\tau _k = \hat{\eta }_{k+1|w}]$$ represents the time delay with the maximum probability. Using this value, the expected time delay values of the median $$\hat{\eta }_{k+1}$$ and standard deviation $$\hat{\varphi }_{k+1}$$ are computed, and hence:
$$\begin{aligned} \hat{\eta } _{k + 1|w} = w_i |P_{\mathop {\max }\limits _i } \left[ w \right] \end{aligned}$$
(2.2)
$$\begin{aligned} \widehat{\varphi }_{k + 1|w} = \sqrt{{\mathrm {var}} \left\{ {\tau _{k - w + 1} , \ldots ,\tau _{k - 1} ,\tau _k } \right\} } \end{aligned}$$
(2.3)
Being the estimated RTT:
$$\begin{aligned} \widehat{\tau }_{k + 1|w} = \widehat{\varphi }_{k + 1|w} + \widehat{\eta }_{k + 1|w} \end{aligned}$$
(2.4)

2.2 Adaptive Fuzzy Model

The strategies for control systems with static time delays is common in literature. Nevertheless, strategies considering variable time delays are uncommon. Among this kind of strategies, it is used optimal control (LQR, LQG) [5, 6], robust control ($$H_\infty $$) [7, 8], vanishing perturbation [9], and others. These strategies aim to keep a control input resilient to variations of time delays, no matter whether this is an optimal input for the NCS.

In this section, an proposed method is introduced using a fuzzy controller, its advantage is to generate optimal control signals for each time delay value. While, it is robust to variations in such time delays. First, the time delays are analyzed an modeled as Sect. 2.1.

The fuzzy control strategy based on TSK considers a variable structure system representation, this shows as:
$$\begin{aligned} \mu _{ij} \left( {x_i \left( k \right) } \right) = e^{ - \left( {\frac{{x_i(k) - \kappa _{ij} }}{{\sigma _{ij} }}} \right) ^2 } \qquad i = 1,\ldots ,n, j = 1,\ldots ,r \end{aligned}$$
(2.5)
where $$x_i(k)$$ is the ith state, n is the number of states, r is the number of fuzzy rules, and $$\mu $$ is the related membership function. Thus:
$$\begin{aligned} g_j = \prod \limits _{i = 1}^n \mu _{ij} (x_i(k)) \qquad j = 1,\ldots ,r \end{aligned}$$
(2.6)
$$\begin{aligned} h_j = \frac{{g_j }}{{\sum \limits _{i = 1}^r {g_i } }} \qquad j = 1 \ldots r \end{aligned}$$
(2.7)
$$\begin{aligned} x\left( {k + 1} \right)= & {} \sum \limits _{j = 1}^r { {h_j ({A_j x\left( k \right) + B_j u\left( k \right) })}} \\ y(k)= & {} \sum _{j = 1}^r h_j C_j x(k) \nonumber \end{aligned}$$
(2.8)
where $$x(k) \in \mathfrak {R}^{n}$$ are the system states (fuzzy inputs), n is the number of states, $$u(k) \in \mathfrak {R}^{m}$$ are the system inputs, m is the number of system inputs, $$y(k) \in \mathfrak {R}^{q}$$ are the system outputs, q is the number of system outputs. Also, $$A_j \in \mathfrak {R}^{n \times n}$$, $$B_j \in \mathfrak {R}^{n \times m}$$, and $$C_j \in \mathfrak {R}^{q \times n}$$ are the plant representation per scenario according to current time delays, where n is the number of states, m is the number of inputs of the system, and r is the number of fuzzy rules, as shown in Fig. 2.4.
Let us define a fuzzy model $$x_p(k)$$ for the plant. The Eq. 2.9 models some kinds of faults using a vector $$\rho _j$$. So, $$\rho _j^p$$ masks the plant faults and the model (2.9) is considering a local variable structure when faults occur and incorporating the time delays $$\tau ^{sc}$$ and $$\tau ^{ca}$$. Remember, the nature of fault is out of the scope of this book. Notice that $$\rho _j^p$$ is the relation of a fault presence through the event.
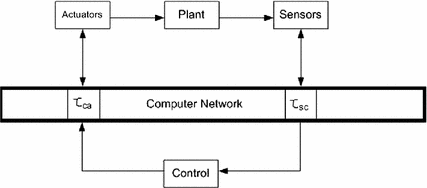
../images/321711_1_En_2_Chapter/321711_1_En_2_Fig4_HTML.gif
Fig. 2.4

Organization of nodes for a NCS

$$\begin{aligned} x_p \left( {k + 1} \right)= & {} \sum \limits _{j = 1}^r h_j (A_j^p x_p(k) + \rho _j^p B_j^p u_c(k - \tau _j^{ca})) \\ y_p(k)= & {} \sum _{j = 1}^r h_j C_j^p x_p(k) \nonumber \end{aligned}$$
(2.9)
where the subindex p corresponds to the dynamics of the plant.
From [10], the time delay representation in terms of discrete system in the range $$[t_i, t_{i+1}]$$ is:
$$\begin{aligned} B_j^p = \sum \limits _{j = 1}^{l_p } {\int \limits _{t_i }^{t_{i + 1} } e^{\hat{A}_j^p t} \hat{B}_j^p dt } \end{aligned}$$
(2.10)
where $$\hat{B}_j^p \in \mathfrak {R}^{n \times m}$$ is the input matrix and $$\hat{A}_j^p \in \mathfrak {R}^{n \times n}$$ is the state matrix of the continuous model of the plant. Remember that $$l_p$$ is the total number of local time delays that appears per scenario, and they respectively are the source of $$\tau _j^{sc}$$ and $$\tau _j^{ca}$$. Suppose that the system is in a stable equilibrium point. Thus, the only perturbations are the time delays, and hence, it is possible to assume the outputs $$(y_{p})$$ of the plant.
Since there is no external perturbation, and the dynamics of actuators and sensors are transparent, that is, they do not modify the control and state signals respectively, the outputs are gathered as follows:
$$\begin{aligned} y_p(k) = \sum \limits _{j = 1}^r {h_j {C_j^p x_p \left( k \right) }} \rightarrow u_c \left( {k - \tau _j^{sc} } \right) = y_p(k - \tau _j^{sc}) \end{aligned}$$
(2.11)
From this equation, substituting in Eq. 2.9, a complete representation of plant is obtained in terms of a system in equilibrium, given as:
$$\begin{aligned} x_p \left( {k + 1} \right) = \sum \limits _{j = 1}^r {h_j \left( {A_j^p x_p \left( k \right) + \rho _j^p B_j^p \sum _{i=1}^r h_j C_i^p x_c(k - \tau _i^{ca})}\right) } \end{aligned}$$
(2.12)
where $$x_c$$ is the feedback state for control.

Since the observed states need to be guaranteed, it is necessary to define a group of observers. The proposal of a control law in Sect. 4.​2 use a group of observers to guarantee as well the system structure and the local time delays are integrated into the dynamic structure. Therefore, stability, in terms of time delays and misleading structure, should be accomplished. A review of the control law is developed through the following chapters. The related observer states are presented as z(k). In this case $$N_j, M_j, L_j$$ and $$T_2$$ are the observer parameters, to be defined in Sect. 4.​2 [11].

2.3 Sampling Frequency Model

One of the strategies implemented for NCS control is feedback scheduling, where the goal is to know the performance of the communication network to modify the transmission of each node and improve the performance of the whole system.

The proposal for feedback scheduling into a real-time distributed system modifies the transmission frequency of each node into a region where the performance in each node is acceptable. This approach is a representation of the transmission frequencies using a time-invariant space state system, whose state variables are the desired transmission frequencies $$f_d^i$$ with $$i=1,\ldots ,n$$ of the n nodes involved in the NCS.

The objective of the space state system is to obtain the next desired frequencies. Each node i is bounded into a minimum $$f_m^i$$ and maximum $$f_x^i$$ transmission frequency computed offline. The $$f_m^i$$ are defined by the steady-state stability requirements associated to the node i and the $$f_x^i$$ are defined by the capacity of the node i itself without generating an excessive transmission cost into the network i.e. in a distributed system with n nodes, each one performing a task $$t_i$$ with a maximum frequency $$f_x^i$$ and consumption time per transmission packet $$\varepsilon _i$$, for $$i = 1,2,\ldots ,n$$ the following computational constraint needs to be accomplished:
$$\begin{aligned} U = \sum \limits _{i = 1}^n {{\varepsilon _i }*{f_x^i } \le 1} \end{aligned}$$
(2.13)
This equation implies that consumptions due to message transmission with the maximum frequencies should not exceed the network utilisation in order to avoid packet losses and time delays.

So, the state variables $$x=\{x_1, x_2,\ldots ,x_n\}$$ are the desired frequencies of the n nodes in the network control system. The objective of the proposed controller is to stabilize the current frequency of the system $$f_r$$ to the desired reference frequency $$f_d$$, through an optimal trajectory using a LQR controller.

By defining a discrete state space model as
$$\begin{aligned} x[k + 1]= & {} Ax[k] + Bu[k] \\ y[k]= & {} Cx[k] \nonumber \end{aligned}$$
(2.14)
where $$A \in \mathfrak {R}^{n \times n}$$ is the matrix of relationships between frequencies of the nodes, $$B \in \mathfrak {R}^{n \times n}$$ is the weighted frequency matrix, $$C \in \mathfrak {R}^{n \times n}$$ is the output matrix, $$x \in \mathfrak {R}^n$$ is a real frequency vector, and $$y \in \mathfrak {R}^n$$ is the next frequency vector.
Let $$a_{ij} \in A$$ be given by a function of minimal frequencies $$f_m^i$$ and $$b_{ij} \in B$$ given by a function of maximal frequencies $$f_x^i$$, where $$i = 1,2,\ldots ,n$$, $$j = 1,2,\ldots ,n$$ and n nodes:
$$\begin{aligned} a_{ij} = \varphi ( {f_m, f_r }) \end{aligned}$$
(2.15)
$$\begin{aligned} b_{ij} = \gamma ( {f_m, f_x }) \end{aligned}$$
(2.16)
The elements $$a_{ij}$$ and $$b_{ij}$$ in Eq. 2.14 are defined as follows:
$$\begin{aligned} a_{ij} = \left\{ {\begin{array}{*{20}c} \frac{f_m^i}{f_r^i } &{} i = j \\ 0 &{} i \ne j \end{array}} \right. \end{aligned}$$
(2.17)
$$\begin{aligned} b_{ij} = \left\{ {\begin{array}{*{20}c} \frac{f_m^i}{f_x^i} &{} i = j \\ \frac{f_m^i}{f_x^j } &{} i \ne j \end{array}} \right. \end{aligned}$$
(2.18)
$$\begin{aligned} c_{ij} = \left\{ {\begin{array}{*{20}c} 1 &{} i = j \\ 0 &{} i \ne j \\ \end{array}} \right. \end{aligned}$$
(2.19)
This will provide a model to modify the transmission frequency of each node depending on the current frequency. It is a reconfigurable system where indirectly the behaviours of the network imperfections and the NCS system are modified.

2.4 Control-Scheduling Codesign Model

Another approach for controlling NCSs with variable time delays is to take into consideration actuation periods. Here, the objective is to bound the variation space of the time delay to discrete values, making use of an estimated time delay with values that are multiples of the actuation period, and generate optimal control signals for such an estimated time delay. The configuration of a NCS takes into consideration the sensor node driven in time, whereas the controller and actuator nodes are event-driven. Using a space-state model of a discrete time linear system in invariant discrete time, with a sampling period h [12]:
$$\begin{aligned} x(k + 1)= & {} \varPhi (h) x(k) + \varGamma (h) u(k) \\ y(k)= & {} Cx(k) \nonumber \end{aligned}$$
(2.20)
where x(k) is the state of the plant, u(k) and y(k) are respectively the inputs and outputs of the plant, matrix $$C \in \mathfrak {R}^{p \times n}$$ is the output matrix, and matrices $$\varPhi (h)$$ y $$\varGamma (h)$$ are obtained using:
$$\begin{aligned} \varPhi (h) = e^{Ah} \qquad \varGamma (h) = \int \limits _0^h {e^{A} Bds} \end{aligned}$$
(2.21)
with $$A \in \mathfrak {R}^{n \times n}$$ and $$B \in \mathfrak {R}^{n \times m}$$ as the matrices of the system and input of the model in continuous form:
$$\begin{aligned} \dot{x}(t)= & {} Ax(t) + Bu(t) \\ y(t)= & {} Cx(t) \nonumber \end{aligned}$$
(2.22)
In the specific case of NCS, I/O latencies result from computing the control algorithm or due to the insertion of the network in the control loop. The standard model that comprises the time delay $$\tau $$, with $$\tau < h$$, is [12]:
$$\begin{aligned} x(k + 1) = \varPhi (h) x(k) + \varPhi (h - \tau ) \varGamma (\tau ) u(k - 1) + \varGamma (h - \tau ) u(k) \end{aligned}$$
(2.23)
The model in Eq. 2.23 is the simplest form used for analyzing and designing controllers for NCS. This model assumes a reference time, given by the sampling instants with a fixed time delay, starting at sampling, and until actuation. But if the time delay is variant and larger than the sampling period and/or the sampling interval is variant, then this model is not very feasible for NCS [13].
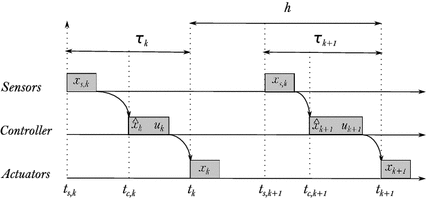
../images/321711_1_En_2_Chapter/321711_1_En_2_Fig5_HTML.gif
Fig. 2.5

Execution time of control tasks with instants of actuation

Here, a execution time of control tasks that synchronizes the operation of each control loop at the instant of actuation is proposed (Fig. 2.5). The sampling instants are labelled by t(s, k) where the system states $$x(s,k) \in [t(k-1),t(k)]$$ are obtained, and the instants of actuation are labelled by t(k) where the control signals u(k) are applied. Hence, the time elapsed between consecutive instants of actuation $$[t(k-1),t(k)]$$, has a actuating period h. The difference between the sampling instant t(s, k) and the following actuation instant t(k) is a variable time delay:
$$\begin{aligned} \tau (k) = t(k) - t(s,k) \end{aligned}$$
(2.24)
and it is used for estimating the state in the actuation instant:
$$\begin{aligned} \hat{x}(k) = \varPhi (\tau (k)) x(s,k) + \varGamma (\tau (k)) u(k - 1) \end{aligned}$$
(2.25)
A control strategy relies on the time reference given by the instant of actuation. In addition, samples are not required to be strictly periodic, because $$\tau (k)$$ in Eq. 2.24 can vary at each closed-loop operation. The interested reader is referred to [14] for further reading on this control model.

Each instant of actuation, the actuator node generates the next actuation instant t(k), which is sent to the sensor after applying the control signal $$u(k-1)$$ to the plant. Upon reception of this message or next sampling period, the sensor samples the plant x(s, k), and records the absolute sampling time t(s, k). The latter, together with t(k), is used to compute $$\tau (k)$$. Both x(s, k) and $$\tau (k)$$ are sent to the controller node. Upon reception of this message, the controller node estimates the plant state that applies at $$\tau (k)$$ (Eq. 2.25) with the next estimated time delay $$\tau (k+1)$$, and computes a control command u(k) designed in Chap. 4. This is sent to the actuator that applies it to the plant at the synchronised actuation instant.

The NCS architecture (Fig. 2.6) has four types of nodes connected to an Ethernet network: sensor, controller, actuator, and traffic nodes. A control loop comprises communication between sensor-controller and controller-actuator nodes. Traffic nodes send periodic or sporadic packets into network, like for example, other control loops or monitoring.
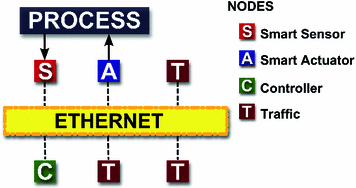
../images/321711_1_En_2_Chapter/321711_1_En_2_Fig6_HTML.gif
Fig. 2.6

NCS configuration

All nodes send User Datagram Protocol (UDP) packets to avoid double traffic into network. However, it is not possible to know whether there is packets loss or a maximum time delay since there is no acknowledgement that the sent packet has been received.

Here, network-induced time delays and variable sampling intervals smaller than a sampling period are compensated by the one-shot model, and the fuzzy model compensates time delays longer than such a sampling period.

The time delay is estimated in the controller using Eqs. (2.1–2.4) (Fig. 2.7). When the control node receives a new packet, this contains the state x(s, k) and the time delay $$\tau (k-1)$$. Once the time delay $$\tau (k-1)$$ is received, an exponential distribution algorithm [15] is used to estimate the next time delay $$\hat{\tau }(k)$$. This algorithm is widely used to estimate delays in real time, where an offline statistical analysis characterises mean and standard deviation $$q_E(\eta ,\phi )$$ of time delays data $$\tau $$ with multiple scenarios of traffic. Those are used to form a generalized exponential distribution with a probability density function (Eq. 2.1).
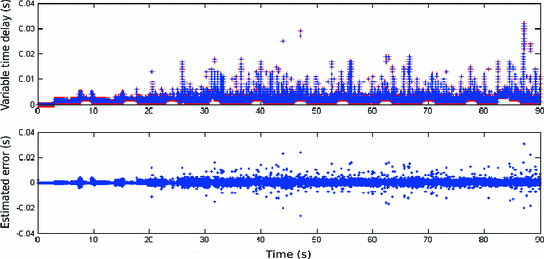
../images/321711_1_En_2_Chapter/321711_1_En_2_Fig7_HTML.gif
Fig. 2.7

Variable time delay ($$\tau _k$$) behaviour and estimation error with algorithm in Sect. 2.1

Once the next time delay $$\hat{\tau }(k)$$ of the system is estimated, it is used to generate a control signal. This controller starts with a fuzzy model of the NCS, designed as follows.

The fuzzy model (Eq. 2.25) is TSK type [16], with the time delay $$\hat{\tau }(k)$$ as input of the antecedent part, and linear discrete models with different sampling periods $$h_j$$ as consequent part. Thus, defining r fuzzy rules, the jth rule has the form:
$$\begin{aligned} if \,\, \hat{\tau }(k) \,\, is \,\, \alpha _j(\hat{\tau }) \,\, then \,\, x_j = \varPhi (h_j) x(s,k) + \varGamma (h) \end{aligned}$$
(2.26)
where $$x(k) \in \mathfrak {R}^{n}$$ is the state vector of system, $$u(k) \in \mathfrak {R}^{n}$$ is the input vector of process, $$\alpha _j(\hat{\tau })$$ is the jth membership function of the estimated time delay $$\hat{\tau }(k)$$.
The overall fuzzy model is:
$$\begin{aligned} \hat{x}(k+\hat{\tau }(k)) = \sum _{j=1}^r \varPsi _j(\varPhi _j x(s,k) + \varGamma _j u(k)) \end{aligned}$$
(2.27)
where the normalized fire strength $$\varPsi _j$$ is:
$$\begin{aligned} \varPsi _j = \frac{\alpha _j}{\sum _{s=1}^r \alpha _s} \qquad \varPsi _j \ge 0 \qquad \sum _{j=1}^r \varPsi _j = 1 \end{aligned}$$
(2.28)
and $$\alpha _j = exp(-(\hat{\tau }(k)-\rho _j)^2/\sigma _j^2)$$ is a Gaussian membership function with parameters $$(\rho _j,\sigma _j)$$. $$(\varPhi _j,\varGamma _j)$$ are the matrices of jth linear discrete model discretised with a sampling period $$h_j$$ ($$j = 1, \ldots , r$$). The discrete local models are:
$$\begin{aligned} x_j = e^{A h_j} x(k) + \int _{0}^{h_j} e^{A s} ds B u(k) = \varPhi _j x(k) + \varGamma _j u(k) \end{aligned}$$
(2.29)
so, $$(h_j, \rho _j, \sigma _j)$$ for $$j = 1, \ldots , r$$ are assigned by user according to offline time delay measurement.

With this fuzzy model, the estimated state of a system is obtained by compensating the time delays and variable sampling intervals. The action is to smoothly switch between discrete models, to generate the best estimate of state, according to the estimated time delay $$\hat{\tau }(k)$$. Once designed the fuzzy model (2.26) using the estimated time delay $$\hat{\tau }(k)$$, a fuzzy controller is proposed in Chap. 4.

2.5 Neuro-Fuzzy Identification

The objective of the neuro-fuzzy model is to define the best linear model for each sampling period representing the system. This model estimates the system states according to the possible time delay calculated by an exponential distribution function defined in Sect. 2.1.

The neuro fuzzy model (Eq. 2.30) is TSK type [17] with variable sampling period $$\hat{\tau }(k)$$ as antecedent input, and discrete models with different sampling periods T as consequent part. So, defining r fuzzy rules, the jth rule has the form:
$$\begin{aligned} \mathrm{if }\ \hat{\tau }(k) \ \mathrm{is} \ \alpha ^j ( {\hat{\tau }})\ \mathrm{then\ x}^j \left( {k + T^j } \right) = { \varPhi } ^j { x}(k) + { \varGamma }^j { u}(k) \end{aligned}$$
(2.30)
where $$x(k) \in \mathfrak {R}^n$$ is the state vector of the system, $$u(k) \in \mathfrak {R}^m$$ is the input vector of the plant, $$\alpha ^j$$ is the jth membership function of variable sampling period $$\hat{\tau }(k)$$.
The overall fuzzy model is:
$$\begin{aligned} { \hat{x}}\left( {k + \hat{\tau }} \right) = \sum _{j = 1}^r {\psi ^j } \left( { \varPhi } ^j { x}\left( k \right) + { \varGamma } ^j { u}\left( k \right) \right) \end{aligned}$$
(2.31)
where the normalized fire strength $$\psi ^j$$ is:
$$\begin{aligned} \psi ^j = \frac{{a^j }}{{\sum _{s = 1}^r {a^s } }},\ \ \psi ^j \ge 0,\ \ \sum _{j = 1}^r {\psi ^j = 1,}\ \ a^j = \exp \left( { - \frac{{\left( {\hat{\tau }_k - \rho ^j } \right) ^2 }}{{\left( {\sigma ^j } \right) ^2 }}} \right) \end{aligned}$$
(2.32)
where $$\alpha ^j$$ is a Gaussian membership function with parameters $$(\rho ^j,\sigma ^j)$$, and $${ \varPhi }^j \in \mathfrak {R}^{n \times n}$$ and $${ \varGamma }^j \in \mathfrak {R}^{n \times n}$$ are the matrices of jth linear model, with m outputs and periods $$T = \{ \rho ^1 , \rho ^2 , \ldots , \rho ^r \}$$.

The system states are approximated with this fuzzy model. The objective is to smoothly switch between discrete models, to generate the best estimate of states according to the variable sampling period$$\hat{\tau }_k$$. However, there are some parameters such as $$({ \varPhi }^j,{ \varGamma }^j,\rho ^j,\sigma ^j)$$ that need to be tuned using a neuro-fuzzy approach [18, 19]. This section uses data of the simulated system with some specific time delays to get the model parameters, although, alternatively techniques like LMI may be used and reviewed in other works as [20]. The neuro-fuzzy model (Eq. 2.30) is identified using inputs-states data with measured variable sampling period $$D = \{x_l,u_l,\tau _l|l=1,\ldots ,L\}$$, obtained from a Truetime simulation of the system [21], with a PID controller and a traffic node on an Ethernet network.

The identification procedure has two algorithms: a clustering algorithm, to create new rules, and a training algorithm, to update the model’s parameters. The procedure is repeated $$\phi $$-epochs. M is maximum firing strength of all rules for variable sampling period and $$K_d$$ is its threshold. $$K_e$$ is a threshold of maximum model error. J is the performance index to update the matrices $$({ \varPhi }^j,{ \varGamma }^j)$$.

Procedure: The first fuzzy rule is created with the discrete model, with sampling period $$\rho _0$$, which is the variable sampling period mean, and $$\sigma _0$$ is the predetermined width. So, matrices $${ \varPhi }^1$$ and $${ \varGamma }^1$$ of the first rule are:
$$\begin{aligned} { \varPhi } ^1 = e^{\left( {{ A}\rho _0 } \right) } \end{aligned}$$
(2.33)
$$\begin{aligned} { \varGamma } ^1 = \int _0^{\rho _0 } {e^{{{ A}s}} ds{ B}} \end{aligned}$$
(2.34)
$$\begin{aligned} \rho ^1 = \rho _0 = mean\left( \tau \right) \ \ \ \ \ \ \sigma ^1 = \sigma _0 \end{aligned}$$
(2.35)
A new rule is created using the $$\varepsilon $$-completeness criterion, which states that, for any input within operation range, there is a rule with fire strength $$\alpha ^j$$ greater than a threshold $$K_d$$ [22]. So, if maximum firing strength M of all rules is less than $$K_d$$ then a new rule is created.
$$\begin{aligned} M = \mathop {\max }\limits _j \mathop {\left( {\alpha ^j } \right) }\limits _{} \end{aligned}$$
(2.36)
$$\begin{aligned} M < K_d \end{aligned}$$
(2.37)
With this clustering algorithm, it is ensured that all variable sampling periods of the training data are represented by the antecedent part of the neuro-fuzzy model.
In the training algorithm, the parameters of local models are estimated using error criterion. It says that, if an output error e is less than a threshold $$K_e$$ (Eq. 2.40), the parameters should be adjusted. The threshold $$K_e$$ is decreased according to the current epoch f.
$$\begin{aligned} e = \left| {y\left( {k + 1} \right) - \hat{y}\left( {k + 1} \right) } \right| \end{aligned}$$
(2.38)
$$\begin{aligned} e > K_e \end{aligned}$$
(2.39)
$$\begin{aligned} K_e = \frac{{e_{\max } + e_{\min } }}{{\phi - 1}}\left( {f - 1} \right) + e_{\max } \end{aligned}$$
(2.40)
where $$e_{max}$$ is the final error expected at the end of training, $$e_{min}$$ is the initial error obtained in the first epoch without training, f is the current training epoch, and $$\phi $$ is the total of epochs.
The backpropagation approach is used for the adjustment of the parameters. So, a performance index J is used to adjust the model with objective to minimise J (modelled error).
$$\begin{aligned} J = \frac{1}{2}\left\| {\hat{x} - x} \right\| ^2 = \frac{{\sum _{p = 1}^n {\left( {\hat{x}_p - x_p } \right) } }}{2} \end{aligned}$$
(2.41)
The coefficients $$a_{p,q}^j$$ and $$b_{p,o}^j$$ of the system $${ \varPhi }^j$$ and control $${ \varGamma }^j$$ matrices, respectively, as well as the centres and standard deviations are adjusted by:
$$\begin{aligned} a_{q,p}^j \left( {k + 1} \right) = a_{q,p}^j \left( k \right) - \eta _a \left( {\hat{x}_p \left( {k + 1} \right) - \hat{x}_p \left( {k + 1} \right) } \right) \psi ^j x_q \left( k \right) \end{aligned}$$
(2.42)
$$\begin{aligned} b_{p,i}^j \left( {k + 1} \right) = b_{p,i}^j \left( k \right) - \eta _b \left( {\hat{x}_p \left( {k + 1} \right) - \hat{x}_p \left( {k + 1} \right) } \right) \psi ^j u_i \left( k \right) \end{aligned}$$
(2.43)
$$\begin{aligned} \rho ^j \left( {k + 1} \right)= & {} \rho ^j \left( k \right) - \eta _\rho \left( {\hat{x}\left( {k + 1} \right) - \hat{x}\left( {k + 1} \right) } \right) \\&\left( {\varPhi ^j \hat{x}\left( k \right) + \varGamma ^j u\left( k \right) } \right) \left( {\psi ^j - \left( {\psi ^j } \right) ^2 } \right) \left( { - 2\frac{{\hat{\tau }- \rho ^j }}{{\left( {\sigma ^j } \right) ^2 }}} \right) \nonumber \end{aligned}$$
(2.44)
$$\begin{aligned} \sigma ^j \left( {k + 1} \right)= & {} \sigma ^j \left( k \right) - \eta _\sigma \left( {\hat{x}\left( {k + 1} \right) - \hat{x}\left( {k + 1} \right) } \right) \\&\left( {\varPhi ^j \hat{x}\left( k \right) + \varGamma ^j u\left( k \right) } \right) \left( {\psi ^j - \left( {\psi ^j } \right) ^2 } \right) \left( { - 2\frac{{\left( {\hat{\tau }- \rho ^j } \right) ^2 }}{{\left( {\sigma ^j } \right) ^3 }}} \right) \nonumber \end{aligned}$$
(2.45)
where $$\eta $$ is the learning rate for each parameter, $$q,p = 1, \ldots , n$$, $$o = 1,\ldots ,m$$; and $$j = 1,\ldots ,r$$. The data used in here is the result of analysis of general scenarios considering local time delays and ethernet channel communication.

Once designed and identified, the fuzzy model (Eqs. 2.30, 2.31, 2.32) is presented a fuzzy controller in Chap. 4, using estimated variable sampling period $$\hat{\tau }(k)$$.

2.6 Concluding Remarks

This chapter presents a statistical model of the time delay through an exponential probability density function that allows estimating the time delay for compensation purposes, the model assumes a variable time delay and greater than the sampling period of the system, Model is validated using experimental data. Three design methodologies are also presented.

The first method presents a model using fuzzy theory to incorporate the estimated time delay with several space-state models. This allows improving the state estimation to be used in the controller with minimal computational cost.

The second method presents a sampling frequency model through a state-space model that represents the dynamic behaviour of the transmission frequency as a function of the actual transmission frequency into the network with longer time delays or lost deadlines.

The third method presents a methodology of codesign where through two fuzzy models are trade-off the control and scheduling performance. The first model incorporates linear models with different sampling periods obtaining delay-dependent system states. The second model uses QsC and QsS to schedule the next stable actuation period and minimise the system error and the effect of network uncertainties.

Finally, a neural strategy is presented to obtain the fuzzy rules that allow to identify the complete NCS system and to improve the estimation of the states of the system.