© Springer International Publishing AG, part of Springer Nature 2019
Héctor Benítez-Pérez, Jorge L. Ortega-Arjona, Paul E. Méndez-Monroy, Ernesto Rubio-Acosta and Oscar A. Esquivel-FloresControl Strategies and Co-Design of Networked Control Systems Modeling and Optimization in Science and Technologies13https://doi.org/10.1007/978-3-319-97044-8_4

4. Design of Networked Control System

Héctor Benítez-Pérez1  , Jorge L. Ortega-Arjona2, Paul E. Méndez-Monroy3, Ernesto Rubio-Acosta1 and Oscar A. Esquivel-Flores1
(1)
Departamento de Ingeniería de Sistemas Computacionales y Automatización, IIMAS—National Autonomous University of Mexico, Mexico City, Mexico
(2)
Departamento de Matemáticas Facultad de Ciencias, National Autonomous University of Mexico, Mexico City, Mexico
(3)
Departamento de Ciencias de la Computación, IIMAS Mérida—National Autonomous University of Mexico, Mérida, Yucatán, Mexico
 
 
Héctor Benítez-Pérez
Email: hector.benitez@iimas.unam.mx

Abstract

This chapter presents the control strategies and codesign based on the NCS models presented in Chap. 2. Three methodologies are proposed focusing on vanishing the perturbations generated by the network, such as time delays larger than a sampling period and lost packets. First, an adaptive fuzzy control is developed according to the scheduling algorithm and the known and bounded time delay, the stategy us a fuzzy model and a LQR control design to modify the control input according to the time delay. A sampling frequency control is presented where the transmission frequiencies are modified into a region according the quality of services into the network. Finally, a codesign strategy is reviewed where the quality of service and the quality of control are trade-off with two fuzzy model, one fuzzy model modifies the input control based on the current sampling period and other fuzzy model modifies the next sampling period based on the time delays and lost packets in a time-lapse.

4.1 Classical Approaches

A feedback control system, in which control loops are closed via a communication network, is called Networked Control System (NCS). Thus, sensors, actuators, controllers and others (monitors, etc.) are interconnected via one or several communication networks. The main advantages of this kind of systems are (a) their low cost, (b) the small volume of wiring, (c) the distributed processing, (d) their simple installation, (e) their maintenance, and (f) their reliability.

Recently, much attention has been paid to control design and stability analysis of NCSs [1–3]. The key problems to solve are minimized the effect of network-induced time delays and packet loss that degrade system performance. In general, time delay has been considered as constant, time varying, or even random. Time delay, as well as packet loss, depends on several factors such as the scheduler, network type, architecture, operating systems, processor conditions, etc. [4] as reviewed in Chap. 3. When the time delay is less than the sampling period of NCS, results indicate that time delay degrades the system performance. However, this situation is possible to be solved [5]. When the time delay is greater than sampling period, with a varying or random behaviour, the performance of a NCS is considerably reduced. Hence, it is necessary to analyse time delays and packet loss to develop an efficient approach for reducing its effect on NCS. For instance, Nilsson analyses important facets of NCSs [4], introducing models for the time delays of a NCS. First, time delays are modelled as fixed values; later, they are modelled as independently random values; and finally, they developed a Markov process. Nilsson introduces optimal stochastic control theorems for NCSs, based on independently random and Markovian delay models, and considering time delays smaller than a sampling period.

Another approach is the well known Takagi-Sugeno-Kang (TSK) fuzzy models, which are qualified to represent a certain class of non-linear dynamic systems [5], and many control techniques have been developed following this approach. In particular, regarding NCS designs that make use of the TSK fuzzy models, some results have recently been published [6, 7]. In [6], a control with fault detection for NCSs with Markov delays is addressed, in which a linear plant is modelled in the discrete-time domain. A set of TSK fuzzy rules is used to deal with network-induced delays. Further, results in [6, 8] are formulated in the continuous time domain, where the TSK fuzzy systems with norm-bounded uncertainties are used to characterise the non-linear NCSs. Nilsson [4] proposes a LQR (Linear Quadratic Regulator) based on Fuzzy Logic. It presents a method for online estimation of the time delays for an invariant sampling period, and it is assumed that delays being less than a sampling period. Takaba [9] shows a robust control design for NCS polytopic systems, with time delays uncertain with PID controllers, but it only presents numerical examples attempting to show the effectiveness of the method.

Regarding the topic of time delays, [10] presents the effect of modelling time delays with a variable sampling period in discrete time systems. A similar approximation has been presented in [9], where a specific study on time delays is reviewed, as well as an application strategy for NCS. Walsh et al. [11] shows a practical approximation of time delays, assuming a regular computer network.

All these previous works provide some control or scheduling strategy, aiming for robustness to constant, and even varying, time delays. Similarly, for packet loss, several approaches assume a linear and available system model, which is periodically sampled. This means that some restrictions have to be taken into consideration for the implementation of control systems. Thus, here it is proposed a controller to stabilise non-linear systems, assuming that there is no model of the system-network. The only knowledge available is a continuous linear model, is used fuzzy controllers and assuming statistical values of RTT delay and packet loss due to the network activity as presented in [12].

NCSs have been focused on how time delays modify the dynamics of the system’s behaviour during time response. Classical approaches have been reviewed in [13]. They suppose beforehand that time delays are mainly static and known. In these cases, when time delays present a dynamic behaviour, the dynamic modelling becomes quite complex, and in terms of the non-linearities presented. Therefore, it is necessary to build a mathematical approximation, capable of tackling the dynamic behaviour of time delays. One approach has been modelling the stochastic behaviour of time delays, as explored in [13], where the behaviour of time delays is modelled in terms of a Brownian system. An alternative approximation makes use of queueing theory, describing system performance in terms of a stochastic procedure for time delays. This approach tends to be appealing, particularly when non-linear computer networks are used, such as Ethernet, in large scale networks, in which several routers are involved for communication [13].

Another approach has been to consider real-time systems in which strictly bounded time is the main goal. Therefore, time delays are known, even during dynamic conditions. Classic approximations are presented by [5]. In this, the results are valid, although restricted by certain conditions like bounded time delays. In this case, the use of scheduling algorithms is explored, with interesting results on system stability.

An interesting approach proposes to control the frequency transmission from the communication channels, to guarantee how time delays behave in short and long terms. In this case [14], they propose a classical approach, using LQG, to guarantee time response from communication channels. However, this is only a first attempt over a complex problem, in which several conditions still have to be explored to overcome the natural restrictions from a LQG approximation. In terms of stability, a strong condition is reviewed by [2]. In this, a Lyapunov Krasovskii strategy is presented as a strong mathematical tool to determine when stochastic varying time delays take place. Time delays tend to be bound to certain realistic conditions, in terms of the behaviour of the computer network. Another approach makes use of the TSK Fuzzy control [15], in which there is a strong gain scheduling technique that combines several linear scenarios into a global stable system. In this, the use of linear matrix inequalities is a mechanism to design and ensure a global stable situation. One important condition is the restriction of the system in terms of observability for global purposes. A holistic review of this case has been studied in [16], in which several time delay conditions are determined, such as oversampling, package loss, long time delays, and stochastically bounded time delays. This work provides a clear approximation to time delays in several local conditions, with the compromise to guarantee global stability.

A final approximation for NCS is based on the synchronisation among nodes belonging to a complex system. Several approximations have been developed to the goal of fixed time delays, like extended states for synchronisation purposes of LMI procedures.

4.2 Adaptive Fuzzy Control

In this section, the objective is to present a adaptive control strategy developed from the time delay knowledge, and following scheduling approximation, where time delays are known and bounded, according to the scheduling algorithm used. The proposed scheduling strategy here has been reviewed in [17, 18]. It pursues to tackle local faults in terms of fault tolerance. In this situation, uncertain time delays would be inevitable.

The case study here makes use of the classical Earliest Deadline First (EDF) and the Priority Exchange (PE) algorithm to decompose timelines, and the respective inherent time delays. For instance, time delays are supervised for a number of tasks as follows:
$$\begin{aligned} \varepsilon _1 \rightarrow \varepsilon _n/T_1 \rightarrow T_n \end{aligned}$$
(4.1)
Priority is provided by the EDF algorithm, in which the process with the closest deadline has the highest priority. However, when an aperiodic task appears, it is necessary to deploy other algorithms to cope with the current conditions. To do so, the PE algorithm is used to manage the spare time from the EDF algorithm. The PE algorithm [18] uses a virtual server that deploys a periodic task with the highest priority, to provide enough computing resources for aperiodic tasks. This simple procedure provides an approximate, deterministic, and dynamic behaviour, within the group of included processes. In this case, time delays can be deterministic and bounded.

Example 4.1

Consider the group of tasks as shown in Table 4.1. In this case, consumption times, as well as periods, are given in terms of integer units. Remember: the server task is the time given for an aperiodic task to take place on the system.

The result of the ordering, based on PE, is presented in Fig. 4.1.

Based on this dynamic scheduling algorithm, time delays are given as current calculations in terms of task ordering. In this case, every time that the scheduling algorithm takes place, the global time delays are modified in the short and long term.

For instance, consider the following example, in which four tasks are set, and two aperiodic tasks take place at different times, giving different events with different time delays (Table 4.2).

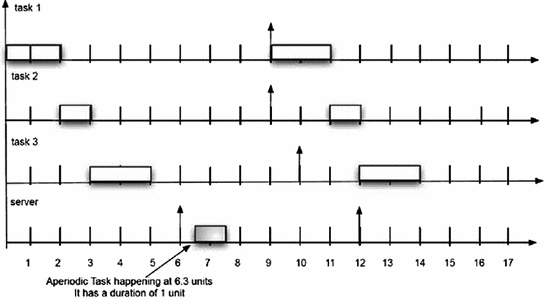
../images/321711_1_En_4_Chapter/321711_1_En_4_Fig1_HTML.gif
Fig. 4.1

Related organization for PE of tasks in Table 4.1

Table 4.1

First example for PE algorithm

Name

Consumption (in units)

Period (in units)

Task 1

1

5

Task 2

2

9

Task 3

1

8

Server

1

11

Table 4.2

Second example of PE

Name

Consumption (in units)

Period (in units)

Task 1

1

5

Task 2

2

9

Task 3

1

8

Server

1

11

Aperiodic task1 (ap1)

0.9

It occurs at 9

Aperiodic task (ap2)

1.0

It occurs at 13

The following task ordering is shown in Fig. 4.2, using the PE algorithm, in which clearly time delays appear.
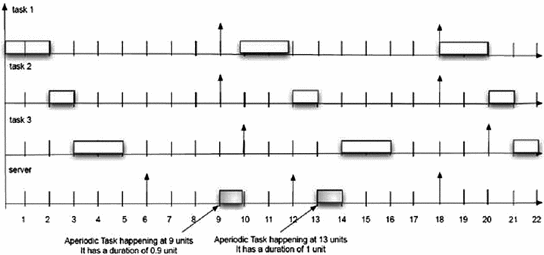
../images/321711_1_En_4_Chapter/321711_1_En_4_Fig2_HTML.gif
Fig. 4.2

Task organizations considering the second example for the PE algorithm

Now, from this, a resulting ordering of these tiny time delays are given for two scenarios, as shown in Fig. 4.3.
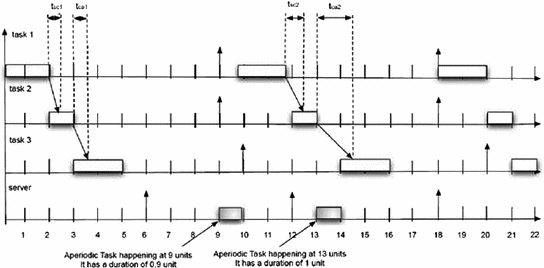
../images/321711_1_En_4_Chapter/321711_1_En_4_Fig3_HTML.gif
Fig. 4.3

Related time delays are depicted according to both scenarios

These two scenarios present two different local time delays that need to be taken into account beforehand to settle the related time delays, according to scheduling approach and control design. These time delays can be expressed in terms of local relations between both dynamical systems. These relations are the actual and possible delays, bounded as marked limits of possible and current scenarios. Then, delays may be expressed as local summations with a high degree of certainty.

In the last example, during the second scenario, a total delay is given as:
$$\begin{aligned} TotalDelay= & {} consumption\,Time\,Delay\,Aperiodic\,Task1 \\+ & {} consumption\,Time\,Delay\,Task1 \nonumber \\+ & {} tsc2 + consumption\,Time\,Delay\,Task2 \nonumber \\+ & {} consumption\,Time\,Delay\,Aperiodic\,Task2 \nonumber \\+ & {} consumption\,TimeDelay\,Task3 \nonumber \end{aligned}$$
(4.2)
Now, from this example, $$lp = 2$$ ($$consumption\,Time\,Delay\,Aperiodic\,Task1 + consumption\,Time\,Delay\,Task1 + tsc2 + consumption\,Time\,Delay\,Task2$$) and $$lc = 3$$ ($$consumption\,Time\,Delay\,Aperiodic\,Task2 + consumption\,Time\,Delay\,Task3$$). lp and lc are the total number of local delays within one scenario, from sensor to control, and from control to actuator, respectively. lp and lc are used as limits of current delays per scenario, as shown in Eqs. 2.​10 and 4.4. These limits are modified according to the allowed scenario that guarantees schedulability during online process. Nevertheless, this execution need to be bounded by the only considered scenarios from TSK modelling as presented in previous chapter.
Having defined time delays as result of a scheduling approximation, several scenarios are potentially present following this time delay behaviour. In fact, the number of scenarios is finite, since the combinatorial formation is bounded. Therefore, any strategy in order to design a control law needs to take into account gain scheduling approximation, and thus, retaking the fuzzy model in Sect. 2.​2, the controller is defined as follows:
$$\begin{aligned} x_c \left( {k + 1} \right)= & {} \sum \limits _{j = 1}^r h_j (A_j^c x_c(k) + \rho _j^c B_j^c u_c(k - \tau _j^{sc})) \\ y_c(k)= & {} \sum _{j = 1}^r h_j C_j^c x_c(k) \nonumber \end{aligned}$$
(4.3)
where the indexes c correspond to the dynamics of the controller.
The time delay representation in discrete system in the range $$[t_i, t_{i+1}]$$ is:
$$\begin{aligned} B_j^c = \sum \limits _{j = 1}^{l_c } {\int \limits _{t_i }^{t_{i + 1} } e^{A_j^c t}\hat{B}_j^c dt } \end{aligned}$$
(4.4)
where $$\hat{B}_j^c$$ are the sets of input matrices of the continuous time models of the controller. According to (2.​5) $$l_c$$ represent the total number of local time delays that appears per scenario, and they are the source of $$\tau _j^{sc}$$. The output is gathering as following:
$$\begin{aligned} y_c(k) = \sum \limits _{j = 1}^r {h_j {C_j^c x_c \left( k \right) }} \rightarrow u_p \left( {k - \tau _j^{ca} } \right) = y_c(k - \tau _j^{ca}) \end{aligned}$$
(4.5)
A complete representation of process and control is obtained in terms of a system in equilibrium, given as:
$$\begin{aligned} x_c \left( {k + 1} \right) = \sum \limits _{j = 1}^r {h_j \left( {A_j^c x_c \left( k \right) + \rho _j^c B_j^c \sum _{i=1}^r h_i C_i^c x_p(k - \tau _i^{sc})}\right) } \end{aligned}$$
(4.6)
From the last equation, the related control dynamics are expressed as $$A_j^c$$, $$B_j^c$$, and $$C_j^c$$, where j is the index with respect to each scenario.
With the fuzzy model in Eq. 2.​12, the estimated state of system is obtained by compensating the time delays and variable sampling intervals. The action is to smoothly switch between discrete models, to generate the best estimate of state, according to the estimated time delay $$\hat{\tau }(k)$$. Thus, let us propose a design for the fuzzy controller, using a fuzzy feedback control law like:
$$\begin{aligned} u(k) = - \sum _{j=1}^r h_j \bar{L}_j x(k) \qquad j = 1, \dots , r \end{aligned}$$
(4.7)
where $$\bar{L}_j$$ is the feedback matrix of the jth fuzzy rule. This control law is designed like a LQR (Linear Quadratic Regulator) [19] to minimize a performance index:
$$\begin{aligned} J_j(x,u) = \sum _{k=0}^\infty [x^T(k) \bar{Q}_j x(k) + u^T(k) R_j u(k)] \qquad j=1,\dots , r \end{aligned}$$
(4.8)
where $$\bar{Q}_j = \bar{Q}_j^T \ge 0$$ and $$R_j = R_j^T \ge 0$$. The control design by LQR for each local model requires the algebraic solution of the Ricatti equation for the $$H_j$$ matrix.
$$\begin{aligned} A_j^T H_j A_j - H_j + \bar{Q}_j - A_j^T H_j B_j (R_j + B_j^T H_j B_j)^{-1} B_j^T H_j A_j = 0 \end{aligned}$$
(4.9)
So, the feedback matrices are calculated like:
$$\begin{aligned} \bar{L}_j = (R_j + B_j^T H_j B_j)^{-1} B_j^T H_j A_j \qquad j=1,\dots ,r \end{aligned}$$
(4.10)
The closed loop system is:
$$\begin{aligned} x(k+1)= & {} \sum _{i=1}^r \sum _{j=1}^r \alpha _i \beta _j (A_i - B_i \bar{L}_j) x(k) \\= & {} \sum _{i=1}^r \sum _{j=1}^r \alpha _i \beta _j \varLambda _{ij} x(k) \nonumber \end{aligned}$$
(4.11)
with $$\varLambda _{ij}=A_i - B_i \bar{L}_j$$, $$i = 1, \dots , r$$ and $$j = 1, \dots , r$$.
The following properties of the antecedent part (Eq. 2.​7) are considered for the stability analysis of fuzzy control (Eq. 4.7):
$$\begin{aligned} h_i h_j \ge 0 \qquad \sum _{i=1}^r \sum _{j=1}^r h_i h_j = 1 \qquad \sum _{i=1}^r h_i^2 + 2\sum _{i,j}^{i < j} h_i h_j = 1 \end{aligned}$$
(4.12)
Based on the properties of fuzzy control, and assuming two-overlapped fuzzy memberships at most, the stability analysis of closed loop fuzzy control is presented.

Theorem 4.1

There is a controller in discrete time such that $$x_c \rightarrow 0$$ and $$x_p \rightarrow 0$$ when $$k \rightarrow \infty $$, if there are two matrices defined positive $$P_1 \in \mathfrak {R}^{n \times n}$$ and $$P_2 \in \mathfrak {R}^{n \times n}$$, such that the following conditions of the LMIs hold:
$$\begin{aligned} (A_j^p - B_{j}^p L_j^p)^T P_1 (A_j^p - B_{j}^p L_j^p) - P_1 < 0 \end{aligned}$$
(4.13)
$$\begin{aligned} \,\,(A_j^c - B_{j}^c L_j^c)^T P_2 (A_j^c - B_{j}^c L_j^c) - P_2 < 0 \end{aligned}$$
(4.14)
In the case of a fault event disruption, the error (as well as time delays) modifies the local structure through time, as an overall situation. Although $$\rho _j^p$$ or $$\rho _j^c$$ in Eq. 4.3 highlight a missing state in terms either plant or controller as described in Chap. 2. The proposal of a current group of observers is to guarantee system structure. Therefore, stability, in terms of time delays and misleading structure, should be accomplished. The related observers states are presented as z(k) following [20]. In this case $$N_j$$, $$M_j$$, $$L_j$$, and $$T_2$$ are the observer parameters to be defined as a classic Unknown Input Observer (UIO).
The UIO is represented as:
$$\begin{aligned} z(k+1) = \sum _{j=1}^{r} h_j (N_j z(k) + M_j u_1^p(k-\hat{\tau }_{1j}^{sc}) + L_j y_p(k)) \end{aligned}$$
(4.15)
$$\begin{aligned} \hat{x}_p(k) = z(k) + T_2 y_p(k) \end{aligned}$$
(4.16)
The objective now is to find the observer’s gains E, G, $$N_j$$, $$M_j$$, $$L_j$$, and $$T_2$$, this is, to design the observer such that the observer error $$e_o(k) \rightarrow 0$$ when $$k \rightarrow \infty $$. Thus, defining $$e_o(k) = x_p(k) - \hat{x}_p(k)$$, and substituting Eq. 4.16:
$$\begin{aligned} e_o(k) = x_p(k) - z(k) - T_2 C x_p(k) - T_2 G u_2^p(k - \hat{\tau }_{2j}^{sc}) \end{aligned}$$
(4.17)
Assuming there is a $$T_1$$ and $$T_2$$ with the following constraints:
$$\begin{aligned} T_1 E + T_2 \sum _{i=1}^r C_i = I_n \end{aligned}$$
(4.18)
With the constraints (4.18), the observer error is:
$$\begin{aligned} e_o(k)= & {} T_1 x_p(k) - z(k) \end{aligned}$$
(4.19)
and its discrete difference is:
$$\begin{aligned} e_o(k+1)= & {} T_1 x_p(k+1) - z(k+1) \end{aligned}$$
(4.20)
Substituting $$x_p(k+1)$$ and $$z(k+1)$$ using Eqs. 2.​12 and 4.15, respectively:
$$\begin{aligned} \begin{aligned} e_o(k+1) = \sum _{j = 1}^r h_j [&T_1 (A_j^p x_p(k) + \rho _j^p B_{1j}^p u_1^p(k-\hat{\tau }_{1j}^{sc}) + B_{2j}^p u_2^p(k-\hat{\tau }_{2j}^{sc})) \\&- N_j z(k) - M_j u_1^p(k-\hat{\tau }_{1j}^{sc}) - L_j y_p(k)] \end{aligned} \end{aligned}$$
(4.21)
Reordering, and using the observer error definition:
$$\begin{aligned} \begin{aligned} e_o(k+1) = \sum _{j = 1}^r h_j [&N_j e_o(k) + \left( T_1 A_j^p - N_j T_1 - L_j \sum _{i=1}^r C_i \right) x_p(k) \\&+ (T_1 B_{1j}^p - M_j ) u_1^p(k-\hat{\tau }_{1j}^{sc}) + T_1 B_{2j}^p u_2^p(k-\hat{\tau }_{2j}^{sc})] \end{aligned} \end{aligned}$$
(4.22)
In terms of augmented states, the estimated states are presented by the observer, since the local variable structure is used when local fault appears as well as the time delays.
Let the augmented state be the union of the fuzzy model, the fuzzy controller, and the fuzzy observer:
$$\begin{aligned} \begin{aligned} \left[ \begin{array}{*{20}c} {x_p \left( {k + 1} \right) } \\ {e_o\left( {k + 1} \right) } \\ {\hat{x}_p \left( {k + 1} \right) } \\ \end{array} \right] = \sum \nolimits _{j = 1}^r h_j \\ \left[ \begin{array}{*{20}c} {A_j^p x_p\left( k \right) + \rho _j^p B_{1j}^p u_1^p(k) + \rho _j^p B_{2j}^p u_2^p(k)} \\ {N_j e_o(k) + (T_1 A_j^p - N_j T_1 - L_j \sum _{i=1}^r C_i) x_p(k) + (T_1 B_{1j}^p - M_j ) u_1^p(k) + T_1 B_{2j}^p u_2^p(k)} \\ {A_j^c x_c\left( k \right) + \rho _j^c B_{1j}^c u_1^c(k) + \rho _j^c B_{2j}^c u_2^c(k)} \end{array} \right] \end{aligned} \end{aligned}$$
(4.23)
Reordering this last equation, and using a matrix representation:
$$\begin{aligned} \left[ \begin{array}{*{20}c} {x_p(k + 1)} \\ {x_c(k + 1)} \\ {e_o(k + 1)} \\ \end{array} \right]= & {} \sum _{j = 1}^r h_j \left[ \begin{array}{*{20}c c c} A_j^p &{} 0 &{} 0 \\ 0 &{} A_j^c &{} 0 \\ T_1 A_j^p + N_j T_1 - L_j \sum _{i=1}^r C_i &{} 0 &{} N_j \end{array} \right] \left[ \begin{array}{*{20}c} {x_p(k)} \\ {x_c(k)} \\ {e_o(k)} \\ \end{array} \right] \nonumber \\+ & {} \sum _{j = 1}^r h_j \left[ \begin{array}{*{20}c} \rho _j^p B_{j}^p &{} 0 \\ 0 &{} \rho _j^c B_{j}^c \\ T_1 B_{1j}^p - M_j &{} 0 \\ \end{array} \right] \left[ \begin{array}{*{20}c} {u_1^p(k-\hat{\tau }_{1j}^{sc})}\\ {u_1^c(k-\hat{\tau }_{1j}^{ca})} \end{array} \right] \nonumber \\ \nonumber \\+ & {} \sum _{j = 1}^r h_j \left[ \begin{array}{*{20}c c} 0 &{} 0 \\ 0 &{} 0 \\ T_1 B_{2j}^p &{} 0 \\ \end{array} \right] \left[ \begin{array}{*{20}c} {u_2^p(k-\hat{\tau }_{2j}^{sc})}\\ {u_2^c(k-\hat{\tau }_{2j}^{ca})} \end{array} \right] \end{aligned}$$
(4.24)
The observer error of the system is:
$$\begin{aligned} \left[ \begin{array}{*{20}c} x_p(k + 1) \\ x_c(k + 1) \\ e_o(k + 1) \\ \end{array} \right]= & {} \sum _{j = 1}^r h_j \left[ \begin{array}{*{20}c c c} \varLambda _j^p &{} 0 &{} 0 \\ 0 &{} \varLambda _j^c &{} 0 \\ 0 &{} 0 &{} N_j \end{array} \right] \left[ \begin{array}{*{20}c} {x_p(k)} \\ {x_c(k)} \\ {e_o(k)} \\ \end{array} \right] \end{aligned}$$
(4.25)
where $$\varLambda _j^p = A_j^p - B_{1j}^p L_j^p$$ and $$\varLambda _j^c = A_j^c - B_{1j}^c L_j^c$$.
Defining a parameter $$Q_j = N_j T_2 - L_j$$, and substituting the feedback Eq. 4.7 for plant and controller:
$$\begin{aligned} \left[ \begin{array}{*{20}c} {x_p(k + 1)} \\ {x_c(k + 1)} \\ {e_o(k + 1)} \\ \end{array} \right]= & {} \sum _{j = 1}^r h_j \left[ \begin{array}{*{20}c c c} A_j^p - B_{1j}^p L_j^p &{} 0 &{} 0 \\ 0 &{} A_j^c - B_{1j}^c L_j^c &{} 0 \\ 0 &{} 0 &{} T_1 A_j + Q_j C_j \end{array} \right] \left[ \begin{array}{*{20}c} {x_p(k)} \\ {x_c(k)} \\ {e_o(k)} \\ \end{array} \right] \end{aligned}$$
(4.26)
This is so if the following constraints are fulfilled:
$$\begin{aligned} I_n= & {} T_1 + T_2 \sum _{i=1}^r C_i \end{aligned}$$
(4.27)
$$\begin{aligned} 0= & {} T_1 B_{2j} \end{aligned}$$
(4.28)
$$\begin{aligned} M_j= & {} T_1 B_{1j} \end{aligned}$$
(4.29)
$$\begin{aligned} L_j= & {} N_j T_2 - Q_j \end{aligned}$$
(4.30)
$$\begin{aligned} N_j= & {} T_1 A_j + Q_j \sum _{i=1}^r C_i \end{aligned}$$
(4.31)
Verifying the constraints of Eqs. 4.27, 4.28, and 4.31, the problem reduces to find a matrix $$\varTheta $$ such that:
$$\begin{aligned} \varTheta X= & {} Y \end{aligned}$$
(4.32)
$$\begin{aligned} N_i= & {} \varTheta Y_i \end{aligned}$$
(4.33)
where $$\varTheta $$, X, Y, and $$Y_i$$ are defined as follows:
$$\begin{aligned} \varTheta = [T_1 T_2 Q_1 Q_2 \dots Q_r] \end{aligned}$$
(4.34)
$$\begin{aligned} X = \left[ \begin{array}{*{20}c c c c} 1 &{} B_{21}^p &{} \dots &{} B_{2r}^p \\ \sum _{i=1}^r C_i &{} 0_{m \times q} &{} \dots &{} 0_{m \times q} \\ \end{array} \right] \end{aligned}$$
(4.35)
$$\begin{aligned} Y = [I_n 0_{n \times rq}] \end{aligned}$$
(4.36)
$$\begin{aligned} Y_i = \left[ \begin{array}{*{20}c} A_i \\ e_i \otimes \sum _{i=1}^r \end{array} \right] \end{aligned}$$
(4.37)

where $$e_i$$ is the column vector with all its components equal to zero except the i-th component, which is 1.

Lemma 4.1

There is a UIO (Eqs. 4.15 and 4.16) such that the following conditions stands:
$$\begin{aligned} rank \ X = rank \ \left[ \begin{array}{*{20}c c c} B_{21}^p &{} \dots &{} B_{2r}^p \\ \end{array} \right] + n \end{aligned}$$
(4.38)
Once defined the existence of the UIO, it is necessary to define the observability of the system. The following lemma states the observability conditions.

Lemma 4.2

The estimation error of the UIO tends to zero ($$e_o \rightarrow 0$$) while time tends to infinity ($$k \rightarrow \infty $$) if there is a matrix $$P \in \mathfrak {R}^{n \times n}$$, and a matrix $$\hat{Z} \in \mathfrak {R}^{n \times (n + m(r+1))}$$ such that the following LMIs are fulfilled for $$i = 1 \dots r$$:
$$\begin{aligned} \left[ \begin{array}{*{20}c c} \varPhi _i &{} (\bar{X} Y_i)^T \hat{Z}^T \\ \hat{Z}(\bar{X} Y_i) &{} -P \end{array} \right] < 0 \end{aligned}$$
(4.39)
where matrix $$\bar{X} = 1 - X X^+$$, and $$X^+$$ is the pseudo inverse of matrix X, and $$\varPhi _i$$ is:
$$\begin{aligned} \varPhi _i = (\bar{X} Y_i)^T \hat{Z}^T (X^{+} Y_i) + (Y X^{+} Y_i)^T Z (\bar{X} Y_i) + (Y X^{+} Y_i)^T P (Y X^{+} Y_i) - P \end{aligned}$$
(4.40)
The complete conditions of the controllers and the UIO are:
$$\begin{aligned} (A_j^p - B_{1j}^p L_j^p)^T P_1 (A_j^p - B_{1j}^p L_j^p) - P_1 < 0 \end{aligned}$$
(4.41)
$$\begin{aligned} (A_j^c - B_{1j}^c L_j^c)^T P_2 (A_j^c - B_{1j}^c L_j^c) - P_2 < 0 \end{aligned}$$
(4.42)
$$\begin{aligned} N_i^T P_3 N_i - P_3 < 0 \end{aligned}$$
(4.43)

These provide the base for the following theorems.

Theorem 4.2

There is a UIO in discrete time, if the condition in Eq. 4.38 holds, and if there is a matrix $$P_3 \in \mathfrak {R}^{n \times n}$$, and a matrix $$\hat{Z} \in \mathfrak {R}^{n \times (n + m(r+1))}$$ such that there exist the LMIs in Eq. 4.39.

For designing the controllers and the UIO in discrete time, the next procedure is followed:
  1. 1.

    Design the controller for the plant $$L_j^p$$ such that the Theorem 4.1 holds.

     
  2. 2.

    Verify the condition of Lemma 4.1.

     
  3. 3.

    Solve the LMIs for $$P_3$$ and $$\hat{Z}$$ (Eq. 4.39).

     
  4. 4.

    Obtain Z with $$Z = P^{-1} \hat{Z}$$.

     
  5. 5.

    Obtain $$N_j$$, $$M_j$$, and $$L_j$$ (Eqs. 4.29, 4.30 and 4.31).

     
Now, the related information amongst local plants and controllers has been reviewed up to this point. Additionally, it is important to consider the nature of time delays, along with a review of the local observers. Here, the time delays are independent, based on the time obtained from the scheduling approximation:
$$\begin{aligned} \tau _i^{sc} + \tau _i^{ca} < T \qquad i = 1, 2, \dots \end{aligned}$$
(4.44)
Further, solving this condition is numerically possible through an LMI solving strategy like [7]. However, the current system representation results quite restrictive, although possible, by using Fuzzy TSK where variables from fuzzy structure control design and observers definitions are tuned through this strategy.

4.3 Sampling Frequency Control

An approximation to schedule a real-time distributed system is based on bounding time delays through modifications on frequency transmission of individual components in the system, as presented in [14]. From this, the scheduling of a distributed system can be accomplished through modifications on transmission frequencies into a region, where the system performance is not affected. This approach drives the periodicity transmission though three parameters: minimum frequency $$f_m$$, real frequency $$f_r$$, and maximum frequency $$f_x$$. The distributed system dynamics can be modeled as a linear time-invariant system, whose state variables are transmission frequencies $$f_i = \frac{1}{p_i}$$ of the n nodes involved in the NCS. Notice that there is a relationship between node frequencies and external input frequencies, which, therefore, serves as coefficients for the linear system. The objective of controlling periodicity is to achieve coordination through the convergence of values. Each sensor i has a minimum $$f_m^i$$ and maximum frequencies $$f_x^i$$ transmission rates, which are computed off-line. Using the model presented in Sect. 2.​3, a control law can be designed to modify the sampling frequencies.

The control input is given by a function of desired frequencies ($$f_d$$) and real frequencies ($$f_r$$) for all the sensors:
$$\begin{aligned} u = -k^s ( {f_d - f_r }) = -k^s x(k) \end{aligned}$$
(4.45)
Note that $$k^s$$ is the control gain, defined as the basics of a LQR algorithm, and $$f_d$$ and $$f_r$$ are vectors. Now, the plant 2.14 is defined as follows, in terms of frequency transmission:
$$\begin{aligned} x(k + 1)= & {} Ax(k) + Bu(k) \\ x(k + 1)= & {} A(f_d - f_r)(k) - Bk^s(f_d(k) - f_r(k)) \nonumber \\ x(k + 1)= & {} Af_d(k) - Af_r(k) - Bk^s f_d(k) + Bk^s f_r(k) \nonumber \\ x(k + 1)= & {} ( {A - Bk^s })(f_d - f_r)(k) \nonumber \end{aligned}$$
(4.46)
In this case, the network constraint (2.​13) needs to be accomplished. Regarding the network utilization, this equation implies that consumptions due to message transmission should not exceed the transmission periods, on order to avoid packet losses and time delays.
Defining $$e(k) = (f_d - f_r)(k)$$, Eq. 4.46 becomes:
$$\begin{aligned} e(k+1) = (A - Bk^s) e(k) \end{aligned}$$
(4.47)
Now defining $$e_5(k) = \varepsilon _d(k) - \varepsilon _r(k)$$ as the augmented state, the system is as follows:
$$\begin{aligned} \left[ {\begin{array}{*{20}c} {e_1 \left( {k + 1} \right) } \\ {e_2 \left( {k + 1} \right) } \\ {e_3 \left( {k + 1} \right) } \\ {e_4 \left( {k + 1} \right) } \\ {e_5 \left( {k + 1} \right) } \\ \end{array}} \right] = \left[ {\begin{array}{*{20}c} {\frac{{\overline{\lambda }}}{{f_m^1 }}} &{} {\frac{{f_m^2 }}{{f_m^1 }}} &{} {\frac{{f_m^3 }}{{f_m^1 }}} &{} {\frac{{f_m^4 }}{{f_m^1 }}} &{} 0 \\ {\frac{{f_m^1 }}{{f_m^2 }}} &{} {\frac{{\overline{\lambda }}}{{f_m^2 }}} &{} {\frac{{f_m^3 }}{{f_m^2 }}} &{} {\frac{{f_m^4 }}{{f_m^2 }}} &{} 0 \\ {\frac{{f_m^1 }}{{f_m^3 }}} &{} {\frac{{f_m^2 }}{{f_m^3 }}} &{} {\frac{{\overline{\lambda }}}{{f_m^3 }}} &{} {\frac{{f_m^4 }}{{f_m^3 }}} &{} 0 \\ {\frac{{f_m^1 }}{{f_m^4 }}} &{} {\frac{{f_m^2 }}{{f_m^4 }}} &{} {\frac{{f_m^3 }}{{f_m^4 }}} &{} {\frac{{\overline{\lambda }}}{{f_m^4 }}} &{} 0 \\ {c_1 } &{} {c_2 } &{} {c_3 } &{} {c_4 } &{} 1 \\ \end{array}} \right] - \end{aligned}$$
$$\begin{aligned} \left[ {\begin{array}{*{20}c} {f_x^1 } &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} {f_x^2 } &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} {f_x^3 } &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} {f_x^4 } &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ \end{array}} \right] \left[ {\begin{array}{*{20}c} {k_1^s } &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} {k_2^s } &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} {k_3^s } &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} {k_4^s } &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} {k_5^s } \\ \end{array}} \right] {\left[ {\begin{array}{*{20}c} {e_1(k)} \\ {e_2(k)} \\ {e_3(k)} \\ {e_4(k)} \\ {e_5(k)} \\ \end{array}} \right] } \end{aligned}$$
(4.48)
$$\begin{aligned} \left[ {\begin{array}{*{20}c} {e_1 \left( {k + 1} \right) } \\ {e_2 \left( {k + 1} \right) } \\ {e_3 \left( {k + 1} \right) } \\ {e_4 \left( {k + 1} \right) } \\ {e_5 \left( {k + 1} \right) } \\ \end{array}} \right] = \left[ {\begin{array}{*{20}c} {\frac{{\overline{\lambda }}}{{f_m^1 }} - f_x^1 k_1^s } &{} {\frac{{f_m^2 }}{{f_m^1 }}} &{} {\frac{{f_m^3 }}{{f_m^1 }}} &{} {\frac{{f_m^4 }}{{f_m^1 }}} &{} 0 \\ {\frac{{f_m^1 }}{{f_m^2 }}} &{} {\frac{{\overline{\lambda }}}{{f_m^2 }} - f_x^2 k_2^s } &{} {\frac{{f_m^3 }}{{f_m^2 }}} &{} {\frac{{f_m^4 }}{{f_m^2 }}} &{} 0 \\ {\frac{{f_m^1 }}{{f_m^3 }}} &{} {\frac{{f_m^2 }}{{f_m^3 }}} &{} {\frac{{\overline{\lambda }}}{{f_m^3 }} - f_x^3 k_3^s } &{} {\frac{{f_m^4 }}{{f_m^3 }}} &{} 0 \\ {\frac{{f_m^1 }}{{f_m^4 }}} &{} {\frac{{f_m^2 }}{{f_m^4 }}} &{} {\frac{{f_m^3 }}{{f_m^4 }}} &{} {\frac{{\overline{\lambda }}}{{f_m^4 }} - f_x^4 k_4^s } &{} 0 \\ {c_1 } &{} {c_2 } &{} {c_3 } &{} {c_4 } &{} 1 - k_5^s \\ \end{array}} \right] \left[ {\begin{array}{*{20}c} {e_1(k)} \\ {e_2(k)} \\ {e_3(k)} \\ {e_4(k)} \\ {e_5(k)} \\ \end{array}} \right] \end{aligned}$$
(4.49)
Hence, the local application of the scheduling algorithm is needed for the partial recovery of the NCS, but this implies that the overall performance of the NCS is now degraded.

4.4 Control—Scheduling Codesign

Codesign has the main objective of mixing the advantages of two or more knowledge areas, while minimising their disadvantages, aiming to adequately solve a common problem. In NCS, the control-communication codesign commonly integrates the feedback control and real-time communications. It is based on the principle that the performance of the system depends on the design of the control algorithms, as well as on the performance of the scheduling of shared communication resources.

Unfortunately, NCS design is frequently based on the principle of separation of concerns [21]. This principle assumes that feedback controllers can be modelled and implemented as periodic tasks with a fixed period, and with a known consumption, for instance, Worst Case Execution Time (WCET), and a rigid deadline. These assumptions focus on the control problem without worrying about how tasks are scheduled in the nodes, and how packets are sent through the network. Nevertheless, it is not quite understood how scheduling impacts on the system’s performance.

The control of tasks does not always make use of the available computing resources in an optimal way, and the assumptions of the model of a simple task are too restrictive regarding the characteristics of many control systems. For example, many deadlines are not always rigid, this is, many practical control systems can occasionally tolerate losing their deadlines. To solve the limitation of resources in a NCS, codesign is made necessary at several different levels. For instance, hardware/software codesign, mechanic/electric codesign, etc. Here, the control/scheduling codesign is presented. In practical terms, the control/communication codesign can be divided into two categories: feedback control of computational systems and real-time control.

The control of computational systems is also known as feedback scheduling [21]. The basic idea is dealing with the scheduling problem as a feedback control problem. A control feedback loop is introduced in the resource scheduler of the computational systems. The objective of feedback scheduling is to increase the flexibility with respect to the uncertainties in resource utilisation. Instead of pre-assigning resources based on an off-line analysis, resources are assigned dynamically on-line, based on a feedback from the actual utilisation of the resource.

A second category of codesign focus on real-time control. Branisky et al. [22] is perhaps one of the first authors to establish that scheduling algorithms and control systems cannot be separately designed. They work the problem of plant regulation as an optimal scheduling problem, studying the limitations of Rate Monotonic (RM) scheduling, as well as the limitations on NCS stability, taking into consideration issues such as induced time delays, packet loss, and multiple packet transmission. Branisky [22] considers a set of NCSs as linear plants with transmission only between sensor and controller, with a period T equal to its deadline, and with a consumption time $$c_i$$. Applying the RM algorithm for scheduling, a static priority is assigned to each controlled plant. A higher priority is assigned to a plant with faster dynamics since it has a higher transmission rate than other slower dynamic plants. The set of N tasks is feasible if the utilisation factor of the network U is less than 1. For optimising the scheduling, it is assumed that each NCS is associated with an average performance function h, which provides with the cost of control as a function of the transmission period $$h_i$$. Selecting such a performance function is essential for the optimisation problem. Normally, a quadratic or exponential cost is chosen. Branisky et al. [22] analyse the allowed percentage of packet loss that secures the stable performance of a NCS. The NCS with packet loss is modelled as a dynamic asynchronous system. It is assumed that the sampling period is constant, and the NCS tolerates a certain amount of lost feedback data. Even though they employ the concept of codesign of a NCS, the method has a few liabilities due to they only consider the data transmission between sensor and controller, and a constant time delay is considered for the analysis of lost packets.

In [23] it is made use of the concept of feedback control of computational resources for scheduling the resources and the workload of a processor. They propose two schemes to manage the systems with a control task or multitask. The design of the control system takes into account unknown time delays, given some uncertainties of time, which are unavoidable. Likewise, they present a new control design method, using state feedback for discrete systems with time delays, formulated as LMI. For feedback scheduling, they consider communication delays mainly as the latency input-output. The objective is to on-line adjust the sampling period of the controller, to cope with the requirements of computational resources, using discrete time systems, in which, for calculating the control input, the communication delay is obtained by the addition of the network induced delay plus the computational cost delay.

Fuzzy Controller

A new modelling method for nonlinear NCS with variable time delays is presented in Sect. 2.​4. It is represented by a TSK fuzzy model [15], with the estimated time delay $$\hat{\tau }(k)$$ as input of the antecedent part, and linear discrete models with different sampling periods $$h_j$$ as consequent part. Once designed the fuzzy model a fuzzy controller is proposed. Thus, defining r fuzzy rules, the jth rule has the form:
$$\begin{aligned} if \,\, \hat{\tau }(k) \,\, is \,\, \alpha _j(\hat{\tau }) \,\, then \,\, u_j = \varPhi (h_j) K_{j} \hat{x}_{k} \end{aligned}$$
(4.50)
where $$x(k) \in \mathfrak {R}^{n}$$ is the state vector of system, $$u(k) \in \mathfrak {R}^{n}$$ is the input vector of process, $$\alpha _j(\hat{\tau })$$ is the jth membership function of the estimated time delay $$\hat{\tau }(k)$$.
The overall fuzzy feedback control is:
$$\begin{aligned} \begin{array}{cc} u_{k} =-\sum \limits _{j=1}^{r}\psi _{j} K_{j} \hat{x}_{k}&j=1,\ldots ,r \end{array} \end{aligned}$$
(4.51)
where $$K_{j}$$ is the feedback matrix of the j-th fuzzy rule. This control law is designed like a LQR (Linear Quadratic Regulator) [19] to minimize a performance index. The control design by LQR for each local model requires the algebraic solution of the Ricatti equation for the $$H_{j}$$ matrix. So, the feedback matrices are calculated like:
$$\begin{aligned} \begin{array}{cc} K_{j} =\left( R_{j} +\varGamma _{j}^{T} H_{j} \varGamma _{j} \right) ^{-1} \varGamma _{j}^{T} H_{j} \varPhi _{j}&j=1-r \end{array} \end{aligned}$$
(4.52)
The closed loop system is:
$$\begin{aligned} \begin{array}{rl} x_{k+1} &{}=\sum \limits _{i=1}^{r}\sum \limits _{j=1}^{r}\alpha _{i} \beta _{j} \left( \varPhi _{i} -\varGamma _{i} K_{j} \right) x_{k} \\ &{}=\sum \limits _{i=1}^{r}\sum \limits _{j=1}^{r}\alpha _{i} \beta _{j} \varLambda _{ij} x_{k} \end{array} \end{aligned}$$
(4.53)
with $$\varLambda _{ij} =\varPhi _{i} -\varGamma _{i} K_{j} \ \ \ i=1,\ldots ,r \ \ \ j=1,\ldots ,r.$$
The following properties of the antecedent part are considered for the stability analysis of fuzzy control (4.51):
$$\begin{aligned} \begin{array}{lll} \psi _{i} \psi _{j} \ge 0 \\ \sum \limits _{i=1}^{r}\sum \limits _{j=1}^{r}\psi _{i} \psi _{j} =1 \\ \sum \limits _{i=1}^{r}\psi _{i}^{2} +2\sum \limits _{i,j}^{i<j}\psi _{i} \psi _{j} =1 \end{array} \end{aligned}$$
(4.54)
Using this properties and assume that two-overlapped fuzzy memberships at most a stability analysis is presented in [24] using the Theorem 4.1.

Theorem 4.3

The equilibrium state $$x_{e}=0$$ of closed loop system with control input (4.53 with two-overlapped fuzzy memberships at most, is asymptotically stable in the large, if there exist $$\mu $$ positive definite matrices $$P_{s} =P_{s}^{ T}>0$$ such that:
$$\begin{aligned} \begin{array}{ccccc} \left( \varLambda _{ij}^s +\varLambda _{ji}^s \right) ^{T}P_{s} \left( \varLambda _{ij}^s+\varLambda _{ji}^s \right) -2P_{s}<0 \\ i\in S_{s} \\ s=1,\ldots ,\mu \end{array} \end{aligned}$$
(4.55)
$$\begin{aligned} \begin{array}{ccccccc} \left( \varLambda _{ii}^{s} \right) ^{ T} P_{s} \varLambda _{ii}^{s} -P_{s}<0 \\ i\in S_{s} \\ j\in S_{s} \\ i<j\in S_{s} \end{array} \end{aligned}$$
(4.56)
$$\varLambda _{ij} =\varPhi ^{i}-\varGamma ^{i} K^{j}$$ where $$S=\left\{ S_{1} ,S_{2} ,\ldots ,S_{\mu } \right\} $$ are $$\mu $$ regions where two fuzzy rules are fired (overlapped fuzzy memberships) at most, where $$S_{s}$$ contains the membership function indexes for fired fuzzy rules in s region.

Scheduling

In this section, scheduling theory is used for designing a feedback scheduler that, online, assigns an execution period for the NCS, based on the control system’s performance and the load conditions of the network. The change in the sampling period is carried out depending on a scheduling period. The basic idea is to keep the lost deadlines (those packets that overpass the deadline or are simply lost), defined as the Quality of Service (QsS), and the system’s performance (QsC) on the desired level, adjusting the sampling period. Here, it is proposed a local fuzzy scheduler for each sensor node present in the communication network, based on external traffic performs a dynamic scheduling, also known as feedback scheduling. This feedback scheduler is codesigning with the Fuzzy controller in the Sect. 4.4.

The configuration of the proposed dynamic scheduling is shown in Fig. 4.4, whose behaviour is described as follows:
  1. 1.

    The sensor sends a packet with period h to the controller. The packet contains system’s information along with its execution period.

     
  2. 2.

    The controller adds the error and control signals as part of the packet and sends it to the actuator.

     
  3. 3.

    The actuator calculates QsC and QsS for each scheduling period and sends the packet to the sensor.

     
  4. 4.

    Finally, the sensor modifies the period h based on QsC and QsS. A lost deadline occurs when a packet arrives at the actuator after the deadline, or when a packet is lost.

     
In control terms, the dependent variable is h, whereas the controlled variables are QsS and QsC.
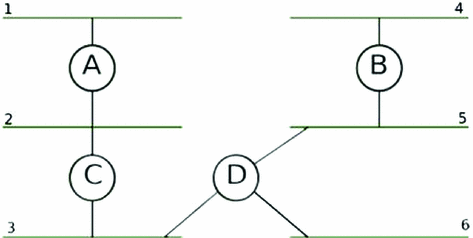
../images/321711_1_En_4_Chapter/321711_1_En_4_Fig4_HTML.gif
Fig. 4.4

Codesign configuration

The actuator computes the system’s performance $$\varDelta e$$ using the Mean Absolute Error (MAE) of n packet, received within a scheduling period $$\delta $$:
$$\begin{aligned} \varDelta e = \frac{\sum _{k \in {n}} {\left| {e_k}\right| }}{n} \end{aligned}$$
(4.57)
On the other hand, the lost packets rate $$\varDelta h$$ is obtained using the information of the total of received packets m that have exceeded their deadline $$h_{max}$$ plus the lost packets $$\lambda $$ during the scheduling period:
$$\begin{aligned} \varDelta h = \frac{m}{\delta } \sum _{k \in {n}} {h_k} \qquad m = \{ \forall {k \in {n} } | \tau _k > h_{max} \} + \lambda \end{aligned}$$
(4.58)
where $$\lambda $$ is the number of lost packets during the scheduling period, $$\tau _k$$ is the time delay between sensor and actuator, measured during the scheduling period, and $$h_{max}$$ is the deadline for the received packet.

The election of the lost deadlines rate, as the controlled variable, is due to it is one of the most common metrics used for Quality of Service (QoS). From a real-time point of view, it is an important factor that affects QoC. The QoS keeps controlled the lost deadline rate in an acceptable low level. Besides, using $$\varDelta h$$ as the controlled variable allows to simultaneously address variable time delays, as well as packet loss.

When $$\varDelta h$$ is kept at a low level, the time delay of most packets is less than the deadline, and the number of lost packets is bounded. As a consequence, the impact on QsC of the time delay and the lost packets diminishes.

The sampling period affects the lost deadlines rate: with a short sampling period, the used of the network increases, which inherently causes an increase of network uncertainties, and vice versa; with a heavy load of traffic, the collision probability between nodes increases, and potentially, grows the time delays and the packet loss, which at the same time increase the lost deadlines. Usually, a largely lost deadline rate may be reduced by increasing the sampling period, particularly when the network is overloaded.

From Digital Control Theory for sampled data, short sampling periods improves QoC. Here, QoC increases by increasing the efficient use of the network, by adjusting the sampling period. This justifies the election of the sampling period as the dependent variable, which is adjusted depending on network conditions, where variations of unpredictable and dynamic traffic in the NCS may be effectively compensated.

With metrics for QsC ($$\varDelta e$$) and QsS ($$\varDelta h$$), a fuzzy scheduler is designed as a control problem in which both metrics compose the IF rules, while the THEN rules are parallel feedback laws. The i-th fuzzy rule has the following form:
$$\begin{aligned} \begin{array}{*{20}c} {Rule}&{i:}&{IF}&{\varDelta e}&{is}&{\beta _1}&{and}&{\varDelta h}&{is}&{\beta _2}&{THEN}&{\overline{h} = Fz} \end{array} \qquad \qquad \end{aligned}$$
(4.59)
where $$\beta _i$$ are the membership functions, and $$z \in \mathfrak {R}^2$$ with $$z = [ \varDelta e \, \, \varDelta h ]$$, and F is the scheduling feedback matrix. The complete fuzzy scheduler is then:
$$\begin{aligned} \overline{h} = \sum _{i = 1}^M {\prod _{j = 1}^{2} {\beta _{ij}F_i z}} \end{aligned}$$
(4.60)
where M is the number of fuzzy rules. The new sampling period is assigned to the interval:
$$\begin{aligned} h^+ = \{ h_{min} \le \overline{h} \le h_{max} \} \end{aligned}$$
(4.61)
Given the absence of a mathematical model describing the relationship between lost deadline rate, the system’s MAE, and the sampling period, the scheduling parameters are set based on simulation.

Any strategy to design a control law needs to take into account a gain scheduling approximation. To do so, a fuzzy control strategy based on Takagi-Sugeno-Kang (TSK) is applied. Using fuzzy control systems [16], and considering a variable structure system representation.

Based on the developments in Chaps. 2 and 4, where the time delays have been extensively worked, it seems important that this representation is useful for conditioning the time delay in terms of a mobile environment, such as the one produced by consensus or context changes in communications. Thus, the time delay representation in terms of a period function or as a product of a stochastic scenario allows concluding in a similar way to the Theorems 4.1 and 4.3. Hence, the time delay is still locally and globally bounded.

The authors consider that even in extreme cases, in which communications are lost, the same theory developed in Chaps. 2 and 4 sustain through packet loss. A scenario of possible interest for the reader is the extensive use of the communication channel, given the local need to establish a group context at each node. This increases the traffic, which conveys to a known situation and modelled before.

4.5 Concluding Remarks

In this chapter we provide a review of the classical control methods for NCS, presenting strategies implemented successfully in real systems. In addition, three controllers are presented using the NCS models of Chap. 2.

The fuzzy control methodology allows generating an optimal control signal in function of the imperfections of the network through its prediction. Generating an optimal control signal for the magnitude of the imperfection while ensuring the global stability of the system.

The sampling frequency scheduling allows minimising network usage, increasing the resources for nodes that need to improve their transmission in the presence of disturbances. The result is a scheduler that modifies the frequencies of each node in the range of its minimum and maximum frequencies, adapting to the network and control performances.

Finally, the codesign strategy employs two fuzzy models. One model with variable actuation periods as input to generate an optimal control signal in function of the next actuation period and another model to schedule the next actuation period in function of QsC and QsS to simultaneously control the system in function of the imperfections of the network.