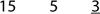
IN THE GRADE 3 CLASS WHERE I TAUGHT FOR A MONTH, ONE OF the boys would peer into his desk from time to time when he thought no one was looking. If I was standing directly behind him, I would bend my knees slightly so I could follow his line of sight, but I never was able to see what he found so fascinating about the interior of his desk. To me, it appeared to be full of books and pencils.
Teachers often forget the gulf that separates them from their students. I dimly remember living in a world where anything was possible, but even if I tried my hardest now, I doubt I could find anything magical in the shadows of an ordinary desk.
When we make assessments of children, we expect them to see the world as we do. But their way of perceiving things is almost unimaginably different from ours. In teaching mathematics, we shouldn’t judge young students too quickly for failing to apply a rule correctly, even after we have shown them a number of examples. Children can be very creative in extending rules to cases they have never seen. A child who learns to apply a rule using small numbers will often believe the rule changes or stops working beyond a certain point, as if a number could grow so enormous it caused things to break. Many rules are also counterintuitive in ways that may not be obvious to an adult. In adding two halves of separate pies, for example, one still has four pieces between the two pies; why then, a child might wonder, isn’t the denominator in the final fraction four?
Learning mathematics, even at the highest levels, is often a matter of getting used to things: there are concepts that only become clear after a great deal of use. A few examples may not be enough to show a child, whose understanding has not been conditioned by years of experience, how to extend a rule to a potentially infinite number of cases. Even the simplest instructions can be ambiguous to a student who is still learning to distinguish shadows from monsters.
All of the books of elementary mathematics I have read recently seem to expect children to master concepts and operations with very little practice, after being shown only a few (or often no) examples. Several weeks ago, I found an exercise in a Grade 3 book that asked students, in each question, to shade a given fraction of an array of boxes. In most of the questions the number of boxes in the array matched the denominator of the fraction, so the student simply had to look at the numerator of the fraction and shade that many boxes. But halfway through the exercise there was an array of 20 boxes with the instruction “Shade one-fifth of the boxes.” Up to that point students had not been taught anything about equivalent fractions, or even how to divide a number into equal parts.
Open almost any current book of elementary mathematics to any page and you are likely to find an example of the sort of conceptual leap I found in that Grade 3 book. The majority of teachers are not trained to fill in such gaps. Nor do they have the time, while supervising and preparing lessons for upwards of 25 children, to rewrite the material they are required to teach.
I was asked by a journalist recently what I thought of the “new math,” a method of teaching now prevalent in Canadian schools in which students solve open-ended problems by discussing and writing down explanations of their work. In the piece she wrote, the journalist made it sound as if I’d advocated a return to more traditional forms of instruction based largely on drills and rote learning. But I had been careful to stress to her that the ideals of the new math were not in themselves responsible for making many children feel incapable of doing mathematics. Rather, it was the way those ideals have been implemented in our schools — with textbooks that appear to have been written in a great hurry and by teachers who have received insufficient training and support — that has caused the current crisis in elementary education.
In the second year of JUMP, I began writing a manual for the program’s tutors. The program had grown from seven to 15 tutors, so I could no longer meet with tutors individually to explain how to teach a particular topic. Before this time, it had never occurred to me to write down the steps I followed in explaining various concepts. As with most of the innovations in JUMP, the idea of producing a set of lesson plans was forced on me by sheer necessity.
The manual is still a work in progress: I constantly test units on my students and make improvements based on their responses. I also rely on tutors to tell me when the units are unclear or difficult to implement. Lately I have added material to bring the manual into line with the curriculum of Ontario, so teachers can use it in the classroom.
In hindsight, I can see it was fortunate that I had planned to teach fractions in my first JUMP lesson. Most programs for remedial students consist of endless drills in addition and multiplication. Because children in special classes are assumed to be intellectually challenged, they gradually lose all confidence and motivation, so that after several years of extra help in math they can scarcely retain even the simplest facts. Many of the students who enter the JUMP program have not, after five or six years of regular school, managed to learn even the three-times table. Based on four years of work with these students, I have come to believe the best way to motivate children who have fallen behind is to skip them ahead — to convince them they are capable of doing work beyond their grade level. JUMP students who complete the first unit of the book are expected to write a test on fractions at a Grade 6–7 level, and they must score 80% or higher to go on to the next unit. Most students accomplish this in three or four months of weekly lessons. Very few need to take the test twice.
The JUMP program was specifically developed to help children who have fallen behind catch up quickly. I would never claim it is the only way to teach mathematics, or even the best. Programs based more on manipulatives, or that introduce concepts in an order different from the order in the manual, might work as well or better. I would claim, however, that whatever method is used, the teacher should never assume that a student who initially fails to understand an explanation is therefore incapable of progressing.
A tutor once told me that one of her students, a girl in Grade 4, had refused to let her teach her how to divide. The girl said that the concept of division was much too hard for her and she would never consent to learn it. I suggested that the tutor teach division as a kind of counting game. In the next lesson, without telling the girl she was about to learn how to divide, the tutor wrote in succession the numbers 15 and 5. Then she asked the child to count on her fingers by multiples of the second number, until she’d reached the first. After the child had repeated this operation with several other pairs of numbers, the tutor asked her to write down, in each case, the number of fingers she had raised when she stopped counting. For instance,
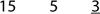
As soon as the student could find the answer to any such question quickly, the tutor wrote, in each example, a division sign between the first and second number, and an equal sign between the second and third.
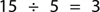
The student was surprised to find she had learned to divide in 10 minutes. (Of course, the tutor later explained to her that 15 divided by 5 is 3 because you can add 5 three times to get 15: that’s what you see when you count on your fingers.)
Any child in Grade 3 or 4, in a regular school, is able to erase or cross out a letter or numeral, or copy a letter or numeral from one part of a page to another. The child is also able, given two numbers between 0 and 9, to say which one is larger than the other. Finally, with a little practice, any child should be able to count, on the fingers of one hand, by ones, twos, and threes (and eventually by higher numbers). These are the only skills children need to have mastered, along with basic addition and subtraction (even if it’s only on their fingers), to carry out the operations in the JUMP manual.
Students in JUMP are always allowed to master the simplest instances of an operation before they are taught the more complicated ones. Two numbers are relatively prime if their lowest common multiple (the lowest number they both divide into evenly) is their product. For instance, 2 and 3 are relatively prime, but 4 and 6 are not (since the product of 4 and 6 is 24, while their lowest common multiple is 12). To add two fractions with relatively prime denominators the student must simply multiply the top and bottom of each fraction by the denominator of the other. (The reason for this is explained in the fractions unit; see Chapter 6.) For instance:
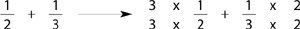
As this is simply a matter of copying numbers from one place on the page to another, any students can carry out this operation, even if they don’t fully understand the concept underlying it. Some students, however, may have very poor memories and visual skills when they start the program: even copying the right numbers in the right places may be a challenge. Several of my students were thrown off if I changed the position of the answer on the page — if I wrote, for instance:
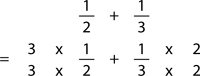
and then wrote:
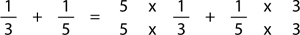
It is always possible, however, even with the weakest student, to make it easier for the student to proceed. You might, for instance, write in the times signs for the student:
so the student simply has to put the right numbers in the right places:
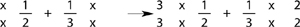
Or you might have them transfer only one symbol at a time:
drawing the circles to help them place the numbers. All of the steps in this manual can be simplified in this way. If a student gets stuck, you can always look for a way to make the step easier.
Once students learn a step, it is important to allow them to repeat it until they have mastered it. When I teach a step I give several examples and then write out two or three questions, leaving enough room under each question for the students to work. After several tests of this sort, when I am sure the students can reproduce the step automatically, I move on to the next step. When they have mastered all of the steps, I give them several tests where they must perform the operation completely. I usually end each lesson with a test that reviews everything we’ve covered.
Of course, it may seem like basic common sense to teach one step at a time, but even an experienced teacher will often compress a number of steps into one without realizing it. In adding fractions with relatively prime denominators, one performs the following steps:
If you teach all three steps at once, a weaker student will not be able to remember the first step by the time you have reached the last. You may well waste a whole lesson and leave the student demoralized, having learned nothing. If, however, you proceed one step at a time, allowing time for repetition, you can teach the weakest student to perform this operation in half a lesson.
Students should never be expected, when learning a new operation, to employ knowledge or a skill that they haven’t mastered. It would be unwise, for instance, to teach a student who has a shaky grasp of the six-times table to add fractions by producing examples with denominators divisible by six. The strain of trying to recall the six-times table could only interfere with the student’s ability to remember the steps.
While this might seem like an obvious principle, it is, I believe, regularly ignored in the schools. Students in JUMP are taught first to count on their fingers by twos, threes, and fives (which they quickly master). All operations taught in the first unit are introduced with fractions whose denominators are divisible by those numbers.
In explaining elementary mathematics, it is all too easy to introduce concepts that are beyond a student’s level of understanding. A JUMP tutor once told a beginning student that the fraction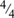 
was equal to 1 because 4 “goes into itself” once. The tutor then wrote “10,000/10,000 = ___” and asked the student to fill in the answer. As the student had no real familiarity with the concept of division, she had no idea what “goes into” meant. She just saw the huge numbers and panicked. (The tutor had to spend half a lesson rebuilding the student’s confidence.)
The problem of reducing fractions like to whole numbers can be turned into an entirely mechanical procedure. For instance, students might simply write the word “same” beside a fraction in which the numerator and denominator are the same, and then write “= 1” in cases where they have written “same.” Similarly, the concept of a number “going into” another can be introduced as a mechanical procedure (counting on your fingers by the first number and checking to see if you ever say the second).
In developing the JUMP manual, I was surprised to see the extent to which mathematics can be reduced to pre-conceptual operations like counting, crossing out a number or symbol, moving a number or symbol from one place on a page to another place, and so on. The fractions unit and the ratios and percents unit in this book were written to illustrate how far this approach can be taken (see Chapters 6 and 7). In working with weaker students, a teacher can always break an operation into steps the student cannot fail to perform. This style of teaching need not be followed indefinitely; even the most delayed student, in my experience, will eventually begin to skip steps and deduce explanations for themselves. But unless teachers begin with extremely simple tasks, they are not likely to help the majority of their students.
As far as I am aware, no program in mathematics was ever developed with the expectation that every child in the program would excel. To most educators, the idea of an entire class doing well in any subject seems absurd. A teacher who gave out only As would soon be called before the principal. Even in the present curriculum, which demands relatively little of students, no one would believe such marks were legitimate.
In working with the students in JUMP, I have come to understand why so many children have trouble learning mathematics. Our schools fail to produce, in the majority of children, skills and attitudes that are essential to abstract thought. Teachers who neglect to develop these basic capacities in their students do not have a hope of succeeding with their whole class.
Before children are introduced to mathematical concepts, they must, above all, be confident they will not be allowed to fail. They must be attentive and excited about learning. They must be able to recognize simple patterns in numbers and be capable of making elementary deductions — deciding, for instance, when to use one algorithm rather than another to carry out an operation. They must be able to follow basic rules and have some idea of what it means to extend a rule to a new case. Finally, they must be able to concentrate long enough to carry out operations of several steps and manipulate numbers well enough to carry out each step without hesitation.
The fractions unit in Chapter 6 of this book is designed to build the skills and attitudes a student needs to learn genuine mathematics. While the steps in every exercise are easy to follow (so that even the weakest student need never be discouraged), the conceptual work inherent in the unit is far from trivial. The goal of even the most mechanical exercises is to prepare a student for more advanced mathematics.
I am convinced, after observing a great many delayed students, that the problems these students face often stem from the same source. Students who have struggled with math for a number of years will likely have developed a kind of guessing mechanism that serves them well at school. No matter what you are teaching, even if it is quite simple, they probably won’t have a clue what you are saying. They will try to get a vague sense of your meaning, while most of their attention is being diverted to formulating a good guess. The method of teaching followed in the fractions unit is very effective at breaking such habits. If students are always able to carry out a given step, they soon develop a faith that they can understand anything the teacher expects them to learn. The startling improvements I have seen in my students are, I believe, largely due to one cause: for the first time these students have been given enough confidence to listen.
Nothing focuses the attention of children more sharply than the feeling that they are meeting a series of challenges and succeeding brilliantly. When adding fractions with different denominators, JUMP students will first count by the smaller denominator, checking to see whether they reach the larger. In this way, by repeatedly adding fractions, the students quickly learn how to divide. A fact learned while practising challenging mathematics is more readily recalled than one learned by rote drill. In JUMP, students who required four years to memorize a single times table at school become capable, in four months, of manipulating fractions at a Grade 7 level. The rapid progress made by our students shows the enormous role a student’s perception plays in learning. Clearly, students learn more quickly if they feel they are doing advanced work and succeeding.
By the time students complete section F-6 in the fractions unit of the manual, they will know how to add fractions in the following cases: when the denominators of the fractions are the same; when one denominator divides the other; and when the denominators are relatively prime. By learning to distinguish between these cases, these students will have taken a significant first step in their conceptual development: they will have learned how to choose between one of a set of algorithms for carrying out an extended sequence of logical or computational steps. While the students’ understanding of fractions will still be quite rudimentary, the effect of their growing mechanical facility often can be quite dramatic. I have observed marked improvements in memory, concentration, and numerical ability in many students after only a month of tutoring (see Chapter 4).
In the fractions unit, students are taught to extend rules to new cases, starting with simple examples. For example, once students know how to add a pair of fractions with the same denominator, they can be asked to deduce for themselves how to add three fractions with the same denominator, how to subtract a pair of fractions with the same denominator, and how to proceed when addition and subtraction are combined.
As students learn to follow increasingly complex rules, and as they become adept at generalizing simple rules, they become motivated to remember and articulate why the rules for the various operations work as they do. Eventually, the teacher can return to concepts that were first presented as mechanical operations, adding layer after layer to students’ understanding. The questions and exercises at the end of the fractions unit are to be introduced when students are ready. These exercises illustrate how to teach, in simple steps, concepts such as proportion and fractional equivalence. The teaching methods outlined above can easily be adapted to material that is normally considered beyond the reach of the majority of students. (Some educators believe that students should not be taught how to perform operations before they fully understand the concepts underlying the operations. I discuss this view in the Introduction to Part 2.)
A typical problem given to a Grade 6 enriched student runs as follows: “You have six blocks numbered one to six. You must build two towers, three blocks high, so that in each tower a block with a lower number never appears above a block with a higher number. How many solutions does this problem have?” If you give this problem to weaker students, they will likely have no idea how to begin. Even when they find an arrangement that satisfies the rule, they will not know how to determine whether they have found all valid arrangements.
Most teachers would conclude that the student was simply not mathematically minded, and that nothing could be done to change this fact. But a little reflection shows that the problem’s solution requires only one skill, a skill that every working mathematician relies on to explore new mathematical terrain: the student must know only how to search systematically through a set of possible solutions, listing the ones that are valid. This skill can easily be taught. You might, for instance, give students three blocks numbered one to three and ask them to build a tower of two blocks satisfying the rule. You could even prepare them by asking, “Could the block with three on it appear on the bottom?” (thus introducing the idea of a necessary condition for the solution of a problem). As students try different arrangements, you might teach them to list the solutions systematically, by first placing the block with one on the bottom, then the block with two. After they have solved the problem with three blocks you might ask them to find all arrangements of four blocks in a tower of three. In this way students are led to solve more complex instances of the problem on their own. The units in Part 2 of this book introduce, step-by-step, basic conceptual skills that underlie all mathematical work.