CHAPTER 4
Getting Started: A Simple Straw Man Quantitative Model

Build a little. Test a little. Learn a lot.

—REAR ADMIRAL WAYNE MEYER, AEGIS WEAPON SYSTEM PROGRAM MANAGER

In the next several chapters I will be reviewing what the research says about the performance of popular qualitative methods and certain quantitative, probabilistic methods. Some readers may be a lot more familiar with the former methods and will need at least some kind of reference for the latter. Some may want to start experimenting with a simple quantitative model even before hearing the details about the relative performance of various methods. In either case, it makes sense to introduce a very simple quantitative model early.

Or perhaps some readers may have misconceptions about what qualifies as a quantitative method and may prematurely dismiss them as infeasibly complex requiring a PhD in statistics or actuarial science or requiring unrealistic amounts of data. Nothing could be further from the truth. There is a whole spectrum of quantitative solutions from the very simple to very complex. The concern that anything quantitative must be unmanageable in practice is just another issue we need to address early.

My team at HDR once created quantitative decision models for infrastructure investments in a power utility. They had previously developed their own version of the risk matrix briefly described in chapter 2, and there was resistance to adopting more quantitative models. One concern they had is that they would end up developing an extremely complex and onerous-to-manage quantitative model similar to the ones their colleagues used in risk assessment for nuclear power generation. (Nuclear power, as mentioned in that same chapter 2, was one of the earliest users of Monte Carlo simulations.) Out of the extreme caution we would expect in that industry, the probabilistic risk assessment engineers developed very detailed and sophisticated simulations. They apparently saw the adoption of probabilistic models as an all-or-nothing choice of extreme complexity. In fact, there are many levels of sophistication in quantitative models and even the simplest can have benefits. We will start with one of the simplest.

As an initial straw man quantitative model, I will introduce what I've called the one-for-one substitution model. This is the simplest probabilistic model that is a direct substitution for a risk matrix. For most risk managers, the one-for-one substitution counts as “better” on the “Risk Management Success-Failure Spectrum” mentioned at the end of chapter 3. Once we've introduced that concept, we will gradually introduce additional ideas to further develop this model.

This model is something I introduced in a previous book, How to Measure Anything in Cybersecurity Risk. The idea of introducing that solution early and then building on it later seemed to work well for the readers and the idea is certainly applicable well beyond cybersecurity. I've made just a few changes to generalize it beyond cybersecurity, but if you are familiar with this concept from the previous book, you might skim or skip this section.

In part 3, we will explore more detailed models and more advanced methods. But for now, we will start with a model that merely replaces the common risk matrix with the simplest equivalent in quantitative terms. We will still just capture subjective estimates of likelihood and impact, but probabilistically. Some of the concepts we need to introduce (such as how to provide subjective probabilities) will be developed in more detail later, but this should get you started.

To make the quantitative models as accessible as possible, we will provide a solution native to Excel—no Visual Basic, macros, or add-ins required. Excel has such a large user base and most readers of this book will have some familiarity with Excel even if they don't have a background in programming, statistics, or mathematical modeling. You will not need to develop this model from scratch, either. An entire working example is ready for you to download at www.howtomeasureanything.com/riskmanagement.

When you are done with this chapter, you will have a foundation to build on for the rest of the book. Later, we will incrementally add further improvements. You will learn how to test your subjective assessments of probability and improve on them. You will learn how even a few observations can be used in mathematically sound ways to improve your estimates further. And you will learn how to add more detail to a model if needed.

A SIMPLE ONE-FOR-ONE SUBSTITUTION

We can start down a path for better risk assessment by replacing elements of the method many risk managers are already familiar with—the risk matrix. Again, similar to the risk matrix, we will depend only on the judgment of subject matter experts in the relevant areas of risk. They continue to make a subjective, expert judgment about likelihood and impact, just as analysts now do with the risk matrix. No data are required other than the information that cybersecurity analysts may already use to inform their judgments with a risk matrix. As now, experts can use as much data as they like to inform what ultimately comes down to a subjective judgment.

We only propose that instead of using the scales such as high, medium, low, or 1 to 5, experts learn how to subjectively assess the actual quantities behind those scales—that is, probability and dollar impact. In exhibit 4.1, we summarize how we propose to substitute each element of the common risk matrix with a method that uses explicit probabilities.

The method proposed is, similar to the risk matrix, really just another expression of your current state of uncertainty. It does not yet reflect a proper measurement in the sense that we are using empirical data about the external world. We are merely stating our current uncertainty about it. But now we have expressed this level of uncertainty in a way that enables us to unambiguously communicate risk and update this uncertainty with new information. We will see how each dot on the traditional risk matrix is substituted with one row in the spreadsheet you download.

EXHIBIT 4.1 Simple Substitution of Quantitative versus the Risk Matrix

Instead of …	We Substitute (more to come on each of the substitutes) …
Rating likelihood on a scale of 1 to 5 or low to high Example: “Likelihood of x is a 2” or “likelihood of x is medium.”	Estimate the probability of the event occurring in a given period of time (e.g., 1 year) “Event x has a 10 percent chance of occurring in the next 12 months.”
Rating impact on a scale of 1 to 5 or “low” to “high” Example: “Impact of x is a 2” or “impact of x is medium.”	Estimate a 90 percent confidence interval for a monetized loss “If event x occurs, there is a 90 percent chance the loss will be between $1 million and $8 million.”
Plotting likelihood and impact scores on a risk matrix	Use the quantitative likelihood and impact to generate a loss exceedance curve—a quantitative approach to expressing risk—using a simple Monte Carlo simulation done in a spreadsheet.
Further dividing the risk matrix into risk categories such as low, medium, high or green, yellow, red and guessing whether you should do something and what you should do	Compare the loss exceedance curve to a risk tolerance curve and prioritize actions based on return on mitigation.

Let's put together the pieces of this approach, starting with how we come up with subjective estimates of probability. Then we will explain how we do the math with those estimates, how we roll them up into a total risk (with a loss exceedance curve), and how we can start to make decisions with this output.

THE EXPERT AS THE INSTRUMENT

In the spirit of the one-for-one substitution we will start with, we will use the same source for an estimate as the current risk matrix—a subject matter expert from the business. Perhaps the person is an expert in supply chains, project management, cybersecurity, product liabilities, or some other area of the organization. They are the same experts you would use to populate the risks listed in any conventional risk matrix or other qualitative risk model. Just as experts already assess likelihood and impact on the conventional risk matrix, they can simply assess these values using meaningful quantities.

We will deal with how to incorporate additional external information in a later step. But simply capturing your current state of uncertainty is an important starting point in any measurement problem. We just need to set up a basic structure with the following steps.

1. Define a list of risks. There are different options for categorizing risks, but for now let's just say that it is the same list that would have been plotted on the conventional risk matrix. For each dot on your risk matrix, create one row for input on the downloaded spreadsheet. Whatever the name of that risk is, type that name in the “Risk Name” column of the spreadsheet.
2. Define a specific period of time over which the risk events could materialize. It could be one year, a decade or whatever time frame makes sense - just use it consistently for all the risks.
3. For each risk, subjectively assign a probability (0 percent to 100 percent) that the stated event will occur in the specified time (e.g., “There is a 10 percent chance a data breach of system x will occur in the next twelve months”). Technically, this is the probability that the event will occur at least once in that time period. (We will consider later how we model events that could happen multiple times in a period.)
4. For each risk, subjectively assign a range for a monetary loss if such an event occurs as a 90 percent confidence interval. In other words, this is a range wide enough that you are 90 percent certain that the actual loss will be within the stated range (e.g., if there is a data breach in application x, then it is 90 percent likely that there will be a loss equal to somewhere between $1 million and $10 million). Don't try to capture the most extreme outcomes possible. (Note: In a 90 percent confidence interval, there is still a 5 percent chance of being below the lower bound and a 5 percent chance of being above the upper bound.)
5. Get the estimates from multiple experts if possible, but don't all have a meeting and attempt to reach consensus. Simply provide the list of defined events and let individuals answer separately. If some individuals give very different answers than others, then investigate whether they are simply interpreting the problem differently. For example, if one person says something is 5 percent likely to happen in a year, and another says it is 100 percent likely to happen every day, then they probably interpreted the question differently. (I have personally seen this very result.) But as long as they at least interpret the question similarly, then just average their responses. That is, average all event probabilities to get one probability, and average the lower bounds to produce one lower bound and upper bounds to produce one upper bound.
6. Once we have recorded the likelihood and 90 confidence interval of losses for each risk in the table, we are ready for the next step: running a simulation to add up the risks.

I need to briefly address some perceived obstacles to using a method like this. Some may object to the idea of subjectively assessing probabilities. Some analysts who had no problem saying likelihood was a 4 on a scale of 1 to 5 or a medium on a verbal scale will argue that there are requirements for quantitative probabilities that make quantification infeasible. Somehow, the problems that were not an issue using more ambiguous methods are major roadblocks when attempting to state meaningful probabilities.

This is a common misunderstanding. There is nothing mathematically invalid about using a subjective input to a calculation. In fact, as we will see, there are problems in statistics that can only be solved by using a probabilistically expressed prior state of uncertainty. And these are actually the very situations most relevant to decision-making in any field, especially risk management. Later, we will discuss the sources supporting this approach, including some very large empirical studies demonstrating its validity. Additionally, we will show how readers can measure and improve their own skills at assessing probabilities using a short series of exercises that can help them continue to improve it over time. We call this calibrated probability assessment, and we will show that there is quite a bit of research backing up the validity of this approach. For now, just recognize that most experts can be trained to subjectively assess probabilities and that this skill is objectively measurable (as ironic as that sounds).

The expert can also be improved by using methods that account for two other sources of error in judgment: the high degree of expert inconsistency and a tendency to make common inference errors when it comes to thinking probabilistically. These improvements will also be addressed in upcoming chapters.

Of course, these sources of error are not dealt with in the typical risk matrix at all. If the primary concern about using probabilistic methods is the lack of data, then you also lack the data to use nonquantitative methods. As we've stated, both the risk matrix and the one-for-one substitution methods are based on the same source of data so far—that is, the opinion of experts in the relevant domain of risk. And we cannot assume that whatever errors you may be introducing to the decision by using quantitative probabilities without being trained are being avoided by using mathematically ambiguous qualitative methods. The lack of data is not alleviated by nonquantitative methods. Ambiguity does not offset uncertainty. We will address more objections to the use of quantitative methods, whether simple or complex, in later chapters.

A QUICK OVERVIEW OF “UNCERTAINTY MATH”

Now that we have recorded the likelihoods and ranges of impacts for a list of potential events, we need a way of summarizing them quantitatively. If we were using exact, deterministic point values—where we pretend to predict all the outcomes exactly—then the math is as simple as adding up the known losses. But because we want to capture and summarize uncertainty, we have to use probabilistic modeling methods to add them up.

So how do we add, subtract, multiply, and divide in a spreadsheet when we have no exact values, only ranges? Fortunately, there is a practical, proven solution, and it can be performed on any modern personal computer—the Monte Carlo simulation briefly mentioned in the short history of risk management in chapter 2. A Monte Carlo simulation uses a computer to generate a large number of scenarios based on probabilities for inputs. For each scenario, a specific value would be randomly generated for each of the unknown variables. Then these specific values would go into a formula to compute an output for that single scenario. This process usually goes on for thousands of scenarios.

For a little more history, we need to go back to the Manhattan Project, America's program to develop the first atomic bomb during World War II. Some mathematicians and scientists working in that project started using simulations of thousands of random trials to help solve certain very hard mathematical problems. Stanislaw Ulam, Nicholas Metropolis, and later John von Neumann had developed a way to use this method on the rudimentary computers available at the time to help solve math problems related to the development of the atomic bomb.¹ They found that randomly running thousands of trials was a way to work out the probabilities of various outcomes when a model has a number of highly uncertain inputs. At the suggestion of Metropolis, Ulam named this computer-based method of generating random scenarios after Monte Carlo, a famous gambling hotspot, in honor of Ulam's uncle, a gambler. Now, with the advantage of greater computing power (easily billions of times greater than what was available on the Manhattan Project, by almost any measure), Monte Carlo simulations assess uncertainties and risks as varied as power generation, supply chain, product development, investment portfolios, cybersecurity, and more.

We are going to use a Monte Carlo simulation to compute an answer to questions such as, “Given all of my stated risks, what is the chance we will lose more than x in the next year?” and “How much does that change if I implement risk mitigation y?” and “What is the return on a given risk mitigation?” A qualitative method such as a risk matrix does not answer these kinds of questions. To answer these questions, we will generate the loss exceedance curve (LEC) briefly shown in exhibit 4.2.

An LEC is a method of visualizing risk in a mathematically unambiguous way. LECs are already used in financial portfolio risk assessment, actuarial science, and what is known as probabilistic risk assessment in nuclear power and other areas of engineering. In these other fields, it is also variously referred to as a probability of exceedance or even complementary cumulative probability function. Exhibit 4.2 shows an example of an LEC.

EXHIBIT 4.2 Example of a Loss Exceedance Curve

To generate an LEC, the spreadsheet you can download from the website will generate ten thousand scenarios using the risks you entered. The spreadsheet simply counts the number of the ten thousand scenarios that had losses exceeding a given amount shown on the horizontal axis of the LEC chart. For example, if there were nine hundred scenarios out of ten thousand that had a total loss exceeding $10 million, then there would be a point on the LEC at $10 million on the horizontal axis and 9 percent on the vertical axis. If there were one hundred scenarios with losses greater than $60 million, then there would be a point at $60 million and 1 percent, and so on. The chart simply shows a series of those points connected in a curve.

To generate the random scenarios, we use what is called a pseudo random number generator, or PRNG. There is a random number–generating function in Excel written as “rand()” that will generate a value between 0 and 1. But we will actually use a different PRNG developed by my staff and me at Hubbard Decision Research. There are two reasons I decided to use my own PRNG instead of Excel's rand() function. First, in statistical tests of randomness the HDR PRNG outperforms Excel's rand(). Very subtle patterns in PRNGs, which can only be detected in sophisticated statistical tests using millions of generated values, are less common in the HDR PRNG than Excel's rand() function. In other words, our method appears to be statistically more random.

Additionally, the HDR PRNG, unlike the Excel rand() function, can be reversed and replayed exactly like fast forward and rewind on a video. It uses a unique identifier for each random scenario and that “trial ID” will always produce the same result. In our spreadsheet, you will see a scroll bar at the top of the spreadsheet. This will enable you to scroll through all the scenarios one by one. If you want to go back to scenario number 9,214, you can do so and get exactly the same result you saw the first time. The Excel rand() function doesn't keep the previous results. If you recalculate a table, the previous values are gone unless you saved them. I find it very useful to exactly re-create specific scenarios in order to validate results.

Using our PRNG, one of these random numbers is generated for each event probability and each impact range for each risk listed for each scenario. In other words, if you have ten risks listed in your one-for-one substitution table, you will have ten risks times two random values per risk (the probability and impact of the event) times ten thousand scenarios (i.e., two hundred thousand individual random values). These ten thousand scenarios are stored using a feature in Excel called a what-if data table. Simply referred to as a data table (confusingly, I think, because many users might think any table of data in Excel is a kind of “data table”), this feature in Excel lets you compute different results in some formula or model by changing one or more values at a time. In this case, we are changing trial ID to generate different results for each random scenario (i.e., trial) in our model. Each row in that table shows a total of all the events in a given scenario.

Note that a data table contains functions written as “{=TABLE(cell address)}.” You cannot directly write this function in the spreadsheet. Excel will create it if you go through the simple process of creating a data table using the what-if features of Excel. (You can review help in Excel to see how to create it in your current version but the downloadable table already has one created for you.)

If you have no experience with Monte Carlo simulations, they're probably easier than you think. My staff and I routinely apply Monte Carlo simulations on a variety of practical business problems. We have seen that many people who initially were uncomfortable with the idea of using Monte Carlo simulations eventually became avid supporters after tinkering with the tools themselves.

Now let's summarize what is going on with our Monte Carlo. I have provided additional details about the Excel formulas in the first appendix and there are also further instructions provided on the downloaded spreadsheet.

1. For each risk we previously listed in the spreadsheet, we determine if the event occurred. If the event had a 5 percent chance of happening per year, then the simulation uses a formula to make the event occur randomly in 5 percent of the scenarios.
2. If the event occurs, the simulation will determine the impact. It will use the range provided as a 90 percent confidence interval particular type of distribution called a “lognormal” distribution. Ninety percent of the time the simulation will choose a random value within that interval, 5 percent of the time the simulated value will be above the upper bound, and 5 percent of the time the value will be below the lower bound. This distribution is useful for impacts because of the way it is shaped. It can't produce a zero or negative value, which would not make sense in the cost of the impact of a risk event, but it could potentially produce values well above the upper bound.
3. The simulation runs ten thousand scenarios for each risk. In each scenario, all the impacts, if there are any, of all the risks are added up and shown in the data table. Each row in the data table shows the total of all the impacts that occurred in a given scenario.
4. Another table is created that counts up the number of scenarios that have losses exceeding a given amount. This creates a series of points used to draw the loss exceedance curve.

ESTABLISHING RISK TOLERANCE

How much risk can we bear? There is actually a well-developed theory for how to quantify this (more on that later). But in the spirit of keeping this straw man as simple as possible yet still quantitative, we will draw another curve to compare to the LEC. If our LEC is under this “risk tolerance” curve, the risk is acceptable.

Ideally, the risk tolerance curve is gathered in a meeting with a level of management that is in a position to state, as a matter of policy, how much risk the organization is willing to accept. I have gathered risk tolerance curves of several types from many organizations, including risk tolerance for multiple cybersecurity applications.

The required meeting is usually done in about ninety minutes. It involves simply explaining the concept to management and then asking them to establish a few points on the curve. We also need to establish which risk tolerance curve we are capturing (e.g., the per-year risk for an individual system, the per-decade risk for the entire enterprise, etc.). But once we have laid the groundwork, we could simply start with one arbitrary point and ask the following:

Analyst:	Okay, today we are establishing your tolerance for risk. Imagine we add up all the (previously discussed) sources of risk. In total, would you accept a 10 percent chance, per year, of losing more than $5 million due to the listed risks?
Executive:	I prefer not to accept any risk.
Analyst:	Me too, but you accept risk right now in many areas. You could always spend more to reduce risks, but obviously there is a limit.
Executive:	True. I suppose I would be willing to accept a 10 percent chance per year of a $5 million loss or greater from these risks.
Analyst:	How about a 20 percent chance?
Executive:	That feels like pushing it. Let's stick with 10 percent.
Analyst:	Great, 10 percent, then. Now, how much of a chance would you be willing to accept for a much larger loss, like $50 million or more? Would you say even 1 percent?
Executive:	I think I'm more risk averse than that. I might accept a 1 percent chance per year of accepting a loss of $25 million or more …

And so on. After plotting three or four points, we can interpolate the rest and give it to the executive for final approval. There is a small table in the spreadsheet just for entering these points you need to draw the risk tolerance curve.

It is not a technically difficult process, but it is important to know how to respond to some potential questions or objections. Some executives may point out that this exercise feels a little abstract. In that case, give them some real-life examples from their firm or other firms of given losses and how often those happen.

Also, some may prefer to consider such a curve only for a given budget—as in, “That risk is acceptable depending on what it costs to avoid it.” This is also a reasonable concern. You could, if the executive was willing to spend more time, state more risk tolerance at different expenditure levels for risk avoidance.

Executives who want to address that issue should consider taking the concept of risk tolerance beyond the simple “ceiling” for an LEC. This is what the field of decision analysis addresses. We will introduce this version of it later as a way to think about how to trade off risks with potential rewards. For now, however, the simple one-for-one substitution model will use the term risk tolerance here to mean a kind of maximum bearable pain the organization is willing to accept, regardless of reward.

SUPPORTING THE DECISION: A RETURN ON MITIGATION

Ultimately, the point of risk analysis—even with the risk matrix we are replacing—is to support decisions. But the difficulty we had before was making specific resource-allocation choices for specific risk mitigation efforts or controls. What is it worth, after all, to move one high risk to a medium level? Is it $5,000 or $5 million? Or what if we have a budget of $8 million in, for example, supply chain–related risks, and we have eighty lows, thirty mediums, and fifteen highs? And what if we can mitigate more lows for the same money as one medium?

If you have observed (as I have) someone asking a question such as, “If we spent another million dollars, can we move this risk from a red to a yellow?” then you may have felt the dissatisfaction from this approach. Clearly the traditional risk matrix offers little guidance once management actually has to make choices about allocating limited resources. Some might feel they can move from the qualitative to specific decisions based on experience and gut feel, but, as we will show later, this has even more problems.

What organizations need is a “return on control” calculation. That is the monetized value of the reduction in expected losses divided by the cost of the control. To express the return as a percentage return comparable to other returns, it would be conventional to show it as expected value of a risk reduction divided by the cost of the risk reduction, then subtract one from the result, and displayed as a percentage. The minus one is to show return as a percentage of benefits in excess of the costs.

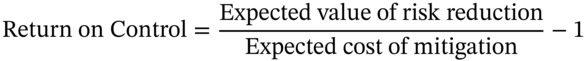
The term expected in the context of quantitative decision methods generally refers to the probability-weighted average of some amount. So expected loss is the average of the Monte Carlo simulation losses. If we applied a control to reduce risks and then we simulated a new set of losses, the average of those losses would be less (by either reducing the chance of any loss, reducing the impact if the loss event occurred, or both). The difference in the loss before and after the control is the reduction in expected losses in the simple formula just given. If the reduction in expected losses was exactly as much as the cost, then this formula would say the return on control was 0 percent. This would be the convention for other forms of investment.

You would also have to identify over what period of time this expected reduction in losses would occur. If the control was just an ongoing expense that could be started and stopped at any time, then this simple formula could just be applied to a year's worth of benefits (loss reduction) and a year's worth of costs. If the control is a one-time investment that could provide benefits over a longer period of time, then follow the financial conventions in your firm for capital investments. You will probably be required then to compute the benefits as a present value of a stream of investments at a given discount rate. Or you may be asked to produce an internal rate of return. We won't spend time on those methods here, but there are fairly simple financial calculations that can, again, be done entirely with simple functions in Excel.

MAKING THE STRAW MAN BETTER

George Box, a statistician famous for his work in quality control, time series forecasts, and many other areas of statistics, once said, “Essentially, all models are wrong, but some are useful.” I add one corollary to this quote: some models are measurably more useful than others. We will increase this usefulness incrementally with additional features though the rest of this book, especially in part 3.

Even with this very simple quantitative model, the component testing methods we discussed in chapter 2 can help us determine if we are really classifying something as better according to the Risk Management Success-Failure Spectrum mentioned in that same chapter. There is existing research that indicates we have improved our assessment of risk just by the act of avoiding the ambiguity of qualitative methods, decomposing uncertain quantities, and even using Monte Carlo simulations. More on that research later.

Now, how much you choose to add to this model to make it even better will be a function of how much detail you are willing to manage and the size of criticality of your risks. If you have very large risks, especially risks existential to the firm or risks involving human safety, you could probably justify a lot more detail. For readers who have had even basic programing, math, or finance courses, they may be able to add more detail without much trouble. But, because everything we are doing in this book was can be handled entirely within Excel, any of these tools would be optional.

We will introduce more about each of these improvements later in the book, but we have demonstrated what a simple one-for-one substitution would look like. Here is a quick summary of some of the ways we will make this model “less wrong” in the chapters ahead:

• Improving subjective judgment: Research shows that subjective expert input can be very useful—if we can adjust for issues such as overconfidence and inconsistency. We also know how some methods of eliciting judgments or aggregating the judgments of many experts are better than other methods.
• Adding more inputs: We can add a lot more detail by decomposing the likelihood and impact of the event. That is, we can compute the probabilities or impacts of events from other inputs instead of just estimating them directly. For example, the impact of a product recall could involve loss of revenue, legal liabilities, operational costs of the recall, and more.
• Considering interconnections: Some events may be correlated. Perhaps some events are necessary conditions for other events and some events may cause possible chain reactions. Now that we have adopted quantitative methods in modeling risks, any of these kinds of relationships can be modeled just by adding more rules to our spreadsheet.
• Additional types of distributions: We started out using a simple binary (did the event happen or not) distribution and a lognormal distribution. There are many more to pick from that may better fit the intentions of the subject matter expert estimating them or will better fit the data they are meant to represent.
• Using empirical data: Useful statistical inferences can be made even in situations where many people might assume that the data are very limited or otherwise imperfect. Contrary to the common misconception that you need some large number of observations to make any inferences at all, single events can update probabilities if we use a set of methods that are part of what is called Bayesian statistics.
• Incorporating decision analysis methods: As discussed earlier in this chapter, there is more to add regarding the concept of risk tolerance. Later, we will introduce additional methods that come from expected utility theory and decision analysis. When risk analysis becomes part of decision analysis and risk management is fully incorporated into management decision-making, then you will need ways of trading off risk and return.

Now that we have introduced what is just about the simplest quantitative method you could use in risk management, let's step back and discuss why there is need for a change at all. In part 2, we will review various conflicting and confusing ideas about risk, research on the performance of experts, problems with popular qualitative methods, and some valid and invalid objections to some quantitative methods. But we will start part 2 by expanding further on the brief history of risk management mentioned in chapter 2 so that we can better see how all these competing methods came about in the first place.

NOTE

1.  1. Stanislaw Ulam, Adventures of a Mathematician (Berkeley: University of California Press, 1991).