2 SINCE ANTIQUITY
The core methods and beliefs of mathematical music have been accumulating gradually since antiquity. Many ideas behind today’s approaches have been around for differing amounts of time. Now, they are gradually coming together in a form that can be seen as something like a piece of writing that has been written over many times. Each of the many layers on this imagined document is visible, even if only barely. The specialist’s name for such a source is palimpsest.
Deriving from with this image, I will treat the history of mathematical music as a kind of a palimpsest of ideas. It has formed as some historical approaches were overlaid with others—a process which almost never made the older ones disappear completely. Accordingly, the chapters in this part of the book will be called “Since Antiquity,” “Since the Middle Ages,” and so on to underscore the continuing relevance of centuries-old ideas even in today’s mathematical music.
In antiquity, we find some of the earliest attempts to formalize mathematically the basic building blocks of music. The most famous example is the mystical-philosophical teachings of the mathematically inclined ancient Greek theorist Pythagoras who is reported to have lived during the 6th century BCE. His teachings, transmitted through later authors, contain a crucial musical–mathematical concept: ratio.1
Ratios are descriptions of relations. A ratio of 1:2 means that one thing is two times bigger, or wider, or louder, and so on, than another. Ratios are at the core of many cultural concepts. We find them in architecture, sculpture, painting, even literature, and, of course, music and mathematics. Additionally, their use in culture is often connected to the idea that the human mind somehow derives special pleasure from being able to grasp the underlying mathematical order.
In principle, any relation expressed by two positive integers (whole numbers) is a ratio, in the everyday sense of the word. 1:2 is one, as is 38,146:69,531. However, in this example, only the former ratio can be understood and remembered easily and intuitively. Accordingly, only relations between relatively small numbers were historically regarded as the kind of a ratio likely to elicit a special aesthetic response.
The central idea that links ratios and music, a thought that has been permanently associated with Pythagoras since antiquity, is that such ratios made from small integers (especially 1, 2, 3, and 4) are the underlying hidden order enabling the aesthetic appeal of sound.
This aesthetic appeal is almost always linked to the idea of harmony. It has been often postulated that a harmonious acoustic impression is created in the listener when the sound is somehow structured by simple ratios. In the mystical-philosophical system of Pythagoreanism, and in later similar systems, these relations between small numbers are in fact expressions of a larger divine and cosmic order.2 One example is the concept that proportions in music represent the proportions in the movements of celestial bodies—the so-called music of the spheres.
If we take a break at this moment to look back at the argument so far, we can see that it is deeply mathematical: hidden order manifests itself in form of properties that can be understood with the help of arithmetic. From now on, this idea will accompany our historical journey. The mathematical tools themselves will gradually become more complicated, but the core belief in the revelatory powers of mathematics to help with the creation of impressive aesthetic works will remain.
Also, it is worth stressing here that most mathematical musical theories are speculative. The authors of these theories believe, and are indeed often firmly convinced, that the internal logic of music works in some particular way which can be explained with the help of mathematics. Yet, proving a specific hypothesis by a specific author in such a way as to convince everyone is mostly impossible. In addition, speculative theories tend to be somewhat detached from musical practice and pedagogy of their time. Today, different traditions, schools of thought, and idiosyncratic approaches by individuals continue to coexist despite innumerous claims to “singular” or “universal” musical truth by various historical and contemporary theorists.
In this situation, it is little wonder that music theorists, like their colleagues in the sciences, have often relied on the persuasive power of illustrations to mobilize support for their ideas. The simple ratios in the historical theories of the Pythagorean tradition were a “natural” candidate for this kind of visual argument. Such illustrations have sometimes grown into very intricate depictions whose stunning visual beauty was obviously meant to validate the musical speculation (see Figure 2.1).
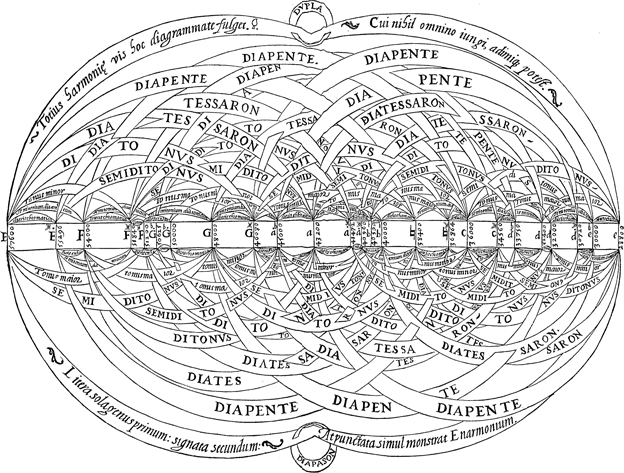
The modern educated person is often accustomed to using certain mathematical notions without thinking about their origin. Yet, considering an unfamiliar, historical perspective on them can help appreciate the work that has led to the shaping of these ideas in the first place. For ratios to become thinkable, the notions of a number, and of relations between numbers, needed to exist.
A whole prehistory of gradual development of mathematical ways of thinking has preceded Pythagoras and his theories. At some point in this prehistory, the idea must have emerged that continuous qualities (such as, for example, length) can be meaningfully represented by discrete (non-continuous) elements. How long a road is, can be measured with increasing, almost endless, precision. But saying that its length is 100 steps is often good enough. At this point the road mutates from a continuous mental figure into a discrete one, sufficiently described by a number.
Ancient board games have survived that beautifully illustrate the early existence of this mental discretization of the world. The so-called “Royal Game of Ur,” found during excavations in Iraq, is an exquisitely crafted wooden game whose principle is based on moving the pieces on a board which is divided into quadratic fields.3 The player needs to move a piece along a certain path, but this movement is discretized: although continuous in the real world of the players who hold the pieces in their hands, it is thought of as consisting of “jumps” from one field to another. It is fascinating to consider that the modern division of musical pitch (tone height) into discrete steps is based on the same figure of thought as the Mesopotamian board game from the third millennium BCE!
Ratios based on such discrete thinking can be applied to different aspects of music ranging from the tuning of the instruments to musical form. The famous idea associated with Pythagoras is that relations between pitches can be made harmonious by adhering to a system of tuning based on proportions. In the canonical example, a string is shortened by half, by two thirds, and so forth, creating proportions of 1:2 or 1:3 between the pitches of the whole string and the shorter part. A second famous example associated with Pythagoras, which is, however, unlike the previous one, not really convincing from the point of view of physics, is that he was inspired by the sounds of different hammers.4
Building upon this approach, whole scales containing the notes from which the performer could choose to create a melody were calculated. Given the link to divine order described above, it is not surprising that, historically, such calculations were destined to be accompanied by claims of their superior aesthetic and mystical-philosophical qualities.
Mathematical attempts at rationalizing musical practice in form of scales and other calculation-based theories were not confined to the ancient Greek culture. In ancient China, for example, the Lü system of tuning brought mathematics into music in a similar way. Other impressive uses of mathematical devices in music can be found in various cultures of the world.5
Given such an early and global spread of the idea to use mathematics in music, one is tempted to see it as “natural.” After all, it seems natural to base the tuning of the different strings of an instrument on ratios, especially now that modern physics has shown that vibrating strings simultaneously produce many harmonics (tones), and that these harmonics do represent ratios such as 1:2 and 1:3. And, certainly, ratios have played a central role in the centuries-long tradition of Western music theory, enabling a gradual build-up of a large and complex conceptual apparatus.
But does music theory have to rely on small-integer ratios?
From today’s point of view there are several problems with this approach. First, it is now known that humans are unable to hear small deviations of pitch.6 According to widespread assumptions, a ratio between the frequencies of two tones that is made up of small integers (like 2:3) will produce a harmonious result, whereas one made up of large integers will not. But a ratio such as 20,000,001:30,000,001 will, despite its monstrous numbers, yield frequencies that are so close to the ones produced by 2:3 that nobody will be able to distinguish between the two results.
Second, humans tend to perceive sounds (and everything else) using the categories they learned from previous examples. Therefore, a person who has repeatedly encountered a ratio like 2:3 in music, even without knowing about the musical theory behind the sound, is very likely to also perceive a slightly deviating sound as being the same—even if it is perfectly capable of hearing the difference when instructed to do so.
In addition, humans seem to have formed a common vocabulary of perception tactics such as grouping phenomena together according to similarity or continuation that are so strong that they even lead to manifold distortions of heard reality in form of auditive illusions.7
These aspects combined, the boundaries of perception and the tendency to “adjust” impressions to fit known models, put a question mark above the claims to “natural” legitimacy of musical theories relying on ratios. Yet, the fact that a theory is not “natural” does not prevent it from becoming widespread and influential. Over time, it can begin to feel natural to everyone who is accustomed to it.
Some ratio-centered theories have remained popular throughout the centuries since Pythagoras, and are used even today by those musicians and theoreticians who are especially interested in so-called “pure,” or “just” intonation.
Pure intonation theories claim that only music based on tunings derived from small-integer ratios is truly harmonious and aesthetically satisfying. Their enemy is the tuning system commonly used today, which has abandoned simple ratios by making the distance between all tones equal.
The mathematical “problem” with the modern system is that the distance between tones is not just not expressible as a relation between small integers, it is not even expressible as a relation of integers at all (a so-called irrational number). Traditionally, scales of Western music were, and still are, theorized as further subdivisions of a big musical interval represented by the ratio 1:2, called the octave. A modern piano has twelve keys inside each octave, and, to make the distance between the tones equal, each tone has to be higher than the previous one by the twelfth root of two, which is an irrational number.
Simple ratios do still inhabit this modern system, but only as ideal models which today’s tuning is capable of approximating, but not of reaching exactly. In the eyes of pure intonation musicians, the modern system is detuned. In the eyes of others, this is a neat observation, but one that is rather irrelevant in practical situations.
Furthermore, modern sound analysis technology shows that expressiveness in music is often linked to variations in pitch: an experienced singer or violinist, for example, is capable of making a tone a little too low or too high, or to play around with pitch in a myriad other ways, conveying subtle changes in emotion that would otherwise become lost. An artificially created “perfect” tuning of a singing voice with absolutely no variation in pitch (something that can only be achieved by technological means) is, by way of contrast, commonly perceived as mechanical.
Also, the idea that harmonious sounds are the building blocks of music leaves out the other important component: disharmony. It is probably impossible to create a musical impression of tension, drama, or of negative emotions, using only deeply harmonious and calming sounds. This observation is another problem for ratio-based ideas of music: even if a musician truly believes that only sounds based on small-integer ratios are pleasant, why not add in some unpleasant ones for the sake of dramatic development? In fact, descriptions of possibilities for tones to move from a more tense (“dissonant”) to a more relaxed (“consonant”) combination have been a staple of music theory for many centuries.
As can be seen from the description above, the issue of ratios in music is a multifaceted and difficult one. Still, it is obvious that the core idea that ratios are somehow centrally important has never disappeared. Some people are deeply invested in pure intonation, others simply remember that the octave is a proportion, still others play string instruments and therefore constantly have in front of them the equivalent of the Pythagorean string to be divided by 2, by 3 and so on.
In all these situations, the thought that music is deeply connected to mathematics is reinforced. Again, it seems completely “natural” to connect these two activities. And, again, we should remind ourselves that a different view of things is also possible, that music is, in fact, thinkable without mathematics.
Trying to understand why it has been consistently linked to the tools of mathematics is a topic of cultural history that exceeds the scope of this book. But I would like to at least offer one explanation that seems probable to me. My stance is that music was often used as a vehicle to show the effectiveness of some idea or method in areas other than music.
Arithmetic is a powerful tool. It can help measure land, construct buildings of needed volume, predict the movements of celestial bodies, or plan the agricultural season. By taking harmonious musical sounds as something (seemingly) obvious and natural, and by linking them to arithmetic operations such as multiplication or division, the Pythagoreans made a case for the usefulness of their mathematical knowledge in all areas, not just in music.
This demonstration of the power of mathematics through its application in music is another theme that will constantly accompany us on our journey through history. In 17th century, the Baroque theorist Kircher would use variations of his wooden box not only for composition, but also for encryption.8 Later, 21st-century AI based on machine learning would be capable of segmentation and generation not only of musical scores, but of all kinds of information. Having a wooden box, or a machine learning algorithm, help with the composition of music means that these ideas and technologies do actually work, and can be applied in more “serious” situations.
Notes
- André Barbera, “Pythagoras,” Grove Music Online, 2001; Manuel Pedro Ferreira, “Proportions in Ancient and Medieval Music,” in Mathematics and Music. A Diderot Mathematical Forum, ed. Gerard Assayag, Hans Georg Feichtinger, and Jose Francisco Rodrigues (Berlin: Springer, 2002), 1–26.
- Catherine Nolan, “Music Theory and Mathematics,” in The Cambridge History of Western Music Theory, ed. Thomas Christensen (Cambridge: Cambridge University Press, 2006), 273.
- “The Royal Game of Ur,” The British Museum, https://www.britishmuseum.org/collection/object/W_1928-1009-378; Irving L. Finkel, ed., Ancient Board Games in Perspective. Papers from the 1990 British Museum Colloquium (London: British Museum Press, 2007).
- Calvin M. Bower, “The Transmission of Ancient Music Theory into the Middle Ages,” in The Cambridge History of Western Music Theory, ed. Thomas Christensen (Cambridge: Cambridge University Press, 2006), 142–143.
- Nick Collins, “Origins of Algorithmic Thinking in Music,” in The Oxford Handbook of Algorithmic Music, ed. Alex McLean and Roger T. Dean (Oxford: Oxford University Press, 2018), 74–75.
- Gareth Loy, Musimathics: The Mathematical Foundations of Music (Cambridge; London: MIT Press, 2006), Vol. 1, “6.4 Pitch”, 156–166.
- Diana Deutsch, The Psychology of Music (San Diego; London: Academic Press, 1999), “Grouping Mechanisms in Music”, 299–348. For an example of an optical illusion, see the circular diagram of connections between letters in this book. The area inside the circle seems to be darker than the surrounding area.
- Siegfried Zielinski, Deep Time of the Media. Toward an Archaeology of Hearing and Seeing by Technical Means (Cambridge, MA: The MIT Press, 2006), 141–157.