3 SINCE THE MIDDLE AGES
The Middle Ages bring about an intermediary step in the history of mathematical music. It first happens outside of music itself, but it will influence it several hundreds of years later. This crucial new development is the use of combinatorics for the purposes of communication (later also including aesthetics).
Combinatorics is a branch of mathematics concerned with counting and listing possible arrangements of individual elements.1 For example, it can count all possible pairings of A, B, and C (there are nine if the order of the elements in the pair is essential), and it can list them: AA, AB, AC, BA, BB, BC, CA, CB, CC.
Combinatorics itself is older than its medieval use discussed here. Since antiquity, combinatorial approaches emerged in different cultures around the world. One of the most famous examples is the Chinese treatise I Ching, which is structured around a basically combinatorial idea: variations of a graphical symbol are created from six stacked lines, each of which can be either broken or unbroken. Given the two possible states for lines (broken and unbroken), and the number of lines (six), a total of sixty-four symbols is presented in the book and interpreted in relation to divination practices.2
Combinatorial approaches create large amounts of material. The sixty-four possibilities in I Ching are actually a rather modest example of the numbers that can be achieved with just a handful of initial elements. The medieval Christian mystic, author and theorist Ramon Llull (ca. 1232–1316) appropriated this method to the generation of religious statements, effectively bringing combinatorics into the realm of communication.
His idea was to formalize the process of coming up with sentences. The first step was to let letters of the alphabet represent certain building blocks of language from which sentences are constructed. By doing so, he divided form (sentence structure) from contents (the respective religious concepts in his case), enabling further mathematization of argumentation. The next step was to postulate that letters could be chosen randomly, bringing into play the power of combinatorics. A graphical representation of his system in the form of circles inscribed with the letters was the crucial final step that both made the method easier to use and proved visually its power by the many lines connecting the letters.3
Figure 3.1 shows sixteen letters, arranged in a circle, with each letter connected to all the others. It is derived from an illustration in a medieval manuscript of one of Llull’s systems.4 The sheer number of connecting lines and the intricate symmetry of the figures that they form turn Llull’s circular diagrams into visually impressive, enigmatic symbols reminiscent of the mandala—a round figure used for meditation in Eastern religious traditions.
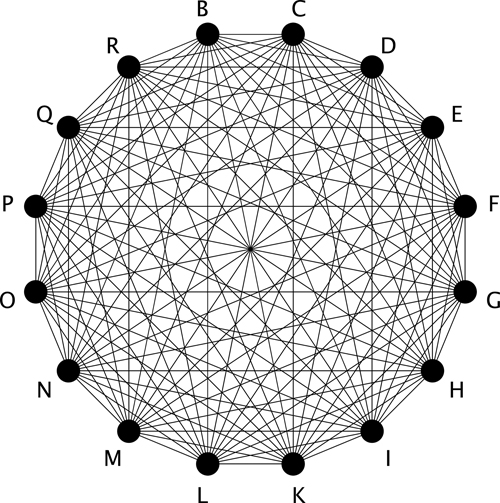
Yet, the diagram also works as a practical tool for the combinatorial creation of pairs of notions, to be used as material religious (in Llull’s case) writing and arguments. In the original manuscript, each letter represents one divine attribute such as goodness, greatness, or eternity.5 The circular diagram thus clearly suggests that each of them can be considered in relation to any other one, and that there are numerous possibilities for doing so.
By creating this combinatorial procedure for communication, Llull basically hoped to make interreligious arguments and conversion as easy as ABC (or BAC, or CAB…). Yet, his most important contribution was that he demonstrated the conceivability of mechanized thinking and communication between humans. From there, it was later only a small step to try to mechanize the process of coming up with melodies.
Llull’s approach can be subdivided into several constitutive parts:
- The combinatorial idea that arrangements of a finite number of elements can yield a virtually endless richness of material.
- The idea to use a circular arrangement of elements.
- The idea to also use multiple circles to help with the mental work of combination.
Arranging letters in a single circle already enables geometric play that can be aesthetically interesting as well as symbolical in a mystical sense.6 For example, one can choose letters in such a way that the lines that connect them represent a recognizable figure such as a triangle or a square. This figure, in turn, can be seen as representing a religious concept. The longer the sequence of letters, the more intricate will be the resulting path through the circle. At some point, tracing it can become a meditative, unworldly experience.
If one wishes to stay more alert during the mind-numbing work of combining strings of letters, one can employ a very simple, but powerful mechanism: multiple circles placed inside each other. With it, creating and remembering a sequence of letters is easy. Each circle, rotated into the needed position, will stay that way, helping with the construction of the arguments that Llull hoped to automate. Historical manuscripts of Llull’s works contain such combinatorial aids, with multiple circles of different sizes on top of each other, all held together by a string going through the page.7
Like the holes of the prehistoric bone flute that mechanized the mental work of remembering pitch, these movable circles mechanize the work of remembering and combining letters and the concepts that they represent in Llull’s system. And even if one does not cut out and assemble the circles into a thinking machine with movable parts, the visual representation of the system on a sheet of paper already makes the combinatorial work much easier than it would have been when conducted entirely in imagination.
Various historical sources have been suggested for Llull’s method, including Jewish and Arabic influences. Notable parallels in its reliance on combinations of letters exist to the Jewish cosmological treatise Sefer Yezira which in the 12th century became a staple of the then-new Jewish mystical tradition of Kabbalism. Sefer Yezira enumerates the possible combinations of two letters of the alphabet, and it even contains the more general combinatorial calculation of the number of possible arrangements of up to seven letters. Likewise, Arabic za'irajah “letter magic” which is based on operations with circles inscribed with letters, and which has been later described in detail in the treatise The Muqaddimah, comes remarkably close to Llull’s circular arrangements.8
Music seems predestined for combinatorial exploration. Sefer Yezira already lets us know that just seven different elements can already be rearranged in 5,040 ways. Accordingly, a musician is able to create this astounding number of melodies from just seven different notes. This is an inspiring and somehow liberating idea. It mitigates the fear (known to many creative individuals) of not being able to come up with anything. It feels great to know that fourteen notes already give rise to much more possible melodies than there are people in the world, without even taking the melody’s rhythm into consideration!9
Of course, several difficulties arise. Listeners might not accept most of these melodies either because they contradict written and unwritten rules of musical tradition or because they seem to represent no clear musical gesture that one can relate to. They can also grow tired of the uniformity of the musical system’s output. And probably, they would see a melody written by a real person as more valuable, even if it happened to be the same sequence of notes as one of the millions of combinations produced by an automaton.
Still, combinatorial play is fascinating. The unusually large numbers of possibilities created by combinatorial methods are deeply counterintuitive. It is difficult to believe that shuffling around a small group of elements (which we can count and clearly imagine in our mind) gives rise to thousands, millions, and billions of combinations, counting which obviously exceeds our mental capabilities. This circumstance has been called combinatorial explosion.
Being an “explosion,” it carries in itself not only positive connotations such as the unexpected richness of produced material, but also hints of danger: the amount of automatically created artefacts can be too much to manage effectively, or it can destabilize the cultural production economy by devaluing “manually” produced works.
By bringing a mechanical aid into the realm of human creativity (in this case, the creation of arguments), Llull therefore transgressed a boundary which is still likely to cause irritation. Missionaries and theologians of Llull’s time were probably as unwilling to be automated away as are today’s factory employees, office workers, or musicians. Even unpaid creative work conducted purely for recreation might start to feel less attractive to some people if they were to learn that a machine is capable of producing very similar results. Exaggerated versions of such feelings seem to have recently erupted in popular culture and everyday discourse in form of doomsday scenarios of machine domination and the ensuing humiliation and enslavement of humanity by a future form of AI.10
In the end, Llull’s idea has probably failed in religious disputes, but it proved influential in broader culture. During the so-called early modern period which followed the Middle Ages, Kircher was deeply inspired by it, as was the famous mathematician Gottfried Leibniz and many others. The next step after Llull introduced combinatorics into communication was to actually employ it in the creation of cultural artefacts. The early modern period was to become the time when people began to see some of the promises of automatic composition based on mathematics.
Notes
- To ensure greater readability, the word “arrangement” is used here not according to its strict mathematical definition as an ordered selection from a set of elements, but in a more everyday sense.
- Andrea Bréard, “China,” in Combinatorics: Ancient and Modern, ed. Robin Wilson and John J. Watkins (Oxford: Oxford University Press, 2013), 66.
- Teun Koetsier, “The Art of Ramon Llull (1232–1350). From Theology to Mathematics,” Studies in Logic, Grammar and Rhetoric 44, no. 57 (2016): 55–80; J. Gray, “Computational Imaginaries. Some Further Remarks on Leibniz, Llull, and Rethinking the History of Calculating Machines,” in Dia-Logos: Ramon Llull’s Method of Thought and Artistic Practice, ed. Amador Vega, Peter Weibel, and Siegfried Zielinski (Minneapolis: University of Minnesota Press, 2018), 293–300.
- Reprinted in Donald E. Knuth, “Two Thousand Years of Combinatorics,” in Combinatorics: Ancient and Modern, ed. Robin Wilson and John J. Watkins (Oxford: Oxford University Press, 2013), 15. The original illustration additionally has the letter A in the center.
- Donald E. Knuth, “Two Thousand Years of Combinatorics,” 15.
- Teun Koetsier, “The Art of Ramon Llull,” 63.
- Anthony Bonner, The Art and Logic of Ramon Llull. A User’s Guide (Leiden; Boston: Brill, 2007), 60–61.
- Teun Koetsier, “The Art of Ramon Llull,” 76; J. Gray, “Computational Imaginaries,” 297–298; Joseph Dan, Kabbalah. A Very Short Introduction (Oxford: Oxford University Press, 2006), 15–18; Victor J. Katz, “Jewish Combinatorics,” in Combinatorics: Ancient and Modern, ed. Robin Wilson and John J. Watkins (Oxford: Oxford University Press, 2013), 110–113.
- The factorial of 14 is 87178291200.
- Mark Coeckelbergh, AI Ethics (Cambridge, MA: MIT Press, 2020), 11–17.