

“THE HAPPIEST THOUGHT”
November 1907.
Albert Einstein was always a conscientious employee. He had been a model civil servant since 1902, when the Swiss national patent office took a chance on the then-unemployed recent graduate with a bachelor’s degree in physics. In 1905 he had experienced what would later be called his annus mirabilis, his miracle year—really just six months—when, to a much greater extent than most realize, he laid the foundations of the twentieth-century revolution in physics. Almost instantly, he was transformed: no longer a mere amateur, stealing time to calculate at his government desk, he became a full participant at the highest level of international physics. And yet, he was still a bureaucrat. In 1906 his superiors promoted him to Technical Examiner Second Class—undoubtedly the most famous patent clerk in Europe.
He still did his job and did it well, delivering an extremely competent day’s work for a day’s pay. He reviewed the documents and technical drawings that crossed his desk. He wrote his evaluations, doing his part to maintain the legal framework for invention. Even so, he couldn’t keep himself from pausing every little while to think about what truly moved him. So it was one day in 1907, he found himself staring out the window. Across the way, he saw a man fixing something on a roof. His imagination took over. In his mind’s eye, that suddenly luckless roofer slipped, slid, fell—and there it was, what Einstein would call “the happiest thought of my life.” It had just come to him that “if a man falls freely he will not feel his own weight.”
A man crashing to his death would seem to be an odd image to evoke joy in anyone. And that treacherous roof was a very long way from the limb of the sun and the realm Vulcan had been supposed to roam. Even so: there stood an anonymous laborer, unaware of the mental play going on in the office across the way and, equally unknowing, about to take on a vital role in settling the fate of an undiscovered planet.
Of course, the work to come did not emerge wholly formed from that first insight. Einstein’s greatest discovery built on an earlier one from his almost ridiculously profligate outpouring in the first half of 1905, when he produced four papers spread across huge swaths of theoretical physics. The first emerged from what might seem like a surprisingly narrow investigation into a phenomenon called the photoelectric effect, originally observed in 1887. A better picture of the phenomenon came at the turn of the century, through the work of the great experimentalist (and horrible man) Philipp Lenard. Lenard studied what happened when he varied the intensity of the electromagnetic radiation—light—striking a metal target. The expected result, based on Maxwell’s description of light as a field of waves, was that a bigger wave (brighter light) should impart more energy to the electrons. But Lenard found that while dimming or adding light altered the amount of current produced—the number of electrons emitted—it didn’t affect the energy of each individual electron as it left a metal surface. That varied only with the color of light he chose, its frequency or wavelength. Ultraviolet radiation, for example, imparted a bigger kick than did longer wavelengths—lower frequency visible colors. Lenard, who won a Nobel Prize for his experiments, couldn’t explain this fissure between theory and observation. In 1905, with no formal training beyond his undergraduate degree in physics, Einstein did.
What if, he asked, light could be understood not simply as a wave, but as a kind of particle, a quantum of light—what is now called a photon. Starting from that physical intuition, interpreting Lenard’s experiments becomes simple (though not easy). If light is made up of particles, then more photons (more light) would produce a bigger flux of electrons and hence more current—as observed. But the energy imparted to each of those electrons would depend on the energy of the photon that whacked it, not the total number of particles that struck the target. Once Einstein represented light as quanta in his equations, the calculation that followed reproduced Lenard’s results…and helped form the foundations of quantum mechanics, a set of ideas that is utterly intertwined with every facet of twenty-first-century life.*1
That came in March. April brought Einstein’s proof of the existence and size of atoms and molecules, an exercise in statistical physics that remains the most frequently cited of his 1905 works, with applications that range from mixing of paint to Einstein’s own definitive explanation for why the sky is blue.
He followed that up with a related analysis that solved the long-standing mystery of Brownian motion—first observed in the random motion of dust or pollen in water. That sounds like a sidelight, a minor result, except that Einstein’s method of accounting for the outrageously large number of molecular collisions required to produce the wandering track of a pollen grain was a significant step in building perhaps the single most powerful idea in twentieth- and twenty-first-century science: the recognition that the fundamental nature of reality in many of its facets is determined by the behavior of crowds that can only be understood in statistical terms, and not by direct links in a chain of cause and effect.
Einstein sent off the Brownian motion paper in the second week of May. With that he’d completed work that would have been the pride of at least two careers—and when he finally won his Nobel, the prize committee cited his account of the photoelectric effect instead of the more popularly celebrated work to come. But he had one more shot to fire. The last of Einstein’s “big four” papers arrived at the offices of Annalen der Physik on June 30, 1905. It came under a seemingly bland title, “On the Electrodynamics of Moving Bodies”—which masked the radical, almost subversive idea it contained, what we know as the special theory of relativity. It took him about six weeks to produce it, but once he was done, he was able to express his ideas in astonishingly simple, clear language, almost a story, in which he asks his readers to question what almost no one had ever paused to consider. What does it mean, he asked, to say that an event happens at a certain time? “If,” he wrote, “I say that ‘the train arrives here at 7’o’clock’ that means, more or less, ‘the pointing of the small hand of my clock to 7 and the arrival of the train are simultaneous.’ ” In other words—to describe any event in nature you need a rigorous concept of time: how it is to be measured and how any two people can come to agree on when anything may be said to have happened.
From there, Einstein lays down the two pillars on which all the rest of his new idea will rest. One was the “relativity principle,” originally defined by Galileo. It holds that “the laws governing the change of state of any physical system do not depend” on whether someone observes that event from within a system or from the outside, looking in—as long as both vantage points “are in uniform motion relative to each other.” That is: it doesn’t matter whether you are standing by the track or riding a train. Newton’s laws of motion (and any other natural laws, of course) behave the same way in both circumstances, even if, say, the path of a ball thrown on the train looks different to people watching from either vantage point.
Einstein’s second axiom was that the speed of light in a vacuum must be a constant, identical for all observers throughout the universe. The problem with that idea—and this had troubled scientists for decades before Einstein—is that if the speed of light truly does remain constant for all observers, that would seem to contradict Newton’s ideas about motion. Here’s the difficulty: imagine that a person turns on a lantern and stands still, while another runs down its beam of light. If Newton were right, the person at rest should find light traveling at the usual number—very nearly 300,000 kilometers (186,000 miles) per second. But the person in motion should come up with a different answer: 300,000 kilometers per second, less the speed at which she runs, say twenty kilometers an hour.*2 To Einstein’s predecessors, that’s how a properly organized universe would behave. Yet stubbornly, throughout the last years of the nineteenth century, the measured speed of light never complied, no matter how precise the experiment, no matter the state of motion of the experimental apparatus.
Einstein’s insight was to take seriously the implications of that evidence of a constant velocity for light. If the speed of light does not change with the motion of an observer, he argued, then to reconcile that fact with the rest of experience requires a change in the way one must think about the elements of speed—distance and time. Another thought experiment captures what he was trying to express: imagine a train traveling at a steady pace along a straight stretch of track, with one person equipped with a clock on the train at its midpoint, and another with an identical clock standing on the embankment. Now picture two bolts of lightning striking each end of the train at the instant that the watcher on the train passed her luckless counterpart, standing by the tracks amid the storm. So here’s the question: do both observers agree that the two bolts of lightning hit the train at the same time?
Special relativity began to form as Einstein understood that the answer has to be “no.” The bystander sees the strikes as simultaneous, but the train’s rider does not. How can this be, given that both of them are describing the same events? Einstein’s answer is, in effect: think about how the constancy of the speed of light affects your ability to decide when something happens, when the event and the tick of your clock occur at the same time. The images of the lightning bolts from both ends of the train have to cross some distance from where they strike to where the two watchers happen to be. To reach the observer standing on the embankment, the signal—the light from each bolt—has to cover the same distance: half the length of the train. Each signal will take the same amount of time (the speed of light is a constant, fixed for both bolts) to cover an identical amount of ground—and the observer can clearly describe the event: he sees the two strikes as simultaneous.
But for the watcher on the train, the situation is different. She’s still moving as the bolts hit. In the time it takes for the light to travel from the strikes to where she stands, she and the train will have traveled forward just a little. The light from the strike at the front will have a slightly shorter stretch to cross before it reaches the eye of the traveling observer than the light from the rear, chasing the advancing motion of the train. This observer will see first the flash from the forward bolt, and then after a moment, the flash from the trailing one. In other words, two strikes occur at different times for this observer, one slightly before her counterpart standing next to the train sees his “simultaneous” flashes, and one slightly after. These two people in two different states of motion cannot agree on the timing of the identical events.
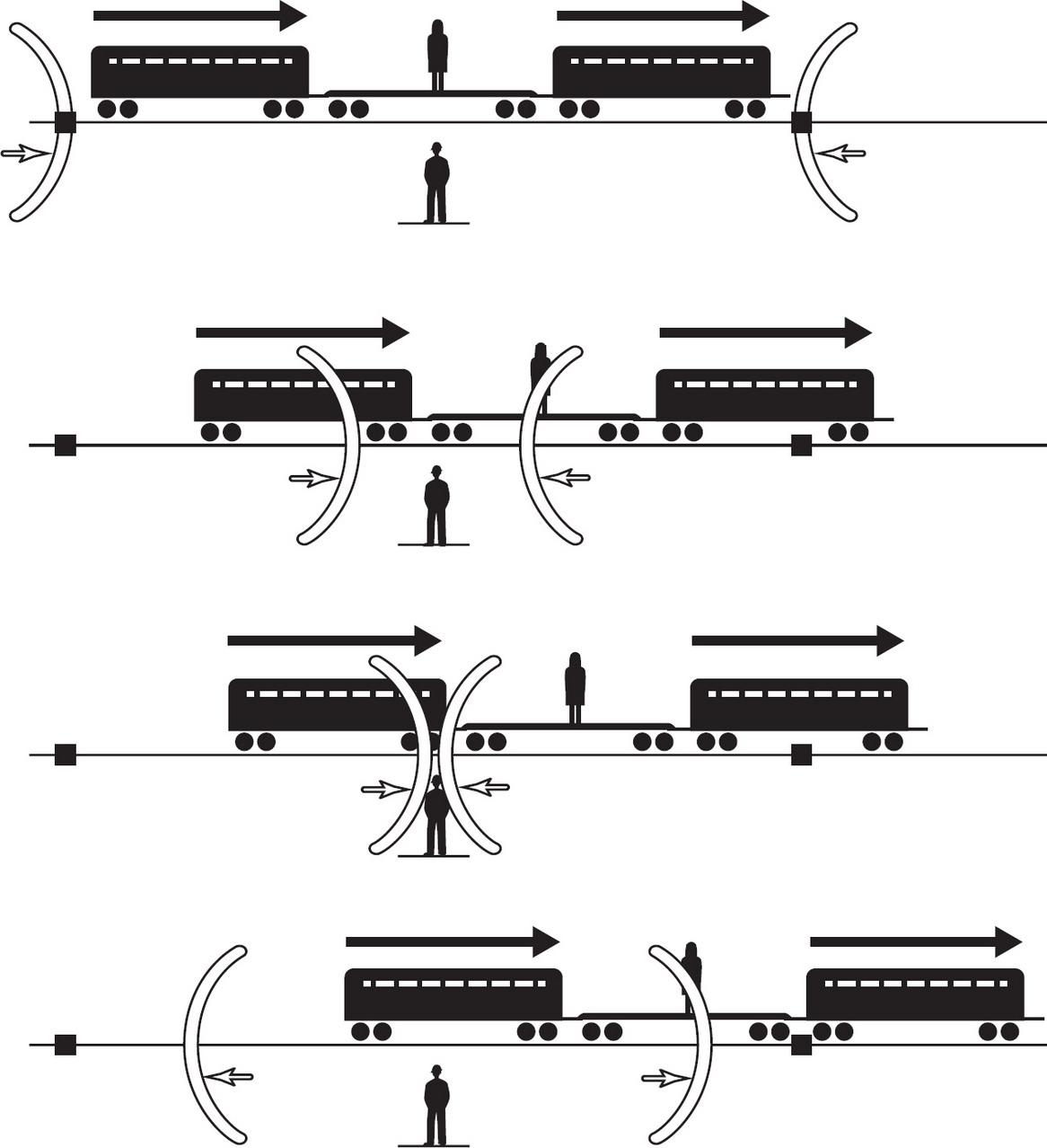

This version of Einstein’s simultanaeity thought experiment depicts what happens from the point of view of a trainspotter on the embankment. Lightning bolts strike both ends of the train as a passenger riding at the train’s midpoint passes the observer (top drawing). Einstein wanted to know if both the observer and the passenger would agree on the timing of the strikes. In the second drawing, the train moves forward, shortening the distance the light from the bolt at the front of the train has to travel to reach the passenger—which results in that light reaching the passenger before the trainspotter. In the third drawing, light from the forward bolt arrives at the trainspotter just as light from the back bolt reaches him too. To him, the lightning bolts hit simultaneously. Finally, in the bottom drawing, as the train moves yet farther, light from the rear bolt catches up to the passenger, who thus concludes that the two strikes hit at different times, disagreeing—in good faith—with the observer at trackside.
What’s more, Einstein realized, this disagreement holds true for distance too. Following the same reasoning as he did for time, Einstein emphasized the importance of the measuring apparatus, in this case an ordinary ruler. Imagine the passenger measuring her legroom with a ruler as she passes the train-spotter beside the track. As the rider notes her result, her measuring stick is moving past the observer on the other side of the window. The observer on the embankment measures the time it takes for the front and the rear of the measuring stick to pass him by. But as we already know through the lightning bolt thought experiment, those times will be different from the measured flow of time on the train—and from that follows that each observer, with their differing measurements of time have to disagree about the length of the measuring rod. Space and time are relative.
One step more remained. In his version of relativity, Galileo had worked out a set of mathematical rules—now called the Galilean transformations—to enable two people in motion relative to each other to see that their different perceptions were really equivalent accounts of the same event. Einstein’s relativity established the physics within an updated set—called the Lorentz transformations—that use that single constant, the velocity of light, to reconcile any two observers’ differing observations.
Newton’s God kept absolute time and absolute space throughout the universe, a divine clock striking the same hours at every point throughout all creation. That article of faith helped Newton to his genuinely revolutionary insight that the heavens above and the earth below are governed by a single set of laws, just one system of the world. As the flight of comets and the discoveries of planets seemed to prove, cosmic history seemed to possess a universal constancy, the same everywhere for all people at all times. Two centuries on, Einstein’s homely images of trains and timepieces and rulers laid waste to all that. His clocks tallied their seconds beautifully, but to a beat that varied in the eye of the beholder.
The second half of Einstein’s relativity paper extended its concepts beyond the realm of the motion of material objects. Relativity, he showed, held for objects in space; for the constituents of atoms; for electromagnetic fields, seemingly, for everything. Three months later, Einstein wrote again to show how deeply the concept penetrated into the fabric of what had seemed to be settled physics. In just two pages, he investigated what happens when a chunk of matter emits energy—any form of radiation for example. From that starting point, he performed a brief calculation that revealed that within relativity energy and mass can be shown to be equivalent. He wrote his conclusion in a very different form from the way we now know it, as the most famous equation in science: E=mc2.
On its own the demonstration that matter and energy were really two sides of a single coin would have been a fine piece of work. Though the calculation was easy—trivial, almost—it still seems almost unbelievable that an argument about kinematics, the properties of motion, could morph into such a deep claim. Common sense says that energy is something that happens to matter, the strike of a bat on a ball or the explosion that throws a shell out the cannon’s mouth. But common sense is wrong. Einstein’s equation forces us to conceive of matter and energy as intertwined, capable of transforming, one into the other.
If that weren’t strange enough, this little paper went deeper still, embodying an insight that Einstein grasped before anyone else: relativity wasn’t so much a specific law of nature as a condition to which all the more ordinary patterns in nature had to conform. E=mc2 translated the concept of inertia into relativistic terms. Through Einstein’s further work and that of others, the laws of motion fell into line. The electromagnetic equations of Maxwell had to be reinterpreted to account for the relativity of space and time…and so on. In the metaphor of the day, relativity was an imperialist, colonizing ever greater tracts of physics. The logic of empire is to grow, and the special theory’s next target was, if not obvious, then inevitable.
Einstein would remain at the patent office into 1909—among other virtues, it paid better than entry-level academic jobs—but long before he finally moved into the professoriat, his miracle year made it clear that he was a rising star, just coming into the full play of his powers. Thus, in the autumn of 1907 it made perfect sense that he would be asked to write a retrospective, charting the progress of relativity over the previous two years. That kind of invitation is an honor—but this one came with a barb. The request reached him late, leaving him only two months before the December 1 deadline. At first, that didn’t seem to be a problem. The larger half of the review went quickly. In four sections Einstein described the application of the relativistic worldview to measurements of time, the study of motion, the behavior of electromagnetic fields, and the implications of Einstein’s discovery of the equivalence of energy and matter. That was, in fact, more or less all that he’d been asked to do. His editor had sought a survey of current developments in relativity theory, and he’d written one.
He hung up on one last question, though. The “special” in the special theory of relativity refers to the fact that it is a limited concept. It described the behavior of space and time perfectly for almost all physical situations, with one major caveat: as Einstein understood it at the time, the special theory applied only to motion at a constant rate. That left those circumstances in which speeds change, accelerating or slowing down.*3 For Einstein, this left an intolerable gap. Acceleration is ubiquitous throughout the cosmos. Most important: anything subject to gravity accelerates.
With all the weight of the Einstein legend between us and that very young researcher—he was still just twenty-eight—stealing time for science in the ebb and flow of patent applications, it’s hard to recapture now just how much raw intellectual confidence was required to take this step. Thinking beyond special relativity would inevitably force him to confront the most famous idea—universal gravitation—produced by the most famous physicist in history: Newton. But if his theory really did form a part of the logic of nature, then no idea, not even the most iconic, should be able to escape it.
November 1907. Einstein reported each working day to the Patent Office. He wrote; he thought; he stared into space. Through his window he looked over at the rooftops of Bern. One day—we don’t know exactly when—he saw that anonymous roofer; he imagined the accident; and the missing piece, his happy thought, burst into his mind. The realization that a falling man won’t feel his own weight provided the crucial hint that led Einstein to think about gravity along similar lines to those he used to analyze the relativity of time and space. Einstein formalized this insight as the “equivalence principle”—an axiom that would become as important to his thinking as the relativity principle had proved to be in 1905. In its simplest form, equivalence simply holds that a person in free fall—like the imaginary roofer—cannot distinguish between two possible descriptions of his circumstances. He can’t say whether he is falling under the influence of gravity, or just floating in a gravity-free region of space.
In other words, never mind that from where Einstein sits, the roofer is accelerating, speeding up as he plummets. The roofer himself feels no change (until he hits the ground)—only weightlessness, no push or tug of any sort—which is the signature of uniform, inertial motion, the sort the special theory of relativity describes. The two states—free-fall and un-accelerated motion—thus had to be seen as equivalent, both accurate descriptions of the same phenomenon. The inverse is also true: it’s impossible for someone (in a closed room) to decide whether the tug she feels as she stands on the floor is that of the earth’s gravitational field, or something—say a rocket motor—accelerating beneath her, pushing upward on the soles of her shoes.
Epiphany! This new principle pointed Einstein directly to the essential connection special relativity on its own couldn’t make: the link between inertia, which is the measure of mass, and weight, which is mass multiplied by whatever force affects an object. Someone visiting the moon retains the same mass she has anywhere else. But because the moon exerts about 16 percent of the earth’s gravitational tug, her weight will be just one sixth what it would measure back home. More generally, weight can be understood as the perception of a change in the motion of any object, no matter whether that shift comes from acceleration or gravity. Free fall produces the same experience as the weightlessness of empty space, far from any source of gravity; acceleration produces the identical perception—that of weight—as does standing still in the grip of the earth’s gravitational field. That tumbling roofer and the equivalence principle he inspired told Einstein the bare minimum of what any relativistic theory of gravity would have to include: a mathematical account that could express the still undiscovered physics that established the connection between the inertial path of anyone or thing and the pull of gravity that exerts its hold on all of us as we travel across the universe.
November came to its end. Einstein finished his paper, including its final section on the equivalence principle and what it implied for a relativistic theory of gravity. It was barely a sketch, a hint toward something richer to come. All he really knew at this point was that it was possible to think about gravity in relativistic terms, in the language of inertia and acceleration.
There was one more mundane matter that caught his attention shortly after he sent off his review. Nowhere in that paper did he mention any real-world challenge to Newton’s gravitation, no anomalies or suspicious phenomena. Instead, then and for the next eight years, the central issue remained one of theoretical consistency, of reconciling the formal disagreement between special relativity and Newton’s ideas. Privately, though, Einstein had a perfectly fine grasp of the tactics as well as the strategy of intellectual combat. He knew that he could win if and only if he could clearly demonstrate that his theory modeled reality better than Newton’s. On Christmas Eve he wrote to Conrad Habicht, an old friend, not a physicist, that he was working on a new, relativistic law of gravitation. His aim? “To explain the still unexplained secular changes in the perihelion of Mercury.”
Vulcan had long since drifted to the far penumbra of possibility. But now, Albert Einstein, constructing a cosmos on a foundation of relativity, was taking dead aim at the undiscovered planet. From the beginning of his investigation of gravity, Einstein grasped the crucial either/or of Vulcan’s existence or absence. He wouldn’t mention Mercury again for several years, even in his private correspondence. But he didn’t forget it either.
*1 It would take another book—and at least thousands have already been written on this theme—to trace the tendrils of quantum mechanics in contemporary life. From the electrical phenomena that allow my computer to turn the motion of my fingers into letters on a screen and thence a page, to the specific properties of the materials within the seat upon which I sit, to the high poetry of the theories of the cosmos with which this book is partly concerned…quantum ideas are implicated everywhere. Most of the way we move around our world is classical, Newtonian, accessible. The secret life that underpins that overt one is inconceivable except as expressed in the language of the quantum revolution. Here the sermon endeth.
*2 In more detail: Maxwell’s equations yield a constant velocity for an electromagnetic wave (of which visible light is simply a particular set of wavelengths). By Galilean invariance, the assertion that the laws of physics remain the same for every observer in uniform motion, that constant velocity remains a constant in every frame of reference. But as Newton developed his mechanics based in part on Galileo’s work, the speed of light was no more a constant than any other velocity, and the claim of Galilean invariance did not apply; hence the conflict.
*3 Special relativity does apply to accelerated systems; the famous twin “paradox,” in which a twin accelerating away from and then returning to the earth ages more slowly than her stay-at-home brother, is an example of a special relativistic analysis of nonuniform motion. But in his initial framing of special relativity, Einstein considered uniform motion, and as he first began to think about generalizing the theory, he continued to think about this distinction between different states of motion.