What is two more than 3 times a certain number x ?
| 3x − 2 | |
| 3x | |
| 2x − 3 | |
| 2x + 3 | |
| 3x + 2 |
Algebra is usually all about writing equations. In this chapter, we’ll show you a fool-proof way to write the equations you need to write, give you a review of the quadratic formula, and teach you how to do simultaneous equations. Plus, you’ll learn two fantastic techniques that will allow you to avoid writing equations on most GMAT questions: Plugging In and Plugging In the Answers (PITA).
More than one quarter of the problems on the computer-adaptive GMAT Math section will involve traditional algebra.
In this chapter we’ll show you some powerful techniques that will enable you to solve these problems without using traditional algebra. The first half of this chapter will discuss these new techniques. The second half will show you how to do the few algebra problems that must be tackled algebraically.
There are certain problems in math that aren’t meant to have just one specific number as an answer. Here’s an example:
What is two more than 3 times a certain number x ?
To find one specific number that answers this question, we would need to know the value of that “certain number x.” Here’s the way it would look on the GMAT:
What is two more than 3 times a certain number x ?
| 3x − 2 | |
| 3x | |
| 2x − 3 | |
| 2x + 3 | |
| 3x + 2 |
In other words, this is kind of a cosmic problem. GMAC asks you to write an equation that will answer this question no matter what the “certain number” is. x could be any number, and that equation would still give you the correct answer.
The test writers expect you to use algebra to answer this question, but there is a better way. Because the correct answer will work for every value of x, why not just pick one value for x ?
We call this Plugging In. It is perhaps our most powerful math technique and will allow you to solve complicated problems more quickly than you might ever have thought possible. Plugging In is easy. There are three steps involved:
Let’s look at that same problem again:
![]()
What is two more than 3 times a certain number x ?
| 3x − 2 | |
| 3x | |
| 2x − 3 | |
| 2x + 3 | |
| 3x + 2 |
Let’s pick a number for x. How about 4 ? In your scratch booklet, write down “x = 4” so you will remember what number you’ve plugged in. By substituting 4 for the x, we now have a specific rather than a cosmic problem. The question now reads,
“What is two more than 3 times 4 ?”
3 × 4 = 12
What is 2 more than 12 ?
14
Using the number we chose for x, the answer to this question is 14. Write 14 down on the erasable board and circle it to indicate that it is your answer. All you need to do now is figure out which of the answer choices equals 14 when you substitute 4 for x.
When you’re plugging values in for variables, always start with the first answer choice (what we call choice A). If that doesn’t work, try the last choice (choice E), then B, then D, then C. In other words, start from the outside and work toward the center.
Let’s start with choice A, 3x − 2. Plugging in 4 for x, do we get 14 ? No, we get 10. Eliminate it.
Go to choice E, 3x + 2. Plugging in 4 for x, we get 12 + 2, or 14. This is the answer we wanted. To be absolutely sure, check all the answer choices, but choice E is the correct answer to this question.
![]()
You might be thinking, “Wait a minute. It was just as easy to solve this problem algebraically. Why should I plug in?” There are two answers:
The students in our GMAT course learn to automatically do scratch work. When plugging in, always write down the number you are plugging in for the variable, and then once you find the answer to the problem in terms of that number, write it down and circle it. Then try each of the answer choices, crossing them off as you eliminate them. Here’s what your scratch work should have looked like for that last problem:

While such a problem is designed to work with any number, you’ll find that certain numbers work better than others. Plugging in a number that’s simple to use is obviously a good idea. In general, you should stick with small numbers. But if the problem concerns hours and days, it might make sense to pick a multiple of 24, such as 48. If the problem concerns minutes and hours, a good number would probably be a multiple of 60, such as 120. Remember, when you are deciding what number(s) to plug in, the question to ask is: “What number(s) make this problem easy for me?”
Sometimes the best way to select a number is to use a little common sense. Here’s an example:
![]()
If Jim drives k miles in 50 minutes, at the same rate, how many minutes will it take him to drive 10 miles?
|
|
|
|
|
|
| 60k |
|
| 10k |
|
|
|
GMAC wants you to write a complicated equation based on the formula rate × time = distance, or perhaps set up a proportion. But this isn’t necessary. Because there are variables in the answer choices, you can simply plug in.
Any number you choose to plug in for k will eventually give you the answer to this problem, but there are some numbers that will make your task even easier.
If it takes Jim 50 minutes to drive k miles, how long will it take him to drive 10 miles at the same rate?
We need a number for k. What if we made k = half of 10 ? See how the question reads now:
If it takes Jim 50 minutes to drive 5 miles, how long will it take him to drive 10 miles at the same rate?
Suddenly the problem is simple. It will take him twice as long: 100 minutes. Now all we need to know is which of the answer choices equals 100, given that k = 5. Start with answer choice A. Divide 500 by 5 and you have 100. Bingo! To double-check, plug 5 into the other answer choices as well. None of them give us the correct answer of 100.
The answer to this question is choice A.
![]()
You can plug numbers into any problem in which the answer choices are not specific numbers. Try Plugging In if you see:
GMAC wants you to use algebra on problems that have variables in the answers, but Plugging In is easier, faster, and less likely to produce errors. Here’s an example:
![]()
At a photocopy center, the first 10 copies cost x cents each. Each of the next 50 copies costs 5 cents less per copy. From the 61st copy on, the cost is 2 cents per copy. Which of the following expressions shows the cost, in cents, to make 200 copies?
| 60x + 30 | |
| 50x − 10 | |
| 50(x − 5) | |
| 60x − 110 | |
| 10x + 490 |
Pick a number for x. How about 8 ? Write x = 8 on your scratch paper so you don’t forget.
The first 10 copies = 10 × 8 = 80 cents
The next 50 copies each cost 5 cents less than the first 10, so each of these copies costs 8 − 5, or 3 cents each.
The next 50 copies = 50 × 3 = 150 cents
From now on, the cost is 2 cents for any additional copies. We need a total of 200 copies. So far, we’ve done 60 copies. We need an additional 140 copies.
The final 140 copies = 140 × 2 = 280 cents
Let’s add it all up. 
This is the answer to the question. All we have to do is find out which answer choice equals 510. Start with choice A, 60x + 30, and remember that we plugged in 8 for x. Does 60(8) + 30 = 510 ? Yes, it does. The answer to this question is choice A. (Try the other choices just to be certain.)
![]()
GMAC also expects you to use algebra on certain problems that have percents in the answers. Plugging In is the better method. Here’s an example:
![]()
A merchant was selling an item at a certain price, then marked it down 20% for a spring sale. During the summer, he marked the item down another 20% from its spring price. If the item sold at the summer price, what percent of the original price did it sell for?
| 40% | |
| 60% | |
| 64% | |
| 67% | |
| 80% |
This is a difficult question. The first thing to do here is eliminate any answers that are too good to be true. The number 20 appears twice in this problem. Adding them together gives you answer choice A. Eliminate choice A. Joe’s favorite answer is probably choice B. Joe reasons that if an item is discounted 20% and then another 20%, there must be 60% left. Eliminate choice B. Choice E seems too large. The answer is probably C or D.

You may have noticed that while this problem gave us lots of information, it never told us the original price of the item. This is another cosmic problem. GMAC wants you to write an equation that will work regardless of the original price of the item. But because this problem is supposed to work for any original amount, we may as well pick one amount.
Let’s plug in 100. When you are dealing with a percent problem, 100 is usually a convenient number. The merchant was selling the item for $100. He discounted it by 20% for the spring sale. Twenty percent of $100 is $20, so the spring price was $80. For the summer, he discounted it again, by 20% of the spring price. Twenty percent of $80 is $16. Therefore he took $20 and then $16 off the original price. The summer price is $64.
The question asks what percent of the original price the item sold for. It sold for $64. What percent of 100 is 64 ? 64%. The answer is choice C.
![]()
You could use traditional math on problems with fractions or ratios in the answer choices, and that’s what GMAC wants. However, as we’ve seen before, you’ll work more quickly and make fewer mistakes if you use Plugging In. Here’s an example:
![]()
Half the graduating class of a college was accepted by a business school. One-third of the class was accepted by a law school. If one-fifth of the class was accepted to both types of school, what fraction of the class was accepted only by a law school?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
You may have noticed that while this problem gave us lots of fractions to work with, it never told us how many people were in the graduating class. This is yet another cosmic problem. The test writers want you to find a fractional part without knowing what the specific whole is. Because this problem is supposed to work with any number of people in the graduating class, we may as well pick one number.
This problem will work with any number, but some numbers are easier to work with than others. For example, if we chose 47 for the number of people in the graduating class, that would mean that ![]() people were accepted by a business school. While this might make a good plot for a Stephen King novel, wouldn’t it be easier to pick a number that can be
divided evenly by all the fractions in the problem? One number that is evenly divisible by 2, 3, and 5 is 30. So let’s plug in 30 for the number of people in the graduating class.
people were accepted by a business school. While this might make a good plot for a Stephen King novel, wouldn’t it be easier to pick a number that can be
divided evenly by all the fractions in the problem? One number that is evenly divisible by 2, 3, and 5 is 30. So let’s plug in 30 for the number of people in the graduating class.
One half of the class got into business school. ![]()
One third of the class got into law school. ![]()
One fifth of the class got into both. ![]()
GMAC wants to know what fraction of the class was accepted only by a law school. Ten people were accepted by a law school, but 6 of those 10 were also accepted by a business school. Therefore, 4 people out of 30 were accepted only by a law school. Reduced, ![]() is
is ![]() , so the answer is choice B.
, so the answer is choice B.
![]()
What about a problem that asks for a specific numeric answer?
A company’s profits have doubled for each of the 4 years it has been in existence. If the total profits for those 4 years were $30 million, what were the profits in the first year of operation?
There is only one number in the whole world that will answer this question. If you tried plugging in amounts for the first year of operation in hopes of happening upon the correct answer, you would be busy for a very, very long time.
GMAC expects you to use algebra to answer this question. It wants you to assign a variable for the first year’s profits, say x, in which case the second year’s profits would be 2x, the third year’s profits would be 4x, and the fourth year’s profits would be 8x. Altogether, we get 15x = 30, and x = 2.
Unfortunately, it is extremely easy to make a mistake when you set up an equation. You could add up the number of x’s incorrectly, or think that the profits of the third year were equal to 3x. While this is not a difficult problem, it does represent the potential difficulties of using algebra.
So why not solve this problem a better way? Take advantage of the fact that each time GMAC asks you to find a specific numeric answer, it is forced to give you five clues. Here is how GMAC would ask this question:
![]()
A company’s profits have doubled for each of the 4 years it has been in existence. If the total profits for the last 4 years were $30 million, what were the profits in the first year of operation?
| $1 million | |
| $2 million | |
| $4 million | |
| $4.5 million | |
| $6 million |
Without answer choices, this problem is complicated, and the only way to solve it is to use algebra. With answer choices, there are only five possible answers; one of them has to be correct. Why not work backward and plug the answer choices back into the problem?
Plugging In the Answers is easy. There are three steps involved:
Let’s try answer choice C:
| If the first year’s profits were | $4 million |
| the second year’s profits would be | $8 million |
| the third year’s profits would be | $16 million |
| and the fourth year’s profits would be | $32 million |
| The total profits = | $60 million |
This is too big. The total profits were only $30 million. We don’t even have to look at choice D or E, which are even bigger. We can eliminate choices C, D, and E.
Let’s try answer choice B:
| If the first year’s profits were | $2 million |
| the second year’s profits would be | $4 million |
| the third year’s profits would be | $8 million |
| and the fourth year’s profits would be | $16 million |
| The total profits = | $30 million |
Bingo! The correct answer is choice B. Note that if choice B had been too big, the only possible answer would have been choice A.
![]()
PITA can also be used in situations where you may be unsure about how to solve a problem algebraically.
![]()
If x is a positive number such that x2 + 5x − 14 = 0, what is the value of x ?
| −7 | |
| −5 | |
| 0 | |
| 2 | |
| 5 |
Notice that the question specifies that x must be a positive number. Don’t waste your time with choices A, B, or C—cross them off immediately. Now let’s try choice D. (Two squared) plus (5 times 2)—we’re up to 14 so far—minus 14 does equal 0. The answer is choice D.
Easy Eliminations
Obviously, if x is a positive number, choices A, B, and C are out of the question. Don’t waste time with those three—cross them off and move on.

![]()
Sometimes when you’re Plugging In the Answers you’ll be able to eliminate choice C, but you may not be sure whether you need a larger number or a smaller number. Rather than waste time trying to decide, just try all the answer choices until you hit the right one. You’ll never have to try more than four of them.
![]()
Today, Jim is twice as old as Fred, and Sam is 2 years younger than Fred. Four years ago, Jim was 4 times as old as Sam. How old is Jim now?
| 8 | |
| 12 | |
| 16 | |
| 20 | |
| 24 |
One of these five answer choices is the right answer. Let’s work backward and find out which one it is.
Start with C. Jim is 16 years old today. He is twice as old as Fred, so Fred is 8. Sam is 2 years younger than Fred, so Sam is 6. Therefore, 4 years ago Jim was 12 and Sam was 2. If these numbers agree with the rest of the problem, then choice C is the answer to this question. The problem says that 4 years ago Jim was 4 times as old as Sam. Does 2 times 4 equal 12 ? No. Choice C is the wrong answer. Does anybody want to guess which direction to go in now? Rather than hem and haw, just try the other answers until you get the right one.
Let’s try choice D. Jim is 20 years old today. He is twice as old as Fred, so Fred is 10. Sam is 2 years younger than Fred, so Sam is 8. Therefore, 4 years ago Jim was 16 and Sam was 4. If these numbers agree with the rest of the problem, choice D is the right answer. The problem says that 4 years ago Jim was 4 times as old as Sam. Does 4 times 4 equal 16 ? Yes. The answer is choice D.
![]()
From time to time, the test writers will give you a question that contains the words “must be,” “could be,” or “cannot be.” This type of problem can almost always be solved by Plugging In, but you may need to plug in more than one number. Here’s an example:
![]()
If x and y are consecutive positive integers, which of the following must be an even integer?
|
x
|
|
|
y
|
|
|
|
|
|
|
|
|
xy
|
Plug In numbers for x and y. How about 2 for x and 3 for y ? Now go through each of the answer choices. Using these numbers, choice A is even, but because of the words “must be,” we cannot assume that it will always be even, or that this is necessarily the right answer. Keep going. Using the numbers we plugged in, choices B and C turn out to be odd, and D is not an integer. Because the question asks us for an answer that is always even, we can eliminate all of these. However, choice E is also even. We’re down to either choice A or E. Which is correct?
Try plugging in a different set of numbers. The problem concerns even and odd numbers, so this time let’s try an odd number first. How about 3 and 4 ? This time choice A is odd. Eliminate it. Choice E is still even; this must be our answer. In “must be” or “could be” problems, it often helps to plug in “weird numbers” such as 1 or 0—the kind of numbers we told you to avoid in regular Plugging In problems. This is because, when solving these problems, we’re often looking for a weird, exceptional answer.
![]()
Plugging In will take care of most of your algebraic needs, but there are a few types of problems that require some knowledge of basic algebra.
Even the simplest equalities can be solved by Plugging In the Answers, but it’s probably easier to solve a simple equation algebraically. If there is one variable in an equation, isolate the variable on one side of the equation and solve it. Let’s try an example of this type, although a question this easy wouldn’t actually be seen on the GMAT. This one is just for practice.
![]()
If x − 5 = 3x + 2, then x =
| −8 |
|
|
|
|
| −7 |
|
|
|
|
|
|
Get all of the x’s on one side of the equation. If we subtract x from both sides we have:

Now subtract 2 from both sides:

Finally, divide both sides by 2:

The answer is choice B.
![]()
To solve inequalities, you must be able to recognize the following symbols:
| > | is greater than |
| < | is less than |
| ≥ | is greater than or equal to |
| ≤ | is less than or equal to |
As with an equation, you can add a number to or subtract a number from both sides of an inequality without changing it; you can collect similar terms and simplify them. In fact, an inequality behaves just like a regular equation except in one way:
If you multiply or divide both sides of an inequality by a negative number, the direction of the inequality symbol changes.
−2x > 5
To solve for x, you would divide both sides by −2, just as you would in an equality. But when you do, the sign flips:

Q: Are the following
equations distinct?
(1) 3x + 21y = 12
(2) x + 7y = 4
Simultaneous equations are almost always tested in data sufficiency format on the GMAT. It’s impossible to solve one equation with two variables. But if there are two equations, both of which have the same two variables, then it is possible to solve for both variables. An easy problem might look like this:
If 3x + 2y = 6 and 5x − 2y = 10, then x = ?
To solve simultaneous equations, add or subtract the equations so that one of the variables disappears.

In more difficult simultaneous equations, you’ll find that neither of the variables will disappear when you try to add or subtract the two equations. In such cases you must multiply both sides of one of the equations by some number in order to get the coefficient in front of the variable that you want to disappear to be the same in both equations. This sounds more complicated than it is. A difficult problem might look like this:
If 3x + 2y = 6 and 5x − y = 10, then x = ?
Let’s set it up the same way:
3x + 2y = 6
5x − y = 10
Unfortunately, in this example, neither adding nor subtracting the two equations gets rid of either variable. But look what happens when we multiply the bottom equation by 2:
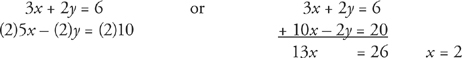
A: No. Look at what
equation #2 looks like
multiplied by 3:
3(x + 7y) = 3(4)
or 3x + 21y = 12.
Multiply both sides
by 3 and
equations
#1 and #2 are identical.
When one equation
can be multiplied to
produce the other, the
equations are identical,
not distinct.
On the GMAT, quadratic equations always come in one of two forms: factored or expanded. Here’s an example:
![]()
The first thing to do when solving a problem that involves a quadratic equation is to see which form the equation is in. If the quadratic equation is in an unfactored form, factor it immediately. If the quadratic equation is in a factored form, unfactor it. The test writers like to see whether you know how to do these things.
To unfactor a factored expression, just multiply it out using FOIL (First, Outer, Inner, Last):

To factor an unfactored expression, put it into the following format and start by looking for the factors of the first and last terms.
![]()
For the first term of the unfactored expression to be x2, the first term of each parentheses of the factored expresstion has to be x.
![]()
For the last term of the unfactored expression to be 15, the last term in each parentheses of the factored expression must be either 5 and 3 or 15 and 1. Since there is no way to get a middle term for the unfactored expression with a coefficient of 2 if the terms were 15 and 1, we are left with
![]()
To decide where to put the pluses and minuses in the factored expression, look to see how the inner and outer terms of the factored equation would combine to form the middle term. If we put a minus in front of the 5 and a plus in front of the 3, then the middle term would be −2x (not what we wanted). Therefore, the final factored expression looks like this
![]()
Quadratic equations are usually set equal to 0. Here’s an example:
![]()
What are all the values of x that satisfy the equation x2 + 4x + 3 = 0 ?
| −3 | |
| −1 | |
| −3 and −1 | |
| 3 and 4 | |
| 4 |
This problem contains an unfactored equation, so let’s factor it.

In order for this equation to be correct, x must be either −3 or −1. The correct answer is choice C.
Note: This problem would also have been easy to solve by Plugging In the Answers. It asked a specific question, and there were five specific answer choices. One of them was correct. All you had to do was try the choices until you found the right one. Bear in mind, however, that in a quadratic equation there are usually two values that will make the equation work.
![]()
There are three types of quadratic equations the GMAT test writers find endlessly fascinating. These equations appear on the GMAT with great regularity in both the problem-solving format and the data-sufficiency format:
(x + y)2 = x2 + 2xy + y2
(x + y)(x − y) = x2 − y2
(x − y)2 = x2 − 2xy + y2
Memorize all three of these. As with all quadratic equations, if you see the equation in factored form, you should immediately unfactor it; if it’s unfactored, factor it immediately. Here’s an example:
![]()
If ![]() = 5, then x =
= 5, then x =
| 3 | |
| 5 | |
| 6 | |
| 7 | |
| 9 |
It is unfactored, so let’s factor it:

The (x + 2)s cancel out, leaving us with (x − 2) = 5. So x = 7, and the answer is choice D.
![]()
(x + y)2 = x2 + 2xy + y2
(x + y)(x − y) = x2 − y2