In this chapter, we’ll show you how to master data-sufficiency problems, how to decipher the intermediate and advanced math hidden beneath the unfamiliar format, and how to use POE to eliminate tempting traps.
Now that you’ve reviewed all the important math concepts covered on the GMAT, it’s time to take a second look at how these concepts are used in data-sufficiency questions.
First, a quick review:
Every data-sufficiency problem consists of a question followed by two statements:
What is x ?
(1) x2 = 4.
(2) x is negative.
You have to decide NOT what the answer is, but WHETHER the question can be answered based on the information in the two statements. There are five possible answer choices:
| |
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient. |
| |
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. |
| |
BOTH statements TOGETHER are sufficient, but NEITHER statement alone is sufficient. |
| |
EACH statement ALONE is sufficient. |
| |
Statements (1) and (2) TOGETHER are not sufficient |
The best way to answer data-sufficiency problems is to look at one statement at a time—so ignore Statement (2), and look only at Statement (1). Based on Statement (1), x2 = 4, can we answer the question, “What is x ?”
At first glance, you might think so. If x2 = 4, then x = 2, right?
Well, not necessarily; x could also equal −2. And since Statement (1) gives us two different possible answers to this question, Statement (1) is NOT sufficient to answer the question. Choices A and D are out of the question; we are down to B, C, or E.
Now, ignore Statement (1) and look ONLY at Statement (2). Based on Statement (2), “x is negative,” can we answer the question, “What is x ?”
Nope, x could be any negative number. We are now down to C or E.
Look at both statements together. If x2 = 4 and x is negative, can we answer the question, “What is x ?”
Yup! Now there is only one unique number in the world that x could be: −2. The correct answer is C.
Here’s a flowchart that walks you through each step of solving a data-sufficiency question. If you need more information about how to use the chart or the basic strategy for solving a data-sufficiency question, check out Chapter 9.
In terms of mathematical content, data-sufficiency questions test the same kinds of topics tested by problem-solving questions (as we told you in Chapter 9). You’ll find problems involving integers, percents, averages, ratios, algebra, and geometry. Only the format is different.
Your familiarity with the math content, however, can give you an advantage when working a data-sufficiency question. Most people read the question and then immediately read the statements. But that’s not how you would normally work a math problem. Normally, you would read the problem and then ask yourself, “What do I already know?” and “What do I need?”
You should always attempt to do the same thing when working a data-sufficiency question. Before proceeding to the statements take stock of the information that you already know. Then, see if you can determine what sort of information the statements need to provide so that you could solve the problem.
We call this approach Pieces of the Puzzle. In a sense, data-sufficiency questions are just like jigsaw puzzles. When you work a jigsaw puzzle, you know what piece you are looking for based on the shapes of the pieces that fit around it. In a data-sufficiency question, you’ll often know what sort of information you need from the statements based on what you already know from the question stem.
Here’s an example:
If a store sold 30 more televisions this month than last month, by what percent has the number of televisions sold increased from last month to this month?
(1) This month the store sold 150 televisions.
(2) Last month the store sold 80% as many televisions as this month.
Start by asking, “What do I know?”
You know two things. First, the problem asks for a percent increase. That should get you thinking about the formula for percent change:
Next, notice that you already know the change, since the question states that the store sold 30 more televisions this month than last month. So, you can plug the difference into the formula to get:
Now, it’s time to ask yourself, “What do I need?” By looking at the formula, you can see that you’ll be able to answer the question if the statements give you a way to determine the original. So, as soon as you know how many televisions the store sold last month, you have sufficient information.
Now, remember to read only Statement (1). If the store sold 150 televisions this month and that represents an increase of 30 televisions, you know that the store sold 120 televisions last month. So, write down AD.
Now, forget about Statement (1) and read Statement (2). This statement is a little trickier than the first. If last month’s sales were 80% of this month’s sales, you know that the additional 30 televisions that were sold this month represent 20% of the total. Now, you set up a part-to-whole relationship:
Can you find the value of x from this equation? Of course. Therefore, Statement (2) is also sufficient and the answer to this question is D.
Let’s try the approach again on a difficult question.
What is the average (arithmetic mean) of a list of 6 consecutive two-digit integers?
(1) The remainder when the fourth integer is divided by 5 is 3.
(2) The ratio of the largest integer to the smallest integer is 5:4.
As before, apply the Pieces of the Puzzle approach by asking, “What do I know?”
Since the question asks you to find the average, you should remember that you can find an average if you have the sum of the items being averaged and the number of those items. In this case, you know that there are six integers. You also know that the integers are consecutive. Finally, since the question states that the integers are two digit, you know that each integer is between 9 and 100.
Now, it’s time to ask, “What do I need?” There are lots of possibilities. The statements could give you the sum of the six numbers. Or, the statements could give you the value of one of the integers and its position in the list. For example, if you know that the second integer is 12, you could certainly find the average.
Now, read and evaluate only Statement (1). It’s best to think about the information in this statement by plugging in some possible numbers. For example, the fourth integer could be 18 because the remainder when 18 is divided by 5 is 3. If the fourth integer is 18, the first integer is 15. The complete list would be 15, 16, 17, 18, 19, 20 and their average is 17.5. However, the fourth integer could also be 33, making the first integer 30 and the average of the six integers 32.5.
So, Statement (1) does not provide sufficient information to find the average of the six integers. Write down BCE.
Now, forget what you know from the first statement and evaluate only Statement (2). At first, Statement (2) may not seem like much help either. After all, if you are going too quickly, you may be tempted to think that the largest integer could be 15 and the smallest 12 or the largest could be 20 and the smallest 16.
However, here’s where you need to remember the puzzle piece that you already have—there are six consecutive integers on the list. So, while 12 and 15 may seem to fit the ratio provided in the second statement, those numbers really don’t satisfy the statement and the problem because there wouldn’t be six numbers for the list.
The only way to satisfy the information in the second statement and in the problem is to make the smallest number 20 and the largest number 25.
Therefore, the answer to this difficult question is B.
The answers can be found in Part V.
1. If only people who paid deposits attended the Rose Seminar, how many people attended this year?
(1) 70 people sent in deposits to attend the Rose Seminar this year.
(2) 60% of the people who sent deposits to attend the Rose Seminar this year actually went.
| |
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient. |
| |
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. |
| |
BOTH statements TOGETHER are sufficient, but NEITHER statement alone is sufficient. |
| |
EACH statement ALONE is sufficient. |
| |
Statements (1) and (2) TOGETHER are NOT sufficient. |
2. Luxo paint contains only alcohol and pigment. What is the ratio of alcohol to pigment in Luxo paint?
(1) Exactly 7 ounces of pigment are contained in a 12-ounce can of Luxo paint.
(2) Exactly 5 ounces of alcohol are contained in a 12-ounce can of Luxo paint.
| |
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient. |
| |
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. |
| |
BOTH statements TOGETHER are sufficient, but NEITHER statement alone is sufficient. |
| |
EACH statement ALONE is sufficient. |
| |
Statements (1) and (2) TOGETHER are NOT sufficient. |
3. A car drives along a straight road from Smithville to Laredo, going through Ferristown along the way. What is the total
distance by car from Smithville to Laredo?
(1) The distance from Smithville to Ferristown is 
of the distance from Smithville to Laredo.
(2) The distance from Ferristown to Laredo is 12 miles.
| |
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient. |
| |
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. |
| |
BOTH statements TOGETHER are sufficient, but NEITHER statement alone is sufficient. |
| |
EACH statement ALONE is sufficient. |
| |
Statements (1) and (2) TOGETHER are NOT sufficient. |
For problem solving questions, the figures are generally drawn to scale. Chapter 13 discussed how you can ballpark by using the figure so long as it wasn’t clearly marked that it wasn’t drawn to scale.
For data-sufficiency questions, however, you should be very careful when using the figure. The figures are drawn so that they represent the information in the question stem, but they need not accurately represent the information in the statements. So, you should base your conclusions about whether you have sufficient information on the statements rather than any figures provided with a data-sufficiency question.
When data-sufficiency questions are about geometry, however, you can often make very effective use of the Pieces of the Puzzle approach. The Pieces of the Puzzle approach works very well in situations in which you can use formulas and take stock of facts.
Here’s an example of a medium question to illustrate:
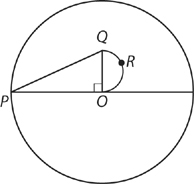
In the figure above, arc QRO is a semicircle. What is the area of the circle with center O ?
(1) The area of triangle PQO is 30.
(2) The length of QRO is 2.5π.
Apply the Pieces of the Puzzle approach by asking, “What do I know?”
For this problem, you actually know a lot. You know that arc QRO is half a circle and that its diameter is one side of a right triangle. Of course, you also know that triangle PQO is a right triangle, so the Pythagorean theorem applies.
Now, ask, “What do I need?” The question asks for the area of the circle. Since the formula for the area of a circle is A = πr2, you’ll need a way to find the radius of the circle. If the statements provide either the length of PO or a way to find that length, you’ll have sufficient information.
Your next step is to look only at the information provided in Statement (1). The formula for the area of a triangle is A = 
. You know the area but neither the base nor the height, so you have insufficient information. Write down BCE.
Next, look only at Statement (2). Now, it’s time to remember that QRO is a semicircle. The statement gives you half of the circumference of a circle. You can use the circumference formula to find the diameter, QO. In this case, you actually have half the circumference, so use 2C = πd or 2(2.5π) = πd and d = 5. So, now you know the length of QO, but you still don’t have the radius of the circle. (You may think that you recognize a 5:12:13 right triangle, but remember that you need two sides of the triangle to use the Pythagorean theorem.) Cross off B.
Finally, put the statements together. Now, you know both the area of the triangle and its height, so you can plug those values into the formula for the area of a triangle to get −30 = 1/2(b)(5). Can you use this formula to find PO ? Yes. So, the answer to the problem is C.
The data-sufficiency question type is particularly well suited to testing your knowledge of the rules of equations and the strange powers of powers. Let’s review this important information:
For example, x = y + 1 cannot be solved, but x = y + 1 and 2x = −y − 6 can be added together, eliminating one variable so the other may be solved.
For example, if x2 = 4, then x could equal either 2 or −2. If x3 = 8, then x can only equal 2.
Let’s look at some problems that use these rules.
Mr. Jones spends $25 on movie tickets for a party of adults and children. How many children’s tickets did he buy?
(1) Adult movie tickets cost $3 each and children’s tickets cost $2 each.
(2) Mr. Jones buys a total of 11 tickets.
Start by asking, “What do I know?” In this case, you know that Mr. Jones spends $25 and that there are two variables—adult tickets and children’s tickets.
Next, ask, “What do I need?” It’s time to start thinking “two equations, two unknowns.”
Now, evaluate Statement (1). From this statement, you get 3x + 2y = 25. That’s only one equation but two variables, so you do not have sufficient information. So, write down BCE.
Next, evaluate Statement (2), from which you can get the equation x + y = 11. Again, there’s only one equation and two variables, so cross off B.
When the statements are combined, you have two distinct equations with two variables, which means that you can solve. So, the answer is C.
Here’s a harder example. This example would be an upper-medium problem.
What is the value of 
?
(1) 7a − 3b = 0
(2) b = 5
| |
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient. |
| |
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. |
| |
BOTH statements TOGETHER are sufficient, but NEITHER statement alone is sufficient. |
| |
EACH statement ALONE is sufficient. |
| |
Statements (1) and (2) TOGETHER are not sufficient. |
You’re not going to get much mileage out of the Pieces of the Puzzle approach for this question. All you really know is that there are two variables involved.
So, ignore Statement (2). Based on Statement (1) ALONE, can you answer this question? At first glance, you might think not—because there are two variables in one equation. But the question is not asking you to solve for a and for b, but for 
. If you add 3b to both sides of the equation in Statement (1), you get
7a = 3b. If you then divide both sides of the equation by b, you get 
, which reduces to 
=3. By dividing both sides by 7, you get 
, which answers the
question. Statement (1) is sufficient, and you are down to AD. Looking at Statement (2) alone, of course, you can’t answer the question, so the correct answer to the problem is choice A.
The problem we just solved made use of the third rule in our review. Notice that C was a trap answer for this problem. Sure, you could find the value of a and b by combining the statements. However, answer C states that you need to put the statements together because neither statement provides sufficient information by itself. So, you’ll want to remember that it’s possible to know the value of an expression without knowing the values of the variables that make up that expression.
Here’s one more example. This one doesn’t sound that bad, but it’s actually a very difficult problem.
Mr. Jones spends $76 on movie tickets for a group of adults and children. How many children’s tickets did he purchase?
(1) Adult movie tickets cost $11 each and children’s movie tickets cost $7 each.
(2) Mr. Jones bought two more adult tickets than children’s tickets.
As always, start by asking, “What do I know?” In this case, Mr. Jones spends $76 on movie tickets, and there are two variables. But, notice that there is actually one more thing that you know—movie tickets must be bought in integer quantities.
Next, ask, “What do I need?” You’ll probably need two equations, but the fact that the variables can only take on integer values may change things.
Now, it’s time to look at Statement (1), which gives you the equation 11x + 7y = 76. Before dismissing this single equation with two variables as insufficient, remember that both x and y must be integers. Also, notice that the coefficients, 11 and 7, are large enough to limit the possibilities. Mr. Jones must buy fewer than 7 adult tickets. It’s probably worthwhile to investigate how many of those integer values for x produce an integer value for y. As it happens, y is only an integer when x = 5. So, Mr. Jones bought 5 adult tickets and 3 children’s tickets. So, write down AD.
Statement (2), however, does not provide sufficient information by itself. Remember that you don’t even know how much the tickets cost based only on the second statement. So, the answer is A.
So, how was this problem different from the first problem in which Mr. Jones bought movie tickets? Why didn’t we need to worry about the integer quantities on the first problem? Well, actually, we did. However, for the first problem, the first statement gave us the equation 3x + 2y = 25. Had we taken some time to investigate this equation, we would have quickly discovered that there are several sets of integer solutions. For example, Mr. Jones could have bought 3 adult tickets and 8 children’s tickets, or he could have bought 5 adult tickets and 5 children’s tickets.
So, how do you know when to look for a single integer solution? Well, first make sure that the variables can only be integers! Since you can’t buy half a movie ticket, that was part of the tip-off. Next, if there is going to be only one integer solution, it is likely that at least one of the coefficients will be a larger prime number like 11 or 17 or 29.
Finally, think about your current scoring level. A problem like that last one would show up only in one of the GMAT’s most difficult question bins—because the test writers think so few people will get it right. You aren’t likely to encounter this problem on your computer-adaptive GMAT unless you are scoring in the mid to high 40s on your practice math tests.
The answers can be found in Part V.
1. What is the value of x ?
(1) x2 = 4
(2) x < 0
| |
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient. |
| |
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. |
| |
BOTH statements TOGETHER are sufficient, but NEITHER statement alone is sufficient. |
| |
EACH statement ALONE is sufficient. |
| |
Statements (1) and (2) TOGETHER are NOT sufficient. |
2. What is the value of xy ?
(1) x2 = 4
(2) y = 0
| |
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient. |
| |
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. |
| |
BOTH statements TOGETHER are sufficient, but NEITHER statement alone is sufficient. |
| |
EACH statement ALONE is sufficient. |
| |
Statements (1) and (2) TOGETHER are NOT sufficient. |
| |
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient. |
| |
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. |
| |
BOTH statements TOGETHER are sufficient, but NEITHER statement alone is sufficient. |
| |
EACH statement ALONE is sufficient. |
| |
Statements (1) and (2) TOGETHER are NOT sufficient. |
We covered the basics of Yes/No Data Sufficiency in Chapter 9.
First, let’s do a quick review by looking at a problem.
Is integer x prime?
(1) 47 < x < 53
(2) x > 0
Notice that this question is phrased so that you would need to respond by saying “yes,” “no,” or “maybe” rather than by giving a numerical answer. That’s why this is a yes/no question. As you know from Chapter 9, you use the same process to answer a yes/no data-sufficiency question.
So, start by evaluating only Statement (1). There are 5 integers between 47 and 53—48, 49, 50, 51, and 52. Are any of these integers prime? No. But, notice that means that you can answer the question. Is x prime? No, it isn’t. So, you have sufficient information. (Remember that a statement can be sufficient for a yes/no question if it allows you to answer the question in either the affirmative or the negative.) So, write down AD.
Now, look only at Statement (2). Based on Statement (2), you don’t know whether x is prime. If x is 3, for example, the answer to the question is yes. However, if x is 4, the answer to the question is no. The best answer you could give to the question “Is x prime?” based on Statement (2) is “maybe.” So, the answer to the problem is A.
Because as many as half of the data-sufficiency problems you’ll see on the GMAT will be yes/no questions, it’s a good idea to have a strategy for these questions. When yes/no questions involve variables, you can plug into the statement and use those numbers to see if you always get the same answer to the question.
In the problem we just looked at, we plugged into the second statement. Because we were able to find examples of numbers that satisfied the statement but that gave different answers to the question, we knew that Statement (2) wasn’t sufficient.
Now, let’s look at another example.
Is x an integer?
(1) 5x is a positive integer.
(2) 5x = 1
As always, ignore Statement (2) and look only at Statement (1). Since this question is phrased as a yes/no question and there are variables involved, let’s plug in.
When you plug in on a yes/no data-sufficiency question, you start by picking a number that satisfies the statement. For example, we can start with a nice, simple number such as x = 2. Notice that we can use x = 2 because 5 × 2 = 10 and 10 is a positive integer.
Now that we’ve found a number that satisfies the first statement, it’s time to use that number to answer the question. Be sure that you use the value that you picked for x, not the result of the statement. So, the question becomes “Is 2 a positive integer?” and the answer is, of course, yes. Careful! Don’t write down AD yet!
All we’ve done is find one example of a number that satisfies the first statement and used that number to answer the question. Now that we have an answer of yes, we actually want to see if it’s possible to get an answer of no to the question based on a number that satisfies the first statement.
What if we make x = 
? We’ve satisfied the statement because 5 × = 1 and 1 is a positive integer. However, now we need to use our number to get an answer to the question.
Is a positive integer? No.
So, some numbers that satisfy the first statement produce an answer of yes to the question, while other numbers that satisfy the statement produce an answer of no. So, we don’t have sufficient information to state whether x is an integer. Write down BCE.
Now it’s time to look at the second statement. In this case, we have an equation that we can solve to find that x = . So, we ask, “Is an integer?” and give a definite answer of no.
The answer to the problem is B.
Plugging In is your most important strategy for handling yes/no data sufficiency questions.
To see how effective Plugging In can be, let’s try it on a more difficult question.
Is 3n > 2k ?
(1) k = n + 1
(2) n is a positive integer.
This is a yes/no question involving variables, so Plugging In is a good idea.
Start by evaluating Statement (1) alone. Pick an easy number for n. If n = 2, then k = 3. The numbers satisfy the statement, so it’s time to use them to answer the question. Is 32 > 23? Yes.
Remember, however, that you can’t properly evaluate the statement based on the results from only one set of numbers. Suppose we tried something a little weirder for n ? If n = −1, then k = 0. Is 3−1 > 20? No. (Remember that negative exponents are just another way of writing a reciprocal and that any nonzero number raised to 0 is 1.)
So, we don’t actually know what the answer to the question is based only on Statement (1). It looks as though the answer depends on the numbers we choose. Write down BCE.
For Statement (2), we can also plug in. Notice that the statement doesn’t tell us anything about k, however. So, we could say that n = 2 and k = 1 to get an answer of yes to the question. But, we could also say that n = 2 and k = 4 to get an answer of no. Cross off B.
When we combine the statements, we can still use n = 2 and k = 3, which, as we saw when we looked at Statement (1), gives us an answer of yes to the question. However, we could also use n = 1 and k = 2 to satisfy the combined statements. Is 31 > 22? No. So, the answer to this problem is E.
Yes or No Plugging In Checklist
The answers can be found in Part V.
1. If x is a positive number, is x < 1 ?
(1) 2x < 1
(2) 2x ≤ 2
| |
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient. |
| |
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. |
| |
BOTH statements TOGETHER are sufficient, but NEITHER statement alone is sufficient. |
| |
EACH statement ALONE is sufficient. |
| |
Statements (1) and (2) TOGETHER are NOT sufficient. |
| |
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient. |
| |
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. |
| |
BOTH statements TOGETHER are sufficient, but NEITHER statement alone is sufficient. |
| |
EACH statement ALONE is sufficient. |
| |
Statements (1) and (2) TOGETHER are NOT sufficient. |
3. Are x and y integers?
(1) The product xy is an integer.
(2) x + y is an integer.
| |
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient. |
| |
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. |
| |
BOTH statements TOGETHER are sufficient, but NEITHER statement alone is sufficient. |
| |
EACH statement ALONE is sufficient. |
| |
Statements (1) and (2) TOGETHER are NOT sufficient. |
As you have just seen, Plugging In can be a very helpful tool to evaluate whether the statements provide sufficient information to answer the question on yes/no data-sufficiency question. Sometimes, however, Plugging In can also help you discover what the question is asking.
Often, test writers make a question harder by writing the question stem in a way that hides the concept being tested. After all, if you’re having a hard time understanding the question, you’ll almost certainly have a hard time answering the question. You should remember, however, that no matter how confusing the question stem appears when you first read it, that GMAT questions really only test fairly straightforward math concepts. Plugging In can help you decipher the question stem.
Here’s an example of how the test writers might ask a difficult question:
If l1 and l2 are distinct lines in the xy coordinate system such that the equation for l1 is y = ax + b and the equation for l2 is y = cx + d, is ac = a2 ?
(1) d = b + 2
(2) For each point (x, y) on l1, there is a corresponding point (x, y + k) on l2 for some constant x.
One of the hardest things about this question is understanding the question stem. It’s going to be impossible to evaluate the information in the statements before we understand what we’re being asked.
Let’s try applying the Pieces of the Puzzle approach by first asking, “What do we know?” We know there are two lines. And, since the question tells us that the lines are distinct, we know that they are different. We also sort of have the equations for each line, but we recognize that the equations we’re given are really just the general equation for any line—y = mx + b.
At this point, it might be a good idea to take stock of what we know about lines. In the equation y = mx + b, m is the slope and b is the y-intercept. For our two lines in question, a and c represent the slopes and b and d represent the y-intercepts.
Okay, now we’re getting somewhere. The question is asking us something about the slopes of the lines, since a and c represent the slopes. Now, let’s plug in. If we let a = 2 and b = 3, then (2)(3) ≠ 22. How could ac = a2? That could only happen if a = c.
Now we’ve got it. If a = c, the slopes of the lines are equal. If the slopes of two lines are equal, the lines are parallel. This question is really just asking, “Is l1 parallel to l2?” If the test writers had asked the question this way, the difficulty of the question would have dropped.
Let’s check out the statements. If we look only at Statement (1), all we know is that the y-intercept of l2 is 2 more than the y-intercept of l1. In that case, the slopes could be the same—producing an answer of yes to the question—or the slopes could be different—producing an answer of no. So, Statement (1) is insufficient. Write down BCE.
Now, let’s look at Statement (2). Plugging In is a good way to evaluate this statement. Start by picking a value of k, which must be a constant. We’ll let k = 2. Let’s say that points (2,6) and (3,8) are on line l1, which would mean that (2,8) and (3,10) are on l2. Using those points, we can calculate that the slope of each line is 2. Since the slopes are the same, the lines are parallel. We have an answer of yes to the question.
Of course, when you plug in on yes/no data sufficiency, you shouldn’t stop after plugging in just one set of numbers. This time, let k = 3. Let’s also say that (2,8) and (3,11) are on l1, which would mean that (2,11) and (3,14) are on l2. Once again, we can calculate the slope of each line. In this case, both slopes turn out to be 3. Again, since the slopes are the same, the lines are parallel. (Don’t be thrown by the fact that the slopes are different for each plug in. We’re only trying to see if the slopes of the lines are the same each time we plug in.)
If you remain unconvinced, you could try plugging in again, but you’ll again find that the slopes of the lines are equal. In effect, the second statement tells us that for each point on l1 there is a corresponding point on l2 that is a distance of k units away. That can only happen if the lines are parallel. So, the answer is B.
If that question left you shaking your head, you’re not alone. It’s a very difficult question. Only a handful of test takers will wind up getting it right. In effect, the test writers pulled out every trick in their book to make this question difficult. Understanding the various ways that the GMAT test writers make questions difficult can help you improve your score dramatically.
Data-sufficiency questions that you find difficult and confusing are a distinct possibility when you take the GMAT, so you need to be prepared for them. After all, if the computer is doing its job properly—and you can pretty much count on that—it will keep feeding you progressively harder questions in the hopes that it will find one that you don’t know how to do.
In other words, almost every GMAT test taker hits a wall at some point. You’ve just gotten a string of questions right and suddenly there’s a question on your screen that you find confusing. You need to answer it to move on to the next question, but you’d like to do better than a blind guess. In fact, if you narrow your available choices, you may just guess correctly, dodge the bullet, get the next couple of questions right, and wind up with a higher score than if you didn’t have a plan for handling those tough, confusing questions. Good test takers always have a good guessing plan in hand.
Part of the key to using a guessing strategy effectively is to know your current GMAT math score. If your current score indicates that you are answering mostly easy questions (a score up to roughly 25), continue to concentrate on mastering the principles that we’ve already covered. As you master those principles, you’ll start to see more questions on practice tests that will make use of the traps that we’ll discuss in a minute. To make further improvements, you’ll need to learn how to spot and avoid the test writers’ favorite traps.
If your score is above 25, you’re already seeing data-sufficiency questions on your practice tests that contain the traps we’re about to discuss. The first step to avoiding the traps is to learn to spot them. Learning to avoid the traps can be a very effective way to improve your GMAT score.
We’ve already been using Process of Elimination (POE) throughout this section. On data-sufficiency questions, a little knowledge can go a long way. Suppose you saw the following data-sufficiency question:
What is the area of square ABCD ?
(1) The length of the side of square ABCD is 2.
(2) For square EFGH, which has sides that are 6 longer than those of square ABCD, the ratio of the perimeter to the area is the reciprocal of the corresponding ratio for square ABCD.
When we don’t know something about a problem, our first impulse is to just skip the whole thing. Or to assume that there’s no way to solve it. However, you can’t skip questions on the GMAT, and you may not get your best score possible if you assume that everything that looks hard can’t be solved.
Obviously, the second statement of this problem is wordy and confusing. You may not be sure what it says or whether it provides sufficient information to answer the question, but that doesn’t mean you need to make a random guess.
Let’s focus on what you DO know. To find the area of a square, you need to know the length of the side of the square—exactly what the first statement provides. Since the first statement is sufficient, your possible answers are A or D.
In other words, you have a fifty-fifty chance of getting the question right. And you get there even if you find the second statement confusing.
As long as you know something about a data-sufficiency question, you can do some shrewd guessing. Take a look at this variation of the problem we’ve been discussing:
What is the area of square ABCD ?
(1) The length of the side of square ABCD is greater than 1.
(2) For square EFGH, which has sides that are 6 longer than those of square ABCD, the ratio of the perimeter to the area is the reciprocal of the corresponding ratio for square ABCD.
You still know that you need the length of the side of the square to find its area. However, now the first statement does not provide that length. If the first statement is insufficient, your can narrow your choices down to B, C, or E.
This time, you have a 1 in 3 chance of getting the question right. As before, you didn’t need to tackle the second statement to better your odds of getting the question right.
Joe can help you avoid several types of traps on data-sufficiency questions. The single most important thing to remember about Joe is that he tends to choose his answers very quickly. Anytime that you are tempted to answer a data-sufficiency question in only a few seconds, you may be about to fall for a Joe Bloggs answer. That’s not to say that you aren’t about to pick the correct answer. However, you should take a few more seconds just to make sure that you aren’t missing anything.
There are several common traps that Joe falls for. Let’s take a look at them.
Let’s revisit that hard question from the More Ways to Plug In section to see how Joe might approach it.
If l1 and l2 are distinct lines in the xy coordinate system such that the equation for l1 is y = ax + b and the equation for l2 is y = cx + d, is ac = a2?
(1) d = b + 2
(2) For each point (x, y) on l1, there is a corresponding point (x, y + k) on l2 for some constant x.
This question really confuses Joe. He has no idea what the question is asking. As a result, he has no idea how he’s supposed to evaluate the information in the statements. But Joe doesn’t want to admit that he doesn’t know what to do. Joe’s not alone in feeling that way—most people don’t like to admit that they don’t know how to solve a problem.
Joe tends to pick E on questions that he doesn’t understand. That’s because Joe thinks that answer E means “I don’t know how to do this problem.” Of course, answer E really means “I know exactly how to do the problem and that’s how I know that the statements don’t provide sufficient information.”
If you want to pick E on a question that you find confusing, make sure that you can explain why you don’t have enough information. Otherwise, you may be equating answer E with “I don’t know how to do this problem.”
Sometimes Joe picks answer E because he’s convinced that the statements need to provide more information. Of course, Joe arrived at his conclusion pretty quickly, so it’s likely that he may have missed some way to use the information provided.
Consider this example:
What is the value of r2 + s ?
(1) t − u = 8
(2) r2t − su + st − r2u = 24
Joe’s first impulse is to pick E on this question. He sees two variables in the question stem but 4 variables in the statements. He doesn’t know what t and u have to do with finding the values of r2 and s. With four variables, Joe thinks that he needs more equations to find the values of r and s so that he can answer the question. Joe is convinced that he’s missing necessary information. So, he goes with E.
Joe’s answer is not correct, however. He’s fallen for the trap.
Statement (1) is obviously insufficient. There’s no way to determine anything about r and s from information about t and u. So, write down BCE.
Now, let’s take a good look at Statement (2). The equation provided does contain the two variables we’re interested in. Let’s try grouping the expressions differently:
r2t − su + st − r2u = 24
(r2t + st) − (r2u + su) = 24
t(r2 + s) − u(r2 + s) = 24
(r2 + s)(t − u) = 24
So, Statement (2) is insufficient. Cross off B.
However, if the statements are combined, we can see that the value of r2 + s is 3. The correct answer is C.
To Joe’s credit, he did try to think about what information he needed to solve this question. However, Joe didn’t really try to evaluate the second statement. He just saw all those variables and concluded that he needed a lot more information and went for E.
How can you avoid Joe’s mistake? Make sure that you take the time to fairly evaluate the information in each statement. You may need to do a little algebraic manipulation or plug in some numbers to see what’s going on.
As previously mentioned, Joe doesn’t like to admit that he doesn’t understand something. So, sometimes the test writers will match up a fairly easy statement with one that is difficult to understand. Let’s see how Joe responds.
What is the volume of a certain rectangular solid?
(1) The solid can be cut into 16 cubes, each of which has a volume of 1.
(2) The base of the rectangular solid is a square, which has a diagonal length of 2√2, and the ratio of the height of the solid to its length is 2:1.
Joe understands Statement (1), and he knows that it tells him that the volume of the rectangular solid is 16. He doesn’t know what to make of the second statement, however. He’s read it a couple of times and finds it pretty confusing. So, Joe—reluctant as he is to pick anything that he doesn’t understand—quickly picks A for this question and moves on to the next problem.
Obviously, the first statement is sufficient, so write down AD. We’ll need to take a better look at that second statement, however.
If the base of the rectangular solid is a square, the diagonal divides the square into two 45-45-90 triangles. For a 45-45-90 triangle, the hypotenuse is s√2. In this case, the side of the square turns out to be 2. So, for the rectangular solid, we now know both its length and width. The statement tells us that the ratio of the height of the solid to its length is 2:1, which means that the height of the solid is 4. So, we now know all three dimensions of the solid. Since the second statement was also sufficient, the correct answer is D.
How can you avoid Joe’s mistake? This question had a very particular format. An easy to understand statement was matched with a statement that was much harder to understand. Joe didn’t want to say that the statement he didn’t understand was sufficient, so he went with A. Typically, however, when the test writers match an easy statement with a statement that is wordy and confusing, the harder statement is also sufficient. If the hard statement didn’t work, the question would be an easy problem.
Obviously, you need to be careful in employing this guessing strategy. The easy statement needs to be so easy that very few people will evaluate it incorrectly. If that’s the case, ask yourself why you’re tempted to say that the more confusing statement is insufficient. Do you know what information it doesn’t supply? Or are you saying, “I really am not sure what this statement says”? If your reason boils down to not fully understanding the statement, your better bet is to say that the confusing statement probably does supply sufficient information.
Joe thinks that many of the hard problems he sees are actually pretty easy. That’s how he winds up with an average score. Every time he starts to do well and the computer feeds him harder questions, Joe gets a lot of those harder questions wrong.
What was the average (arithmetic mean) attendance for baseball games played at Memorial Stadium during the months of June and July?
(1) The average numbers of people attending baseball games at Memorial Stadium for June and July were 23,100 and 25,200, respectively.
(2) There were 20 baseball games played in June at the stadium and 22 games played in July.
Joe thinks this question is pretty easy. Statement (1) gives us the average attendance for June and the average attendance for July. Joe thinks he has all the information he needs because he thinks that he can get the average for the two months by averaging the two averages. (You—having completed our chapter on arithmetic—know better.) Joe looks at Statement (2) and doesn’t see any attendance figures at all. He quickly picks answer choice A.
But, of course, Joe is wrong. The answer to this question is C. An average is the total sum of values divided by the total number of values. We need to know the number of games in each month in order to find out the total number of people attending.
How can you avoid Joe’s mistake? First, slow down! Joe goes too fast and that causes him to make a lot of mistakes. Second, remember that data-sufficiency questions most likely are not as easy as they seem.
Data-sufficiency questions try to get test takers to make bad assumptions. The test writers know how most people think about math, and they often write the questions to take advantage of the assumptions that people routinely make.
For example, consider the following medium question:
What is the value of x ?
(1) x > 8
(2) x < 10
Joe assumed that numbers are always integers and chose C. As always, Joe chooses his answer very quickly.
Of course, numbers are not always integers. Statement (1) is insufficient, so write down BCE. Statement (2) is also insufficient, so cross off B. Combining the statements only tells us that x is any number between 8 and 10—x could be 9, but it could also be 8.5. The answer is E.
How can you avoid Joe’s mistake? Again, slow down! When a problem seems too easy, go back and reread the information. Are you, for example, assuming anything about the types of numbers that fit the statements?
Joe sometimes tries to use information that he learned in Statement (1) while evaluating Statement (2).
At a business dinner, people were offered coffee or tea. If all the diners had either coffee or tea, how many of the diners had tea?
(1) Of the 60 people at the dinner, 10% had tea.
(2) Fifty-four people had coffee.
Joe likes D for this question. He thinks the first statement is pretty easy. Joe has correctly determined that the first statement tells him that 6 people had tea. When Joe looks at the second statement, however, he thinks “54 people had coffee so that means that 6 had tea. Yeah, that works.” So, he selects D.
There’s only one small problem with Joe’s reasoning—the second statement does not tell us the number of diners. So, based on the second statement, we have no idea how many people had tea. The correct answer is A.
How can you avoid Joe’s mistake? Always evaluate the statements independently. Use the AD/BCE approach.
You should also be careful when the statements seem to agree. If the second statement had said “two people had coffee,” it would have been easy to conclude that the second statement was not sufficient. By choosing a number that agreed with the information from the first statement, the test writers made it much easier to fall for the trap. So, remember that just because one statement seems to agree with the other, that doesn’t mean that they say the same thing.
Joe’s biggest problem always boils down to going too fast. While we have run through a list of common ways that Joe gets questions wrong, in all cases, Joe’s first mistake was thinking that it’s OK to answer data-sufficiency questions quickly. Just because you don’t need to compute an answer to a data-sufficiency question, however, doesn’t mean that you can race through the question.
Recognizing the types of errors that Joe makes on data-sufficiency questions can sometimes help you guess your way to the right answer. That can be helpful if you find a question confusing or if you are running short on time close to the end of the section.
Let’s look at one last example.
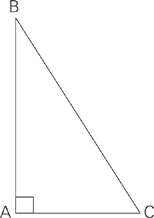
If the perimeter of right triangle ABC above is 
, what is the area of the triangle?
(1) AC ≠ AB
(2) angle ABC = 30°
The area of a triangle is 
. Joe looks at Statements (1) and (2) and sees neither the base nor the height of the triangle. So, he quickly concludes that the answer is E because he doesn’t see any way to get the area of the triangle from the information in the statements.
Let’s see how close we can get to the answer using Process of Elimination. Ignore Statement (2). The first statement only tells us that the base and height have different lengths. Even with the value for the perimeter, there’s no way we’re going to get the values of the base or height. So, cross off AD.
We’re down to B, C, or E. We know that E, Joe’s answer, is very unlikely, so let’s cross that off. The remaining choices are B or C. Now, let’s look at that second statement. From it, we can conclude that this triangle is a 30-60-90 triangle. If the triangle is 30-60-90, that would also mean that the base and the height of the triangle are different—exactly what the first statement told us. It doesn’t sound like combining the statements adds anything that we don’t know from just the second statement. So, C is unlikely. It seems very likely that the correct answer is B.
And the correct answer is B. If you were running out of time or not exactly sure how to solve this question, you can get to the right answer just by knowing how Joe would respond and employing a little deductive reasoning.
Statement (2) tells us that the right triangle is a 30-60-90 triangle. If you have already read our chapter on geometry, you know that the dimensions of a 30-60-90 triangle are always in the same proportion: x: x
: 2x. (Remember that the x in the proportion is the side opposite the 30-degree angle.) Since you can find the
perimeter of any figure by adding up the sides, the perimeter of a 30-60-90 triangle is 3x + x. And we can use what we know from the question stem to solve for the short side of the triangle:
Remember that you don’t need to solve. You just need to know that you can solve, since this is a data-sufficiency problem. (Just in case you’re curious, x = ). Once you’ve got the length of the base, you can find the height and then find the area of the triangle.
So, Statement (2) is sufficient and the answer is B.
This question was very difficult and very time-consuming if you tried to solve it as the test writers wanted you to. Almost every test taker battles the clock on the GMAT. Knowing how to use Process of Elimination and what Joe would choose can help you make informed guesses when you are stuck on a problem and starting to run out of time.
Our guessing strategies are not infallible. However, if you must guess, it’s better to make an informed guess than a random guess.