… because it seems to be true that many things have, as it were, an epoch in which they are discovered in several places simultaneously, just as the violets appear on all sides in the springtime.
WOLFGANG BOLYAI
The character of necessity ascribed to the truths of mathematics and even the peculiar certainty attributed to them is an illusion.
JOHN STUART MILL
Amidst all the complex technical creations of the nineteenth century the most profound one, non-Euclidean geometry, was technically the simplest. This creation gave rise to important new branches of mathematics but its most significant implication is that it obliged mathematicians to revise radically their understanding of the nature of mathematics and its relation to the physical world. It also gave rise to problems in the foundations of mathematics with which the twentieth century is still struggling. As we shall see, non-Euclidean geometry was the culmination of a long series of efforts in the area of Euclidean geometry. The fruition of this work came in the early nineteenth century during the same decades in which projective geometry was being revived and extended. However, the two domains were not related to each other at this time.
Though the Greeks had recognized that abstract or mathematical space is distinct from sensory perceptions of space, and Newton emphasized this point,1 all mathematicians until about 1800 were convinced that Euclidean geometry was the correct idealization of the properties of physical space and of figures in that space. In fact, as we have already noted, there were many attempts to build arithmetic, algebra, and analysis, whose logical foundation was obscure, on Euclidean geometry and thereby guarantee the truth of these branches too.
Many men actually voiced their absolute trust in the truth of Euclidean geometry. For example, Isaac Barrow, who built his mathematics including his calculus on geometry, lists eight reasons for the certainty of geometry: the clearness of the concepts, the unambiguous definitions, the intuitive assurance and universal truth of its axioms, the clear possibility and easy imaginability of its postulates, the small number of its axioms, the clear conceivability of the mode by which magnitudes are generated, the easy order of the demonstrations, and the avoidance of things not known.
Barrow did raise the question, How are we sure that the geometric principles do apply to nature ? His answer was that these are derived from innate reason. Sensed objects are merely the agents which awaken them. Moreover the principles of geometry had been confirmed by constant experience and would continue to be so because the world, designed by God, is immutable. Geometry is then the perfect and certain science.
It is relevant that the philosophers of the late seventeenth and the eighteenth century also raised the question of how we can be sure that the larger body of knowledge that Newtonian science had produced was true. Almost all, notably Hobbes, Locke, and Leibniz, answered that the mathematical laws, like Euclidean geometry, were inherent in the design of the universe. Leibniz did leave some room for doubt when he distinguished between possible and actual worlds. But the only significant exception was David Hume, who in his Treatise of Human Nature (1739) denied the existence of laws or necessary sequences of events in the universe. He contended that these sequences were observed to occur and human beings concluded that they always will occur in the same fashion. Science is purely empirical. In particular the laws of Euclidean geometry are not necessary physical truths.
Hume’s influence was negated and indeed superseded by Immanuel Kant’s. Kant’s answer to the question of how we can be sure that Euclidean geometry applies to the physical world, which he gave in his Critique of Pure Reason (1781), is a peculiar one. He maintained that our minds supply certain modes of organization—he called them intuitions—of space and time and that experience is absorbed and organized by our minds in accordance with these modes or intuitions. Our minds are so constructed that they compel us to view the external world in only one way. As a consequence certain principles about space are prior to experience; these principles and their logical consequences, which Kant called a priori synthetic truths, are those of Euclidean geometry. The nature of the external world is known to us only in the manner in which our minds oblige us to interpret it. On the grounds just described Kant affirmed, and his contemporaries accepted, that the physical world must be Euclidean. In any case whether one appealed to experience, relied upon innate truths, or accepted Kant’s view, the common conclusion was the uniqueness and necessity of Euclidean geometry.
Though confidence in Euclidean geometry as the correct idealization of physical space remained unshaken from 300 B.C. to about 1800, one concern did occupy the mathematicians during almost all of that long period. The axioms adopted by Euclid were supposed to be self-evident truths about physical space and about figures in that space. However, the parallel axiom in the form stated by Euclid (Chap. IV, sec. 3) was believed to be somewhat too complicated. No one really doubted its truth and yet it lacked the compelling quality of the other axioms. Apparently even Euclid himself did not like his own version of the parallel axiom because he did not call upon it until he had proved all the theorems he could without it.
A related problem which did not bother as many people but which ultimately came to the fore as equally vital is whether one may assume the existence of infinite straight lines in physical space. Euclid was careful to postulate only that one can produce a (finite) straight line as far as necessary so that even the extended straight line was still finite. Also the peculiar wording of Euclid’s parallel axiom, that two lines will meet on that side of the transversal where the sum of the interior angles is less than two right angles, was a way of avoiding the outright assertion that there are pairs of lines that will never meet no matter how far they are extended. Nevertheless Euclid did imply the existence of infinite straight lines for, were they finite, they could not be extended as far as necessary in any given context and he proved the existence of parallel lines.
The history of non-Euclidean geometry begins with the efforts to eliminate the doubts about Euclid’s parallel axiom. From Greek times to about 1800 two approaches were made. One was to replace the parallel axiom by a more self-evident statement. The other was to try to deduce it from the other nine axioms of Euclid; were this possible it would be a theorem and so be beyond doubt. We shall not give a fully detailed account of this work because this history is readily available.2
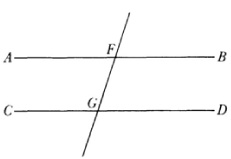
The first major attempt was made by Ptolemy in his tract on the parallel postulate. He tried to prove the assertion by deducing it from the other nine axioms and Euclid’s theorems 1 to 28, which do not depend on the parallel axiom. But Ptolemy assumed unconsciously that two straight lines do not enclose a space and that if AB and CD are parallel (Fig. 36.1) then whatever holds for the interior angles on one side of FG must hold on the other.
The fifth-century commentator Proclus was very explicit about his objection to the parallel axiom. He says, “This [postulate] ought even to be struck out of the postulates altogether; for it is a theorem involving many difficulties, which Ptolemy, in a certain book, set himself to solve, and it requires for the demonstration of it a number of definitions as well as theorems, and the converse of it is actually proved by Euclid himself as a
Figure 36.2
theorem.” Proclus points out that while it is necessary to believe that two lines will tend toward each other on the side of the transversal where the sum of the interior angles is less than two right angles, it is not so clear that these two lines will actually intersect at a finite point. This conclusion is only probable. For, he continues, there are certain curves that approach each other more and more but do not actually meet. Thus, a hyperbola approaches but does not meet its asymptote. Hence might not this be true of the two lines in Euclid’s postulate? He then says that up to a certain sum of the interior angles on one side of the transversal the two lines might indeed meet; however, for a value slightly greater but still less than two right angles, the lines might be asymptotic.
Proclus based his own proof of the parallel postulate on an axiom which Aristotle used to prove the universe is finite. The axiom says, “If from one point two straight lines forming an angle be produced indefinitely, the successive distances between the said straight lines [perpendiculars from one onto the other] will ultimately exceed any finite magnitude.” Proclus’ proof was essentially correct but he substituted one questionable axiom for another.
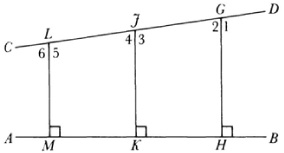
Nasîr-Eddîn (1201-74), the Persian editor of Euclid, likewise gave a “proof” of Euclid’s parallel postulate by assuming that two non-parallel lines approach each other in one direction and diverge in the other. Specifically, if AB and CD (Fig. 36.2) are two lines cut by GH, JK, LM, …, if these latter are perpendicular to AB, and if the angles 1, 3, 5, … are obtuse while 2, 4, 6, … are acute then GH > JK > LM …. This fact, Nasîr-Eddîn says, is clearly seen.
Wallis did some work on the parallel axiom in 1663 which he published in 1693.3 First he reproduced Nasîr-Eddîn’s work on the parallel axiom which he had translated for him by a professor of Arabic at Oxford. Incidentally, this was how Nasîr-Eddîn’s work on the parallel axiom became known to Europe. Wallis then criticized Nasîr-Eddîn’s proof and offered his own proof of Euclid’s assertion. His proof rests on the explicit assumption that to each triangle there is a similar one whose sides have any given ratio to the sides of the original one. Wallis believed that this axiom was more evident than the assumption of arbitrarily small subdivision and arbitrarily large extension. In fact, he said, Euclid’s axiom that we can construct a circle with given center and radius presupposes that there is an arbitrarily large radius at our disposal. Hence one can just as well assume the analogue for rectilinear figures such as a triangle.
The simplest of the substitute axioms was suggested by Joseph Fenn in 1769, namely, that two intersecting lines cannot both be parallel to a third straight line. This axiom also appears in Proclus’ comments on Proposition 31 of Book I of Euclid’s Elements. Fenn’s statement is entirely equivalent to the axiom given in 1795 by John Playfair (1748-1819): Through a given point P not on a line l, there is only one line in the plane of P and l which does not meet l. This is the axiom used in modern books (which for simplicity usually say there is “one and only one line…”).
Legendre worked on the problem of the parallel postulate over a period of about twenty years. His results appeared in books and articles including the many editions of his Elements de géométrie.4 In one attack on the problem he proved the parallel postulate on the assumption that there exist similar triangles of different sizes; actually his proof was analytical but he assumed that the unit of length does not matter. Then he gave a proof based on the assumption that given any three noncollinear points there exists a circle passing through all three. In still another approach he used all but the parallel postulate and proved that the sum of the angles of a triangle cannot be greater than two right angles. He then observed that under these same assumptions the area is proportional to the defect, that is, two right angles minus the sum of the angles. He therefore tried to construct a triangle twice the size of a given triangle so that the defect of the larger one would be twice that of the given one. Proceeding in this way he hoped to get triangles with larger and larger defects and thus angle sums approaching zero. This result, he thought, would be absurd and so the sum of the angles would have to be 180°. This fact in turn would imply the Euclidean parallel axiom. But Legendre found that the construction reduced to proving that through any given point within a given angle less than 60° one can always draw a straight line which meets both sides of the angle. This he could not prove without Euclid’s parallel postulate. In each of the twelve editions (12th ed., 1813) of Legendre’s version of Euclid’s Elements he added appendices which supposedly gave proofs of the parallel postulate but each was deficient because it assumed something implicitly which could not be assumed or assumed an axiom as questionable as Euclid’s.
In the course of his researches Legendre,5 using the Euclidean axioms except for the parallel axiom, proved the following significant theorems: If the sum of the angles of one triangle is two right angles, then it is so in every triangle. Also if the sum is less than two right angles in one triangle it is so in every triangle. Then he gives the proof that if the sum of the angles of any triangle is two right angles, Euclid’s parallel postulate holds. This work on the sum of the angles of a triangle was also fruitless because Legendre failed to show (without the aid of the parallel axiom or an equivalent axiom) that the sum of the angles of a triangle cannot be less than two right angles.
The efforts described thus far were mainly attempts to find a more self-evident substitute axiom for Euclid’s parallel axiom and many of the proposed axioms did seem intuitively more self-evident. Consequently their creators were satisfied that they had accomplished their objective. However, closer examination showed that these substitute axioms were not really more satisfactory. Some of them made assertions about what happens indefinitely far out in space. Thus, to require that there be a circle through any three points not in a straight line requires larger and larger circles as the three points approach collinearity. On the other hand the substitute axioms that did not involve “infinity” directly, for example, the axiom that there exist two similar but unequal triangles, were seen to be rather complex assumptions and by no means preferable to Euclid’s own parallel axiom.
The second group of efforts to solve the problem of the parallel axiom sought to deduce Euclid’s assertion from the other nine axioms. The deduction could be direct or indirect. Ptolemy had attempted a direct proof. The indirect method assumes some contradictory assertion in place of Euclid’s statement and attempts to deduce a contradiction within this new body of ensuing theorems. For example, since Euclid’s parallel axiom is equivalent to the axiom that through a point P not on a line I there is one and only one parallel to I, there are two alternatives to this axiom. One is that there are no parallels to I through ? and the other is that there is more than one parallel to I through P. If by adopting each of these in place of the “one parallel” axiom one could show that the new set led to a contradiction, then these alternatives would have to be rejected and the “one parallel” assertion would be proved.
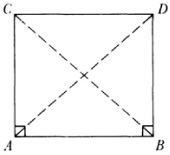
The most significant effort of this sort was made by Gerolamo Saccheri (1667-1733), a Jesuit priest and professor at the University of Pavia. He studied the work of Nasîr-Eddîn and Wallis carefully and then adopted his own approach. Saccheri started with the quadrilateral (Fig. 36.3) ABCD in which A and ? are right angles and AC = BD. It is then easy to prove that 
C = Z). Now Euclid’s parallel axiom is equivalent to the assertion that angles ? and D are right angles. Hence Saccheri considered the two possible alternatives:
(1) the hypothesis of the obtuse angle: C and D are obtuse;
(2) the hypothesis of the acute angle: C and D are acute.
On the basis of the first hypothesis (and the other nine axioms of Euclid)
Saccheri proved that angles ? and D must be right angles. Thus with this hypothesis he did deduce a contradiction.
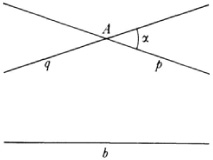
Saccheri next considered the second hypothesis and proved many interesting theorems. He continued until he reached the following theorem: Given any point A and a line b (Fig. 36.4), on the hypothesis of the acute angle there exist in the pencil (family) of lines through A two lines p and q which divide the pencil into two parts. The first of these consists of the lines which intersect b, and the second consists of those lines (lying in angle a) which have a common perpendicular with b somewhere along b. The lines p and q themselves are asymptotic to b. From this result and a lengthy subsequent argument Saccheri deduced that p and b would have a common perpendicular at their common point, which is at infinity. Saccheri believed that this result was at odds with the “nature of the straight line” and therefore concluded that he had arrived at a contradiction.
There remained only the hypothesis that angles C and D of Figure 36.3 are right angles. Saccheri had previously proved that when C and D are right angles, the sum of the angles of any triangle equals 180° and that this fact implies Euclid’s parallel postulate. He therefore felt justified in concluding that Euclid was upheld and so published his Euclides ab Omni Naevo Vindicatus (Euclid Vindicated from All Faults, 1733). However, since Saccheri did not obtain a contradiction on the basis of the acute angle hypothesis the problem of the parallel axiom was still open.
The efforts to find an acceptable substitute for the Euclidean axiom on parallels or to prove that the Euclidean assertion must be a theorem were so numerous and so futile that in 1759 d'Alembert called the problem of the parallel axiom “the scandal of the elements of geometry.”
In his dissertation of 1763 Georg S. Klügel (1739-1812), professor of mathematics at the University of Helmstädt, who knew Saccheri’s book, made the remarkable observation that the certainty with which men accepted the truth of the Euclidean parallel axiom was based on experience. This observation introduced for the first time the thought that experience rather than self-evidence substantiated the axioms. Klügel expressed doubt that the Euclidean assertion could be proved. He realized that Saccheri had not arrived at a contradiction but merely at results that seemed at variance with experience. introduced for the first time the thought that experience rather than self-evidence substantiated the axioms. Klugel expressed doubt that the Euclidean assertion could be proved. He realized that Saccheri had not arrived at a contradiction but merely at results that seemed at variance with experience.
KlügePs paper suggested work on the parallel axiom to Lambert. In his book, Theorie der Parallellinien written in 1766 and published in 1786,6Lambert, somewhat like Saccheri, considered a quadrilateral with three right angles and considered the possibilities of the fourth angle being right, obtuse, and acute. Lambert did discard the obtuse angle hypothesis because it led to a contradiction. However, unlike Saccheri, Lambert did not conclude that he had obtained a contradiction from the acute angle hypothesis.
The consequences Lambert deduced from both the obtuse and acute angle hypothesis, respectively, even though the former did lead to a contradiction, are noteworthy. His most remarkable result is that under either hypothesis the area of a polygon of ? sides is proportional to the difference between the sum of the angles and In — 4 right angles. (Saccheri had this result for a triangle.) He also noted that the obtuse angle hypothesis gave rise to theorems just like those which hold for figures on the surface of a sphere. And he conjectured that the theorems that followed from the acute angle hypothesis would apply to figures on a sphere of imaginary radius. This led him to write a paper7 on the trigonometric functions of imaginary angles, that is, iA, where ? is a real angle and i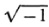 
, which in effect introduced the hyperbolic functions (Chap. 19, sec. 2). We shall see a little more clearly later just what Lambert’s observations mean.
Lambert’s views on geometry were quite advanced. He realized that any body of hypotheses which did not lead to contradictions offered a possible geometry. Such a geometry would be a valid logical structure even though it might have little to do with real figures. The latter might be suggestive of a particular geometry but do not control the variety of logically developable geometries. Lambert did not reach the more radical conclusion that was introduced somewhat later by Gauss.
Still another forward step was made by Ferdinand Karl Schweikart (1780-1859), a professor of jurisprudence, who devoted spare time to mathematics. He worked on non-Euclidean geometry during the period in which Gauss devoted some thought to the subject but Schweikart arrived at his conclusions independently. He was, however, influenced by Saccheri’s and Lambert’s work. In a memorandum of 1816 which he sent to Gauss in 1818 for approval, Schweikart actually distinguished two geometries. There is the geometry of Euclid and a geometry based on the assumption that the sum of the angles of a triangle is not two right angles. This latter geometry he
called astral geometry, because it might hold in the space of the stars, and its theorems were those which Saccheri and Lambert had established on the basis of the acute angle hypothesis.
Franz Adolf Taurinus (1794-1874), a nephew of Schweikart, took up his uncle’s suggestion to study astral geometry. Though he established in his Geometriae Prima Elementa (1826) some new results, notably some analytic geometry, he concluded that only Euclid’s geometry could be true of physical space but that the astral geometry was logically consistent. Taurinus also showed that the formulas which would hold on a sphere of imaginary radius are precisely those that hold in his astral geometry.
The work of Lambert, Schweikart, and Taurinus constitutes advances that warrant recapitulation. All three and other men such as Klügel and Abraham G. Kästner (1719-1800), a professor at Göttingen, were convinced that Euclid’s parallel axiom could not be proven, that is, it is independent of Euclid’s other axioms. Further, Lambert, Schweikart, and Taurinus were convinced that it is possible to adopt an alternative axiom contradicting Euclid’s and build a logically consistent geometry. Lambert made no assertions about the applicability of such a geometry; Taurinus thought it is not applicable to physical space; but Schweikart believed it might apply to the region of the stars. These three men also noted that the geometry on a real sphere has the properties of the geometry based on the obtuse angle hypothesis (if one leaves aside the contradiction which results from the latter) and the geometry on a sphere of imaginary radius has the properties of the geometry based on the acute angle hypothesis. Thus all three recognized the existence of a non-Euclidean geometry but they missed one fundamental point, namely, that Euclidean geometry is not the only geometry that describes the properties of physical space to within the accuracy for which experience can vouch.
No major branch of mathematics or even a major specific result is the work of one man. At best, some decisive step or proof may be credited to an individual. This cumulative development of mathematics applies especially to non-Euclidean geometry. If one means by the creation of non-Euclidean geometry the recognition that there can be geometries alternative to Euclid’s then Klügel and Lambert deserve the credit. If non-Euclidean geometry means the technical development of the consequences of a system of axioms containing an alternative to Euclid’s parallel axiom then most credit must be accorded to Saccheri and even he benefited by the work of many men who tried to find a more acceptable substitute axiom for Euclid’s. However, the most significant fact about non-Euclidean geometry is that it can be used to describe the properties of physical space as accurately as Euclidean geometry does. The latter is not the necessary geometry of physical space; its physical truth cannot be guaranteed on any a priori grounds. This realization, which did not call for any technical mathematical development because this had already been done, was first achieved by Gauss.
Carl Friedrich Gauss (1777-1855) was the son of a mason in the German city of Brunswick and seemed destined for manual work. But the director of the school at which he received his elementary education was struck by Gauss’s intelligence and called him to the attention of Duke Karl Wilhelm. The Duke sent Gauss to a higher school and then in 1795 to the University of Göttingen. Gauss now began to work hard on his ideas. At eighteen he invented the method of least squares and at nineteen he showed that the 17-sided regular polygon is constructible. These successes convinced him that he should turn from philology to mathematics. In 1798 he transferred to the University of Helmstedt and there he was noticed by Johann Friedrich Pfaff who became his teacher and friend. After finishing his doctor’s degree Gauss returned to Brunswick where he wrote some of his most famous papers. This work earned for him in 1807 the appointment as professor of astronomy and director of the observatory at Göttingen. Except for one visit to Berlin to attend a scientific meeting he remained at Göttingen for the rest of his life. He did not like to teach and said so. However, he did enjoy social life, was married twice, and raised a family.
Gauss’s first major work was his doctoral thesis in which he proved the fundamental theorem of algebra. In 1801 he published the classic Disquisitiones Arithmeticae. His mathematical work in differential geometry, the “Disquisitiones Generales circa Superficies Curvas” (General Investigations of Curved Surfaces, 1827), which, incidentally, was the outcome of his interest in surveying, geodesy, and map-making, is a mathematical landmark (Chap. 37, sec. 2). He made many other contributions to algebra, complex functions, and potential theory. In unpublished papers he recorded his innovative work in two major fields: the elliptic functions and non-Euclidean geometry.
His interests in physics were equally broad and he devoted most of his energy to them. When Giuseppe Piazzi (1746-1826) discovered the planet Ceres in 1801 Gauss undertook to determine its path. This was the beginning of his work in astronomy, the activity that absorbed him most and to which he devoted about twenty years. One of his great publications in this area is his Theoria Motus Corporum Coelestium (Theory of Motion of the Heavenly Bodies, 1809). Gauss also earned great distinction in his physical research on theoretical and experimental magnetism. Maxwell says in his Electricity and Magnetism that Gauss’s studies of magnetism reconstructed the whole science, the instruments used, the methods of observation, and the calculation of results. Gauss’s papers on terrestrial magnetism are models of physical research and supplied the best method of measuring the earth’s magnetic field. His work on astronomy and magnetism opened up a new and brilliant period of alliance between mathematics and physics.
Though Gauss and Wilhelm Weber (1804-91) did not invent the idea of telegraphy, in 1833 they improved on earlier techniques with a practical device which made a needle rotate right and left depending upon the direction of current sent over a wire. Gauss also worked in optics, which had been neglected since Euler’s days, and his investigations of 1838-41 gave a totally new basis for the handling of optical problems.
The universality of Gauss’s activities is all the more remarkable because his contemporaries had begun to confine themselves to specialized investigations. Despite the fact that he is acknowledged to be the greatest mathematician at least since Newton, Gauss was not so much an innovator as a transitional figure from the eighteenth to the nineteenth century. Although he achieved some new views which did engage other mathematicians he was oriented more to the past than to the future. Felix Klein describes Gauss’s position in these words: We could have a tableau of the development of mathematics if we would imagine a chain of high mountains representing the men of the eighteenth century terminated by an imposing summit— Gauss—then a large and rich region filled with new elements of life. Gauss’s contemporaries appreciated his genius and by the time of his death in 1855 he was widely venerated and called the “prince of mathematicians.”
Gauss published relatively little of his work because he polished whatever he did partly to achieve elegance and partly to achieve for his demonstrations the maximum of conciseness without sacrificing rigor, at least the rigor of his time. In the case of non-Euclidean geometry he published no definitive work. He said in a letter to Bessel of January 27, 1829, that he probably would never publish his findings in this subject because he feared ridicule, or, as he put it, he feared the clamor of the Boeotians, a figurative reference to a dull-witted Greek tribe. Gauss may have been overly cautious, but one must remember that though some mathematicians had been gradually reaching the climax of the work in non-Euclidean geometry the intellectual world at large was still dominated by Kant’s teachings. What we do know about Gauss’s work in non-Euclidean geometry is gleaned from his letters to friends, two short reviews in the Göttingische Gelehrte Anzeigen of 1816 and 1822 and some notes of 1831 found among his papers after his death.8
Gauss was fully aware of the vain efforts to establish Euclid’s parallel postulate because this was common knowledge in Göttingen and the whole history of these efforts was thoroughly familiar to Gauss’s teacher Kästner. Gauss told his friend Schumacher that as far back as 1792 (Gauss was then fifteen) he had already grasped the idea that there could be a logical geometry in which Euclid’s parallel postulate did not hold. By 1794 Gauss had found that in his concept of non-Euclidean geometry the area of a quadrangle must be proportional to the difference between 360° and the sum of the angles. However, at this later date and even up to 1799 Gauss was still trying to deduce Euclid’s parallel postulate from other more plausible assumptions and he still believed Euclidean geometry to be the geometry of physical space even though he could conceive of other logical non-Euclidean geometries. However, on December 1 7, 1799, Gauss wrote to his friend the Hungarian mathematician Wolfgang Farkas Bolyai (1775-1856),
As for me I have already made some progress in my work. However, the path I have chosen does not lead at all to the goal which we seek [deduction of the parallel axiom], and which you assure me you have reached. It seems rather to compel me to doubt the truth of geometry itself. It is true that I have come upon much which by most people would be held to constitute a proof; but in my eyes it proves as good as nothing. For example, if we could show that a rectilinear triangle whose area would be greater than any given area is possible, then I would be ready to prove the whole of [Euclidean] geometry absolutely rigorously.
Most people would certainly let this stand as an axiom; but I, no! It would, indeed, be possible that the area might always remain below a certain limit, however far apart the three angular points of the triangle were taken.
This passage shows that by 1799 Gauss was rather convinced that the parallel axiom cannot be deduced from the remaining Euclidean axioms and began to take more seriously the development of a new and possibly applicable geometry.
From about 1813 on Gauss developed his new geometry which he first called anti-Euclidean geometry, then astral geometry, and finally non-Euclidean geometry. He became convinced that it was logically consistent and rather sure that it might be applicable. In reviews of 1816 and 1822 and in his letter to Bessel of 1829 Gauss reaffirmed that the parallel postulate could not be proved on the basis of the other axioms in Euclid. His letter to Olbers written in 18179 is a landmark. In it Gauss says, “I am becoming more and more convinced that the [physical] necessity of our [Euclidean] geometry cannot be proved, at least not by human reason nor for human reason. Perhaps in another life we will be able to obtain insight into the nature of space, which is now unattainable. Until then we must place geometry not in the same class with arithmetic, which is purely a priori, but with mechanics.”
To test the applicability of Euclidean geometry and his non-Euclidean geometry Gauss actually measured the sum of the angles of the triangle formed by three mountain peaks, Brocken, Hohehagen, and Inselsberg. The sides of this triangle were 69, 85, and 197 km. He found10 that the sum exceeded 180° by 14!85. The experiment proved nothing because the experimental error was much larger than the excess and so the correct sum could have been 180° or even less. As Gauss realized, the triangle was a small one and since in the non-Euclidean geometry the defect is proportional to the area only a large triangle could possibly reveal any significant departure from an angle sum of 180°.
We shall not discuss the specific non-Euclidean theorems that are due to Gauss. He did not write up a full deductive presentation and the theorems he did prove are much like those we shall encounter in the work of Lobatchevsky and Bolyai. These two men are generally credited with the creation of non-Euclidean geometry. Just what is to their credit will be discussed later but they did publish organized presentations of a non-Euclidean geometry on a deductive synthetic basis with the full understanding that this new geometry was logically as legitimate as Euclid’s.
Nikolai Ivanovich Lobatchevsky (1793-1856), a Russian, studied at the University of Kazan and from 1827 to 1846 was professor and rector at that university. He presented his views on the foundations of geometry in a paper before the department of mathematics and physics of the University in 1826. However, the paper was never printed and was lost. He gave his approach to non-Euclidean geometry in a series of papers, the first two of which were published in Kazan journals and the third in the Journal für Mathematik. 11 The first was entitled “On the Foundations of Geometry” and appeared in 1829-30. The second, entitled “New Foundations of Geometry with a Complete Theory of Parallels” (1835-37), is a better presentation of Lobatchevsky’s ideas. He called his new geometry imaginary geometry for reasons which are perhaps already apparent and will be clearer later. In 1840 he published a book in German, Geometrische Untersuchungen zur Theorie der Parallellinien (Geometrical Researches on the Theory of Parallels12). In this book he laments the slight interest shown in his writings. Though he became blind he dictated a completely new exposition of his geometry and published it in 1855 under the title Pangéométrie.
John (János) Bolyai (1802-60), son of Wolfgang Bolyai, was a Hungarian army officer. On non-Euclidean geometry, which he called absolute geometry, he wrote a twenty-six-page paper “The Science of Absolute Space.”13This was published as an appendix to his father’s book Tentamen Juventutem Studiosam in Elementa Matheseos (Essay on the Elements of Mathematics for Studious Youths). Though the two-volume book appeared in 1832-33 and therefore after a publication by Lobatchevsky, Bolyai seems to have worked out his ideas on non-Euclidean geometry by 1825 and was convinced by that time that the new geometry was not self-contradictory. In a letter to his father dated November 23, 1823, John wrote, “ I have made such wonderful discoveries that I am myself lost in astonishment.” Bolyai’s work was so much like Lobatchevsky’s that when Bolyai first saw the latter’s work in 1835 he thought it was copied from his own 1832-33 publication. On the other hand, Gauss read John Bolyai’s article in 1832 and wrote to Wolfgang14that he was unable to praise it for to do so would be to praise his own work.
Gauss, Lobatchevsky, and Bolyai had realized that the Euclidean parallel axiom could not be proved on the basis of the other nine axioms and that some such additional axiom was needed to found Euclidean geometry. Since the parallel axiom was an independent fact it was then at least logically possible to adopt a contradictory statement and develop the consequences of the new set of axioms.
To study the technical content of what these men created, it is just as well to take Lobatchevsky’s work because all three did about the same thing. Lobatchevsky gave, as we know, several versions which differ only in details. We shall use his 1835-37 paper as the basis for the account here.
Since, as in Euclid’s Elements, many theorems can be proved which do not depend at all upon the parallel axiom, such theorems are valid in the new geometry. Lobatchevsky devotes the first six chapters of his paper to the proof of these basic theorems. He assumes at the outset that space is infinite, and he is then able to prove that two straight lines cannot intersect in more than one point and that two perpendiculars to the same line cannot intersect.
In his seventh chapter Lobatchevsky boldly rejects the Euclidean parallel axiom and makes the following assumption: Given a line AB and a point ? (Fig. 36.5) then all lines through ? fall into two classes with respect to AB, namely, the class of lines which meet AB and the class of lines which do not. To the latter belong two lines p and q which form the boundary between the two classes. These two boundary lines are called parallel lines. More precisely, if C is a point at a perpendicular distance a from the line AB, then there exists an angle15 π(a) such that all lines through C which make with the perpendicular CD an angle less than π (a) will intersect AB; all other lines through C do not intersect AB.16 The two lines which make the
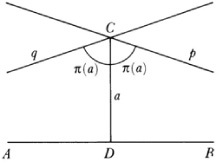
angle π(a) with AB are the parallels and π(a) is called the angle of parallelism. Lines through C other than the parallels and which do not meet AB are called non-intersecting lines, though in Euclid’s sense they are parallel to AB and so in this sense Lobatchevsky’s geometry contains an infinite number of parallels through C.
If π(a) = π/2 then the Euclidean axiom results. If not, then it follows that π(a) increases and approaches π/2 as a decreases to zero, and π(a) decreases and approaches zero as a becomes infinite. The sum of the angles of a triangle is always less than π, decreases as the area of the triangle increases, and approaches π as the area approaches zero. If two triangles are similar then they are congruent.
Now Lobatchevsky turns to the trigonometric part of his geometry. The first step is the determination of π(a). The result, if a complete central angle is 2π, is 17.
from which it follows that π(0) = π/2 and π(+ ∞) = 0. The relation (1) is significant in that with each length x it associates a definite angle π (x). When x = 1, tan [π(1)/2] = e-1 so that π(1) = 40°24’. Thus the unit of length is that length whose angle of parallelism is 40°24'. This unit of length does not have direct physical significance. It can be physically one inch or one mile. One would choose the physical interpretation which would make the geometry physically applicable.18
Then Lobatchevsky deduces formulas connecting sides and angles of the plane triangles of his geometry. In a paper of 1834 he had defined cos ?
where k is a constant, called the space constant. For theoretical purposes the value of k is immaterial. Bolyai also gives the form (a).
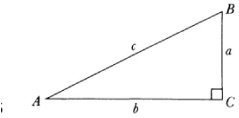
and sin x for real imaginary parts of eix. Lobatchevsky’s point was to give a purely analytical foundation for trigonometry and so make it independent of Euclidean geometry. The main trigonometric formulas of his geometry are (Fig. 36.6)
cot π(a) = cot π(c) sin A
sin A = cos B sin π(b)
sin π(c) = sin π(a) sin π(b).
These formulas hold in ordinary spherical trigonometry provided that the sides have imaginary lengths. That is, if one replaces a, b, and ? in the usual formulas of spherical trigonometry by ia, ib, and ic one obtains Lobatchevsky’s formulas. Since the trigonometric functions of imaginary angles are replaceable by hyperbolic functions one might expect to see these latter functions in Lobatchevsky’s formulas. They can be introduced by using the relation tan (π(x)/2 = e-x/k. Thus the first of the formulas above can be converted into
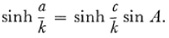
Also whereas in the usual spherical geometry the area of a triangle with angles A, B, and C is r2(A + B + C — π), in the non-Euclidean geometry it is r2[π — (A + B C)] which amounts to replacing r by ir in the usual formula.
By working with an infinitesimal triangle Lobatchevsky derived in his first paper (1829-30) the formula
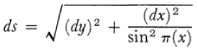
for the element of arc on a curve y = f(x) at the point (x, y). Then the entire circumference of a circle of radius r can be calculated. It is
C = π(er – e-r/2)2
The expression for the area of a circle proves to be
A = π(er/2 – e-r/12)2.
He also gives theorems on the area of plane and curved regions and volumes of solids.
The formulas of Euclidean geometry result from the non-Euclidean formulas when the magnitudes are small. Thus if we use the fact that
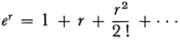
and neglect for small r all but the first two terms then, for example,
C = π(er – e-r) ~ π {1 + r – (1 – r)} = 2–r.
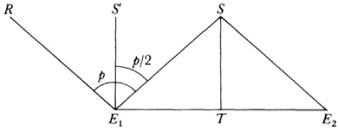
In the first paper (1829-30) Lobatchevsky also considered the applicability of his geometry to physical space. The essence of his argument rests on the parallax of stars. Suppose Ex and E2 (Fig. 36.7) are the positions of the earth six months apart and S is a star. The parallax/; of S is the difference in the directions of EX S S and E2 S S measured, say, from the perpendicular EX S S′. If EX R R is the Euclidean parallel to E2 S S, then since EX SSE2 is an isosceles triangle, π/2 — iSEx EE2 is half of the change in direction of the star, that is, p¡2. This angle is 1 “24 for the star Sirius (Lobatchevsky’s value). As long as such an angle is not zero, the line from Ex to the star cannot be the parallel to TS because the line cuts TS. If, however, there were a lower bound to the various parallaxes of all the stars then any line from Ex making a smaller angle with EX S S′ than this lower bound could be taken to be a parallel to TS through Ex and this geometry would be equally useful so far as stellar measurements are concerned. But then Lobatchevsky showed that the unit of length in his geometry would have to be, physically, more than a half a million times the radius of the earth’s path. In other words, Lobatchevsky’s geometry could be applicable only in an enormously large triangle.
The creation of non-Euclidean geometry is often used as an example of how an idea occurs independently to different people at about the same time. Sometimes this is regarded as pure coincidence and sometimes as evidence of the spirit of the time working its influence in widely separated quarters. The creation of non-Euclidean geometry by Gauss, Lobatchevsky, and Bolyai is not an example of a simultaneous creation nor is the great credit given to Lobatchevsky and Bolyai justified. It is true, as already noted, that they were the first to publish an avowed non-Euclidean geometry and in this act showed more courage than Gauss did. However, the creation of non-Euclidean geometry is hardly their contribution. We have already pointed out that even Gauss was preceded by Lambert, that Schweikart and Taurinus were independent creators, and that Lambert and Taurinus published their work. Moreover the realization that the new geometry may be applicable to physical space is due to Gauss.
Both Lobatchevsky and Bolyai owe much to Gauss. Lobatchevsky’s teacher in Kazan was Johann Martin Bartels (1769-1836), a good friend of Gauss. In fact they spent the years 1805 to 1807 together in Brunswick. Subsequently Gauss and Bartels kept in communication with each other. It is extremely unlikely that Bartels did not pass on to Lobatchevsky, who remained at Kazan as a colleague, Gauss’s progress in non-Euclidean geometry. In particular Bartels must have known Gauss’s doubts as to the truth of Euclidean geometry.
As for John Bolyai, his father Wolfgang was also a close friend of Gauss and a fellow student in Göttingen from 1796 to 1798. Wolfgang and Gauss not only continued to communicate with each other but discussed the specific subject of the parallel axiom, as one of the quotations above indicates. Wolfgang continued to work hard on the problem of the parallel axiom and sent a purported proof to Gauss in 1804. Gauss showed him that the proof was fallacious. By 1817 Gauss was certain not only that the axiom could not be proved but that a logically consistent and physically applicable non-Euclidean geometry could be constructed. Beyond his communication of 1799 to this effect, Gauss transmitted his later thoughts freely to Wolfgang. Wolfgang continued to work on the problem until he published his Tentamen of 1832-33. Since he recommended to his son that he take up the problem of the parallel axiom he almost certainly retailed what he knew.
There are contrary views. The mathematician Friedrich Engel (18611941) believed that though Lobatchevsky’s teacher Bartels was Gauss’s friend, Lobatchevsky could hardly have learned more through this connection than that Gauss doubted the physical correctness of the parallel axiom. But this fact in itself was crucial. However, Engel doubted that Lobatchevsky learned even this much from Gauss, for Lobatchevsky had tried from 1816 on to prove the Euclidean parallel axiom; then recognizing the hopelessness of such efforts finally in 1826 created the new geometry. John Bolyai also tried to prove the Euclidean parallel axiom until about 1820 and then turned to the construction of a new geometry. But these continuing efforts to prove the parallel axiom do not imply ignorance of Gauss’s thoughts.19 Since no one, not even Gauss, had shown that Euclid’s parallel axiom could not be deduced from the other nine axioms both Lobatchevsky and Bolyai may have decided to try their hand at the problem. Having failed, they could appreciate all the more readily the wisdom of Gauss’s views on the subject.
As for the technical content contributed by Lobatchevsky and John Bolyai, though they may have created this independently of their predecessors and of each other, Saccheri’s and Lambert’s work, to say nothing of Schweikart’s and Taurinus’s, was widely known in Göttingen and was certainly known to Bartels and Wolfgang Bolyai. And when Lobatchevsky refers in his 1835-37 paper to the futility of the efforts over two thousand years to settle the question of the parallel axiom, by inference he admits to the knowledge of the earlier work.
We have already stated that the creation of non-Euclidean geometry was the most consequential and revolutionary step in mathematics since Greek times. We shall not treat all the implications of the subject at this time. Instead we shall follow the historical course of events. The impact of the creation and the full realization of its significance were delayed because Gauss did not publish his work on this subject and Lobatchevsky’s and Bolyai’s work was ignored for about thirty years. Though these men were aware of the importance of their work, the mathematicians generally exhibited their usual reluctance to entertain radical ideas. Also, the key subject in the geometry of the 1830s and 1840s was projective geometry and for this reason too the work on non-Euclidean geometry did not attract the English, French, and German mathematicians. When Gauss’s notes and correspondence on non-Euclidean geometry were published after his death in 1855 attention was drawn to the subject. His name gave weight to the ideas and soon thereafter Lobatchevsky’s and Bolyai’s work was noted by Richard Baltzer (1818-87) in a book of 1866-67. Subsequent developments finally brought mathematicians to the realization of the full import of non-Euclidean geometry.
Gauss did see the most revolutionary implication. The first step in the creation of non-Euclidean geometry was the realization that the parallel axiom could not be proved on the basis of the other nine axioms. It was an independent assertion and so it was possible to adopt a contradictory axiom and develop an entirely new geometry. This Gauss and others did. But Gauss, having realized that Euclidean geometry is not necessarily the geometry of physical space, that is, is not necessarily true, put geometry in the same class with mechanics, and asserted that the quality of truth must be restricted to arithmetic (and its development in analysis). This confidence in arithmetic is in itself curious. Arithmetic at this time had no logical foundation at all. The assurance that arithmetic, algebra, and analysis offered truths about the physical world stemmed entirely from reliance upon experience.
The history of non-Euclidean geometry reveals in a striking manner how much mathematicians are influenced not by the reasoning they perform but by the spirit of the times. Saccheri had rejected the strange theorems of non-Euclidean geometry and concluded that Euclid was vindicated. But one hundred years later Gauss, Lobatchevsky, and Bolyai confidently accepted the new geometry. They believed that their new geometry was logically consistent and hence that this geometry was as valid as Euclid’s. But they had no proof of this consistency. Though they proved many theorems and obtained no evident contradictions, the possibility remained open that a contradiction might still be derived. Were this to happen, then the assumption of their parallel axiom would be invalid and, as Saccheri had believed, Euclid’s parallel axiom would be a consequence of his other axioms.
Actually Bolyai and Lobatchevsky considered this question of consistency and were partly convinced of it because their trigonometry was the same as for a sphere of imaginary radius and the sphere is part of Euclidean geometry. But Bolyai was not satisfied with this evidence because trigonometry in itself is not a complete mathematical system. Thus despite the absence of any proof of consistency, or of the applicability of the new geometry, which might at least have served as a convincing argument, Gauss, Bolyai, and Lobatchevsky accepted what their predecessors had regarded as absurd. This acceptance was an act of faith. The question of the consistency of non-Euclidean geometry remained open for another forty years.
One more point about the creation of non-Euclidean geometry warrants attention and emphasis. There is a common belief that Gauss, Bolyai, and Lobatchevsky went off into a corner, played with changing the axioms of Euclidean geometry just to satisfy their intellectual curiosity and so created the new geometry. And since this creation has proved to be enormously important for science—a form of non-Euclidean geometry which we have yet to examine has been used in the theory of relativity—many mathematicians have contended that pure intellectual curiosity is sufficient justification for the exploration of any mathematical idea and that the values for science will almost surely ensue as purportedly happened in the case of non-Euclidean geometry. But the history of non-Euclidean geometry does not support this thesis. We have seen that non-Euclidean geometry came about after centuries of work on the parallel axiom. The concern about this axiom stemmed from the fact that it should be, as an axiom, a self-evident truth. Since the axioms of geometry are our basic facts about physical space and vast branches of mathematics and of physical science use the properties of Euclidean geometry the mathematicians wished to be sure that they were relying upon truths. In other words, the problem of the parallel axiom was not only a genuine physical problem but as fundamental a physical problem as there can be.
Bonola, Roberto: Non-Euclidean Geometry, Dover (reprint), 1955.
Dunnington, G. W.: Carl Friedrich Gauss, Stechert-Hafner, 1960.
Engel, F., and P. Staeckel: Die Theorie der Parallellinien von Euklid bis auf Gauss, 2 vols., B. G. Teubner, 1895.
–––: Urkunden zur Geschichte der nichteuklidischen Geometrie, B. G. Teubner, 1899-1913, 2 vols. The first volume contains the translation from Russian into German of Lobatchevsky’s 1829-30 and 1835-37 papers. The second is on the work of the two Bolyais.
Enriques, F.: “ Prinzipien der Geometrie,” Encyk. der Math. Wiss., B. G. Teubner, 1907-10, III ABI, 1-129.
Gauss, Carl F.: Werke, B. G. Teubner, 1900 and 1903, Vol. 8, 157-268; Vol. 9, 297-458.
Heath, Thomas L.: Euclid’s Elements, Dover (reprint), 1956, Vol. 1, pp. 202-20.
Kagan, V.: Lobatchevsky and his Contribution to Science, Foreign Language Pub. House, Moscow, 1957.
Lambert, J. H.: Opera Mathematica, 2 vols., Orell Fussli, 1946-48.
Pasch, Moritz, and Max Dehn: Vorlesungen über neuere Geometrie, 2nd ed., Julius Springer, 1926, pp. 185-238.
Saccheri, Gerolamo: Euclides ab Omni Naevo Vindicatus, English trans, by G. B. Halsted in Amer. Math. Monthly, Vols. 1-5, 1894-98; also Open Court Pub. Co., 1920, and Chelsea (reprint), 1970.
Schmidt, Franz, and Paul Staeckel: Briefwechsel zwischen Carl Friedrich Gauss und Wolfgang Bolyai, B. G. Teubner, 1899; Georg Olms (reprint), 1970.
Smith, David E.: A Source Book in Mathematics, Dover (reprint), 1959, Vol. 2, pp. 351-88.
Sommerville, D. M. Y.: The Elements of Non-Euclidean Geometry, Dover (reprint), 1958.
Staeckel, P.: “Gauss als Geometer,” Nachrichten König. Ges. der Wiss. zu Gött., 1917, Beiheft, pp. 25-142. Also in Gauss: Werke, X2.
von Walterhausen, W. Sartorius: Carl Friedrich Gauss, S. Hirzel, 1856; Springer-Verlag (reprint), 1965.
Zacharias, M.: “Elementargeometrie und elementare nicht-euklidische Geometrie in synthetischer Behandlung,” Encyk. der Math. Wiss., B. G. Teubner, 1914-31, III AB9, 859-1172.