1 What Is Artificial Intelligence?
In today’s terms, artificial intelligence (AI) is best understood as a special branch of computer science. Historically, the boundary between AI and computer science was in fact less clear-cut. The history of computer science is intimately linked with the history of AI. When Alan Turing invented the general-purpose computer in 1936 (on paper!), he was evidently thinking about how to model a person doing something clever—namely, a specific kind of mathematical calculation. Turing was also one of the first to speculate that the machine he invented for that purpose could be used to reproduce humanlike intelligence more generally. In this sense, the father of computer science is also the father of AI. But other computer pioneers also thought about computing machinery in human (indeed anthropomorphic) terms. For instance, John von Neumann, in a famous 1945 paper introducing the architecture still used by computers today, used a term from psychology, “memory,” to refer to a computer’s storage units.
In a sense, we can still think of computers as exhibiting “intelligence” in their general operation. By chaining together simple logical operations in myriad ways, they accomplish an extraordinary and impressive range of tasks. But these days, AI is very clearly a subfield of computer science. As AI and computer science evolved, AI focused more squarely on the tasks that humans are good at. A famous definition of AI states that AI is the science of making computers produce behaviors that would be considered intelligent if done by humans.1 Of course, this is no easy undertaking. Computers, we noted in the prologue, are exceptionally good at many tasks we find extremely difficult, such as solving complex mathematical equations in split seconds, but often spectacularly bad at tasks we find a breeze, such as walking, opening doors, engaging in conversation, and the like.
This human-centered definition of AI still works pretty well, but needs a little updating. It’s true that many of the central applications of modern AI involve reproducing human abilities, in language, perception, reasoning, and motor control. To this extent, AI involves making computers “in our own image,” so to speak. But nowadays AI systems are also used in many other more arcane areas to accomplish tasks whose scale or speed far exceed human capabilities. For instance, they’re used in high-frequency stock trading, internet search engines, and the operation of social media sites. In fact, it’s useful to think of modern industrial-scale AI systems as possessing a mixture of both subhuman and superhuman abilities.
There’s obviously a great deal more to AI than this potted history can get across, but it’s enough to get you started and enough also to situate the focus of this book. In this book, we’re going to focus on the most influential approach to AI today called “machine learning.” We describe machine learning as an “approach” to AI because it’s not concerned with any specific task or application. Rather, machine learning comprises a set of techniques for solving any number of AI problems. For instance, natural language processing, speech recognition, and computer vision have each been pursued within the general approach to AI known as machine learning.
As the name suggests, machine learning harnesses both the power of computers as well as the sheer volume of data now available (thanks to the internet) to enable computers to learn for themselves. In the usual case, what are learned are patterns in the data. From now on, when we refer to AI, we’ll refer to machine learning, unless the context dictates otherwise.
The rest of this chapter will introduce and then deploy a few concepts that you might not have encountered since high school algebra. Some of you might not have encountered them at all. Here we have in mind concepts like a mathematical “function,” a “parameter,” and a “variable.” These terms are sometimes used in ordinary speech, but they have specific, technical meanings in mathematics and computer science, and their technical definitions are what we’ll mean when we use them. We’ll do our best to explain the gist of these as we go along, as the gist is all you’ll need. But if you find the explanations glib or unsatisfactory in any way, do take heart. We don’t go into much detail precisely because all you need is the gist. So, if you’re turned off by anything remotely mathy, get out of this chapter what you can, and then definitely proceed with the rest of the book. If you don’t completely grasp something, chances are it won’t matter. Again, the book is intended to be primarily political, not technical.
By the way, you can dip into this book at any point—each chapter can be read on its own without having read any of the others first. If there are relevant bits of other chapters we think you might like to read in conjunction, we’ll refer back (or forward) to that chapter.
Machine Learning and Prediction
In this book, we’re going to focus on a particular class of machine learning technologies, which we term “predictive models.” This focus doesn’t include all machine learning models, but it does encompass the technologies at the center of the current “AI revolution” that’s causing so much disruption in industry and government. Importantly, it also encompasses systems that have been in use in industry and government for decades—and in some cases, much longer. In the media, AI is often portrayed as a brand new arrival—something that’s suddenly, and recently, started to affect public life. In our introduction to AI, we want to emphasize that the AI models currently affecting public life are very much a continuous development of statistical methods that have been in use for a long time in both the private and public sectors. There is a long tradition of statistical modeling in both government and commerce, and the statistical models used historically in these fields actually have much in common with the predictive AI models that are now becoming prevalent. To emphasize these commonalities, it’s helpful to focus on the predictive models that are at the core of modern AI.
Our focus on predictive models will also be helpful in emphasizing that the AI models used in government departments are technically very similar to those used in modern commercial settings. For instance, the models used in finance ministries to hunt for tax evaders or in justice departments to assess defendants’ risks of reoffending are the same kind of model that Amazon uses to recommend books we might be interested in and that Google uses to decide which ads we see. When, toward the end of the book, we come to consider how AI techniques in government and business should be regulated, it will be helpful to understand that the technical methods under scrutiny in these two areas are largely the same. Regulation of the use of AI models in government may look quite different from regulation of their use in industry owing to the very different social functions of the institutions in these two spheres. But the models that are the object of regulation in these two areas are basically the same.
Predictive Modeling Basics
We’ll begin with a simple definition of a predictive model. A predictive model is a mathematical procedure that makes predictions about the value of some unknown variable based on one or more known variables. A “variable” can be any measurable aspect of the world. For instance, a predictive model might predict a person’s weight based on their height. Such a model would be useful if for some reason we can readily get information about people’s height but not about their weight (and we are nevertheless interested in their weight).
Note that a predictive model doesn’t have to predict an occurrence in the future. The unknown variable might relate to the current moment or even to times in the past. The key thing is that we need to guess it because we can’t measure it directly (the word “guess” is probably more to the point than the word “predict” here). Thus we can define a predictive model as a tool that can make guesses about some outcome variable based on a set of input variables.
To build a predictive model, the key ingredient is a training set of cases where we know the outcome variables as well as the input variables. In the above example, the training set would be measurements of the height and weight of a number of sample people. There is a (loose) relationship between people’s height and weight. The training set provides information about this relationship. A predictive model uses this information to compute a general hypothesis about the relationship between height and weight that it can use to make a guess about someone’s weight given their height. A training set is in essence a database of facts about known cases. The larger this database, the more information is provided about the outcome variable. We will take it as part of the definition of a “predictive model” that it is derived from training data through a training process of some kind.
A Brief History of Predictive Models
Mathematical methods have been in use for centuries to guess an unknown variable by consulting a database of known facts. The first serious applications were in the insurance industry. The Lloyd’s register, which developed in 1688 and assessed the likely risks of shipping ventures, is a well-known early example.2 Our survey of predictive models will begin slightly later with the Equitable Life insurance company, which was the first company to use data systematically to make predictions. Equitable Life was founded in 1762.3
The earliest predictive models with relevance to government date from around this same time. For instance, in the 1740s the German statistician Johann Süssmilch used data from church records to devise a model that systematically used the availability of land in a given region to predict marriage age and marriage rate (and, through these, birth rates).4 Governments have been maintaining databases of information about their citizens from time immemorial, largely for the purposes of assessing their tax obligations. As the science of predictive modeling developed, these databases could be reused for other government functions, particularly those relating to financial planning. The British Government employed its first official actuary in the 1830s, an employee who worked in naval pensions and is credited with saving the government hundreds of millions of pounds in today’s money.5 Already at that time, the predictive models used in government mirrored those used in business—a trend that continues to this day.
To begin with, developing predictive models involved calculations done by hand, using databases stored in written ledgers. Computers can help in two ways: they facilitate the storage of large amounts of data, and they can perform calculations automatically. Predictive models are now routinely implemented as computer programs that consult databases held in computer memory.
When computers were first introduced, their only users were governments and large corporations owing to their great expense. Both companies and governments started to develop computer-based predictive models almost as soon as computers were invented. For instance, the US government used computers to predict missile trajectories in the 1940s,6 to predict weather in the 1950s,7 and to predict suitability of military personnel for missions in the 1960s.8 In industry, the FICO corporation in the United States, which specializes in predicting credit risk, produced its first computerized model of risk scores in 1958.
We will introduce modern predictive AI systems by first presenting some older predictive statistical models, and then showing how the AI models extend (and differ from) these.
Actuarial Tables
The Equitable Life company made a novel contribution to insurance when it produced a table showing, for each age, the probability that a person will die at that age (based on available mortality statistics), and computing an associated insurance premium for that age. This kind of table came to be known as an “actuarial table.” This venerable insurance practice counts as a predictive model by our definition. The input variable is “age”; the outcome variable is “chance of dying”; and the training data are the mortality statistics used to compile the table. The innovation of the actuarial table lay in its systematically charting the outcome variable for each possible input variable within a given range.
As actuarial science progressed, more complex tables were developed, taking into account factors other than age so that more accurate predictions could be made and more accurate premiums charged. These tables implemented more complex predictive models with more input variables.
Geometric Approaches to Predictive Modeling
A drawback with actuarial tables is that they treat ages as discrete categories and then compute probabilities for each age separately, without regard for one another. But age varies continuously, and the probability of dying varies smoothly as a function of age. A function is a special type of relationship between input and output variables. What makes the relationship special is that the value of the output variable depends on and can be determined by the value of the input variable. In the earlier example we gave, height and weight are related in this special way. The “value” of your weight—that is, how much you weigh—is (partly) dependent on and can be determined by your height. The taller you are, the more you’ll weigh. Many variables of interest to scientists in the real world are related in this way. In technical terms, we say that the relationship between such variables defines a function. And as you may recall from high school, these relationships can be plotted as curves on graphs (the famous Cartesian number plane). That is, we can think of functions geometrically as curves with different shapes.
Actually it’s useful to be able to think about probabilities geometrically. For instance, we can define a mathematical function that maps the variable “age” represented on the x axis of a graph onto a probability of dying represented on the y axis, as shown in figure 1.1. This idea was pioneered by the nineteenth century actuary Benjamin Gompertz who found that the probability of dying can be modeled quite accurately by a simple mathematical function. Importantly, the function is continuous, meaning there are no breaks in it. For absolutely any age in figure 1.1, including, theoretically, something very precise like 7.78955 years of age, we can find the corresponding probability of dying. You wouldn’t easily be able to do this using an actuarial table because the age increments would soon get unwieldy if years were expressed correct to three or four decimal places.
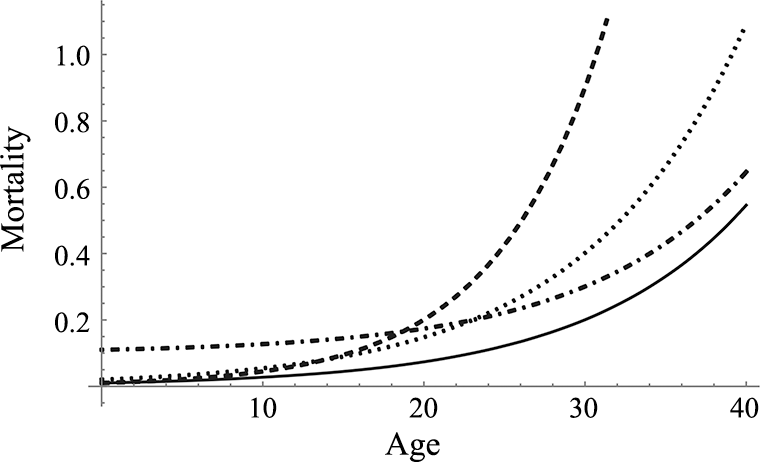
Examples of the Gompertz curve, a mathematical function mapping age onto probability of dying.
Note there are several curves in figure 1.1. Like many mathematical functions, Gompertz’s function has various parameters that can be adjusted. The four curves in this figure show the same function with different sets of parameter values. You might remember from high school that the same function y = 2x2 would come out looking different on a graph if, instead of a 2 in front of the x2, you had a 4 in front of it. Here, 2 and 4 are called “parameters,” but the underlying function y = ax2 is the same function, regardless of what its parameters might be (i.e., regardless of the value of a). In this new geometric approach to prediction, we don’t use our training data to estimate many separate probabilities, as we would in creating actuarial tables. Instead, we use the data to find the parameters of a function that best “fit” the data. If we model mortality with a “parameterizable” function, we can use our training set to find the parameter values that make the function most closely approximate the known facts about mortality. Of course, we have to begin by choosing a parameterizable function that’s suitable for modeling our data in the first place. But having made this choice, the process of finding the parameters that best fit the data can be automated in various ways. In this paradigm, the predictive model is nothing more than a mathematical function, with certain specified parameter values.
A particularly influential method for fitting a function to a given set of training data is called regression, which was first developed in the nineteenth century.
Regression Models
Take that “loose” relationship between height and weight we mentioned earlier. To quantify this relationship, we can gather a set of known height-weight pairs to serve as a “training set” for a model that maps height onto weight. An example training set is shown in figure 1.2, as a set of data points on a two-dimensional graph, where the x axis depicts height, and the y axis depicts weight.
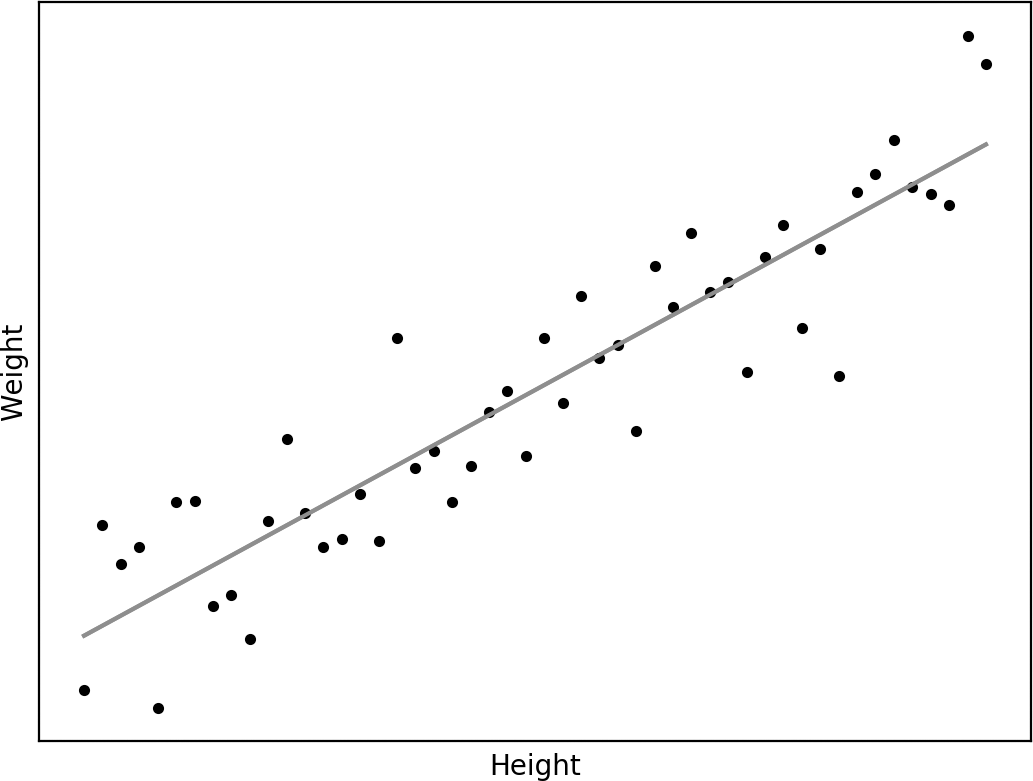
A function defining a relation between people’s height and weight, learned by linear regression from the data points shown in black.
Crucially, having represented the training set as points in a graph, we can “learn” a mathematical function that maps every possible height onto a weight, as shown by the red line in figure 1.2. (The training points include “noise,” miscellaneous factors that are relevant to weight but aren’t included in the model.) The line gives an answer even for heights that aren’t included in the training set and thus can be used to estimate weights for people who aren’t exactly like those in the training set. Note that the line doesn’t go through many of the training points. (It might not go through any at all!) In the presence of noise, we have to make a “best guess.”
Let’s say we decide we’re going to use a straight line to model our data. We can draw all sorts of straight lines on the graph in figure 1.2, but which of these most accurately represents the data points? Answering this amounts to finding the parameters of our straight-line function that best “fits” the training points. Linear regression is a way of finding the parameter values that provably minimize the amount of “error” the line makes in its approximation of the training points. The regression technique takes a set of training points and gives us the best parameter values for our function. We can then use this function as a general predictive model of the kind that is our focus—it will make a prediction about a weight for any given height.
Modern Regression Models
Regression is a key technique in modern statistical modeling. The basic method outlined above has been expanded in a multitude of different ways. For instance, linear regression models can involve many variables, not just two. If we have exactly three variables, for example, data points can be visualized in a three-dimensional space, and regression can be understood as identifying a three-dimensional plane that best fits the points. Moreover, regression modelers are free to decide how complex the function that fits the training data points should be. In figure 1.2, the function is a straight line, but we can also allow the function to be a curve, with different amounts of “squiggliness”—or, in three dimensions or more, a plane with different amounts of “hilliness.”
Regression techniques can also be used to model relationships between variables that vary discretely rather than continuously. (An example of a discrete variable is the outcome of a coin toss: there are just two possibilities here, unlike the continuous range of possibilities for height or weight.) This is done using “logistic regression” models, which are useful for classification tasks (we’ll say more about classification below when we discuss decision trees). Finally, there are many varieties of regression model specialized for particular tasks. An important variety for many government applications is “survival analysis,” which is a method for estimating the likely amount of time that will elapse before some event of interest happens. The original applications of these methods were in drug trials in which the “event of interest” was the death of a patient under some form of therapy. But there are many applications in government or commercial planning in which it is very useful to have a way of predicting how far in the future some event may be for different people or groups. Again, the same regression methods are used both within government and industry.
We should also note that regression models don’t have to be used in these action-guiding, practical ways. Scientists who use it are often just interested in stating relationships between variables in some domain. A scientist might, for instance, want to be able to state as an empirical finding that “there is a relationship between height and weight.” Methods relating to regression can be used to quantify the strength of this relationship.
We’ll now introduce two newer machine learning techniques that are often associated with the field of AI: decision trees and neural networks. These two techniques share a focus on the process of learning, which distinguishes them from regression modeling, where the focus is on fitting mathematical models to data.
Decision Trees
Decision trees are a fairly simple machine learning method and are often used to introduce machine learning models. Their origins date back to the 1930s, but they didn’t become popular until the mid-1980s.9 A decision tree is a set of instructions for guessing the value of some outcome variable by consulting the values of the input variables one by one. A toy example in the domain of criminal justice is shown in figure 1.3. This decision tree provides a way of guessing whether a prisoner up for bail will reoffend (the outcome variable), based on whether they have behaved well in prison and whether they committed a violent offense (two toy input variables).
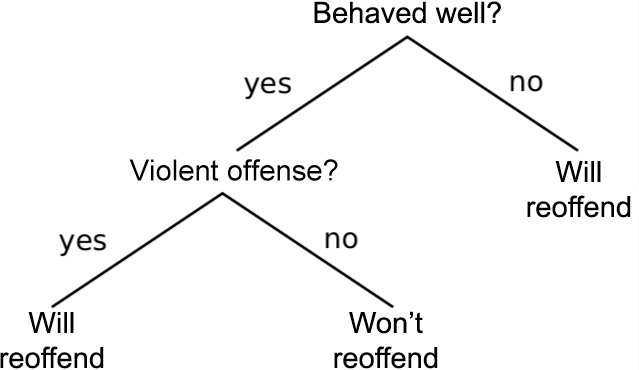
A simple decision tree for predicting a prisoner’s reoffending.
The tree states that if the prisoner didn’t behave well, they will reoffend, regardless of whether their original offense was violent. If they did behave well, they will reoffend if their original offense was violent, and they won’t if it wasn’t. (We use this crude example for illustration, but in real life they will take many more variables into account.)
The key task in decision tree modeling is to devise an algorithm that creates a good decision tree from the training data it’s given.* In the classic algorithm, we build the decision tree progressively, starting from the top. At each point in the tree, we find the input variable that supplies the most “information” about the outcome variable in the training set and add a node consulting that variable at that point.
An attractive feature of decision trees is that the procedure for reaching a decision can be readily understood by humans. At base, a decision tree is just a complex “if–then” statement. Understandability is an important attribute for machine learning systems making important decisions. However, modern decision tree models often use multiple decision trees embodying a range of different decision procedures and take some aggregate over the decisions reached. “Random forests” are the dominant model of this kind at present. For various reasons, these aggregate methods are more accurate. There is often (although not always) a tradeoff between a machine learning system’s explainability and its predictive performance.
Decision trees provide a useful opportunity to introduce the concept of a “classifier,” which is widely used in machine learning. A classifier is simply a predictive model whose outcome variable can take a number of discrete values. These discrete values represent different classes that the input items can be grouped into. Decision trees have to operate on variables with discrete values so they can easily implement classifiers. Our decision tree for reoffending can be understood as a classifier that sorts prisoners into two classes: “will reoffend” and “won’t reoffend.” To implement classifiers with regression techniques, we must use logistic regression models, which are specifically designed to handle discrete outcome variables.
Neural Networks
Neural networks (sometimes called “connectionist” networks) are machine learning techniques that are loosely inspired by the way brains perform computation. The first neural network was developed by Frank Rosenblatt in 1958,10 drawing on ideas about neural learning processes developed by Donald Hebb in the late 1940s.11
A brain is a collection of neurons, linked together by synapses. Each neuron is a tiny, very simple processor. The brain can learn complex representations and produce complex behavior because of the very large number of neurons it has and the even larger number of synapses that connect them together. Learning in the brain happens through the adjustment of the “strength” of individual synapses—the strength of a synapse determines how efficiently it communicates information between the neurons it connects. We are still far from understanding how this learning process works and how the brain represents information, but neural networks have been very roughly based on this model of the brain, imperfect as it is.
A neural network is a collection of neuron-like units that perform simple computations and can have different degrees of activation. These units are connected by synapse-like links that have adjustable weights. There are many different types of neural networks, but networks that learn a predictive model are predominantly “feedforward networks” of the kind illustrated (very crudely) in figure 1.4. A feedforward network used to learn a predictive model has a set of input units that encode the input variables of training items (or test items), a set of output units that encode the outcome variable for these same items, and a set of intermediate “hidden units.” Activity flows from the input units through the hidden units to the output units. Through this process, the network implements a function from input variables to the outcome variable, much like a regression model. Often there are many “layers” of hidden units, each connected to the layer before and the layer after. (The network in figure 1.4 has one hidden layer.)
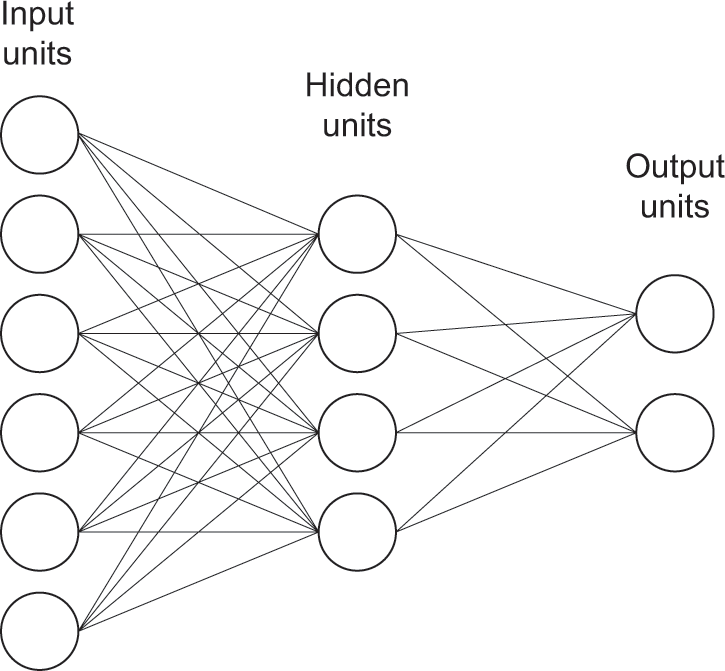
A simple feedforward network.
To give a simple example, imagine the network in figure 1.4 is a very simple image classifier that takes a tiny image comprising six pixels, and decides whether these pixels represent an image of type A or type B. The intensity of each pixel would be encoded in the activity of one of the input units. The activity of the output units encodes the type, in some designated scheme. (For instance, type A could be encoded by setting the activity of one unit to one, and the other unit to zero, whereas type B could be encoded by setting the activity of the former unit to zero, and the latter unit to one.)
There are many different learning algorithms for feedforward networks. But the basic principle for all of them is “supervised learning.” In this learning algorithm, we begin by setting the weights of all the links in the network to random values. The network then implements a function from inputs to outputs in successive rounds of training. To train an image classifier in this fashion, we would first present it with training inputs and let it guess—essentially randomly—what it was “seeing.” The classifier will invariably produce errors, and a crucial step in the training process involves calculating what these errors are. This is done by comparing, after each guess, the network’s actual output values to those it should have produced. Errors are then reduced by making small changes to the weights of all links in the network—changes which gradually improve the network’s performance as the process is repeated many times.
All the smarts in a supervised learning algorithm relate to how to tweak its weights so as to reduce error. A big breakthrough in this area is the technique of “error backpropagation,” which was invented (or at least made prominent) in 1986 by David Rumelhart and colleagues at the University of California, San Diego. This algorithm allowed the weights of neurons in a network’s hidden layer(s) to be sensibly adjusted. The invention of backpropagation led to a wave of academic interest in neural networks, but not to immediate practical effect. Then in the late 1990s and early 2000s, various innovations to the feedforward network were devised that culminated in dramatic improvements to backpropagation.12 These innovations, combined with the huge increases in computing power that occurred around that time, led to a new generation of “deep networks” that have revolutionized AI and data science.
The most salient feature of deep networks is that they have many layers of hidden units (unlike the single layer in figure 1.4). There are now several varieties of deep networks deployed in many different areas of machine learning. Deep networks of one sort or another are often the best performing models. The field of machine learning has in fact undergone a paradigm shift. The majority of researchers in this area currently focus their attention on deep networks. There are several open-source software packages that support the implementation, training, and testing of deep networks (e.g., Google’s TensorFlow and Facebook’s PyTorch). These packages have undoubtedly helped consolidate the new paradigm, and their ongoing development helps progress it further.
Nevertheless, a significant drawback of deep networks is that the models they learn are so complex that it’s essentially impossible for humans to understand their workings. Humans have a reasonable chance of being able to understand a decision tree (or even a set of decision trees) or to understand a regression model that succinctly states the relationships between variables. But they have no chance of understanding how a deep network computes its output from its inputs. If we want our machine learning tools to provide human-understandable explanations of their decisions, we need to supplement them with additional tools that generate explanations. The development of “explanation tools” is a growth area of AI and sufficiently important that we’ll discuss explanation systems separately in chapter 2.
Protocols for Testing Predictive Models
So far we’ve said little about methods to test and evaluate algorithms. Here we’ll mention just one device that can be used to evaluate an algorithm’s performance.
Often, a predictive algorithm can make several different types of error that have very different implications for its use in the field. Consider a “binary classifier” that’s trained to recognize members of one particular class. During testing, this classifier labels each test individual either as “positive” (a member of the class in question), or “negative” (not a member). If we also know the actual class of the test individuals, we can chart how often it’s right and wrong in its assignment of these labels and express these results in a “confusion matrix.” An example of a confusion matrix is shown in table 1.1. The classifier in this case is a system trained to predict fraudsters. It makes a “positive” response for people it predicts will commit fraud and a “negative” response for everyone else.
Confusion Matrix for a Fraud Detection Algorithm
|
Did commit fraud |
Did not commit fraud |
|||
|---|---|---|---|---|
|
Predicted to commit fraud |
True positives |
False positives (type 1 errors) |
||
|
Predicted not to commit fraud |
False negatives (type 2 errors) |
True negatives |
The confusion matrix shows how frequently the system is right or wrong in both kinds of prediction. A “false positive” is a case in which the system wrongly predicts someone to commit fraud (a false alarm, so to speak); a “false negative” is a case in which it fails to detect an actual fraudster (a miss). If a system isn’t perfect, there will always be a tradeoff between false positives and false negatives (and between true positives and true negatives). For example, an algorithm that judges everyone to be a fraudster will have no false negatives, while one judging nobody to be a fraudster will have no false positives. Importantly, in different domains, we might want to err on one side or the other. For instance, if we’re predicting suitability for a rehabilitation project, we might want to err on the side of false positives, whereas if we’re predicting guilt in a criminal case, we might want to err on the side of false negatives (on the assumption that it’s better to let many more guilty persons go free than to imprison a single innocent one). For many applications, then, we’d like the evaluation criterion for a classifier to specify what counts as acceptable performance in relation to the confusion matrix—that is, what sorts of error we would prefer the system to make.
A confusion matrix is just a simple means of keeping track of what types of errors an algorithm is making and assessing whether or not it’s performing acceptably. But there’s obviously a lot more to testing and evaluating algorithms than confusion matrices. For one thing, if it’s not to be a merely perfunctory, rubber-stamping exercise, testing has to be frequent. People’s habits, preferences, and lifestyles can be expected to change over time, so the items used to train an algorithm need to be constantly updated to ensure they’re truly representative of the people on whom it’ll be used. If test items aren’t routinely updated, the performance of an algorithm will deteriorate, and biases of various kinds may be (re)introduced. Another requirement is for testing to be rigorous. It’s not enough to test an algorithm’s performance on standard cases—cases involving “average” people on “average” incomes, for example. It must be tested in borderline cases involving unusual circumstances and exceptional individuals.
Mind you, frequent, rigorous testing isn’t just important for safety and reliability; it’s also crucial to fostering trust in AI. We humans are a suspicious lot, but we’re generally willing to go along with a technology if repeated testing under adverse conditions has shown that it’s safe to do so. That’s why we’re happy to board planes. The tests to which Boeing subjects its commercial airliners are famously—even eccentrically—tough-going. The same should go for AI. Until autonomous vehicles clock up enough evidence of safety from rigorous stress-testing in all sorts of conditions (heavy traffic, light traffic, wet weather, with and without pedestrians, with and without cyclists, etc.), it’s unlikely we’ll be as willing to hand over control to a Google car as we are to an air traffic control system or autopilot.
Summing Up
We’ve just presented the main varieties of predictive models currently used by government departments and corporations around the world. Our aim has been to emphasize the continuity of modeling techniques. Today’s models are extensions of predictive models that have been in use since the dawn of the computer age, and in some cases well before that. We have also emphasized that although these models are often referred to in current discussions as “AI” models, they are often equally well described as “statistical” models. The main novelty of modern AI predictive models is that they often perform better than traditional models, partly because of improvements in techniques, and partly owing to the many new data sources that are coming online in the age of big data. As a result, they’re becoming more widely adopted.
In the case of modern AI technologies, it has to be said that commercial companies have taken the lead in development and adoption. The big tech companies (Google, Facebook, Amazon, Facebook, and their Chinese equivalents) are the world leaders in AI, employing the largest, best-qualified and best-funded teams of researchers with access to the largest datasets and greatest computer processing power ever. Academic AI research is lagging some distance behind on all of these metrics. Government departments are lagging even further behind, but they are deploying the same kinds of AI tools as the big tech companies. And in both cases, the focus is very much on prediction.
We should emphasize that we haven’t covered all of AI, or even all of machine learning, in this chapter. There are many other important machine learning technologies that contribute to modern AI systems, in particular, unsupervised learning methods, which look for patterns in data without guidance, and reinforcement learning methods, where the system’s guidance takes the form of rewards and punishments. (Readers interested in these methods can read about them in the appendix to this chapter.) But predictive models as we have defined them are still at the center of the AI technologies that are impacting our world. And as we will show in this book, they are also at the center of citizens’ discussions about how AI technologies should be regulated. For instance, the fact that predictive models can all be evaluated in the same basic way makes them a natural focus for discussions about quality control and bias (chapter 3); the fact that they perform clearly defined tasks makes them a natural focus for discussions about human oversight and control (chapter 5); and the fact that their performance is often achieved at the expense of simplicity makes them a natural focus for discussions about transparency (chapter 2). In summary, the class of predictive models is coherent both from a technical perspective and from the perspective of regulation and oversight: it is thus a good starting point for a citizen’s guide.
Appendix: Other Machine Learning Systems
Our introduction to machine learning has focused on “predictive models” and the history of their use in industry and government. Most of the discussion in this book will be focused on these tools. However, there are other types of machine learning that find widespread application alongside predictive models—and these should have some introduction too.
One of these is called “unsupervised” machine learning. Although supervised learning algorithms are told how they should map their input variables onto outcome variables, unsupervised algorithms are given no instruction. They simply look for patterns in large datasets that human analysts might miss. Unsupervised algorithms are often used to build profiles of “typical” customers or “typical” citizens. This can be very helpful in simplifying a complex dataset and re-expressing it in terms of the typical patterns it contains. If we know that people who buy dog biscuits also frequently buy flea collars and visit websites aimed at pet owners, we can create a rough and ready class of people who do all these things. This “customer segmentation,” among other uses, makes potential customers easier to target with advertising.
It’s hard to measure the performance of unsupervised learning systems because they don’t have a specific task to do. In the above example, they simply find groupings of customers based on shared characteristics. This makes the regulatory objectives for these systems hard to define. However, unsupervised learning systems are sometimes used in conjunction with predictive models. For instance, the inputs to a predictive model are sometimes simplified classes created by unsupervised learning algorithms. Let’s say we want to construct a classifier that sorts people into two groups: high credit risk and low credit risk. But let’s also assume we don’t know what features distinguish low-risk from high-risk borrowers. Before constructing the classifier, we can run an unsupervised learning algorithm and see if it detects this particular grouping. If it does, it may reveal features that all low-risk borrowers share (e.g., high savings and medium income) and that all high-risk customers share (e.g., low savings and low income). In this case, we can measure the unsupervised system indirectly by seeing whether it improves the performance of the predictive system. Here, regulatory objectives are easier to formulate. The law could mandate that an unsupervised algorithm meet a certain benchmark in respect of predictive accuracy for credit scoring.
A final type of machine learning worth mentioning is “reinforcement learning.” This form of learning is used to train an agent-like system that acts in some environment, the state of which it can sense in some ways. The system takes as its input the current state of this environment, as revealed by its senses, and produces as its output an action. Typically, it produces a sequence of actions, with each action bringing about a change in its environment. Its stream of perceptions is thus influenced by the actions it performs. A good example of this kind of system is an AI agent playing a video game. As input it might take the current pixel values of the game display, and as output it might generate a reaction by a character in the game.
A system trained by reinforcement learning is like a predictive model, in that it learns to map “inputs” onto “outputs.” But there are two main differences. First, it doesn’t just “predict” an output; it actually performs its prediction, bringing about a change in its environment. Second, it doesn’t just make one-off, isolated predictions; it makes a stream of predictions, each one related to the new state it finds itself in.
Reinforcement learning is like supervised learning, in that the system learns from some external source how to map inputs onto outputs. But in reinforcement learning, there’s less spoon-feeding. The agent isn’t told at each step what it should do. Instead, the agent stumbles upon rewards and punishments in the environment it’s exploring. These stimuli are often sparse, as they are in the real world. Thus, it often has to learn sequences of actions that achieve rewards, or that avoid punishments, some distance into the future. A lot of learning in humans, and other animals, happens through this kind of reinforcement, rather than direct supervision. Our supervisor is the school of hard knocks.
Under the hood, a system trained by reinforcement learning is still a kind of predictive model, in our terms. And these days, the predictive model is typically a deep network, trained using backpropagation at each time step. But in reinforcement learning, it’s the system’s job to work out how to train this model—that is, it has to come up with its own set of training examples, mapping inputs onto “desired” outputs. This has implications for the way reinforcement learning systems are evaluated. The system developer doesn’t typically have a “test set” of unseen input–output mappings on which performance can be rated. Instead, as learning progresses, the developer evaluates the system by simply seeing how good the system gets at maximizing reward and minimizing punishment.
Notes
1. Marvin Minsky, ed. Semantic Information Processing (Cambridge, MA: MIT Press, 1968).
2. Nigel Watson, Barbara Jones, and Louise Bloomfield, Lloyd’s Register: 250 Years of Service (London: Lloyd’s Register, 2010).
3. Maurice Ogborn, Equitable Assurances: The Story of Life Assurance in the Experience of the Equitable Life Assurance Society 1762–1962 (London: Routledge, 1962).
4. Samuel Kotz, “Reflections on Early History of Official Statistics and a Modest Proposal for Global Coordination,” Journal of Official Statistics 21, no. 2 (2005): 139–144.
5. Martin Clarke, “Why Actuaries Are Essential to Government,” UK Civil Service Blog, December 4, 2018, https://civilservice.blog.gov.uk/2018/12/04/why-actuaries-are-essential-to-government.
6. Martin H. Weik, “The ENIAC Story,” Ordnance, the Journal of the American Ordnance Association (January–February 1961): 3–7.
7. George W. Platzman, The ENIAC Computation of 1950: Gateway to Numerical Weather Prediction (Chicago: University of Chicago Press, 1979).
8. Judy D. Roomsburg, “Biographical Data as Predictors of Success in Military Aviation Training,” Paper presented to the Faculty of the Graduate School of the University of Texas at Austin, December 1988.
9. Wei-Yin Loh, “Fifty Years of Classification and Regression Trees,” International Statistical Review 82, no. 3 (2014): 329–348.
10. Frank Rosenblatt, The Perceptron: A Perceiving and Recognizing Automaton (Buffalo: Cornell Aeronautical Laboratory, 1958).
11. Donald Hebb, The Organization of Behavior: A Neuropsychological Theory (Oxford: Wiley, 1949).
12. Alex Krizhevsky et al., “ImageNet Classification with Deep Convolutional Neural Networks,” Communications of the ACM 60, no. 6 (May 2017): 84–90.
* For example, you can imagine the sort of data that would lead an algorithm to create the decision tree in figure 1.3: data on good behavior, episodes of violence, and so on.