 |
GROUP (p. 1) |
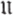 |
SUBGROUP (p. 10) |
 |
INDEX of  with respect to with respect to 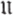 = number of left (right) cosets (p. 10) = number of left (right) cosets (p. 10) |
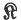 |
COMPLEX = subset of a group (p. 19) |
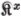 |
Complex transformed by x = set of all xKx–1 (p. 25) |
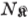 |
NORMALIZER of 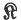 = group of all x which transform = group of all x which transform 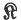 into itself (p. 26) into itself (p. 26) |
 |
CENTRALIZER of 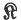 = group of all x which are permutable with every element of = group of all x which are permutable with every element of 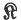 (p. 50) (p. 50) |
 |
NORMAL SUBGROUP = subgroup which is transformed into itself by all elements (p. 23) |
 |
FACTOR GROUP of  over over 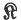 = group of cosets of = group of cosets of  by by 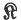 (p. 38) (p. 38) |
 |
CENTER OF = group of all elements commuting with every element of = group of all elements commuting with every element of  (p. 27) (p. 27) |
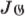 |
Group of all INNER AUTOMORPHISMS (transformations) of  (p. 48) (p. 48) |
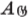 |
Group of all AUTOMORPHISMS of  (p. 48) (p. 48) |
| A / J |
Group of OUTER AUTOMORPHISMS of  (p. 48) (p. 48) |
| Φ |
A subgroup of  = intersection of = intersection of  with its maximal subgroups (p. 49) with its maximal subgroups (p. 49) |
| (a, b) = aba–1b–1 |
COMMUTATOR of a with b (p. 18) |
| (a, b, c) = (a, (b, c)) |
(p. 81) |
 |
mutual COMMUTATOR GROUP = group of all (U, V) (p. 81) |
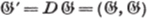 |
COMMUTATOR GROUP of  (p. 67) (p. 67) |
 |
FACTOR COMMUTATOR GROUP (p. 67) |
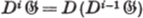 |
i-TH DERIVATIVE of  (p. 79) (p. 79) |
| k |
degree of METABELIAN group  , so that , so that  (p. 79) (p. 79) |
 |
DESCENDING CENTRAL SERIES (p. 155) so that |
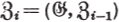 |
is the i-th Reidemeister commutator group |
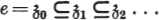 |
ascending central series (p. 50) so that |
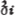 |
is the i-th center of  , hence , hence 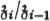 is the center of is the center of  |
| c |
Class of the nilpotent group  , hence , hence 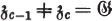 and and  |
 |
is a SYLOW p-GROUP of  (p. 135) (p. 135) |
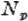 |
Normalizer of  (p. 135) (p. 135) |
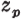 |
Center  (p. 135) (p. 135) |
 |
The minimal number of independent generators of  (p. 141) (p. 141) |
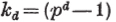 |
(pd−1—1) ... (p — 1) (p. 142) |
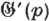 |
p-commutator group = intersection of all normal subgroups with abelian p-factor group (p. 158) |
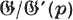 |
p-factor commutator group = maximal abelian p-factor group (p. 158) |
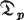 |
Intersections of all normal subgroups with index a power of p (p. 159) |
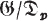 |
Maximal p-factor group (p. 159) |
| ∈ |
 means: x is an element of means: x is an element of  |
 |
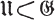 means: means: 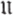 is a proper subgroup of is a proper subgroup of  |
 |
 is the sum of the sets is the sum of the sets 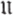 and and 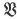 |
 |
 is the intersections of is the intersections of 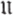 and and 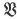 |
 |
 means: means: 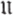 is a subgroup of is a subgroup of  |
 |
 means: means: 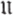 is a normal subgroup of is a normal subgroup of  |
  |
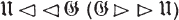 means: means: 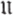 is a subnormal subgroup of is a subnormal subgroup of  |
{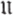 , , 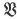 } } |
or 〈 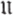 , , 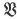 〉 denotes the subgroup generated by the two subgroups 〉 denotes the subgroup generated by the two subgroups 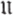 , , 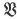 of a group of a group |
| × |
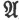 × × 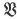 denotes the direct product of the groups denotes the direct product of the groups 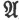 , , 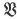 |
| * |
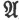 * * 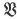 denotes the free product of the groups denotes the free product of the groups 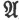 , , 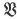 |
| ≤ |
a ≤ b (b ≥ a or a C b) means: the poset element a is contained in the poset element b |
| < |
a < b means: a ≤ b, but not b ≥ a; also denoted by: a > b |
| K |
a K b means: the lattice element a is Kurosh-invariant in the lattice element b |
| N |
a N b means: a is normal in b |
| NN |
a NN b means: a is subnormal in b |
| J |
a J b denotes the join of a and b |
| M |
a M b denotes the meet of a and b |
| a/b |
denotes the factor lattice of a over b |