Chapter 6
Lumber Stress Grades and Design Properties
Lumber sawn from a log, regardless of species and size, is quite variable in mechanical properties. Pieces may differ in strength by several hundred percent. For simplicity and economy in use, pieces of lumber of similar mechanical properties are placed in categories called stress grades, which are characterized by (a) one or more sorting criteria, (b) a set of properties for engineering design, and (c) a unique grade name.
This chapter briefly discusses the U.S. Department of Commerce American Softwood Lumber Standard PS20 (1994) sorting criteria for two stress-grading methods, and the philosophy of how properties for engineering design are derived. The derived properties are then used in one of two design formats: (a) the load and resistance factor design (LRFD), which is based on a reference strength at the 5th percentile 5-min bending stress (AF&PA 1996), or (b) the allowable stress design (ASD), which is based on a design stress at the lower 5th percentile 10-year bending stress. The properties depend on the particular sorting criteria and on additional factors that are independent of the sorting criteria. Design properties are lower than the average properties of clear, straight-grained wood tabulated in Chapter 4.
From one to six design properties are associated with a stress grade: bending modulus of elasticity for an edgewise loading orientation and stress in tension and compression parallel to the grain, stress in compression perpendicular to the grain, stress in shear parallel to the grain, and extreme fiber stress in bending. As is true of the properties of any structural material, the allowable engineering design properties must be either inferred or measured nondestructively. In wood, the properties are inferred through visual grading criteria, nondestructive measurement such as flatwise bending stiffness or density, or a combination of these properties. These nondestructive tests provide both a sorting criterion and a means of calculating appropriate mechanical properties.
The philosophies contained in this chapter are used by a number of organizations to develop visual and machine stress grades. References are made to exact procedures and the resulting design stresses, but these are not presented in detail.
Responsibilities and Standards for Stress Grading
An orderly, voluntary, but circuitous system of responsibilities has evolved in the United States for the development, manufacture, and merchandising of most stress-graded lumber. The system is shown schematically in Figure 6–1. Stress-grading principles are developed from research findings and engineering concepts, often within committees and subcommittees of the American Society for Testing and Materials.
American Lumber Standard Committee
Voluntary product standards are developed under procedures published by the U.S. Department of Commerce. The Department of Commerce National Institute of Standards and Technology (NIST), working with rules-writing agencies, lumber inspection agencies, lumber producers, distributors and wholesalers, retailers, end users, and members of Federal agencies, work through the American Lumber Standard Committee (ALSC) to maintain a voluntary consensus softwood standard, called the American Softwood Lumber Standard (PS 20–94). The PS 20–94 Standard prescribes the ways in which stress-grading principles can be used to formulate grading rules designated as conforming to the American Lumber Standard. Under the auspices of the ALSC is the National Grading Rule, which specifies grading characteristics for different grade specifications.
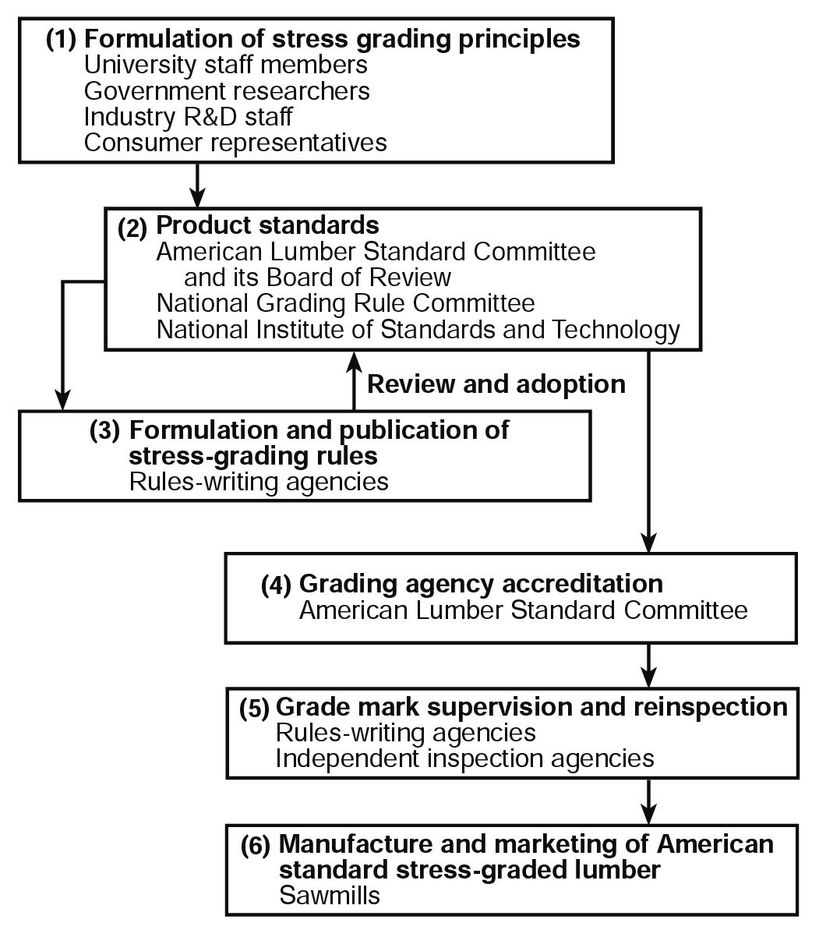
Figure 6–1. Voluntary system of responsibilities for stress grading under the American Softwood Lumber Standard.
Organizations that write and publish grading rule books containing stress-grade descriptions are called rules-writing agencies. Grading rules that specify American Softwood Lumber Standard PS 20–94 must be certified by the ALSC Board of Review for conformance with this standard. Organizations that write grading rules, as well as independent agencies, can be accredited by the ALSC Board of Review to provide grading and grade-marking supervision and reinspection services to individual lumber manufacturers. Accredited rules-writing and independent agencies are listed in Table 6–1. The continued accreditation of these organizations is under the scrutiny of the ALSC Board of Review.
Most commercial softwood species manufactured in the United States are stress graded under American Lumber Standard practice. Distinctive grade marks for each species or species grouping are provided by accredited agencies. The principles of stress grading are also applied to several hardwood species under provisions of the American Softwood Lumber Standard. Lumber found in the marketplace may be stress graded under grading rules developed in accordance with methods approved by the ALSC or by some other stress-grading rule, or it may not be stress graded. Only those stress grades that meet the requirements of the voluntary American Softwood Lumber Standard system are discussed in this chapter.
Table 6–1. Sawn lumber grading agenciesa
| Rules-writing agencies | |
|---|---|
| Northeastern Lumber Manufacturers Association (NELMA) | |
| Northern Softwood Lumber Bureau (NSLB) | |
| Redwood Inspection Service (RIS) | |
| Southern Pine Inspection Bureau (SPIB) | |
| West Coast Lumber Inspection Bureau (WCLIB) | |
| Western Wood Products Association (WWPA) | |
| National Lumber Grades Authority (NLGA) | |
| Independent agencies | |
| California Lumber Inspection Service | |
| Pacific Lumber Inspection Bureau, Inc. | |
| Renewable Resource Associates, Inc. | |
| Timber Products Inspection | |
| Alberta Forest Products Association | |
| Canadian Lumbermen’s Association | |
| Canadian Mill Services Association | |
| Canadian Softwood Inspection Agency, Inc. | |
| Cariboo Lumber Manufacturers Association | |
| Central Forest Products Association | |
| Coniferous Lumber Inspection Bureau | |
| Council of Forest Industries of British Columbia | |
| Interior Lumber Manufacturers Association | |
| MacDonald Inspection | |
| Maritime Lumber Bureau | |
| Newfoundland Lumber Producers Association | |
| Northern Forest Products Association | |
| Ontario Lumber Manufacturers Association | |
| Pacific Lumber Inspection Bureau | |
| Quebec Lumber Manufacturers Association | |
| aFor updated information, contact American Lumber Standard Committee, P.O. Box 210, Germantown, MD 20874. | |
National Grading Rule
Stress grading under the auspices of the ALSC is applied to many sizes and several patterns of lumber that meet the American Softwood Lumber Standard provision. However, most stress-graded lumber is dimension lumber (standard 38 to 89 mm (nominal 2 to 4 in.) thick) and is governed by uniform specifications under the National Grading Rule. The National Grading Rule provides guidelines for writing grading rules for lumber in this thickness range and specifies grading characteristics for different grade specifications. American Softwood Lumber Standard dimension lumber in this thickness range is required to conform to the National Grading Rule, except for special products such as scaffold planks. Grade rules for other sizes, such as nominal 5-in. (standard 114-mm) or larger structural timbers may vary between rules-writing agencies or species.
The National Grading Rule establishes the lumber classifications and grade names for visually stress-graded dimension lumber (Table 6–2) and also provides for the grading of dimension lumber by a combination of machine and visual methods. Visual requirements for this type of lumber are developed by the respective rules-writing agencies for particular species grades.
Table 6–2. Visual grades described in National Grading Rule
| Lumber classificationa | Grade name | Bending strength ratio (%) |
|---|---|---|
| Light framingb | Construction | 34 |
| Standard | 19 | |
| Utility | 9 | |
| Structural light framingb | Select Structural | 67 |
| 1 | 55 | |
| 2 | 45 | |
| 3 | 26 | |
| Studc | Stud | 26 |
| Structural joists and planksd | Select Structural | 65 |
| 1 | 55 | |
| 2 | 45 | |
| 3 | 26 | |
| aContact rules-writing agencies for additional information. | ||
| bStandard 38 to 89 mm (nominal 2 to 4 in.) thick and wide. Widths narrower than 89 mm (4 in.) may have different strength ratio than shown. | ||
| cStandard 38 to 89 mm (nominal 2 to 4 in.) thick, ≥38 mm (≥4 in.) wide. | ||
| dStandard 38 to 89 mm (nominal 2 to 4 in.) thick, ≥140 mm (≥6 in.) wide. | ||
Standards
Table 6–2 also shows associated minimum bending strength ratios to provide a comparative index of quality. The strength ratio is the hypothetical ratio of the strength of a piece of lumber with visible strength-reducing growth characteristics to its strength if those characteristics were absent. Formulas for calculating strength ratios are given in American Society of Testing and Materials (ASTM) standard D245. The corresponding visual description of the dimension lumber grades can be found in the grading rule books of the rules-writing agencies listed in Table 6–1. Design properties will vary by species. The design properties for each species and grade are published in the appropriate rule books and in the National Design Specification for Wood Construction (AF&PA 1997).
Grouping of Species
Most species are grouped together and the lumber from them treated as equivalent. Species are usually grouped when they have about the same mechanical properties, when the wood of two or more species is very similar in appearance, or for marketing convenience. For visual stress grades, ASTM D2555 contains procedures for calculating clear wood properties for groups of species to be used with ASTM D245. ASTM D1990 contains procedures for calculating design properties for groups of species tested as full-sized members. The properties assigned to a group by such procedures will often be different from those of any species that make up the group. The group will have a unique identity, with nomenclature approved by the Board of Review of the ALSC. The identities, properties, and characteristics of individual species of the group are found in the grade rules for any particular species or species grouping. In the case of machine stress grading, the inspection agency that supervises the grading certifies by testing that the design properties in that grade are appropriate for the species or species grouping and the grading process.
Foreign species
Currently, the importation of structural lumber is governed by two ALSC guidelines that describe the application of the American Lumber Standard and ASTM D1990 procedures to foreign species. The approval process is outlined in Table 6–3.
Visually Graded Structural Lumber
Visual Sorting Criteria
Visual grading is the original method for stress grading. It is based on the premise that mechanical properties of lumber differ from mechanical properties of clear wood because many growth characteristics affect properties and these characteristics can be seen and judged by eye. Growth characteristics are used to sort lumber into stress grades. The typical visual sorting criteria discussed here are knots, slope of grain, checks and splits, shake, density, decay, heartwood and sapwood, pitch pockets, and wane.
Table 6–3. Approval process for acceptance of design values for foreign species
| 1 | Rules-writing agency seeks approval to include species in grade-rule book. |
| 2 | Agency develops sampling and testing plan, following American Lumber Standard Committee (ALSC) foreign importation guidelines, which must then be approved by ALSC Board of Review. |
| 3 | Lumber is sampled and tested in accordance with approved sampling and testing plan. |
| 4 | Agency analyzes data by ALSC Board of Review and ASTM D1990 procedures and other appropriate criteria (if needed). |
| 5 | Agency submits proposed design values to ALSC Board of Review. |
| 6 | Submission is reviewed by ALSC Board of Review and USDA Forest Service, Forest Products Laboratory. |
| 7 | Submission is available for comment by other agencies and interested parties. |
| 8 | ALSC Board of Review approves (or disapproves) design values, with modification (if needed) based on all available information. |
| 9 | Agency publishes new design values for species. |
Knots
Knots cause localized cross grain with steep slopes. A very damaging aspect of knots in sawn lumber is that the continuity of the grain around the knot is interrupted by the sawing process.
In general, knots have a greater effect on strength in tension than compression; in bending, the effect depends on whether a knot is in the tension or compression side of a beam (knots along the centerline have little or no effect). Intergrown (or live) knots resist (or transmit) some kinds of stress, but encased knots (unless very tight) or knotholes resist (or transmit) little or no stress. On the other hand, distortion of grain is greater around an intergrown knot than around an encased (or dead) knot of equivalent size. As a result, overall strength effects are roughly equalized, and often no distinction is made in stress grading between intergrown knots, dead knots, and knotholes.
The zone of distorted grain (cross grain) around a knot has less “parallel to piece” stiffness than does straight-grained wood; thus, localized areas of low stiffness are often associated with knots. However, such zones generally constitute only a minor part of the total volume of a piece of lumber. Because overall stiffness of a piece reflects the character of all parts, stiffness is not greatly influenced by knots.
The presence of a knot has a greater effect on most strength properties than on stiffness. The effect on strength depends approximately on the proportion of the cross section of the piece of lumber occupied by the knot, knot location, and distribution of stress in the piece. Limits on knot sizes are therefore made in relation to the width of the face and location on the face in which the knot appears. Compression members are stressed about equally throughout, and no limitation related to location of knots is imposed. In tension, knots along the edge of a member cause an eccentricity that induces bending stresses, and they should therefore be more restricted than knots away from the edge. In simply supported structural members subjected to bending, stresses are greater in the middle of the length and at the top and bottom edges than at midheight. These facts are recognized in some grades by differing limitations on the sizes of knots in different locations.
Knots in glued-laminated structural members are not continuous as in sawn structural lumber, and different methods are used for evaluating their effect on strength (Ch. 11).
Slope of Grain
Slope of grain (cross grain) reduces the mechanical properties of lumber because the fibers are not parallel to the edges. Severely cross-grained pieces are also undesirable because they tend to warp with changes in moisture content. Stresses caused by shrinkage during drying are greater in structural lumber than in small, clear straight-grained specimens and are increased in zones of sloping or distorted grain. To provide a margin of safety, the reduction in design properties resulting from cross grain in visually graded structural lumber is considerably greater than that observed in small, clear specimens that contain similar cross grain.
Checks and Splits
Checks are separations of the wood that normally occur across or through the annual rings, usually as a result of seasoning. Splits are a separation of the wood through the piece to the opposite surface or to an adjoining surface caused by tearing apart of the wood cells. As opposed to shakes, checks and splits are rated by only the area of actual opening. An end-split is considered equal to an end-check that extends through the full thickness of the piece. The effects of checks and splits on strength and the principles of their limitation are the same as those for shake.
Shake
Shake is a separation or a weakness of fiber bond, between or through the annual rings, that is presumed to extend lengthwise without limit. Because shake reduces resistance to shear in members subjected to bending, grading rules therefore restrict shake most closely in those parts of a bending member where shear stresses are highest. In members with limited cross grain, which are subjected only to tension or compression, shake does not affect strength greatly. Shake may be limited in a grade because of appearance and because it permits entrance of moisture, which results in decay.
Density
Strength is related to the mass per unit volume (density) of clear wood. Properties assigned to lumber are sometimes modified by using the rate of growth and percentage of latewood as measures of density. Typically, selection for density requires that the rings per unit length and the percentage of latewood be within a specified range. It is possible to eliminate some very low-strength pieces from a grade by excluding those that are exceptionally low in density.
Decay
Decay in most forms should be prohibited or severely restricted in stress grades because the extent of decay is difficult to determine and its effect on strength is often greater than visual observation would indicate. Decay of the pocket type (for example, Fomes pini) can be permitted to some extent in stress grades, as can decay that occurs in knots but does not extend into the surrounding wood.
Heartwood and Sapwood
Heartwood does not need to be taken into account in stress grading because heartwood and sapwood have been assumed to have equal mechanical properties. However, heartwood is sometimes specified in a visual grade because the heartwood of some species is more resistant to decay than is the sapwood; heartwood may be required if untreated wood will be exposed to a decay hazard. On the other hand, sapwood takes preservative treatment more readily than heartwood and it is preferable for lumber that will be treated with preservatives.
Pitch Pockets
Pitch pockets ordinarily have so little effect on structural lumber that they can be disregarded in stress grading if they are small and limited in number. The presence of a large number of pitch pockets, however, may indicate shake or weakness of bond between annual rings.
Wane
Wane refers to bark or lack of wood on the edge or corner of a piece of lumber, regardless of cause (except eased edges). Requirements of appearance, fabrication, or ample bearing or nailing surfaces generally impose stricter limitations on wane than does strength. Wane is therefore limited in structural lumber on those bases.
Procedures for Deriving Design Properties
The mechanical properties of visually graded lumber may be established by (a) tests of a representative sample of full-size members (ASTM D1990 in-grade testing procedure) or (b) appropriate modification of test results conducted on small clear specimens (ASTM D245 procedure for small clear wood). Design properties for the major commercial softwood dimension lumber species given in current design specification and codes in the United States have been derived from full-size member test results. However, design properties for most hardwood dimension and structural timbers (larger than standard 89-mm- (nominal 4-in.-, actual 3-1/2-in.-) thick “timbers”) of all species are still derived using results of tests on small clear samples.
Procedure for Small Clear Wood
The derivation of mechanical properties of visually graded lumber was historically based on clear wood properties with appropriate modifications for the lumber characteristics allowed by visual sorting criteria. Sorting criteria that influence mechanical properties are handled with “strength ratios” for the strength properties and with “quality factors” for the modulus of elasticity.
From piece to piece, there is variation in both the clear wood properties and the occurrence of growth characteristics. The influence of this variability on lumber properties is handled differently for strength properties than for modulus of elasticity.
Strength Properties—Each strength property of a piece of lumber is derived from the product of the clear wood strength for the species and the limiting strength ratio. The strength ratio is the hypothetical ratio of the strength of a piece of lumber with visible strength-reducing growth characteristics to its strength if those characteristics were absent. The true strength ratio of a piece of lumber is never known and must be estimated. Therefore, the strength ratio assigned to a growth characteristic serves as a predictor of lumber strength. Strength ratio is expressed as a percentage, ranging from 0 to 100.
Estimated strength ratios for cross grain and density have been obtained empirically; strength ratios for other growth characteristics have been derived theoretically. For example, to account for the weakening effect of knots, the assumption is made that the knot is effectively a hole through the piece, reducing the cross section, as shown in Figure 6–2. For a beam containing an edge knot, the bending strength ratio can be idealized as the ratio of the bending moment that can be resisted by a beam with a reduced cross section to that of a beam with a full cross section:
SR = 1 − (k/h)2
where SR is strength ratio, k knot size, and h width of face containing the knot. This is the basic expression for the effect of a knot at the edge of the vertical face of a beam that is deflected vertically. Figure 6–3 shows how strength ratio changes with knot size according to the formula.
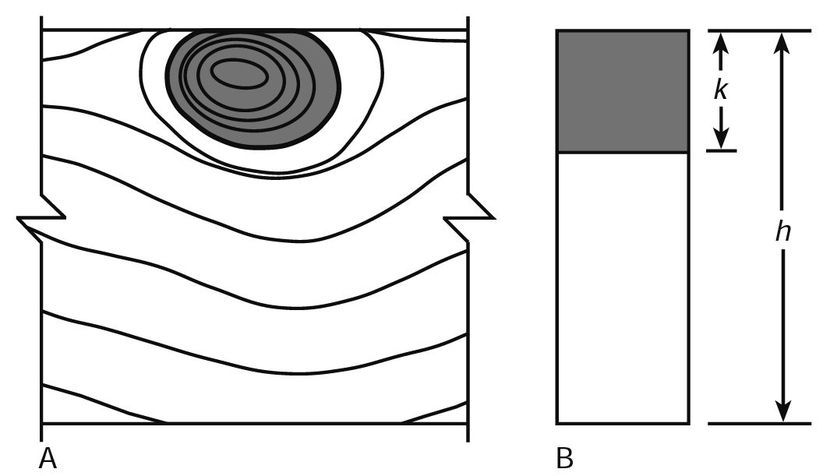
Figure 6–2. Effect of edge knot: A, edge knot in lumber and B, assumed loss of cross section (cross-hatched area).
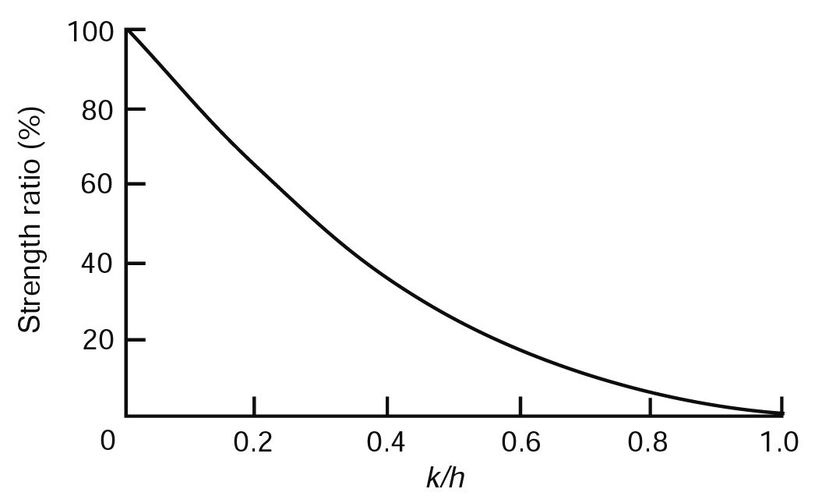
Figure 6–3. Relation between bending strength ratio and size of edge knot expressed as fraction of face width. k is knot size; h, width of face containing the knot.
Strength ratios for all knots, shakes, checks, and splits are derived using similar concepts. Strength ratio formulas are given in ASTM D245. The same reference contains guidelines for measuring various growth characteristics.
An individual piece of lumber will often have several characteristics that can affect any particular strength property. Only the characteristic that gives the lowest strength ratio is used to derive the estimated strength of the piece. In theory, a visual stress grade contains lumber ranging from pieces with the minimum strength ratio permitted in the grade up to pieces with the strength ratio just below the next higher grade. In practice, there are often pieces in a grade with strength ratios of a higher grade. This is a result of grade reduction for appearance factors such as wane that do not affect strength.
The range of strength ratios in a grade and the natural variation in clear wood strength give rise to variation in strength between pieces in the grade. To account for this variation and to ensure safety in design, it is intended that the actual strength of at least 95% of the pieces in a grade exceed the design properties (before reduction for duration of load and safety) assigned to that grade. In visual grading, according to ASTM D245, this is handled by using a near-minimum clear wood strength as a base value and multiplying it by the minimum strength ratio permitted in the grade to obtain the grade strength property. The near-minimum value is called the 5% exclusion limit. ASTM D2555 provides clear wood strength data and gives a method for estimating the 5% exclusion limit.
For example, suppose a 5% exclusion limit for the clear wood bending strength of a species in the green condition is 48 MPa (7,000 lb/in2). Suppose also that among the characteristics allowed in a grade of lumber, one characteristic (a knot, for example) provides the lowest strength ratio in bending—assumed in this example as 40%. Using the numbers, the bending strength for the grade is estimated by multiplying the strength ratio (0.40) by 48 MPa (7,000 1b/2in), equaling 19 MPa (2,800 1b/2in) (Fig. 6–4). The bending strength in the green condition of 95% of the pieces in this species in a grade that has a strength ratio of 40% is expected to be ≥19 MPa (≥2,800 lb/in2). Similar procedures are followed for other strength properties, using the appropriate clear wood property value and strength ratio. Additional multiplying factors are then applied to produce properties for design, as summarized later in this chapter.
Modulus of Elasticity—Modulus of elasticity E is a measure of the ability of a beam to resist deflection or of a column to resist buckling. The assigned E is an estimate of the average modulus, adjusted for shear deflection, of the lumber grade when tested in static bending. The average modulus of elasticity for clear wood of the species, as recorded in ASTM D2555, is used as a base. The clear wood average is multiplied by empirically derived “quality factors” to represent the reduction in modulus of elasticity that occurs by lumber grade for pieces tested in an edgewise orientation. This procedure is outlined in ASTM D245.
For example, assume a clear wood average modulus of elasticity of 12.4 GPa (1.8 × 106 lb/in2) for the example shown earlier. The limiting bending strength ratio was 40%. ASTM D245 assigns a quality multiplying factor of 0.80 for lumber with this bending strength ratio. The modulus of elasticity for that grade would be the product of the clear wood modulus and the quality factor; that is, 12.4 × 0.8 = 9.9 GPa (1.8 × 0.8 = 1.44 × 106 lb/in2).
Actual modulus of elasticity of individual pieces of a grade varies from the average assumed for design (Fig. 6–5). Small individual lots of lumber can be expected to deviate from the distribution shown by this histogram. The additional multiplying factors used to derive final design values of modulus of elasticity are discussed later in this chapter.
In-Grade Procedure
To establish the mechanical properties of specified grades of lumber from tests of full-size specimens, a representative sample of the lumber population is obtained following procedures in ASTM D2915 and D1990. The specimens are tested using appropriate procedures given in ASTM D198 or D4761. Because the range of quality with any one specific grade may be large, it is necessary to assess the grade quality index (GQI) of the sampled material in relation to the assumed GQI. In the North American In-Grade Program, GQI was the strength ratio calculated according to formulas in ASTM D245. The sample GQI and the assumed GQI are compared to see if adjustment to the test data is necessary. An average value for the edgewise modulus of elasticity or a near-minimum estimate of strength properties is obtained using ASTM D1990 procedures. The grade GQI is also used as a scaling perimeter that allows for modeling of strength and modulus of elasticity with respect to grade. These properties are further modified for design use by consideration of service moisture content, duration of load, and safety.
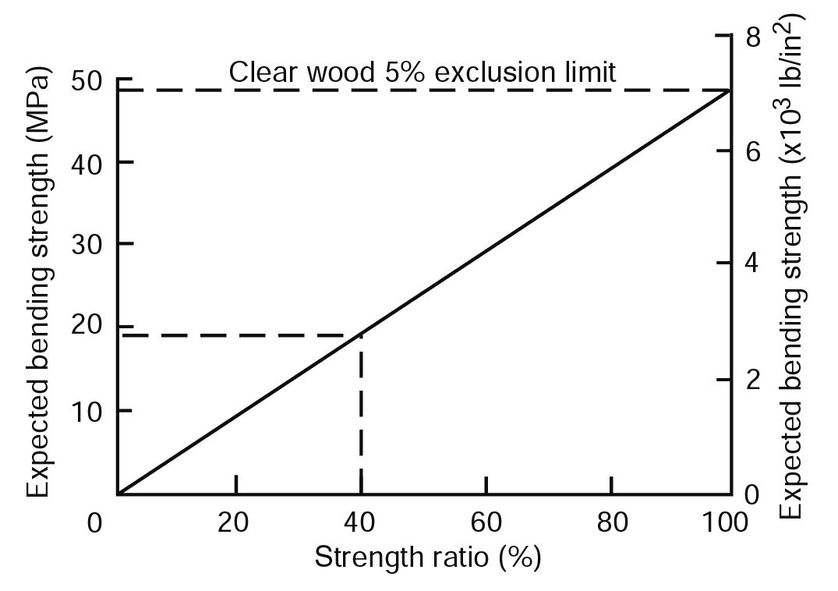
Figure 6–4. Example of relation between strength and strength ratio.
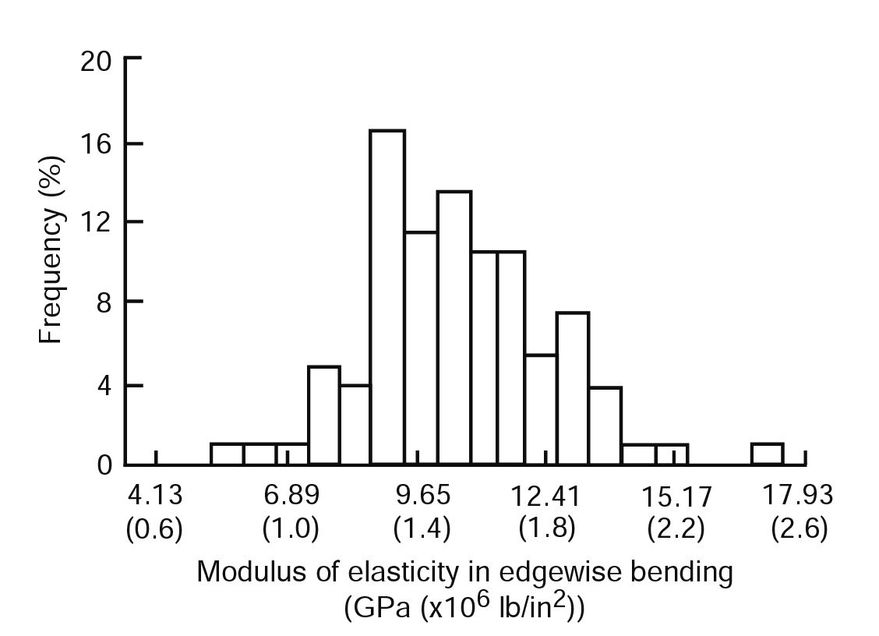
Figure 6–5. Histogram of modulus of elasticity observed in a single visual grade, from pieces selected over a broad geographical range.
Machine-Graded Structural Lumber
Machine-graded lumber is lumber evaluated by a machine using a nondestructive test followed by visual grading to evaluate certain characteristics that the machine cannot or may not properly evaluate. Machine-stress-rated (MSR), machine-evaluated-lumber (MEL), and E-rated lumber are three types of machine-graded lumber. Machine-graded lumber allows for better sorting of material for specific applications in engineered structures. The basic components of a machine-grading system are as follows:
- sorting and prediction of strength through machinemeasured nondestructive determination of properties coupled with visual assessment of growth characteristics,
- assignment of design properties based on strength prediction, and
- quality control to ensure that assigned properties are being obtained. The quality control procedures ensure
- proper operation of the machine used to make the nondestructive measurements,
- appropriateness of the predictive parameter-bending strength relationship, and
- appropriateness of properties assigned for tension and compression.
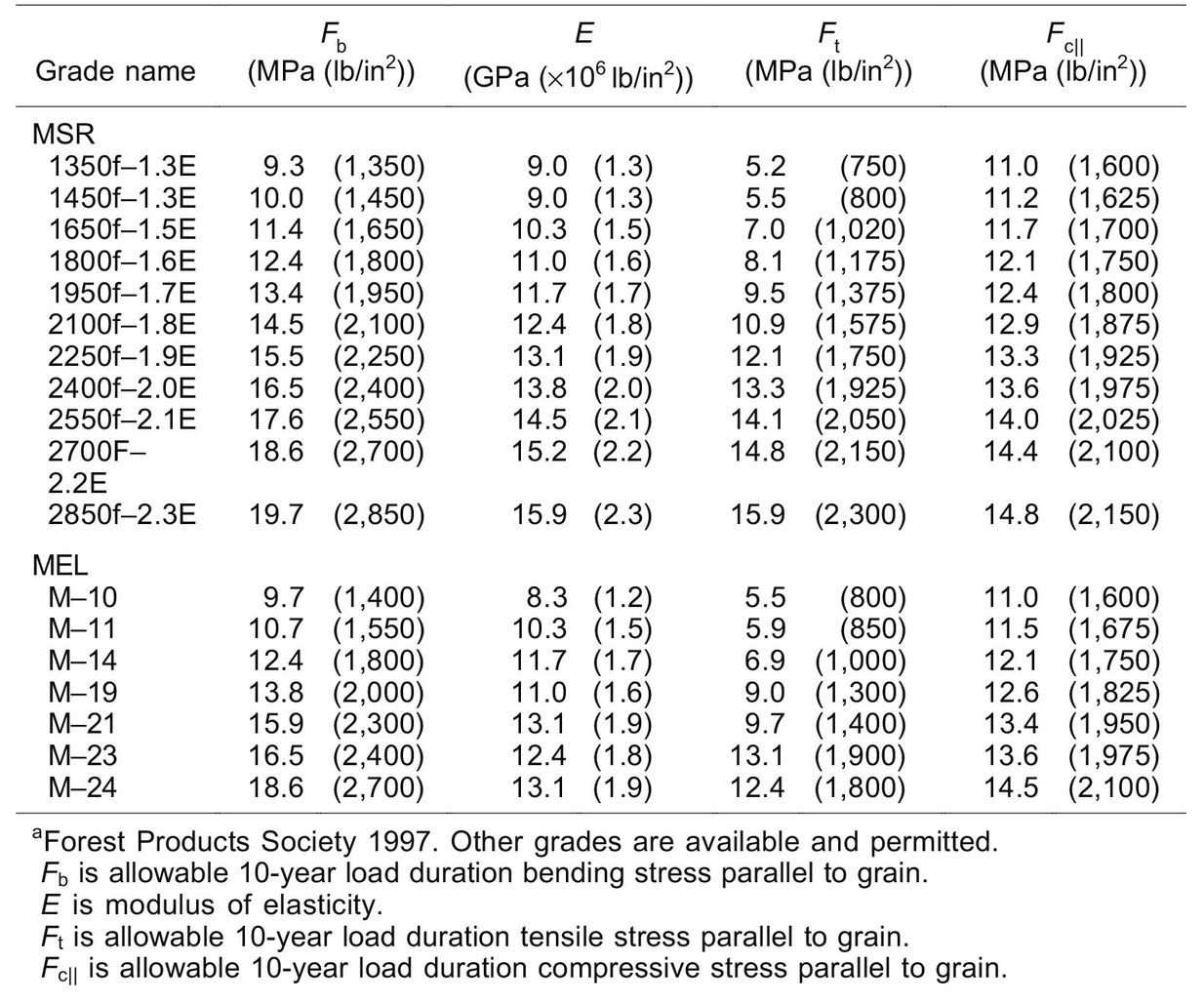
The MSR and MEL systems differ in grade names, quality control, and coefficient of variation (COV) for E values. Grade names for MSR lumber are a combination of the design bending stress and average modulus of elasticity, whereas grade names for MEL lumber start with an M designation. For quality control, MSR requires pieces to be tested daily for at least one strength property and bending modulus of elasticity in an edgewise orientation, whereas MEL requires daily tension quality control and edgewise bending strength and stiffness testing. Finally, MSR grades are assigned a COV = 11% on E, whereas MEL grades are assigned a COV ≤ 15% on E. Grade names for a wide range of machine-graded lumber commonly available across North America are given in Table 6–4. Not all grades are available in all sizes or species.
Machine Sorting Criteria
The most common method of sorting machine-graded lumber is modulus of elasticity E. When used as a sorting criterion for mechanical properties of lumber, E can be measured in a variety of ways. Usually, the apparent E, or deflection related to stiffness, is actually measured. Because lumber is heterogeneous, the apparent E depends on span, orientation (edge- or flatwise in bending), load speed of test (static or dynamic), and method of loading (tension, bending, concentrated, or uniform). Any of the apparent E values can be used, as long as the grading machine is properly calibrated, to assign the graded piece to a “not to exceed” grade category. Most grading machines in the United States are designed to detect the lowest flatwise bending E that occurs in any approximately 1.2-m (4-ft) span and the average flatwise E for the entire length of the piece.
Table 6–4. Common grades for machine-graded lumbera
Another method of sorting machine-graded lumber is using density measurements to estimate knot sizes and frequency. X-ray sources in conjunction with a series of detectors are used to determine density information. Density information is then used to assign the graded piece to a “not to exceed” grade category.
In the United States and Canada, MSR and MEL lumber are also subjected to a visual override because the size of edge knots in combination with E is a better predictor of strength than is E alone. Maximum edge knots are limited to a specified proportion of the cross section, depending on grade level. Other visual restrictions, which are primarily appearance rather than strength criteria, are placed on checks, shake, skips (portions of board “skipped” by the planer), splits, wane, and warp.
Procedures for Deriving Design Properties
Allowable Stress for Bending
A stress grade derived for machine-graded lumber relates design strength to a nondestructive parameter. For this example, it will be considered to be E. Because E is an imperfect predictor of strength, lumber sorted solely by average E falls into one of four categories, one of which is sorted correctly and three incorrectly (Fig. 6–6).
Consider, for example, the most simple case (sometimes referred to as “go” or “no go”) where lumber is sorted into two groups: one with sufficient strength and stiffness for a specific application, the other without. In Figure 6–6a, a regression line relating E and strength is used as the prediction model. The “accept-reject” groups identified by the regression sort can be classified into four categories:
- Category 1—Material that has been accepted correctly, that is, pieces have sufficient strength and stiffness as defined
- Category 2—Material that has been accepted incorrectly, that is, pieces do not have sufficient strength
- Category 3—Material that has been rejected correctly because it does not have sufficient strength
- Category 4—Material that has been rejected correctly because it does not have sufficient stiffness
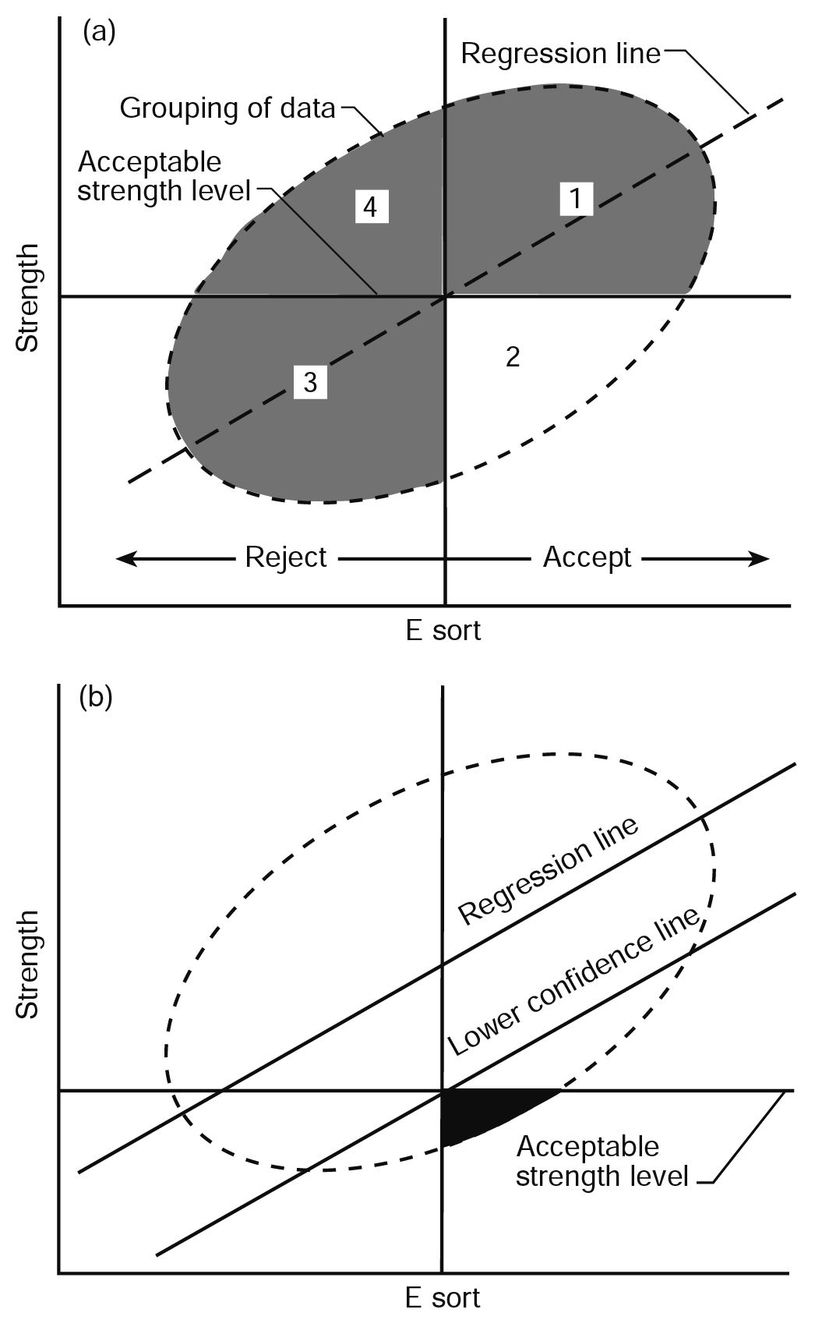
Figure 6–6. Schematic E sort: (a) using a regression line as the predictor showing four categories: 1—accepted correctly; 2—accepted incorrectly; 3—rejected correctly; and 4—rejected correctly; (b) using a lower confidence line as the predictor and showing the relatively low proportion of material in the accepted incorrectly category (lower right).
Thus, the sort shown in Figure 6–6a has worked correctly for categories 1, 3, and 4 but incorrectly for category 2. Pieces in category 2 present a problem. These pieces are accepted as having sufficient strength but in reality they do not, and they are mixed with the accepted pieces of category 1. The number of problem pieces that fall in category 2 depends on the variability in the prediction model.
To minimize the material that falls into category 2, adjustments are made to the property assignment claims made about the sorted material. An appropriate model is one that minimizes the material in category 2 or at least reduces it to a lower risk level. Additional grading criteria (edge-knot limitations, for example) are also added to improve the efficiency of the sorting system relative to the resource and the claimed properties.
Commonly, a lower confidence line is used as the prediction model (Fig. 6–6b). The number of pieces that fall into category 2 is now low compared with the regression line model. Furthermore, the probability of a piece (and thus the number of pieces) falling into category 2 is controlled by the confidence line selected.
In actual MSR systems, the lumber is sorted (graded) into E classes. In the United States and Canada, the number of grades has increased as specific market needs have developed for MSR lumber. Today, individual grading agencies list as many as 13 E classifications and more than 20 different grades. The grades are designated by the recommended extreme fiber stress in bending Fb and edgewise modulus of elasticity E. For example, “2100F-1.8E” designates an MSR grade with a design stress Fb = 14 MPa (2,100 lb/in2) and E = 12.4 GPa (1.8 × 106 lb/in2).
In theory, any F-E combination can be marketed that can be supported by test data. In practice, a mill will usually produce only a few of the possible existing F-E classifications depending on the potential of the timber being harvested, mill production capabilities, and product or market demand. When a mill has determined the grades it would like to produce (based on their lumber resource and marketing issues), grade boundary machine settings are used to separate the lumber into F-E classifications. A qualification sample of lumber is tested by a grading agency for strength and stiffness, to verify that the proper machine settings are being used. After initial qualification, additional quality control tests are performed during production.
Figure 6–7 illustrates how Fb-E classifications have been developed historically for species groups. Data for a particular species group are collected, the relationship of E and MOR is evaluated, and a lower confidence line is established for the species, as illustrated in Figure 6–6b. Using the lower confidence line of this relationship, an MOR value corresponding to the “minimum E” assigned to the grade is determined. The “minimum E” assigned to the grade represents the 5th percentile of the E distribution. The 5th percentile value is expected to be exceeded by 95% of the pieces in a grade or class. In this example, for a grade with an assigned E of 13.8 GPa (2.0 × 106 lb/in2), the “minimum E” is 11.3 GPa (1.64 × 106 lb/in2). The corresponding MOR value from the lower confidence line prediction model, approximately a 5th percentile MOR value, is 34.8 MPa (5.04 × 103 lb/in2). This value is then adjusted by a factor (2.1) for assumed 10-year duration of load and safety to obtain Fb. This factor applied to an estimated 5th percentile MOR value of 34.8 MPa (5.04 × 103 lb/in2) yields an Fb of 16.5 MPa (2.40 × 103 lb/in2) for the 2.0E grade; in other words, a 2400f -2.0E MSR grade.
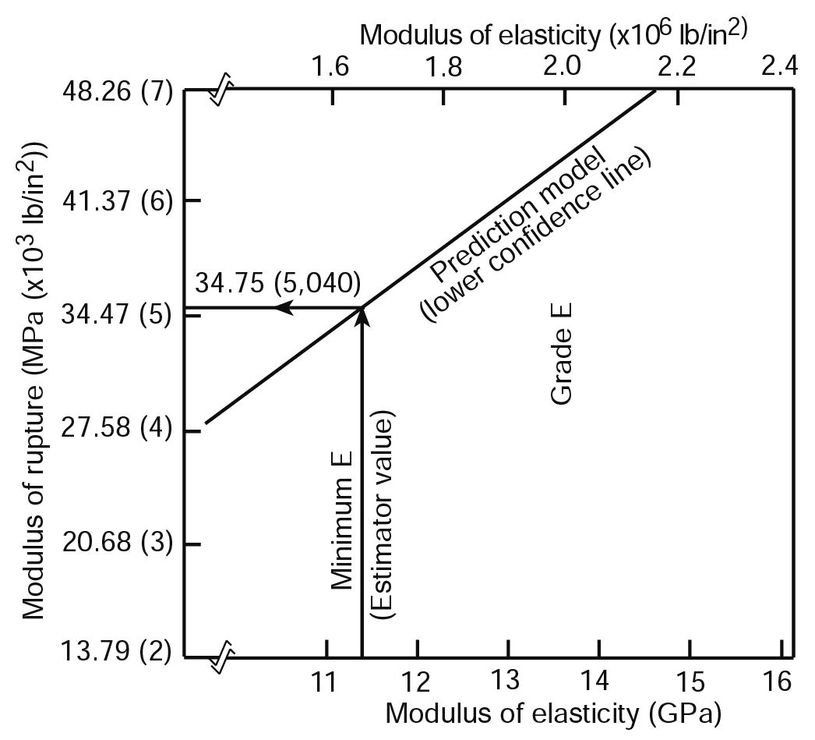
Figure 6–7. Typical assignment of Fb-E values for MSR lumber in United States (solid lines are minimum E for the Fb-E classification and bending strengths predicted by minimum E values).
Design Stresses for Other Properties
Properties in tension and compression are commonly developed from relationships with bending rather than estimated directly by the nondestructive parameter E. In Canada and the United States, the relationships between the 5th percentile 10-year bending stress and those in tension and compression are based upon limited lumber testing for the three properties but supported by years of successful experience in construction with visual stress grades of lumber. For tension, it is assumed that the ratio of design bending stress Fb to design tensile stress Fc is between 0.5 and 0.8, depending on the grade, whereas the relationship between Fb and fiber stress in design compressive stress Fc is assumed to be
Fc = [0.338 (2.1Fb) + 2060.7]/1.9
Strength in shear parallel to the grain and in compression perpendicular to the grain is poorly related to modulus of elasticity. Therefore, in machine stress grading these properties are assumed to be grade-independent and are assigned the same values as those for visual lumber grades, except when predicted from specific gravity on a mill-by-mill basis. It is permissible to assign higher allowable stress for shear parallel to grain and compression perpendicular to grain to specific grades based on additional specific gravity research.
Quality Control
Quality control procedures are necessary to ensure that stresses assigned by a machine-grading system reflect the actual properties of the lumber graded. These procedures must check for correct machine operation. Verification of the relationships between bending and other properties may also be required by the rules-writing agency, particularly for fiber stress in tension Ft.
Daily or even more frequent calibration of machine operation may be necessary. Depending upon machine principle, calibration may involve operating the machine on a calibration bar of known stiffness, comparing grading machine E values to those obtained on the same pieces of lumber by calibrated laboratory test equipment, determining if machine-predicted density matches a calibration sample density, or in some instances, using two or more procedures. Machine operation should be certified for all sizes of lumber being produced. Machine settings may need to be adjusted to produce the same grade material from different widths.
Quality control procedures of the MSR prediction model (E-bending strength relationship) have been adopted in Canada and the United States. Daily, or more frequently, lumber production is representatively sampled and proof-loaded, usually in bending, with supplementary testing in tension. The pieces are proof-loaded to at least twice the design stress (Fb or Ft) for the assigned Fb -E classification. In bending, the pieces are loaded on a random edge with the maximum-edge defect within the maximum moment area (middle one-third span in third-point loading) or as near to that point as possible. In tension, the pieces are tested with a 2.4-m (8-ft) gauge length.
If the number of pieces in the sample failing the proof-test load indicates a high probability that the population from which the pieces came does not meet the minimum grade criteria, a second sampling and proof test are conducted immediately. If the second sample confirms the results of the first sample, the MSR grading system is declared “out of control” and the operation is shut down to isolate and correct the problem. The lumber that was incorrectly labeled is then correctly labeled.
Cumulative machine calibration records are useful for detecting trends or gradual change in machine operation that might coincide with use and wear of machine parts. The proof-test results are also accumulated. Standard statistical quality control procedures (such as control charts) are used to monitor the production process so that it can be modified as needed in response to change in the timber resource, and to make the output fit the assumed model.
Too many failures in one, or even consecutive, samples do not necessarily indicate that the system is out of control. If the prediction line is based on 95% confidence, it can be expected by chance alone that 1 sample in 20 will not meet the proof-load requirements. One or more out-of-control samples may also represent a temporary aberration in material properties (E-strength relationship). In any event, this situation would call for inspection of the cumulative quality control records for trends to determine if machine adjustment might be needed. A “clean” record (a period when the system does not go out of control) rectifies the evaluation of a system thought to be out of control.
Adjustment of Properties for Design Use
The mechanical properties associated with lumber quality are adjusted to give design unit stresses and a modulus of elasticity suitable for engineering uses. First, a lower confidence level is determined for the material, and this value is then adjusted for shrinkage, size, duration of load, and in ASD, an additional factor of safety. These adjustment factors are discussed in the following text (specific adjustments are given in ASTM designations D245 and D1990).
Shrinkage
As described in Chapter 3, lumber shrinks and swells with changes in moisture content. The amount of dimensional change depends on a number of factors, such as species and ring angle. The American Softwood Lumber Standard, PS 20, lists specific shrinkage factors from green to 15% moisture content that were used historically to set green lumber dimensions for most species (2.35% for thickness and 2.80% for width). The standard does not provide a means of adjusting lumber dimensions to any other moisture content. The standard also does not provide specific shrinkage factors for species such as redwood and the cedars, which shrink less than most species. Using the PS 20 recommendations and an assumed green moisture content Mg, we derive equations that can be used with most species to calculate the shrinkage of lumber as a function of percentage of moisture content M. The equation is applicable to lumber of all annual ring orientations. For dimension lumber, the dimensions at different moisture contents can be estimated with the following equation:
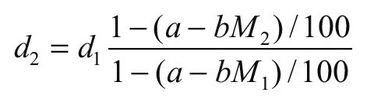
where d1 is dimension (mm, in.) at moisture content M1, d2 dimension (mm, in.) at moisture content M2, M1 moisture content (%) at d1, M2 moisture content (%) at d2, and a and b are variables from Table 6–5.
Size Factor
In general, a size effect causes small members to have a greater unit strength than that of large members. There are two procedures for calculating size-adjustment factors, small clear and In-grade.
Table 6–5. Coefficients for equations to determine dimensional changes with moisture content change in dimension lumber
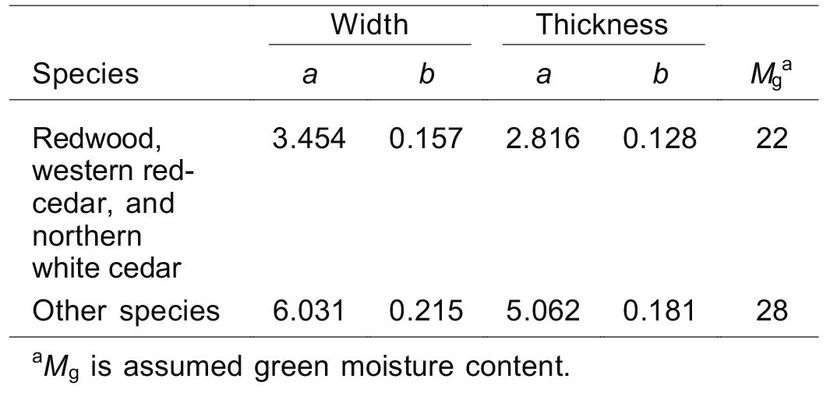
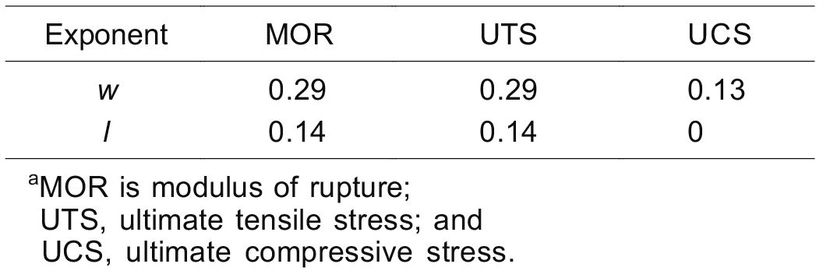
Table 6–6. Exponents for adjustment of dimension lumber mechanical properties with change in sizea
Small Clear Procedure
ASTM D245 provides only a formula for adjusting bending strength. The bending strength for lumber is adjusted to a new depth Fn other than 2 in. (51 mm) using the formula
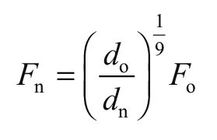
where do is original depth (51 mm, 2 in.), dn new depth, and Fo original bending strength.
This formula is based on an assumed center load and a span-todepth ratio of 14. A depth effect formula for two equal concentrated loads applied symmetrical to the midspan points is given in Chapter 8.
In-Grade Test Procedures
ASTM D1990 provides a formula for adjusting bending, tension, and compression parallel to grain. No size adjustments are made to modulus of elasticity or for thickness effects in bending, tension, and compression. The size adjustments to dimension lumber are based on volume using the formula
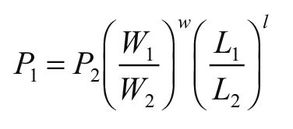
where P1 is property value (MPa, lb/in2) at volume 1, P2 property value (MPa, lb/in2) at volume 2, W1 width (mm, in.) at P1, W2 width (mm, in.) at P2, L1 length (mm, in.) at P1, and L2 length (mm, in.) at P2. Exponents are defined in Table 6–6.
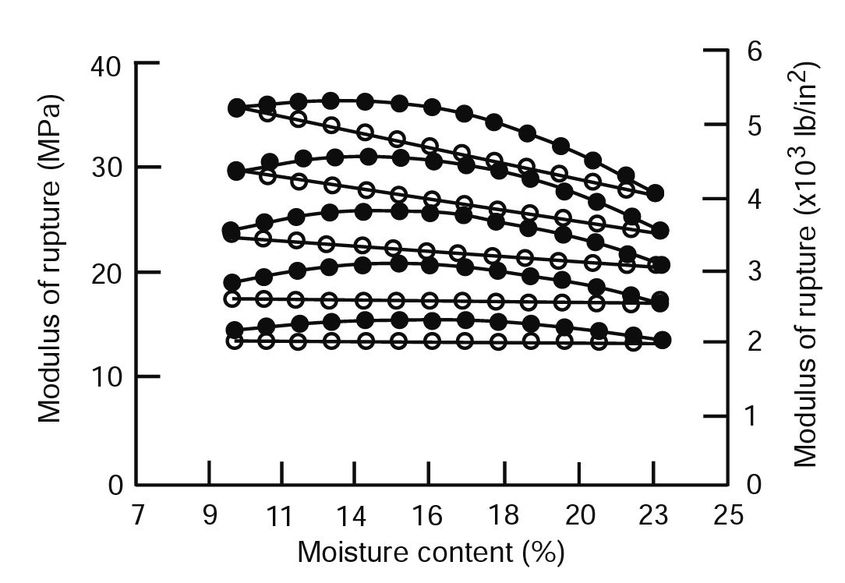
Figure 6–8. Modulus of rupture as a function of moisture content for dimension lumber. Open dots represent the ASTM D1990 model, and solid dots represent the more precise quadratic surface model on which the ASTM D1990 model was based.
Moisture Adjustments
For lumber ≤102 mm (≤4 in.) thick that has been dried, strength properties have been shown to be related quadratically to moisture content. Two relationships for modulus of rupture at any moisture content are shown in Figure 6–8. Both models start with the modulus of elasticity of green lumber. The curves with solid dots represent a precise quadratic model fit to experimental results. In typical practice, adjustments are made to correspond to average moisture contents of 15% and 12% with expected maximum moisture contents of 19% and 15%, respectively, using simplified expressions represented by the open dot curves. Below about 8% moisture content, some properties may decrease with decreasing moisture content values, and care should be exercised in these situations. Equations applicable to adjusting properties to other moisture levels between green and 10% moisture content are as follows:
For MOR, ultimate tensile stress (UTS), and ultimate compressive stress (UCS), the following ASTM D1990 equations apply:

P1=P2
Thus, there is no adjustment for stresses below these levels.

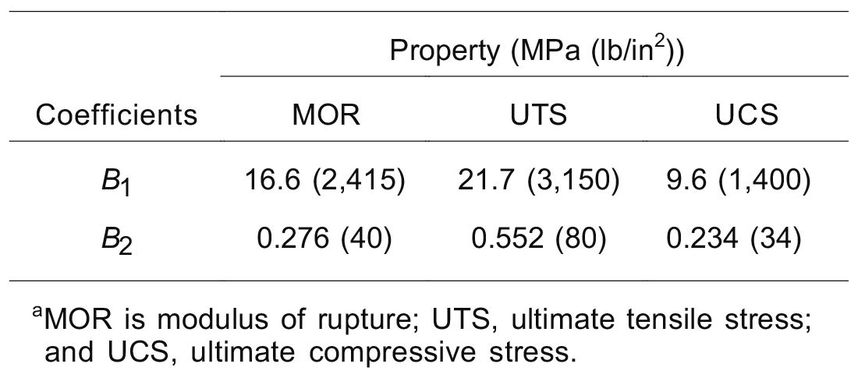
where M1 is moisture content 1 (%), M2 is moisture content 2 (%), and B1, B2 are constants from Table 6–7.
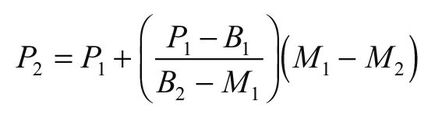
Table 6–7. Coefficients for moisture adjustment of dimension lumber mechanical properties with change in moisture contenta
For E, the following equation applies:
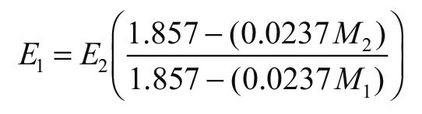
where E1 is property (MPa, lb/in2) at moisture content 1 and E2 is property (MPa, lb/in2) at moisture content 2.
For lumber thicker than 102 mm (4 in.), often no adjustment for moisture content is made because properties are assigned on the basis of wood in the green condition. This lumber is usually put in place without drying, and it is assumed that drying degrade offsets the increase in strength normally associated with loss in moisture.
Duration of Load
Design may be based on either design stresses and a duration of load factor or on ultimate limit state design stresses and a time effects factor. Both the duration of load and time effects factor describe the same phenomenon. In allowable stress design, design stresses are based on an assumed 10-year loading period (called normal loading). If duration of loading, either continuously or cumulatively, is expected to exceed 10 years, design stresses are reduced 10%. If the expected duration of loading is for shorter periods, published design stresses can be increased using Figure 6–9. Ultimate limit-state design stresses are based on a 5-min loading period. If the duration of loading is expected to exceed 5 min, limit-state design stresses are reduced by applying the time effects factor. Intermittent loading causes cumulative effects on strength and should be treated as continuous load of equivalent duration. The effects of cyclic loads of short duration must also be considered in design (see discussion of fatigue in Ch. 4). These duration of load modifications are not applicable to modulus of elasticity.
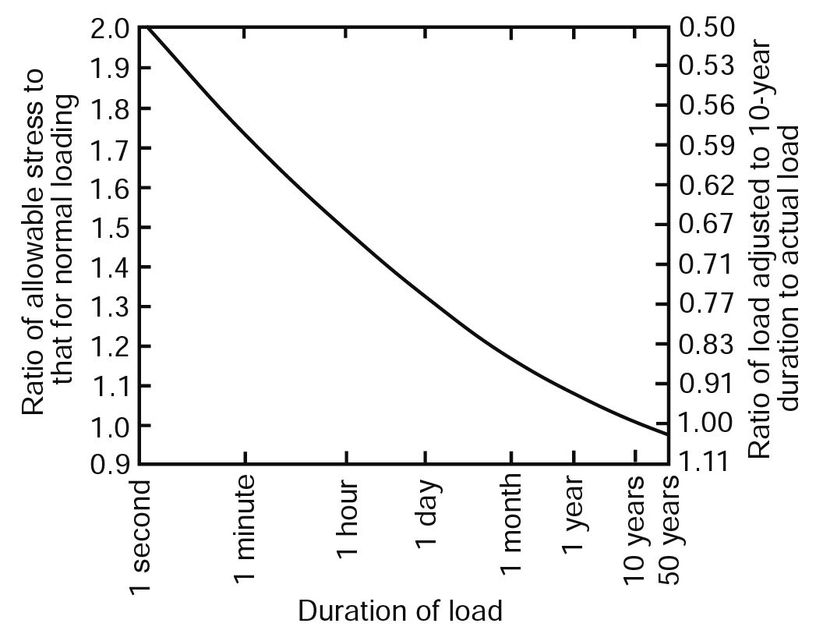
Figure 6–9. Relation of strength to duration of load.
In many design circumstances there are several loads on the structure, some acting simultaneously and each with a different duration. When loads of different time duration are applied, the load duration factor corresponding to the shortest time duration is used. Each increment of time during which the total load is constant should be treated separately, and the most severe condition governs the design. Either the design stress or the total design load (but not both) can be adjusted using Figure 6–9.
For example, suppose a structure is expected to support a load of 4.8 kPa (100 lb/ft2) on and off for a cumulative duration of 1 year. Also, it is expected to support its own dead load of 0.96 kPa (20 lb/ft2) for the anticipated 50-year life of the structure. The adjustments to be made to arrive at an equivalent 10-year design load are listed in Table 6–8.
The more severe design load is 5.36 kPa (112 lb/ft2), and this load and the design stress for lumber would be used to select members of suitable size. In this case, it was convenient to adjust the loads on the structure, although the same result can be obtained by adjusting the design stress.
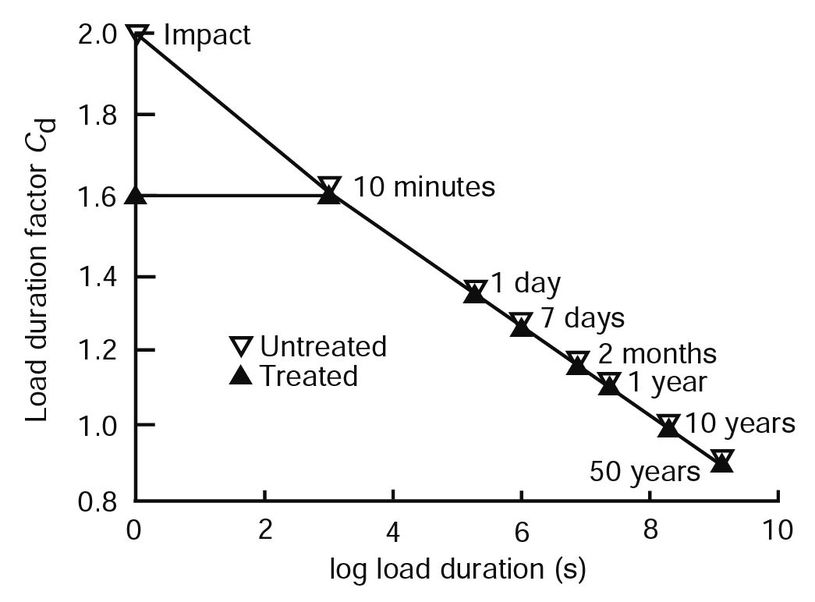
Figure 6–10. Load duration factor for material treated with waterborne preservative.
Treatment Effects
Treatments have been shown to affect the final strength of wood (Ch. 4 for detailed discussion). There is a 5% reduction in E and a 15% reduction in strength properties of incised and treated dimension lumber for both dry- and wet-use conditions in the United States. In Canada, a 10% reduction in E and a 30% reduction in all strength properties from incising is applied to dry-use conditions whereas 5% and 15% reductions are used for wet-use conditions. The wet-use factors are applied in addition to the traditional wet-use service factor. Reductions in energy-related properties are about 1.5 to 2 times those reported for static strength properties. There is no difference in long-term duration of load behavior between treated and untreated material (Fig. 6–10). Current design standards prohibit increases in design stresses beyond the 1.6 factor for short-term duration of load when considering impact-type loading for material treated with waterborne preservative.
Table 6–8. Example of duration of load adjustments
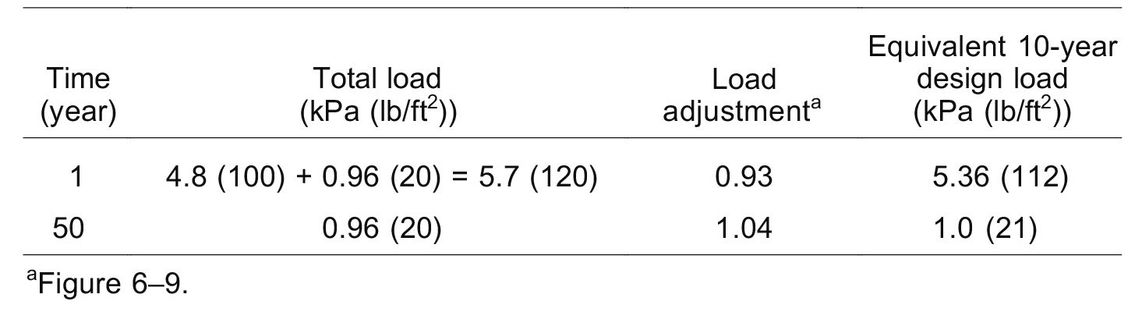
Table 6–9. Property adjustment factors for in-service temperature exposures
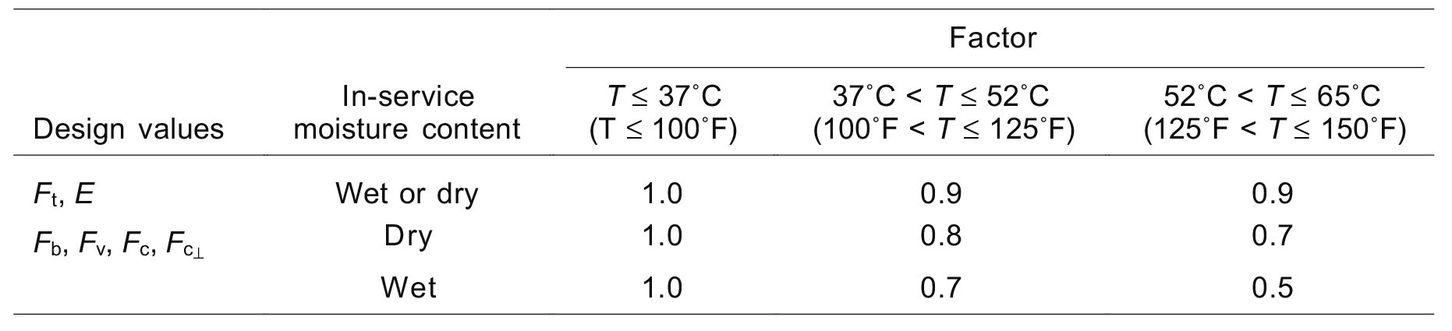
Temperature Effects
As wood is cooled below normal temperatures, its properties increase. When heated, its properties decrease. The magnitude of the change depends upon moisture content. Up to 65°C (150°F), the effect of temperature is assumed by design codes to be reversible. For structural members that will be exposed to temperatures up to 65°C (150°F), design values are multiplied by the factors given in Table 6–9 (AF&PA 1997). Prolonged exposure to heat can lead to a permanent loss in strength (see Ch. 4).
References
AF&PA. 1997. Washington, DC: American Forest & Paper Association.
National design specification for wood construction.
Design values for wood construction—a supplement to the national design specification for wood construction.
AF&PA. 1996. Load and resistance factor design manual for engineered wood construction. Washington, DC: American Forest & Paper Association.
ASTM. 1998. West Conshohocken, PA: American Society for Testing and Materials.
ASTM D198–97. Standard methods of static tests of timbers in structural sizes.
ASTM D245–93. Standard methods for establishing structural grades for visually graded lumber.
ASTM D1990–97. Standard methods for establishing allowable properties for visually-graded dimension lumber from In-grade tests of full-size specimens.
ASTM D2555–96. Standard methods for establishing clear wood strength values.
ASTM D2915–94. Standard method for evaluating properties for stress grades of structural lumber.
ASTM D4761–96. Standard methods for mechanical properties of lumber and wood-base structural materials.
Forest Products Society. 1997. Machine-graded lumber. Madison, WI: Forest Products Society. Wood Design Focus. 8(2): 1–24.
Galligan, W.L.; Green, D.W.; Gromala, D.S.; Haskell, J.H. 1980. Evaluation of lumber properties in the United States and their application to structural research. Forest Products Journal. 30(10): 45–51.
Gerhards, C.C. 1977. Effect of duration and rate of loading on strength of wood and wood based materials. Res. Pap. FPL–RP–283. Madison, WI: U.S. Department of Agriculture, Forest Service, Forest Products Laboratory.
Green, D.W. 1989. Moisture content and the shrinkage of lumber. Res. Pap. FPL–RP–489. Madison, WI: U.S. Department of Agriculture, Forest Service, Forest Products Laboratory.
Green, D.W.; Evans, J.W. 1987. Mechanical properties of visually graded dimension lumber. Vol. 1–Vol. 7. Springfield VA: National Technical Information Service. PB–88–159–371.
Green, D.W.; Kretschmann, D.E. 1992. Properties and grading of Southern Pine timbers. Forest Products Journal. 47(9): 78–85.
Green, D.W.; Shelley, B.E. 1992. Guidelines for assigning allowable properties to visually grade foreign species based on test data from full sized specimens. Germantown, MD: American Lumber Standards Committee.
Green, D.W.; Shelley, B.E. 1993. Guidelines for assigning allowable properties to mechanically graded foreign species. Germantown, MD: American Lumber Standards Committee.
Green, D.W.; Shelley, B.E.; and Vokey, H.P. 1989. In-grade testing of structural lumber. In: Proceedings of workshop sponsored by In-grade Testing Committee and Forest Products Society. Proceedings 47363. Madison, WI: Forest Products Society.
Kretschmann, D.E.; Green D.W. 1996. Modeling moisture content-mechanical property relationships for clear Southern Pine. Wood and Fiber Science. 28(3): 320–337.
U.S. Department of Commerce. 1994. American softwood lumber standard. Prod. Stand. PS20–94. Washington, DC: U.S. Department of Commerce.
Winandy, J.E. 1995. The influence of time-to-failure on the strength of CCA-treated lumber. Forest Products Journal. 45(2): 82–85.