3
THE SIMPLICITY, UNITY, AND COMPLEXITY OF LIFE
As emphasized in the opening chapter, living systems, from the smallest bacteria to the largest cities and ecosystems, are quintessential complex adaptive systems operating over an enormous range of multiple spatial, temporal, energy, and mass scales. In terms of mass alone, the overall scale of life covers more than thirty orders of magnitude (1030) from the molecules that power metabolism and the genetic code up to ecosystems and cities. This range vastly exceeds that of the mass of the Earth relative to that of our entire galaxy, the Milky Way, which covers “only” eighteen orders of magnitude, and is comparable to the mass of an electron relative to that of a mouse.
Over this immense spectrum, life uses essentially the same basic building blocks and processes to create an amazing variety of forms, functions, and dynamical behaviors. This is a profound testament to the power of natural selection and evolutionary dynamics. All of life functions by transforming energy from physical or chemical sources into organic molecules that are metabolized to build, maintain, and reproduce complex, highly organized systems. This is accomplished by the operation of two distinct but closely interacting systems: the genetic code, which stores and processes the information and “instructions” to build and maintain the organism, and the metabolic system, which acquires, transforms, and allocates energy and materials for maintenance, growth, and reproduction. Considerable progress has been made in elucidating both of these systems at levels from molecules to organisms, and later I will discuss how it can be extended to cities and companies. However, understanding how information processing (“genomics”) integrates with the processing of energy and resources (“metabolics”) to sustain life remains a major challenge. Finding the universal principles that underlie the structures, dynamics, and integration of these systems is fundamental to understanding life and to managing biological and socioeconomic systems in such diverse contexts as medicine, agriculture, and the environment.

The extraordinary scale of life from complex molecules and microbes to whales and sequoias in relation to galactic and subatomic scales.
A unified framework for understanding genetics has been developed that can account for phenomena from the replication, transcription, and translation of genes to the evolutionary origin of species. Slower to emerge has been a comparable unified theory of metabolism that links processes by which the energy and material transforming processes that are generated by biochemical reactions within cells are scaled up to sustain life, power biological activities, and set the timescales of vital processes at levels from organisms to ecosystems.
The search for fundamental principles that govern how the complexity of life emerges from its underlying simplicity is one of the grand challenges of twenty-first-century science. Although this has been, and will continue to be, primarily the purview of biologists and chemists, it is becoming an activity where other disciplines, and in particular physics and computer science, are playing an increasingly important role. Understanding more generally the emergence of complexity from simplicity, an essential characteristic of adaptive evolving systems, is one of the founding cornerstones of the new science of complexity.
The field of physics is concerned with fundamental principles and concepts at all levels of organization that are quantifiable and mathematizable (meaning amenable to computation), and can consequently lead to precise predictions that can be tested by experiment and observation. From this perspective, it is natural to ask if there are “universal laws of life” that are mathematizable so that biology could also be formulated as a predictive, quantitative science much like physics. Is it conceivable that there are yet-to-be-discovered “Newton’s Laws of Biology” that would lead, at least in principle, to precise calculations of any biological process so that, for instance, one could accurately predict how long you and I would live?
This seems very unlikely. After all, life is the complex system par excellence, exhibiting many levels of emergent phenomena arising from multiple contingent histories. Nevertheless, it may not be unreasonable to conjecture that the generic coarse-grained behavior of living systems might obey quantifiable universal laws that capture their essential features. This more modest view presumes that at every organizational level average idealized biological systems can be constructed whose general properties are calculable. Thus we ought to be able to calculate the average and maximum life span of human beings even if we’ll never be able to calculate our own. This provides a point of departure or baseline for quantitatively understanding actual biosystems, which can be viewed as variations or perturbations around idealized norms due to local environmental conditions or historical evolutionary divergence. I will elaborate on this perspective in much greater depth below, as it forms the conceptual strategy for attacking most of the questions posed in the opening chapter.
1. FROM QUARKS AND STRINGS TO CELLS AND WHALES
Before launching into some of the big questions that have been raised, I want to make a short detour to describe the serendipitous journey that led me from investigating fundamental questions in physics to fundamental questions in biology and eventually to fundamental questions in the socioeconomic sciences that have a bearing on pivotal questions concerning global sustainability.
In October 1993 the U.S. Congress with the consent of President Bill Clinton officially canceled the largest scientific project ever conceived after having spent almost $3 billion on its construction. This extraordinary project was the mammoth Superconducting Super Collider (SSC), which, together with its detectors, was arguably the greatest engineering challenge ever attempted. The SSC was to be a giant microscope designed to probe distances down to a hundred trillionth of a micron with the aim of revealing the structure and dynamics of the fundamental constituents of matter. It would provide critical evidence for testing predictions derived from our theory of the elementary particles, potentially discover new phenomena, and lay the foundations for what was termed a “Grand Unified Theory” of all of the fundamental forces of nature. This grand vision would not only give us a deep understanding of what everything is made of but would also provide critical insights into the evolution of the universe from the Big Bang. In many ways it represented some of the highest ideals of mankind as the sole creature endowed with sufficient consciousness and intelligence to address the unending challenge of unraveling some of the deepest mysteries of the universe—perhaps even providing the very reason for our existence as the agents through which the universe would know itself.
The scale of the SSC was gigantic: it was to be more than fifty miles in circumference and would accelerate protons up to energies of 20 trillion electron volts at a cost of more than $10 billion. To give a sense of scale, an electron volt is a typical energy of the chemical reactions that form the basis of life. The energy of the protons in the SSC would have been eight times greater than that of the Large Hadron Collider now operating in Geneva that was recently in the limelight for discovering the Higgs particle.
The demise of the SSC was due to many, almost predictable, factors, including inevitable budget issues, the state of the economy, political resentment against Texas where the machine was being built, uninspired leadership, and so on. But one of the major reasons for its collapse was the rise of a climate of negativity toward traditional big science and toward physics in particular.1 This took many forms, but one that many of us were subjected to was the oft-repeated pronouncement I have already quoted earlier that “while the nineteenth and twentieth centuries were the centuries of physics, the twenty-first century will be the century of biology.”
Even the most arrogant hard-nosed physicist had a hard time disagreeing with the sentiment that biology would very likely eclipse physics as the dominant science of the twenty-first century. But what incensed many of us was the implication, oftentimes explicit, that there was no longer any need for further basic research in this kind of fundamental physics because we already knew all that was needed to be known. Sadly, the SSC was a victim of this misguided parochial thinking.
At that time I was overseeing the high energy physics program at the Los Alamos National Laboratory, where we had a significant involvement with one of the two major detectors being constructed at the SSC. For those not familiar with the terminology, “high energy physics” is the name of the subfield of physics concerned with fundamental questions about the elementary particles, their interactions and cosmological implications. I was a theoretical physicist (and still am) whose primary research interests at that time were in this area. My visceral reaction to the provocative statements concerning the diverging trajectories of physics and biology was that, yes, biology will almost certainly be the predominant science of the twenty-first century, but for it to become truly successful, it will need to embrace some of the quantitative, analytic, predictive culture that has made physics so successful. Biology will need to integrate into its traditional reliance on statistical, phenomenological, and qualitative arguments a more theoretical framework based on underlying mathematizable or computational principles. I am embarrassed to say that I knew very little about biology at that time, and this outburst came mostly from arrogance and ignorance.
Nevertheless, I decided to put my money where my mouth was and started to think about how the paradigm and culture of physics might help solve interesting challenges in biology. There have, of course, been several physicists who made extremely successful forays into biology, the most spectacular of which was probably Francis Crick, who with James Watson determined the structure of DNA, which revolutionized our understanding of the genome. Another is the great physicist Erwin Schrödinger, one of the founders of quantum mechanics, whose marvelous little book titled What Is Life?, published in 1944, had a huge influence on biology.2 These examples were inspirational evidence that physics might have something of interest to say to biology, and had stimulated a small but growing stream of physicists crossing the divide, giving rise to the nascent field of biological physics.
I had reached my early fifties at the time of the demise of the SSC, and as I remarked at the opening of the book, I was becoming increasingly conscious of the inevitable encroachment of the aging process and the finiteness of life. Given the poor track record of males in my ancestry, it seemed natural to begin my thinking about biology by learning about aging and mortality. Because these are among the most ubiquitous and fundamental characteristics of life, I naively assumed that almost everything was known about them. But, to my great surprise, I learned that not only was there no accepted general theory of aging and death but the field, such as it was, was relatively small and something of a backwater. Furthermore, few of the questions that would be natural for a physicist to ask, such as those I posed in the opening chapter, seemed to have been addressed. In particular, where does the scale of one hundred years for human life span come from, and what would constitute a quantitative, predictive theory of aging?
Death is an essential feature of life. Indeed, implicitly it is an essential feature of the theory of evolution. A necessary component of the evolutionary process is that individuals eventually die so that their offspring can propagate new combinations of genes that eventually lead to adaptation by natural selection of new traits and new variations leading to the diversity of species. We must all die so that the new can blossom, explore, adapt, and evolve. Steve Jobs put it succinctly3:
No one wants to die. Even people who want to go to heaven don’t want to die to get there. And yet death is the destination we all share. No one has ever escaped it, and that is how it should be, because death is very likely the single best invention of life. It’s life’s change agent. It clears out the old to make way for the new.
Given the critical importance of death and of its precursor, the aging process, I assumed that I would be able to pick up an introductory biology textbook and find an entire chapter devoted to it as part of its discussion of the basic features of life, comparable to discussions of birth, growth, reproduction, metabolism, and so on. I had expected a pedagogical summary of a mechanistic theory of aging that would include a simple calculation showing why we live for about a hundred years, as well as answering all of the questions I posed above. No such luck. Not even a mention of it, nor indeed was there any hint that these were questions of interest. This was quite a surprise, especially because, after birth, death is the most poignant biological event of a person’s life. As a physicist I began to wonder to what extent biology was a “real” science (meaning, of course, that it was like physics!), and how it was going to dominate the twenty-first century if it wasn’t concerned with these sorts of fundamental questions.
This apparent general lack of interest by the biological community in aging and mortality beyond a relatively small number of devoted researchers stimulated me to begin pondering these questions. As it appeared that almost no one was thinking about them in quantitative or analytic terms, there might be a possibility for a physics approach to lead to some small progress. Consequently, during interludes between grappling with quarks, gluons, dark matter, and string theory, I began to think about death.
As I embarked on this new direction, I received unexpected support for my ruminations about biology as a science and its relationship to mathematics from an unlikely source. I discovered that what I had presumed was subversive thinking had been expressed much more articulately and deeply almost one hundred years earlier by the eminent and somewhat eccentric biologist Sir D’Arcy Wentworth Thompson in his classic book On Growth and Form, published in 1917.4 It’s a wonderful book that has remained quietly revered not just in biology but in mathematics, art, and architecture, influencing thinkers and artists from Alan Turing and Julian Huxley to Jackson Pollock. A testament to its continuing popularity is that it still remains in print. The distinguished biologist Sir Peter Medawar, the father of organ transplants, who received the Nobel Prize for his work on graft rejection and acquired immune tolerance, called On Growth and Form “the finest work of literature in all the annals of science that have been recorded in the English tongue.”
Thompson was one of the last “Renaissance men” and is representative of a breed of multi- and transdisciplinary scientist-scholars that barely exists today. Although his primary influence was in biology, he was a highly accomplished classicist and mathematician. He was elected president of the British Classical Association, president of the Royal Geographical Society, and was a good enough mathematician to be made an honorary member of the prestigious Edinburgh Mathematical Society. He came from an intellectual Scottish family and had a name, much like Isambard Kingdom Brunel, that one might associate with a minor fictional character in a Victorian novel.
Thompson begins his book with a quote from the famous German philosopher Immanuel Kant, who had remarked that the chemistry of his day was “eine Wissenschaft, aber nicht Wissenschaft,” which Thompson translates as: chemistry is “a science, but not Science,” implying that “the criterion of true science lay in its relation to mathematics.” Thompson goes on to discuss how there now existed a predictive “mathematical chemistry” based on underlying principles, thereby elevating chemistry from “science” with a small s to “Science” with a capital S. On the other hand, biology had remained qualitative, without mathematical foundations or principles, so that it was still just “a science” with a lowercase s. It would only graduate to becoming “Science” when it incorporated mathematizable physical principles. Despite the extraordinary progress that has been made in the intervening century, I began to discover that the spirit of Thompson’s provocative characterization of biology still has some validity today.
Although he was awarded the prestigious Darwin Medal by the Royal Society in 1946, Thompson was critical of conventional Darwinian evolutionary theory because he felt that biologists overemphasized the role of natural selection and the “survival of the fittest” as the fundamental determinants of the form and structure of living organisms, rather than appreciating the importance of the role of physical laws and their mathematical expression in the evolutionary process. The basic question implicit in his challenge remains unanswered: are there “universal laws of life” that can be mathematized so that biology can be formulated as a predictive quantitative Science? He put it this way:
It behoves us always to remember that in physics it has taken great men to discover simple things. . . . How far even then mathematics will suffice to describe, and physics to explain, the fabric of the body, no man can foresee. It may be that all the laws of energy, and all the properties of matter, and all the chemistry of all the colloids are as powerless to explain the body as they are impotent to comprehend the soul. For my part, I think it is not so. Of how it is that the soul informs the body, physical science teaches me nothing; and that living matter influences and is influenced by mind is a mystery without a clue. Consciousness is not explained to my comprehension by all the nerve-paths and neurons of the physiologist; nor do I ask of physics how goodness shines in one man’s face, and evil betrays itself in another. But of the construction and growth and working of the body, as of all else that is of the earth earthy, physical science is, in my humble opinion, our only teacher and guide.
This pretty much expresses the credo of modern-day “complexity science,” including even the implication that consciousness is an emergent systemic phenomenon and not a consequence of just the sum of all the “nerve-paths and neurons” in the brain. The book is written in a scholarly but eminently readable style with surprisingly little mathematics. There are no pronouncements of great principles other than the belief that the physical laws of nature, written in the language of mathematics, are the major determinant of biological growth, form, and evolution.
Although Thompson’s book did not address aging or death, nor was it particularly helpful or sophisticated technically, its philosophy provided support and inspiration for contemplating and applying ideas and techniques from physics to all sorts of problems in biology. In my own thinking, this led me to perceive our bodies as metaphorical machines that need to be fed, maintained, and repaired but which eventually wear out and “die,” much like cars and washing machines. However, to understand how something ages and dies, whether an animal, an automobile, a company, or a civilization, one first needs to understand what the processes and mechanisms are that are keeping it alive, and then discern how these become degraded with time. This naturally leads to considerations of the energy and resources that are required for sustenance and possible growth, and their allocation to maintenance and repair for combating the production of entropy arising from destructive forces associated with damage, disintegration, wear and tear, and so on. This line of thinking led me to focus initially on the central role of metabolism in keeping us alive before asking why it can’t continue doing so forever.
2. METABOLIC RATE AND NATURAL SELECTION
Metabolism is the fire of life . . . and food, the fuel of life. Neither the neurons in your brain nor the molecules of your genes could function without being supplied by metabolic energy extracted from the food you eat. You could not walk, think, or even sleep without being supplied by metabolic energy. It supplies the power organisms need for maintenance, growth, and reproduction, and for specific processes such as circulation, muscle contraction, and nerve conduction.
Metabolic rate is the fundamental rate of biology, setting the pace of life for almost everything an organism does, from the biochemical reactions within its cells to the time it takes to reach maturity, and from the rate of uptake of carbon dioxide in a forest to the rate at which its litter breaks down. As was discussed in the opening chapter, the basal metabolic rate of the average human being is only about 90 watts, corresponding to a typical incandescent lightbulb and equivalent to the approximately 2,000 food calories you eat every day.
Like all of life, we evolved by a process of natural selection, interacting with and adapting to our fellow creatures, whether bacteria and viruses, ants and beetles, snakes and spiders, cats and dogs, or grass and trees, and everything else in a continuously challenging and evolving environment. We have been coevolving together in a never-ending multidimensional interplay of interaction, conflict, and adaptation. Each organism, each of its organs and subsystems, each cell type and genome, has therefore evolved following its own unique history in its own ever-changing environmental niche. The principle of natural selection, introduced independently by Charles Darwin and Alfred Russell Wallace, is key to the theory of evolution and the origin of species. Natural selection, or the “survival of the fittest,” is the gradual process by which a successful variation in some inheritable trait or characteristic becomes fixed in a population through the differential reproductive success of organisms that have developed this trait by interacting with their environment. As Wallace expressed it, there is sufficiently broad variation that “there is always material for natural selection to act upon in some direction that may be advantageous,” or as put more succinctly by Darwin: “each slight variation, if useful, is preserved.”
Out of this melting pot, each species evolves with its suite of physiological traits and characteristics that reflect its unique path through evolutionary time, resulting in the extraordinary diversity and variation across the spectrum of life from bacteria to whales. So after many millions of years of evolutionary tinkering and adaptation, of playing the game of the survival of the fittest, we human beings have ended up walking on two legs, being around five to six feet high, living for up to one hundred years, having a heart that beats about sixty times a minute, with a systolic blood pressure of about 100 mm Hg, sleeping about eight hours a day, an aorta that’s about eighteen inches long, having about five hundred mitochondria in each of our liver cells, and a metabolic rate of about 90 watts.
Is all of this solely arbitrary and capricious, the result of millions of tiny accidents and fluctuations in our long history that have been frozen in place by the process of natural selection, at least for the time being? Or is there some order here, some hidden pattern reflecting other mechanisms at work?
Indeed there is, and explaining it is the segue back to scaling.
3. SIMPLICITY UNDERLYING COMPLEXITY: KLEIBER’S LAW, SELF-SIMILARITY, AND ECONOMIES OF SCALE
We need about 2,000 food calories a day to live our lives. How much food and energy do other animals need? What about cats and dogs, mice and elephants? Or, for that matter, fish, birds, insects, and trees? These questions were posed at the opening of the book where I emphasized that despite the naive expectation from natural selection, and despite the extraordinary complexity and diversity of life, and despite the fact that metabolism is perhaps the most complex physical-chemical process in the universe, metabolic rate exhibits an extraordinarily systematic regularity across all organisms. As was shown in Figure 1, metabolic rate scales with body size in the simplest possible manner one could imagine when plotted logarithmically against mass, namely, as a straight line indicative of a simple power law scaling relationship.
The scaling of metabolic rate has been known for more than eighty years. Although primitive versions of it were known before the end of the nineteenth century, its modern incarnation is credited to the distinguished physiologist Max Kleiber, who formalized it in a seminal paper published in an obscure Danish journal in 1932.5 I was quite excited when I first came across Kleiber’s law because I had presumed that the randomness and unique historical path dependency implicit in how each species had evolved would have resulted in a huge uncorrelated variability among them. Even among mammals, after all, whales, giraffes, humans, and mice don’t look very much alike except for some very general features, and each operates in a vastly different environment facing very different challenges and opportunities.
In his pioneering work, Kleiber surveyed the metabolic rates for a spectrum of animals ranging from a small dove weighing about 150 grams to a large steer weighing almost 1,000 kilograms. Over the ensuing years his analysis has been extended by many researchers to include the entire spectrum of mammals ranging from the smallest, the shrew, to the largest, the blue whale, thereby covering more than eight orders of magnitude in mass. Remarkably, and of equal importance, the same scaling has been shown to be valid across all multicellular taxonomic groups including fish, birds, insects, crustacea, and plants, and even to extend down to bacteria and other unicellular organisms.6 Overall, it encompasses an astonishing twenty-seven orders of magnitude, perhaps the most persistent and systematic scaling law in the universe.
Because the range of animals in Figure 1 spans well over five orders of magnitude (a factor of more than 100,000), from a little mouse weighing only 20 grams (0.02 kg) to a huge elephant weighing almost 10,000 kilograms, we are forced to plot the data logarithmically, meaning that the scales on both axes increase by successive factors of ten. For instance, mass increases along the horizontal axis from 0.001 to 0.01 to 0.1 to 10 to 100 kilograms, and so on, rather than linearly from 1 to 2 to 3 to 4 kilograms, et cetera. Had we tried to plot this on a standard-size piece of paper using a conventional linear scale, all of the data points except the elephant would pile up in the bottom left-hand corner of the graph because even the next lightest animals after the elephant, the bull and the horse, are more than ten times lighter. To be able to distinguish all of them with any reasonable resolution would require a ridiculously large piece of paper more than a kilometer wide. And to resolve the eight orders of magnitude between the shrew and the blue whale it would have to be more than 100 kilometers wide.
So as we saw when discussing the Richter scale for earthquakes in the previous chapter, there are very practical reasons for using logarithmic coordinates for representing data such as this which span many orders of magnitude. But there are also deep conceptual reasons for doing so related to the idea that the structures and dynamics being investigated have self-similar properties, which are represented mathematically by simple power laws, as I will now explain.
We’ve seen that a straight line on a logarithmic plot represents a power law whose exponent is its slope (⅔ in the case of the scaling of strength, shown in Figure 7). In Figure 1 you can readily see that for every four orders of magnitude increase in mass (along the horizontal axis), metabolic rate increases by only three orders of magnitude (along the vertical axis), so the slope of the straight line is ¾, the famous exponent in Kleiber’s law. To illustrate more specifically what this implies, consider the example of a cat weighing 3 kilograms that is 100 times heavier than a mouse weighing 30 grams. Kleiber’s law can straightforwardly be used to calculate their metabolic rates, leading to around 32 watts for the cat and about 1 watt for the mouse. Thus, even though the cat is 100 times heavier than the mouse, its metabolic rate is only about 32 times greater, an explicit example of economy of scale.
If we now consider a cow that is 100 times heavier than the cat, then Kleiber’s law predicts that its metabolic rate is likewise 32 times greater than the cat’s, and if we extend this to a whale that is 100 times heavier than the cow, its metabolic rate would be 32 times greater than the cow’s. This repetitive behavior, the recurrence in this case of the same factor 32 as we move up in mass by the same repetitive factor of 100, is an example of the general self-similar feature of power laws. More generally: if the mass is increased by any arbitrary factor at any scale (100, in the example), then the metabolic rate increases by the same factor (32, in the example) no matter what the value of the initial mass is, that is, whether it’s that of a mouse, cat, cow, or whale. This remarkably systematic repetitive behavior is called scale invariance or self-similarity and is a property inherent to power laws. It is closely related to the concept of a fractal, which will be discussed in detail in the following chapter. To varying degrees, fractality, scale invariance, and self-similarity are ubiquitous across nature from galaxies and clouds to your cells, your brain, the Internet, companies, and cities.
We just saw that a cat that is 100 times heavier than a mouse requires only about 32 times as much energy to sustain it even though it has approximately 100 times as many cells—a classic example of an economy of scale resulting from the essential nonlinear nature of Kleiber’s law. Naive linear reasoning would have predicted the cat’s metabolic rate to have been 100 times larger, rather than only 32 times. Similarly, if the size of an animal is doubled it doesn’t need 100 percent more energy to sustain it; it needs only about 75 percent more—thereby saving approximately 25 percent with each doubling. Thus, in a systematically predictable and quantitative way, the larger the organism the less energy has to be produced per cell per second to sustain a gram of tissue. Your cells work less hard than your dog’s, but your horse’s work even less hard. Elephants are roughly 10,000 times heavier than rats but their metabolic rates are only 1,000 times larger, despite having roughly 10,000 times as many cells to support. Thus, an elephant’s cells operate at about a tenth the rate of a rat’s, resulting in a corresponding decrease in the rates of cellular damage, and consequently to a greater longevity for the elephant, as will be explained in greater detail in chapter 4. This is an example of how the systematic economy of scale has profound consequences that reverberate across life from birth and growth to death.
4. UNIVERSALITY AND THE MAGIC NUMBER FOUR THAT CONTROLS LIFE
The systematic regularity of Kleiber’s law is pretty amazing, but equally surprising is that similar systematic scaling laws hold for almost any physiological trait or life-history event across the entire range of life from cells to whales to ecosystems. In addition to metabolic rates, these include quantities such as growth rates, genome lengths, lengths of aortas, tree heights, the amount of cerebral gray matter in the brain, evolutionary rates, and life spans; a sampling of these is illustrated in Figures 9-12. There are probably well over fifty such scaling laws and—another big surprise—their corresponding exponents (the analog of the ¾ in Kleiber’s law) are invariably very close to simple multiples of ¼.
For example, the exponent for growth rates is very close to ¾, for lengths of aortas and genomes it’s ¼, for heights of trees ¼, for cross-sectional areas of both aortas and tree trunks ¾, for brain sizes ¾, for cerebral white and gray matter 5⁄4, for heart rates minus ¼, for mitochondrial densities in cells minus ¼, for rates of evolution minus ¼, for diffusion rates across membranes minus ¼, for life spans ¼ . . . and many, many more. The “minus” here simply indicates that the corresponding quantity decreases with size rather than increases, so, for instance, heart rates decrease with increasing body size following the ¼ power law, as shown in Figure 10. I can’t resist drawing your attention to the intriguing fact that aortas and tree trunks scale in the same way.
Particularly fascinating is the emergence of the number four in the guise of the ¼ powers that appear in all of these exponents. It occurs ubiquitously across the entire panoply of life and seems to play a special, fundamental role in determining many of the measurable characteristics of organisms regardless of their evolved design. Viewed through the lens of scaling, a remarkably general universal pattern emerges, strongly suggesting that evolution has been constrained by other general physical principles beyond natural selection.
These systematic scaling relationships are highly counterintuitive. They show that almost all the physiological characteristics and life-history events of any organism are primarily determined simply by its size. For example, the pace of biological life decreases systematically and predictably with increasing size: large mammals live longer, take longer to mature, have slower heart rates, and have cells that work less hard than those of small mammals, all to the same predictable degree. Doubling the mass of a mammal increases all of its timescales such as its life span and time to maturity by about 25 percent on average and, concomitantly, decreases all rates, such as its heart rate, by the same amount.
Whales live in the ocean, elephants have trunks, giraffes have long necks, we walk on two legs, and dormice scurry around, yet despite these obvious differences, we are all, to a large degree, nonlinearly scaled versions of one another. If you tell me the size of a mammal, I can use the scaling laws to tell you almost everything about the average values of its measurable characteristics: how much food it needs to eat each day, what its heart rate is, how long it will take to mature, the length and radius of its aorta, its life span, how many offspring it will have, and so on. Given the extraordinary complexity and diversity of life, this is pretty amazing.


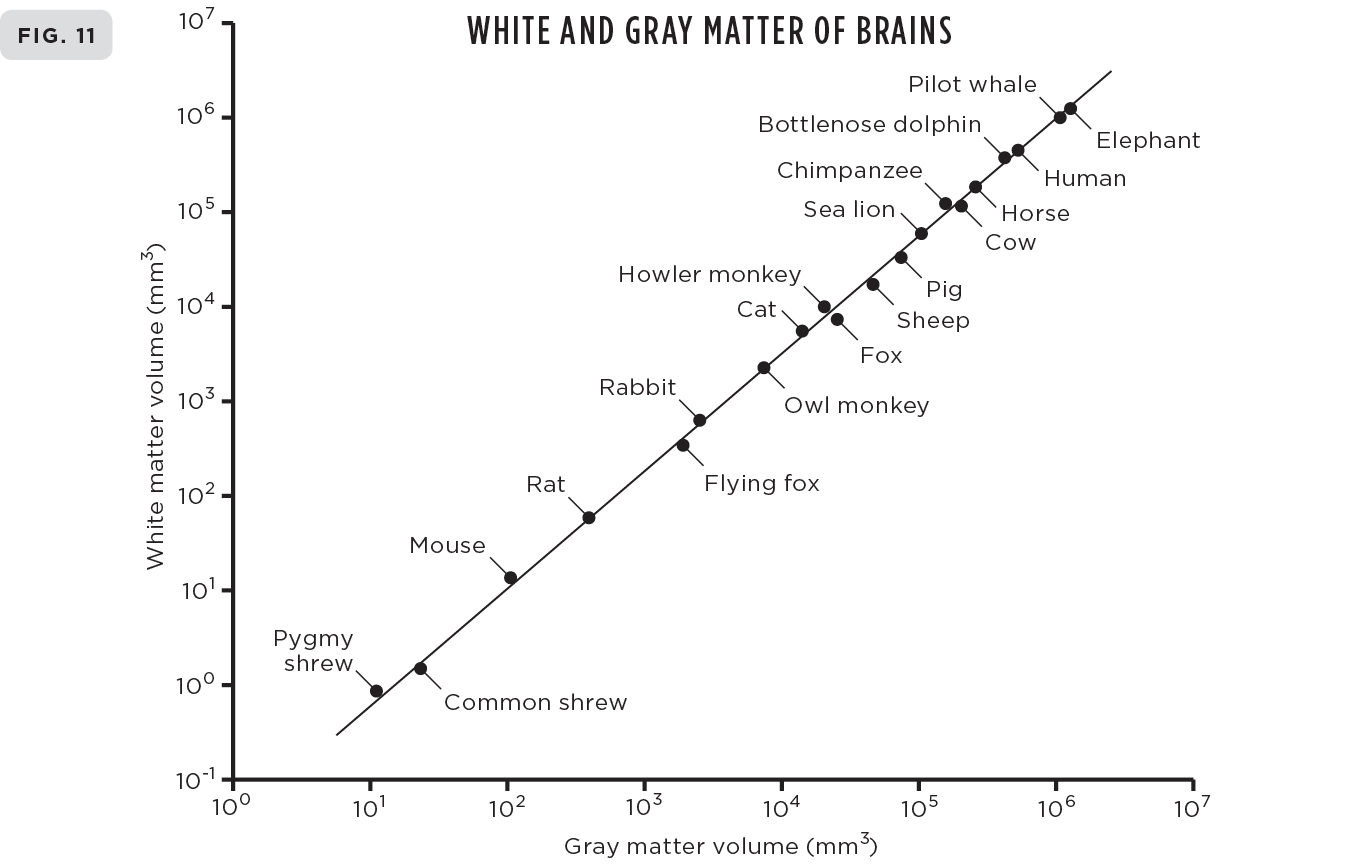
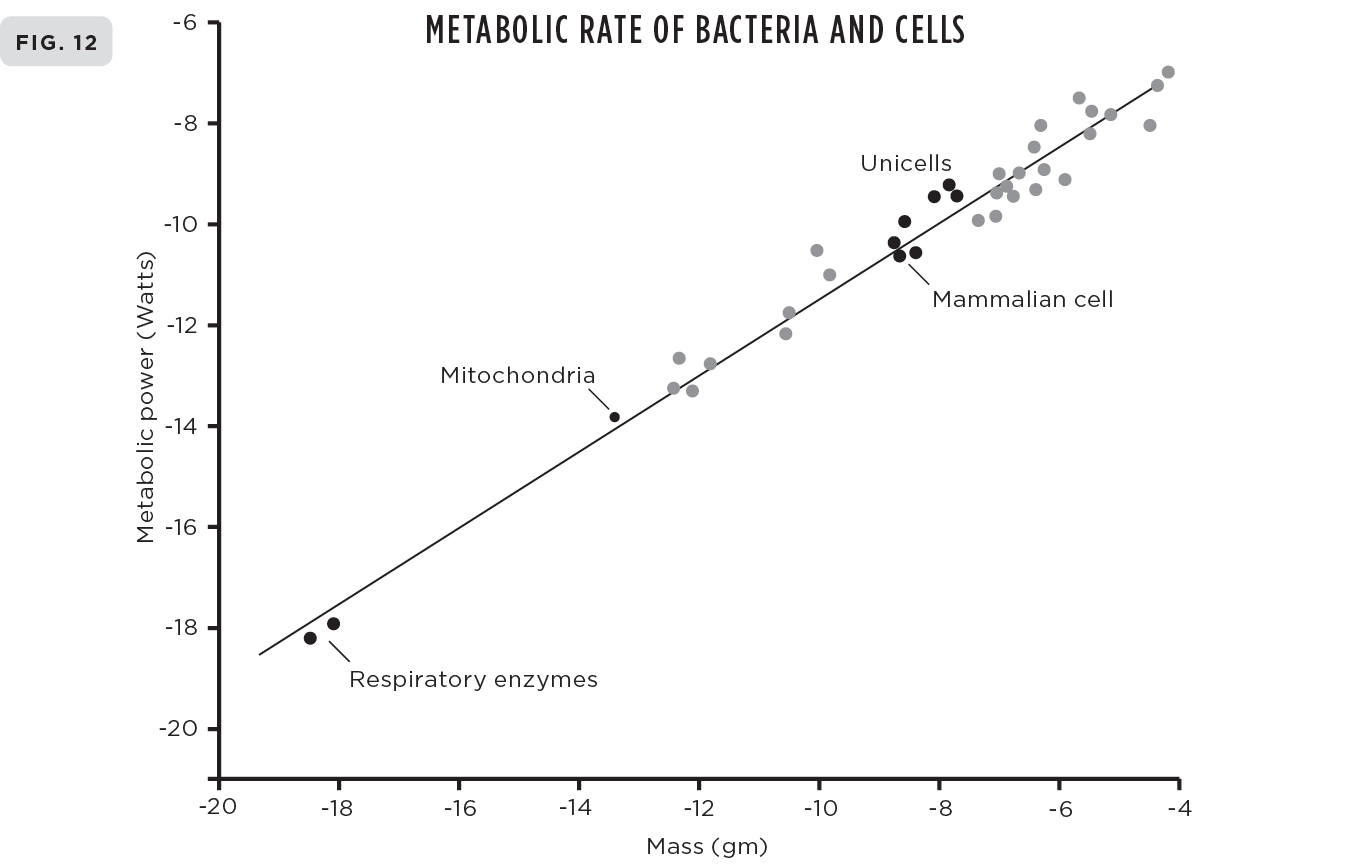
Here and here: A small sampling of the many examples of scaling showing their remarkable universality and diversity. (9) Biomass production of both individual insects and insect colonies showing how they both scale with mass with an exponent of ¾, just like metabolic rate of animals shown in Figure 1. (10) Heart rates of mammals scale with mass with an exponent of -¼. (11) The volume of white matter in mammalian brains scales with the volume of gray matter with an exponent of 5⁄4. (12) The scaling of metabolic rate of single cells and bacteria with their mass following the classic ¾ exponent of Kleiber’s law for multicellular animals.
I was very excited when I realized that my quest to learn about some of the mysteries of death had unexpectedly led me to learn about some of the more surprising and intriguing mysteries of life. For here was an area of biology that was explicitly quantitative, expressible in mathematical terms, and, at the same time, manifested a spirit of “universality” beloved of physicists. In addition to the surprise that these “universal” laws seemed to be at odds with a naive interpretation of natural selection, it was equally surprising that they seemed not to have been fully appreciated by most biologists, even though many were aware of them. Furthermore, there was no general explanation for their origin. Here was something ripe for a physicist to get his teeth into.
Actually, it isn’t quite true that scaling laws had been entirely unappreciated by biologists. Scaling laws had certainly maintained an ongoing presence in ecology and, until the advent of the molecular and genomics revolution in biology in the 1950s, had attracted the attention of many eminent biologists, including Julian Huxley, J. B. S. Haldane, and D’Arcy Thompson.7 Indeed, Huxley coined the term allometric to describe how physiological and morphological characteristics of organisms scale with body size, though his focus was primarily on how that occurred during growth. Allometric was introduced as a generalization of the Galilean concept of isometric scaling, discussed in the previous chapter, where body shape and geometry do not change as size increases, so all lengths associated with an organism increase in the same proportion; iso is Greek for “the same,” and metric is derived from metrikos, meaning “measure.” Allometric, on the other hand, is derived from allo, meaning “different,” and refers to the typically more general situation where shapes and morphology change as body size increases and different dimensions scale differently. For example, the radii and lengths of tree trunks, or for that matter the limbs of animals, scale differently from one another as size increases: radii scale as the ⅜ power of mass, whereas lengths scale more slowly with ¼ power (that is, as the 2⁄8 power). Consequently, trunks and limbs become more thickset and stockier as the size of a tree or animal increases; just think of an elephant’s legs relative to those of a mouse. This is a generalization of Galileo’s original argument regarding the scaling of strength. Had it been isometric, then radii and lengths would have scaled in the same way and the shape of trunks and limbs would have remained unchanged, making the support of the animal or tree unstable as it increases in size. An elephant whose legs have the same spindly shape as a mouse would collapse under its own weight.
Huxley’s term allometric was extended from its more restrictive geometric, morphological, and ontogenetic origins to describe the kinds of scaling laws that I discussed above, which include more dynamical phenomena such as how flows of energy and resources scale with body size, with metabolic rate being the prime example. All of these are now commonly referred to as allometric scaling laws.
Julian Huxley, himself a very distinguished biologist, was the grandson of the famous Thomas Huxley, the biologist who championed Charles Darwin and the theory of evolution by natural selection, and the brother of the novelist and futurist Aldous Huxley. In addition to the word allometric, Julian Huxley brought several other new words and concepts into biology, including replacing the much-maligned term race with the phrase ethnic group.
In the 1980s several excellent books were written by mainstream biologists summarizing the extensive literature on allometry.8 Data across all scales and all forms of life were compiled and analyzed and it was unanimously concluded that quarter-power scaling was a pervasive feature of biology. However, there was surprisingly little theoretical or conceptual discussion, and no general explanation was given for why there should be such systematic laws, where they came from, or how they related to Darwinian natural selection.
As a physicist, it seemed to me that these “universal” quarter-power scaling laws were telling us something fundamental about the dynamics, structure, and organization of life. Their existence strongly suggested that generic underlying dynamical processes that transcend individual species were at work constraining evolution. This therefore opened a possible window onto underlying emergent laws of biology and led to the conjecture that the generic coarse-grained behavior of living systems obeys quantifiable laws that capture their essential features.
It would seem impossible, almost diabolical, that these scaling laws could be just a coincidence, each an independent phenomenon, a “special” case reflecting its own unique dynamics and organization, a wicked series of accidents of evolutionary dynamics, so that the scaling of heart rates is unrelated to the scaling of metabolic rates and the heights of trees. Of course, every individual organism, biological species, and ecological assemblage is unique, reflecting differences in genetic makeup, ontogenetic pathways, environmental conditions, and evolutionary history. So in the absence of any additional physical constraints, one might have expected that different organisms, or at least each group of related organisms inhabiting similar environments, might exhibit different size-related patterns of variation in structure and function. The fact that they don’t—that the data almost always closely approximate a simple power law across a broad range of size and diversity—raises some very challenging questions. The fact that the exponents of these power laws are nearly always simple multiples of ¼ poses an even greater challenge.
The question as to what the underlying mechanism for their origin could be seemed a wonderful conundrum to think about, especially given my morbid interest in aging and death and the fact that even life spans seem to scale allometrically with ¼ power (albeit with large variance).
5. ENERGY, EMERGENT LAWS, AND THE HIERARCHY OF LIFE
As I have emphasized, no aspect of life can function without energy. Just as every muscle contraction or any activity requires metabolic energy, so does every random thought in your brain, every twitch of your body even while you sleep, and even the replication of your DNA in your cells. At the most fundamental biochemical level metabolic energy is created in semiautonomous molecular units within cells called respiratory complexes. The critical molecule that plays the central role in metabolism goes by the slightly forbidding name of adenosine triphosphate, usually referred to as ATP. The detailed biochemistry of metabolism is extremely complicated but in essence it involves the breaking down of ATP, which is relatively unstable in the cellular environment, from adenosine triphosphate (with three phosphates) into ADP, adenosine diphosphate (with just two phosphates), thereby releasing the energy stored in the binding of the additional phosphate. The energy derived from breaking this phosphate bond is the source of your metabolic energy and therefore what is keeping you alive. The reverse process converts ADP back into ATP using energy from food via oxidative respiration in mammals such as ourselves (that’s why we have to breathe in oxygen), or via photosynthesis in plants. The cycle of releasing energy from the breakup of ATP into ADP and its recycling back from ADP to store energy in ATP forms a continuous loop process much like the charging and recharging of a battery. A cartoon of this process is shown here. Unfortunately it doesn’t do justice to the beauty and elegance of this extraordinary mechanism that fuels most of life.
Given its central role, it’s not surprising that the flux of ATP is often referred to as the currency of metabolic energy for almost all of life. At any one time our bodies contain only about half a pound (about 250 g) of ATP, but here’s something truly extraordinary that you should know about yourself: every day you typically make about 2 × 1026 ATP molecules—that’s two hundred trillion trillion molecules—corresponding to a mass of about 80 kilograms (about 175 lbs.). In other words, each day you produce and recycle the equivalent of your own body weight of ATP! Taken together, all of these ATPs add up to meet our total metabolic needs at the rate of the approximately 90 watts we require to stay alive and power our bodies.
These little energy generators, the respiratory complexes, are situated on crinkly membranes inside mitochondria, which are potato-shaped objects floating around inside cells. Each mitochondrion contains about five hundred to one thousand of these respiratory complexes . . . and there about five hundred to one thousand of these mitochondria inside each of your cells, depending on the cell type and its energy needs. Because muscles require greater access to energy, their cells are densely packed with mitochondria, whereas fat cells have many fewer. So on average each cell in your body may have up to a million of these little engines distributed among its mitochondria working away night and day, collectively manufacturing the astronomical number of ATPs needed to keep you viable, healthy, and strong. The rate at which the total number of these ATPs is produced is a measure of your metabolic rate.
Your body is composed of about a hundred trillion (1014) cells. Even though they represent a broad range of diverse functionalities from neuronal and muscular to protective (skin) and storage (fat), they all share the same basic features. They all process energy in a similar way via the hierarchy of respiratory complexes and mitochondria. Which raises a huge challenge: the five hundred or so respiratory complexes inside your mitochondria cannot behave as independent entities but have to act collectively in an integrated coherent fashion in order to ensure that mitochondria function efficiently and deliver energy in an appropriately ordered fashion to cells. Similarly, the five hundred or so mitochondria inside each of your cells do not act independently but, like respiratory complexes, have to interact in an integrated coherent fashion to ensure that the 1014 cells that constitute your body are supplied with the energy they need to function efficiently and appropriately. Furthermore, these hundred trillion cells have to be organized into a multitude of subsystems such as your various organs, whose energy needs vary significantly depending on demand and function, thereby ensuring that you can do all of the various activities that constitute living, from thinking and dancing to having sex and repairing your DNA. And this entire interconnected multilevel dynamic structure has to be sufficiently robust and resilient to continue functioning for up to one hundred years!
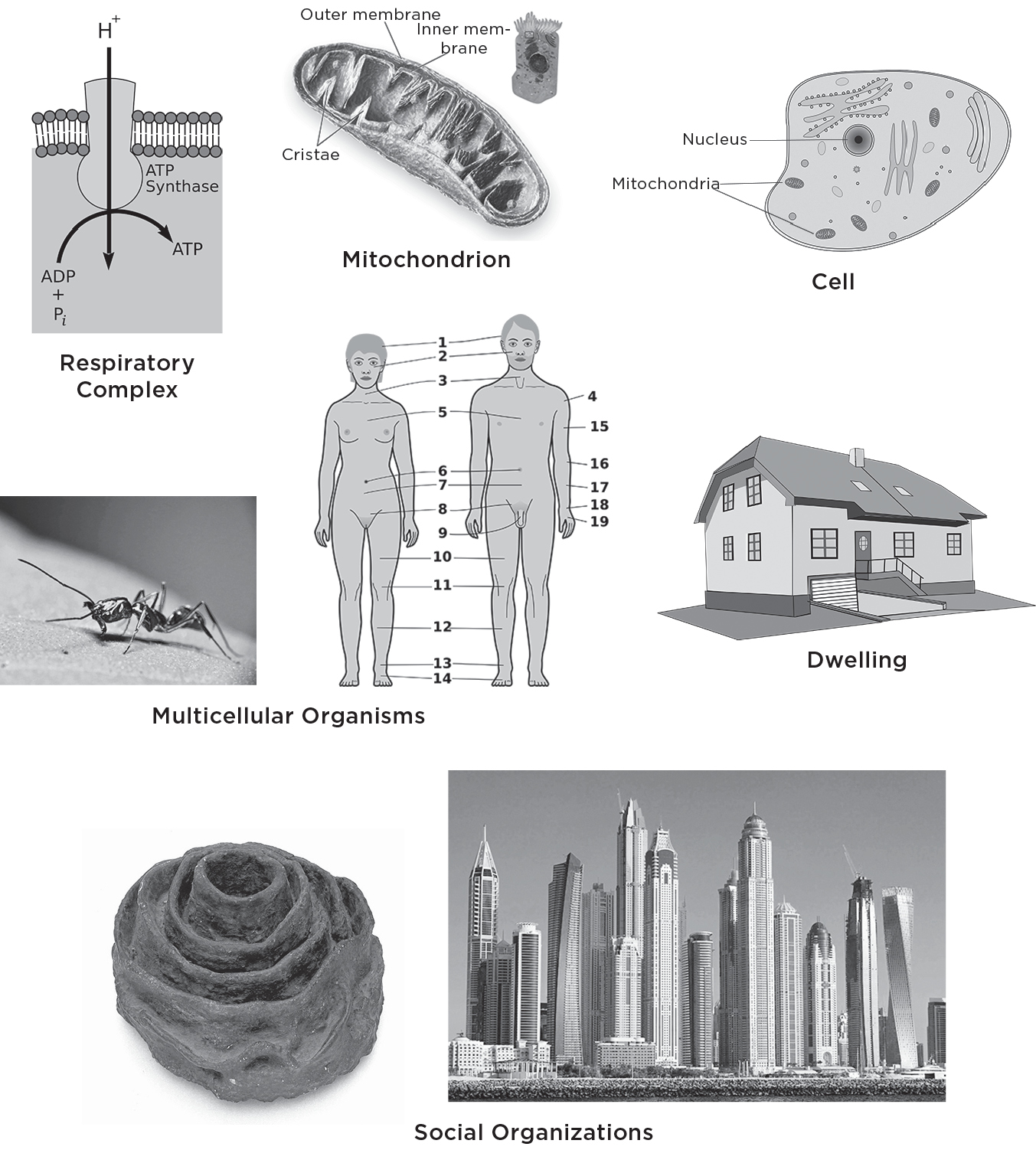
The energy flow hierarchy of life beginning with respiratory complexes (top left) that produce our energy up through mitochondria and cells (middle and top right) to multicellular organisms and community structures. From this perspective, cities are ultimately powered and sustained by the ATP produced in our respiratory complexes. Although each of these looks quite different with very different engineered structures, energy is distributed through each of them by space-filling hierarchical networks having similar properties.
It’s natural to generalize this hierarchy of life beyond individual organisms and extend it to community structures. Earlier I talked about how ants collectively cooperate to create fascinating social communities that build remarkable structures by following emergent rules arising from their integrated interactions. Many other organisms, such as bees and plants, form similar integrated communities that take on a collective identity.
The most extreme and astonishing version of this is us. In a very short period of time we have evolved from living in small, somewhat primitive bands of relatively few individuals to dominating the planet with our mammoth cities and social structures encompassing many millions of individuals. Just as organisms are constrained by the integration of the emergent laws operating at the cellular, mitochondrion, and respiratory complex levels, so cities have emerged from, and are constrained by, the underlying emergent dynamics of social interactions. Such laws are not “accidents” but the result of evolutionary processes acting across multiple integrated levels of structure.
This hugely multifaceted, multidimensional process that constitutes life is manifested and replicated in myriad forms across an enormous scale ranging over more than twenty orders of magnitude in mass. A huge number of dynamical agents span and interconnect the vast hierarchy ranging from respiratory complexes and mitochondria to cells and multicellular organisms and up to community structures. The fact that this has persisted and remained so robust, resilient, and sustainable for more than a billion years suggests that effective laws that govern their behavior must have emerged at all scales. Revealing, articulating, and understanding these emergent laws that transcend all of life is the great challenge.
It is within this context that we should view allometric scaling laws: their systematic regularity and universality provides a window onto these emergent laws and underlying principles. As external environments change, all of these various systems must be scalable in order to meet the continuing challenges of adaptability, evolvability, and growth. The same generic underlying dynamical and organizational principles must operate across multiple spatial and temporal scales. The scalability of living systems underlies their extraordinary resilience and sustainability both at the individual level and for life itself.
6. NETWORKS AND THE ORIGINS OF QUARTER-POWER ALLOMETRIC SCALING
As I began to ponder what the origins of these surprising scaling laws might be, it became clear that whatever was at play had to be independent of the evolved design of any specific type of organism, because the same laws are manifested by mammals, birds, plants, fish, crustacea, cells, and so on. All of these organisms ranging from the smallest, simplest bacterium to the largest plants and animals depend for their maintenance and reproduction on the close integration of numerous subunits—molecules, organelles, and cells—and these microscopic components need to be serviced in a relatively “democratic” and efficient fashion in order to supply metabolic substrates, remove waste products, and regulate activity.
Natural selection has solved this challenge in perhaps the simplest possible way by evolving hierarchical branching networks that distribute energy and materials between macroscopic reservoirs and microscopic sites. Functionally, biological systems are ultimately constrained by the rates at which energy, metabolites, and information can be supplied through these networks. Examples include animal circulatory, respiratory, renal, and neural systems, plant vascular systems, intracellular networks, and the systems that supply food, water, power, and information to human societies. In fact, when you think about it, you realize that underneath your smooth skin you are effectively an integrated series of such networks, each busily transporting metabolic energy, materials, and information across all scales. Some of these are below.

Examples of biological networks, counterclockwise from the top left-hand corner: the circulatory system of the brain; microtubial and mitochondrial networks inside cells; the white and gray matter of the brain; a parasite that lives inside elephants; a tree; and our cardiovascular system.
Because life is sustained at all scales by such hierarchical networks, it was natural to conjecture that the key to the origin of quarter-power allometric scaling laws, and consequently to the generic coarse-grained behavior of biological systems, lay in the universal physical and mathematical properties of these networks. In other words, despite the great diversity in their evolved structure—some are constructed of tubes like the plumbing in your house, some are bundles of fibers like electrical cables, and some are just diffusive pathways—they are all presumed to be constrained by the same physical and mathematical principles.
7. PHYSICS MEETS BIOLOGY: ON THE NATURE OF THEORIES, MODELS, AND EXPLANATIONS
As I was struggling to develop the network-based theory for the origin of quarter-power scaling, a wonderful synchronicity occurred: I was serendipitously introduced to James Brown and his then student Brian Enquist. They, too, had been thinking about this problem and had also been speculating that network transportation was a key ingredient. Jim is a distinguished ecologist (he was president of the Ecological Society of America when we met) and is well known, among many other things, for his seminal role in inventing an increasingly important subfield of ecology called macroecology.9 As its name suggests, this takes a large-scale, top-down systemic approach to understanding ecosystems, having much in common with the philosophy inherent in complexity science, including an appreciation of using a coarse-grained description of the system. Macroecology has whimsically been referred to as “seeing the forest for the trees.” As we become more concerned about global environmental issues and the urgent need for a deeper understanding of their origins, dynamics, and mitigation, Jim’s big-picture vision, articulated in the ideas of macroecology, is becoming increasingly important and appreciated.
When we first met, Jim had only recently moved to the University of New Mexico (UNM), where he is a Distinguished Regents Professor. He had concomitantly become associated with the Santa Fe Institute (SFI), and it was through SFI that the connection was made. Thus began “a beautiful relationship” with Jim, SFI, and Brian and, by extension, with the ensuing cadre of wonderful postdocs and students, as well as other senior researchers who worked with us. Over the ensuing years, the collaboration between Jim, Brian, and me, begun in 1995, was enormously productive, extraordinarily exciting, and tremendous fun. It certainly changed my life, and I venture to say that it did likewise for Brian and Jim, and possibly even for some of the others. But like all excellent, fulfilling, and meaningful relationships, it has also occasionally been frustrating and challenging.
Jim, Brian, and I met every Friday beginning around nine-thirty in the morning and finishing in mid-afternoon by around three with only short breaks for necessities (neither Jim nor I eat lunch). This was a huge commitment, as both of us ran sizable groups elsewhere—Jim had a large ecology group at UNM and I was still running high energy physics at Los Alamos. Jim and Brian very generously drove up most weeks from Albuquerque to Santa Fe, which is about an hour’s drive, whereas I did the reverse trip only every few months or so. Once the ice was broken and some of the cultural and language barriers that inevitably arise between fields were crossed, we created a refreshingly open atmosphere where all questions and comments, no matter how “elementary,” speculative, or “stupid,” were encouraged, welcomed, and treated with respect. There were lots of arguments, speculations, and explanations, struggles with big questions and small details, lots of blind alleys and an occasional aha moment, all against a backdrop of a board covered with equations and hand-drawn graphs and illustrations. Jim and Brian patiently acted as my biology tutors, exposing me to the conceptual world of natural selection, evolution and adaptation, fitness, physiology, and anatomy, all of which were embarrassingly foreign to me. Like many physicists, I was horrified to learn that there were serious scientists who put Darwin on a pedestal above Newton and Einstein. Given the primacy of mathematics and quantitative analysis in my own thinking, I could hardly believe it. However, since I became seriously engaged with biology my appreciation for Darwin’s monumental achievements has grown enormously, though I must admit that it’s still difficult for me to see how anyone could rank him above the even more monumental achievements of Newton and Einstein.
For my part, I tried to reduce complicated nonlinear mathematical equations and technical physics arguments to relatively simple, intuitive calculations and explanations. Regardless of the outcome, the entire process was a wonderful and fulfilling experience. I particularly enjoyed being reminded of the primal excitement of why I loved being a scientist: the challenge of learning and developing concepts, figuring out what the important questions were, and occasionally being able to suggest insights and answers. In high energy physics, where we struggle to unravel the basic laws of nature at the most microscopic level, we mostly know what the questions are and most of one’s effort goes into trying to be clever enough to carry out the highly technical calculations. In biology I found it to be mostly the other way around: months were spent trying to figure out what the problem actually was that we were trying to solve, the questions we should be asking, and the various relevant quantities that were needed to be calculated, but once that was accomplished, the actual technical mathematics was relatively straightforward.
In addition to a strong commitment to solving a fundamental long-standing problem that clearly needed close collaboration between physicists and biologists, a crucial ingredient of our success was that Jim and Brian, as well as being outstanding biologists, thought a lot like physicists and were appreciative of the importance of a mathematical framework grounded in underlying principles for addressing problems. Of equal importance was their appreciation that, to varying degrees, all theories and models are approximate. It is often difficult to see that there are boundaries and limitations to theories, no matter how successful they might have been. This does not mean that they are wrong, but simply that there is a finite range of their applicability. The classic case of Newton’s laws is a standard example. Only when it was possible to probe very small distances on the atomic scale or very large velocities on the scale of the speed of light did serious deviations from the predictions from Newton’s laws become apparent. And these led to the revolutionary discovery of quantum mechanics to describe the microscopic, and to the theory of relativity to describe ultrahigh speeds comparable to the speed of light. Newton’s laws are still applicable and correct outside of these two extreme domains. And here’s something of great importance: modifying and extending Newton’s laws to these wider domains led to a deep and profound shift in our philosophical conceptual understanding of how everything works. Revolutionary ideas like the realization that the nature of matter itself is fundamentally probabilistic, as embodied in Heisenberg’s uncertainty principle, and that space and time are not fixed and absolute, arose out of addressing the limitations of classical Newtonian thinking.
Lest you think that these revolutions in our understanding of fundamental problems in physics are just arcane academic issues, I want to remind you that they have had profound consequences for the daily life of everyone on the planet. Quantum mechanics is the foundational theoretical framework for understanding materials and plays a seminal role in much of the high-tech machinery and equipment that we use. In particular, it stimulated the invention of the laser, whose many applications have changed our lives. Among them are bar code scanners, optical disk drives, laser printers, fiber-optic communications, laser surgery, and much more. Similarly, relativity together with quantum mechanics spawned atomic and nuclear bombs, which changed the entire dynamic of international politics and continue to hang over all of us as a constant, though often suppressed and sometimes unacknowledged, threat to our very existence.
To varying degrees, all theories and models are incomplete. They need to be continually tested and challenged by increasingly accurate experiments and observational data over wider and wider domains and the theory modified or extended accordingly. This is an essential ingredient in the scientific method. Indeed, understanding the boundaries of their applicability, the limits to their predictive power, and the ongoing search for exceptions, violations, and failures has provoked even deeper questions and challenges, stimulating the continued progress of science and the unfolding of new ideas, techniques, and concepts.
A major challenge in constructing theories and models is to identify the important quantities that capture the essential dynamics at each organizational level of a system. For instance, in thinking about the solar system, the masses of the planets and the sun are clearly of central importance in determining the motion of the planets, but their color (Mars red, the Earth mottled blue, Venus white, etc.) is irrelevant: the color of the planets is irrelevant for calculating the details of their motion. Similarly, we don’t need to know the color of the satellites that allow us to communicate on our cell phones when calculating their detailed motion.
However, this is clearly a scale-dependent statement in that if we look at the Earth from a very close distance of, say, just a few miles above its surface rather than from millions of miles away in space, then what was perceived as its color is now revealed as a manifestation of the huge diversity of the Earth’s surface phenomena, which include everything from mountains and rivers to lions, oceans, cities, forests, and us. So what was irrelevant at one scale can become dominant at another. The challenge at every level of observation is to abstract the important variables that determine the dominant behavior of the system.
Physicists have coined a concept to help formalize a first step in this approach, which they call a “toy model.” The strategy is to simplify a complicated system by abstracting its essential components, represented by a small number of dominant variables, from which its leading behavior can be determined. A classic example is the idea first proposed in the nineteenth century that gases are composed of molecules, viewed as hard little billiard balls, that are rapidly moving and colliding with one another and whose collisions with the surface of a container are the origin of what we identify as pressure. What we call temperature is similarly identified as the average kinetic energy of the molecules. This was a highly simplified model which in detail is not strictly correct, though it captured and explained for the first time the essential macroscopic coarse-grained features of gases, such as their pressure, temperature, heat conductivity, and viscosity. As such, it provided the point of departure for developing our modern, significantly more detailed and precise understanding not only of gases, but of liquids and materials, by refining the basic model and ultimately incorporating the sophistication of quantum mechanics. This simplified toy model, which played a seminal role in the development of modern physics, is called the “kinetic theory of gases” and was first proposed independently by two of the greatest physicists of all time: James Clerk Maxwell, who unified electricity and magnetism into electromagnetism, thereby revolutionizing the world with his prediction of electromagnetic waves, and Ludwig Boltzmann, who brought us statistical physics and the microscopic understanding of entropy.
A concept related to the idea of a toy model is that of a “zeroth order” approximation of a theory, in which simplifying assumptions are similarly made in order to give a rough approximation of the exact result. It is usually employed in a quantitative context as, for example, in the statement that “a zeroth order estimate for the population of the Chicago metropolitan area in 2013 is 10 million people.” Upon learning a little more about Chicago, one might make what could be called a “first order” estimate of its population of 9.5 million, which is more precise and closer to the actual number (whose precise value from census data is 9,537,289). One could imagine that after more detailed investigation, an even better estimate would yield 9.54 million, which would be called a “second order” estimate. You get the idea: each succeeding “order” represents a refinement, an improved approximation, or a finer resolution that converges to the exact result based on more detailed investigation and analysis. In what follows, I shall be using the terms “coarse-grained” and “zeroth order” interchangeably.
This was the philosophical framework that Jim, Brian, and I were exploring when we embarked on our collaboration. Could we first construct a coarse-grained zeroth order theory for understanding the plethora of quarter-power allometric scaling relations based on generic underlying principles that would capture the essential features of organisms? And could we then use it as a point of departure for quantitatively deriving more refined predictions, the higher order corrections, for understanding the dominant behavior of real biological systems?
I later learned that compared with the majority of biologists, Jim and Brian were the exception rather than the rule in appreciating this approach. Despite some of the seminal contributions that physics and physicists have made to biology, a prime example being the unraveling of the structure of DNA, many biologists appear to retain a general suspicion and lack of appreciation of theory and mathematical reasoning.
Physics has benefited enormously from a continuous interplay between the development of theory and the testing of its predictions and implications by performing dedicated experiments. A great example is the recent discovery of the Higgs particle at the Large Hadron Collider at CERN in Geneva. This had been predicted many years earlier by several theoretical physicists as a necessary and critical component of our understanding of the basic laws of physics, but it took almost fifty years for the technical machinery to be developed and the large experimental team assembled to mount a successful search for it. Physicists take for granted the concept of the “theorist” who “only” does theory, whereas by and large biologists do not. A “real” biologist has to have a “lab” or a field site with equipment, assistants, and technicians who observe, measure, and analyze data. Doing biology with just pen, paper, and laptop, in the way many of us do physics, is considered a bit dilettantish and simply doesn’t cut it. There are, of course, important areas of biology, such as biomechanics, genetics, and evolutionary biology, where this is not the case. I suspect that this situation will change as big data and intense computation increasingly encroach on all of science and we aggressively attack some of the big questions such as understanding the brain and consciousness, environmental sustainability, and cancer. However, I agree with Sydney Brenner, the distinguished biologist who received the Nobel Prize for his work on the genetic code and who provocatively remarked that “technology gives us the tools to analyze organisms at all scales, but we are drowning in a sea of data and thirsting for some theoretical framework with which to understand it. . . . We need theory and a firm grasp on the nature of the objects we study to predict the rest.” His article begins, by the way, with the astonishing pronouncement that “biological research is in crisis.”10
Many recognize the cultural divide between biology and physics.11 Nevertheless, we are witnessing an enormously exciting period as the two fields become more closely integrated, leading to new interdisciplinary subfields such as biological physics and systems biology. The time seems right for revisiting D’Arcy Thompson’s challenge: “How far even then mathematics will suffice to describe, and physics to explain, the fabric of the body, no man can foresee. It may be that all the laws of energy, and all the properties of matter, all . . . chemistry . . . are as powerless to explain the body as they are impotent to comprehend the soul. For my part, I think it is not so.” Many would agree with the spirit of this remark, though new tools and concepts, including closer collaboration, may well be needed to accomplish his lofty goal. I would like to think that the marvelously enjoyable collaboration between Jim, Brian, and me, and all of our colleagues, postdocs, and students has contributed just a little bit to this vision.
8. NETWORK PRINCIPLES AND THE ORIGINS OF ALLOMETRIC SCALING
Prior to this digression into the interrelationship between the cultures of biology and physics, I argued that the mechanistic origins of scaling laws in biology were rooted in the universal mathematical, dynamical, and organizational properties of the multiple networks that distribute energy, materials, and information to local microscopic sites that permeate organisms, such as cells and mitochondria in animals. I also argued that because the structures of biological networks are so varied and stand in marked contrast to the uniformity of the scaling laws, their generic properties must be independent of their specific evolved design. In other words, there must be a common set of network properties that transcends whether they are constructed of tubes as in mammalian circulatory systems, fibers as in plants and trees, or diffusive pathways as in cells.
Formulating a set of general network principles and distilling out the essential features that transcend the huge diversity of biological networks proved to be a major challenge that took many months to resolve. As is often the case when moving into uncharted territory and trying to develop new ideas and ways of looking at a problem, the final product seems so obvious once the discovery or breakthrough has been made. It’s hard to believe that it took so long, and one wonders why it couldn’t have been done in just a few days. The frustrations and inefficiencies, the blind alleys, and the occasional eureka moments are all part and parcel of the creative process. There seems to be a natural gestation period, and this is simply the nature of the beast. However, once the problem comes into focus and it’s been solved it is extremely satisfying and enormously exciting.
This was our collective experience in deriving our explanation for the origin of allometric scaling laws. Once the dust had settled, we proposed the following set of generic network properties that are presumed to have emerged as a result of the process of natural selection and which give rise to quarter-power scaling laws when translated into mathematics. In thinking about them it might be useful to reflect on their possible analogs in cities, economies, companies, and corporations, to which we will turn in some detail in later chapters.
I. Space Filling
The idea behind the concept of space filling is simple and intuitive. Roughly speaking, it means that the tentacles of the network have to extend everywhere throughout the system that it is serving, as is illustrated in the networks here. More specifically: whatever the geometry and topology of the network is, it must service all local biologically active subunits of the organism or subsystem. A familiar example will make it clear: Our circulatory system is a classic hierarchical branching network in which the heart pumps blood through the many levels of the network beginning with the main arteries, passing through vessels of regularly decreasing size, ending with the capillaries, the smallest ones, before looping back to the heart through the venal network system. Space filling is simply the statement that the capillaries, which are the terminal units or last branch of the network, have to service every cell in our body so as to efficiently supply each of them with sufficient blood and oxygen. Actually, all that is required is for capillaries to be close enough to cells for sufficient oxygen to diffuse efficiently across capillary walls and thence through the outer membranes of the cells.
Quite analogously, many of the infrastructural networks in cities are also space filling: for example, the terminal units or end points of the utility networks—gas, water, and electricity—have to end up supplying all of the various buildings that constitute a city. The pipe that connects your house to the water line in the street and the electrical line that connects it to the main cable are analogs of capillaries, while your house can be thought of as an analog to cells. Similarly, all employees of a company, viewed as terminal units, have to be supplied by resources (wages, for example) and information through multiple networks connecting them with the CEO and the management.
II. The Invariance of Terminal Units
This simply means that the terminal units of a given network design, such as the capillaries of the circulatory system that we just discussed, all have approximately the same size and characteristics regardless of the size of the organism. Terminal units are critical elements of the network because they are points of delivery and transmission where energy and resources are exchanged. Other examples are mitochondria within cells, cells within bodies, and petioles (the last branch) of plants and trees. As individuals grow from newborn to adult, or as new species of varying sizes evolve, terminal units do not get reinvented nor are they significantly reconfigured or rescaled. For example, the capillaries of all mammals, whether children, adults, mice, elephants, or whales, are essentially all the same despite the enormous range and variation of body sizes.
This invariance of terminal units can be understood in the context of the parsimonious nature of natural selection. Capillaries, mitochondria, cells, et cetera, act as “ready-made” basic building blocks of the corresponding networks for new species, which are rescaled accordingly. The invariant properties of the terminal units within a specific design characterize the taxonomic class. For instance, all mammals share the same capillaries. Different species within that class such as elephants, humans, and mice are distinguished from one another by having larger or smaller, but closely related, network configurations. From this perspective, the difference between taxonomic groups, that is, between mammals, plants, and fish, for example, is characterized by different properties of the terminal units of their various corresponding networks. Thus while all mammals share similar capillaries and mitochondria, as do all fish, the mammalian ones differ from those of fish in their size and overall characteristics.
Analogously, the terminal units of networks that service and sustain buildings in a city, such as electrical outlets or water faucets, are also approximately invariant. For example, the electrical outlets in your house are essentially identical to those of almost any building anywhere in the world, no matter how big or small it is. There may be small local variations in detailed design but they are all pretty much the same size. Even though the Empire State Building in New York City and many other similar buildings in Dubai, Shanghai, or São Paulo may be more than fifty times taller than your house, all of them, including your house, share outlets and faucets that are very similar. If outlet size was naively scaled isometrically with the height of buildings, then a typical electrical outlet in the Empire State Building would have to be more than fifty times larger than the ones in your house, which means it would be more than ten feet tall and three feet wide rather than just a few inches. And as in biology, basic terminal units, such as faucets and electrical outlets, are not reinvented every time we design a new building regardless of where or how big it is.
III. Optimization
The final postulate states that the continuous multiple feedback and fine-tuning mechanisms implicit in the ongoing processes of natural selection and which have been playing out over enormous periods of time have led to the network performance being “optimized.” So, for example, the energy used by the heart of any mammal, including us, to pump blood through the circulatory system is on average minimized. That is, it is the smallest it could possibly be given its design and the various network constraints. To put it slightly differently: of the infinite number of possibilities for the architecture and dynamics of circulatory systems that could have evolved, and that are space filling with invariant terminal units, the ones that actually did evolve and are shared by all mammals minimize cardiac output. Networks have evolved so that the energy needed to sustain an average individual’s life and perform the mundane tasks of living is minimized in order to maximize the amount of energy available for sex, reproduction, and the raising of offspring. This maximization of offspring is an expression of what is referred to as Darwinian fitness, which is the genetic contribution of an average individual to the next generation’s gene pool.
This naturally raises the question as to whether the dynamics and structure of cities and companies are the result of analogous optimization principles. What, if anything, is optimized in their multiple network systems? Are cities organized to maximize social interactions, or to optimize transport by minimizing mobility times, or are they ultimately driven by the ambition of each citizen and company to maximize their assets, profits, and wealth? I will return to these issues in chapters 8, 9, and 10.
Optimization principles lie at the very heart of all of the fundamental laws of nature, whether Newton’s laws, Maxwell’s electromagnetic theory, quantum mechanics, Einstein’s theory of relativity, or the grand unified theories of the elementary particles. Their modern formulation is a general mathematical framework in which a quantity called the action, which is loosely related to energy, is minimized. All the laws of physics can be derived from the principle of least action which, roughly speaking, states that, of all the possible configurations that a system can have or that it can follow as it evolves in time, the one that is physically realized is the one that minimizes its action. Consequently, the dynamics, structure, and time evolution of the universe since the Big Bang, everything from black holes and the satellites transmitting your cell phone messages to the cell phones and messages themselves, all electrons, photons, Higgs particles, and pretty much everything else that is physical, are determined from such an optimization principle. So why not life?
This question returns us to our earlier discussion concerning the differences between simplicity and complexity. You may recall that almost all the laws of physics come under the umbrella of simplicity, primarily because they can be expressed in a parsimonious way in terms of just a few compact mathematical equations such as Newton’s laws, Maxwell’s equations, Einstein’s theory of relativity, and so on, all of which can be formulated and elegantly derived from the principle of least action. This is one of the crowning achievements of science and has contributed enormously to our understanding of the world around us and to the remarkable development of our modern technological society. Is it conceivable that the coarse-grained dynamics and structure of complex adaptive systems, whether organisms, cities, or companies, could be analogously formulated and derived from such a principle?
It is important to recognize that the three postulates enunciated above are to be understood in a coarse-grained average sense. Let me explain. It may have occurred to you that there must be variation among the almost trillion capillaries in any individual human body, as there must be across all the species of a given taxonomic group, so strictly speaking capillaries cannot be invariant. However, this variation has to be viewed in a relative scale-dependent way. The point is that any variation among capillaries is extremely small compared with the many orders of magnitude variation in body size. For instance, even if the length of mammalian capillaries varied by a factor of two, this is still tiny compared with the factor of 100 million in the variation of their body masses. Similarly, there is relatively little variation in petioles, the last branch of a tree prior to the leaf, or even in the size of leaves themselves, during the growth of a tree from a tiny sapling to a mature tree that might be a hundred or more feet high. This is also true across species of trees: leaves do vary in size but by a relatively small factor, despite huge factors in the variation of their heights and masses. A tree that is just twenty times taller than another does not have leaves whose diameter is twenty times larger. Consequently, the variation among terminal units within a given design is a relatively small secondary effect. The same goes for possible variations in the other postulates: networks may not be precisely space filling or precisely optimized. Corrections due to such deviations and variations are considered to be “higher order” effects in the sense we discussed earlier.
These postulates underlie the zeroth order, coarse-grained theory for the structure, organization, and dynamics of biological networks, and allow us to calculate many of the essential features of what I referred to as the average idealized organism of a given size. In order to carry out this strategy and calculate quantities such as metabolic rates, growth rates, the heights of trees, or the number of mitochondria in a cell, these postulates have to be translated into mathematics. The goal is to determine the consequences, ramifications, and predictions of the theory and confront them with data and observations. The details of the mathematics depend on the specific kind of network being considered. As discussed earlier, our circulatory system is a network of pipes driven by a beating heart, whereas plants and trees are networks of bundles of thin fibers driven by a steady nonpulsatile hydrostatic pressure. Fundamental to the conceptual framework of the theory is that, despite these completely different physical designs, both kinds of networks are constrained by the same three postulates: they are space filling, have invariant terminal units, and minimize the energy needed to pump fluid through the system.
Carrying out this strategy proved to be quite a challenge, both conceptually and technically. It took almost a year to iron out all of the details, but ultimately we showed how Kleiber’s law for metabolic rates and, indeed, quarter-power scaling in general arises from the dynamics and geometry of optimized space-filling branching networks. Perhaps most satisfying was to show how the magic number four arises and where it comes from.12
In the following subsections I am going to translate the mathematics of how all of this comes about into English to give you an insight into some surprising ways that our bodies work and how we are intimately related not only to all of life but to the entire physical world around us. This was an extraordinary experience that I hope you will find as fascinating and exciting as I did. Equally satisfying was to extend this framework to address all sorts of other problems such as forests, sleep, rates of evolution, and aging and mortality, some of which I will turn to in the following chapter.
9. METABOLIC RATE AND CIRCULATORY SYSTEMS IN MAMMALS, PLANTS, AND TREES
As was explained earlier, oxygen is crucial for maintaining the continuous supply of ATP molecules that are the basic currency of the metabolic energy that keeps us alive—that’s why we have to be continuously breathing. Inhaled oxygen is transported across the surface membranes of our lungs, which are suffused with capillaries, where it is absorbed by our blood and pumped through the cardiovascular system to be delivered to our cells. Oxygen molecules bind to the iron-rich hemoglobin in blood cells, which act as the carriers of oxygen. It is this oxidation process that is responsible for our blood being red in much the same way that iron turns red when it oxidizes to rust in the atmosphere. After the blood has delivered its oxygen to the cells, it loses its red color and turns bluish, which is why veins, which are the vessels that return blood back to the heart and lungs, look blue.
The rate at which oxygen is delivered to cells and likewise the rate at which blood is pumped through our circulatory system are therefore measures of our metabolic rate. Similarly, the rate at which oxygen is inhaled through our mouths and into the respiratory system is also a measure of metabolic rate. These two systems are tightly coupled together so blood flow rates, respiratory rates, and metabolic rates are all proportional to one another and related by simple linear relationships. Thus, hearts beat approximately four times for each breath that is inhaled, regardless of the size of the mammal. This tight coupling of the oxygen delivery systems is why the properties of the cardiovascular and respiratory networks play such an important role in determining and constraining metabolic rate.
The rate at which you use energy to pump blood through the vasculature of your circulatory system is called your cardiac power output. This energy expenditure is used to overcome the viscous drag, or friction, on blood as it flows through increasingly narrower and narrower vessels in its journey through the aorta, which is the first artery leaving your heart, down through multiple levels of the network to the tiny capillaries that feed cells. A human aorta is an approximately cylindrical pipe that is about 18 inches long (about 45 cm) and about an inch (about 2.5 cm) in diameter, whereas our capillaries are only about 5 micrometers wide (about a hundredth of an inch), which is somewhat smaller than a hairbreadth.13 Although a blue whale’s aorta is almost a foot in diameter (30 cm), its capillaries are still pretty much the same size as yours and mine. This is an explicit example of the invariance of the terminal units in these networks.
It’s much harder to push fluid through a narrow tube than a wider one, so almost all of the energy that your heart expends is used to push blood through the tiniest vessels at the end of the network. It’s a bit like having to push juice through a sieve, in this case one that is made up of about 10 billion little holes. On the other hand, you use relatively little energy pumping blood through your arteries or indeed through any of the other larger tubes in the network, even though that’s where most of your blood resides.
One of the basic postulates of our theory is that the network configuration has evolved to minimize cardiac output, that is, the energy needed to pump blood through the system. For an arbitrary network where the flow is driven by a pulsatile pump such as our hearts there is another potential source of energy loss in addition to that associated with the viscous drag of blood flowing through capillaries and smaller vessels. This is a subtle effect arising from its pulsatile nature and nicely illustrates the beauty of the design of our cardiovascular system that has resulted from optimizing its performance.
When blood leaves the heart, it travels down through the aorta in a wave motion that is generated by the beating of the heart. The frequency of this wave is synchronous with your heart rate, which is about sixty beats a minute. The aorta branches into two arteries, and when blood reaches this first branch point some of it flows down one tube and some down the other, both in a wavelike motion. A generic feature of waves is that they suffer reflections when they meet a barrier, a mirror being the most obvious example. Light is an electromagnetic wave, so the image that you see is just the reflection from the surface of the mirror of the light waves that originate from your body. Other familiar examples are the reflection of water waves from a barrier, or an echo in which sound waves are reflected from a hard surface.
In a similar fashion, the blood wave traveling along the aorta is partially reflected back when it meets the branch point, the remainder being transmitted down through the daughter arteries. These reflections have potentially very bad consequences because they mean that your heart is effectively pumping against itself. Furthermore, this effect gets hugely enhanced as blood flows down through the hierarchy of vessels because the same phenomenon occurs at each ensuing branch point in the network, resulting in a large amount of energy being expended by your heart just in overcoming these multiple reflections. This would be an extremely inefficient design, resulting in a huge burden on the heart and a huge waste of energy.
To avoid this potential problem and minimize the work our hearts have to do, the geometry of our circulatory systems has evolved so that there are no reflections at any branch point throughout the network. The mathematics and physics of how this is accomplished is a little bit complicated, but the result is simple and elegant: the theory predicts that there will be no reflections at any branch point if the sum of the cross-sectional areas of the daughter tubes leaving the branch point is the same as the cross-sectional area of the parent tube coming into it.
As an example, consider the simple case where the two daughter tubes are identical and therefore have the same cross-sectional areas (which is approximately correct in real circulatory systems). Suppose that the cross-sectional area of the parent tube is 2 square inches; then, in order to ensure that there are no reflections, the cross-sectional area of each daughter has to be 1 square inch. Because the cross-sectional area of any vessel is proportional to the square of its radius, another way of expressing this result is to say that the square of the radius of the parent tube has to be just twice the square of the radius of each of the daughters. So to ensure that there is no energy loss via reflections as one progresses down the network, the radii of successive vessels must scale in a regular self-similar fashion, decreasing by a constant factor of the square root of two (√2) with each successive branching.
This so-called area-preserving branching is, indeed, how our circulatory system is constructed, as has been confirmed by detailed measurements across many mammals—and many plants and trees. This at first seems quite surprising given that plants and trees do not have beating hearts—the flow through their vasculature is steady and nonpulsatile, yet their vasculature scales just like the pulsatile circulatory system. However, if you think of a tree as a bundle of fibers all tightly tied together beginning in the trunk and then sequentially spraying out up through its branches, then it’s clear that the cross-sectional area must be preserved all the way up through the hierarchy. This is illustrated below, where this fiber bundle structure is compared with the pipe structure of mammals. An interesting consequence of area-preserving branching is that the cross-sectional area of the trunk is the same as the sum of the cross-sectional areas of all the tiny branches at the end of the network (the petioles). Amazingly, this was known to Leonardo da Vinci. I have reproduced the requisite page of his notebook where he demonstrates this fact.
Although this simple geometric picture demonstrates why trees obey area-preserving branching, it is in actuality an oversimplification. However, area preserving can be derived from a much more realistic model for trees using the general network principles of space filling and optimization enunciated above, supplemented with biomechanical constraints that require branches to be resilient against perturbations from wind by bending without breaking. Such an analysis shows that in almost all respects plants and trees scale just like mammals, both within individuals as well as across species, including the ¾ power law for their metabolic rates, even though their physical design is quite different.14


(Above) A schematic of the hierarchical branching pipe structure of mammals (left) and the fiber bundle structure of the vasculature of plants and trees (right); the sequential “unraveling” of fibers forms their physical branch structure. In both cases cutting across any level of branching and adding up the cross-sectional areas results in the same value throughout the network. (Left) A page from da Vinci’s notebooks showing that he understood the area-preserving branching of trees.
10. DIGRESSION ON NIKOLA TESLA, IMPEDANCE MATCHING, AND AC/DC
It’s a lovely thought that the optimum design of our circulatory system obeys the same simple area-preserving branching rules that trees and plants do. It’s equally satisfying that the condition of nonreflectivity of waves at branch points in pulsatile networks is essentially identical to how national power grids are designed for the efficient transmission of electricity over long distances.
This condition of nonreflectivity is called impedance matching. It has multiple applications not only in the working of your body but across a very broad spectrum of technologies that play an important part in your daily life. For example, telephone network systems use matched impedances to minimize echoes on long-distance lines; most loudspeaker systems and musical instruments contain impedance matching mechanisms; and the bones in the middle ear provide impedance matching between the eardrum and the inner ear. If you have ever witnessed or been subject to an ultrasound examination you will be familiar with the nurse or technician smearing a gooey gel over your skin before sliding the probe over it. You probably thought that this was for lubrication purposes but in fact it’s actually for matching impedances. Without the gel, the impedance mismatch in ultrasound detection would result in almost all of the energy being reflected back from the skin, leaving very little to go into the body to be reflected back from the organ or fetus under investigation.
The term impedance matching can be a very useful metaphor for connoting important aspects of social interactions. For example, the smooth and efficient functioning of social networks, whether in a society, a company, a group activity, and especially in relationships such as marriages and friendships, requires good communication in which information is faithfully transmitted between groups and individuals. When information is dissipated or “reflected,” such as when one side is not listening, it cannot be faithfully or efficiently processed, inevitably leading to misinterpretation, a process analogous to the loss of energy when impedances are not matched.
As we became more and more reliant on electricity as a major source of power, the necessity for transmitting it across long distances became a matter of some urgency as the nineteenth century progressed. Not surprisingly, Thomas Edison was a major player in thinking about how this could be accomplished. He subsequently became the great proponent of direct current (DC) transmission. You are probably familiar with the idea that electricity comes in two major varieties: direct current (DC), beloved of Edison, in which electricity flows in a continuous fashion like a river, and alternating current (AC), in which it flows in a pulsatile wave motion much like ocean waves or the blood in your arteries. Until the 1880s all commercial electrical current was DC, partly because AC electrical motors had not yet been invented and partly because most transmission was over relatively short distances. However, there were good scientific reasons for favoring AC transmission, especially for long distances, not least of which is that one can take advantage of its pulsatile nature and match impedances at branch nodes in the power grid so as to minimize power loss, just as we do in our circulatory system.
The invention of the AC induction motor and transformer in 1886 by the brilliant charismatic inventor and futurist Nikola Tesla marked a turning point and signaled the beginning of the “war of currents.” In the United States this turned into a battle royal between the Thomas Edison Company (later General Electric) and the George Westinghouse Company. Ironically, Tesla had come to the United States from his native Serbia to work for Edison to perfect DC transmission. Despite his success in this endeavor, he moved on to develop the superior AC system, ultimately selling his patents to Westinghouse. Although AC eventually won out and now dominates electrical transmission globally, DC persisted well into the twentieth century. I grew up in houses in England with DC electricity and well remember when our neighborhood was converted to AC and we joined the twentieth century.
You have no doubt heard of Nikola Tesla primarily because his name was co-opted by the much-publicized automobile company that produces sleek upscale electric cars. Until recently he had been all but forgotten except by physicists and electrical engineers. He was famous in his lifetime not only for his major achievements in electrical engineering technology but for his somewhat wild ideas and outrageous showmanship, so much so that he made it onto the cover of Time magazine. His research and speculations on lightning, death rays, and improving intelligence via electrical impulses, as well as his photographic memory, his apparent lack of the need for sleep or close human relationship, and his Central European accent led him to become the prototype of the “mad scientist.” Although his patents earned him a considerable fortune, which he used to fund his own research, he died destitute in New York in 1943. Over the last twenty years his name has experienced a major resurgence in the popular culture, culminating fittingly in its use for the automobile company.
11. BACK TO METABOLIC RATE, BEATING HEARTS, AND CIRCULATORY SYSTEMS15
The theoretical framework discussed in the previous sections explains how cardiovascular systems scale across species from the shrew to the blue whale. Equally important, it also explains how they scale within an average individual from the aorta to the capillaries. So if for some perverse reason you wanted to know the radius, length, blood flow rate, pulse rate, velocity, pressure, et cetera, in the fourteenth branch of the circulatory system of the average hippopotamus, the theory will provide you with the answer. In fact, the theory will tell you the answer for any of these quantities for any branch of the network in any animal.
As blood flows through smaller and smaller vessels on its way down through the network, viscous drag forces become increasingly important, leading to the dissipation of more and more energy. The effect of this energy loss is to progressively dampen the wave on its way down through the network hierarchy until it eventually loses its pulsatile character and turns into a steady flow. In other words, the nature of the flow makes a transition from being pulsatile in the larger vessels to being steady in the smaller ones. That’s why you feel a pulse only in your main arteries—there’s almost no vestige of it in your smaller vessels. In the language of electrical transmission, the nature of the blood flow changes from being AC to DC as it progresses down through the network.
Thus, by the time blood reaches the capillaries its viscosity ensures that it is no longer pulsatile and that it is moving extremely slowly. It slows down to a speed of only about 1 millimeter per second, which is tiny compared with its speed of 40 centimeters per second when it leaves the heart. This is extremely important because this leisurely speed ensures that oxygen carried by the blood has sufficient time to diffuse efficiently across the walls of the capillaries and be rapidly delivered to feed cells. Interestingly, the theory predicts that these velocities at the two extremities of the network, the capillaries and the aorta, are the same for all mammals, as observed. You are very likely aware of this huge difference in speeds between capillaries and the aorta. If you prick your skin, blood oozes out very slowly from the capillaries with scant resulting damage, whereas if you cut a major artery such as your aorta, carotid, or femoral, blood gushes out and you can die in just a matter of minutes.
But what’s really surprising is that blood pressures are also predicted to be the same across all mammals, regardless of their size. Thus, despite the shrew’s heart weighing only about 12 milligrams, the equivalent of about 25 grains of salt, and its aorta having a radius of only about 0.1 millimeter and consequently barely visible, whereas a whale’s heart weighs about a ton, almost the weight of a Mini Cooper, and its aorta has a radius of about 30 centimeters, their blood pressures are approximately the same. This is pretty amazing—just think of the enormous stresses on the walls of the shrew’s tiny aorta and arteries compared with the pressures on yours or mine, let alone those on a whale’s. No wonder the poor creature dies after only a year or two.
The first person to study the physics of blood flow was the polymath Thomas Young. In 1808 he derived the formula for how its velocity depends on the density and elasticity of the arterial walls. His seminal results were of great importance in paving the way for understanding how the cardiovascular system works and for using measurements on pulse waves and blood velocities to probe and diagnose cardiovascular disease. For example, as we age, our arteries harden, leading to significant changes in their density and elasticity, and therefore to predictable changes in the flow and pulse velocity of the blood.
In addition to his work on the cardiovascular system, Young was famous for several other quite diverse and profound discoveries. He is perhaps best known for establishing the wave theory of light, in which each color is associated with a particular wavelength. But he also contributed to early work in linguistics and Egyptian hieroglyphics, including being the first person to decipher the famous Rosetta Stone now sitting in the British Museum in London. As a fitting tribute to this remarkable man, Andrew Robinson wrote a spirited biography of Young titled The Last Man Who Knew Everything: Thomas Young, the Anonymous Polymath Who Proved Newton Wrong, Explained How We See, Cured the Sick, and Deciphered the Rosetta Stone, Among Other Feats of Genius. I have a certain soft spot for Young because he was born in Milverton, in the county of Somerset in the West of England, just a few short miles from Taunton, where I was born.
12. SELF-SIMILARITY AND THE ORIGIN OF THE MAGIC NUMBER FOUR
Most biological networks like the circulatory system exhibit the intriguing geometric property of being a fractal. You’re probably familiar with the idea. Simply put, fractals are objects that look approximately the same at all scales or at any level of magnification. A classic example is a cauliflower or a head of broccoli shown opposite. Fractals are ubiquitous throughout nature, appearing everywhere from lungs and ecosystems to cities, companies, clouds, and rivers. I want to spend this section elaborating on what they are, what they mean, how they are related to power law scaling, and how they are manifested in the circulatory system that we have been discussing.
If broccoli is broken into smaller pieces, each piece looks like a reduced-size version of the original. When scaled back up to the size of the whole, each piece appears indistinguishable from the original. If each of these smaller pieces is likewise broken into even smaller pieces, then these too look like reduced-size versions of the original broccoli. You can imagine repeating this process over and over again with basically the same result, namely that each subunit looks like a scaled-down version of the original whole. To put it slightly differently: if you took a photograph of any of the pieces of broccoli, whatever their size, and blew it up to the size of the original head, you would have a difficult time telling the difference between the blown-up version and the original.
This is in marked contrast to what we normally see when, for example, we use a microscope to zoom in on an object using a higher and higher resolution in order to reveal greater detail and new structure that is qualitatively different from those of the whole. Obvious examples are cells in tissue, molecules in materials, or protons in atoms. If, on the other hand, the object is a fractal, no new pattern or detail arises when the resolution is increased: the same pattern repeats itself over and over again. In reality, this is an idealized description for, of course, the images at various levels of resolution differ very slightly from one another and eventually the recursive repetition ceases and new patterns of structural design appear. If you continue breaking down broccoli to increasingly smaller pieces, these eventually lose the geometric characteristics of broccoli and eventually reveal the structure of its tissue, its cells, and its molecules.

Examples of classic fractals and scale invariance; in all cases it’s not straightforward to discern the absolute scale. (A) and (B): Romanesco cauliflower at two different resolutions showing its self-similarity. (C): A dried-up riverbed in California. The similarity with a tree in winter, a dried leaf, or our circulatory system is obvious. (D): The Grand Canyon. It could just as well be erosion along the dirt roadway to my house after the runoff following a big storm.
This repetitive phenomenon is called self-similarity and is a generic characteristic of fractals. Analogous to the repetitive scaling exhibited by broccoli are the infinite reflections in parallel mirrors, or the nesting of Russian dolls (matryoshka) of regularly decreasing sizes inside one another. Long before the concept was invented, self-similarity was poetically expressed by the Irish satirist Jonathan Swift, the author of Gulliver’s Travels, in this whimsical quatrain:
So, naturalists observe, a flea
Hath smaller fleas that on him prey;
And these have smaller still to bite ’em;
And so proceed ad infinitum.
—
So it is with the hierarchical networks we have been discussing. If you cut a piece out of such a network and appropriately scale it up, then the resulting network looks just like the original. Locally, each level of the network essentially replicates a scaled version of the levels adjacent to it. We saw an explicit example of this when discussing the consequences of impedance matching in the pulsatile regime of the circulatory system where area-preserving branching resulted in the radii of successive vessels decreasing by a constant factor (√2 = 1.41 . . .) with each successive branching. So, for example, if we compare the radii of vessels separated by 10 such branchings, then they are related by a scale factor of (√2)10 = 32. Because our aorta has a radius of about 1.5 centimeters, this means that the radii of vessels at the tenth branching level are only about half a millimeter.
Because blood flow changes from pulsatile to nonpulsatile as one progresses down the network, our circulatory system is actually not continuously self-similar nor therefore a precise fractal. In the nonpulsatile domain where the flow is dominated by viscous forces, minimizing the amount of power being dissipated leads to a self-similarity in which the radii of successive vessels decrease by a constant factor of the cube root of two 3√2 (= 1.26 . . .), rather than the square root √2 (= 1.41 . . .) as in the pulsatile region. Thus the fractal nature of the circulatory system subtly changes from the aorta to the capillaries, reflecting the change in the nature of the flow from pulsatile to nonpulsatile. Trees, on the other hand, maintain approximately the same self-similarity from the trunk to their leaves, with radii successively decreasing by the area-preserving ratio of √2.
The space-filling requirement that the network must service the entire volume of the organism at all scales also requires it to be self-similar in terms of the lengths of the vessels. To fill the three-dimensional space, lengths of successive vessels have to decrease by a constant factor of 3√2 with each successive branching and, in contrast to radii, this remains valid down through the entire network, including both the pulsatile and nonpulsatile domains.
Having determined how networks scale within individuals following these simple rules, the last piece of the derivation is to determine how this connects across species of different weights. This is accomplished from a further consequence of the energy minimization principle: namely, that the total volume of the network—that is, the total volume of blood in the body—must be directly proportional to the volume of the body itself, and therefore proportional to its weight, as observed. In other words, the volume of blood is a constant proportion of the volume of the body, regardless of size. For a tree this is obvious because the network of its vessels constitutes the entire tree—there is no analog of flesh in between all of its branches, so the volume of the network is the volume of the tree.16
Now, the volume of the network is just the sum of the volumes of all of its vessels or branches, and these can be straightforwardly calculated from knowing how their lengths and radii scale, thereby connecting the self-similarity of the internal network to body size. It is the mathematical interplay between the cube root scaling law for lengths and the square root scaling law for radii, constrained by the linear scaling of blood volume and the invariance of the terminal units, that leads to quarter-power allometric exponents across organisms.
The resulting magic number four emerges as an effective extension of the usual three dimensions of the volume serviced by the network by an additional dimension resulting from the fractal nature of the network. I shall go into this in more detail in the following chapter, where I discuss the general concept of fractal dimension, but suffice it to say here that natural selection has taken advantage of the mathematical marvels of fractal networks to optimize their distribution of energy so that organisms operate as if they were in four dimensions, rather than the canonical three. In this sense the ubiquitous number four is actually 3 + 1. More generally, it is the dimension of the space being serviced plus one. So had we lived in a universe of eleven dimensions, as some of my string theory friends believe, the magic number would have been 11 + 1 = 12, and we would have been talking about the universality of 1⁄12 power scaling laws rather than ¼ power ones.
13. FRACTALS: THE MYSTERIOUS CASE OF THE LENGTHENING BORDERS
Mathematicians had recognized for a long time that there were geometries that lay outside of the canonical boundaries of the classical Euclidean geometry that has formed the basis for mathematics and physics since ancient times. The traditional framework that many of us have been painfully and joyfully exposed to implicitly assumes that all lines and surfaces are smooth and continuous. Novel ideas that evoked concepts of discontinuities and crinkliness, which are implicit in the modern concept of fractals, were viewed as fascinating formal extensions of academic mathematics but were not generally perceived as playing any significant role in the real world. It fell to the French mathematician Benoit Mandelbrot to make the crucial insight that, quite to the contrary, crinkliness, discontinuity, roughness, and self-similarity—in a word, fractality—are, in fact, ubiquitous features of the complex world we live in.17
In retrospect it is quite astonishing that this insight had eluded the greatest mathematicians, physicists, and philosophers for more than two thousand years. Like many great leaps forward, Mandelbrot’s insight now seems almost “obvious,” and it beggars belief that his observation hadn’t been made hundreds of years earlier. After all, “natural philosophy” has been one of the major categories of human intellectual endeavor for a very long time, and almost everyone is familiar with cauliflowers, vascular networks, streams, rivers, and mountain ranges, all of which are now perceived as being fractal. However, almost no one had conceived of their structural and organizational regularities in general terms, nor the mathematical language used to describe them. Perhaps, like the erroneous Aristotelian assumption that heavier things “obviously” fall faster, the Platonic ideal of smoothness embodied in classical Euclidean geometry was so firmly ingrained in our psyches that it had to wait a very long time for someone to actually check that it was valid with real-life examples. That person was an unusual British polymath named Lewis Fry Richardson, who almost accidentally laid the foundation for inspiring Mandelbrot’s invention of fractals. The tale of how Richardson came to this is an unusually interesting one, which I shall recount very briefly.
Mandelbrot’s insights imply that when viewed through a coarse-grained lens of varying resolution, a hidden simplicity and regularity is revealed underlying the extraordinary complexity and diversity in much of the world around us. Furthermore, the mathematics that describes self-similarity and its implicit recursive rescaling is identical to the power law scaling discussed in previous chapters. In other words, power law scaling is the mathematical expression of self-similarity and fractality. Consequently, because animals obey power law scaling both within individuals, in terms of the geometry and dynamics of their internal network structures, as well as across species, they, and therefore all of us, are living manifestations of self-similar fractals.
Lewis Fry Richardson was a mathematician, physicist, and meteorologist who at the age of forty-six also earned a degree in psychology. He was born in 1881 and early in his career made seminal contributions to our modern methodology of weather forecasting. He pioneered the idea of computationally modeling the weather using the fundamental equations of hydrodynamics (the Navier-Stokes equations introduced earlier when discussing the modeling of ships), augmented and updated with continuous feedback from real-time weather data, such as changes in air pressure, temperature, density, humidity, and wind velocity. He conceived this strategy early in the twentieth century, well before the development of modern high-speed computers, so his computations had to be carried out painfully slowly by hand, resulting in very limited predictive power. Nevertheless, this strategy and the general mathematical techniques he developed provided the foundation for science-based forecasts and pretty much form the template now used to give us relatively accurate weather forecasts for up to several weeks into the future. The advent of high-speed computers, coupled with almost minute-by-minute updating from huge amounts of local data gathered across the globe, has enormously improved our ability to forecast weather.
Both Richardson and Mandelbrot came from relatively unusual backgrounds. Although both were trained in mathematics, neither followed a standard academic career path. Richardson, who was a Quaker, had been a conscientious objector during the First World War and was consequently prevented from having any subsequent university academic position, a rule that might strike us today as particularly vindictive. And Mandelbrot did not get his first tenured professorial appointment until he was seventy-five years old, thereby becoming the oldest professor in Yale’s history to receive tenure. Perhaps it requires outliers and mavericks like Richardson and Mandelbrot working outside mainstream research to revolutionize our way of seeing the world.
Richardson had worked for the British Meteorological Office before the war and rejoined it after the war ended only to resign his post a couple of years later, again on conscientious grounds, when the office became part of the Air Ministry in charge of the Royal Air Force. It is curiously fitting that his deeply felt pacifism and consequent fringe connection to the world of mainstream academic research led to his most interesting and seminal observation, namely that measuring lengths isn’t as simple as it might appear, thereby bringing to consciousness the role of fractals in our everyday world. To appreciate how he came to this I need to make a small detour into his other accomplishments.
Stimulated by his passionate pacifism, Richardson embarked on an ambitious program to develop a quantitative theory for understanding the origins of war and international conflict in order to devise a strategy for their ultimate prevention. His aim was nothing less than to develop a science of war. His main thesis was that the dynamics of conflict are primarily governed by the rates at which nations build up their armaments and that their continued accumulation is the major cause of war. He viewed the accumulation of weapons as a proxy for the collective psychosocial forces that reflect, but transcend, history, politics, economics, and culture and whose dynamics inevitably lead to conflict and instability. Richardson used the mathematics developed for understanding chemical reaction dynamics and the spread of communicable diseases to model the ever-increasing escalation of arms races in which the arsenal of each country increases in response to the increase in armaments of every other country.
His theory did not attempt to explain the fundamental origins of war, that is, why we collectively resort to force and violence to settle our conflicts, but rather to show how the dynamics of arms races escalate, resulting in catastrophic conflict. Although his theory is highly oversimplified, Richardson had some success in comparing his analyses with data, but more important, he provided an alternative framework for quantitatively understanding the origins of war that could be confronted with data. Furthermore, it had the virtue of showing what parameters were important, especially in providing scenarios under which a potentially peaceful situation could be achieved and sustained. In contrast to conventional, more qualitative theories of conflict, the roles of leadership, cultural and historical animosity, and specific events and personalities play no explicit role in his theory.18
In his desire to create a testable scientific framework, Richardson collected an enormous amount of historical data on wars and conflicts. In order to quantify them he introduced a general concept, which he called the deadly quarrel, defined as any violent conflict between human beings resulting in death. War is then viewed as a particular case of a deadly quarrel, but so is an individual murder. He quantified their magnitudes by the subsequent number of deaths: for an individual murder the size of the deadly quarrel is therefore just one, whereas for the Second World War it is more than 50 million, the exact number depending on how civilian casualties are counted. He then took the bold leap of asking whether there was a continuum of deadly quarrels beginning with the individual and progressing up through gang violence, civil unrest, small conflicts, and ending up with the two major world wars, thereby covering a range of almost eight orders of magnitude. Trying to plot these on a single axis leads to the same challenge we faced earlier when trying to accommodate all earthquakes or all mammalian metabolic rates on a simple linear scale. Practically, it simply isn’t possible, and one has to resort to using a logarithmic scale to see the entire spectrum of deadly quarrels.
Thus, by analogy with the Richter scale, the Richardson scale begins with zero for a single individual murder and ends with a magnitude of almost eight for the two world wars (eight orders of magnitude would represent a hundred million deaths). In between, a small riot with ten victims would have magnitude one, a skirmish in which one hundred combatants were killed would be two, and so on. Obviously there are very few wars of magnitude seven but an enormous number of conflicts with magnitude zero or one. When he plotted the number of deadly quarrels of a given size versus their magnitude on a logarithmic scale, he found an approximately straight line just like the straight lines we saw when physiological quantities like metabolic rate were plotted in this way versus animal size (see Figure 1).
Consequently, the frequency distribution of wars follows simple power law scaling indicating that conflicts are approximately self-similar.19 This remarkable result leads to the surprising conclusion that, in a coarse-grained sense, a large war is just a scaled-up version of a small conflict, analogous to the way that elephants are approximately scaled-up mice. Thus underlying the extraordinary complexity of wars and conflicts seems to be a common dynamic operating across all scales. Recent work has confirmed such findings for recent wars, terrorist attacks, and even cyberattacks.20 No general theory has yet been advanced for understanding these regularities, though they very likely reflect the fractal-like network characteristics of national economies, social behavior, and competitive forces. In any case, any ultimate theory of war needs to account for them.
This, at last, leads to the main point of telling the story of Lewis Richardson. He had viewed the power law scaling of conflicts as just one of potentially other systematic regularities concerning war from which he hoped to discover the general laws governing human violence. In trying to develop a theory, he hypothesized that the probability of war between neighboring states was proportional to the length of their common border. Driven by his passion to test his theory, he turned his attention to figuring out how the lengths of borders are measured . . . and in so doing inadvertently discovered fractals.
To test his idea, he set about collecting data on lengths of borders and was surprised to discover that there was considerable variation in the published data. For example, he learned that the length of the border between Spain and Portugal was sometimes quoted as 987 kilometers but other times as 1,214 kilometers, and similarly that the border between the Netherlands and Belgium was sometimes 380 kilometers and at other times 449 kilometers. It was hard to believe that such large discrepancies were errors in measurement. By that time surveying was already a highly developed, well-established, and accurate science. For instance, the height of Mount Everest was known to within a few feet by the end of the nineteenth century. So discrepancies of hundreds of kilometers in the lengths of borders were totally weird. Clearly something else was going on.
Until Richardson’s investigation, the methodology of measuring lengths was taken completely for granted. The idea seems so simple it’s hard to see what could go wrong. Let’s then analyze the process of how we measure lengths. Suppose you want to make a rough estimate of the length of your living room. This can be straightforwardly accomplished by laying down a meter stick end to end (in a straight line) and counting how many times it fits in between the walls. You discover that it takes just over 6 times and so conclude that the room is roughly 6 meters long. Sometime later you find that you need a more accurate estimate and so use the finer-grained resolution of a 10-centimeter ruler to make the estimate. Carefully placing it end to end you find that it takes just under 63 times to fit it across the room, leading to a more accurate approximation for its length of 63 × 10 centimeters, which is 630 centimeters, or 6.3 meters. Obviously you can repeat this process over and over again with finer and finer resolutions depending on how accurately you want to know the answer. If you were to measure the room to an accuracy of millimeters, you might find that its length is 6.289 meters.
In actuality, we don’t usually lay down rulers end to end but, for convenience, employ appropriately long continuous tape measures or other measuring devices to relieve us of this tedious process. But the principle remains exactly the same: a tape measure or any other measuring device is simply a sequence of shorter rulers of a given standard length, such as a meter or 10 centimeters, sewed together end to end.
Implicit in our measurement process, whatever it is, is the assumption that with increasing resolution the result converges to an increasingly accurate fixed number, which we call the length of the room, a presumably objective property of your living room. In the example, its length converged from 6 to 6.3 to 6.289 meters as the resolution increased. This convergence to a well-defined length seems completely obvious and, indeed, was not questioned for several thousand years until 1950, when Richardson stumbled upon the surprising mystery of the lengthening borders and coastlines.
Let’s now imagine measuring the length of the border between two neighboring countries, or the length of a country’s coastline, following the standard procedure outlined above. To get a very rough estimate we might start by using 100-mile segments laid end to end to cover its entire length. Suppose we find that with this resolution the border is approximated by just over 12 such segments so that its length is roughly a little over 1,200 miles. To get a more accurate measurement we might then use 10-mile segments to estimate the length. According to the usual “rules of measurement” articulated with the living room example, we might find something like 124 segments, leading to a better estimate of 1,240 miles. Greater accuracy could then be obtained by increasing the resolution to one mile, in which case we might expect to find 1,243 segments, say, leading to a value of 1,243 miles. This can be continued using progressively finer and finer resolutions to obtain as accurate a number as needed.
However, to his great surprise, Richardson found that when he carried out this standard iterative procedure using calipers on detailed maps, this simply wasn’t the case. In fact, he discovered that the finer the resolution, and therefore the greater the expected accuracy, the longer the border got, rather than converging to some specific value! Unlike lengths of living rooms, the lengths of borders and coastlines continually get longer rather than converging to some fixed number, violating the basic laws of measurement that had implicitly been presumed for several thousand years. Equally surprising, Richardson discovered that this increase in length progressed in a systematic fashion. When he plotted the length of various borders and coastlines versus the resolution used to make the measurements on a logarithmic scale, it revealed a straight line indicative of the power law scaling we’ve seen in many other places (see Figure 14). This was extremely strange, as it indicated that contrary to conventional belief, these lengths seem to depend on the scale of the units used to make the measurement and, in this sense, are not an objective property of what is being measured.21
So what’s going on here? A moment’s reflection and you will quickly realize what it is. Unlike your living room, most borders and coastlines are not straight lines. Rather, they are squiggly meandering lines either following local geography or having “arbitrarily” been determined via politics, culture, or history. If you lay a straight ruler of length 100 miles between two points on a coastline or border, as is effectively done when surveying, then you will obviously miss all of the many meanderings and wiggles in between (see Figure 13). If, however, you were to instead use a 10-mile-long ruler then you become sensitive to all of those meanderings and wiggles that you missed whose scale is bigger than 10 miles. This finer resolution can see these finer details and follow the wiggles, thereby leading to an estimate that is necessarily larger than that obtained with the coarser 100-mile scale. Likewise, the 10-mile scale will be blind to similar meanderings and wiggles whose scale is smaller than 10 miles, but which would be included if we increased the resolution to one mile, leading to a further increase in the length. Thus, for lines like the borders and coastlines that Richardson studied with many wiggles and squiggles, we can readily understand how their measured lengths continuously increase with resolution.
Because the increase follows simple power law behavior, these borders are in fact self-similar fractals. In other words, the wiggles and squiggles at one scale are, on average, scaled versions of the wiggles and squiggles at another. So when you’ve marveled at how the erosion on the bank of a stream looks just like a scaled-down version of the erosion you’ve seen on a large river, or that it even looks like a mini-version of the Grand Canyon, you weren’t fantasizing, it actually is (see here).
This is wonderful stuff. Once again we see that underlying the daunting complexity of the natural world lies a surprising simplicity, regularity, and unity when viewed through the coarse-grained lens of scale. Although Richardson discovered this strange, revolutionary, nonintuitive behavior in his investigations of borders and coastlines and understood its origins, he didn’t fully appreciate its extraordinary generality and far-reaching implications. This bigger insight fell to Benoit Mandelbrot.

Measuring the lengths of coastline using different resolutions (Britain in the example). (13) The lengths increase systematically with resolution following a power law as indicated by the examples in the graph. (14) The slope gives the fractal dimension for the coastline: the more squiggly it is, the steeper the slope.
Richardson’s discovery was almost entirely ignored by the scientific community. This is not too surprising because it was published in a relatively obscure journal and, in addition, it was buried in the middle of his investigations into the origins of war. His paper, published in 1961, carries the marvelously obscure title “The Problem of Contiguity: An Appendix to Statistics of Deadly Quarrels,” barely revealing, even to the cognoscenti, what the content might be. Who was to know that this was to herald a paradigm shift of major significance?
Well, Benoit Mandelbrot did. He deserves great credit not only for resurrecting Richardson’s work but for recognizing its deeper significance. In 1967 he published a paper in the high-profile journal Science with the more transparent title “How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension.”22 This brought Richardson’s work to light by expanding on his findings and generalizing the idea. Crinkliness, later to become known as fractality, is quantified by how steep the slopes of the corresponding straight lines are on Richardson’s logarithmic plots: the steeper the slope, the more crinkly the curve. These slopes are just the exponents of the power laws relating length to resolution and are the analog of the ¾ exponent relating metabolic rate to mass for organisms. For very smooth traditional curves, like circles, the slope or exponent is zero because its length does not change with increasing resolution but converges to a definite value, as in the living room example. However, for rugged, crinkly coastlines the slope is nonzero. For example, for the west coast of Britain, it’s 0.25. For more crinkly coastlines like those of Norway with its magnificent fjords and multiple levels of bays and inlets that successively branch into increasingly smaller bays and inlets, the slope has the whopping value of 0.52. On the other hand, Richardson found that the South African coast is unlike almost any other coastline, with a slope of only 0.02, closely approximating a smooth curve. As for the frontier between Spain and Portugal, whose “discrepancies” had originally piqued his interest in this problem, he found a slope of 0.18; see Figure 14.
To appreciate what these numbers mean in English, imagine increasing the resolution of the measurement by a factor of two; then, for instance, the measured length of the west coast of Britain would increase by about 25 percent and that of Norway by over 50 percent. This is an enormous effect, which had been completely overlooked until Richardson stumbled across it just seventy years ago. So for the process of measurement to be meaningful, knowing the resolution is crucial and integral to the entire process.
The take-home message is clear. In general, it is meaningless to quote the value of a measured length without stating the scale of the resolution used to make it. In principle, it is as meaningless as saying that a length is 543, 27, or 1.289176 without giving the units it’s measured in. Just as we need to know if it is in miles, centimeters, or angstroms, we also need to know the resolution that was used.
Mandelbrot introduced the concept of a fractal dimension, defined by adding 1 to the exponent of the power law (the value of the slopes). Thus the fractal dimension of the South African coast is 1.02, Norway 1.52, and so on. The point of adding the 1 was to connect the idea of fractals to the conventional concept of ordinary dimensions discussed in chapter 2. Recall that a smooth line has dimension 1, a smooth surface dimension 2, and a volume dimension 3. Thus the South African coast is very close to being a smooth line because its fractal dimension is 1.02, which is very close to 1, whereas Norway is far from it because its fractal dimension of 1.52 is so much greater than 1.
You could imagine an extreme case of this in which the line is so crinkly and convoluted that it effectively fills an entire area. Consequently, even though it’s still a line with “ordinary” dimensions 1, it behaves as if it were an area in terms of its scaling properties, therefore having a fractal dimension of 2. This curious gain of an effective additional dimension is a general feature of space-filling curves, to which I will return in the next chapter.
In the natural world almost nothing is smooth—most things are crinkly, irregular, and crenulated, very often in a self-similar way. Just think of forests, mountain ranges, vegetables, clouds, and the surfaces of oceans. Consequently, most physical objects have no absolute objective length, and it is crucial to quote the resolution when stating the measurement. So why did it take more than two thousand years for people to recognize something so basic and which now seems almost obvious? Very likely this has its origins in the duality that emerged as we gradually separated from a close connection to the natural world and became more and more distant from the forces of nature that have determined our biology. Once we invented language, learned how to take advantage of economies of scale, formed communities, and began making artifacts, we effectively changed the geometry of our daily world and its immediate surroundings. In designing and manufacturing human-engineered artifacts, whether primitive pots and tools or modern sophisticated automobiles, computers, and skyscrapers, we employed and aspired to the simplicity of straight lines, smooth curves, and smooth surfaces. This was brilliantly formalized and reflected in the development of quantified measurement and the invention of mathematics, manifested, in particular, in the idealized paradigm of Euclidian geometry. This is the mathematics appropriate to the world of artifacts we created around us as we evolved from being a mammal like any other to become social Homo sapiens.
In this new world of artifacts we inevitably became conditioned to seeing it through the lens of Euclidian geometry—straight lines, smooth curves, and smooth surfaces—blinding ourselves, at least as scientists and technologists, to the seemingly messy, complex, convoluted world of the environment from which we had emerged. This was mostly left to the imagination of artists and writers. Although measurement plays a central role in this new, more regular artificial world, it has the elegant simplicity of Euclid, so there is no need to be concerned with awkward questions like that of resolution. In this new world, a length is a length is a length, and that’s it. Not so, however, in the immediate “natural” world around us, which is highly complex and dominated by crinkles, wrinkles, and crenulations. As Mandelbrot succinctly put it: “Smooth shapes are very rare in the wild but extremely important in the ivory tower and the factory.”
From the beginning of the nineteenth century mathematicians had already contemplated curves and surfaces that were not smooth but they had not been motivated by the pervasiveness of such geometries in the natural world. Their motivation was simply to explore new ideas and concepts that were primarily of academic interest, such as whether it was possible to formulate consistent geometries that violate the sacred tenets of Euclid.
To which the answer was yes, and Mandelbrot was well positioned to take advantage of this. In contrast to Richardson, Mandelbrot had been educated in the more formal tradition of classical French mathematics and was familiar with the strange world of abstract, densely crinkled, non-Euclidean curves and surfaces. His great contribution was to see that what Richardson had discovered could be put on a firm mathematical basis and that the weird geometries that academic mathematicians had been playing with and which seemed to have nothing to do with “reality” had, in fact, everything to do with reality—and, in some respects, possibly even more so than Euclidean geometry.
Perhaps of greater importance is that he realized that these ideas are generalizable far beyond considerations of borders and coastlines to almost anything that can be measured, even including times and frequencies. Examples include our brains, balls of crumpled paper, lightning, river networks, and time series like electrocardiograms (EKGs) and the stock market. For instance, it turns out that the pattern of fluctuations in financial markets during an hour of trading is, on average, the same as that for a day, a month, a year, or a decade. They are simply nonlinearly scaled versions of one another. Thus if you are shown a typical plot of the Dow Jones average over some period of time, you can’t tell if it’s for the last hour or for the last five years—the distributions of dips, bumps, and spikes is pretty much the same, regardless of the time frame. In other words, the behavior of the stock market is a self-similar fractal pattern that repeats itself across all timescales following a power law that can be quantified by its exponent or, equivalently, its fractal dimension.
You might think that with this knowledge you might soon become rich. Although this certainly gives new insight into hidden regularities in stock markets, unfortunately it has predictive power only in an average coarse-grained sense and does not give specific information about the behavior of individual stocks. Nevertheless, it’s an important ingredient for understanding the dynamics of the market over different timescales. This has stimulated the development of a new transdisciplinary subfield of finance called econophysics and motivated investment companies to hire physicists, mathematicians, and computer scientists to use these sorts of ideas to develop novel investment strategies.23 Many have done very well, though it is unclear just how big a role their physics and mathematics actually played in their success.
Likewise, the self-similarity observed in EKGs is a potentially important gauge of the condition of our hearts. You might have thought that the healthier the heart the smoother and more regular would be the EKG, that is, that a healthy heart would have a low fractal dimension compared with a more diseased one. Quite the contrary. Healthy hearts have relatively high fractal dimensions, reflecting more spiky and ragged EKGs, whereas diseased hearts have low values with relatively smooth EKGs. In fact, those that are most seriously at risk have fractal dimensions close to one with an uncharacteristically smooth EKG. Thus the fractal dimension of the EKG provides a potentially powerful complementary diagnostic tool for quantifying heart disease and health.24
The reason that being healthy and robust equates with greater variance and larger fluctuations, and therefore a larger fractal dimension as in an EKG, is closely related to the resilience of such systems. Being overly rigid and constrained means that there isn’t sufficient flexibility for the necessary adjustments needed to withstand the inevitable small shocks and perturbations to which any system is subjected. Think of the stresses and strains your heart is exposed to every day, many of which are unexpected. Being able to accommodate and naturally adapt to these is critical for your long-term survival. These continuous changes and impingements require all of your organs, including your brain as well as its psyche, to be both flexible and elastic and therefore to have a significant fractal dimension.
This can be extended, at least metaphorically, beyond individuals to companies, cities, states, and even life itself. Being diverse and having many interchangeable, adaptable components is another manifestation of this paradigm. Natural selection thrives on and consequently manufactures greater diversity. Resilient ecosystems have greater diversity of species. It is no accident that successful cities are those that offer a greater spectrum of job opportunities and businesses, and that successful companies have a diversity of products and people with the flexibility to change, adapt, and reinvent in response to changing markets. I shall discuss this further in chapters 8 and 9 when I turn to cities and companies.
In 1982 Mandelbrot published a highly influential and very readable semipopular book titled The Fractal Geometry of Nature.25 This inspired tremendous interest in fractals by showing their ubiquity across both science and the natural world. It stimulated a mini industry searching for fractals, finding them everywhere, measuring their dimensions, and showing how their magical properties result in wonderfully exotic geometric figures.
Mandelbrot had shown how relatively simple algorithmic rules based on fractal mathematics can produce surprisingly complex patterns. He, and later many others, produced amazingly realistic simulations of mountain ranges and landscapes, as well as intriguing psychedelic patterns. This was enthusiastically embraced by the film and media industries, so much so that a great deal of what you now see on the screen and in advertisements, whether “realistic” battle scenes, glorious landscapes, or futuristic fantasy, is based on fractal paradigms. The Lord of the Rings, Jurassic Park, and Game of Thrones would be drab versions of realistic fantasies without the early work and insights on fractals.
Fractals even showed up in music, painting, and architecture. It is claimed that the fractal dimensions of musical scores can be used to quantify the signature nature and characteristics of different composers, such as between Beethoven, Bach, and Mozart, while the fractal dimensions of Jackson Pollock’s paintings were used to distinguish fakes from the real thing.26
Although there is a mathematical framework for describing and quantifying fractals, no fundamental theory based on underlying physical principles for mechanistically understanding why they arise in general, or for calculating their dimensions, has been developed. Why are coastlines and borders fractal, what were the dynamics that gave rise to their surprising regularity and determined that South Africa should have a relatively smooth coastline, whereas Norway a rugged one? And what are the common principles and dynamics that link these disparate phenomena to the behavior of stock markets, cities, vascular systems, and EKGs?
A fractal dimension is just one single metric out of many that characterize such systems. It is amazing how much store we put into single metrics such as these. For example, the Dow Jones Industrial Average is almost religiously perceived as the indicator of the overall state of the U.S. economy, just as body temperature is typically used as an indicator of our overall health. Better is to have a suite of such metrics such as you get from an annual physical examination, or what economists generate in order to get a broader picture of the state of the economy. But much better still is to have a general quantitative theory and conceptual framework supplemented by dynamical models for mechanistically understanding why the various metrics are the sizes they are and to be able to predict how they will evolve.
In this context, just knowing Kleiber’s law for how metabolic rates scale, or even knowing all of the other allometric scaling laws obeyed by organisms, does not constitute a theory. Rather, these phenomenological laws are a sophisticated summary of enormous amounts of data that reveal and encapsulate the systematic, generic features of life. Being able to derive them analytically from a parsimonious set of general underlying principles such as the geometry and dynamics of networks at increasingly finer levels of granularity provides a deep understanding of their origins, leading to the possibility of addressing and predicting other and new phenomena. In the following chapter I will show how the network theory provides such a framework and present a few chosen examples to illustrate the point.
One final note: Mandelbrot showed surprisingly little interest in understanding the mechanistic origins of fractals. Having revealed to the world their extraordinary universality, his passion remained more with their mathematical description than with their physical origins. His attitude seemed to be that they were a fascinating property of nature and we should delight in their ubiquity, simplicity, complexity, and beauty. We should develop a mathematics to describe and use them, but we should not be too concerned about the underlying principles for how they are generated. In a word, he approached them more as a mathematician than as a physicist. This may have been one of the reasons that his great discovery did not receive quite the appreciation in the physics community and scientific establishment that it perhaps deserved and, as a result, he did not receive the Nobel Prize, despite broad recognition in many quarters and a litany of prestigious awards and prizes.