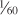of a degree. Minutes, in turn, are broken into seconds of arc or arc seconds, where 1 second is equal to 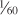of a minute. When units smaller than 1 second of arc are needed, decimal fractions are used.What do you suppose prehistoric people thought about the sky? Why does the Sun move differently from the Moon? Why do the stars move in yet another way? Why do star patterns change with the passing of many nights? Why do certain stars wander among the others? Why does the Sun sometimes take a high course across the sky and sometimes a low course? Are the Sun, the Moon, and the stars attached to a dome over Earth, or do they float free? Are some objects farther away than others?
A thousand generations ago, people had no quantitative concept of the sky. In the past few millennia, we have refined astronomical measurement as a science and an art. Mathematics, and geometry in particular, has made this possible.
It is natural to imagine the sky as a dome or sphere at the center of which we, the observers, are situated. This notion has always been, and still is, used by astronomers to define the positions of objects in the heavens. It’s not easy to specify the locations of points on a sphere by mathematical means. We can’t wrap a piece of quadrille paper around a globe and make a rectangular coordinate scheme work neatly with a sphere. However, there are ways to uniquely define points on a sphere and, by extension, points in the sky.
You’ve seen globes that show lines of longitude and latitude on Earth. Every point has a unique latitude and a unique longitude. These lines are actually half circles or full circles that run around Earth.
The lines of longitude, also called meridians, are half circles with centers that coincide with the physical center of Earth (Fig. 1-1A). The ends of these arcs all come together at two points, one at the north geographic pole and the other at the south geographic pole. Every point on Earth’s surface, except for the north pole and the south pole, can be assigned a unique longitude.
The lines of latitude, also called parallels, are all full circles, with two exceptions: the north and south poles. All the parallels have centers that lie somewhere along Earth’s axis of rotation (Fig. 1-1B), the line connecting the north and south poles. The equator is the largest parallel; above and below it, the parallels get smaller and smaller. Near the north and south poles, the circles of latitude are tiny. At the poles, the circles vanish to points.
All the meridians and parallels are defined in units called degrees and are assigned values with strict upper and lower limits.
There are 360 degrees in a complete circle. Why 360 and not 100 or 1000, which are “rounder” numbers, or 256 or 512, which can be divided repeatedly in half all the way down to 1?
No doubt ancient people noticed that there are about 360 days in a year and that the stellar patterns in the sky are repeated every year. A year is like a circle. Various familiar patterns repeat from year to year: the general nature of the weather, the Sun’s way of moving across the sky, the lengths of the days, the positions of the stars at sunset. Maybe some guru decided that 360, being close to the number of days in a year, was a natural number to use when dividing up a circle into units for angular measurement. Then people could say that the stars shift in the sky by 1 degree, more or less, every night. Whether this story is true or not doesn’t matter; different cultures came up with different ideas anyway. The fact is that we’re stuck with degrees that represent 1/360 of a circle (Fig. 1-2), whether we like it or not.
For astronomical measurements, the degree is not always exact enough. The same is true in geography. On Earth’s surface, 1 degree of latitude represents about 112 kilometers or 70 miles. This is okay for locating general regions but not for pinpointing small towns or city blocks or individual houses. In astronomy, the degree may be good enough for locating the Sun or the Moon or a particular bright star, but for dim stars, distant galaxies, nebulae, and quasars, smaller units are needed. Degrees are broken into minutes of arc or arc minutes, where 1 minute is equal to 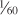of a degree. Minutes, in turn, are broken into seconds of arc or arc seconds, where 1 second is equal to 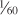of a minute. When units smaller than 1 second of arc are needed, decimal fractions are used.
Figure 1-1. At A, circles of longitude, also called meridians. At B, circles of latitude, also called parallels.
Figure 1-2. There are 360 degrees in a complete circle.
Let’s take a close look at how latitude and longitude coordinates are defined on the surface of Earth. It will help if you use a globe as a visual aid.
In geography classes you were taught that latitude can range from 90 degrees south to 90 degrees north. The north geographic pole is at 90 degrees north, and the south geographic pole is at 90 degrees south. Both the poles lie on the Earth’s axis. The equator is halfway between the poles and is assigned 0 degrees latitude. The northern hemisphere contains all the north-latitude circles, and the southern hemisphere contains all the south-latitude circles.
As the latitude increases toward the north or south, the circumferences of the latitude circles get smaller and smaller. Earth is about 40,000 kilometers (25,000 miles) in circumference, so the equator measures about 40,000 kilometers around. The 45-degree-latitude circle measures about 28,000 kilometers (17,700 miles) in circumference. The 60-degree-latitude circle is half the size of the equator, or 20,000 kilometers (12,500 miles) around. The 90-degree-latitude “circles” are points with zero circumference. Every latitude circle lies in a geometric plane that slices through Earth. All these planes are parallel; this is why latitude circles are called parallels. Every parallel, except for the poles, consists of infinitely many points, all of which lie on a circle and all of which have the same latitude.
There is no such thing as a latitude coordinate greater than 90 degrees, either north or south. If there were such points, the result would be a redundant set of coordinates. The circle representing “100 degrees north latitude” would correspond to the 80-degree north-latitude circle, and the circle representing “120 degrees south latitude” would correspond to the 60-degree south-latitude circle. This would be confusing at best because every point on Earth’s surface could be assigned more than one latitude coordinate. At worst, navigators could end up plotting courses the wrong way around the world; people might mistakenly call 3:00 P.M. the “wee hours of the morning”!
An ideal coordinate system is such that there is a one-to-one correspondence between the defined points and the coordinate numbers. Every point on Earth should have one, and only one, ordered pair of latitude-longitude numbers. And every ordered pair of latitude/longitude numbers, within the accepted range of values, should correspond to one and only one point on the surface of Earth. Mathematicians are fond of this sort of neatness and, with the exception of paradox lovers, dislike redundancy and confusion.
Latitude coordinates often are designated by abbreviations. Forty-five degrees north latitude, for example, is written “45 deg N lat” or “45°N.” Sixty-three degrees south latitude is written as “63 deg S lat” or “63°S.” Minutes of arc are abbreviated “min” or symbolized by a prime sign (′). Seconds of arc are abbreviated “sec” or symbolized by a double prime sign (″). So you might see 33 degrees, 12 minutes, 48 seconds north latitude denoted as “33 deg 12 min 48 sec N lat” or as “33°12′48″N.”
As an exercise, try locating the above-described latitude circles on a globe. Then find the town where you live and figure out your approximate latitude. Compare this with other towns around the world. You might be surprised at what you find when you do this. The French Riviera, for example, lies at about the same latitude as Portland, Maine.
Longitude coordinates can range from 180 degrees west, down through zero, and then back up to 180 degrees east. The zero-degree longitude line, also called the prime meridian, passes through Greenwich, England, which is near London. (Centuries ago, when geographers, lexicographers, astronomers, priests, and the other “powers that were” decided on the town through which the prime meridian should pass, they almost chose Paris, France.) The prime meridian is also known as the Greenwich meridian. All the other longitude coordinates are measured with respect to the prime meridian. Every half-circle representing a line of longitude is the same length, namely, half the circumference of Earth, or about 20,000 kilometers (12,500 miles), running from pole to pole. The eastern hemisphere contains all the east-longitude half circles, and the western hemisphere contains all the west-longitude half circles.
There is no such thing as a longitude coordinate greater than 180 degrees, either east or west. The reason for this is the same as the reason there are no latitude coordinates larger than 90 degrees. If there were such points, the result would be a redundant set of coordinates. For example, “200 degrees west longitude” would be the same as 160 degrees east longitude, and “270 degrees east longitude” would be the same as 90 degrees west longitude. One longitude coordinate for any point is enough; more than one is too many. The 180-degree west longitude arc, which might also be called the 180-degree east-longitude arc, is simply called “180 degrees longitude.” A crooked line, corresponding approximately to 180 degrees longitude, is designated as the divider between dates on the calendar. This so-called International Date Line meanders through the western Pacific Ocean, avoiding major population centers.
Longitude coordinates, like their latitude counterparts, can be abbreviated. One hundred degrees west longitude, for example, is written “100 deg W long” or “100°W.” Fifteen degrees east longitude is written “15 deg E long” or “15°E.” Minutes and seconds of arc are used for greater precision; you might see a place at 103 degrees, 33 minutes, 7 seconds west longitude described as being at “103 deg 33 min 7 sec W long” or “103°33′07′″W.”
Find the aforementioned longitude half circles on a globe. Then find the town where you live, and figure out your longitude. Compare this with other towns around the world. As with latitude, you might be in for a shock. For example, if you live in Chicago, Illinois, you are further west in longitude than every spot in the whole continent of South America.
The latitude and longitude of a celestial object is defined as the latitude and longitude of the point on Earth’s surface such that when the object is observed from there, the object is at the zenith (exactly overhead).
Suppose that a star is at x degrees north celestial latitude and y degrees west celestial longitude. If you stand at the point on the surface corresponding to x°N and y°W, then a straight, infinitely long geometric ray originating at the center of Earth and passing right between your eyes will shoot up into space in the direction of the star (Fig. 1-3).
As you might guess, any star that happens to be at the zenith will stay there for only a little while unless you happen to be standing at either of the geographic poles (not likely). Earth rotates with respect to the stars, completing a full circle approximately every 23 hours and 56 minutes. In a few minutes, a star that is straight overhead will move noticeably down toward the western horizon. This effect is exaggerated when you look through a telescope. The greater the magnification, the more vividly apparent is the rotation of Earth.
Figure 1-3. Celestial latitude and longitude.
The next time you get a chance, set up a telescope and point it at some star that is overhead. Use the shortest focal-length eyepiece that the telescope has so that the magnification is high. Center the star in the field of view. If that star is exactly overhead, then its celestial latitude and longitude correspond to yours. For example, if you’re on the shore of Lake Tahoe, your approximate latitude is 39°N and your approximate longitude is 120°W. If you have a telescope pointing straight up and a star is centered in the field of view, then that star’s celestial coordinates are close to 39°N, 120°W. However, this won’t be the case for long. You will be able to watch the star drift out of the field of view. Theoretically, a star stays exactly at a given celestial longitude coordinate (x, y) for an infinitely short length of time—in essence, for no time at all. However, the celestial latitude of each and every star remains constant, moment after moment, hour after hour, day after day. (With the passage of centuries, the celestial latitudes of the stars change gradually because Earth’s axis wobbles slowly. However, this effect doesn’t change things noticeably to the average observer over the span of a lifetime.)
The celestial longitude of any natural object in the sky (except those at the north and south geographic poles) revolves around Earth as the planet rotates on its axis. No wonder people thought for so many centuries that Earth must be the center of the universe! This makes the celestial latitude/longitude scheme seem useless for the purpose of locating stars independently of time. What good can such a coordinate scheme be if its values have meaning only for zero-length micromoments that recur every 23 hours and 56 minutes? This might be okay for the theoretician, but what about people concerned with reality?
It turns out that the celestial latitude/longitude coordinate system is anything but useless. Understanding it will help you understand the more substantial coordinate schemes described in the next sections. And in fact, there is one important set of objects in the sky, a truly nuts-and-bolts group of hardware items, all of which stay at the same celestial latitude and longitude as viewed from any fixed location. These are the geostationary satellites, which lie in a human-made ring around our planet. These satellites orbit several thousand kilometers above the equator, and they revolve right along with Earth’s rotation (Fig. 1-4).
Figure 1-4. Geostationary satellites are all at 0 degrees celestial latitude, and each has a constant celestial longitude.
When it is necessary to point a dish antenna, such as the sort you might use to receive digital television or broadband Internet signals, at a geostationary “bird,” the satellite’s celestial coordinates must be known, in addition to your own geographic latitude and longitude, with great accuracy. The celestial latitude and longitude of a geostationary satellite are constant for any given place on Earth. If a satellite is in a geostationary orbit precisely above Quito, Ecuador, then that is where the “bird” will stay, moment after moment, hour after hour, day after day.
An Internet user fond of broadband and living in the remote South American equatorial jungle might use a dish antenna to transmit and receive data to and from a “bird” straight overhead. The dish could be set to point at the zenith and then left there. (It would need a hole near the bottom to keep it from collecting rain water!) A second user on the shore of Lake Tahoe, in the western United States, would point her dish at some spot in the southern sky. A third user in Tierra del Fuego, at the tip of South America, would point his dish at some spot in the northern sky (Fig. 1-5). None of the three dishes, once positioned, would ever have to be moved and, in fact, should never be moved.
Figure 1-5. A geostationary satellite has constant celestial latitude and longitude, so dish antennas can be aimed at it and then left alone.
If you’re astute, you’ll notice that although the geostationary satellite is directly above the equator, its celestial latitude is zero only with respect to observers located at the equator. If viewed from north of the equator, the satellite shifts a little bit into the southern celestial hemisphere; when observed from south of the equator, the satellite shifts slightly into the northern celestial hemisphere. The reason for this is parallax. The satellite is only a few thousand kilometers away, whereas the stars, whose celestial latitudes remain fixed, are trillions and quadrillions of kilometers distant. This is why the signal paths in Fig. 1-5 aren’t exactly parallel. On a small scale, the phenomenon of parallax allows us to perceive depth with binocular vision. On a large scale, parallax is used to measure the distance to the Sun, the Moon, the other planets in the solar system, and even a few of the nearer stars.
For centuries, navigators and casual observers have used a celestial coordinate system that is in some ways simpler than latitude/longitude and in other ways more complicated. This is the so-called azimuth/elevation scheme. It’s often called az/el for short.
The azimuth of a celestial object is the compass bearing, in degrees, of the point on the horizon directly below that object in the sky. Imagine drawing a line in the sky downward from some object until it intersects the horizon at a right angle. The point at which this intersection occurs is the azimuth of the object. If an object is straight overhead, its azimuth is undefined.
Azimuth bearings are measured clockwise with respect to geographic north. The range of possible values is from 0 degrees (north) through 90 degrees (east), 180 degrees (south), 270 degrees (west), and up to, but not including, 360 degrees (north again). This is shown in Fig. 1-6A. The azimuth bearing of 360 degrees is left out to avoid ambiguity, so the range of possible values is what mathematicians call a half-open interval. Azimuth bearings of less than 0 degrees or of 360 degrees or more are reduced to some value in the half-open interval (0°, 360°) by adding or subtracting the appropriate multiple of 360 degrees.
The elevation of an object in the sky is the angle, in degrees, subtended by an imaginary arc running downward from the object until it intersects the horizon at a right angle. This angle can be as small as 0 degrees when the object is on the horizon, or as large as 90 degrees when the object is directly overhead. If the terrain is not flat, then the horizon is defined as that apparent circle halfway between the zenith and the nadir (the point directly below you, which would be the zenith if you were on the exact opposite side of the planet).
Elevation bearings for objects in the sky are measured upward from the horizon (Fig. 1-6B). Such coordinates are, by convention, not allowed to exceed 90 degrees because that would produce an ambiguous system. Although you might not immediately think of them, elevation bearings of less than 0 degrees are possible, all the way down to –90 degrees. These bearings represent objects below the horizon. While we can’t see such objects, they are there nevertheless. At night, for example, the Sun has a negative elevation. Technically, elevation bearings always have values within the closed interval [–90°, 90°].
Figure 1-6A. Azimuth is the compass bearing. The observer is shown as a black dot.
Figure 1-6B. Elevation is the angle above the horizon. The observer is shown as a black dot.
Various Internet sites provide up-to-the-minute maps of the sky for stargazers. One excellent site can be found by pointing your browser to Weather Underground at the following URL
http://www.wunderground.com
and then clicking on the link that says “Astronomy.” From there, it’s a simple matter of following the online instructions.
Some star maps are drawn so that the sky appears as it would if you lie on your back with your head facing north and your feet facing south. Thus west appears on your right, and east appears on your left (Fig. 1-7a). Others are drawn so that the sky appears as it would if your head were facing south and your feet were facing north, so west appears on your left and east appears on your right (Fig. 1-7b). Points having equal elevation form concentric circles, with the zenith (90 degrees) being a point at the center of the map and the horizon (0 degrees) being a large circle representing the periphery of the map. Simplified sets of grid lines for such az/el maps are shown in both illustrations of Fig. 1-7.
These maps show the Sun and the pole star Polaris as they might appear at midafternoon from a location near Lake Tahoe (or anyplace else on Earth at the same latitude as Lake Tahoe). The gray line represents the path of the Sun across the sky that day. From this you might get some idea of the time of year this map represents. Go ahead and take an educated guess! Here are two hints:
• The Sun rises exactly in the east and sets exactly in the west.
• The situation shown can represent either of two approximate dates.
There are two points in time every year when the Sun’s elevation, measured with respect to the center of its disk, is positive for exactly 12 hours and negative for exactly 12 hours. One of these time points, the vernal equinox, occurs on March 21, give or take about a day; the other, the autumnal equinox, occurs on September 22, give or take about a day. At the equinoxes, the Sun is exactly at the celestial equator; it rises exactly in the east and sets exactly in the west, assuming that the observer is not at either of the geographic poles.
Figure 1-7. Az/el sky maps for viewer lying flat, face-up. At A, top of head facing north; at B, top of head facing south.
The crude celestial maps of Fig. 1-7 show the situation at either of the equinoxes. That is, the date is on or around March 21 or September 22. You can deduce this because the Sun rises exactly in the east and sets exactly in the west, so it must be exactly at the celestial equator. At the latitude of Lake Tahoe, the Sun is 39 degrees away from the zenith (51 degrees above the southern horizon) at high noon on these days. Polaris is 39 degrees above the northern horizon all the time. The entire heavens seem to rotate counterclockwise around Polaris.
What’s this about the Sun being above the horizon for exactly 12 hours and below the horizon for exactly 12 hours at the equinoxes? The stars in the heavens seem to revolve around Earth once every 23 hours and 56 minutes, approximately. Where do the 4 extra minutes come from?
The answer is that the Sun crosses the sky a little more slowly than the stars. Every day, the Sun moves slightly toward the east with respect to the background of stars. On March 21, the Sun is at the celestial equator and is located in a certain position with respect to the stars. This point among the stars is called, naturally enough, the vernal equinox (just as the date is called). It represents an important reference point in the system of celestial coordinates most often used by astronomers: right ascension (RA) and declination (dec). As time passes, the Sun rises about 4 minutes later each day relative to the background of stars. The sidereal (star-based) day is about 23 hours and 56 minutes long; the synodic (sun-based) day is precisely 24 hours long. We measure time with respect to the Sun, not the stars.
Declination is the same as celestial latitude, except that “north” is replaced by “positive” and “south” is replaced by “negative.” The south celestial pole is at dec = –90 degrees; the equator is at dec = 0 degrees; the north celestial pole is at dec = +90 degrees. In the drawings of Fig. 1-7, the Sun is at dec = 0 degrees. Suppose that these drawings represent the situation on March 21. This point among the stars is the zero point for right ascension (RA = 0 h). As springtime passes and the Sun follows a higher and higher course across the sky, the declination and right ascension both increase for a while. Right ascension is measured eastward along the celestial equator from the March equinox in units called hours. There are 24 hours of right ascension in a complete circle; therefore, 1 hour (written 1 h or 1h) of RA is equal to 15 angular degrees.
As the days pass during the springtime, the Sun stays above the horizon for more and more of each day, and it follows a progressively higher course across the sky. The change is rapid during the early springtime and becomes more gradual with approach of the summer solstice, which takes place on June 22, give or take about a day.
At the summer solstice, the Sun has reached its northernmost declination point, approximately dec = +23.5 degrees. The Sun has made one-quarter of a complete circuit around its annual “lap” among the stars and sits at RA = 6 h. This situation is shown in Fig. 1-8 using the same two az/el coordinate schemes as those in Fig. 1-7. The gray line represents the Sun’s course across the sky. As in Fig. 1-7, the time of day is midafternoon. The observer’s geographic latitude is the same too: 39°N.
After the summer solstice, the Sun’s declination begins to decrease, slowly at first and then faster and faster. By late September, the autumnal equinox is reached, and the Sun is once again at the celestial equator, just as it was at the vernal equinox. Now, however, instead of moving from south to north, the Sun is moving from north to south in celestial latitude. At the autumnal equinox, the Sun’s RA is 12 h. This corresponds to 180 degrees.
Now it is the fall season in the northern hemisphere, and the days are growing short. The Sun stays above the horizon for less and less of each day, and it follows a progressively lower course across the sky. The change is rapid during the early fall and becomes slower and slower with approach of the winter solstice, which takes place on December 21, give or take about a day.
At the winter solstice, the Sun’s declination is at its southernmost point, approximately dec = –23.5 degrees. The Sun has made three-quarters of a complete circuit around its annual “lap” among the stars and sits at RA = 18 h. This is shown in Fig. 1-9 using the same two az/el coordinate schemes as those in Figs. 1-7 and 1-8. The gray line represents the Sun’s course across the sky. As in Figs. 1-7 and 1-8, the time of day is midafternoon. The observer hasn’t moved either, at least in terms of geographic latitude; this point is still at 39°N. (Maybe the observer is in Baltimore now or in the Azores. Winter at Lake Tahoe can be rough unless you like to ski.)
Figure 1-8. Az/el sky maps for midafternoon at 39 degrees north latitude on or around June 21.
Figure 1-9. Az/el sky maps for midafternoon at 39 degrees north latitude on or around December 21.
After the winter solstice, the Sun’s declination begins to increase gradually and then, as the weeks pass, faster and faster. By late March, the Sun reaches the vernal equinox again and crosses the celestial equator on its way to warming up the northern hemisphere for another spring and summer. The “lap” is complete. The Sun’s complete circuit around the heavens takes about 365 solar days plus 6 hours and is the commonly accepted length of the year in the modern calendar. In terms of the stars, there is one extra “day” because the Sun has passed from west to east against the far reaches of space by a full circle.
The path that the Sun follows against the background of stars during the year is a slanted celestial circle called the ecliptic. Imagine Earth’s orbit around the Sun; it is an ellipse (not quite a perfect circle, as we will later learn), and it lies in a flat geometric plane. This plane, called the plane of the ecliptic, is tilted by 23.5 degrees relative to the plane defined by Earth’s equator. If the plane of the ecliptic were made visible somehow, it would look like a thin gray line through the heavens that passes through the celestial equator at the equinoxes, reaching a northerly peak at the June solstice and a southerly peak at the December solstice. If you’ve ever been in a planetarium, you’ve seen the ecliptic projected in that artificial sky, complete with RA numbers proceeding from right to left from the vernal equinox.
Suppose that you convert the celestial latitude and longitude coordinate system to a Mercator projection, similar to those distorted maps of the world in which all the parallels and meridians show up as straight lines. The ecliptic would look like a sine wave on such a map, with a peak at +23.5 degrees (the summer solstice), a trough at –23.5 degrees (the winter solstice), and two nodes (one at each equinox). This is shown in Fig. 1-10. From this graph, you can see that the number of hours of daylight, and the course of the Sun across the sky, changes rapidly in March, April, September, and October and slowly in June, July, December, and January. Have you noticed this before and thought it was only your imagination?
Figure 1-10. The ecliptic (gray line) is the path that the Sun follows in its annual “lap around the heavens.”
QuizRefer to the text if necessary. A good score is 8 correct. Answers are in the back of the book.
1. Which of the following points or objects seems to stay fixed in the sky all the time?
(a) The vernal equinox
(b) The background of stars
(c) The Sun
(d) Polaris
2. What is the declination represented by the south celestial pole?
(a) 18 h
(b) 0°
(c) –90
(d) It cannot be defined because it changes with time.
3. What is the celestial longitude of the winter solstice?
(a) 18 h
(b) 0°
(c) –90
(d) It cannot be defined because it changes with time.
4. A point is specified as having a celestial latitude of 45°30′00″N. This is equivalent to how many degrees as a decimal fraction?
(a) 45.5°
(b) 45.3°
(c) 30.00°
(d) There is not enough information to tell.
5. How many hours of right ascension correspond to one-third of a circle?
(a) 3 h
(b) 6 h
(c) 12 h
(d) None of the above
6. How many sidereal days are there in one full calendar year?
(a) Approximately 366.25
(b) Approximately 365.25
(c) Approximately 364.25
(d) It depends on the celestial latitude of the observer.
7. One second of arc represents what fraction of a complete circle?
(a) 1/60
(b) 1/3600
(c) 1/86,400
(d) 1/1,296,000
8. The celestial latitude/longitude frame of reference
(a) is fixed relative to the background of stars.
(b) is fixed relative to the Sun.
(c) is fixed relative to geostationary satellites.
(d) is not fixed relative to anything.
9. Which of the following represents an impossible or improperly expressed coordinate value?
(a) RA = 12 h
(b) dec = +100
(c) 103 deg 00 min 20 sec W long
(d) 23°S
10. Azimuth is another name for
(a) right ascension.
(b) compass bearing.
(c) celestial latitude.
(d) celestial longitude.
