Relativity theory has a reputation as something only geniuses can understand. However, the basics of relativity are no more difficult to grasp than the fundamentals of any other theory. Some of the ideas put forth to explain astronomical observations before Einstein came up with his theory were more esoteric than relativity itself. This chapter contains a little bit of mathematics, but it doesn’t go beyond the middle-school level.
There are two aspects to relativity theory: the special theory and the general theory. The special theory involves relative motion, and the general theory involves acceleration and gravitation.
Before we get into relativity, let’s find out what follows from the hypotheses that the speed of light is absolute, constant, and finite and that it is the highest speed anything can attain.
When he became interested in light, space, and time, Einstein pondered the results of experiments intended to find out how the Earth moves relative to the supposed medium that carries electromagnetic (EM) waves such as visible light. Einstein decided that such a medium doesn’t exist—EM waves can travel through a perfect vacuum.
Before Einstein’s time, physicists determined that light has wavelike properties and in some ways resembles sound. However, light travels much faster than sound. Also, light can propagate through a vacuum, whereas sound cannot. Sound waves require a material medium such as air, water, or metal to get from one place to another. Many scientists suspected that light also must need some sort of medium to travel through space. What could exist everywhere, even between the stars and galaxies, and even in a jar from which all the air was pumped out? This mysterious medium was called luminiferous ether, or simply ether.
If the ether exists, some scientists wondered, how could it pass right through everything, even the entire Earth, and get inside an evacuated chamber? How could the ether be detected? One idea was to see if the ether “blows” against the Earth as our planet orbits around the Sun, as the Solar System orbits around the center of the Milky Way galaxy, and as our galaxy drifts through the Cosmos. If there is an “ether wind,” then the speed of light ought to be different in different directions. This, it was reasoned, should occur for the same reason that a passenger on a fast-moving truck measures the speed of sound waves coming from the front as faster than the speed of sound waves coming from behind.
In 1887, an experiment was done by two physicists named Albert Michelson and Edward Morley in an attempt to find out how fast the “ether wind” is blowing and from what direction. The Michelson-Morley experiment, as it became known, showed that the speed of light is the same in all directions. This cast doubt on the ether theory. If the ether exists, then according to the results obtained by Michelson and Morley, it must be moving right along with the Earth. This is quite a coincidence; it implies that the Earth is stationary relative to absolute space, and no one believed that in 1887. Attempts were made to explain away this result by suggesting that the Earth drags the ether along with itself. Einstein could not believe this. He decided that the results of the Michelson-Morley experiment had to be taken at face value: The speed of light is constant in every direction. Einstein believed that the Michelson-Morley experiment would have the same outcome for observers on the Moon, on any other planet, on a space ship, or anywhere in the Universe.
Einstein rejected the notion of luminiferous ether. Instead, he proposed an axiom, a fundamental rule of the Universe: The speed at which light (and any other EM field) travels in a vacuum is the same no matter what the direction and regardless of the motion of the observer with respect to the EM energy source. Then he set out to deduce what logically follows from this assumption.
Einstein did all his work by using a combination of mathematics and daydreaming that he called “mind journeys.” He wasn’t an experimentalist but a theorist. There is a saying in physics: “One experimentalist can keep a dozen theorists busy.” Einstein turned this inside out. His theories have kept thousands of experimentalists occupied.
One of the first results of Einstein’s speed-of-light axiom is the fact that there can be no such thing as an absolute time standard. It is impossible to synchronize the clocks of two obervers so that they will see both clocks as being in exact agreement unless both observers occupy the exact same point in space.
In recent decades we have built atomic clocks, and we claim that they are accurate to within billionths of a second (where a billionth is 0.000000001 or 10–9). However, this has meaning only when we are right next to such a clock. If we move a little distance away, then the light (or any other signal that we know of) takes some time to get to us, and this throws the clock’s reading off.
The speed of EM-field propagation, the fastest speed known, is approximately 300 million meters per second (3.00 × 108 m/s), or 186,000 miles per second (1.86 × 105 mi/s). A beam of light therefore travels about 300 m (984 ft) in 0.000001 s (one microsecond or 1 µs). If you move a little more than the length of a football field away from a superaccurate billionth-of-a-second atomic clock, the clock will appear to be in error by a microsecond, or 1,000 billionths of a second. If you go to the other side of the world, where the radio signal from that clock must travel 20,000 km (12,500 mi) to reach you, the time reading will be off by 0.067 s, or 67 thousandths of a second. If you go to the Moon, which is about 400,000 km (250,000 mi) distant, the clock will be off by approximately 1.33 s.
If scientists ever discover an energy field that can travel through space instantaneously regardless of the distance, then the conundrum of absolute time will be resolved. In practical scenarios, however, the speed of light is the fastest possible speed. (Some recent experiments suggest that certain effects can propagate faster than the speed of light over short distances, but no one has demonstrated this on a large scale yet, much less used such effects to transmit any information such as data from an atomic clock.) We can say that the speed of light is the speed of time. Distance and time are inextricably related.
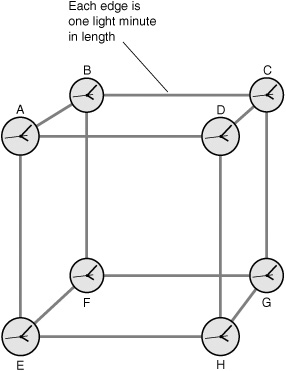
Imagine that there are eight clocks in space arranged at the vertices of a gigantic cube. Each edge of the cube measures 1 light-minute, or approximately 18 million km (11 million mi) long, as shown in Fig. 16-1. We are given a challenge: Synchronize the clocks so that they agree within the limit of visibility, say, to within 1 second of each other. Do you suppose that this will be easy?
Because the clocks are so far apart, the only way we can ascertain what they say is to equip them with radio transmitters that send time signals. Alternatively, if we have a powerful enough telescope, we can observe them and read them directly by sight. In either case, the information that tells us what the clocks say travels to us at the speed of light. We get in our space ship and maneuver ourselves so that we are in the exact center of the cube, equidistant from all eight clocks. Then we proceed to synchronize them using our remote-control, wireless two-way data communications equipment. Thank heaven for computers! The task is accomplished in a just a few minutes. It can’t be done instantaneously, of course, because our command signals take the better part of a minute to reach the clocks from our central location, and then the signals coming back from the clocks take just as long to get to us so that we can see what they say. Soon, however, everything is in agreement. Clocks A through H all tell the same time to within a fraction of a second.
Figure 16-1. A hypothetical set of eight clocks, arranged at the vertices of a cube that measures one light-minute on each edge. How will we synchronize these clocks?
Satisfied with our work, we cruise out of the cube because there’s nothing there of any real interest except a few small meteoroids. We take a look back at the clocks, mainly to admire our work but also because, as technicians, we are instinctively programmed to suspect that something can always go wrong. What do we see? To our dismay, the clocks have already managed to get out of sync. Muttering a curse or two, we take our ship back to the center of the cube to correct the problem. However, when we get there, there is no problem to correct! The clocks are all in agreement again.
You can guess what is happening here. The clock readings depend on how far their signals must travel to reach us. For an observer at the center of the cube, the signals from all eight clocks, A through H, arrive from exactly the same distance. However, this is not true for any other point in space. We have synchronized the clocks for one favored vantage point; if we go somewhere else, we will have to synchronize them all over again. This can be done, but then the clocks will be synchronized only when observed from the new favored vantage point. There is a unique sync point—the spot in space from which all eight clocks read the same—for each coordination of the clocks.
No sync point is more valid than any other from a scientific standpoint. If the cube happens to be stationary relative to some favored reference point such as Earth, we can synchronize the clocks, for convenience, from that reference point. However, if the cube is moving relative to our frame of reference, we will never be able to keep the clocks synchronized. Time depends on where we are and on whether or not we are moving relative to whatever device we use to indicate the time. Time is not absolute, but relative, and there is no getting around it.
The relative location of an observer in space affects the relative readings of clocks located at different points. Similarly, relative motion in space affects the apparent rate at which time “flows.” Isaac Newton hypothesized that time flows in an absolute way and that it constitutes a fundamental constant in the Universe. Einstein showed that this is not the case; it is the speed of light, not time, that is constant. In order to understand why relativistic time dilation occurs based on Einstein’s hypothesis, let’s conduct a “mind experiment.”
Suppose that we have a space ship equipped with a laser/sensor on one wall and a mirror on the opposite wall (Fig. 16-2). Imagine that the laser/sensor and the mirror are positioned so that the light ray from the laser must travel perpendicular to the axis of the ship, perpendicular to its walls, and (once we get it moving) perpendicular to its direction of motion. The laser and mirror are adjusted so that they are separated by 3 m. Because the speed of light in air is approximately 300 million (3 × 108) m/s, it takes 10–8 s, or 10 nanoseconds (10 ns), for the light ray to get across the ship from the laser to the mirror and another 10 ns for the ray to return to the sensor. The ray therefore requires 20 ns to make one round trip from the laser/sensor to the mirror and back again.
Our laser emits pulses of extremely brief duration, much shorter than 20 ns. We measure the time increment using an extremely sophisticated oscilloscope so that we can observe the pulses going out and coming back and measure the time lag between them. This is a special clock; its timekeeping ability is based on the speed of light, which Einstein proposed is constant no matter from what point of view it is observed. There is no better way to keep time.
Figure 16-2. A space ship equipped with a laser clock. This is what an observer in the ship always sees.
Suppose that we start up the ship’s engines and get moving. We accelerate faster and faster, with the goal of eventually reaching speeds that are nearly the speed of light. Suppose that we manage to accelerate to a sizable fraction of the speed of light, and then we shut off the engines so that we are coasting through space. You ask, “Relative to what are we moving?” This, as we shall see, is an important question! For now, suppose that we measure speed with respect to Earth.
We measure the time it takes for the laser to go across the ship and back again. We are riding along with the laser, the mirror, and all the luxuries of a spacecraft that is only 3 m (about 10 ft) wide. We find that the time lag is still exactly the same as it was when the ship was not moving relative to Earth; the oscilloscope still shows a delay of 20 ns. This follows directly from Einstein’s axiom. The speed of light has not changed because it cannot. The distance between the laser and the mirror has not changed either. Therefore, the round trip takes the same length of time as it did before we got the ship moving.
If we accelerate so that the ship is going 60 percent, then 70 percent, and ultimately 99 percent of the speed of light, the time lag will always be 20 ns as measured from a reference frame, or point of view, inside the ship.
Let’s add another axiom to Einstein’s: In free space, light beams always follow the shortest possible distance between two points. Normally, this is a straight line. You ask, “How can the shortest path between two points in space be anything other than a straight line?” This is another good question. We’ll deal with it later in this chapter. For now, note that light beams appear to follow straight lines through free space as long as the observer is not accelerating relative to the light source. Relative motion does not affect the “straightness” of light rays. (As we will see, acceleration does.)
Imagine now that we are outside the ship and are back on Earth. We are equipped with a special telescope that allows us to see inside the ship as it whizzes by at a significant fraction of the speed of light. We can see the laser, the mirror, and even the laser beam itself because the occupants of the space vessel have temporarily filled it with smoke to make the viewing easy for us. (They have their pressure suits on so that they can breathe.)
What we see is depicted in Fig. 16-3. The laser beam still travels in straight lines, and it still travels at 3 × 108 m/s relative to us. This is true because of Einstein’s axiom concerning the speed of light and our own hypothesis to the effect that light rays always appear to travel in straight lines as long as we are not accelerating. However, the rays have to travel farther than 3 m to get across the ship. The ship is going so fast that by the time the ray of light has reached the mirror from the laser, the ship has moved a significant distance forward. The same thing happens as the ray returns to the sensor from the mirror. As a result of this, it will seem to us, as we watch the ship from Earth, to take more than 20 ns for the laser beam to go across the ship and back.
As the ship goes by, time appears to slow down inside it, as seen from a “stationary” point of view. Inside the ship, though, the “speed of time” seems entirely normal. The faster the ship goes, the greater is this discrepancy. As the speed of the ship approaches the speed of light, the time dilation factor can become large indeed; in theory, there is no limit to how great it can become. You can visualize this by imagining Fig. 16-3 stretched out horizontally so that the light rays have to travel almost parallel to the direction of motion, as seen from the “stationary” reference frame.
There exists a mathematical relationship between the speed of the space ship in the foregoing “mind experiment” and the extent to which time is dilated. Let tship be the number of seconds that appear to elapse on the moving ship as 1 s elapses as measured by a clock next to us as we sit in our Earth-based observatory. Let u be the speed of the ship as a fraction of the speed of light. Then
Figure 16-3. This is what an external observer sees as the laser-clock-equipped space ship whizzes by at a sizable fraction of the speed of light.
tship = (1 – u2)1/2
The 1/2 power is an alternative and popular way to denote the square root. The time dilation factor (let’s call it k) is the reciprocal of this:
k = 1 / [ (1 – u2)1/2 ] = (1 – u2)–1/2
Let’s see how great the time dilation factor is if the space ship is going half the speed of light. In this case, u = 0.5. If 1 s passes on Earth, then according to an Earthbound observer:
tship = (1 – 0.52)1/2
= (1 – 0.25)1/2
= 0.751/2
= 0.87 s
That is, 0.87 s will seem to pass on the ship as 1 s passes as we measure it while watching the ship from Earth. This means that the time dilation factor is 1/0.87, or approximately 1.15. Of course, on the ship, time will seem to flow normally.
Just for fun, let’s see what happens if the ship is going 99 percent of the speed of light. In this case, u = 0.99. If 1 s passes on Earth, then we, as Earthbound observers, will see this:
tship = (1 – 0.992)1/2
= (1 – 0.98)1/2
= 0.021/2
= 0.14 s
That is, 0.14 s will seem to pass on the ship as 1 s passes on Earth. The time dilation factor k in this case is 1/0.14, or approximately 7.1. Time flows more than seven times more slowly on a ship moving at 99 percent of the speed of light than it flows on Earth—from the reference frame of someone on Earth.
As you can imagine, this has implications for time travel. According to the special theory of relativity, if you could get into a space ship and travel fast enough and far enough, you could propel yourself into the future. You might travel to a distant star, return to Earth in what seemed to you to be only a few months, and find yourself in the year A.D. 5000. When science-fiction writers realized this in the early 1900s just after Einstein published his work, they took advantage of it.
Relativistic speeds—that is, speeds high enough to cause significant time dilation—cause objects to appear foreshortened in the direction of their motion. As with time dilation, relativistic spatial distortion occurs only from the point of view of an observer watching an object speed by at a sizable fraction of the speed of light.
If we travel inside a space ship, regardless of its speed, everything appears normal as long as our ship is not accelerating. We can cruise along at 99.9 percent of the speed of light relative to the Earth, but if we are inside a space ship, it is always stationary relative to us. Time, space, and mass appear normal from the point of view of passengers on a relativistic space journey. However, as we watch the space ship sail by from the vantage point of Earth, its length decreases as its speed increases. Its diameter is not affected. The extent to which this happens is the same as the extent to which time slows down.
Let L be the apparent length of the moving ship as a fraction of its length when it is standing still relative to an observer. Let u be the speed of the ship as a fraction of the speed of light. Then
L = (1 – u2)1/2
This effect is shown in Fig. 16-4 for various relative forward speeds. The foreshortening takes place entirely in the direction of motion. This produces apparent physical distortion of the ship and everything inside, including the passengers. It’s sort of like those mirrors in fun houses that are concave in only one dimension and reflect your image all scrunched up. As the speed of the ship approaches the speed of light, its observed length approaches zero.
Figure 16-4. As an object moves faster and faster, it grows shorter and shorter along the axis of its motion.
Spatial distortion is a curious phenomenon. You might wonder, based on this result, about the shapes of photons. They are the particles of which visible light and all other EM radiation are comprised. Photons travel at the speed of light. Does that mean they are infinitely thin, flat disks or squares or triangles hurtling sidelong through space? No one has ever seen a photon, so no one knows how they are shaped. It is interesting to suppose that they are two-dimensional things and, as such, have zero volume. However, if they have zero volume, how can we say that they exist?
Scientists know a lot about what happens to objects as they approach the speed of light, but it’s intellectually dangerous to extrapolate and claim to know what would happen if the speed of light could be attained by a material thing. We will see shortly that no physical object (such as a space ship) can reach the speed of light, so the notion of a real object being squeezed down to zero thickness is nothing more than an academic fantasy. As for photons, comparing them with material particles such as bullets or baseballs is an unjustified intuitive leap. We cannot bring a photon to rest, nor can we shoot a bullet or throw a baseball at the speed of light. As they might say in certain places, “Baseballs and photons ain’t the same animals.”
Another interesting effect of relativistic speeds is an increase in the masses of objects as they move faster and faster. This increase occurs to the same extent as the decrease in length and the slowing down of time.
If we travel inside a space ship, regardless of its speed, the masses of all the objects in the ship with us appear normal as long as our ship is not accelerating. However, from the vantage point of Earth, the mass of the ship and the masses of all the atoms inside it increase as its speed increases.
Let m be the mass of the moving ship as a multiple of its mass when it is stationary relative to an observer. Let u be the speed of the ship as a fraction of the speed of light. Then
m = 1/(1 – u2)1/2 = (1 – u2)–1/2
This is the same as the factor k that we defined a little while ago. It is always greater than or equal to 1.
Look again at Fig. 16-4. As the space ship moves faster, it scrunches up. Imagine now that it also becomes more massive. The combination of smaller size and greater mass produces a dramatic increase in density at relativistic speeds.
Suppose that the rest mass (the mass when stationary) of our ship is 10 metric tons. When it speeds by at half the speed of light, its mass increases to a little more than 11 metric tons. At 80 percent of the speed of light, its mass is roughly 17 metric tons. At 95 percent of the speed of light, the ship’s mass is about 32 metric tons. At 99.9 percent of the speed of light, the ship’s mass is more than 220 metric tons. And so it can go indefinitely. As the speed of the ship approaches the speed of light, its mass grows larger and larger without limit.
It’s tempting to suppose that the mass of an object, if it could be accelerated all the way up to the speed of light, would become infinite. After all, as u approaches 1 (or 100 percent), the value of m in the preceding formula increases without limit. However, it’s one thing to talk about what happens as a measured phenomenon or property approaches some limit; it is another thing entirely to talk about what happens when that limit is actually reached, assuming that it can be reached.
No one has ever seen a photon at rest. No one has ever seen a space ship moving at the speed of light, nor will they ever. No finite amount of energy can accelerate any real object to the speed of light. This is so because of the way in which the mass increases as the speed of an object approaches the speed of light. Even if it were possible to move a real object at the speed of light relative to some point of observation, the mass-increase factor, as determined by the preceding formula, would be meaningless. To calculate it, we would have to divide by zero, and division by zero is not defined. (If you tell a theoretical mathematician that “one over zero equals infinity,” you will get, at the very least, a raised eyebrow.)
The more massive a speeding space ship becomes, the more powerful is the rocket thrust necessary to get it moving faster. As a space ship approaches the speed of light, its mass becomes arbitrarily great. This makes it harder and harder to give it any more speed. Using a mathematical technique called integral calculus, astronomers and physicists have proven that no finite amount of energy can propel a space ship to the speed of light. The mass increases too fast. The function “blows up.”
You’ve heard expressions such as electron rest mass, which refers to the theoretical mass of an electron when it is not moving relative to an observer. If an electron is observed whizzing by at relativistic speed, it has a mass greater than its rest mass and thus will have momentum and kinetic energy greater than is implied by the formulas used in classical physics. This, unlike spatial distortion, is more than a mere “mind experiment.” There is little practical concern about spatial distortion in most situations, at least nowadays. (A thousand years from now, when we are roaming among the stars, we should expect that things will be different!) When electrons move at high enough speed, they attain properties of much more massive particles and acquire some of the properties of x-rays or gamma rays such as are emitted by radioactive substances. There is a name for high-speed electrons that act this way: beta particles.
Physicists take advantage of the relativistic effects on the masses of protons, helium nuclei, neutrons, and other subatomic particles. When these particles are subjected to powerful electrical and magnetic fields in a device called a particle accelerator, they get moving so fast that their mass increases because of relativistic effects. When the particles strike atoms of matter, the nuclei of those target atoms are fractured. It takes quite a wallop to break up the nucleus of an atom! When this happens, energy can be released in the form of infrared, visible light, ultraviolet, x-rays, and gamma rays, as well as a potpourri of exotic particles.
If astronauts ever travel long distances through space in ships moving at speeds near the speed of light, relativistic mass increase will be a dire concern. While the astronaut’s own bodies won’t seem unnaturally massive, and the objects inside the ship will appear to have normal mass too, the particles whizzing by outside will gain real mass. It is scary enough to think about what will happen when a 1-kg meteoroid strikes a space ship traveling at 99.9 percent of the speed of light. But that 1-kg stone will mass more than 22 kg when u = 0.999, that is, at 99.9 percent of the speed of light. As if this is not bad enough, every atomic nucleus outside the ship will strike the vessel’s shell at relativistic speed, producing deadly radiation.
Relativistic time dilation and mass increase have been measured under controlled conditions, and the results concur with Einstein’s formulas stated earlier. Thus these effects are more than mere tricks of the imagination.
To measure time dilation, a superaccurate atomic clock was placed on board an aircraft, and the aircraft was sent up in flight to cruise around for a while at several hundred kilometers per hour. Another atomic clock was kept at the place where the aircraft took off and landed. Although the aircraft’s speed was only a tiny fraction of the speed of light and the resulting time dilation was exceedingly small, the accumulated discrepancy was large enough to measure. When the aircraft arrived back at the terminal, the clocks, which had been synchronized (when placed right next to each other, of course!) before the trip began, were compared. The clock that had been on the aircraft was a little behind the clock that had been resting comfortably on Earth.
To measure mass increase, particle accelerators are used. It is possible to determine the mass of a moving particle based on its known rest mass and the kinetic energy it possesses as it moves. When the mathematics is done, Einstein’s formula is always shown to be correct.
There is no absolute standard for position in the Universe, nor is there an absolute standard for velocity. Another way of saying this is that any reference frame is just as valid as any other as long as acceleration does not take place. The notions of “the center of the Universe” and “at rest” are relative. If we measure position or velocity, we must do so with respect to something, such as Earth or the Sun or a space ship coasting through the void.
Einstein noticed something special about accelerating reference frames compared with those that are not accelerating. This difference is apparent if we consider the situation of an observer who is enclosed in a chamber that is completely sealed and opaque.
Imagine that you are in a space ship in which the windows are covered up and the radar and navigational equipment have been placed on standby. There is no way for you to examine the surrounding environment and determine where you are, how fast you are moving, or what direction you are moving. However, you can tell whether or not the ship is accelerating. This is so because acceleration always produces a force on objects inside the ship.
When the ship’s engines are fired and the vessel gains speed in the forward direction, all the objects in the ship (including your body) are subjected to a force directed backward. If the ship’s retro rockets are fired so that the ship slows down (decelerates), everything in the ship is subjected to a force directed forward. If rockets on the side of the ship are fired so that the ship changes direction without changing its speed, this too is a form of acceleration and will cause sideways forces on everything inside the ship. Some examples are illustrated in Fig. 16-5.
The greater the acceleration, or change in velocity, to which the space ship is subjected, the greater is the force on every object inside it. If m is the mass of an object in the ship (in kilograms) and a is the acceleration of the ship (in meters per second per second), then the force F (in newtons) is their product:
Figure 16-5. When a vessel in deep space is not accelerating, there is no force on the objects inside. When the ship accelerates, there is always a force on the objects inside.
F = ma
This is one of the most well-known formulas in physics.
This “acceleration force” occurs even when the ship’s windows are covered up, the radar is switched off, and the navigational equipment is placed on standby. There is no way the force can be blocked out. In this way, Einstein reasoned, it is possible for interstellar travelers to determine whether or not their ship is accelerating. Not only this, but they can calculate the magnitude of the acceleration as well as its direction. When it comes to acceleration, there are absolute reference frames.
Imagine that our space ship, instead of accelerating in deep space, is set down on the surface of a planet. It might be tail-downward, in which case the force of gravity pulls on the objects inside as if the ship is accelerating in a forward direction. It might be nose-downward so that gravity pulls on the objects inside as if the ship is decelerating. It could be oriented some other way so that the force of gravity pulls on the objects inside as if the ship is changing course in a lateral direction. Acceleration can consist of a change in speed, a change in direction, or both.
If the windows are kept covered, the radar is shut off, and the navigational aids are placed on standby, how can passengers in such a vessel tell whether the force is caused by gravitation or by acceleration? Einstein’s answer: They can’t tell. In every respect, acceleration force manifests itself in precisely the same way as gravitational force.
From this notion came the equivalence principle, also known as Einstein’s principle of equivalence. The so-called acceleration force is exactly the same as gravitation. Einstein reasoned that the two forces act in an identical way on everything, from human bodies to subatomic particles and from light rays to the very fabric of space-time. This is the cornerstone of the theory of general relativity.
Imagine that you are in a space ship traveling through deep space. The ship’s rockets are fired, and the vessel accelerates at an extreme rate. Suppose that the laser apparatus described earlier in this chapter is in the ship, but instead of a mirror on the wall opposite the laser, there is a screen. Before the acceleration begins, you align the laser so that it shines at the center of the screen (Fig. 16-6). What will happen when the rockets are fired and the ship accelerates?
Figure 16-6. As seen from within a nonaccelerating space ship, a laser beam travels in a straight line across the vessel.
In a real-life scenario, the spot from the laser will not move on the screen enough for you to notice. This is so because any reasonable (that is, non-life-threatening) rate of acceleration will not cause sufficient force to influence the path of the beam. However, let’s suspend our disbelief and imagine that we can accelerate the vessel at any rate, no matter how great, without being squashed against the ship’s rear wall. If we accelerate fast enough, the ship pulls away from the laser beam as the beam travels across the ship. We, looking at the situation from inside the ship, see the light beam follow a curved path (Fig. 16-7). A stationary observer on the outside sees the light beam follow a straight path, but the vessel pulls out ahead of the beam (Fig. 16-8).
Regardless of the reference frame, the ray of light always follows the shortest possible path between the laser and the screen. When viewed from any nonaccelerating reference frame, light rays appear straight. However, when observed from accelerating reference frames, light rays can appear curved. The shortest distance between the two points at opposite ends of the laser beam in Fig. 16-7 is, in fact, curved. The apparently straight path is in reality longer than the curved one, as seen from inside the accelerating vessel! It is this phenomenon that has led some people to say that “space is curved” in a powerful acceleration field. According to the principle of equivalence, powerful gravitation causes the same sort of spatial curvature as acceleration.
For spatial curvature to be as noticeable as it appears in Figs. 16-7 and 16-8, the vessel must accelerate at an extremely large pace. The standard unit of acceleration is the meter per second per second, or meter per second squared (m/s2). Astronauts and aerospace engineers also express acceleration in units called gravities (symbolized g), where one gravity (1 g) is the acceleration that produces the same force as the gravitational field of Earth at the surface, approximately 9.8 m/s2. (Don’t confuse the abbreviation for gravity or gravities with the abbreviation for grams. Pay attention to the context if you see a unit symbolized g.) Figures 16-7 and 16-8 show the situation for an acceleration of many thousands of gravities. If you weigh 150 pounds on Earth, you would weigh many tons in a ship accelerating at a rate, or in a gravitational field of such intensity, so as to cause that much spatial curvature. In real life, no one could survive such force. No living human being will ever directly witness the sort of light-beam curvature shown in these illustrations.
Figure 16-7. As seen from within a space ship accelerating at an extreme rate, a laser beam travels in a curved path across the vessel.
Figure 16-8. When viewed from a “stationary” reference frame outside the ship, the accelerating vessel pulls away from the straight-line path of the laser beam, so the beam strikes the screen off-center.
Is all this a mere academic exercise? Are there actually gravitational fields powerful enough to bend light rays significantly? Yes. They exist near the event horizons of black holes.
The spatial curvature caused by intense acceleration or gravitation produces an effective slowing down of time. Remember the fundamental axiom of special relativity: The speed of light is constant no matter what the point of view. The laser beam traveling across the space ship, as shown in many of the illustrations in this chapter, always moves at the same speed. This is one thing about which all observers, in all reference frames, must agree.
The path of the light ray, as it travels from the laser to the screen, is longer in the situation shown by Fig. 16-7 than in the situation shown by Fig. 16-6. This is so in part because the ray takes a diagonal path rather than traveling straight across. In addition, however, the path is curved. This increases the time interval even more. From the vantage point of a passenger in the space ship, the curved path shown in Fig. 16-7 represents the shortest possible path the light ray can take across the vessel between the point at which it leaves the laser and the point at which it strikes the screen. The laser device itself can be turned slightly, pointing a little bit toward the front of the ship; this will cause the beam to arrive at the center of the screen (Fig. 16-9) instead of off-center. However, the path of the beam is still curved and is still longer than its path when the ship is not accelerating (see Fig. 16-6). The laser represents the most accurate possible timepiece, because it is based on the speed of light, which is an absolute constant. Thus time dilation is produced by acceleration not only as seen by observers looking at the ship from the outside but also for passengers within the vessel itself. In this respect, acceleration and gravitation are more powerful “time dilators” than relative motion.
Suspending our disbelief again, and assuming that we could experience such intense acceleration force (or gravitation) without being physically crushed, we will actually perceive time as slowing down inside the vessel under conditions such as those that produce spatial curvature, as shown in Fig. 16-7 or Fig. 16-9. Clocks will run more slowly even from reference frames inside the ship. In addition, everything inside the ship will appear warped out of shape.
Figure 16-9. Even if the laser is turned so the light ray hits the center of the screen, the path of the ray is curved when the ship accelerates at a high rate.
If the acceleration or gravitation becomes far more powerful still (Fig. 16-10), the spatial curvature and the time dilation will be considerable. You will look across the ship at your fellow travelers and see grotesquely elongated or foreshortened faces (depending on which way you are oriented inside the vessel). Your voices will deepen. It will be like a science-fiction movie. You and all the other passengers in the ship will know that something extraordinary is happening. This same effect will be observed by people foolish enough to jump into a black hole (yet again ignoring the fact that they would be stretched and crushed at the same time by the force).
When Einstein developed his general theory of relativity, some of the paradoxes inherent in special relativity were resolved. (These paradoxes are avoided here because discussing them would only confuse you.) In particular, light rays from distant stars were observed as they passed close to the Sun to see whether or not the Sun’s gravitational field, which is quite strong near its surface, would bend the light rays. This bending would be observed as a change in the apparent position of a distant star in the sky as the Sun passes close to it.
Figure 16-10. If the acceleration is great enough, the spatial curvature becomes extreme.
The problem with this type of observation was, as you might guess, the fact that the Sun is far brighter than any other star in the sky, and the Sun’s glare normally washes out the faint illumination from distant stars. However, during a total solar eclipse, the Sun’s disk is occulted by the Moon. The angular diameter of the Moon in the sky is almost exactly the same as that of the Sun, so light from distant stars passing close to the Sun can be seen by Earthbound observers during a total eclipse. When this experiment was carried out, the apparent position of a distant star was offset by the presence of the Sun, and this effect took place to the same extent as Einstein’s general relativity formulas said it should.
More recently, the light from a certain quasar has been observed as it passes close to a suspected black hole. On its way to us, the light from the quasar follows multiple curved paths around the dark, massive object. This produces several images of the quasar, arranged in the form of a cross with the dark object at the center.
The curvature of space in the presence of a strong gravitational field has been likened to a funnel shape (Fig. 16-11), except that the surface of the funnel is three-dimensional rather than two-dimensional. The shortest distance in three-dimensional space between any two points near the gravitational source is always a curve with respect to four-dimensional space. This is impossible for most (if not all) people to envision directly without “cheating” by taking away one dimension. But the mathematics is straightforward enough, and observations have shown that it correctly explains the phenomenon.
Figure 16-11. Spatial curvature in the vicinity of an object that produces an intense gravitational field.
We have conducted “mind experiments” in this chapter, many of which require us to suspend reality. In real life, scenarios such as these would kill anyone attempting to make the observations. So why is relativity theory important? If space is bent and time is slowed by incredibly powerful gravitational fields, so what?
The theory of general relativity plays an important role in astronomers’ quests to unravel the mysteries of the structure and evolution of the Universe. On a cosmic scale, gravitation acquires a different aspect than on a local scale. A small black hole, such as that surrounding a collapsed star, is dense and produces gravitation strong enough to destroy any material thing crossing the event horizon. However, if a black hole contains enough mass, the density within the event horizon is not so large. Black holes with quadrillions of solar masses can exist, at least in theory, without life-threatening forces at any point near their event horizons. If such a black hole is ever found, and if we develop space ships capable of intergalactic flight, we will be able to cross its event horizon unscathed and enter another Universe. We can be sure someone will try it if they think they can do it, even if they are never able to communicate back to us what they find.
According to some theorists, we need not travel far to find the ultimate black hole. It has been suggested that our entire Universe is such an object and that we are inside it.
 Quiz
QuizRefer to the text if necessary. A good score is 8 correct. Answers are in the back of the book.
1. A common unit of acceleration is the
(a) meter per second.
(b) kilometer per second.
(c) kilometer per hour.
(d) gravity.
2. Suppose that you have a spherical ball with mass of a hundred grams (100 g) at rest. If you throw the ball at three-quarters of the speed of light, what will its mass become, as measured from a stationary point of view?
(a) 100 g
(b) 133 g
(c) 151 g
(d) It cannot be calculated from this information.
3. Suppose that the ball in Problem 2 has an apparent diameter, as measured laterally (sideways to the direction of its motion), of a hundred millimeters (100 mm) when it is speeding along at three-quarters of the speed of light. What will its diameter be when it comes to rest?
(a) 100 mm
(b) 133 mm
(c) 151 mm
(d) It cannot be calculated from this information.
4. If a space ship is slowing down, that is, losing speed in the forward direction, the acceleration force inside the ship is directed
(a) toward the rear.
(b) toward the front.
(c) toward the side.
(d) nowhere; there is no acceleration force.
5. The Michelson-Morley experiment
(a) showed that the speed of light depends on the direction in which it is measured.
(b) showed that the speed of light depends on the velocity of the observer.
(c) showed that the speed of light does not depend on the direction in which it is measured.
(d) proved that the ether passes right through the Earth.
6. If you are in a spacecraft accelerating at 9.8 m/s2 through interplanetary space, you will feel the same force as you feel if you are sitting still on the surface of the Earth. This is an expression of
(a) a complete falsehood! Traveling through space is nothing at all like being on Earth.
(b) the fact that the speed of light is absolute, finite, and constant and is the fastest known speed.
(c) Einstein’s equivalence principle.
(d) the results of the Michelson-Morley experiment.
7. Suppose that you see a space ship whiz by at the speed of light. What is the time dilation factor k that you observe when you measure the speed of a clock inside that ship and compare it with the speed of a clock that is stationary relative to you?
(a) 1
(b) 0
(c) Infinity
(d) It is not defined.
8. Some light beams will follow curved paths
(a) under no circumstances.
(b) when measured inside a space ship that is coasting at high speed.
(c) when measured in the presence of an extreme gravitational field.
(d) when measured from a reference frame that is not accelerating.
9. Suppose that you get on a space ship and travel toward the star Sirius at 150,000 km/s, which is approximately half the speed of light. If you measure the speed of the light arriving from Sirius, what figure will you obtain?
(a) 150,000 km/s
(b) 300,000 km/s
(c) 450,000 km/s
(d) It cannot be calculated from this information.
10. Clocks in different locations are impossible to synchronize from every possible reference frame because
(a) the speed of light is absolute, finite, and constant and is the fastest known speed.
(b) the speed of light depends on the location of the reference frame from which it is measured.
(c) the speed of light depends on velocity of the reference frame from which it is measured.
(d) there is no such thing as a perfect clock.