Until a few hundred years ago, the only instrument available for astronomical observation was the human eye. This changed in the 1600s when several experimenters, including such notables as Galileo Galilei and Isaac Newton, combined lenses and mirrors to make distant objects look closer. Since then, optical telescopes have become larger and more sophisticated. So have the ways in which the light they gather is scrutinized.
You have learned that visible light always take the shortest path between two points and that it always travels at the same speed. These are the cornerstones of relativity theory and can be taken as axiomatic as long as the light stays in a vacuum. However, if the medium through which light passes is significantly different from a vacuum, and especially if the medium changes as the light ray travels through it, these principles of relativity do not apply.
Let’s focus our attention on what happens when light passes through a medium such as glass or is reflected by mirrors. If a ray of light passes from air into glass or from glass into air, the path of the ray is bent. Light rays change direction when they are reflected from mirrors. This has nothing to do with relativity. It happens all the time, everywhere you look. It even takes place within your own eyes.
What is a ray of light? Definitions vary. Informally, a thin shaft of light, such as that which passes from the Sun through a pinhole in a piece of cardboard, can be called a ray or beam of light. In a more technical sense, a ray can be considered to be the path that an individual photon (light particle) follows through space, air, glass, water, or any other medium.
Light rays have properties of both particles and waves. This duality has long been a topic of interest among physicists. In some situations, the particle model or corpuscular model explains light behavior very well, and the wave model falls short. In other scenarios, the opposite is true. No one has actually seen a ray of light; all we can see are the effects produced when a ray of light strikes something. Yet there are certain things we can say about the way in which rays of light behave. These things are predictable, both qualitatively and quantitatively. When we know these facts about light, we can build high-quality instruments for observing the Cosmos at visible wavelengths.
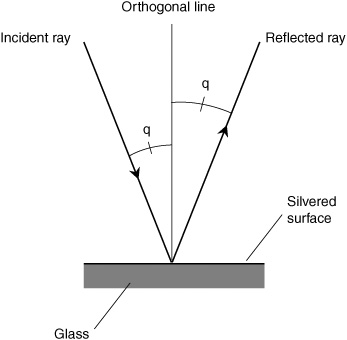
Prehistoric people knew about reflection. It would not take an intelligent creature very long to figure out that the “phantom in the pond” actually was a reflection of himself or herself. Any smooth, shiny surface reflects some of the light that strikes it. If the surface is perfectly flat, perfectly shiny, and reflects all the light that strikes it, then any ray that encounters the surface is reflected away at the same angle at which it hits. You have heard the expression, “The angle of incidence equals the angle of reflection.” This principle, known as the law of reflection, is illustrated in Fig. 17-1. The angle of incidence and the angle of reflection are both measured relative to a normal line (also called an orthogonal or perpendicular). In the figure, these angles are denoted q. They can range from as small as 0 degrees, where the light ray strikes at a right angle, to almost 90 degrees, a grazing angle.
If the reflective surface is not perfectly flat, then the law of reflection still applies for each ray of light striking the surface at a specific point. In such a case, the reflection is considered with respect to a flat plane passing through the point tangent to the surface at that point. When many parallel rays of light strike a curved or irregular reflective surface at many different points, each ray obeys the law of reflection, but the reflected rays do not all emerge parallel. In some cases they converge; in other cases they diverge. In still other cases the rays are scattered haphazardly.
Figure 17-1. When a ray of light is reflected from a shiny flat surface, the angle of incidence is equal to the angle of reflection. Here, both angles are denoted q.
Prehistoric people noticed refraction as well as reflection; a clear pond looks shallower than it actually is because of this effect. People who used spears to catch fish learned to compensate for the effects of refraction; the images of fish were displaced more or less depending on the angle at which they were observed. The cause and the far-reaching uses of visible-light refraction were not known or understood until quite recently. There is evidence that ancient Greeks and Romans knew how to make crude lenses for the purpose of focusing light beams, but more refined applications apparently evaded them.
When light rays cross a flat boundary from one clear medium into another having different light-transmission properties, the rays are bent, or refracted. An example is shown in Fig. 17-2 when the refractive index of the initial medium, called medium X in the figure, is higher than that of the final medium, called Y. (The refractive index, also called the index of refraction, is defined in the next section.) A ray striking the boundary at a right angle passes through without changing direction. However, a ray that hits at some other angle is bent; the greater the angle of incidence, the sharper is the turn. When the angle of incidence reaches a critical angle, then the light ray is not refracted at the boundary but is reflected back into medium X. This is total internal reflection.
Figure 17-2. Rays of light are bent more or less as they cross a boundary between media having different properties.
If the directions of the light rays in Fig. 17-2 are reversed, they still follow the same paths. Thus a ray originating in medium Y and striking the boundary at a grazing angle is bent downward at a considerable angle. This causes significant distortion of images when viewed from underwater. You have surely seen this effect if you are a scuba diver. The entire landscape above the water looks as if it is viewed through a wide-angle lens.
If the refracting boundary is not perfectly flat, then the principle shown by Fig. 17-2 still applies for each ray of light striking the boundary at a specific point. The refraction is considered with respect to a flat plane passing through the point tangent to the boundary at that point. When many parallel rays of light strike a curved or irregular refractive boundary at many different points, each ray obeys the same principle individually. As a whole, however, the effect can be much different than is the case for a flat boundary. In some cases parallel rays converge after crossing the boundary; in other cases they diverge. In still other cases the rays are scattered.
Different media transmit light at different speeds. This does not violate the fundamental principle of relativity theory. The speed of light is absolute in a vacuum, where it travels at 299,792 km/s or 186,282 mi/s expressed to six significant digits. However, light travels more slowly than this in other media because the relativistic principle only applies for a vacuum.
In air, the difference in the speed of light is slight, although it can be significant enough to produce refractive effects at near-grazing angles between air masses having different densities. In water, glass, quartz, diamond, and other transparent media, light travels quite a lot more slowly than it does in a vacuum. The refractive index of a particular medium is the ratio of the speed of light in a vacuum to the speed of light in that medium. If c is the speed of light in a vacuum and cx is the speed of light in medium X, then the index of refraction for medium X, call it rx, can be calculated simply:
rx = c/cx
Always use the same units when expressing c and cx. According to this definition, the index of refraction of any transparent material is always greater than or equal to 1.
The greater the index of refraction for a transparent substance, the more a ray of light is bent when it passes the boundary between that substance and air. Different types of glass have different refractive indices. Quartz refracts more than glass, and diamond refracts more than quartz. The high refractive index of diamond is responsible for the multicolored shine of diamond stones.
The index of refraction for a particular substance depends on the wavelength of the light passing through it. Glass slows down light the most at the shortest wavelengths (blue and violet) and the least at the longest wavelengths (red and orange). This variation of the refractive index with wavelength is known as dispersion. It is the principle by which a prism works (Fig. 17-3). The more the light is slowed down by the glass, the more its path is deflected when it passes through the prism. This is why prisms cast rainbows when white light shines through them.
Dispersion is important in optical astronomy for two reasons. First, a prism can be used to make a spectrometer, which is a device for examining the intensity of visible light at specific wavelengths. (Gratings are also used for this.) Second, dispersion degrades the quality of white-light images viewed through lenses unless those lenses are specially made to cancel out the effect.
Figure 17-3. Dispersion is responsible for the fact that a glass prism “splits” white light into its constituent colors.
The ways in which visible light is reflected and refracted can be used to advantage. This was first discovered when experimenters noticed that specially shaped pieces of glass could make objects look larger or smaller. The refractive properties of glass have been used for centuries to help correct nearsightedness and farsightedness. Lenses work because they refract light more or less depending on where and at what angle the light strikes their surfaces. Curved mirrors have much the same effect when they reflect light.
You can buy a convex lens in almost any novelty store or department store. In a good hobby store you should be able to find a magnifying glass up to 10 cm (4 in) or even 15 cm (6 in) in diameter. The term convex arises from the fact that one or both faces of the glass bulge outward at the center. A convex lens is sometimes called a converging lens. It brings parallel light rays to a sharp focus or focal point, as shown in Fig. 17-4A, when those rays are parallel to the axis of the lens. It also can collimate (make parallel) the light from a point source, as shown in Fig. 17-4B.
Figure 17-4. At A a convex lens focuses parallel light rays to a point. At B the same lens collimates light from a point source at the focus.
The properties of a convex lens depend on the diameter of the lens, as well as on the difference in thickness between the edges and the center. The larger the diameter, the greater is the light-gathering power. The greater the difference in thickness between the center and the edges, the shorter is the distance between the lens and the point at which it brings parallel light rays to a focus. The effective area of the lens, measured in a plane perpendicular to the axis, is known as the light-gathering area. The distance between the center of the lens and the focal point (as shown in Fig. 17-4A or B) is called the focal length. If you look through a convex lens at a close-up object such as a coin, the features are magnified; they appear larger than they look with the unaided eye.
The surfaces of convex lenses generally are spherical. This means that if you could find a large ball having just the right diameter, the curve of the lens face would fit neatly inside the ball. Some convex lenses have the same radius of curvature on each face; others have different radii of curvature on their two faces. Some converging lenses have one flat face; these are called planoconvex lenses.
You will have some trouble finding a concave lens in a department store, but you should be able to order them from specialty catalogs or Web sites. The term concave refers to the fact that one or both faces of the glass bulge inward at the center. This type of lens is also called a diverging lens. It spreads parallel light rays outward (Fig. 17-5A). It can collimate converging rays if the convergence angle is correct (see Fig. 17-5B).
Figure 17-5. At A a concave lens spreads parallel light rays. At B the same lens collimates converging light rays.
As with convex lenses, the properties of a concave lens depend on the diameter and the extent to which the surface(s) depart from flat. The greater the difference in thickness between the edges and the center of the lens, the more the lens will cause parallel rays of light to diverge. If you look through a concave lens at a close-in object such as a coin, the features are reduced; they appear smaller than they look with the unaided eye.
The surfaces of concave lenses, like those of their convex counterparts, generally are spherical. Some concave lenses have the same radius of curvature on each face; others have different radii of curvature on their two faces. Some diverging lenses have one flat face; these are called planoconcave lenses.
A convex mirror reflects light rays in such a way that the effect is similar to that of a concave lens. Incident rays, when parallel, are spread out (Fig. 17-6A) after they are reflected from the surface. Converging incident rays, if the angle of convergence is just right, are collimated by a convex mirror (see Fig. 17-6B). When you look at the reflection of a scene in a convex mirror, the objects all appear reduced. The field of vision is enlarged, a fact that is used to advantage in some automotive rear-view mirrors.
Figure 17-6. At A a convex mirror spreads parallel incident light rays. At B the same mirror collimates converging incident light rays.
The extent to which a convex lens spreads light rays depends on the radius of curvature. The smaller the radius of curvature, the greater is the extent to which parallel incident rays diverge after reflection.
A concave mirror reflects light rays in a manner similar to the way a convex lens refracts them. When incident rays are parallel to each other and to the axis of the mirror, they are reflected so that they converge at a focal point (Fig. 17-7A). When a point source of light is placed at the focal point, the concave mirror reflects the rays so that they emerge parallel (see Fig. 17-7B).
The properties of a concave mirror depend on the size of the reflecting surface, as well as on the radius of curvature. The larger the light-gathering area, the greater is the light-gathering power. The smaller the radius of curvature, the shorter is the focal length. If you look at your reflection in a convex mirror, you will see the same effect that you would observe if you placed a convex lens up against a flat mirror.
Figure 17-7. At A a concave mirror focuses parallel light rays to a point. At B the same mirror collimates light from a point source at the focus.
Concave mirrors can have spherical surfaces, but the finest mirrors have surfaces that follow the contour of an idealized three-dimensional figure called a paraboloid. A paraboloid results from the rotation of a parabola, such as that having the equation y = x2 in rectangular coordinates, around its axis. When the radius of curvature is large compared with the size of the reflecting surface, the difference between a spherical mirror and a paraboloidal mirror (more commonly called a parabolic mirror) is not noticeable to the casual observer. However, it makes a big difference when the mirror is used in a telescope.
The first telescopes were developed in the 1600s and used lenses. Any telescope that enlarges distant images with lenses alone is called a refracting telescope.
Galileo devised a telescope consisting of a convex-lens objective and a concave-lens eyepiece. His first telescope magnified the apparent diameters of distant objects by a factor of only a few times. Some of his later telescopes magnified up to 30 times. The Galilean refractor (Fig. 17-8A) produces an erect image, that is, a right-side up view of things. In addition to appearing right-side-up, images are also true in the left-to-right sense. The magnification factor, defined as the number of times the angular diameters of distant objects are increased, depends on the focal length of the objective, as well as on the distance between the objective and the eyepiece.
Galilean refractors are still available today, mainly as novelties for terrestrial viewing. Galileo’s original refractors had objective lenses only 2 or 3 cm (about 1 in) across; the same is true of most Galilean telescopes found today. Some of these telescopes have sliding, concentric tubes, providing variable magnification. When the inner tube is pushed all the way into the outer one, the magnification factor is the lowest; when the inner tube is pulled all the way out, the magnification is highest. The image remains fairly clear over the entire magnification-adjustment range. These instruments are sometimes called spy glasses.
Figure 17-8. The Galilean refractor (A) uses a convex objective and a concave eyepiece. The Keplerian refractor (B) has a convex objective and a convex eyepiece.
Johannes Kepler’s refracting telescope employed a convex-lens objective with a long focal length and a smaller convex-lens eyepiece with a short focal length. Unlike the Galilean telescope, the Keplerian refractor (see Fig. 17-8B) produces an inverted image; it is upside-down and backwards. The distance between the objective and the eyepiece must be exactly equal to the sum of the focal lengths of the two lenses in order for the image to be clear. The magnification factor depends on the ratio between the focal lengths of the objective and the eyepiece.
The Keplerian telescope is preferred over the Galilean type mainly because the Keplerian design provides a larger apparent field of view. This is the angular diameter, as seen directly by the eyes, of the circular region in which objects appear through the telescope. Galilean telescopes have apparent fields of view so narrow that looking through them is an uncomfortable experience.
The magnification factor of a Keplerian telescope can be changed by using eyepieces with longer or shorter focal lengths. The shorter the focal length of the eyepiece, the greater is the magnification factor, informally known as power, assuming that the focal length of the objective lens remains constant.
The largest refracting telescope in the world is a Keplerian refractor, located at the Yerkes Observatory in Wisconsin. Its objective lens has a diameter of 40 in, or slightly more than 1 m. Keplerian refractors are used by thousands of amateur astronomers worldwide.
A well-designed refracting telescope is a pleasure to use. Nevertheless, there are certain problems inherent in their design. These are known as spherical aberration, chromatic aberration, and lens sag.
Spherical aberration results from the fact that spherical convex lenses don’t bring parallel light rays to a perfect focus. Thus a refracting telescope with a spherical objective will focus a ray passing through its edge a little differently than a ray passing closer to the center. The actual focus of the objective is not a point but a very short line along the lens axis. This effect causes slight blurring of images of objects that have relatively large angular diameters, such as nebulae and galaxies. The problem can be corrected by grinding the objective lens so that it has paraboloidal rather than spherical surfaces.
Chromatic aberration occurs because the glass in an objective lens refracts the shortest wavelengths of light slightly more than the longest wavelengths. The focal length of any given convex lens therefore is shorter for violet light than for blue light, shorter for blue light than for yellow light, and shorter for yellow light than for red light. This produces rainbow-colored halos around star images, as well as along sharply defined edges in objects with large angular diameters. Chromatic aberration can be corrected by the use of compound lenses. These lenses have two or more sections made of different types of glass; the sections are glued together with a special transparent adhesive. Such objectives are called achromatic lenses and are standard issue in refracting telescopes these days.
Lens sag occurs in the largest refracting telescopes. When an objective is larger than approximately 1 m (about 40 in) across, it becomes so massive that its own weight distorts its shape. Glass is not perfectly rigid, as you have noticed if you have seen the reflection of the landscape in a large window on a windy day. There is no way to get rid of this problem with a refractor except to take the telescope out of Earth’s gravitational field.
The problems inherent in refracting telescopes, particularly chromatic aberration and lens sag, can be largely overcome by using mirrors instead of lenses as objectives. A first-surface mirror, with the silvering on the outside so that the light never passes through glass, can be ground so that it brings light to a focus that does not vary with wavelength. Mirrors can be supported from behind, so it is possible to make them larger than lenses without running into the sag problem.
Isaac Newton designed a reflecting telescope that was free of chromatic aberration. His design is still used in many reflecting telescopes today. The Newtonian reflector employs a concave objective mounted at one end of a long tube. The other end of the tube is open to admit incoming light. A small, flat mirror is mounted at a 45-degree angle near the open end of the tube to reflect the focused light through an opening in the side of the tube containing the eyepiece (Fig. 17-9A).
The flat mirror obstructs some of the incoming light, slightly reducing the effective surface area of the objective mirror. As a typical example, suppose that a Newtonian reflector has an objective mirror 20 cm in diameter. The total surface area of this mirror is approximately 314 centimeters squared (cm2). If the eyepiece mirror is 3 cm square, its total area is 9 cm2, which is about 3 percent of the total surface area of the objective.
Newtonian reflectors have limitations. Some people find it unnatural to “look sideways” at objects. If the telescope has a long tube, it is necessary to use a ladder to view objects at high elevations. These annoyances can be overcome by using a different way to get the light to the eyepiece.
Figure 17-9. The Newtonian reflector (A) has an eyepiece set into the side of the tube. In the Cassegrain reflector (B), the eyepiece is in the center of the objective mirror.
Figure 17-9B shows the design of the Cassegrain reflector. The eyepiece mirror is closer to the objective than in the Newtonian design. It is not angled, but it is convex. The convexity of this mirror increases the effective focal length of the objective mirror. Light reflects from the convex mirror and passes through a small hole in the center of the objective containing the eyepiece.
The Cassegrain reflector can be made with a physically short tube and an objective mirror having a smaller radius of curvature than that of a Newtonian telescope having the same diameter. Thus the Cassegrain telescope is less massive and less bulky. Cassegrain reflectors with heavy-duty mountings are physically stable, and they can be used at low magnification to obtain wide views of the sky.
Several parameters are significant when determining the effectiveness of a telescope for various applications. Here are the most important ones.
The magnification, also called power and symbolized ×, is the extent to which a telescope makes objects look closer. Actually, telescopes increase the observed sizes of distant objects, but they do not look closer in terms of perspective. The magnification is a measure of the factor by which the apparent angular diameter of an object is increased. A 20× telescope makes the Moon, whose disk subtends about 0.5 degrees of arc as observed with the unaided eye, appear 10 degrees of arc in diameter. A 180× telescope makes a crater on the Moon with an angular diameter of only 1 minute of arc (1/60 of a degree) appear 3 degrees across.
Magnification is calculated in terms of the focal lengths of the objective and the eyepiece. If fo is the effective focal length of the objective and fe is the focal length of the eyepiece (in the same units as fo), then the magnification factor m is given by this formula:
m = fo/fe
For a given eyepiece, as the effective focal length of the objective increases, the magnification of the whole telescope also increases. For a given objective, as the effective focal length of the eyepiece increases, the magnification of the telescope decreases.
The resolution, also called resolving power, is the ability of a telescope to separate two objects that are not in exactly the same place in the sky. It is measured in an angular sense, usually in seconds of arc (units of 1/3,600 of a degree). The smaller the number, the better the resolving power.
The best way to measure a telescope’s resolving power is to scan the sky for known pairs of stars that appear close to each other in the angular sense. Astronomical data charts can determine which pairs of stars to use for this purpose. Another method is to examine the Moon and use a detailed map of the lunar surface to ascertain how much detail the telescope can render.
Resolving power increases with magnification, but only up to a certain point. The greatest image resolution a telescope can provide is directly proportional to the diameter of the objective lens or mirror, up to a certain maximum dictated by atmospheric turbulence. In addition, the resolving power depends on the acuity of the observer’s eyesight (if direct viewing is contemplated) or the coarseness of the grain of the photographic or detecting surface (if an analog or digital camera is used).
The light-gathering area of a telescope is a quantitative measure of its ability to collect light for viewing. It can be defined in centimeters squared (cm2) or meters squared (m2), that is, in terms of the effective surface area of the objective lens or mirror as measured in a plane perpendicular to its axis. Sometimes it is expressed in inches squared (in2).
For a refracting telescope, given an objective radius of r, the light-gathering area A can be calculated according to this formula:
A = πr2
where π is approximately equal to 3.14159. If r is expressed in centimeters, then A is in centimeters squared; if r is in meters, then A is in meters squared.
For a reflecting telescope, given an objective radius of r, the light-gathering area A can be calculated according to this formula:
A = πr2–B
where B is the area obstructed by the secondary mirror assembly. If r is expressed in centimeters and B is expressed in centimeters squared, then A is in centimeters squared; if r is in meters and B is in meters squared, then A is in meters squared.
When you look through the eyepiece of a telescope, you see a circular patch of sky. Actually, you can see anything within a cone-shaped region whose apex is at the telescope (Fig. 17-10). The absolute field of view is the angular diameter q of this cone; q can be specified in degrees, minutes, and/or seconds of arc. Sometimes the angular radius is specified instead of the angular diameter.
Figure 17-10. A telescope’s absolute field of view, q, is measured in angular degrees, minutes, and/or seconds of arc.
The absolute field of view depends on several factors. The magnification of the telescope is important. When all other factors are held constant, the absolute field of view is inversely proportional to the magnification. If you double the magnification, you cut the absolute field of view in half. If you reduce the magnification by a factor of 4, you increase the absolute field of view by a factor of 4.
The viewing angle provided by the eyepiece—the apparent field of view—is important. Some types of eyepieces have a wide apparent field, such as 60 degrees or even 90 degrees. Others have narrower apparent fields, in some cases less than 30 degrees. Galileo’s first refracting telescope had an apparent field of view only a few degrees wide.
Another factor that affects the absolute field of view is the focal ratio or f-ratio: the objective’s focal length divided by its actual diameter as measured in the same units. A telescope’s f-ratio is denoted by writing f, followed by a forward slash, followed by the ratio expressed as a number. Thus, for example, if the focal length of the objective is 200 cm and its actual diameter is 20 cm, the f-ratio is f/10. In general, the larger the f-ratio, the smaller is the maximum apparent field of view that can be obtained with the telescope. Long, narrow telescopes have the smallest maximum apparent fields of view; short, fat ones have the widest maximum fields.
The quality of the image obtainable with a telescope depends on some things the astronomer can control, such as the objective diameter, the quality of the optics, and the location of the observatory. Other problems are unavoidable. Here are some of the factors that affect the performance of telescopes.
The greatest useful magnification a telescope can provide is approximately 20× per centimeter of objective diameter, or 50× per inch. Visible light has properties of a wave disturbance, and the waves have physical length in space. The objective lens or mirror must measure at least a certain number of wavelengths in diameter to provide a given image resolution.
If you have a telescope that is 10 cm (4 in) across, you can obtain up to approximately 200× of magnification with it. Beyond this, you can get things to “look bigger,” but they also become more blurred, so the resolution of the images you see does not improve.
The importance of good optics (that is, high-quality lenses and mirrors) is obvious. The best optics can be expensive, and the cheapest optics are usually not so good. However, the quality of the optics is not an absolute and direct function of expense.
It is important to keep the objective lens or mirror, the secondary mirror (if any), and the eyepieces clean and free of condensation. In some locations, the formation of dew can be a constant problem. Frost can form if the temperature is low enough and the humidity is relatively high. Dew and frost not only cloud the optics, but they also accelerate the accumulation of dirt.
When a telescope is aimed at an object, you expect it to stay there. Vibration transmitted from the ground can cause blurring of the image. Swaying produced by the wind can make viewing difficult. Either of these effects, when they occur in conjunction with the use of a time-exposure camera attached to a telescope, injure the image quality.
The mounting that secures the telescope to the base must be physically rugged so that the telescope will not waver once it is aimed at an object. The platform on which the entire observatory is placed likewise must be solid. The effects of vibration and swaying are exaggerated by high magnification.
When a telescope is aimed at a certain spot in the sky, celestial objects move across the field of view because Earth rotates on its axis. For most regions of the sky, this apparent motion is from east to west. Depending on the type of mounting used, image rotation also can take place. This rotation does not occur with objects on the celestial equator, but it does happen with all other objects unless an equatorial mounting and motor drive are used to compensate for Earth’s rotation.
The atmosphere interferes with observation of celestial objects. The main trouble is the fact that the air is not uniformly dense at every point above the surface. Pockets of warmer and cooler air are constantly swirling and tumbling, and these have the effect of slightly refracting the light passing from space to the surface. This refraction is responsible for the twinkling of stars, whose angular diameters are virtually zero even when viewed through a telescope. It blurs the images of planets, their moons, and the details within distant galaxies.
Air turbulence limits the practical magnification of any telescope to about 500× no matter how large the objective. It can be somewhat greater than 500× for observatories atop high mountains in regions where the atmosphere is relatively stable, such as Mauna Kea in Hawaii. In many locations, however, it is less than 500×. The only way to completely get around this limitation is to put the telescope in outer space.
The atmosphere scatters visible light, particularly at the shorter wavelengths (blue and violet). This produces an effect called airglow. It is responsible for the blue color of the daytime sky. Daytime airglow makes it impossible to see any stars or planets, except Venus and, of course, the Sun. Airglow occurs at night to a much lesser extent. It washes out the dimmest stars and limits the faintness of objects that can be observed through large telescopes. Airglow at night is worst at the time of the full Moon, and it is aggravated by the proximity of large cities because of myriad human-made lights. Dust and air pollution aggravate airglow problems.
In outer space, there is some scattering of light even though there is no airglow because space itself is not a perfect vacuum. One example of this is the gegenschein (counterglow) that occurs in a direction opposite the Sun. Atoms in space scatter light from the Sun and also from the distant stars and galaxies. This skyglow places a theoretical limit on the faintness of objects that can be observed, no matter how large the telescope and regardless of where it is located. In general, however, it is possible to see much fainter objects from space than from Earth’s surface.
At the world’s large observatories, the astronomers make use of instruments to record, analyze, and enhance the images. Rarely does a telescope operator simply peer through an eyepiece.
Sometimes it is necessary to measure the brightness of a celestial object rather than merely making a good guess or a subjective comparison. A photometer is an instrument that does this. An astronomical photometer is a sophisticated version of the lightmeter, which is used by photographers to determine camera exposure time. The device consists of a photosensor placed at the focal point of the telescope. An amplification circuit multiplies the sensitivity of the sensor. The output of the amplifier can be connected to a circuit that plots the light intensity as a function of time.
Many celestial objects, such as variable stars and visible pulsars, change in visual magnitude with time. Variable stars fluctuate slowly, but some pulsars blink so fast that they look like ordinary stars until a graph is plotted using a photometer capable of resolving into brief intervals of time. Photometers can be made sensitive in the infrared (IR) and ultraviolet (UV) ranges as well as in the visible spectrum.
Visible light can be broken down into the colors of the rainbow, each hue representing a specific wavelength. This can be done by a prism with a triangular or trapezoidal cross section. It also can be done by passing the light through or reflecting it from a diffraction grating, which is a clear plate or mirror with thousands of tiny parallel opaque bands etched on it. The grating works because of the interference patterns produced by light waves passing through the gaps between the dark bands. This is an entirely different phenomenon from the refraction that occurs in a prism, but the practical effect is similar.
A spectrometer, also known as a spectroscope, is a device intended for analyzing visible light at all its constituent wavelengths. Some spectrometers also work at IR or UV wavelengths. Stars, galaxies, quasars, and some nebulae have spectra that contain dark absorption lines at certain wavelengths. Other nebulae are dark except at specific emission wavelengths that manifest themselves as bright lines in a spectrum. The patterns of lines allow scientists to determine the amounts of various chemicals that comprise celestial objects after corrections are made for the absorption effects of Earth’s atmosphere.
Figure 17-11A is a functional diagram of a simple spectrometer. The light-sensitive surface can be photographic film or a matrix of optoelectronic sensors. The maximum image resolution obtainable by a spectrometer of this type is limited by the grain of the film or the number of pixels per centimeter in the sensor. Higher resolution can be achieved by a scheme such as that diagrammed in Fig. 17-11B. The rotating prism causes the spectrum to sweep across the objective of a viewing scope. A light sensor connected to the scope measures the intensity of the rays. The angle of the prism at any given moment in time is fed to a computer along with the sensor output. This produces a graph of the spectrum that is called, not surprisingly, a spectrograph.
Figure 17-11. Functional diagrams of a simple spectrometer (A) and a high-resolution spectrometer (B).
Astrophotography is the art of recording the images from a telescope on photographic film. Long exposures make it possible for astronomers to “see” objects much dimmer than they could by looking directly through the telescope.
The sensitivity of an astrophotographic system depends on the light-gathering area of the telescope, on the speed of the film, and on the length of time the film is exposed to the image. The image resolution depends on the size of the emulsion particles in the film, as well as on the telescope’s magnification and light-gathering area. Some cameras and films can record images at near-IR or near-UV wavelengths as well as in the visible range.
Film behaves in strange ways when exposed to visible light over long periods of time. This is one of the reasons digital imaging systems are gradually replacing film cameras in astrophotography.
A charge-coupled device (CCD) is a camera that converts visible-light images into digital signals. Some CCDs also work with IR or UV. Astronomers use CCDs to record and enhance images of all kinds of celestial objects. Common digital cameras work on a principle similar to that of the CCD.
The image focused on the retina of your eye or on the film of a camera is an analog image. It can have infinitely many configurations and infinitely many variations in hue, brightness, contrast, and saturation. However, a digital computer needs a digital image to make sense of and enhance what it “sees.” Binary digital signals have only two possible states: on and off. These are also called high and low or 1 and 0. It is possible to get an excellent approximation of an analog image in the form of high and low digital signals. This allows a computer program to process the image, bringing out details and features that otherwise would be impossible to detect.
A simplified block diagram of a CCD is shown in Fig. 17-12. The image falls on a matrix containing thousands or millions of tiny sensors. Each sensor produces one pixel (picture element). The computer (not shown) can employ all the tricks characteristic of any good graphics program. In addition to rendering high-contrast or false-color images, the CCD and computer together can detect and resolve images much fainter than is possible with conventional camera film.
Once astronomers realized the extent to which Earth’s atmosphere limits the resolution and faintness of objects that can be seen or photographed with telescopes, they began to dream about putting a telescope in space. The Hubble Space Telescope (HST) was the first major optical instrument to be placed in Earth orbit and used for intensive observation within the visible-light range.
Figure 17-12. Functional diagram of a charge-coupled device (CCD) and basic image-processing system. A computer can provide additional image enhancement.
Space telescopes get above the “dirty window” of gases that absorb, disperse, and scatter the light. They are also freed from the constraints imposed by gravity. This makes it possible to build gigantic instruments without concern for lens or mirror sag. The HST has a mirror approximately 2.4 m (94 in) across. This is not particularly large as telescopes go, but we should expect that some future space telescopes will have much larger mirrors.
Problems caused by dew and frost are eliminated in outer space because there is no water vapor to condense on the optics. There is no atmospheric dust to accumulate on instruments either. The HST can be covered when not in use, so meteoric dust can be kept out. The telescope contains on-board computers and steering devices and is powered by batteries recharged with solar panels.
The HST uses a Cassegrain design. The f-ratio is optimized. Several instruments are available to obtain, process, and analyze images. These include:
 High-speed photometer
High-speed photometer
 Wide-field camera
Wide-field camera
 Faint-object camera
Faint-object camera
 Faint-object spectrometer
Faint-object spectrometer
 Multiobject spectrometer
Multiobject spectrometer
 IR camera
IR camera
Operating a telescope in space presents certain problems that users of Earth-based telescopes don’t have to deal with. The most obvious constraint, at least with the HST, is the fact that the observer is not physically present to attend to the apparatus. The telescope must be aimed and the instruments operated by remote control.
Pointing and tracking of the HST are somewhat more complicated than is the case with an Earth-based telescope. This is so because the instrument is not fixed with respect to Earth but is in orbit. The telescope is also subject to instability because of the action-reaction principle of physics, also known as Newton’s third law. If anything moves in the telescope assembly, its momentum produces a reaction that causes the whole machine to slowly tumble unless corrective action is taken. The telescope is kept “on target” using star trackers that follow the images of certain reference stars in fixed positions relative to the telescope axis. Gyroscopes add stability.
Temperature fluctuations affect all large telescopes. A change of even a few degrees Celsius can cause the optics to expand and contract enough to affect the focal length and sharpness of the image. Even in the relatively temperature-stable environment of Earth’s atmosphere, the cooling that takes place after sundown can cause problems unless measures are taken to minimize the effect. In an orbiting telescope such as HST, the difference in temperature between “day” (telescope in sunlight) and “night” (telescope in Earth’s shadow) is much greater. Sophisticated temperature-compensation equipment is necessary to prevent this from severely degrading the performance of the telescope.
A space telescope can be placed in an orbit directly above the terminator, also known as the gray line or twilight line, on Earth’s surface. In this way, the telescope is kept in sunlight all the time. This evens out the temperature fluctuations, although some variation still occurs as the Sun shines on different parts of the instrument when the telescope is aimed at different parts of the sky. This type of orbit also ensures that the solar panels are constantly exposed to plenty of light so that there is solar power available all the time.
 Quiz
QuizRefer to the text if necessary. A good score is 8 correct. Answers are in the back of the book.
1. A simple convex lens has a focal length that varies slightly depending on the wavelength of the light passing through it. When such a lens is used as the objective of a telescope, this effect results in
(a) dispersion.
(b) spherical aberration.
(d) nothing! The premise is wrong. A convex lens has the same focal length for all wavelengths of light passing through it.
2. At the surface of Earth, the maximum useful magnification of a telescope, no matter how large the objective, is approximately 500× because of
(a) skyglow.
(b) air turbulence.
(c) dispersion.
(d) diffraction.
3. A spectrometer can record its image on
(a) photographic film.
(b) an eyepiece.
(c) a secondary mirror.
(d) a gegenschein device.
4. The use of a CCD with a telescope can enhance the
(a) focal length.
(b) magnification.
(c) image contrast.
(d) spectral output.
5. According to the law of reflection,
(a) a ray of light traveling from a medium having a low refractive index to a medium having a higher refractive index is reflected at the boundary.
(b) a ray of light traveling from a medium having a high refractive index to a medium having a lower refractive index is reflected at the boundary.
(c) a ray of light always reflects from a shiny surface in a direction exactly opposite the direction from which it arrives.
(d) None of the above
6. A Cassegrain type reflecting telescope has an objective mirror with a diameter of 300 mm and an eyepiece with a focal length of 30 mm. The magnification is
(a) 100×.
(b) 10×.
(c) 9,000×.
(d) impossible to calculate from this information.
7. A diverging lens
(a) can collimate converging rays of light.
(b) can focus the Sun’s rays to a brilliant point.
(c) is also known as a convex lens.
(d) is ideal for use as the objective in a refracting telescope.
8. Suppose that the speed of red visible light in a transparent medium is 270,000 km/s. What, approximately, is the index of refraction for this substance with respect to red light?
(a) 0.900
(b) 1.11
(c) 0.810
(d) It cannot be calculated from this information.
9. As the magnification of a telescope is increased,
(a) the image resolution decreases in direct proportion.
(b) physical stability becomes more and more important.
(c) the light-gathering area increases in direct proportion.
(d) dimmer and dimmer objects can be seen.
10. An advantage of space telescopes over Earthbound telescopes is the fact that
(a) space telescopes have less mass.
(b) space telescopes do not need power supplies.
(c) space telescopes are not subject to temperature changes.
(d) space telescopes are not subject to airglow.