Anyone who has read and understood appendixes A through D will have no misperceptions about the Divisia monetary index. But students and nonexperts, who see the index without first knowing the underlying theory, sometimes read into the index the wrong interpretations. This appendix is intended to clarify the economic interpretation of the Divisia monetary aggregates for readers who are not index-number-theory professionals. Particular emphasis is placed on the need for proper understanding of the Divisia weights and of their source in theory. Whereas part I of this book assumes little, if any, prior knowledge of economic theory, the first four appendixes in part II assume extensive knowledge of the relevant background in aggregation and index-number theory. This appendix E addresses a middle ground relevant to a large percentage of those who are potential users of the Divisia monetary aggregates, without being experts in aggregation and index-number theory.
The purpose of this appendix is to present the underlying theory of Divisia monetary aggregation in a form that would permit a potential user to understand the aggregates without the need to acquire extensive prior background of aggregation theory and index-number theory, as can be found in appendixes A through D. In this appendix only knowledge of basic microeconomic theory is needed. While this appendix and most of this book emphasize the Divisia index formula for financial aggregation, the emphasis on the Divisia index is largely for expositional convenience. All other reputable index numbers, including the Fisher ideal, can be put into a form such that this appendix becomes equally as applicable (see Barnett and Choi 2008).
The issues addressed in this appendix are equally as applicable to the data produced by the Commerce Department’s BEA, the Labor Department’s BLS, and the Department of Agriculture. But those US governmental agencies have been applying index-number theory for so long that users of their data rarely ask to see the formulas that produced the data. Such concerns are left to the experts in index-number theory employed by those agencies. If the Federal Reserve Board had adopted index-number theory for aggregation, when monetary assets began yielding interest, potential users of the Divisia monetary aggregates would be equally as uninterested in the underlying aggregation formula as they are about the index-number formulas being used by other governmental agency in Washington, DC. But since that unfortunately did not happen, it is not unreasonable for economists without expertise in index-number theory and aggregation theory to want to acquire a basic understanding of the economics of Divisia monetary aggregation.
Difficulties in understanding the Divisia monetary aggregates can almost invariably be traced to misunderstandings of the Divisia “weights.” In order to understand those weights, the source of the Divisia index number must be understood. The following discussion presents that source in terms of easily understood microeconomic theory. In particular, we now present a more detailed and transparent derivation of lemma 2 in section D.9.1 of appendix D.
Suppose that the economy’s transactions technology (or the “representative consumer’s” utility function) over monetary assets is Q(x), where x is the vector of n component asset quantities. In aggregation theory Q(x) then is the economic quantity aggregate. The aggregation theoretic procedure for selecting the n component assets, as a weakly separable cluster, is described in Barnett (1982).
Take the total differential of Q to get
Since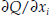 
contains the unknown parameters of the function, Q, we replace each of those marginal products (or marginal utilities) by 
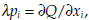which is a first-order condition for expenditure constrained maximization of Q, where is λ the Lagrange multiplier and pi is the user-cost price of asset i. We get
which has no unknown parameters on the right-hand side.
In order for a quantity aggregate to be useful, it must be linearly homogeneous. If there is one case in which the correct growth rate of an aggregate is entirely obvious, it is in the case where all components are growing at the same rate. As required by linear homogeneity, we should certainly expect that the quantity aggregate then would grow at that same rate. Hence we assume Q is linearly homogeneous.
Define P(p) to be the dual price index, satisfying Fisher’s factor reversal test, P(p)Q(x) = p’x. In other words, define P(p) to equal p’x/Q(x), which can be shown to depend only on p when Q is linearly homogeneous. The proof replaces Q(x) by the corresponding indirect utility function, factors m = p’x out of the indirect utility function, and cancels m out of the numerator and denominator of the expression for P(p). Then the following lemma holds.
Lemma 1 λ = 1/P(p).
Proof Let m = p’x, and let x = D(m, p) be the solution to maximization of Q(x) subject to p’x = m. By the linear homogeneity of Q(x), we know that there must exist ϕ(p) such that D(m, p) = ϕ(p)m. Substituting for x into Q(x), we get
Since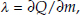 
we have from equation (E.3) that 
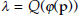. In addition from Q(x)P(p)=m and from equations (E.3) we have that P(p)= 
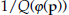. Hence
From equation (E.3) we therefore find that
Manipulating equation (E.4) algebraically to convert to growth rate (log change) form, we find that
where ωi = pixi/ m is the ith asset’s value share in total expenditure on monetary asset services. Equation (E.5) is the Divisia index in growth rate terms. In short, the growth rate of the Divisia index, Q(x), is the share weighted average of the growth rates of the components. The index, as provided in appendix A, equation (A.79), was originated by the French economist, François Divisia (1925, 1926a, b).
To be able to use (E.5) with discrete-time economic data, we need a finite change approximation to (E.5). The Törnqvist-Theil approximation in equation (A.80) of appendix A is very accurate in discrete time. That approximation is explained in section A.6.1 of appendix A along with its relationship to equation (E.5). In brief, the Törnqvist–Theil approximation is exact for the translog aggregator function, as proved by Diewert (1976). Since the translog is a second-order approximation to any aggregator function, it follows that the Törnqvist–Theil approximation is a second-order approximation to the Divisia index, (E.5). The Divisia index (E.5) exactly tracks any aggregator function in continuous time, since (E.5) is directly derived from aggregation theory.
Finally, in order to be able to apply (E.5) to monetary aggregation, we need the user cost of each monetary asset. As in equation (A.5) of appendix A, Barnett (1978, 1980a) proved that the user cost of monetary asset i is
where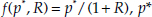 
is the true cost-of-living index, ri, is the own yield on asset i, and R is the maximum expected holding-period yield available in the economy.
Substituting (E.6) into (E.5), we see that f(p*, R) cancels out of the numerator and denominator of each share, and hence f(p*, R) does not appear in the Divisia index formula. As a result we could use the simpler form of the user-cost prices,
Clearly, (E.7) is just the interest forgone (and therefore the opportunity cost) of holding asset i.
The Divisia monetary aggregates are acquired by using (E.7) for the user-cost prices in the Törnqvist–Theil discrete time.
The most widely asked questions regarding the Divisia monetary aggregates relate to the “weights” and to the relationship between the weights and interest rates. In this section we consider that subject in light of the derivation in the last section.
If ri is high, for example, as was the case for money market funds in the late 1970s, then pi is low in (E.7). Hence, if the yield on money market funds were high and if the “weight” attached to money market funds in a monetary aggregate were its user cost, money market funds would have little influence on the aggregate. Observations of that sort have occasionally led to misunderstandings of the Divisia aggregates. However, the user costs are not the weights. As can be seen from (E.4), the prices weight the marginal component changes, dxi, to get the dollar value of the marginal change in the aggregate, P(p)dQ(x). This elementary fact, which follows directly from microeconomic theory, does not apply either to the growth rate or to the level of the quantity aggregate. In addition the role of prices in (E.4) applies only at the margin.
The role of prices at the margin should be no surprise, since the relationship between prices and marginal utilities or marginal products is well known. The fallacies that can arise from misinterpreting the role of prices in economics are also well known. For example, the familiar “diamonds and water paradox” illustrates that high price and therefore high marginal utility do not necessarily imply high utility. In fact, if a utility function is strictly concave, then marginal utility and total utility are inversely related. Hence, if we view Q(x) as a utility function, we see that low user-cost price of money-market funds (and therefore low marginal utility, as reflected in equation E.4) does not imply low contribution of money market funds to total utility, Q(x).
If we look at (E.5) rather than (E.4), we see the source of the common interpretation of the shares, ωi as being the Divisia weights. This interpretation is useful, both because (E.5) does define the Divisia index and also because (E.5) illustrates that the shares weight the component growth rates to get the growth rate of the aggregate. Since the growth rates of monetary aggregates are the most closely watched properties of the aggregates’ time paths, the Divisia share weights are important. But note that each share depends on all prices and all quantities. This observation further emphasizes the fact that the user-cost prices are not the weights. Without knowing the own price elasticity of demand for asset i, it is impossible to predict the direction of the change in ωi, when Pi increases. Hence high or rising pi need not imply high or rising ωi. For example, if Q(x) were Cobb–Douglas, then ωi would be independent of pi.
As weights, the value shares are far more meaningful than the user costs. The user costs are prices. Every quantity index contains prices in its weights. The Laspeyres, Paasche, and Fisher-ideal quantity indexes all contain prices in their weights. Although each such index uses the same vector of prices, each index certainly does not have the same weights.
Nevertheless, the value shares, ωi also need to be interpreted with care, when viewed as “weights.” If understood clearly in terms of their role in weighting growth rates in (E.5), the shares are indeed weights. However, in common usage, the term “weight” frequently refers to the contribution of the level of a component to the level of the aggregate. The shares do not serve that role for the Divisia index. In fact, in the Divisia index and in general aggregation theory, no such level weights exist. When components are not perfect substitutes, economic aggregates always are nonlinear and therefore cannot be completely strongly separable (“additive”). Without additivity, the concept of weights in levels has no meaning.
To see this problem, suppose that the economic quantity aggregate, Q(x), is completely additive, so that it can be written in the form
for some fi (i = 1,. . ., n). Then we equivalently can write
where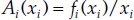 
is the average product (or average utility) of asset (or good) i. Clearly, Ai(xi) also is the weight imputed to component quantity level, xi, to get the level of the aggregate, Q(x). Since the user costs measure marginal products (or marginal utilities), the user costs do not measure the aggregation theoretic level weights, Ai(xi). Furthermore, unless Q(x) can be written in the form (E.8), Q(x) cannot be written as a weighted average of component levels, as in (E.9). Yet most misunderstandings of the Divisia monetary aggregates result from viewing the user costs as the level weights, Ai(xi), in (E.9). Clearly, both (E.9) and therefore the resulting level weights, Ai(xi), usually do not exist, and, even when they do, the level weights, Ai(xi), do not equal the user costs. Furthermore the level weights do not equal the shares, ωi.
In short, misunderstandings of the Divisia monetary aggregates generally stem from confusing marginal products (or user costs) with average products (or level weights, when they exist) or with growth rate weights (or value shares). Understanding of the derivation and discussion above should permit potential users of the Divisia aggregates to avoid such easily made errors.
Finally, to summarize all of the above in one equation, we will solve the differential equation (E.5) for the level of the index, Q(x). First we rewrite (E.5) as the explicit differential equation
where x(t), t ∊ T, is the time path of the asset quantities and ωi(t), t ∊ T, is the time path of the ith value share. Clearly, ωi(t) = pi(t)xi(t) / p(t)’x(t), where p(t), t ∊ T, is the time path of the user-cost prices.
Solving the differential equation (E.10) for Q(t), we get
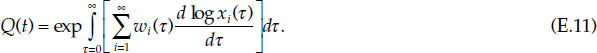
In discrete time we would use the Törnqvist–Theil approximation to the line integral (E.11). Inspecting (E.11), we see that Q(t) does not have the simple linearly weighted form of (E.9). Reading “weights” into a deeply nonlinear function such as (E.11) clearly is a hazardous enterprise.
A deeper understanding of the Divisia index is acquired when one realizes that the weights and even the user-cost prices are really not there at all. One should learn to see through the weights and user costs to the fact that the resulting index equals Q(x), which depends only on quantities. Clearly, the only arguments of Q(x) are the quantities, x. No prices appear as arguments of Q. In short Q(x) is a quantity index, not a price index.
The paradox that may appear to be evident from the appearance of prices on the right-hand side of (E.5) is easily explained through the derivation of (E.5) from (E.2). The prices were used to eliminate the marginal products from (E.2), so that no unknown parameters would exist in the index. However, the marginal products depend only on quantities, and hence the right-hand side of (E.5) continues to track the quantity aggregate on the left side exactly.
Once one has recognized the fact that the Divisia quantity index measures Q(x), which contains no prices, one can see that the Divisia monetary aggregates can be controlled. Federal Reserve policy instruments affect the economy’s equilibrium value for Q(x), which measures a true structural economic variable. Since the Divisia monetary aggregates accurately measure Q(x), a stable relationship can be expected to exist between Federal Reserve instruments (e.g., the monetary base or nonborrowed reserves) and the Divisia monetary aggregates. Since the simple-sum aggregates do not measure Q(x), we cannot expect to find a stable relationship between Federal Reserve instruments and the simple-sum aggregates. These theoretical conjectures have been verified empirically repeatedly, as illustrated by figures 3.5 and 3.6 in part I of this book.
The prices in (E.5) affect Q(x) only to the degree that changes in prices induce changes in component quantities, x, affecting Q(x). Similarly prices appear in revealed preference theory, despite the fact that the preferences being revealed are defined only over quantities. Nevertheless, if the Federal Reserve were to adopt the Divisia monetary aggregates as policy targets, it is conceivable that some aspects of the targeting and control procedures might require forecasting of the share weights, ωi (i = 1, . . ., n), rather than direct forecasting of Q(x). However, it would be preferable to treat the Divisia monetary aggregates themselves as elementary variables, and target or forecast them directly, rather than to operate indirectly through the weights. Such targeting in the short run would require deep understanding of the underlying theory and its nonlinear dynamics, but a long-run Divisia “anchor” for policy would require little more than a clear understanding of what it measures.
Since quantities and own prices tend to move in opposite directions along demand curves, value shares tend to be more stable over time than either prices or quantities alone. Hence the value shares can more easily be forecasted than either component quantities or prices alone. In fact a no-change extrapolation, which uses the current-period shares as next-period shares, is usually hard to beat. Hence even the simplest means of forecasting the Divisia share weights is likely to result in far less weighting error than the use of the greatly inaccurate simple-sum weighting scheme.
Finally the possibility of controlling the Divisia monetary aggregates as a long-run policy anchor would be facilitated by the existing institutional arrangements in the money markets. The simple-sum aggregates, at high levels of aggregation, heavily weight high yielding money substitutes, which typically are backed by either zero or low-reserve requirements. The Divisia monetary aggregates, however, frequently impute lower weights to such high yielding component assets. Hence the problems of controlling component assets having low reserve requirements are less serious for the Divisia than the simple-sum aggregates. When treated directly as an elementary variable, the Divisia quantity aggregates are more heavily reserve backed than the simple-sum aggregates computed over the same components.
But it should be emphasized that the validity of the Divisia monetary aggregates as measures of monetary service flows, as opposed to the simple-sum monetary aggregates, which are not validly based on reputable index-number theory, is unrelated to whether or not a monetary long-run target is adopted by the central bank. The Divisia monetary aggregates measure perceived service flow on the demand side, regardless of whether markets are or are not in equilibrium, so long as demanders are price takers. But an understanding of the index-number theory’s implications for control of the monetary service flow should give pause to any proposal based on short-term active control of money, since control brings in both demand and supply. The dependency on general equilibrium theory means that short-term active control could require a sophisticated model of the transmission mechanism and of the economy. Use as an indicator, rather than as a short term target, requires far weaker assumptions. Use as a long-run anchor also is far less demanding on the central bank’s abilities than short-term active control
The Divisia monetary aggregate over x measures Q(x). With the prices, p, measured as user costs rather than stock prices, Q(x) measures the service flow produced by x. The simple-sum aggregates measure the stock. This result also can be seen by exploring the mathematical relationship between (E.5) and the simple-sum aggregate.
To determine that relationship, we need only write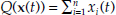 
and take the time derivative of log Q(x(t)) in continuous time. We find that we again get (E.10), but with the shares equaling 
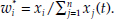Hence in continuous time the Divisia aggregates reduce to the simple-sum aggregates, when all prices are equal. That simple-sum special case can be acquired in one of two ways. One method would be to use Q(x) as a service-flow measure under the assumption that all components are perfect substitutes in identical units. In that case all equilibrium user-cost prices would be equal. The other method would be to treat Q(x) as an accounting (as opposed to economic) stock aggregate. In that case each monetary asset would be a “numéraire” good with price of one dollar. But as shown in appendix B, that latter approach measures the accounting stock of a joint product, not the capital stock of money. The relationship between the Divisia aggregates and service flows can further be seen through the form of the user-cost prices, (E.7). The theory views the services of monetary assets as being of two types: investment services and other services, such as transactions services. At the margin, ri fully values the investment services of asset i. The other marginal services are valued by R – ri, which measures the potential investment services forgone by holding asset i at yield rt when R was potentially available on an asset providing nothing but investment services. In cases of rate regulated assets, the own market yield, ri, may not fully measure the asset’s investment yield. An implicit rate of return then is needed.
This appendix derives the Divisia index. The discussion examined the concept of “weights” and has pointed out that level weights, as commonly defined, do not exist in this nonlinear context. As shown, the Divisia index is a quantity index that depends only on quantities. The simple-sum stock measure is special case of the Divisia service-flow index, when the user cost or price of all included assets is the same.
