Chapter 11
Spreadsheet-Based Concept Design and Examples
Having finished the outline constraint analysis, a more complete concept model can be constructed. Typically a finished concept design will be specified in around 100 numbers, of which perhaps 20 will relate directly to geometry – if greater detail is entered into, there is a danger that the design team will lose understanding of what parameters are controlling which aspects of the design. There does, however, need to be sufficient detail to enable simple sketches of the concept to be generated. The resulting design also needs to be balanced. Balance implies, for example, that lift is equal to weight (in level flight or a turn), available thrust is equal to drag (again in level flight or during takeoff or climb), the center of gravity lies close to the center of lift, and fuselage volume is sufficient for fuel, avionics, and payload, and so on, without being over-sized. Achieving balance almost always requires an iterative process to adjust key dimensions, something that can generally be specified in the form of an optimization problem and which can be set up and solved in a spreadsheet or similar environment. Constraint analysis provides the starting point for this process, enabling the design team to specify likely initial wing sizes and powerplant choices.
It is normal at the concept level to avoid using physics-based analysis codes to assess a design geometry, particularly during the iterative steps needed to balance the project. Rather, various design rules and equations will be invoked as in the previous chapter, see also, for example, the texts by Raymer [11] or Gudmundsson [15]. The problem with a physics-based approach is the need for more complete geometry data than is commonly available and the much longer calculation times involved. Research is progressing in this area but such tools tend to be limiting in the restrictions they impose on the design team. Thus CFD and FEA are not commonly used in concept design balancing work. They can, however, be invoked once a balanced design has been achieved to check whether the assumptions used in the design are still valid for the final concept. If they are not, assumptions can be adapted and a rebalancing carried out. It cannot be stressed too strongly that getting a design correctly balanced is of critical importance if the final product is to be satisfactory. It is clearly highly undesirable if the aircraft when finally built has an incorrect location of the center of gravity (CoG) and ballast has to be added – this might sound obvious but some quite major engineering projects have suffered because basic issues of balance and trim had not been dealt with correctly at the outset. When comparing configurations, it is again critical that all designs have been worked up properly into balanced possibilities to allow a fair decision. If it is intended to run more complex calculations, these should be completed and any subsequent rebalancing carried out before decisions are taken. In all cases, some measure of design merit will be needed to support the choices being made. This will have to take account of a range of possible performance and cost measures in some statement of overall value.
For the purposes of this chapter, we will begin with unmanned air vehicles (UAVs) with a dry take-off weight less than 40 kg. Initially, these will be taken to be powered by a single pusher propeller and piston engine system. Twin carbon tail booms and a U-shaped tail will be adopted. The fuselage can be nylon or glass-fiber-covered laser-cut foam with additional longitudinal stringers if desired. Reinforcement in laser-cut plywood or laser-sintered nylon will be possible. Molds and fiber layout will not be considered so as to reduce tooling and manpower costs. This information represents our topology and manufacturing choices and becomes embedded in the rules used to estimate weights for structural and fuselage components.
The designer starts with a given payload mass as well as landing and cruise speed combination (i.e., a design brief): here we begin with a payload of 2 kg, and landing, take-off, and cruise speeds of 15, 16, and 30 m/s, respectively. Maximum endurance is desired within an all-up maximum take-off weight (MTOW) – including payload and fuel – of 15 kg as used in the previous chapter.
The following sections set out the basic principles we use for sizing such a small, propeller-driven, piston-engine UAV. Most of the approaches we use are covered in Anderson [19] and Gudmundsson [15] with some additional data from Raymer [11], together with engine data sheets and propeller data sheets based on manufacturers' data and some results from our own experimental work. An extensive collection of independent propeller data can be found on the UIUC Propeller Data Site as compiled by John Brandt, Robert Deters, Gavin Ananda, and Michael Selig.1 The Web-based program javaProp2 can also be used to further check propeller behavior.
11.1 Concept Design Algorithm
The basic steps of the UAV platform concept design process used here are as follows:
- 1. Decide target payload mass, MTOW, and cruise speed (at a maximum cruise ceiling, for us typically 400 ft as set by UK CAA regulations) – we aim to maximize range within this MTOW budget and speed setting – other choices of start point are possible.
- 2. Choose the overall aircraft configuration (canard, monocoque, tail booms, etc.) – here taken as a tail boom pusher as already noted.
- 3. Choose the landing speed and take-off speed (or set take-off speed to be the same as landing speed), which govern wing loadings if we assume we do not have high lift devices – typical values are in the 12–18 m/s range. Higher landing speeds give faster, smaller aircraft with greater range but which are more likely to have accidents on landing!
- 4. Choose values for various fixed parameters – many of these are aerodynamic, all are nondimensional or do not depend on the airframe size and here are based on typical aircraft, operational speeds, previous designs and simple calculations (such as
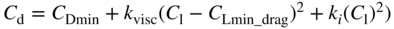 , see, for example, Table 11.1.
, see, for example, Table 11.1. - 5. Place some limits on what is possible or acceptable for the design under consideration – examples are given in Table 11.2.
- 6. To start the design process, choose the total main wing area from the constraint diagram along with likely coefficients of lift at cruise and landing (these are based on the chosen wing loading and the expected aerodynamic performance, including allowance for flaps or other landing aids if fitted), together with the fuel weight and longitudinal positions of tail-plane spar (to control static pitch stability) and payload (e.g., assumed to be forward of the front bulkhead and hence fixed by the location of this bulkhead) – ultimately we adjust these to balance the design and also ensure that they do not go outside the limits just set.
Table 11.1 Typical fixed parameters in concept design.
Item Value Aspect ratio (span  /area)
/area)9 Reserve fuel fraction 0.1 Minimum (wing) coefficient of drag at cruise speed, 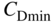
0.0143 Viscous drag constant, 
0.0329 Pressure and induced drag constant, 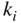
0.0334 Minimum drag (wing) coefficient of lift at cruise speed, 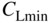
0.1485 Coefficient of parasitic drag at cruise speed 0.0375  at landing speed
at landing speed5 Coefficient of parasitic drag at landing speed 0.05  at take-off speed
at take-off speed5 Coefficient of parasitic drag at take-off speed 0.035 Equivalent rolling coefficient of friction 0.225 Propulsive efficiency at cruise speed 0.6 Tail-plane aspect ratio (span 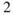 /area)
/area)4 Fin aspect ratio, ((twice fin height) 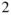 /area) assuming two fins
/area) assuming two fins3 Bank angle in level turn 60° Minimum rate of climb from cruise 5m/s Percentage extra thrust desired to start ground roll 0% Table 11.2 Typical limits on variables in concept design.
Item Value Maximum wing  at cruise speed
at cruise speed16 Maximum wing lift to total drag at cruise speed (allows for all drag elements) 8 Maximum coefficient of lift at landing speed 1.3 Minimum allowable rotation at take-off before grounding happens 17° Minimum static margin (expressed in fractions of main wing chord) 0.1 - 7. Choose the installed power needed from the constraint diagram or try and estimate the likely lift and drag of the aircraft at cruise, level turn, climb, takeoff, and landing for the given MTOW, so as to try and see what kind of installed power will be needed. If MTOW is fixed, this can be done without having to estimate the mass of the vehicle from its components, which is a distinct advantage of starting from a fixed MTOW.
- 8. Choose an engine/propeller combination and some likely dimensions for the aircraft fuselage (we set the datum on the center-line in way of the main wing spar, which is taken to lie at the quarter chord point). These dimensions can be used to sketch the aircraft; for the 15 kg Decode-1 aircraft used as the first example in this chapter, which has twin tail booms and conventional U-shaped rear control surfaces, they are as shown in Table 11.3. For other designs, they will need setting to different but appropriate values, based on prior experience or educated guesses.
Table 11.3 Estimated secondary airframe dimensions.
Item Value Units Fuselage depth 200 mm Fuselage width 150 mm Nose length (forward of front bulkhead) 150 mm Diameter of main undercarriage wheels 100 mm Longitudinal position of engine bulkhead  200
200mm Vertical position of base of fuselage  110
110mm Vertical position of tail-plane 0.0 mm Vertical position of engine 60 mm Vertical position of center of main undercarriage wheels  300
300mm - 9. Assess the likely empty weight based on the dimensions now available and the structural construction philosophy adopted, together with the components required to operate the aircraft (such as avionics, undercarriage, servos, and so on, that is, an outline list of component parts) plus the maximum fuel weight (without reserve). Ultimately MTOW includes
- payload weight
- structural weight
- avionics, systems, and servo weight
- propulsion system weight
- undercarriage and miscellaneous weight
- fuel weight including reserve.
- 10. Check if the following conditions have been met:
- the aircraft can rotate by at least the minimum angle specified at takeoff without fouling any part of the structure,
- the static margin is greater than the minimum required without being excessive,
- if a nose wheel is not fitted, the pitching moment caused by the propeller thrust and wheel drag (set equal and opposite to the thrust) will not cause the aircraft to pitch nose down into the ground, given the position of the CoG,
- there is enough weight difference between the MTOW, the structural weight, and the payload to carry some fuel!
- the wing
 ratio at cruise is below the maximum chosen,
ratio at cruise is below the maximum chosen, - the wing lift to total drag ratio at cruise is below the maximum chosen,
- the
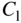 at landing is below the permitted maximum,
at landing is below the permitted maximum, - the installed static thrust is enough to start the aircraft rolling and to permit takeoff (assume that static thrust does not change until after the aircraft leaves the runway – in fact, it is likely to rise slightly for a well chosen propeller),
- the installed power is sufficient to achieve the cruise speed and to carry out acceptably banked level turns and climbs,
- the calculated aircraft weight including fuel is no more than the target MTOW (if it is less, more fuel is carried to simply increase the range),
- 11. Adjust the guessed inputs to maximize the range while meeting the constraints.
When this process is completed, the overall geometry of the balanced platform can then be used to begin the next stage of the design process. To carry out the above calculations, information is needed on a number of other aspects as described in the following sections.
11.2 Range
Range is given by the Breguet equation (for piston engined aircraft):  where SFC is in kg/kWh and the resulting range is in km.
where SFC is in kg/kWh and the resulting range is in km. 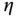 is the propulsive efficiency at the cruise speed, typically around 0.6 but clearly varies with propeller choice and also speed. Note that here
is the propulsive efficiency at the cruise speed, typically around 0.6 but clearly varies with propeller choice and also speed. Note that here 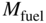 does not include the fuel reserve.
does not include the fuel reserve.
11.3 Structural Loading Calculations
To size spars and booms, and hence estimate their weights, some form of maximum 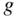 to design against will be needed. This will come from gust or maneuver loads or some arbitrary choice such as
to design against will be needed. This will come from gust or maneuver loads or some arbitrary choice such as 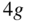 . Then simple beam theory can be used alongside design decisions on the likely form and materials to be selected for these items (typical materials are carbon-fiber tubes, solid or box-section plywood beams, or aluminum rods or tubes). Note that the FAA regulations (FARS 14, CFR, part 25) state that the maximum maneuver load factor is normally to be 2.5 but if the airplane weighs less than 50 000 lbs, the load factor is to be given by
. Then simple beam theory can be used alongside design decisions on the likely form and materials to be selected for these items (typical materials are carbon-fiber tubes, solid or box-section plywood beams, or aluminum rods or tubes). Note that the FAA regulations (FARS 14, CFR, part 25) state that the maximum maneuver load factor is normally to be 2.5 but if the airplane weighs less than 50 000 lbs, the load factor is to be given by 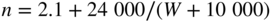 , though
, though 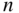 need not be greater than 3.8; while UK JAR 25 says: “the limit load maneuvering load factor
need not be greater than 3.8; while UK JAR 25 says: “the limit load maneuvering load factor 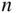 for any speed up to
for any speed up to 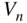 may not be less than
may not be less than 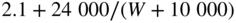 except that
except that  may not be less than 2.5 and need not be greater than 3.8, where
may not be less than 2.5 and need not be greater than 3.8, where 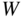 is the design MTOW.” Here the unit of weight is lbs. JAR-VLA (the equivalent standard for very light aircraft) simply says the limits should be between 1.5 and 3.8.
is the design MTOW.” Here the unit of weight is lbs. JAR-VLA (the equivalent standard for very light aircraft) simply says the limits should be between 1.5 and 3.8.
11.4 Weight and CoG Estimation
To estimate the total weight of the aircraft, a list must be made of all items carried (such as individual components of the avionics, including the wiring harness, undercarriage components, fuel tanks, servos, engine, etc.) and the locations of each item relative to the chosen datum noted, typically on a separate weights sheet (a relatively detailed example of a weights table is given in Chapter 15). For wing and fuselage structure, some construction method must be chosen and then estimates made using projected areas and lengths. Any spars or booms must be suitably sized with simple beam theory calculations as noted above. Monocoque areas subject to significant structural loads are difficult to estimate weights for accurately during concept sizing, but typically a surface area and thickness plus allowance for any rib stiffening has to suffice. Typical materials for stressed monocoques are carbon-fiber lay-up (possibly using foam sandwich techniques) or selective laser sintered (SLS) Nylon – in this chapter we restrict designs to SLS nylon or glass-fiber-covered hot-wire-cut foam. Tables 11.4 and 11.5 list some of the variables that might be used to scale weights and the items which might be scaled from them, respectively. Table 11.6 lists items whose weights are rather less easy to estimate, but which nonetheless may vary with aircraft size and must be allowed for.
Table 11.4 Variables that might be used to estimate UAV weights
| Name | Long name/definition | Typical value | Unit |
| Awing | Total wing area | 1.54 | m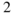 |
| AR | Aspect ratio (spanˆ2/area) | 9.00 | — |
| Thick | Aerodynamic mean thickness | 62.1 | mm |
| Atail | Tailplane area | 226 222 | mm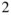 |
| Afin | Fin area | 203 600 | mm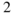 |
| y_ tail_ boom | Horizontal position of tail booms | 271.5 | mm |
| Span_ tail | Tailplane span | 951.3 | mm |
| Chord_ tail | Tailplane mean chord | 237.8 | mm |
| Height_ fin | Fin height (or semispan) for two fins | 390.8 | mm |
| Chord_ fin | Fin mean chord | 260.5 | mm |
| Vmax_ C | Maximum cruise speed | 30.0 | m/s |
| x_ main_ spar | Long position of main spar | 0.0 | mm |
| x_ fnt_ bkhd | Long position of front bulkhead | 240.3 | mm |
| x_ tail_ spar | Long position of tailplane spar |  |
mm |
| x_ rear_ bkhd | Long position of rear bulkhead | 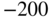 |
mm |
| x_ mid_ bkhd | Long position of middle bulkhead | 20.2 | mm |
| Depth_ Fuse | Fuselage depth | 250 | mm |
| Width_ Fuse | Fuselage width | 190 | mm |
| Len_ Nose | Nose length (forward of front bulkhead) | 200 | mm |
| Len_ Engine | Length of engine | 125 | mm |
| Mengine | Engine mass | 2.072 | kg |
| Dprop | Propeller diameter | 494 | mm |
| DTop | Design topology | 3 | — |
Table 11.5 Items for which weight estimates may be required and possible dependencies
| Item | Typical no. per a/c | Possible dependency |
| Wing spars (incl. center spars) | 2 | Wing area, spar length, speed |
Wing ribs nylon parts nylon parts |
6 | Wing cross-sectional area |
| Wing foam | 2 | Wing box volume |
| Wing covers | 4 | Wing area |
| Ailerons | 2 | Wing box volume |
| Flaps | 2 | Wing box volume |
| Tail boom | 2 | Tail-plane area, spar length, speed |
| Tail fin | 2 | Individual fin area |
| Tailplane | 1 | Tail-plane area |
| Rudder | 2 | Individual fin area |
| Elevators | 1 | Tail-plane area |
| Engine | 2 | List of engine weights |
| Muffler | 2 | List of engine weights |
| Propeller | 2 | Prop dia. |
| Generator | 2 | Engine mass/?fixed |
| Ignition unit | 2 | Engine mass/?fixed |
| Fuel tank | 0 | Engine mass/?fixed |
| Aileron servos | 2 | Wing area |
| Flap servos | 0 | Wing area |
| Throttle servo | 1 | Engine mass/?fixed |
| Rudder servo | 2 | Individual fin area |
| Elevator servo | 1 | Tail-plane area |
| Wheel steering servo | 2 | Wing area |
| Linkages and bell-cranks | 8 | Total wing area/?fixed |
Table 11.6 Other items for which weight estimates may be required
| Item | Typical no. per a/c |
| R/C receiver | 1 |
| Batteries | 2 |
| Autopilot | 2 |
| Misc. avionics | 1 |
| Wiring and aerials | 1 |
| Engine covers | 2 |
| Main fuselage | 0 |
| Rear nacelle fuselage | 2 |
| Mid-wing skin & fuel tank | 1 |
| Rear wing box | 1 |
| Nose | 2 |
| Front bulkhead | 2 |
| Main undercarriage structure | 2 |
| Main wheels | 2 |
| Undercarriage mounting point | 1 |
| Catapult mounting | 1 |
| Tail undercarriage structure | 2 |
| Nose undercarriage structure | 0 |
| Tail wheels | 2 |
| Nose wheel | 0 |
11.5 Longitudinal Stability
Static longitudinal (pitch) stability calculations are always needed, which require suitable downwash data for the elevator surfaces. Here we take the main wing quarter chord point as the datum and center of lift of the main wing:
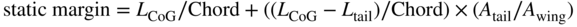

where 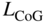 is the longitudinal position of the center of gravity forward (positive) of the main wing quarter chord point,
is the longitudinal position of the center of gravity forward (positive) of the main wing quarter chord point, 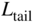 is the longitudinal position of the tail-plane quarter chord behind (negative) the main wing quarter chord point. The value of 2 used twice is from theoretically perfect inviscid two-dimensional thin airfoil theory of 2
is the longitudinal position of the tail-plane quarter chord behind (negative) the main wing quarter chord point. The value of 2 used twice is from theoretically perfect inviscid two-dimensional thin airfoil theory of 2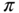 for the lift curve slope – in practice, a value of 1.9 is more likely. The value of 3/4 used twice is the Oswald span efficiency and this is on the pessimistic side, 0.85 might be more likely. However, since both the perfect slope value and the span efficiency are applied to both wing and tail terms, the errors tend to cancel; if the main wing and tail-plane aspect ratios are equal they cancel completely. The terms essentially penalize low-aspect-ratio tail-planes slightly. Also in the downwash term
for the lift curve slope – in practice, a value of 1.9 is more likely. The value of 3/4 used twice is the Oswald span efficiency and this is on the pessimistic side, 0.85 might be more likely. However, since both the perfect slope value and the span efficiency are applied to both wing and tail terms, the errors tend to cancel; if the main wing and tail-plane aspect ratios are equal they cancel completely. The terms essentially penalize low-aspect-ratio tail-planes slightly. Also in the downwash term  can be estimated from data provided in Raymer [11] (p. 482) and depends on wing aspect ratio (span
can be estimated from data provided in Raymer [11] (p. 482) and depends on wing aspect ratio (span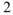 /area); wing semispan (assuming a rectangular wing); vertical position of tailplane compared to the main wing; longitudinal position of tail-plane quarter chord point behind wing quarter chord point; tail aspect ratio;
/area); wing semispan (assuming a rectangular wing); vertical position of tailplane compared to the main wing; longitudinal position of tail-plane quarter chord point behind wing quarter chord point; tail aspect ratio; 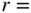 tail-plane longitudinal position/semi-span;
tail-plane longitudinal position/semi-span;  tail-plane vertical position/semispan. We leave consideration of dynamic stability until more detailed analysis is to take place, and instead rely on sensible tail volume coefficients to ensure a reasonable starting point has been chosen.
tail-plane vertical position/semispan. We leave consideration of dynamic stability until more detailed analysis is to take place, and instead rely on sensible tail volume coefficients to ensure a reasonable starting point has been chosen.
11.6 Powering and Propeller Sizing
By examining data from propeller manufacturers and their recommendations, it is possible to derive a simple regression curve that allows probable propeller diameter to be derived from engine capacity and likely pitch from diameter:
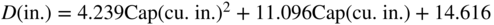
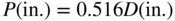
Also, one can estimate the likely engine capacity from engine power by looking at a range of small engines to get
 .
.
Then the (uncorrected) Abbott equations3 link power, thrust, pitch, diameter, and rotational speed as:
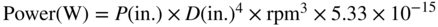
 .
.
Therefore, we can eliminate rpm to link thrust to power:
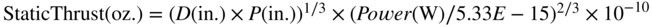 .
.
So, given an engine power, we can estimate its likely static thrust when matched to a suitable propeller. Since we can also estimate the required thrust for cruise, banked turns, climb, and takeoff as described in the previous chapter, it is then possible to make an engine selection given the overall aircraft weight. For example, the estimated thrust needed for takeoff is given by
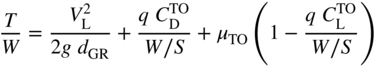
where the three terms represent the kinetic energy required during the ground roll, the mean aerodynamic drag on the runway, and the mean rolling resistance on the runway (recall that here 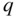 is the dynamic pressure at 70.71% of the take-off speed
is the dynamic pressure at 70.71% of the take-off speed 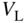 ). The estimated thrust for climb is given by
). The estimated thrust for climb is given by
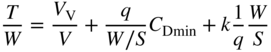
where 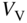 is the vertical velocity in the climb and
is the vertical velocity in the climb and 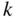 is the lift-induced drag factor.
is the lift-induced drag factor.
Next, using the UIUC Propeller Data Site,4 variations in propeller thrust with airspeed for a given diameter and rotational speed can be deduced by regressing plots of the thrust coefficient 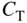 versus the advance
versus the advance 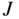 . For example, for thin electric propellers with 12 in. pitch, the thrust coefficient can be approximated from the advance ratio as
. For example, for thin electric propellers with 12 in. pitch, the thrust coefficient can be approximated from the advance ratio as 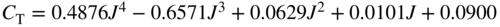 . It is also possible, using JavaProp (and a suitable base propeller design operating at fixed torque), to calculate static thrust and to derive regression curves for thrust and required power as the forward velocity changes. In either case, these can be used to simulate runway roll-out and initial climb to check the results from the above equation and also to check whether the assumed propulsive efficiency is sensible. However, when the design is close to balance, we need to recognize that only existing engines can be specified and one should then switch to data for actual engines. Figure 5.3 given previously shows the powers and thrusts of typical UAV engine/propeller combinations.
. It is also possible, using JavaProp (and a suitable base propeller design operating at fixed torque), to calculate static thrust and to derive regression curves for thrust and required power as the forward velocity changes. In either case, these can be used to simulate runway roll-out and initial climb to check the results from the above equation and also to check whether the assumed propulsive efficiency is sensible. However, when the design is close to balance, we need to recognize that only existing engines can be specified and one should then switch to data for actual engines. Figure 5.3 given previously shows the powers and thrusts of typical UAV engine/propeller combinations.
11.7 Resulting Design: Decode-1
As part of the DECODE program mentioned in the introduction, we designed several aircraft adopting the principles set out in this book. The first of these, Decode-1, was a simple single-engine pusher aircraft that we used to gain information on performance and weights for subsequent design work. A pusher design was selected so as to give an uninterrupted view forward for the payload, but it does mean the fuselage length has to be sufficient to allow the payload mass to balance out the rear-mounted engine mass so as to yield an acceptable center of gravity. The aircraft was also designed to allow a range of different experimental wings to be trialed and was sized so as to fit inside our largest wind tunnel without significant modification. Figures 11.1 and 11.2 show this aircraft with conventional wings attached.

Figure 11.1 Decode-1 in the R.J. Mitchell wind tunnel with wheels and wing tips removed and electric motor for propeller drive.

Figure 11.2 Decode-1 in flight with nose camera fitted.
The basic design brief for the aircraft is given in Table 11.7. If this brief, together with the data from Tables 11.1–11.3, is fed into our spreadsheet system, which follows the algorithm previously outlined, the design details given in Tables 11.8 and 11.9 result; see also Figures 11.3–11.5, which show the inputs, results, and simplified layout sketches we create inside the spreadsheet during design studies5. We find that seeing the aircraft in planform and side view in this way is very helpful when making design judgments early on in the design process; it is immediately apparent how similar this is to the layout of the final aircraft.
Table 11.7 Design brief for Decode-1
| Item | Value | Units |
| Payload mass | 2 | kg |
| Maximum take-off weight set by design | 15 | kg |
| Maximum cruise speed | 30 | m/s |
| Landing speed | 15 | m/s |
| Take-off speed | 16 | m/s |
| Length of ground roll on take-off | 60 | m |
| Runway altitude | 0 | m |
| Cruising height | 121.92 | m |
Table 11.8 Resulting concept design from spreadsheet analysis for Decode-1
| Item | Value | Units |
| Maximum fuel weight (without reserve) | 1.04 | kg |
| Total wing area | 0.966 | m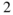 |
| Long position of front bulkhead | 640 | mm |
| Long position of tail-plane spar | 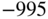 |
mm |
| Coefficient of lift at cruise speed | 0.280 | — |
| Maximum range at cruise speed (Breguet) | 106.9 | km |
| Lift at cruise speed | 147.15 | N |
| Drag at cruise speed | 28.93 | N |
| Endurance at cruise speed | 60.0 | min |
| Limit load factor | 3.80 | g |
| Turn rate | 68.7 |  /s /s |
| Longitudinal position of MTOW CoG fwd of main spar | 42.8 | mm |
| Maximum possible rotation at takeoff | 17.0 |  |
| Engine selected | OS Gemini FT-160 | — |
| Specific fuel consumption at cruise speed | 0.75 | kg/kWh |
| Maximum required power | 1.45 | kW |
| Maximum installed power | 1.49 | kW |
| Coefficient of lift at landing speed | 1.11 | — |
Wing 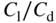 at cruise speed at cruise speed |
16.0 | — |
| Lift to drag ratio at cruise speed | 5.09 | — |
| Static margin | 0.10 | — |
| Thrust to weight ratio | 0.361 | — |
| Wing loading | 15.53 | kg/m |
The first five entries here are manipulated by the solver tool within the spreadsheet to maximize the range.
Table 11.9 Design geometry from spreadsheet analysis for Decode-1 (in units of mm and to be read in conjunction with Tables 11.3 and 11.8)
| Item | Value |
| Total wing span (rect. wing) | 2948.3 |
| Aerodynamic mean chord | 327.6 |
| Propeller diameter | 435.0 |
| Tail-plane span | 797.4 |
| Tail-plane mean chord | 199.3 |
| Fin height (or semi-span) for two fins | 293.0 |
| Fin mean chord | 195.3 |
| Long position of middle bulkhead | 220.0 |
| Horizontal position of tail booms | 239.2 |
Note that three of the constraints set out in Table 11.2 are actively limiting the design: the peak wing 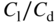 at cruise speed is 16; the allowable rotation at takeoff before grounding happens is 17°; and the static margin (expressed in fractions of main wing chord) is 0.1. Of these, it is the
at cruise speed is 16; the allowable rotation at takeoff before grounding happens is 17°; and the static margin (expressed in fractions of main wing chord) is 0.1. Of these, it is the 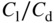 value that is most fundamental aerodynamically, the other two largely dictating the fuselage and tail-boom length. The maximum value of
value that is most fundamental aerodynamically, the other two largely dictating the fuselage and tail-boom length. The maximum value of 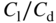 is set by the wing technology being deployed and depends on the detailed choice of planform, sections, twist, and wing tip treatment. The value of 16 used here is intimately related to the wing loading discussed in the previous chapter, and for operations at sea level and 30 m/s gives a wing loading of 15.5 kg/m
is set by the wing technology being deployed and depends on the detailed choice of planform, sections, twist, and wing tip treatment. The value of 16 used here is intimately related to the wing loading discussed in the previous chapter, and for operations at sea level and 30 m/s gives a wing loading of 15.5 kg/m . The value of
. The value of 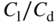 used is something we know we can achieve in practice using the construction methods we have adopted; higher values are possible but these tend to make the wings more difficult and expensive to make. For example, we chose to taper our wings linearly and avoid twist when working with hot-wire-cut foam; twisted or elliptic planform wings would give better control of induced drag, but instead we often make use of quite sophisticated 3D-printed wing tips to limit induced drag, see again Figure 11.2.
used is something we know we can achieve in practice using the construction methods we have adopted; higher values are possible but these tend to make the wings more difficult and expensive to make. For example, we chose to taper our wings linearly and avoid twist when working with hot-wire-cut foam; twisted or elliptic planform wings would give better control of induced drag, but instead we often make use of quite sophisticated 3D-printed wing tips to limit induced drag, see again Figure 11.2.
Once one is happy that the concept is sufficiently well developed to warrant further effort, the basic geometry details can then be used to generate a more realistic and fully three-dimensional outer envelope for the aircraft. To do this, we use the AirCONICS suite of programs,6 which leads to the design shown in Figure 11.6. This can then be used for further analysis or to start the process of building a detailed CAD model suitable for generating manufacturing drawings. Note that the AirCONICS geometry includes wing taper, an aerodynamically shaped circular fuselage, faired in-tail booms, and slab-sided undercarriage legs. These are just working assumptions at this stage, but the resulting model is sufficiently detailed for reasonable CFD and FEA analysis. No attempt at this stage has been made to add control surfaces to the wings, tail, or fins, so any CFD results would be solely for the cruise configuration. These can be added later using AirCONICS, as will be seen in Chapter 13. The final design shown in Figure 11.2 has greater wing taper, wing tips, and a triangular section fuselage, but otherwise is broadly similar to this initial AirCONICS model.

Figure 11.3 Decode-1 spreadsheet snapshot – inputs page.
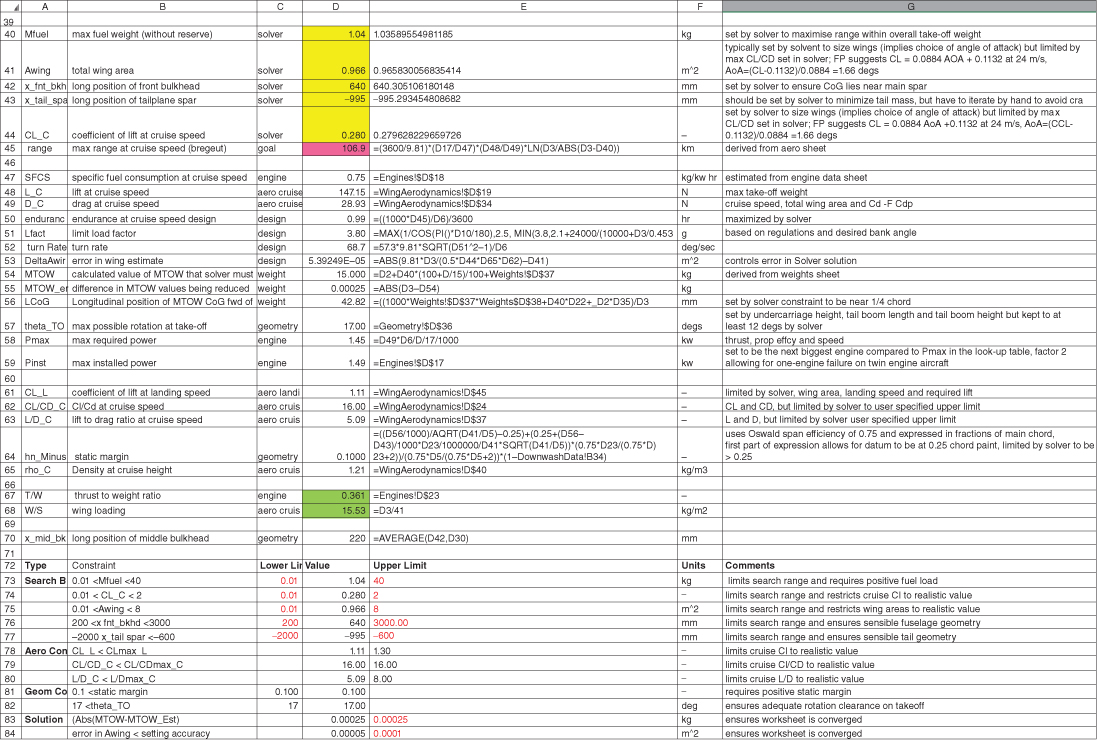
Figure 11.4 Decode-1 spreadsheet snapshot – results summary page.

Figure 11.5 Decode-1 spreadsheet snapshot – geometry page.
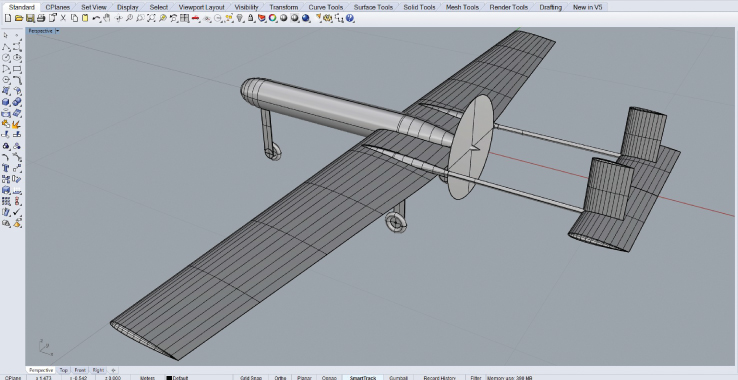
Figure 11.6 Decode-1 outer geometry as generated with the AirCONICS tool suite.
11.8 A Bigger Single Engine Design: Decode-2
The next aircraft we consider is an enlarged variant of Decode-1 that has 50% greater payload capability and endurance, a larger margin on installed power (a shorter ground roll is specified), and usefully lower landing speed, all made possible by the use of an inverted V tail and large flaps. The inverted V tail is allowed in the design process by reducing the tail volume coefficients needed by 30%, which gives a smaller, lighter tail and easier control of the static margin. The flaps allow a greater lift coefficient in the landing configuration and hence lower approach speed. Decode-2 is also a single pusher design with a nose-mounted camera system. The design brief is set out in Table 11.10 and the secondary dimensions in Table 11.11. The wing loading is slightly lower (this is now controlled by the choice of maximum landing  of 1.55) but a slightly less stringent rotation at takeoff of 14° is chosen. The other parameters given in Table 11.2 are held fixed as before.
of 1.55) but a slightly less stringent rotation at takeoff of 14° is chosen. The other parameters given in Table 11.2 are held fixed as before.
Table 11.10 Design brief for Decode-2
| Item | Value | Units |
| Payload mass | 3 | kg |
| Maximum take-off weight set by design | 23.5 | kg |
| Maximum cruise speed | 30 | m/s |
| Landing speed | 12.5 | m/s |
| Take-off speed | 16 | m/s |
| Length of ground roll on take-off | 45 | m |
| Runway altitude | 0 | m |
| Cruising height | 121.92 | m |
Table 11.11 Estimated secondary airframe dimensions for Decode-2
| Item | Value | Units |
| Fuselage depth | 225 | mm |
| Fuselage width | 250 | mm |
| Nose length (forward of front bulkhead) | 200 | mm |
| Diameter of main undercarriage wheels | 125 | mm |
| Longitudinal position of engine bulkhead |  |
mm |
| Vertical position of base of fuselage |  |
mm |
| Vertical position of tail-plane | 0.0 | mm |
| Vertical position of engine | 60 | mm |
| Vertical position of center of main undercarriage wheels |  |
mm |
Table 11.12 Resulting concept design from spreadsheet analysis for Decode-2
| Item | Value | Units |
| Maximum fuel weight (without reserve) | 0.40 | kg |
| Total wing area | 1.554 | m |
| Long position of front bulkhead | 688 | mm |
| Long position of tailplane spar |  1407 1407 |
mm |
| Coefficient of lift at cruise speed | 0.272 | — |
| Maximum range at cruise speed (Breguet) | 37.3 | km |
| Lift at cruise speed | 230.54 | N |
| Drag at cruise speed | 46.17 | N |
| Endurance at cruise speed | 20.7 | min |
| Limit load factor | 3.80 | g |
| Turn rate | 68.7 |  /s /s |
| Longitudinal position of MTOW CoG fwd of main spar | 42.1 | mm |
| Maximum possible rotation at takeoff | 14.00 |  |
| Engine selected | Saito FG-57T | — |
| Specific fuel consumption at cruise speed | 0.5 | kg/kWh |
| Maximum required power | 2.31 | kW |
| Maximum installed power | 3.04 | kW |
| Coefficient of lift at landing speed | 1.55 | — |
 at cruise speed at cruise speed |
15.99 | — |
| Lift to drag ratio at cruise speed | 4.99 | — |
| Static margin | 0.1000 | — |
| Thrust to weight ratio | 0.431 | — |
| Wing loading | 15.12 | kg/m |
The first five entries here are manipulated by the solver tool within the spreadsheet to maximize the range.
The resulting design is detailed in Tables 11.12 and 11.13 along with the screenshot in Figure 11.7. The aircraft is shown in flight in Figure 11.8 and the outer shape modeled with AirCONICS in Figure 11.9. Note that our spreadsheet sketch does not distinguish between an H and an inverted V tail (simple horizontal and vertical projections being provided); this level of detail has to be worked up after the initial spreadsheet-based concept has been defined, which is straightforward to create within AirCONICS.
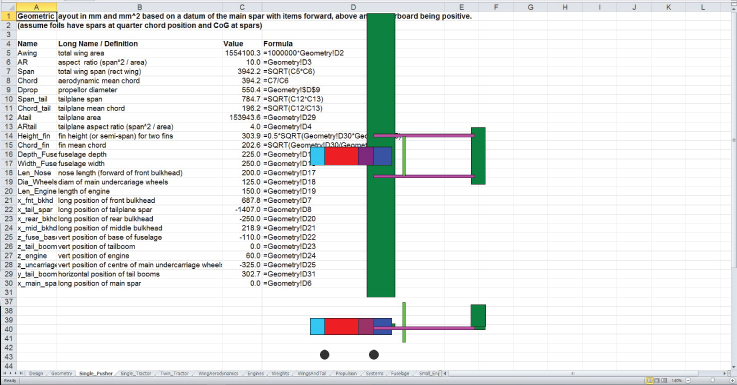
Figure 11.7 Decode-2 spreadsheet snapshot.

Figure 11.8 Decode-2 in flight with nose camera fitted.
Table 11.13 Design geometry from spreadsheet analysis for Decode-2 (in units of mm and to be read in conjunction with Tables 11.11 and 11.12)
| Item | Value |
| Total wing span (rect. wing) | 3942.2 |
| Aerodynamic mean chord | 394.2 |
| Propeller diameter | 550.4 |
| Tail-plane span | 784.7 |
| Tail-plane mean chord | 196.2 |
| Fin height (or semi-span) for two fins | 303.9 |
| Fin mean chord | 202.6 |
| Long position of middle bulkhead | 218.9 |
| Horizontal position of tail booms | 302.7 |
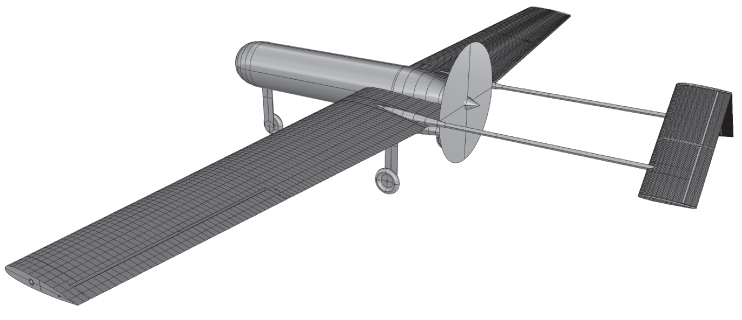
Figure 11.9 Decode-2 outer geometry as generated with the AirCONICS tool suite.
11.9 A Twin Tractor Design: SPOTTER
Our third example is the twin tractor aircraft SPOTTER. This is bigger again and is designed to have a high level of redundancy to ensure better operational resilience. The aircraft is designed to carry an interchangeable underslung payload pod of up to 5 kg weight and makes use of an integral fuel tank. It carries dual on-board charging systems powered from the main engines. The design brief is set out in Table 11.14 and the estimated secondary dimensions in Table 11.15. The wing loading is now slightly lower (this is again controlled by the choice of maximum landing 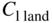 of 1.55), and a rotation at takeoff of 15° is used. The other parameters given in Table 11.2 are held fixed as before. Here the engines are sized so as to be able to maintain flight with one engine nonoperational but not so as to be able to complete a take-off run with only one engine with full fuel and payload. The resulting design is detailed in Tables 11.16 and 11.17 along with the screenshot in Figure 11.10. The aircraft is shown in flight in Figure 11.11 and the outer shape modeled with AirCONICS in Figure 11.12.
of 1.55), and a rotation at takeoff of 15° is used. The other parameters given in Table 11.2 are held fixed as before. Here the engines are sized so as to be able to maintain flight with one engine nonoperational but not so as to be able to complete a take-off run with only one engine with full fuel and payload. The resulting design is detailed in Tables 11.16 and 11.17 along with the screenshot in Figure 11.10. The aircraft is shown in flight in Figure 11.11 and the outer shape modeled with AirCONICS in Figure 11.12.
Table 11.14 Design brief for SPOTTER
| Item | Value | Units |
| Payload mass | 5 | kg |
| Maximum take-off weight set by design | 30 | kg |
| Maximum cruise speed | 30 | m/s |
| Landing speed | 12.5 | m/s |
| Take-off speed | 16 | m/s |
| Length of ground roll on takeoff | 60 | m |
| Runway altitude | 0 | m |
| Cruising height | 121.92 | m |
Table 11.15 Estimated secondary airframe dimensions for SPOTTER
| Item | Value | Units |
| Length of engine | 150 | mm |
| Fuselage depth | 125 | mm |
| Fuselage width | 125 | mm |
| Nose length (forward of front bulkhead) | 200 | mm |
| Diameter of main undercarriage wheels | 150 | mm |
| Longitudinal position of engine bulkhead | 580 | mm |
| Vertical position of base of fuselage | 0.0 | mm |
| Vertical position of tailplane | 0.0 | mm |
| Vertical position of engine | 60 | mm |
| Vertical position of center of main undercarriage wheels | 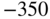 |
mm |
Table 11.16 Resulting concept design from spreadsheet analysis for SPOTTER
| Item | Value | |
| Maximum fuel weight (without reserve) | 1.18 | kg |
| Total wing area | 1.957 | m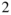 |
| Long position of front bulkhead | 580 | mm |
| Long position of tailplane spar | 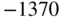 |
mm |
| Coefficient of lift at cruise speed | 0.276 | — |
| Maximum range at cruise speed (Breguet) | 77.7 | km |
| Lift at cruise speed | 313.92 | N |
| Drag at cruise speed | 62.46 | N |
| Endurance at cruise speed | 41.8 | min |
| Limit load factor | 3.80 | g |
| Turn rate | 66.5 |  /s /s |
| Longitudinal position of MTOW CoG fwd of main spar | 47.94 | mm |
| Maximum possible rotation at take-off | 15.00 | 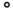 |
| Engine selected | Twin OS GF40 | — |
| Specific fuel consumption at cruise speed | 0.5 | kg/kWh |
| Maximum required power | 2.98 | kW |
| Maximum installed power | 5.60 | kW |
| Coefficient of lift at landing speed | 1.55 | — |
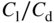 at cruise speed at cruise speed |
15.87 | — |
| Lift to drag ratio at cruise speed | 5.03 | — |
| Static margin | 0.1000 | — |
| Thrust to weight ratio | 0.489 | — |
| Wing loading | 16.36 | kg/m |
The first five entries here are manipulated by the solver tool within the spreadsheet to maximize the range.
Table 11.17 Design geometry from spreadsheet analysis for SPOTTER (in units of mm and to be read in conjunction with Tables 11.15 and 11.16)
| Item | Value |
| Total wing span (rect. wing) | 4196.3 |
| Aerodynamic mean chord | 466.3 |
| Propeller diameter | 493.6 |
| Tail-plane span | 1154.1 |
| Tail-plane mean chord | 288.5 |
| Fin height (or semispan) for two fins | 424.1 |
| Fin mean chord | 282.7 |
| Long position of middle bulkhead | 165.0 |
| Horizontal position of tail booms | 271.5 |

Figure 11.10 SPOTTER spreadsheet snapshot.

Figure 11.11 SPOTTER in flight with payload pod fitted.
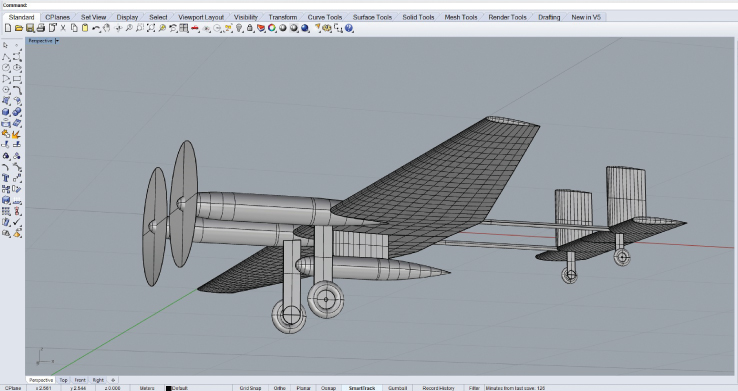
Figure 11.12 SPOTTER outer geometry as generated with the AirCONICS tool suite.