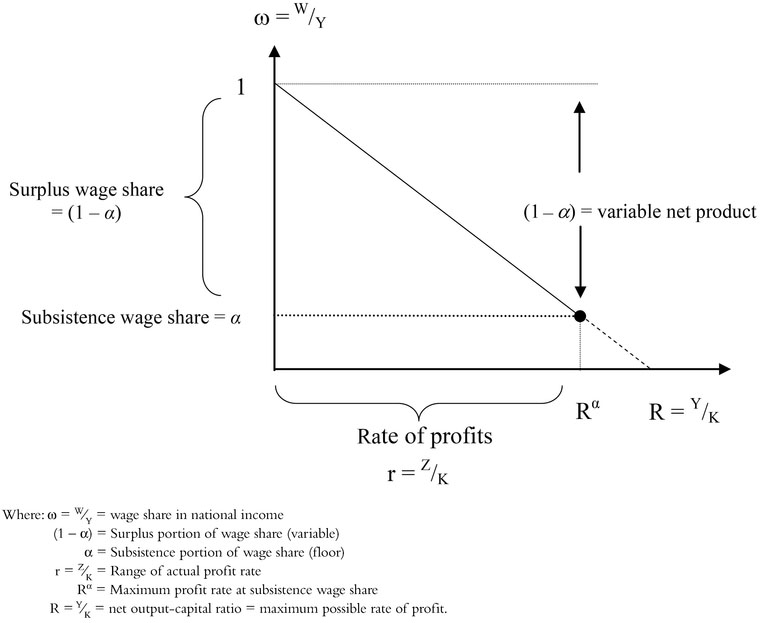
Figure 9.1 Wage share distribution schedule for subsistence and surplus wages
Scott Carter
Economists measure the distribution of income in two ways: the functional distribution of revenue or the size of the distribution of earnings. Functional distribution is older in economic theorizing as it appears in the classical notion of income shares to different economic classes.1 Within the general framework of the classical model, classes are broadly defined by their private property relations in the production process of capitalist market economies. Workers own their laboring capacity and receive wages (W), landlords own non-produced and non-reproducible (‘land’) inputs and receive rent (R), and capitalists own the produced means of production and receive profits (Z); more advanced models include in the profit relation the interest rate and the role of finance generally. In aggregate, the sum of these distributed revenues is equal to the total national income:
National income (Y) = Wages (W) + Rents (R) + [Profits (Z) + Interest (i)]
The importance of the mechanisms (or ‘laws’) that determine distribution in classical theory is made explicit by David Ricardo in the first edition of Principles of Political Economy (1817), where he calls it the “principal problem in Political Economy” (Sraffa 1951: 5). This importance attached to income distribution received less attention from those at the forefront of the marginalist revolution, with perhaps Walras being the more thorough in developing the distributional aspects of the new marginal calculus (Sandmo 2014). With the development of marginal productivity theory in the 1890s, based on the same marginal principle as to utility demonstrated 20 years earlier, authors such as J.B. Clark, Knut Wicksell, and Philip Wicksteed among others were able to wed the diminishing margin of cultivation in Ricardian theory to the newly found theoretical apparatus (Sandmo 2014: 21–27). They developed a purported general theory of the determination of factor income shares by combining theories of productivity, value, and distribution under one theoretical rubric and methodology.
The shape of the size income distribution first appears with the work of Pareto in the 1890s (Persky 1992). Here the (ostensibly) same aggregate income considered in the analysis of functional distribution is now subject to a different conceptualization. Instead of the aggregate shares of various revenue streams to different classes, ‘size distribution’ considers the income stream that accrues to a set of individual units such as households, families, and individual people.
Pareto posited a ‘law of distribution’ that was fundamentally skewed. This means that equal portions of individuals receive different incomes, with ‘less people’ receiving ‘more income,’ and vice versa. Pareto drew this relation in terms of a linear downward sloping double logarithmic curve, which has been henceforth called the Pareto distribution (Persky 1992; Sandmo 2014). Pareto held that the skewed distribution was an empirical fact evident across diverse ranges of societies and peoples, and hence dependent on ‘human nature,’ which led to the view that any attempt to alter this otherwise naturally skewed distribution would result in failure and indeed backfire. Economists of the day who were critical of the view of policy ineffectiveness in altering the skewed income distribution (and the dangerous bedfellows politically that this brought to the surface) included Lorenz, Pigou, and Gini (Persky 1992: 187–188). Ever since, the relationship between functional and size distribution has remained a subject of controversy.
This chapter considers heterodox approaches to the problem of distribution and is organized into three sections. The section that follows this introduction discusses three heterodox theories of distribution: (i) classical and Marxian approaches, (ii) the Cambridge theories in both their ‘physicalist’ and ‘monetary’ expressions, and (iii) recent Neo-Kaleckian approaches. The section after considers theoretical resonances and connections between functional and size distribution which have recently become a cutting edge area of research in heterodox approaches, including advancements in econo-physics. The final section concludes.
This section focuses on three mainstay heterodox theories of distribution. They are (i) the classical and Marxian theory, inclusive of significant Sraffian elements; (ii) the Cambridge theory, inclusive of the ‘physicalist’ natural rate of growth theory of profits as well as the rate of interest-infused monetary theory of profits; and (iii) the Neo-Kaleckian theory that develops the relationship between income distribution and aggregate demand and productive capacity. Broadly speaking the latter two theories are ‘Post Keynesian’ in the sense that the distribution parameter is closed from the output account side of the ledger, although this is less unequivocal in Neo-Kaleckian approaches as labor market struggle can play a role in the determination of the mark-up, leading to a certain degree of closure coming from the wage bargain (hence income account). Modern classical theories including Marxian primarily consider the wage bargain and/or the ‘subsistence wage’ to be the determining factors as regards systemic ‘net’ closure.
One of the features of the classical model is the conception of ‘normal’ conditions that are assumed to govern systems characterized by free competition. Two illustrative (though not exhaustive) approaches along these lines are: (i) the surplus approach to value and distribution of the so-called ‘Sraffian’ school, developed for example by Garegnani (1984, 1987) and given analytical treatment in Kurz & Salvadori (1995); and (ii) the theory of regulating capital in Anwar Shaikh’s (2016) development of the Marxian framework. In both approaches, classical causality is maintained and the closure of the system via the wage relation (specified differently in the different frameworks) runs from the profit rate to the rates of accumulation of capital and the investment of profit, with the nexus linking the two being the propensity to save and to accumulate profits.
The hallmark of the Sraffian approach is the ‘long-period position,’ where wages are determined (via various mechanisms) to some ‘normal’ level which in turn gives rise to ‘normal’ profits, the ‘normal’ prices of production, and the ‘normal’ utilization of capacity. This is termed the fully adjusted situation where the above ‘normal’ categories are adjusted to effective demand (Panico 2011: 168). It is important to emphasize that ‘normality’ does not necessitate full employment. The conditions that determine the normality tend also to ascribe uniformity in the rates of wages and profits under conditions of ‘free competition’ (Kurz & Salvadori 1995: 1–15).
Shaikh’s (2016: 14–15, 259–326) approach to conditions of ‘normality’ conceives of the notion of ‘regulating conditions’ and the theory of ‘real competition,’ the latter conceived not as a game as in neoclassical perfect and imperfect competition but rather warfare as profit-seeking capitals adjust to the highest sustainable rate of return, termed the regulating conditions. The determination of the regulating conditions occurs from a complex mosaic of competitive processes at both the intra- and inter-industrial level. The basic mechanism is that within industries best-practice techniques—that are generally socially reproducible—determine the regulating capital of that industry, and these regulating conditions once identified become subject to competition across industries (Shaikh 1978, 1980, 2016; Botwinick 1993).
Classical closure of the distribution parameter from the wage-side means that wages are ‘given’ and profits a residual. The notion of a ‘given’ wage rate has a long history in political economy, going as far back at least to Quesnay and the Physiocratic school. The argument is basically that certain physiological, social, historical, and/or demographic conditions exist such that systemic social reproduction includes and ensures an ‘efficient laboring class’ (Levrero 2013: 92). The definition of what constitutes an ‘efficient laboring class’ is often a matter of interpretation, as is the necessary bundle of wage goods that brings this about. At one end of the theoretical spectrum is the iron-law of wages where the wage bundle is limited by the bare physiological existence of the workers, which is enforced by means of Malthusian–Ricardian demographic equilibrium of death and birth rates—a notion that Marx himself vehemently rejected (Baumol 1983; Levrero 2013; Shaikh 2016). At the other end of the spectrum there are sociological and historical theories that posit a relatively ‘given’ wage bundle that is above the bare minimum. And although the mechanisms and assumptions by which the ‘given bundle’ are proposed are physiological or socio-historical, what is common to both is the idea that the subsistence wage is determined by the price of the ‘given’—that is non-market determined—bundle of wage goods (Levine 1988; Roncaglia 1988; Green 1991; Chiodi 2010; Bellofiore 2012, 2014; Levrero 2013; Giovannoni 2014; Shaikh 2016).
That the ‘subsistence wage’ is generally acknowledged to not refer to a biological minimum means that ‘subsistence’ is defined broadly to include the socio-historical conditions in the reproduction of the working class, and even here class struggle can play a role in influencing those broad conditions. Levrero (2013) discusses many disparate conditions affecting the level of real wages (see especially the figure on p. 101 and related discussion). He develops the thesis that the minimum wage is a function of the ‘wage inherited from the past’ and argues that workers’ bargaining power determines whether the actual wage will be greater than this minimum wage. Workers’ bargaining power is described as a function of the conditions in the labor market (often proxied by the unemployment rate), the level of worker organization, and the general social and political climate, where
all . . . have some degree of autonomy in determining the strength of the workers in the wage bargain, and thus in determining if the wage rate will be higher or equal to the subsistence wage – the wage inherited from the past, and which forms a minimum floor in wage-bargaining.
Levrero 2013: 101
A recent approach to the specification of the wage in terms of classical closure is given in Shaikh (2016: 638–676). The socio-historical minimum is assumed to be some constant portion (α) of the productivity of labor, leaving the remainder (1 − α) as the maximal surplus wage equal to the productivity of labor (y*). The surplus wage is a different constant proportion α′ between the minimal subsistence wage and labor productivity (the subscript ‘t’ refers to time):
The bracketed term is the class struggle parameter. It consists of the ‘subsistence’ portion (α) out of total productivity (y), which represents the ‘given bundle’ determined by the social and historical conditions necessary for the reproduction of the working class, and a portion, α′(1−α), that represents the surplus wage or share out of net product above the minimum wage. This is depicted in the ‘truncated’ version of the wage share distribution schedule shown in Figure 9.1. The parameters of class struggle include the length and intensity of the working day, the level of working-class organization in making effective changes, and the disciplining mechanism of the unemployment rate (Bellofiore 2014; Petri 2014; Shaikh 2016).
Various forces influence each of the share values on the vertical axis. The lower limit of the subsistence wage itself can vary, as can the relationship with the surplus wage.

Figure 9.1 Wage share distribution schedule for subsistence and surplus wages
The disciplining effect of the unemployment rate, or Marx’s reserve army of labor, is generally a feature of Marxian-inspired models beginning with Goodwin’s (1967) famous article (Rowthorn 1981, 1999; Levine 1988; Bhaduri & Marglin 1990; Green 1991; Glyn 1995, 2009; Levrero 2013; Shaikh 2016). The specification regarding the unemployment rate is the basis of the classical wage curve (Blanchflower & Oswald 1990; Card 1995; Shaikh 2016: 648–650) where the wage rate exhibits an inverse relation to the rate of unemployment.
This determination of income distribution for classical closure on the wage-side relates to the Marxian reserve army of labor story in a two-stage process. In the first instance, social conditions, norms, and class struggle help to shape the particular value of the class struggle parameter, which establishes the share of wages in productivity (Green 1991). This establishes the overall regime of distribution which following Marx’s reserve army idea will be associated with a (dynamicstable) regime of distribution where ‘short-run’ changes in the wage share are cyclically associated with changes in the unemployment rate. When the labor market is ‘tight’ the actual rate of unemployment is less than the critical rate and the wage share rises, and when the labor market is ‘loose’ the actual rate of unemployment is greater than the critical rate and the wage share falls. Leftward or backward shifts in the classical wage curve and/or counter-clockwise rotating shifts indicate decreased worker strength. In this case, a new regime and hence a new wage curve has occurred (Shaikh 2016: 667). There has been a growing interest in Goodwin-type models, including extensions of the model to consider investments and aggregate demand (Skott 1989b), empirical tests across OEDC countries (Harvie 2000), and issues in labor market conflict (Rezai 2011; Palley 2012).
One of the core tenets of Cambridge theory is the causality running to distributional relations (such as profitability, the profit rate, the wage share, and/or wage rate) from some other source. Within this tradition there have been two distinct approaches as to what constitutes that source. The first approach is the ‘physicalist’ growth-theoretic approach and the vast literature and rich discussion around the Cambridge equation where the rate of profit is determined by the so-called ‘natural rate of growth’ or investment-capital ratio divided by the propensity to save out of profit-type revenue (sz). The second approach is the ‘monetary’ interest rate-theoretic approach that is built on the cryptic statement made by Piero Sraffa (1960: 33) in §44 of his Production of Commodities by Means of Commodities, that the money rate of interest determines the profit rate. It is important to emphasize that in both approaches the profit rate is the dependent variable in terms of how the system closes. Once the profit rate is determined from outside of the revenue account it then acts upon the wage element, and (surplus) wages become a residual.
The growth-theoretic approach accepts the causality proposed by Keynes’ widow’s cruse theory of profits (see Kurz & Salvadori 1995; Pasinetti 2000) introduced in the Treatise on Money. The basic idea is that the investment behavior of the capitalist class determines profitability, hence output account relations determine those of the income account. By reversing classical causality, Cambridge theory introduced the role of aggregate and/or effective demand in the determinants of income distribution.
Kaldor (1956) and Pasinetti (1962) developed the basic framework for this approach initially within conditions of full employment and later in models that fully adjusted in the presence of unemployment. Setting the propensities to save out of wage-type and profit-type revenue as sw and sz respectively, and assuming that 0 < sw < sz < 1, the standard derivation of the profit share and profit rate is as follows:
where ω is the wage share, Y aggregate income, Z aggregate profits, I aggregate investments, and K the value of the capital stock. For both the profit share and the profit rate, the investment relation is the determining force; for the profit share it is the investment-output ratio and for the profit rate it is the rate of capital accumulation (called the natural rate of growth) under the assumption of a constant output-capital ratio equal to the maximum rate of profit). The determination of the profit share constitutes the model’s ‘theory’ of distribution, such that the profit share is endogenous and in line with the level of investment spending. Equation (9.2) is the Cambridge equation when workers save; when workers do not save then sw = 0 and Equation (9.2) reduces to the famous form in which the Cambridge equation is mostly known:
In Baranzini & Mari’s (2009) exhaustive survey of Cambridge models, the Cambridge equation is shown to be robust in a variety of different scenarios in which different conditions are relaxed and/or introduced. Perhaps the most important is the relaxation of the full employment assumption in lieu of the possibly less than full employment ‘fully adjusted situation’ associated with normal prices and quantities (Pasinetti 1981: 44). Also important is the development of steady-state growth models compatible with those of both full employment and fully adjusted growth (Bortis 1993).
Among the extensions to the Cambridge theory, one is the inclusion of differentiated interest rates on the wealth of different classes. The upshot is that two rates of return manifest: (i) the rate of profit, which is the rate of return of capitalists’ saving; and (ii) the rate of interest by which “is meant the rate at which the workers place their savings into the hands of capitalists” (Baranzini & Mari 2009: 6). Inclusion of the monetary sector here is expressed in terms of portfolio choice where workers’ savings take the form of bonds issued by firms (Palley 1996, 2002). Park (2006) extends this framework by relaxing the assumption that workers’ consumption is limited by the wage bill and accordingly introduces a credit-money system.
Another extension made to the Cambridge model is the introduction of the analysis of the public sector with respect to the aggregate propensities to consume, save, accumulate, and run budget deficits or surpluses. The works by Steedman (1972) and Fleck & Domenghino (1987) incorporate government spending and direct and indirect taxation and thereby arrive “at a more generalised version of the Cambridge equation according to which the workers’ propensity to save determines . . . the steady state of income distribution” (Baranzini & Mari 2009: 13). There has also been recent literature that relaxes the assumption of exogenous savings propensities of the various classes (Baranzini & Mari 2009: 22–23). Here a differentiated accumulation structure is posited, where workers or wage earners generally accumulate wealth accrued over the life-cycle and capitalists or profit earners adopt a bequest motive approach and accumulate wealth inter-generationally (Wolff 1988; Teixeira et al. 1998; Palley 2010).
Monetary approaches develop the cryptic comment in §44 of Sraffa (1960) that the money rates of interest determine the profit rate in monetary theories of distribution (Garegnani 1979; Panico 1980, 1985, 1988a, b; Pivetti 1985, 1991; Panico et al. 2012; Bellofiore 2014; Deleplace 2014; Biermann 2015). Here the interest rate is the independent variable, which determines the profit rate and accordingly closes the distribution parameter. The mechanisms that determine the interest rate range from monetary authorities’ interventions (Garegnani 1979; Pivetti 1991) to the presence of financial instruments (Panico 1985, 1988a, b). Recently Deleplace (2014) and Biermann (2015) have advanced a thesis similar to Lawlor & Horn (1992) that the rate of interest which determines the profit rate in Sraffa are the commodity own-rates of interest measured in money.
In the Neo-Kaleckian branch of Post Keynesian economics the influence of distribution on aggregate and effective demand emerges as the paramount issue (Bhaduri & Marglin 1990; Taylor 2004; Barbosa-Filho & Taylor 2006; Nikoforos & Foley 2012). Neo-Kaleckian theory generally posits imperfect competition in the product market and conflict in the labor market, and the two are thought to interact in the expression of the mark-up (Lavioe 2014; Palley 2016), with simple versions the mark-up is written directly as a function of the profit share.2
The Neo-Kaleckian school is known for its usage of the Bhaduri-Marglin (1990) (B&M) model although earlier variants of the original model do abound (Rowthorn 1981; Dutt 1990). The B&M model is robust in conceptualizing the growth and distribution process, and provides explanation for a variety of different demand, productivity, and distributive regimes. The key relationship regarding the role of demand and distribution has to do with the slope of the steady-state effective demand IS curve and its intersection with the ‘distributive curve’ drawn in the profit share-capacity utilization space (Taylor 2004; Barbosa-Fihlo & Taylor 2006; Nikoforos & Foley 2012).
The IS schedule is the relationship between distributive shares and capacity on the 'demand' side. The schedule is derived under the assumption that an excess of investment over saving increases the level of capacity, the latter defined as the ratio of actual to potential output This means that the change in capacity is equal to the change in the investment-saving balance. Saving and investment are written as functions of the wage share co and capacity utilization rate (u): I = I(Ω;u) and S = S(ω;u). The IS curve is expressed as the change in capacity with respect to the change in income distribution, as follows:
where the subscripts denote partial derivatives.
The denominator in Equation (9.5) is negative “under the . . . Keynesian stability condition. . . that saving is more responsive than investment to a change in output” (Nikoforos & Foley 2012: 203, emphasis in original), meaning that the sign of the numerator becomes of interest. If saving reacts more than investment to a change in the wage share, the numerator is positive, meaning that as the wage share rises the amount of capacity utilization also rises, thereby increasing output and aggregate demand. Here the demand regime is wage-led. The opposite happens in a profit-led demand regime, when the numerator is negative. Here redistribution to wages decreases the capacity utilization rate thereby decreasing output and aggregate demand; or alternatively expressed in terms of the profit share, the distribution towards profits leads to higher capacity, output, and demand. In terms of the schedule, a wage-led demand regime will have an upward sloping IS curve in the wage share-capacity space and a profit-led demand regime will have a downward sloping IS curve in that same space (Taylor 2004; Barbosa-Fihlo & Taylor 2006; Nikoforos & Foley 2012; Lavoie 2014).
The distributive curve considers the relationship between distributive shares and capacity on the utilization or ‘production’ side. It can also have a positive or negative slope, and in fact Nikoforos & Foley (2012) show evidence of non-linearity in a u-shaped distributive curve, such that it has both slopes at different levels of capacity. The distributive curve expresses the change in the wage share given a change in capacity utilization as the ratio of the difference in the rates of real wage and productivity growth:
where the rate of change of real wages given a change in j, is the rate of change of productivity given a change in j, and j = u, ω.
A positive distributive schedule indicates that the wage share increases with increases in capacity utilization and this scenario relates to wage-inflation and the profit squeeze. A negative distributive schedule is the case of price inflation and forced saving. Combining the IS demand schedule with the distributive curve yields the Neo-Kaleckian equilibrium situation.
The strength of the B&M model is the ability to handle a variety of different scenarios under the same analytical setting, as positive and negative slopes of both the IS and the distributive schedules in the ω-u space are possible. Neo-Kaleckian growth and distribution theory has garnered much use from the B&M model as there has been an explosion of studies that are both theoretical and empirical in exploring the robustness and verifiability of the wage-led and profit-led demand thesis. The main result includes the possibility of an economy to be in either wage-led or profit-led growth regimes, and the regime which dominates an economy is mostly an empirical and historical question.
Wage-led demand growth holds when increases in the wage share lead to increases in the capacity utilization rate, thereby increasing output and aggregate demand, and profit-led demand growth is said to hold when the wage share increases lead to a decrease in those indicators (Barbosa-Filho & Taylor 2006; Hein & Vogel 2008; Stockhammer et al. 2009). To these wage- and profit-led demand effects Lavoie & Stockhammer (2012) add supply-side productivity effects. Wage-led productivity growth is defined as increases in productivity growth when there is an increase in wage growth.3 Profit-led productivity growth is the opposite case, when the growth in wages causes productivity growth to slow down (Lavoie & Stockhammer 2012: 16). The empirical literature inspired by tests of the B&M model has been quite fruitful. Lavoie & Stock-hammer (2012: 18–20) report summary results for 12 studies4 from 1995 to 2012 that have tested the B&M model for a total of seven advanced economies.5 The results reported by the majority of studies find domestic wage-led demand regimes with increasingly profit-led demand once international trade is included.
Heterodox economics in the classical, Marxian, and Post Keynesian traditions at the theoretical level has mostly focused on functional distribution, although the personal distribution of income is becoming a growing area of interest for heterodox economists. A recent empirical study extending the Neo-Kaleckian framework to personal distribution is Carvahlo & Rezai (2016). They begin with the observation of a shift in functional distribution from wage to profit revenue over the past 20 years, and this had been associated with redistribution towards high-income earners in the size distribution of the wage component. In this framework, size distribution affects functional distribution and, through the latter, also regimes of demand according to Neo-Kaleckian theory. The question becomes one of determining the influence on aggregate demand of increased inequality in wage income. Size distribution is incorporated into the B&M model where aggregate income is determined by independent investment and saving decisions. The investment function depends positively on capacity utilization, the profit rate, as well as an autonomous component of ‘animal spirits.’ It is the savings function that Carvahlo & Rezai (2016) make dependent on size distribution and the focus here is on the wage portion of income broadly defined (Bowles & Boyer 1995; Taylor 2004; Barbosa-Filho & Taylor 2006; Tavani & Vasudevan 2014). The distribution of revenue among wage earners influences the propensity to save out of wages, with a decrease in the wage share (increase in the profit share) as the causal mechanism for the increased inequality across the spectrum of wage earners (Carvahlo & Rezai 2016: 495).
Galbraith (1998, 2011), Lavoie (2009), and Palley (2005, 2014, 2016) develop theoretical relationships between functional and size distribution. In Galbraith, for example, the personal dimension in functional distribution turns on the dichotomy of the macroeconomy in terms of different sectors—the consumption sector, the service sector, and the knowledge sector. So sub-aggregating the macroeconomy allows for analysis of the income distribution within each sector according to its specific economic, competitive, structural, etc. conditions. This leads Galbraith (2011: 38–39) to conclude that “we thus have a macroeconomic theory of the evolution of personal income distribution, according to which inequality varies with the movements of aggregate demand, differentiated by sector.”
Lavoie (2009, 2014) and Palley (2005, 2014, 2016) consider the personal-functional relationship to be related to the ‘overhead work’ and income streams consisting of wage-type and profit-type revenues accrued to a third economic class in the system. The possibility of income consisting of both wage-type and profit-type revenues has been discussed ever since Pasinetti’s (1962) extension of Kaldor’s Keynesian growth and distribution model. Palley (2005, 2014, 2016) develops the B&M model to include a measure of income inequality defined as the ratio of capitalists’ to workers’ income, each of whom are able to garner both wage- and profit-type revenues. Key to this relationship is the structure of ownership in the accrual of the respective income streams, denoted in the present context as θij, read as the ownership share of individual agent i in the income stream of type j, where i = workers and capitalists and j = wage-type and profit-type revenue. It is important—with the extension from the functional to the personal—to keep the individual agents (workers versus capitalists) distinct from the revenue-flows (wages versus profits) so that mapping their interaction is as transparent as possible.
Income to laborers (YL) and income to capitalists (YK) are the sums of their respective profit-type (Z) and wage-type (W) income:
Capitalists' income: YK = ΘKWW + θKZZ (9.7a)
Workers* income: YL = θLW W + θLZZ (9.7b)
Dividing each of the income streams by total income (Y) yields the shares of worker and capitalist incomes in the total national income, which Palley (2016: 6) reduces to a function of the ownership structure and distributive shares:
where the measure of inequality, ψ, is equal to the ratio of capitalist to worker income:
From this relation Palley (2016: 6) concludes that “income inequality depends on the functional distribution of income, the division of the wage bill, and the ownership distribution of the capital stock.” This seems to be a fruitful way to move forward in developing specific relationships, accounting or otherwise, in mapping functional to size distribution and vice versa.
These developments can be interwoven with a graphical exposition adapted from the neoclassical approach of Atkinson & Bourguignon (2000) in the development of the structural relationship between functional and size distribution. Here we find that, although neoclassically oriented, their approach once modified provides a broad way to conceive of the functional-size nexus. As with the classical model, it is assumed here that there is uniformity in both the wage and profit rates. The functional distribution of (macro) revenue is by revenue type and size distribution of (micro) earnings by income recipient, the latter designated as the household (HH). The macro revenue type is given by the sum of the wage bill (W) and gross profits (Z), where:
Y=W + Z = (w*L) + (r*p*K) (9.10)
The wage bill is a monetary magnitude determined by the product of the uniform ‘normal’ money wage rate (w*) and the aggregate quantity of labor (L). Gross profits are also a monetary magnitude determined by the product of the uniform ‘normal’ rate profit (r*), the money prices-of-production of aggregate capital inputs (p*), and the quantity of such inputs (K).
At the level of the micro-earning recipient, consider the case when the total number of households (HH) are equal to worker-households (HHW) receiving wage-type revenue plus capitalist households (HHZ) receiving profit-type revenue. In a purely egalitarian society, the ownership across both earned and unearned revenue accrual will be exactly the same.6 However, equitable distribution in income is not only the result of complete social equity in ownership shares across individuals, and a purely class-based society too could equitably distribute revenues and incomes as well, so long as the overall class division of individuals is equal to the wage share of income. The wage share of perfect equality (ωPE)in a pure class system is therefore the share of wages in national income when equal to the aggregate breakdown of individual wage and profit earning streams. To make matters simple we will consider the individual unit to be the ‘household’ which in the two-class society will be divided into worker and capitalist households (HHW and HHZ, respectively).
where hhw is the portion of household wage-type income stream recipients out of total; hh is the cumulative aggregate total income stream of all individuals, that is, hhw + hhz = 1.
We can now relate functional to size distribution. To do so the functional income distribution in Equation (9.10) is transformed into the wage-share variant by dividing both sides by total value-added Y:
Solving for r* yields the well-known equation for the uniform rate of profit written as the product of the profit share and the output-capital ratio qua maximum rate of profit (Sraffa 1960; Kurz & Salvadori 1995; Foley & Michl 1999):
r* = (l - Ω)R (9.12)
where R = output-capital ratio = maximum rate of profit.
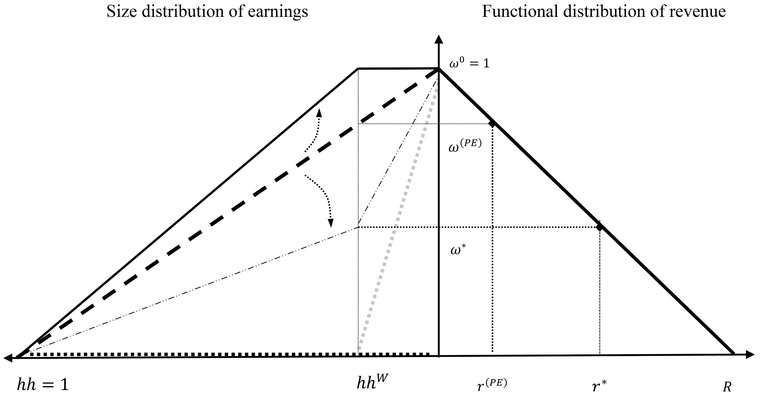
Figure 9.2 Functional and size distribution interface
A two-quadrant graph that links functional distribution in quadrant I to size distribution in quadrant II can be drawn. Functional distribution is the sum of the wage bill and gross profits, whereas the streams of earnings accrue to the different households. Assumed is the limiting case of workers consumption being equal to their wage bill, hence workers do not save. This reduces both the realism as well as the complexity of the exposition, but does provide an indication of the nature of the functional-size interface under such limiting conditions. The wage share of perfect equality corresponds to a one-to-one ratio between the income received and the income recipient. If wages were to increase beyond perfect equality, admittedly a very unlikely scenario, then profit earners receive less revenue resulting in overall inequality in the system. Inequality here is driven by the share of wage revenue exceeding the proportion in wage-recipients. In the more likely scenario of wages decreasing below the threshold of perfect equality, profit earners receive proportionally more revenue. Inequality here is driven by profit revenues accruing in excess proportion to the number of profit earning income recipients. The absolute lower limit to the distribution parameter corresponds to a wage share of zero, although most heterodox theories posit a lower limit to the wage set by the historical and social conditions of society.
Atkinson & Bourguignon (2000: 8) show a graph similar to that of quadrant II shown in Figure 9.2, except they do not posit the case of a wage share of unity (hence no trapezoid). Based on this simple two-class economy they show that the measure of profit-driven inequality is determined by the Gini coefficient calculated as the proportion of wage-earning households minus the share of wages in national income:
Gini =
The overall distribution of income of course does not fit this nice two-class schema, and incorporation of different income types has always presented issues for heterodox and neoclassical theorizing alike. Instead, the above is only meant to provide an overall broad picture to the functional dimension in the size distribution nexus.
One of the most relevant results from empirical studies of the size distribution of earnings at an analytical level shows that the upper tail of the income distribution is of a different character than that of the remaining portion of the income distribution. Shown in various studies (Dragğulescu & Yakovenko 2000, 2001a, b; Silva et al. 2002; Aoyama et al. 2003; Fujiwara et al. 2003; Silva & Yakavenko 2005; Wright 2005, 2011; Shaikh et al. 2014; Shaikh 2016), the income of the ‘rich’ is subject to a Pareto-type power distribution that allows greater intensity of concentration, and the income of the ‘non-rich’ is subject to an exponential distribution with a lessened intensity of concentration. Terming the former ‘superthermal’ and the latter ‘thermal’ income classes, Silva & Yakavenko (2005: 1) characterize this as follows:
We show that the US economy has a well-defined two-class structure. The majority of the population . . . belongs to the lower class and has a very stable in time exponential (‘thermal’) distribution of income. The upper class . . . has a power-law (‘superthermal’) distribution, whose parameters significantly change with the rise and fall of the stock market.
Wright (2011: 19) develops the results described above in terms of an analytical framework and simulation much in line with the precepts of classical and Marxian political economy. His simulation model is called the ‘dynamic computational model of the social relations of production’ or SR model for short. This model develops all sorts of dynamic properties consistent with real capitalist economic systems and reproduces with simulations many of the empirical patterns and results that have emerged from empirical studies, two of which stand out for our purposes: (i) that the “class of capitalists is numerically small, whereas the class of workers, that is those actors who predominantly rely on wage income for their subsistence, constitute the vast majority of the population” (Wright 2011: 11); and (ii) that the “empirical distribution is characterised by a highly unequal distribution of income, in which a very small number of households receive a disproportionate amount of the total” (Wright 2011: 19). Wright develops these results in terms of an analytical framework in line with the precepts of classical and Marxian political economy and concludes that
the higher, property income, regime of income distribution can be fitted to a Pareto (or power) distribution whereas the lower, or wage-income, regime, which represents the vast majority of the population, is normally fitted to a lognormal distribution, but recently researchers report that an exponential (Boltzmann-Gibbs) distribution better describes the empirical data.
Wright 2011: 19
Shaikh (2016: 751–755) calls this evidence the “econo-physics two-class theory of income distribution” or EPTC. In relating this to increased income inequality evidenced since 1979–1980, Shaikh (2016: 755, original emphasis) draws the following conclusions:
If labor income is exponentially distributed . . . a rise in the Gini of overall income distribution must come from a rise in property income relative to labor income. Indeed, the EPTC group explicitly links the rise in property income with the rise in stock market prices . . . [as] the overall Gini depends on the proportion of property income to total income. It follows that the overall degree of income inequality ultimately rests on the ratio of profits to wages, that is, on the basic division of value added. This is a fundamentally classical result.
In this chapter the distribution of income has been considered in terms of three different heterodox theories of distribution: classical/Marxian theory, Cambridge theory, and Neo-Kaleckian theory. Each of the theories was considered in terms of its closure and the basic mechanisms underlying and interacting within each model as well as the functional-size distribution nexus and the implications for various heterodox theories. Finally, the chapter explored the frontiers with other disciplines such as that of econo-physics.
For the classical-Marxian model, fully adjusted normal and/or regulating conditions were posited as the centers-of-gravitation for the system. Classical-Marxian theory closes the system from the wage-side of the ledger and causality runs from profitability to the accumulation of capital and growth. Differences in the mechanisms that determine closure are wages as a ‘given’ and constant bundle of commodities versus wages conceived as a share of net productivity. Important extensions of the model include incorporation of disciplining effects on labor such as the unemployment rate which constitutes a proxy of labor market conditions, and further research could consider the impact of labor market institutions such as union concentration.
Cambridge theory closes the system from rates of accumulation and growth to profitability and income distribution. The Cambridge equation was shown to be robust and susceptible to various implementations and applications, and the research agenda outlined in Baranzini & Mari (2009) is very fruitful including theoretical applications of the functional-size nexus, the introduction of financial variables, and the consideration of other socio-economic classes. The Cambridge theory was also shown to have two variants: the physicalist natural rate of growth or accumulation perspective; and the interest rate monetary sector perspective. Common to both perspectives is the profit rate as the dependent variable as regards aggregate systemic closure, and the rate of capital accumulation as the independent variable as regards income distribution. The latter means that in terms of the distribution parameter it is the profit rate that determines the level of relative wages, exactly the opposite of the classical traditions.
Neo-Kaleckian theory was shown to be a robust way to conceive of the role of income distribution in terms of regimes of demand as well as productivity. The generality of the framework and its applicability across a variety of scenarios makes the model very useful in terms of both theory and policy. The importance of the latter is highlighted by the fact that economic policy can be framed in terms of equitable ways in which the economy can recover and sustain itself, expressed in terms of regimes of wage-led growth. Here economic analysis becomes less of a description of the workings of market forces and more of an application of directing the economy towards ways in which economic activity works for all members of the economy, not just the capital-owning class.
Heterodox theories of distribution have the marked distinction to harken back to the dictum Ricardo made in his Preface that distribution is the ‘principal problem’ of our science. This stands in contrast with orthodox-neoclassical theories where ‘distribution’ is often relegated to the ghetto of being normative rather than positive in its essential form theoretically, and highly problematic when implemented as policy. Many heterodox economists consider this dismissal of the conceptual and practical merit of distribution as apologetics for the capitalist order and status quo. It is to the credit of heterodox approaches to place emphasis on the role of distribution as both a theoretical-category and a policy-target, and this broadens the scope of economic inquiry generally for all theories, orthodox and heterodox.
1 For recent retrospective on the theory of distribution from a history of thought standpoint see: also Atkinson & Bourguignon (2000), Atkinson (2009), and Glyn (2009); other important surveys on income distribution can be found in Marchal & Ducros (1968), Bronfenbrenner (1971), Pen (1971), Ranadive (1978), Sahota (1978), and the entries in Asimakopulos (1988); see also the New Palgrave Dictionary entries for the various schools of thought: neoclassical (Bliss 1987), classical (Pivetti 1987), Keynesian (Baranzini 1987), and Marxian (Gordon 1987).
2 Post Keynesian theories of the mark-up include various mechanisms, some of them being monopoly power, degree of concentration, risk of new entry, and worker resistance (Eichner & Kregel 1975; Skott 1989a; Lee 1998; Shapiro 2000), target return rates that finance a firm’s desired growth rate (Godley & Lavoie 2007; Lavoie 2014), and forward-looking strategic behavior (Shapiro & Sawyer 2003).
3 Lavoie & Stockhammer (2012: 15) and Lavoie (2014: 320) call this the ‘Webb-Effect’ after Sidney Webb and note that this has resonance with the mainstream efficiency wage thesis.
4 These studies are: Bowles & Boyer (1995); Stockhammer & Onaran (2004); Barbosa-Filho & Taylor (2006); Naastepad & Storm (2006–07); Ederer & Stockhammer (2007); Hein & Vogel (2008); Stockhammer et al. (2009); Stockhammer et al. (2011); Stockhammer & Stehrer (2011), and Onaran et al. (2012).
5 The countries are the Euro area, Germany, France, the Netherlands, Austria, the United Kingdom, Japan, and the United States.
6 One Editor of the Handbook pointed out that the scenario posited assumes the wage rate and the profit rate are uniform, and that such proviso is untenable if we wish to talk about the real world. To reiterate, the present exercise is to show in a simple diagram the connections between the functional and size distribution in such a limiting case. The criticism generally against uniformity in the wage and profit rates is an important matter beyond the scope of this chapter.
Aoyama, H., Souma, W., & Fujiwara, Y. 2003. ‘Growth and fluctuations of personal and company’s income.’ Physica A, 324: 352–358.
Asimakopulos, A. (ed.) 1988. Theories of Income Distribution. Boston: Kluwer Academic Press.
Atkinson, A. 2009. ‘Factor shares: the principal problem of political economy?’ Oxford Review of Economic Policy, 25 (1): 3–16.
Atkinson, A. & Bourguignon, F. 2000. ‘Introduction: income distribution and economics,’ in A. Atkinson & F. Bourguignon (eds.), Handbook of Income Distribution. Geneva: Elsevier Science, 1–88.
Baranzini, M. 1987. ‘Distribution: Keynesian,’ in: J. Eatwell, M. Milgate, & P. Newman (eds.), The New Palgrave Dictionary of Economics. Basingstoke, UK: Palgrave Macmillan, 876–8.
Baranzini, M. & Mari, C. 2009. The Cantabrigiensis–Italian school of income distribution. Unpublished Manuscript.
Barbosa-Filho, N. & Taylor, L. 2006. ‘Distributive and demand cycles in the US economy – a structuralist Goodwin model.’ Metroeconomica, 57 (3): 389–411.
Baumol, W. 1983. ‘Marx and the Iron Law of wages.’ American Economic Review, 73 (2): 303–308.
Bellofiore, R. 2012. ‘The “tiresome objector” and old moor: a renewal of the debate on Marx after Sraffa based on the unpublished material at the Wren Library.’ Cambridge Journal of Economics, 36 (6): 1385–1399.
Bellofiore, R. 2014. ‘The loneliness of the long distance thinker: Sraffa, Marx and the critique of political economy,’ in: R. Bellofiore & S. Carter (eds.), Towards a New Understanding of Sraffa: Insights into Archival Research. Basingstoke, UK: Palgrave Macmillan, 198–240.
Bhaduri, A. & Marglin, S. 1990. ‘Unemployment and the real wage: the economic basis for contesting political ideologies.’ Cambridge Journal of Economics, 14 (4): 375–393.
Biermann, A. 2015. Money, interest, and profit in the theory of distribution: a Sraffian approach. Unpublished Manuscript, the University Frankfurt. Available from http://www.boeckler.de/pdf/v_2015_10_23_biermann.pdf [Accessed April 1, 2016]
Blanchflower, D.G. & Oswald, A.J. 1990. The Wage Curve. Cambridge, MA: The MIT Press.
Bliss, C. 1987. ‘Distribution: neoclassical,’ in: J. Eatwell, M. Milgate, & P. Newman. The New Palgrave Dictionary of Economics. Basingstoke, UK: Palgrave Macmillan, 883–886.
Bortis, H. 1993. ‘Notes on the Cambridge equation.’ Journal of Post Keynesian Economics, 16 (1): 105–126.
Botwinick, H. 1993. Persistent Inequalities: Wage Disparity under Capitalist Competition. Princeton, NJ: Princeton University Press.
Bowles, S. & Boyer, R. 1995. ‘Wages, aggregate demand, and employment in an open economy: an empirical investigation,’ in: G. Epstein & H. Gintis (eds.), Macroeconomic Policy after the Conservative Era: Studies in Investment, Saving and Finance. Cambridge: Cambridge University Press, 143–171.
Bronfenbrenner, M. 1971. Income Distribution Theory. New York: Aldine.
Card, D. 1995. ‘The wage curve: a review.’ Journal of Economic Literature, 33 (2): 785–799.
Carvahlo, L. & Rezai, A. 2016. ‘Personal income inequality and aggregate demand.’ Cambridge Journal of Economics, 40 (2): 491–505.
Chiodi, G. 2010. ‘The means of subsistence and the notion of ‘viability’ in Sraffa’s surplus approach,’ in: S. Zambelli (ed.), Computable, Constructive and Behavioural Economic Dynamics: Essays in Honour of Kuma-raswamy (Vela) Velupillai. London: Routledge, 318–330.
Deleplace, G. 2014. ‘The essentiality of money on the Sraffa Papers,’ in: R. Bellofiore & S. Carter (eds.), To w a r d s a New Understanding of Sraffa: Insights into Archival Research. Basingstoke, UK: Palgrave Macmillan, 139–166.
Drag ˘ulescu, A.A. & Yakovenko, V.M. 2000. ‘Statistical mechanics of money.’ The European Physical Journal B, 17: 723–729.
Drag ˘ulescu, A.A. &Yakovenko, V.M. 2001a. ‘Evidence for the exponential distribution of income in the USA.’ The European Physical Journal B, 20: 585–589.
Drag ˘ulescu, A.A. & Yakovenko, V.M. 2001b. ‘Exponential and power-law probability distributions of wealth and income in the United Kingdom and the United States.’ Physica A, 299: 213–221.
Dutt, A. 1990. Growth, Distribution, and Uneven Development. Cambridge: Cambridge University Press.
Ederer, S. & Stockhammer, E. 2007. ‘Wages and aggregate demand in France: an empirical investigation,’ in: E. Hein & A. Truger (eds.), Money, Distribution, and Economic Policy – Alternatives to Orthodox Macroeconomics. Cheltenham, UK: Edward Elgar, 119–138.
Eichner, A. & Kregel, J. 1975. ‘An essay on Post-Keynesian theory: a new paradigm in economics.’ Journal of Economic Literature, 13 (4): 1293–1314.
Fleck, F. & Domenghino, C.-M. 1987. ‘Cambridge (UK) versus Cambridge (Mass): a Keynesian solution of “Pasinetti’s Paradox”.’ Journal of Post Keynesian Economics, 19 (1): 22–36.
Foley, D. & Michl, T. 1999. Growth and Distribution. Cambridge, MA: Harvard University Press.
Fujiwara, Y., Souma, W., Aoyama, H., Kaizoji, T., & Aoki, M. 2003. ‘Growth and fluctuations of personal income.’ Physica A, 321: 598–604.
Galbraith, J.K. 1998. Created Unequal: The Crisis in American Pay. Chicago: University of Chicago Press.
Galbraith, J.K. 2011. ‘Income distribution,’ in: R. Holt & S. Pressman (eds.), A New Guide to Post Keynesian Economics. New York: Routledge, 32–41.
Garegnani, P. 1979. ‘Notes on consumption, investment and effective demand.’ Cambridge Journal of Economics, 3 (1): 83–89.
Garegnani, P. 1984. ‘Value and distribution in the classical economists and Marx.’ Oxford Economics Papers, 36 (2): 291–325.
Garegnani, P. 1987. ‘Surplus approach to value and distribution,’ in: J. Eatwell, M. Milgate, & P. Newman (eds.), The New Palgrave Dictionary of Economics. Basingstoke, UK: Palgrave Macmillan, 560–574.
Giovannoni, O. 2014. What do we know about the labor share and the profit share? Part I: Theories. University of Texas Inequality Project Working Paper No. 65. Available from http://utip.lbj.utexas.edu/papers/UTIP%2064.pdf [Accessed April 1, 2016]
Glyn, A. 1995. ‘Unemployment and inequality.’ Oxford Review of Economic Policy, 11 (1): 196–213.
Glyn, A. 2009. ‘Functional distribution and inequality,’ in: W. Salverda, B. Nolan, & T.M. Smeeding (eds.), Oxford Handbook of Economic Inequality. Oxford: Oxford University Press, 99–124.
Godley, W. & Lavoie, M. 2007. Monetary Economics: An Integrated Approach to Credit, Money, Income, Production, and Wealth. Basingstoke, UK: Palgrave Macmillan.
Goodwin, R. 1967. ‘A growth cycle,’ in: C. Feinstein (ed.), Socialism, Capitalism, and Economic Growth. Cambridge: Cambridge University Press, 54–58.
Gordon, D. 1987. ‘Distribution: Marxian,’ in: J. Eatwell, M. Milgate, & P. Newman (eds.), The New Palgrave Dictionary of Economic s. Basingstoke, UK: Palgrave Macmillan, 878–883.
Green, F. 1991. ‘The relationship of wages to the value of labour-power in Marx’s labour market.’ Cambridge Journal of Econ omics, 15 (2): 199–213.
Harvie, D. 2000. ‘Testing Goodwin: growth cycles in ten OECD countries.’ Cambridge Journal of Economics, 24 (3): 349–376.
Hein, E. & Vogel, L. 2008. ‘Distribution and growth reconsidered – empirical results for six OECD countries.’ Cambridge Journal of Economics, 32 (3): 479–511.
Kaldor, N. 1956. ‘Alternative theories of distribution.’ Review of Economic Studies, 23 (2): 83–100.
Kurz, H. & Salvadori, N. 1995. Theory of Production: A Long Period Analysis. Cambridge: Cambridge University Press.
Lavoie, M. 2009. ‘Cadrisme within a Post-Keynesian model of growth and distribution.’ Review of Political Economy, 21 (3): 369–391.
Lavoie, M. 2014. Post-Keynesian Economics: New Foundations. Northampton, MA: Edward Elgar.
Lavoie, M. & Stockhammer, E. 2012. Wage-led Growth: An Equitable Strategy for Economic Recovery. Basingstoke, UK: Palgrave Macmillan.
Lawlor, M.S. & Horn, B. 1992. ‘Notes on the Sraffa–Hayek exchange.’ Review of Political Economy, 4 (3): 317–340.
Lee, F.S. 1998. Post Keynesian Price Theory. Cambridge: Cambridge University Press.
Levine, D. 1988. ‘Marx’s theory of income distribution,’ in: A. Asimakopulos (ed.), Theories of Income Distribution. Boston: Kluwer Academic, 19–74.
Levrero, E.S. 2013. ‘Marx on absolute and relative wages and the modern theory of distribution.’ Review of Political Economy, 25 (1): 91–116.
Marchal, J. & Ducros, B. (eds.) 1968. The Distribution of National Income. London: Macmillan.
Naastepad, C.W.M. & Storm, S. 2006–07. ‘OECD demand regimes (1960–2000).’ Journal of Post Keynesian Economics, 29 (2): 213–248.
Nikiforos, M. & Foley, D. 2012. ‘Distribution and capacity utilization: conceptual issues and empirical evidence.’ Metroeconomica, 63 (1): 200–229.
Onaran, Ö., Stockhammer, E., & Grafl, L. 2012. ‘The finance-dominated growth regime, distribution, and aggregate demand in the US.’ Cambridge Journal of Economics, 35 (4): 637–661.
Palley, T. 1996. ‘Inside debt, aggregate demand, and the Cambridge theory of distribution.’ Cambridge Journal of Economics, 20 (4): 465–474.
Palley, T. 2002. ‘Financial institutions and the Cambridge theory of distribution.’ Cambridge Journal of Economics, 26 (2): 275–277.
Palley, T. 2005. ‘Class conflict and the Cambridge theory of distribution,’ in: B. Gibson (ed.), The Economics of Joan Robinson: A Centennial Celebration. Cheltenham, UK: Edward Elgar, 203–224.
Palley, T. 2010. ‘The relative permanent income theory of consumption: a synthetic Keynes–Duesenberry– Friedman Model.’ Review of Political Economy, 22 (1): 41–56.
Palley, T. 2012. A Neo-Kaleckian–Goodwin model of capitalistic economic growth: monopoly power, managerial pay, labor market conflict, and endogenous technical progress. Institut für Makroökonomie und Konjunkturforschung Working Paper 105. Available from http://www.boeckler.de/pdf/p_imk_wp_105_2012.pdf [Accessed April 1, 2016]
Palley, T. 2014. ‘Wealth and wealth distribution in the Neo-Kaleckian growth model.’ Journal of Post Keynesian Economics, 34 (3): 453–474.
Palley, T. 2016. Inequality and growth in Neo-Kaleckian and Cambridge growth theory. Political Economy Research Institute Working Paper No. 417. Available from http://www.peri.umass.edu/fileadmin/pdf/working_papers/working_papers_401-450/WP417.pdf[Accessed June 1, 2016]
Panico, C. 1980. ‘Marx’s analysis of the relationship between the rate of interest and the rate of profits.’ Cambridge Journal of Economics, 4 (4): 363–378.
Panico, C. 1985. ‘Market forces and the relation between the rates of interest and profits.’ Contributions to Political Economy, 4 (1): 37–60.
Panico, C. 1988a. ‘Sraffa on money and banking.’ Cambridge Journal of Economics, 12 (1): 2–28.
Panico, C. 1988b. Interest and Profit in the Theories of Value and Distribution. London: Macmillan.
Panico, C. 2011. ‘Monetary influences on distribution: a comparison of Post Keynesian theories,’ in: R. Ciccone, C. Gehrke, & G. Mongiovi (eds.), Sraffa and Modern Economics, Volume II. New York: Routledge, 168–185.
Panico, C., Pinto, A., & Anyul, M.P. 2012. ‘Income distribution and the size of the financial sector: a Sraffian analysis.’ Cambridge Journal of Economics, 36 (6): 1455–1478.
Park, M.-S. 2006. ‘The financial system and the Pasinetti theorem.’ Cambridge Journal of Economics, 30 (2): 201–217.
Pasinetti, L.1962. ‘Rate of profit and income distribution in relation to the rate of economic growth.’ Review of Economic Studies, 29 (4): 267–279.
Pasinetti, L. 1981. Structural Change and Economic Growth: A Theoretical Essay on the Dynamics of the Wealth of Nations. Cambridge: Cambridge University Press.
Pasinetti, L. 2000. ‘Critique of the neoclassical theory of growth and distribution.’ Banca Nazionale del Lavoro Quarterly Review, 23 (3): 383–390.
Pen, J. 1971. Income Distribution: Facts, Theories, Policies. New York: Praeger.
Persky, J. 1992. ‘Pareto’s Law.’ Journal of Economic Perspectives, 6 (2): 181–190.
Petri, D. 2014. ‘On the Neoricardian criticism of irrelevance,’ in: R. Bellofiore & S. Carter (eds.), Towards a New Understanding of Sraffa: Insights into Archival Research. Basingstoke, UK: Palgrave Macmillan, 25–46.
Pivetti, M. 1985. ‘On the monetary explanation of distribution.’ Political Economy: Studies in the Surplus Approach, 1 (2): 73–104.
Pivetti, M. 1987. ‘Distribution: classical,’ in: J. Eatwell, M. Milgate, & P. Newman (eds.), The New Palgrave Dictionary of Economics. Basingstoke, UK: Palgrave Macmillan, 873–876.
Pivetti, M. 1991. An Essay on Money and Distribution. London: Macmillan.
Ranadive, K.R. 1978. Income Distribution: The Unsolved Puzzle. Bombay: Oxford University Press.
Rezai, A. 2011. Goodwin cycles, distributional conflict, and productivity growth. The New School for Social Research Department of Economics Working Paper 10/2011. Available from http://www.economicpolicyresearch.org/econ/2011/NSSR_WP_102011.pdf [Accessed April 1, 2016]
Roncaglia, A. 1988. ‘The neo-Ricardian approach and the distribution of income,’ in: A. Asimakopulos (ed.), Theories of Income Distribution. Boston: Kluwer Academic, 159–180.
Rowthorn, R. 1981. ‘Demand, real wages and economic growth.’ Thames Papers in Political Economy, Autumn: 1–39.
Rowthorn, R. 1999. ‘Unemployment, wage-bargaining and capital–labour substitution.’ Cambridge Journal of Economics, 23 (4): 413–425.
Sahota, G. S. 1978. ‘Theories of personal distribution: a survey.’ Journal of Economic Literature, 16 (1): 1–55.
Sandmo, A. 2014. ‘The principal problem in political economy: income distribution in the history of economic thought,’ in: A. Atkinson & F. Bourguignon (eds.), Handbook of Income Distribution, SET vols. 2A. Amsterdam: Elsevier, 3–66.
Shaikh, A. 1978. ‘Political economy and capitalism: notes on Dobb’s theory of crisis.’ Cambridge Journal of Economics, 2 (2): 233–251.
Shaikh, A. 1980. ‘Marxian competition versus perfect competition: further comments on the so-called ‘choice of technique’.’ Cambridge Journal of Economics, 4 (1): 75–83.
Shaikh, A. 2016. Capitalism: Competition, Conflict, Crises. New York: Oxford University Press.
Shaikh, A., Papanikolaou, N., & Wiener, N. 2014. ‘Race, gender, and the econophysics of income distribution.’ Physica A, 414: 54–60.
Shapiro, N. & Sawyer, M. 2003. ‘Post Keynesian price theory.’ Journal of Post Keynesian Economics, 25 (3): 355–365.
Shapiro, N. 2000. ‘Review of Post Keynesian Price Theory by Frederic S. Lee.’ Journal of Economic Issues, 34 (4): 990–992.
Silva, A.C. & Yakovenko, V.M. 2005. ‘Temporal evolution of the ‘thermal’ and ‘superthermal’ income classes in the USA during 1983–2001.’ Europhysics Letters, 69: 304–310.
Silva, J., Slud, E., & Takamoto, T. 2002. ‘Statistical equilibrium wealth distributions in an exchange economy with stochastic preferences.’ Journal of Economic Theory, 106 (2): 417–435.
Skott, P. 1989a. Conflict and Effective Demand in Economic Growth. Cambridge: Cambridge University Press.
Skott, P. 1989b. ‘Effective demand, class struggle and cyclical growth.’ International Economic Review, 30 (1): 231–247.
Sraffa, P. (ed.) 1951. The Works and Correspondence of David Ricardo, Vol. I. Cambridge: Cambridge University Press.
Sraffa, P. 1960. Production of Commodities by Means of Commodities: Prelude to a Critique of Economic Theory. Cambridge: Cambridge University Press.
Steedman, I. 1972. ‘The state and outcome of the Pasinetti Process.’ The Economic Journal, 82 (328): 1387–1395.
Stockhammer, E. & Onaran, O. 2004. ‘Accumulation, distribution and employment: a structural VAR approach to a Kaleckian macro-model.’ Structural Change and Economic Dynamics, 15 (4): 421–447.
Stockhammer, E. & Stehrer, R. 2011. ‘Goodwin or Kalecki in demand? Functional income distribution and aggregate demand in the short run.’ Review of Radical Political Economics, 43 (4): 506–522.
Stockhammer, E., Hein, E., & Grafl, L. 2011. ‘Globalization and the effects of changes in functional income distribution on aggregate demand in Germany.’ International Review of Applied Economics, 25 (1): 1–23.
Stockhammer, E., Onaran, O., & Ederer, S. 2009. ‘Functional income distribution and aggregate demand in the Euro area.’ Cambridge Journal of Economics, 33 (1): 139–159.
Tavani, D. & Vasudevan, R. 2014. ‘Capitalists, workers, and managers: wage inequality and effective demand.’ Structural Change and Economic Dynamics, 30 (September): 120–131.
Taylor, L. 2004. Reconstructing Macroeconomics: Structuralist Proposals and Critiques of the Mainstream. Cambridge, MA: Harvard University Press.
Teixeira, J.R., Sugahara, R., & Baranzini, M. 1998. ‘On micro-foundations for the Kaldor-Pasinetti growth model with taxation and bequest.’ Anais do XXVI Encontro Nacional de Economia, 1: 505–518.
Wolff, E.N. 1988. ‘Life-cycle savings and the individual distribution of wealth by class,’ in: D. Kessler & A. Masson (eds.), Modelling the Accumulation and Distribution of Wealth. Oxford: Oxford University Press, 261–280.
Wright, I. 2005. ‘The social architecture of capitalism.’ Physica A, 346: 589–620.
Wright, I. 2011. Classical macrodynamics and the labor theory of value. The Open University Discussion Papers in Economics No. 76. Available from http://www.open.ac.uk/socialsciences/main/__assets/lqd8gqeaxeewkdpjof.pdf [Accessed April 1, 2016]