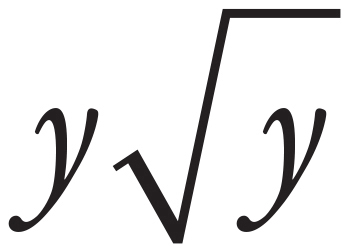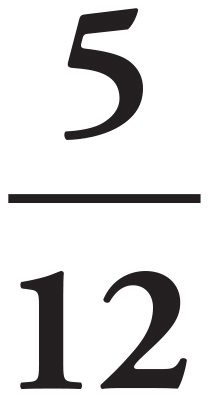Part III
Drill Answers and Explanations
CHAPTER 4
Dual-Passage Drill
38. C
The author mentions infections and cancers as examples of the types of ailments that site-specific and conservative drug doses can more effectively help than other drug delivery systems that are not characterized by these attributes. The answer that best matches this description is (C). Choice (A) is not supported because the passage discusses treating these types of illnesses, not curing them. Choice (D) is also incorrect as it references vaccines, rather than treatments. Choice (B) is disproven by the passage; the paragraph clearly refers to drugs used to predominately treat infections and cancers. This implies that there are currently effective treatments for cancers, but there may be even better ones out there. The best answer is (C).
39. D
The author states that the fibers range in size from nanometers to micrometers, which is an attribute that is intrinsically difficult to obtain from other fiber-fabrication processes. The only answer choice that matches this is (D). Choices (A) and (C) are not correct because precise fiber measurements and cellular measurements are not mentioned in the passage. Choice (B) is deceptively worded; the passage is describing the sizes of the fibers for the first time. Because there is no additional information being given about the size, (B) cannot be correct.
40. B
In context, “residual” refers to the solvent that evaporates, as opposed to that which forms the collection of non-woven fibers, so it is the extra material that results from the electrospinning process. Therefore, the correct answer should match the meaning “extra.” Because durable, steadfast, and inhabiting do not match this meaning, eliminate (A), (C), and (D). The remaining answer does match this meaning, making (B) the best answer.
41. A
The author of Passage 1 prefers natural polymers to synthetic polymers because they possess lower levels of toxicity, immunogenicity, and improved biocompatibility as compared to synthetic polymers. This is best supported by (A). The author of Passage 1 does not discuss blending natural polymers with synthetic polymers—that’s the author of Passage 2, so eliminate (B). Choice (D) is too extreme—while the author states that when combined, these polymers can have greater benefit; it does not go so far to say that when used individually, collagen and elastin are not effective. Choice (C) is not discussed in either passage, so it cannot be the correct answer.
42. A
Passage 2 begins by discussing why there has been an increase in research and use of synthetic polymers as opposed to natural ones and reviews the positive attributes of synthetic. It then goes on to say in the second and final paragraph that researchers should not limit themselves to a purist approach, and a blend of polymer types may result in the most beneficial base yet of electrospun scaffolds. This best matches (A). Choice (C) is the opposite of this—the author does not think a purist approach is important to have. Choice (D) is too specific and does not address the connection between natural and synthetic polymers. Choice (B) goes too far; although the passage does state that synthetic polymers can be created in laboratories, it does not say that they are easier to work with than natural fibers, only that many possible products can be made from them. The correct answer is (A).
43. D
Although the author does state that synthetic polymers have clear benefits over natural ones, he goes on to urge that a blend of the two may create an even better option because they both have positive properties. Choice (D) is the only answer that matches the general point of the paragraph. Choice (A) is too specific because it addresses only the first line of the paragraph. Choice (B) is the opposite of what is stated in the paragraph; the author does not support the purist approach. Choice (C) is not addressed in the passage, so it is not correct. The best answer is (D).
44. B
Don’t forget to use POE! Passage 2 focuses on the positive aspects of synthetic polymers and the importance of keeping an open approach to building these drug delivery systems. Choice (B) is supported by the author’s assertion that because synthetic polymers can be created in laboratories…[they] can be engineered to address any particular clinical need. Choice (A) is too vague and does not match the information presented in Passage 2 regarding synthetic polymers having many benefits over natural polymers. Eliminate (A). The passage states that the hydrophilicity and hydrophobicity of a polymer are related to its solubility, but it never states that one has more affect on solubility than the other. This makes (C) incorrect. Because there is no evidence from Passage 2 to support (D), the only possible answer is (B).
45. C
Hydrophilicity and hydrophobicity are mentioned only in Passage 2, not in both passages. Therefore, eliminate (A). Differing electrical charges and viscosity are mentioned only in Passage 1, so (B) can be eliminated as well. The topics in (C) and (D) are addressed in both passages, but (D) goes too far. Passage 1 states that natural polymers typically possess positive aspects, not that they necessarily do, while Passage 2 argues for trying blended polymer bases. So eliminate (D). Passage 1 does state that site-specificity, stability, and dosage measurement all impact how well electrospun scaffolds work, while Passage 2 states that it is the aim of researchers to precisely fine-tune the properties of electrospun scaffolds. Choice (C) is the best-supported answer.
46. B
Both passages discuss blended polymer bases: Passage 1 discusses the combination of collagen and elastin, while Passage 2 encourages research on synthetic and natural base blends, so eliminate (A). Choice (C) is incorrect because Passage 1 refers to both the efficacy of different drug delivery systems for cancers and infections, while Passage 2 does not refer to disease at all, just merely medical applications. Eliminate (C). Choice (D) is inaccurate for Passage 1 because the author of that passage clearly favors natural polymer bases. Only (B) matches both passages, as Passage 1 explains how electrospinning works, and Passage 2 discusses the need to look at combining polymer bases and continued interest in this field in the last paragraph.
47. C
The tones differ in that Passage 1 strongly believes natural polymers are the best, while Passage 2 believes that, although synthetic polymers have more positive characteristics, both have benefits that should be utilized. This makes (C) the best answer. Choice (B) can be eliminated because biased and subjective mean the same thing. Choices (A) and (D) can be eliminated as the author of Passage 1 is neither belligerent nor pessimistic.
CHAPTER 5
Writing and Language Drill 1
1. Apostrophes; apostrophes and where they go
2. Verbs; verb tense and number
3. Words; transition words (direction)
4. Seem/Seems and their/its; verb number and pronoun number
5. Number of words; conciseness
CHAPTER 6
Writing and Language Drill 2
CHAPTER 7
Writing and Language Drill 3
CHAPTER 8
Writing and Language Drill 4
CHAPTER 9
Drill 1
1. c
Examples: −7, 0, 1, 8
2. d
Examples: .5, 2, 118
3. g
Examples: −.5, −2, −118
4. f
Examples: −4, 0, 10
5. b
Examples: −5, 1, 17
6. a
Examples: Factors of 12 are 1, 2, 3, 4, 6, and 12. Factors of 10 are 1, 2, 5, and 10.
7. i
Examples: Multiples of 12 include −24, −12, 0, 12, 24, and so on. Multiples of 10 include −20, −10, 0, 10, 20, 30, and so on.
8. h
Examples: 2, 3, 5, 7, 11, and so on. There are no negative prime numbers, and 1 is not prime.
9. e
Examples: 3 and 4 are distinct numbers. −2 and 2 are also distinct.
10. j
Examples: In the number 274, 2 is the digit in the hundreds place, 7 is the digit in the tens place, and 4 is the digit in the ones place.
11. p
Examples: −1, 0, 1, and 2 are consecutive numbers. Be careful—sometimes you will be asked for consecutive even or consecutive odd numbers, in which case you would use just the odds or evens in a consecutive list of numbers.
12. n
Examples: 6 is divisible by 2 and 3, but not by 4 or 5.
13. l
Examples: When you divide 26 by 8, you get 3 with a remainder of 2 (2 is left over). When you divide 14 by 5, you get 2 with a remainder of 4 (4 is left over).
14. k
Examples: When you add 2 and 3, you get a sum of 5. When you add −4 and 1, you get a sum of −3.
15. r
Examples: When you multiply 2 and 3, you get a product of 6. When you multiply −4 and 1, you get a product of −4.
16. m
Examples: When you subtract 2 from 3, you get a difference of 1. When you subtract −4 from 1, you get a difference of 5.
17. q
Examples: When you divide 2 by 3, you get a quotient of 
. When you divide −4 by 1, you get a quotient of −4.
18. o
Examples: The absolute value of −3 is 3. The absolute value of 41 is 41.
Drill 2
a. 35
b. 31
c. 36
d. x8
e. x4
f. x12
h. −4
k. −y
3. A
If 34 = 9x, then 81 = 9x. Therefore, x = 2. You could also rewrite 34 as 3 × 3 × 3 × 3 = 9 × 9.
6. C
Square both sides of the equation to get m2 + 39 = 64. Solve for m to get m2 = 25, so m = ±5. Therefore, one possible value for m is 5.
5. B
If (3x)3 = 315, then by the rules of MADSPM, 3x = 15, and x = 5.
8. D
Take the two equations separately, using the rules of MADSPM. If xy × x6 = x54, then y + 6 = 54, and y = 48. If (x3)z = x9, then 3z = 9, and z = 3. Now you know that y = 48 and z = 3, so y + z = 51.
7. D
Add 3 to both sides to get 
= 12. Square both sides of the equation to get s = 144.
8. D
Since x6 doesn’t change form, eliminate (C). y−3 can be rewritten as 
, so eliminate (A). 
can be rewritten as 
, so eliminate (B).
9. A
Start with applying the root to the coefficient: 
= 3. Therefore, eliminate (C) and (D) because these answer choices have the wrong coefficient. To find the fourth root of an exponent, divide the exponent by 4. Therefore,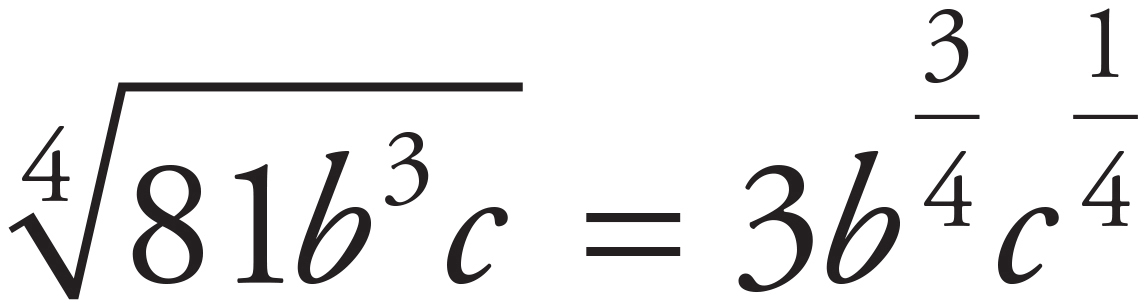 
. The correct answer is (A).
9. A
According to the question, the two functions are equal to each other. Therefore, k0.3x = 
, which means that 0.3x = 
. Multiply both sides by 9 to get 2.7x = Bx. Solve for B to get 2.7 = B. The correct answer is (A).
10. B
When you simplify the fractional exponent, you get 
= 8x. Squaring both sides gives you x5 = 64x2. You can divide by x2 on each side to get x3 = 64 (remember your MADSPM rules!). Finally, taking the cube root of both sides gives you x = 4, which is (B).
11. B
With a fractional exponent, the numerator is the power the number or variable is taken to and the denominator represents the root. Therefore, 
. When taking a power to another power, multiply the exponents: 
. Note, only (B) has 
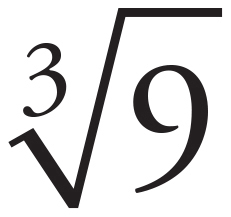as part of its answers. Therefore, the correct answer must be (B). Another approach to these can be to plug in numbers for m and n and let the calculator do the hard work. See Chapter 10 for how to use this approach.
16. D
Start with the left side. Take the cube root of 64 and rewrite: 
= 
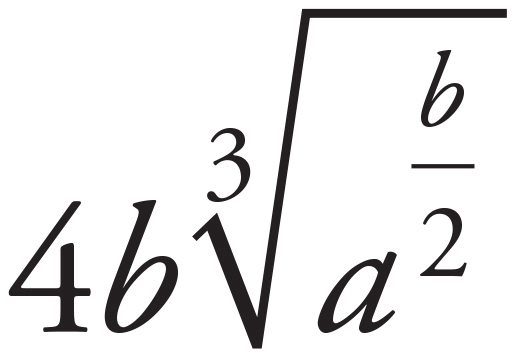. Taking the cube root is the same as raising an expression to the 
power, so continue simplifying the left side: 
= 
. Use the rules of MADSPM to multiply the exponents: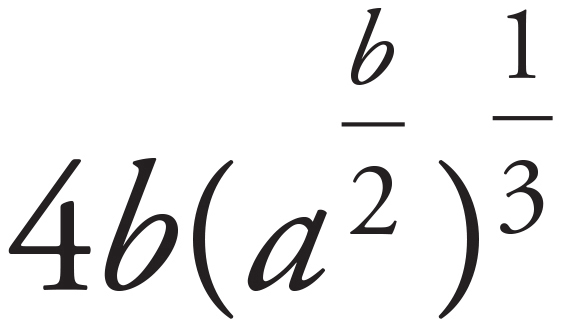 
= 
. Now that the left side is simplified, start working with the right side by squaring each term in the parentheses (be careful!): (4
a)2 = 42 × ()2 × a2 = 16 × 3 × a2 = 48a2. When dealing with exponents, terms that have the same bases also have equal exponents, so set the terms with base a equal to each other to solve for the value of b: a
= a2. Solve for b by setting the exponents equal to each other: = 2, and b = 12. An alternate final step could have been to set 48 equal to 4b and get b = 12.
23. A
Remember MADSPM: when multiplying, add the exponents. Therefore,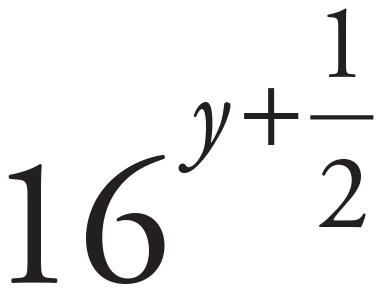 
= 16y × 
and the fraction is equivalent to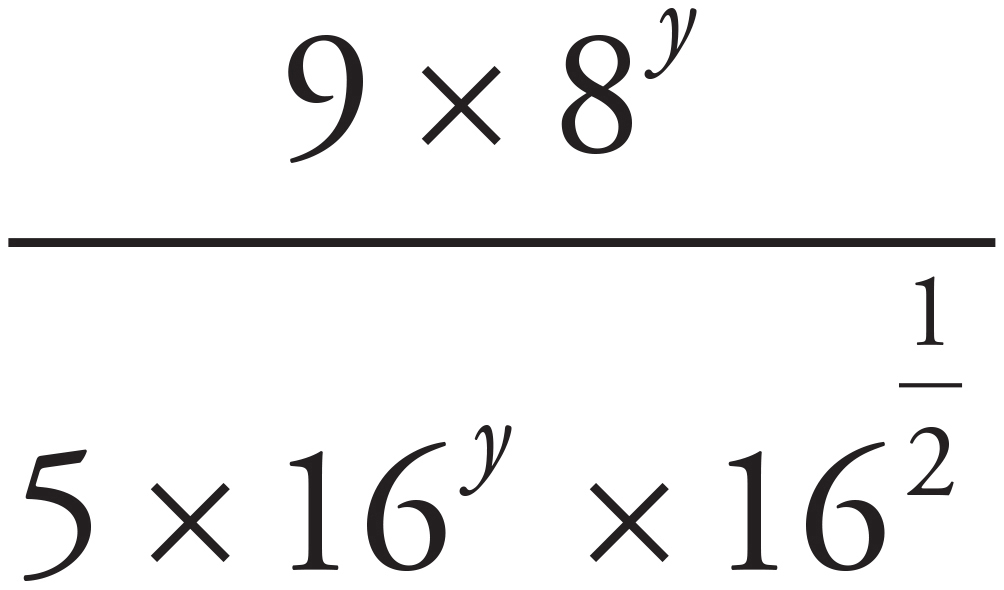 
. Taking a number to the 
power is the same as taking the square root of the number. Therefore, 
. Rewrite 16y as (2 × 8)y or 2y8y. Reduce the fraction to get 
. Simplify the denominator to get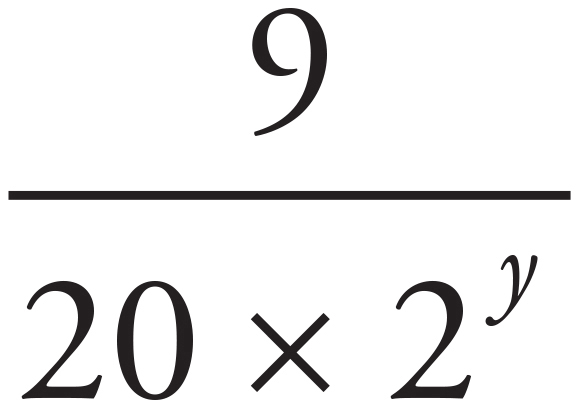 
. Separate the fraction to get 
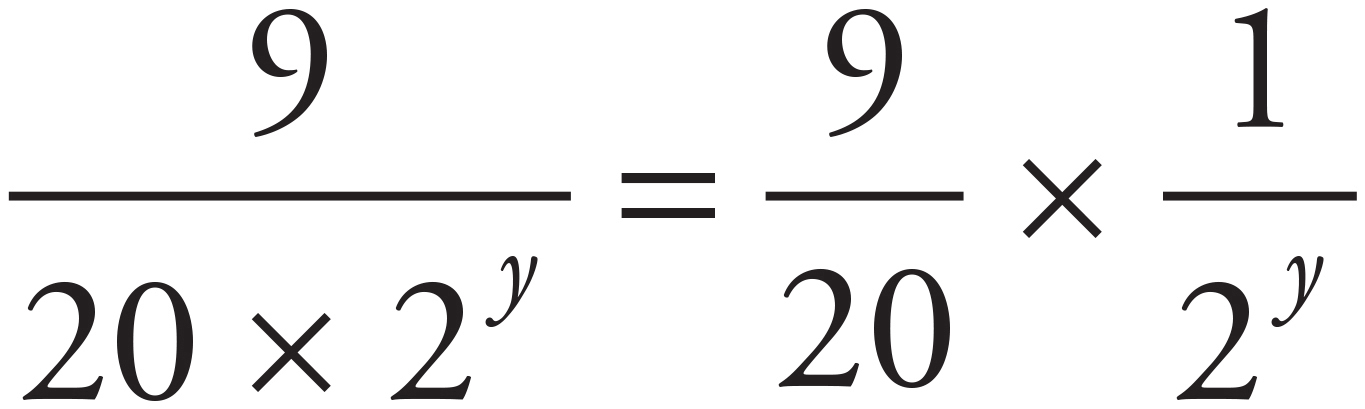. Only (A) includes the correct fractions. The correct answer is (A).
Drill 3
3. C
This is a translation question. Translate the English to math one step at a time to get x = 3 + 7x. Now you can subtract 7x from both sides to leave you with −6x = 3. Divide both sides by −6 and you find that x is equal to 3 divided by −6, which is (C).
2. B
To start to solve the equation for y, cross-multiply to get 7y = (x + 4)(x + 3). Use FOIL on the right side to get 7y = x2 + 3x + 4x + 12 (the FOIL technique is discussed in Chapter 11). Combine like terms to get 7y = x2 + 7x + 12. Divide both sides by 7 to get y = 
. The correct answer is (B).
5. D
Currently Ann has 32 + 18 = 50 recipes. Given that the book will include up to 90 recipes, Ann can include at most 98 − 50 = 48 additional recipes. Therefore, r ≤ 48. Solve for r in (A) to get r ≥ 148. Eliminate (A). Solve for r in (B) to get r ≤ 148. Eliminate (B). In (C), 98 − 50 − r ≤ 0, so 48 − r ≤ 0. Solve for r to get −r ≤ −48 or r ≥ 48. Eliminate (C). In (D), 98 − 50 − r ≥ 0, so 48 − r ≥ 0. Solve for r to get −r ≥ −48 or r ≤ 48. The correct answer is (D).
4. C
Cross-multiply to get 3a × 6d = 4b × 5c. Simplify both sides of the equation to get 18ad = 20bc. Solve for bc to get 
= bc. Reduce to get 
= bc. The correct answer is (C).
28. 6
According to the question, Debbie’s average daily miles walked are equal to one-hundredth of the square of the number of hours in one day. Given that there are 24 hours in a day, the calculation is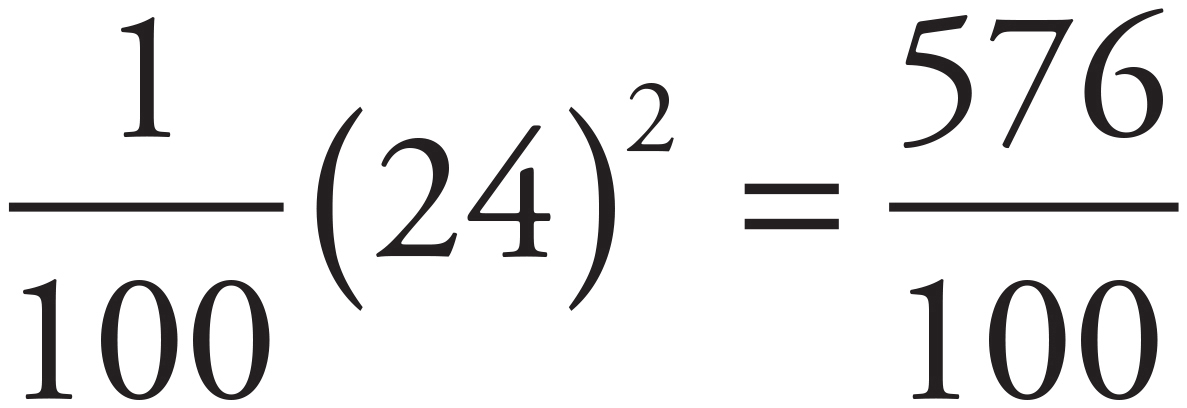 
= 5.76 ≈ 6. The correct answer is 6.
7. A
Since the denominators on both sides of the equation are equal, set the numerators equal and solve for p. The equation becomes 2(p − 2) + 2(3 − p) = 2(3p − 6) + 3(6 − 2p). Distribute on both sides to get 2p − 4 + 6 − 2p = 6p − 12 + 18 − 6p. Combine like terms to get 2 = 6. All the p’s disappeared, leaving a statement that is false. This means that there is no solution, and the correct answer is (A).
8. C
Start with the easier equation and use Process of Elimination. The easier equation is related to the total number of skis and snowboards, s + b, the ski resort rented. According to the problem, the following number of skis and snowboards were rented:
|
Total Skis and Snowboards rented |
|
|
Friday |
40 |
|
Saturday |
55 |
|
Sunday |
85 |
|
Total |
180 |
Therefore, s + b = 180. Eliminate (A) and (D) because neither of these answers includes this equation. The other equation in the set is related to the amount of money the ski resort collected in rental fees. According to the question, the following amounts were collected:
|
Rental Fees Collected |
|
|
Friday |
$1,100 |
|
Saturday |
$1,400 |
|
Sunday |
$2,100 |
|
Total |
$4,600 |
Eliminate (B) because the total in the money equation is wrong. The correct answer is (C).
12. B
First, get rid of the fractions by multiplying both sides of the equation by 21. The equation becomes 
+ 21(2) = 
+ 21(3), which simplifies to 7(m + 9) + 42 = 3(m − 2) + 63. Multiply it out to get 7m + 63 + 42 = 3m − 6 + 63 or 7m + 105 = 3m + 57. Subtract 3m and 105 from both sides, resulting in 4m = − 48; then divide both sides by 4. The result is m = −12, so the correct answer is (B).
9. B
First, eliminate the parentheses by multiplying everything out. Be careful of the negative signs. The equation becomes −4h − 20 = −6 + 3h + 14. Combine like terms to get −4h − 20 = 8 + 3h. Subtract 3h from both sides, resulting in −7h − 20 = 8. Adding 20 to both sides turns the equation into −7h = 28. Divide both sides by −7 to find that h = −4; therefore, the correct answer is (B).
23. C
Let s represent snickerdoodle cookies and c represent cinnamon cookies. Translate the two equations given in the problem as 2s + 7c = 14 and 8s + 3c = 17.5. To solve for one of the variables, try to make the coefficient for one of the variables the same and then add or subtract the two resulting equations from each other to get rid of that variable. In this case, take the first equation and multiply it by −4 to get −8s − 28c = −56. Place the two equations on top of each other and add:
Solve for c to get c = 1.54. Plug 1.54 in for c in the first equation to get 2s + 7(1.54) = 14. Solve for s to get 2s + 10.78 = 14, or 2s = 3.22, so s = 1.61. Plug 1.61 in for s and 1.54 in for c in the answers to see which answer works. Choice (A) becomes 2(1.61) + 3(1.54) = 8.00. Solve the left side of the equation to get 3.22 + 4.62 = 8.00 or 7.84 = 8.00. This is not true, so eliminate (A). Choice (B) becomes 4(1.61) + 6(1.54) = 16.25. Solve the left side of the equation to get 6.44 + 9.24 = 16.25 or 15.68 = 16.25. Eliminate (B). Choice (C) becomes 6(1.61) + 5(1.54) = 17.36. Solve the left side of the equation to get 9.66 + 7.70 = 17.36 or 17.36 = 17.36. The correct answer is (C).
13. A
The question states that there are infinitely many solutions to the equation. That means any real number should work for x, so plug in an easy number for every x in the equation. Avoid 0 in this case—it may make too many things disappear. If x = 1, the equation becomes 10[3(1) + a] − a[4(1) + 2] = 2a[(1) + 4]. This simplifies to 10(3 + a) − a(4 + 2) = 2a(5) or 30 + 10a − 6a = 10a. Combine like terms to get 30 + 4a = 10a; then subtract 4a from both sides, resulting in 30 = 6a. Therefore, a = 5, which matches (A).
25. A
Let e = eggs and f = cups of flour. The two equations that are given in the problem are 5e + 4f = 5.50 and 9e + 8f = 10.50. Whenever there are two equations with the same two variables, think simultaneous equations. The goal with simultaneous equations is to create a common coefficient for one of the variables and then add or subtract the two equations from each other to get rid of that variable. In this case, multiply the first equation through by 2 to get 10e + 8f = 11.00. Place the two equations on top of each other and subtract them:
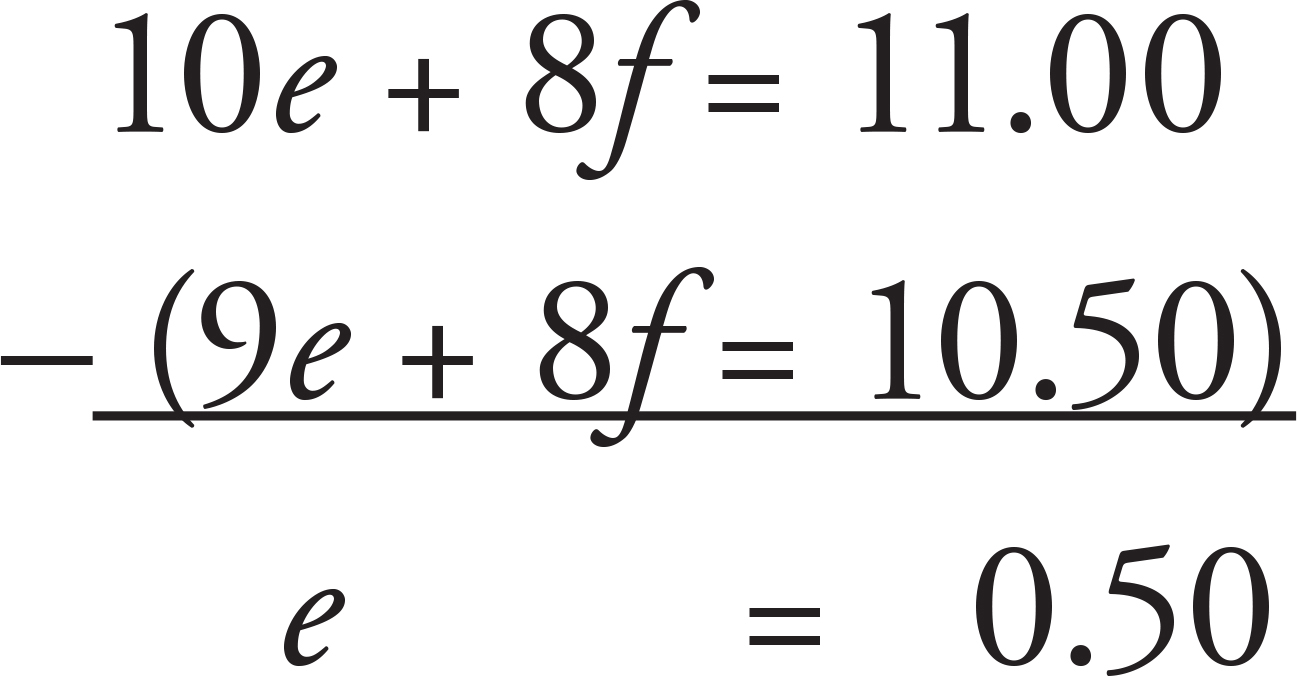
Therefore, 10e = 0.50 × 10 = 5.00. The correct answer is (A).
Drill 4
a. 6
b. 6
c. −1
d. −1
e. 1
f. 6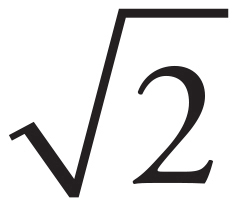
g. (0, 1)
2. B
The slope-intercept form of the equation of a line is y = mx + b, where m is the slope and b is the y-intercept. So the slope of the line given by the first equation is 6. To find the slope of a perpendicular line, you would take the negative reciprocal. So c = −
, which is (B).
6. B
Parallel lines have equal slopes. Therefore, because the line in the graph has a negative slope, the correct answer will also have a negative slope. Eliminate (C) and (D) right away because they have positive slopes. Now find the exact slope of the line shown, and compare it with the remaining answers to see which line equation has the same slope. The slope of a line is determined by the equation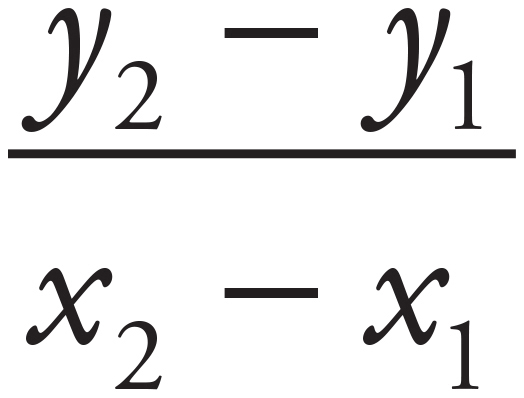 
. Calculate the slope of the line shown to get 
. The answers are all in the slope-intercept form of an equation, y = mx + b, where m = slope. Only (B) has a slope of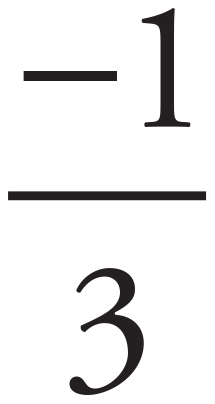 
, so the correct answer is (B).
3. A
The slope-intercept form of the equation of a line is y = mx + b, where m is the slope and b is the y-intercept. So you would manipulate this equation to solve for y. Subtracting 2x from both sides of the equation and then dividing both sides by 3 gives you y = −x + 4, so the y-intercept is 4.
12. D
The x-intercept of a line is where the line crosses the x-axis. The line in the graph has a positive x-intercept, so you can eliminate (A) and (B). To find the x-intercept, first find the slope of the line and then use one of the points given to determine the value of x. The slope of a line is determined by the equation 
. The slope of the line shown is 
. At the x-intercept, y = 0, so the coordinates for the x-intercept are (x, 0). To find x, plug point (x, 0) and (−2, −2) into the slope equation and solve for x: 
, so 
. Cross-multiply to get −2 − x = −4, or −x = −2. Therefore, x = 2, and the correct answer is (D).
7. D
Look for an answer that has the same y-intercept and slope as the line shown in the graph. In the line shown, the point at which the line crosses the y-axis is 1, so the y-intercept is 1. Use the two points on the line—(0, 1) and (8, 0)—to calculate the slope: slope =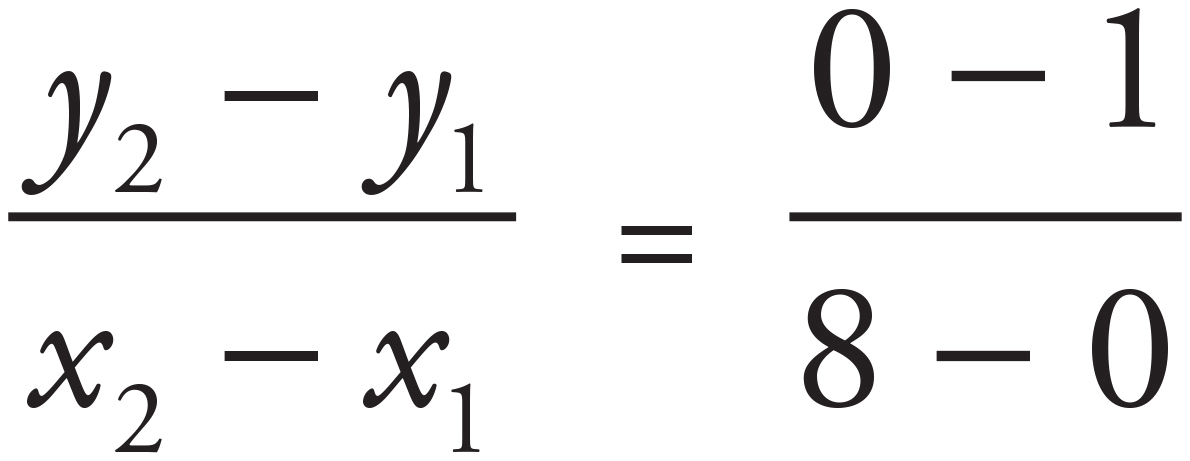 
= − 
. Rewrite the answers in the slope-intercept form of the equations, y = mx + b, where m is the slope of the line and b is the y-intercept. In (A), the equation becomes 2y = x − 8, or y = x − 4. The slope of this line is , and the y-intercept is −4, so eliminate (A). In (B), the equation becomes 4y = −x − 8, or y = −
x − 2. The slope of this line is −, and the y-intercept is −2, so eliminate (B). In (C), the equation becomes 8y = 3x + 8, or y = 
x + 1. The slope of this line is , and the y-intercept is 1, so eliminate (C). Choice (D) is the only one left, so it must be correct. In (D), the equation becomes 8y = −x + 8, or y = −x + 1. The slope of this line is − and the y-intercept is 1, which is the same as the slope and y-intercept of the line shown in the graph.
14. B
The slope of a line is determined by the equation 
. Therefore, the slope of the line shown can be calculated as follows: 
= 
. The correct answer is (B).
15. A
The line shown crosses the y-axis at −2; this point is also known as the y-intercept. The answers are all in the slope-intercept form, y = mx + b, where m is the slope and b is the y-intercept. You can eliminate (B) right away because the y-intercept in (B) is 2, not −2. Next, calculate the slope of the line with the two given points. The slope of a line is determined by the equation 
. Therefore, the slope of the line shown can be calculated as follows: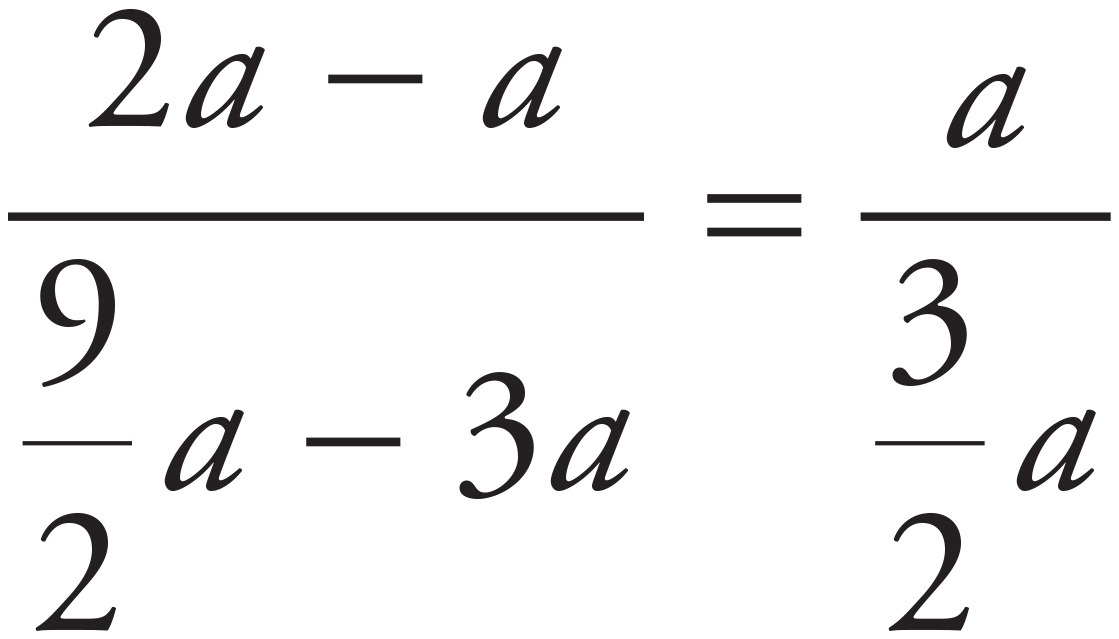 
= 
. The only remaining answer that has a slope equal to is (A), so that is the correct answer.
17. 32
Set the two equations equal to each other to get 4x2 − 6x + 4 = 2x + 4. Set the equation to 0 to get 4x2 − 8x = 0. Divide both sides of the equation by 4 to get x2 − 2x = 0. Factor x out of the equation to get x(x − 2) = 0. Therefore, the two possible values for x are x = 0 and x = 2. Plug both of these values into the second equation to find the corresponding y-values. If x = 0, then y = 2(0) + 4 = 4. If x = 2, then y = 2(2) + 4 = 8. Therefore, the product of the two possible values of y is 4 × 8 = 32. The correct answer is 32.
Drill 5
28. 0.833 or 
Take the number of contracted users, 225, and divide it by the total number of users in 2008, 270: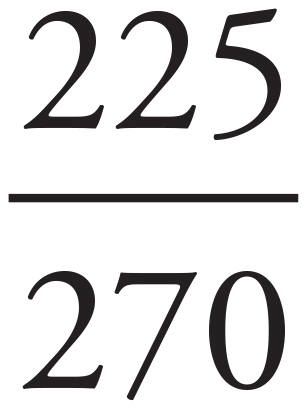 
= 0.833 or .
14. 625
Because 5x2 = 125, you know that x2 = 25 and x = −5 or 5. Since you can grid in only positive numbers, assume x = 5. Therefore, 5x3 = 5 × 125 = 625.
First, simplify inside the parentheses. Be careful with the negative signs: z = 5 − 5(5z − 2 + 2z) becomes z = 5 − 5(7z − 2). Multiply it out to get z = 5 − 35z + 10, or z = 15 − 35z. Adding 35z to both sides results in 36z = 15, so z = 
. This won’t fit in the grid-in box, so reduce the fraction to make it is small enough to fit in the space provided. Divide the numerator and denominator of the fraction by 3. The correct answer is 
.
29. 9
Start by squaring both sides of the equation to get (5 − )(5 − ) = z − 5. Expand the left side of the equation to get 25 − 10 + z = z − 5. Subtract z from both sides to get 25 − 10 = −5. Solve for z to get −10 = −30, so = 3. Square both sides of the equation to get z = 9. The correct answer is 9.
16. 6
Whenever you have two equations with the same two variables, think simultaneous equations. The goal with simultaneous equations is to create a common coefficient for one of the variables and then add or subtract the two equations from each other to get rid of that variable. To get rid of a, multiply the first equation by 7 to get 21a + 14b = 259 and multiply the second equation by −3 to get −21a − 12b = −255. Place the two equations on top of each other and subtract them from each other.
Solve for b to get b = 2. Therefore, b2 + 6b − 10 = 22 + 6(2) − 10 = 4 + 12 − 10 = 6. The correct answer is 6.
30. 5
The conversion from Fahrenheit to Celsius on the first day can be calculated as follows: 
(95 − 32) = (63) = 35. The conversion from Fahrenheit to Celsius on the second day can be calculated as follows: (86 − 32) = (54) = 30. Therefore, the difference between the forecasted temperatures in degrees Celsius is 35 − 30 = 5. The correct answer is 5.
31. 350
Set up an equation using the information from the question. Moriah’s portion is compared with Mathew’s portion, so call Mathew’s portion m. Moriah’s portion is 30 less than twice m, or 2m − 30. Together, they paid $540, so the equation is m + 2m − 30 = 540, or 3m − 30 = 540. Add 30 to both sides to get 3m = 570, so m = 190. That was Mathew’s portion, and the question asks for Moriah’s portion, which is 2(190) − 30 = 380 − 30 = 350. The correct answer is 350.
17. 100
Let x be the amount of Solution 2 that Kimberly adds to Solution 1. Therefore, the total amount of Solution 3 Kimberly creates is 50 + x. The amount of sugar in the portion of the mixture that came from Solution 1 can be calculated as 50 × 0.25 = 12.5, and sugar from Solution 2 can be calculated as x × 0.10. Therefore, the total amount of sugar in Solution 3 can be calculated as 12.5 + 0.1x. Since Solution 3 has a 15% sugar content, this amount of sugar is equal to 15% of the ounces of Solution 3, or 0.15(50 + x). To solve for x, set up the following equation: 12.5 + 0.1x = 0.15(50 + x). Distribute the 0.15 on the right side of the equation to get 12.5 + 0.1x = 7.5 + 0.15x, then 5 + 0.1x = 0.15x, and finally 5 = 0.05x. Therefore, x = 100 ounces of Solution 2, so the correct answer is 100.
CHAPTER 10
Drill 1
5. B
Whenever the question includes variables, Plug In. If m = 10, then David pays $25 + $0.05(10) = $25.50. Now plug in 10 for m in the answers to see which answer is equal to the target number of $25.50. In (A), 25 + 1.05(10) = $35.50. Because this is not equal to the target number, eliminate (A). In (B), 25 + 0.05(10) = $25.50. This is equal to the target number. Leave (B), but check the remaining answers just in case. In (C), 0.05(25 + 10) = $1.75, and in (D), 1.05(25 + 10) = 36.75. Neither of these is the target number, so eliminate (C) and (D). Therefore, the correct answer is (B).
4. D
Pick numbers for a, b, and c such that a = 
. If you pick 4 = 
, the question becomes, what is 
or 
? The answer is 
. When you work through all of the answer choices using a = 4, b = 16, and c = 2, which choice says this? Choice (D) does.
11. D
Whenever there are variables in the problem and in the answer choices, Plug In. If w = 20, then Luciano’s cup has 20 − 2 = 18 ounces at the end of day 1. At the end of 7 days, Luciano’s cup would have 18 − 8 = 10 ounces. After 11 days, Luciano’s cup would hold 10 − 5 = 5 ounces. Plug in 20 for w in the answer choices to see which answer is equal to the target number of 5. Choice (A) becomes 
= 2.25. This does not match the target number of 5, so eliminate (A). Choice (B) becomes 
− 10 =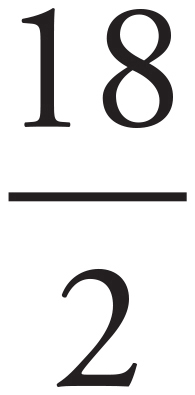 
− 10 = 9 − 10 = −1. Eliminate (B). Choice (C) becomes 
(20) − 10 = 10 − 10 = 0. Eliminate (C). Choice (D) becomes 
= 5. This matches the target number; therefore, the correct answer is (D).
7. A
Pick a number for p. How about 2? Now the problem reads 
. When you plug p = 2 into the answers, (A) turns out to be right.
9. C
Whenever there are variables in the problem and in the answer choices, think Plugging In. Try using c = 46. This would mean the student got 46 questions correct and 4 questions wrong. The student’s score would be 46(1) − 
= 46 − 1 = 45. Plug 46 in for c in the answer choices to see which answer equals 45, the target number. Choice (A) becomes S = 50 − 0.25(46) = 50 − 11.5 = 38.5. Eliminate (A). Choice (B) becomes S = 50 − 0.75(46) = 50 − 34.5 = 15.5. Eliminate (B). Choice (C) becomes 46 − 0.25(50 − 46) = 46 − 0.25(4) = 46 − 1 = 45. Keep (C), but check (D) just in case it also works. Choice (D) becomes 46 − 0.75(50 − 46) = 46 − 0.75(4) = 46 − 3 = 43. Eliminate (D). The correct answer is (C).
18. D
Variables in the answer choices? Absolutely! So plug in your own numbers. For x (Jodi’s account), plug in $18 (hey, who said Jodi had to be rich?). With $18 in her account, for rent is $3 and the car payment is also $3. Subtract that from the $18, and Jodi has $12 left in her account. Now plug in for y (the amount Jodi deposits); make that $8, bringing her account balance to $20. Well, she now purchases a set of knives for $10 ( the amount in her account) and has $10 left. Go through all of the answer choices, using x = 18 and y = 8, and see which one gives you $10. The only one that works is (D).
12. B
Inequalities with an absolute value can be tough to set up; there are two parts, and it’s not always easy to remember how to deal with the negative values. Instead, try plugging in some easy numbers. Start with y = 0. The inequality becomes 2|0 − 5| < 24 or 2(5) < 24. That’s true, so 0 works. Move up to y = 1, which results in 2|4 − 5| < 24 or 2(1) < 24. That’s true, too, so keep going. Plugging in y = 2 results in 2(3) < 24, y = 3 results in 2(7) < 24, and y = 4 results in 2(9) < 24. All these are true, but trying y = 5 results in 2(15) < 24, which isn’t true. So 4 is the greatest integer that works. Now try negative numbers. If y = −1, the inequality is 2(9) < 24, which is true, but if y = −2, the inequality is 2(13) < 24. Therefore, −1 is the smallest integer that works. The integers that satisfy the inequality are −1, 0, 1, 2, 3, and 4, and their sum is 9, (B).
29. 92.3
You don’t know how many students are in the incoming freshman class, so Plug In. Because you’re taking percentages of the class, make the total number of students 100. That means that there are 15 left-handed students in the class. There are also 65 female students and 35 male students. If of the left-handed students are male, then × 15 = 10 of the left-handed students are male, leaving 5 female left-handed students. If 5 of the 65 female students are left-handed, then the other 60 female students are right-handed. To find the percentage of female students who are right-handed, divide: 
= 0.923 = 92.3%. Remember to multiply a decimal by 100 to get the equivalent percentage.
Drill 2
3. D
Start with (B). If n = 3, then the equation becomes 2(3 + 5) = 3(3 − 2) + 8. Work the equation: 2(8) = 3(1) + 8; 16 = 11. This isn’t true, so eliminate (B). You might not know whether you need a bigger or smaller number, so try a larger number. With (C), make n = 4. Now work the equation: 2(4 + 5) = 3(4 − 2) + 8; 2(9) = 3(2) + 8; 18 = 14. Not quite; eliminate (C). Try (D): 2(8 + 5) = 3(8 − 2) + 8; 2(13) = 3(6) + 8; 26 = 26. This works, so pick (D).
8. C
Start by trying (C), 3, for x. Does 35 = 243? Yes! So the answer is (C).
7. C
Whenever there are numbers in the answer choices, think Plugging In the Answers. Start with one of the middle answers. Plug the numbers from (B) into the first equation to get 2(−3) − (−2) > −3. Simplify the left side of the equation to get −6 + 2 > −3, or −4 > −3. Because this statement is not true, eliminate (B). It may not be clear which direction to go next; if so, just pick a direction. Plug the numbers from (C) into the first equation to get 2(−1) − (−1) > −3. Simplify the left side of the equation to get −2 + 1 > −3, or −1 > −3. Because this is a true statement, plug the same numbers into the second equation to get 4(−1) + (−1) < 5. Simplify the left side of the equation to get −4 − 1 < 5, or −5 < 5. Because this is a true statement, plug in the values from (C) into the last equation to get −1 > −6. Because the values given in (C) work in all three equations, the correct answer is (C).
10. D
If you try plugging in (C), , for x, the equation becomes 
+ 4 = 5, which is false. If you try plugging in (D), , for x, the equation becomes 
+ 2 = 5, which is true. Therefore, the correct answer is (D).
20. A
Whenever there are variables in the question and numbers in the answer choices, think Plugging In the Answers. Start with one of the middle answers. In (B), v = −3. Plug v = −3 into the second equation because it is the easier of the two equations, and solve for u. The resulting equation becomes 2(−3) = 7 + 5u. Solve for u to get −6 = 7 + 5u, −13 = 5u, and u = −
. Now, use the same numbers for u and v in the first equation to see if that equation works. Plugging in u = − and v = −3, the first equation becomes −
= −(−3). Solve both sides of the equation to get −
= 3. This is not true, so eliminate (B). It may not be clear which direction to go, so pick a direction. In (A), v = −4. Plug in v = −4 using the second equation and solve for u. The resulting equation becomes 2(−4) = 7 + 5u. Solve for u to get −8 = 7 + 5u, or −15 = 5u. Therefore, u = −3. Now, use the same numbers for u and v in the first equation to see if that equation works. Plugging in u = −3 and v = −4, the first equation becomes −
(−3) = −(−4). Solve both sides of the equation to get −
= 4, or 
= 4. Because this is a true statement, the correct answer is (A).
25. C
Whenever the question includes variables and the answers are numbers, think Plugging In the Answers. According to the question, the alloy needs to contain between 10(0.1) = 1 kg and 10 (0.15) = 1.5 kg of titanium. Choose an x-value that fits into the range of each of the answers to see which answer will create an alloy with an acceptable amount of titanium. Start with one of the answers in the middle. For (B), let x = 3. This means the resulting alloy would contain 10 − 3 = 7 kg of 5% titanium alloy. The amount of titanium in the mixture can be calculated as 3(0.2) + 7(0.05) = 0.6 + 0.35 = 0.95 kg, which is not enough titanium. Eliminate both (B) and (A), because (A) would give you an even smaller amount of titanium. For (C), let x = 3.5. This means the resulting alloy would contain 10 − 3.5 = 6.5 kg of 5% titanium alloy. The amount of titanium in the mixture can be calculated as 3.5(0.2) + 6.5(0.05) = 0.7 + 0.325 = 1.025 kg, which is an acceptable amount of titanium. The correct answer is (C).
Drill 3
k. 
= approximately 14%
The amount of money in a savings account after m months is modeled by the function f(m) = 1,000(1.01)m .
l. $1,000
m. 1%
n. 40
o. 1.5
p. 5 kPa
2. D
This question is asking us to compare pecks and bushels, so let’s make a proportion: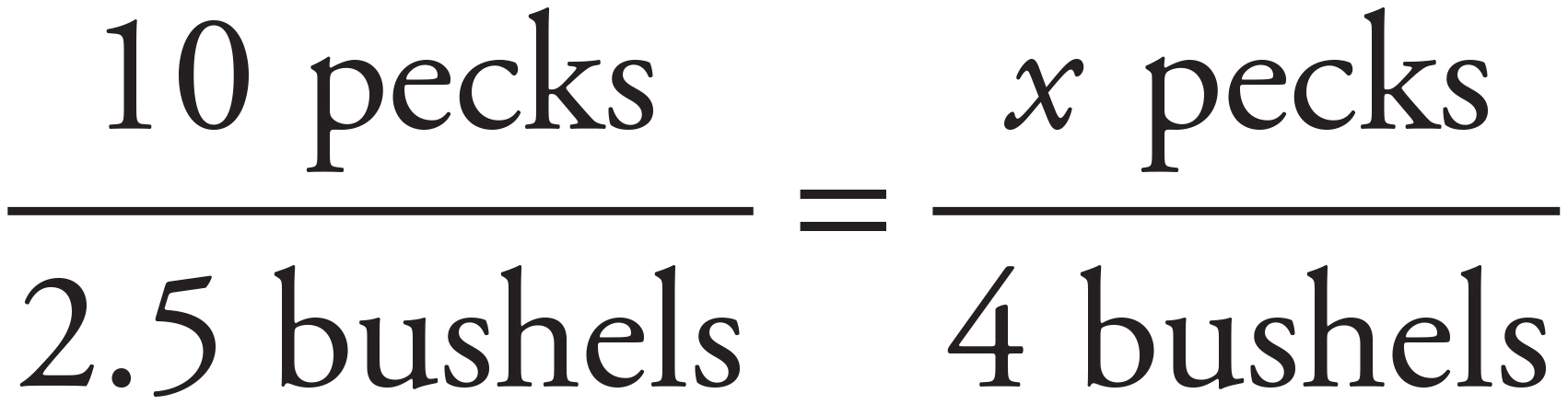 
. Then we can cross-multiply and solve for x, which results in x = 16.
Probability is defined as 0 ≤ 
≤ 1, so start by identifying the values for the numerator and denominator. The question is asking for the probability that a user in 2008 is a contracted user. Reference the 2-way table to find that, for 2008, there were 225 contracted users out of 270 total users. Set up the fraction and reduce: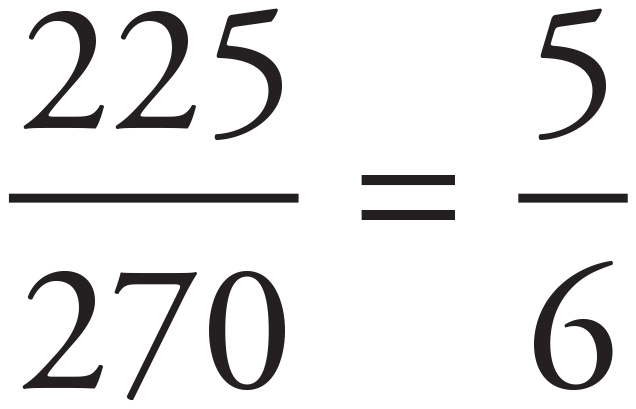 
= 0.83.
12. B
Whenever there are variables in the question and answer choices, think Plugging In. If t = 12, then the air squad was able to reduce the size of the fire by 10 × 0.07 = 0.7 acres, and the area of the forest still on fire is 10 − 0.7 = 9.3. Plug 12 in for t in the answer choices to see which answer equals the target number of 9.3. Choice (A) becomes 10 − (0.93)12×12 = 10 − (0.93)144 ≈ 10. This does not match the target number, so eliminate (A). Choice (B) becomes 10 × 
= 10 × (0.93)1 = 9.3. Keep (B), but check the remaining answers just in case one of them works. Choice (C) becomes 10 − 9312×12 = 10 − 93144, which is a very small negative number, and (D) becomes (0.93)10−12(12) = (0.93)10−144 = (0.93)−134 = 16,721.872. Eliminate (C) and (D). The correct answer is (B).
15. C
Consider each statement one at a time. The last two tests have an average of 90. If the student scored the same on both tests, his score would be 90 on each of those two tests. The two tests have a total of 180 points (2 × 90), so he could have also scored 0 on one test and 180 on the other test, or anything in between. No matter what, there’s at least one test on which the student scored more than 85, so I must be true. Eliminate (B) and (D). Now you only need consider II (because there’s no option remaining which includes III). You already determined that the last two tests have a total of 180 points. If the first three tests were an average of 80, then the total for those tests would be 3 × 80 = 240. The total points over all 5 tests would be 180 + 240 = 420, and the average would be 420 ÷ 5 = 84, which is less than 85. II is true, so choose (C).
19. C
First, you need to calculate how far Maggie runs. For the first five minutes, she runs 1,200 meters before turning around and returning home. She then runs 2,100 more meters after retrieving her iPod. Therefore, she runs a total of 4,500 meters (1,200 + 1,200 + 2,100). Because she was at home for 3 minutes, the total time she spent running was 12 minutes. The question asks for speed in meters per second, so convert the 12 minutes to seconds by multiplying by 60. To find the speed, simply divide the 4,500 meters by the 720 seconds to get (C).
28. 45
If Marcia types 18 pages per hour, and David can type 14 pages per hour, then together they will be able to type 18 + 14, or 32 pages per hour. To see what fraction of an hour it will take them to type 24 pages, set up a proportion: 
.
If you solve for x, you can see that they can type 24 pages in .75 of an hour. But that isn’t the answer! The question asks for the answer in minutes. Three-quarters of an hour is equal to 45 minutes, so the answer is 45.
22. C
To find percent difference, use the equation percent change = 
× 100. Here, because you want to find what percent greater the number of registered Republicans who plan to vote for Candidate B is than the number of registered Democrats who plan to vote for Candidate B, the original will be the smaller number (the Democrats). This makes the equation: 
× 100 = 25%, which matches (C).
25. C
Whenever there are variables in the question and in the answer choices, think Plugging In. Because the problem is dealing with percentages, make x = 100. Remember the distance formula, distance = rate × time, or d = r × t. Therefore, the time it takes Everett’s parents can be calculated as 200 = 45 × t, so t = 4.4. If Everett is driving at a speed 100% greater than his parent’s speed, then he is driving at 90 mph. Therefore, Everett’s time can be calculated as follows: 200 = 90 × t, so Everett’s t = 2.2. The difference in the amount of time it takes Everett versus his parents is 4.4 − 2.2 = 2.2. Plug 100 in for x in each of the answers to see which one is equal to the target of 2.2. Choice (A) becomes 
. Choice (A) is clearly a negative value, so eliminate it. Choice (B) becomes 
. Because 0 cannot be in the denominator of a fraction, (B) is impossible; eliminate it. Choice (C) becomes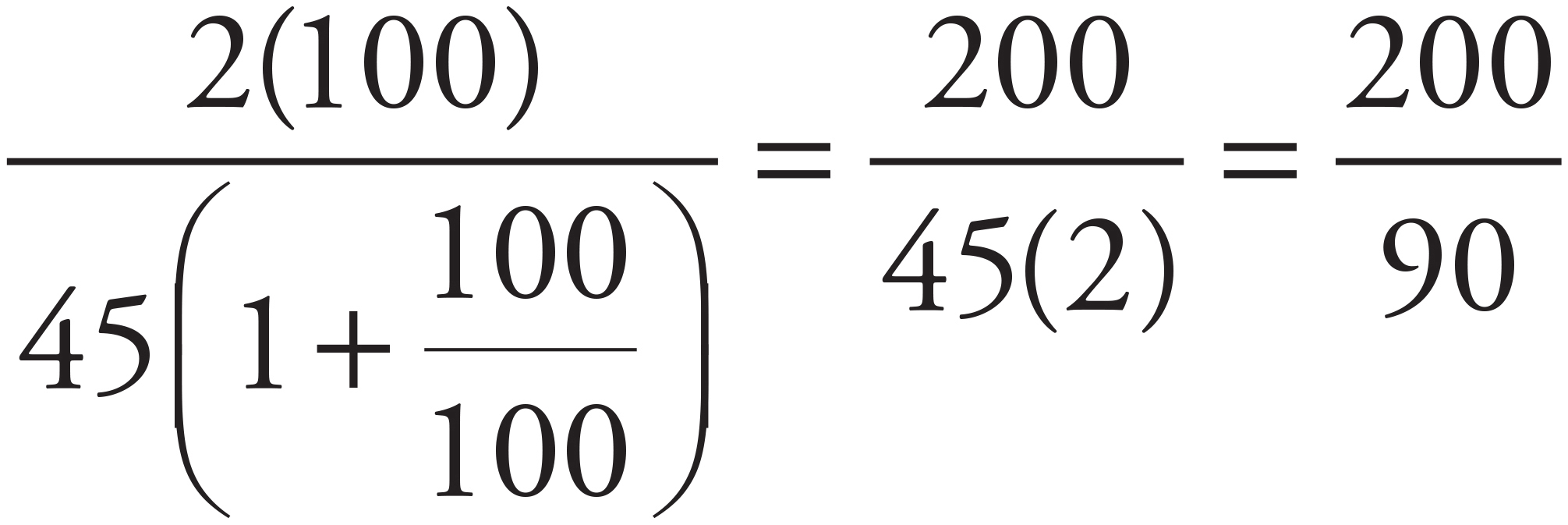 
= 2.2. This matches the target so keep (C), but check (D) just in case it also works. Choice (D) becomes 
= 
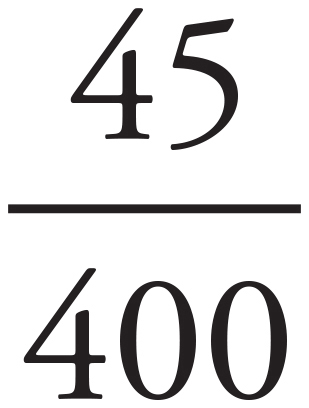= 0.1125. Eliminate (D). The correct answer is (C).
27. A
Start by examining (A). To determine how many people used both forms of transportation in each city, use the Group Equation: Total = Group 1 + Group 2 + Neither − Both. For Boston, this becomes 7,556 = 5,281 + 3,504 + 1,025 − B. Combine like terms: 7,556 = 9,810 − B. Subtract 9,810 from both sides: −2,254 = −B. Divide both sides by −1 to find that 2,254 people use both forms in Boston. Repeat the same for New York: 7,789 = 2,476 + 5,738 + 1,459 − B; 7,789 = 9,673 − B; −1,884 = −B, so 1,884 people in New York use both forms of public transportation. Finally, determine if 20% more people checked both in Boston by using the percent change formula: percent change = 
× 100, so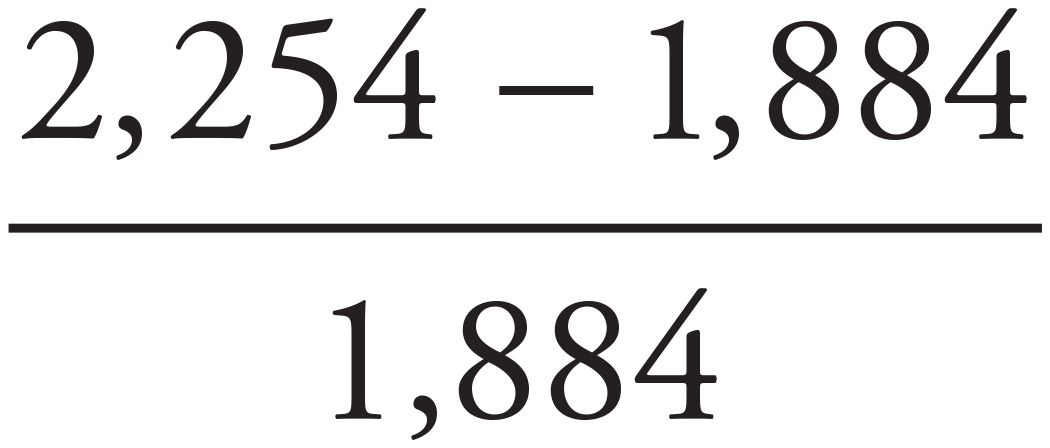 
× 100 = 19.7%. This is approximately 20%, so choose (A).
CHAPTER 11
Drill 1
3. C
The x-intercepts are where the graph crosses the x-axis. At those points, the corresponding y-values are 0. To find the x-intercepts, factor the equation and set each factor equal to zero. In the answer choices, (C) is already fully factored such that it is easy to determine that the x-intercepts are at −3 and −5. Therefore, the correct answer is (C).
4. C
Whenever there are variables in the question and in the answers, think Plugging In. If m = 10, then Monster Truck Inc. receives a down payment of $3,200 plus 10 months’ worth of monthly payments. This can be calculated as 3,200 + 10(380) = 3,200 + 3,800 = $7,000. Plug in 10 for m in the answers to see which function equals 7,000. Choice (A) becomes f(m) = 380 + 3,200(10) = 380 + 32,000 = 32,380. Eliminate (A). Choice (B) becomes f(m) = 3,200 + 36(10) = 3,200 + 360 = 3,560. Eliminate (B). Choice (C) becomes f(m) = 3,200 + 380(10) = 3,200 + 3,800 = 7,000. Keep (C), but check (D) just in case it also works. Choice (D) becomes f(m) = 10,480 − 380(10) = 10,480 − 3,800 = 6,680. Eliminate (D). The correct answer is (C).
15. 3
Since the problem tells you that f(a) = 10, and that f(x) = x2 − x + 4, you can plug a into the function for x so f(a) = a2 − a + 4, and 10 = a2 − a + 4. Now you need to factor to solve for a. If you subtract 10 from both sides of the equation, you get a2 − a − 6 = 0, which you can factor as (a − 3) (a + 2) = 0. The value of a could be 3 or −2, but since the question tells you that a is non-negative, the value of a must be 3.
9. C
The equation for the number of bonus points when the purchases are increased by 4 can be written as a(p + 4) + 7. According to the question, this sum will be 25 greater than ap + 7. Therefore, the following equation can be constructed to solve for a: ap + 7 + 25 = a(p + 4) + 7 or ap + 32 = a(p + 4) + 7. Distribute the a on the right side of the equation to get ap + 32 = ap + 4a + 7. Subtract ap from both sides of the equation to get 32 = 4a + 7. Solve for a to get 25 = 4a, so 6.25 = a. The correct answer is (C).
21. D
Negative exponents mean to take the reciprocal of the positive exponent. For example y−2 = 
, and 2−3 = 
. For fractional exponents, the denominator tells you what root of the number to take and the numerator acts as a normal exponent. So, f(x) is 
. First, find f(8):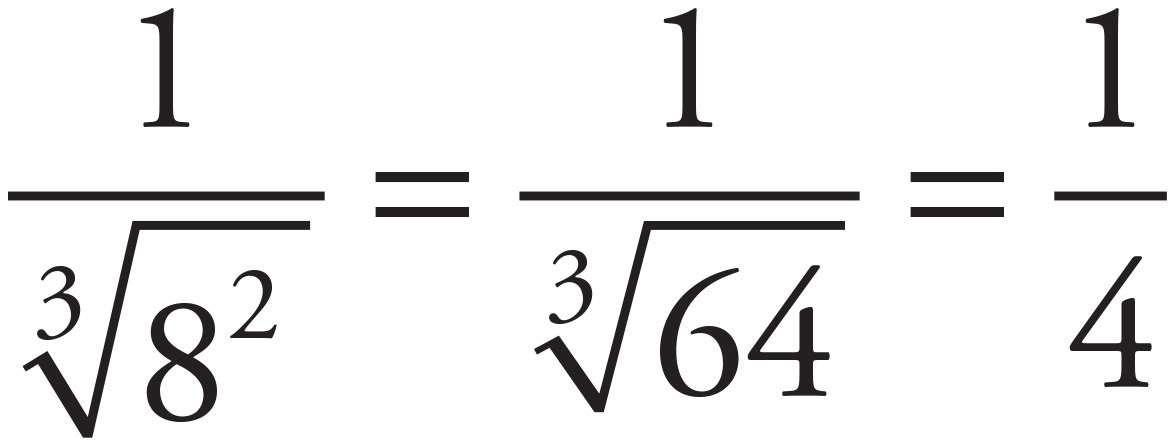 
. Next, find f(3): 
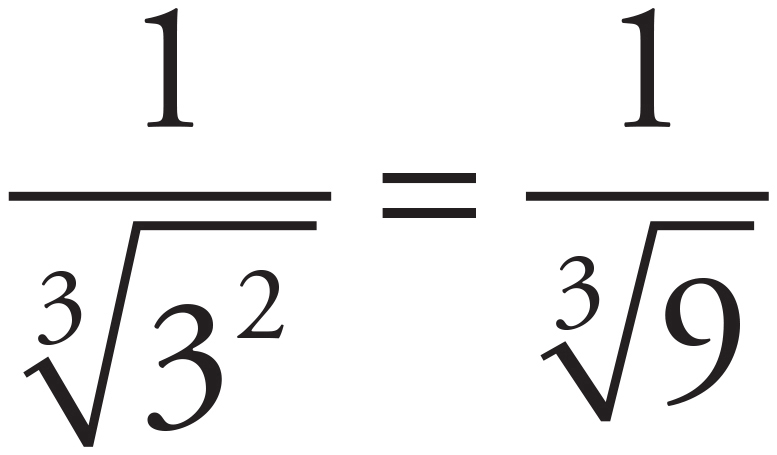. Put these values in for 
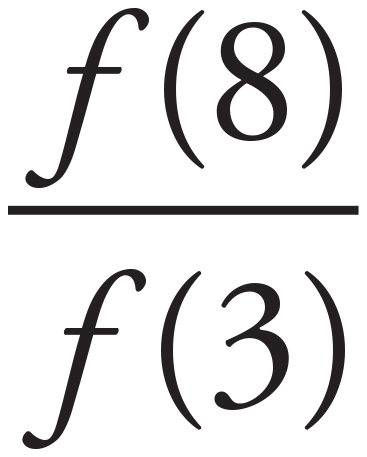. So, 
= 
. Remember to look at the answer choices so you don’t keep trying to simplify when there’s no need to.
23. B
Set the more straightforward equation equal to 0 by subtracting 100 from each side to get 0 = x2 − 24x + 44. Factor the equation to get 0 = (x − 22)(x − 2). Solve for x to get x = 2 or 22. These numbers represent the hours since midnight, and 2 hours after midnight would be 2 A.M. That is not a choice. 22 hours after midnight is 10 P.M. Therefore, the correct answer is (B).
12. B
Remember that the basic function equation states that y = f(x). Given that the question states that f is a linear function, the table shows that 3 points on the line are (−1, 2), (j, j), and (5, −6). Use the slope formula to find the value of j. The slope formula states that given two points on a line slope =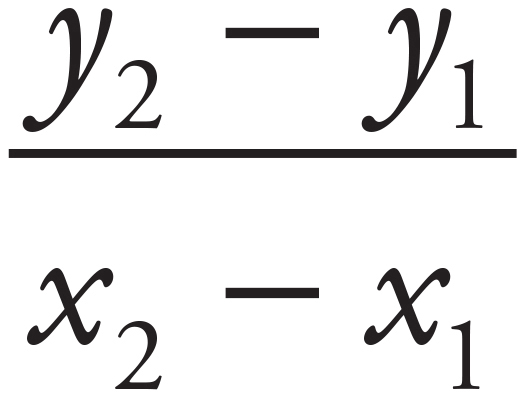 
. Given the two known points (−1, 2) and (5, −6), the slope can be calculated as follows: 
. Next plug the points (j, j) and (−1, 2) into the slope formula to find j :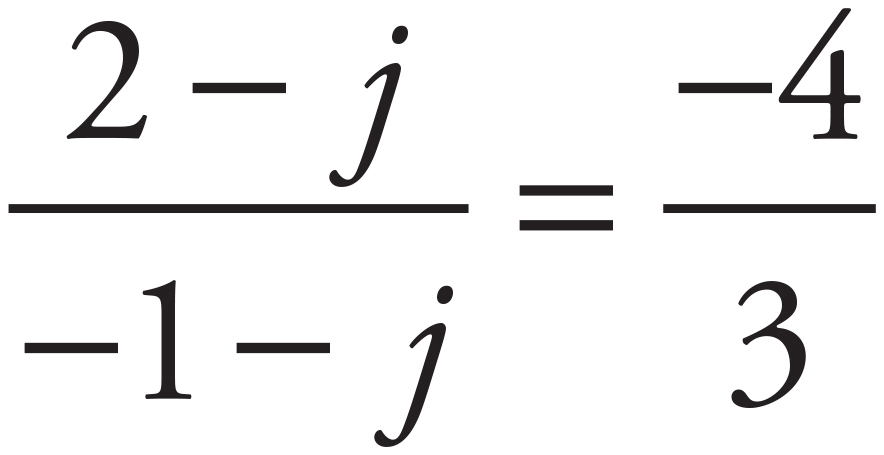 
. Cross-multiply to get −4(−1 − j) = 3(2 − j). Distribute the −4 and the 3 to get 4 + 4j = 6 − 3j. Solve for j to get 4 + 7j = 6, then 7j = 2, and finally j = 
. The correct answer is (B).
30. 148
Make x = 12 in each function: f(12) = (12)2 − 4 = 140 and g(12) = −(12) − 4 = −8. Subtract: 140 − (−8) = 148.
31. 8
Perpendicular lines have negative reciprocal slopes, so the slope of h(x) is 3. You can use the point (−12, 0) to determine the y-intercept by first writing h(x) in y-intercept form and solving for b: h(x) = 3x + b; plugging in (−12, 0) gives you 0 = 3(−12) + b. Multiply and you get 0 = −36 + b. Add 36 to both sides and you find b = 36, so h(x) = 3x + 36. You want a point of intersection between h(x) and f(x), so put the functions equal to one another: x2 − 4 = 3x + 36. This is a quadratic equation, so set it equal to zero: x2 − 3x − 40 = 0. Factors of 40 that have a difference of 3 are 5 and 8, so this quadratic factors to (x + 5)(x − 8) = 0. The solutions are therefore x = −5, 8. Because you cannot input negative numbers into the grid, the answer is 8.
Drill 2
3. A
The initial height of the projectile corresponds to the moment before it is launched. At that point, no time has passed, and so t = 0. Therefore, the correct answer is (A).
4. B
You could solve this one by expanding the squared binomial, setting it equal to zero, factoring, and solving, but look for a faster way. When the question asks for a specific value and there are numbers in the answer choices, think Plugging In the Answers. In (A), if t = −9, the equation becomes 12 − (−9 + 2)2 = 3 or 12 − (−7)2 = 3. This becomes 12 − 49 = 3, which is not true, so eliminate (A). In (B), if t = −5, 12 − (−5 + 2)2 = 3 or 12 − (−3)2 = 3. This becomes 12 − 9 = 3, which is true, so (B) is the correct answer.
6. B
The equations in the answer choices are factored, making it easy to see the roots. The correct answer will have roots at −3 and 1, as shown on the graph. For (A), the roots are x − 3 = 0 or x = 3 and x + 1 = 0 or x = −1, which are the right numbers but the wrong signs. For (B), though, the roots are −3 and 1, so (B) is the correct answer. Another approach would be to plug the given points into the answer choices to see which one works for both points.
9. A
Whenever the question and the answers include variables, think Plugging In. If x = 3 and y = 2, then Aubri’s score can be calculated as 34 − 24 = 81 − 16 = 65. Plug 3 in for x and 2 in for y in the answers to see which answer equals the target number of 65. Choice (A) becomes (3 + 2)(3 − 2)(32 + 22)(5)(1)(9 + 4) = (5)(1)(13) = 65. Keep (A), but check the remaining answers just in case one of them also works. Choice (B) becomes (3 + 2)2(32 + 22) = (5)2(9 + 4) = (25)(13) = 325. Eliminate (B). Choice (C) becomes (3 − 2)2(32 + 22) = (1)2(9 + 4) = (1)(13) = 13. Eliminate (C). Choice (D) becomes (3 + 2)(3 − 2)(32 − 22) = (5)(1)(9 − 4) = (5)(1)(5) = 25. Eliminate (D). The correct answer is (A).
10. C
Plug −5 in for x and 2 in for y in the answers to see which equation contains the point (−5, 2). Choice (A) becomes 2 = (−5 + 5)2 − 2. Solve the right side of the equation to get 2 = (0)2 − 2, or 2 = 0 − 2. Because this statement is not true, eliminate (A). Choice (B) becomes 2 = (−5 − 5)2 − 2. Solve the right side of the equation to get 2 = (−10)2 − 2, or 2 = 100 − 2. Because this statement is not true, eliminate (B). Choice (C) becomes 2 = (−5 + 5)2 + 2. Solve the right side of the equation to get 2 = 2(0)2 + 2, or 2 = 0 + 2. This statement is true so keep (C), but check (D) just in case. Choice (D) becomes 2 = 2(−5 − 5)2 + 2. Solve the right side of the equation to get 2 = 2(−10)2 + 2, then 2 = 2(100) + 2, and finally 2 = 200 + 2. This statement is not true, so eliminate (D). The correct answer is therefore (C).
14. 3
The maximum profit will occur at the vertex of the parabola. The equation is in vertex form, so the vertex is (3, 2,000). The x-coordinate is the price, so the shop should charge $3. If you forget the form, you can use a sort of plugging in. To maximize its profit, the donut shop needs to make the negative part of the equation, −4(x − 3)2, either positive or 0. Because (x − 3)2 is always either positive or 0, it is not possible to make −4(x − 3)2 positive. Therefore, the maximum profits will occur when −4(x − 3)2 = 0. Solve for x by dividing both sides by −4 to get (x − 3)2 = 0. Solve for x to get x = 3. The correct answer is 3.
23. B
Whenever there are variables in the question and numbers in the answers, think Plugging In the Answers. In (A), c = 33 and the equation becomes x2 + 24x + 33 = (x + 9)(x + p). This means that 33 would equal 9p once the right side was multiplied out. Eliminate (A) since 33 is not divisible by 9. In (B), c = 135 and the equation becomes x2 + 24x + 135 = (x + 9)(x + p). Divide 135 by 9 to get x2 + 24x + 135 = (x + 9)(x + 15). Test whether this is the right answer by using FOIL to expand (x + 9)(x + 15) to get x2 + 24x + 135. The middle term is in fact 24x, and the correct answer is therefore (B).
26. B
Use Process of Elimination to solve this question. According to the question, the correct equation should be a parabola. Eliminate (D) because it represents the equation of a straight line. The water shoots up and then down, therefore eliminate (C), which is the equation of a parabola that is upward facing. Because the water shoots out from a spout that is 8 feet above the ground, the point (0, 8) must be on the graph. Plug this point into (A) to get 8 = −02 + 15 and 8 = 15. This is not true, so eliminate (A). Therefore, the correct answer is (B).
Drill 3
3. D
Whenever there are variables in the answer choices, think Plugging In. In the answers, plug in 15 for d to see which answer equals the corresponding oxygen concentration of 0.0022. Choice (A) becomes 
= 0.5 − 0.004 ≈ 0.496. This does not match the target number, so eliminate (A). Choice (B) becomes 
= 0.0006. Eliminate (B). Choice (C) becomes 
= 0.06. Eliminate (C). Therefore, the correct answer is (D).
6. A
Notice that the 40 is being subtracted from the rest of the equation, which means that there is a $40 reduction in the driver’s net pay. Look for other information in the question that suggests some type of reduction. The only information on any type of reduction is that the shipping company “deducts a separate fee daily for the use of the company’s delivery truck.” Therefore, it is reasonable to assume that the 40 represents this fee. The correct answer is (A).
9. B
Focus only on the information that is needed to answer the question. The total number of customers is equal to the number of student customers, s, and the total number of non-student customers, n. Add these two groups together to get the overall total. The calculation for this is s + n. The correct answer is (B).
7. B
Use Process of Elimination to solve this problem. According to the question, T represents temperature. Therefore, eliminate (A). Eliminate (C) because the question says nothing about Fahrenheit. According to the question, k represents the constant rate. Therefore, eliminate (D). The correct answer is (B).
10. D
For this question, you have to find the slope of the best-fit line, which will represent the average yearly change. The formula for slope is 
, so find two points to use. On the graph, the number of carp in 2010 was 25,000 and in 2011, the number of carp was 22,500. You can substitute these x- and y-values from the graph to get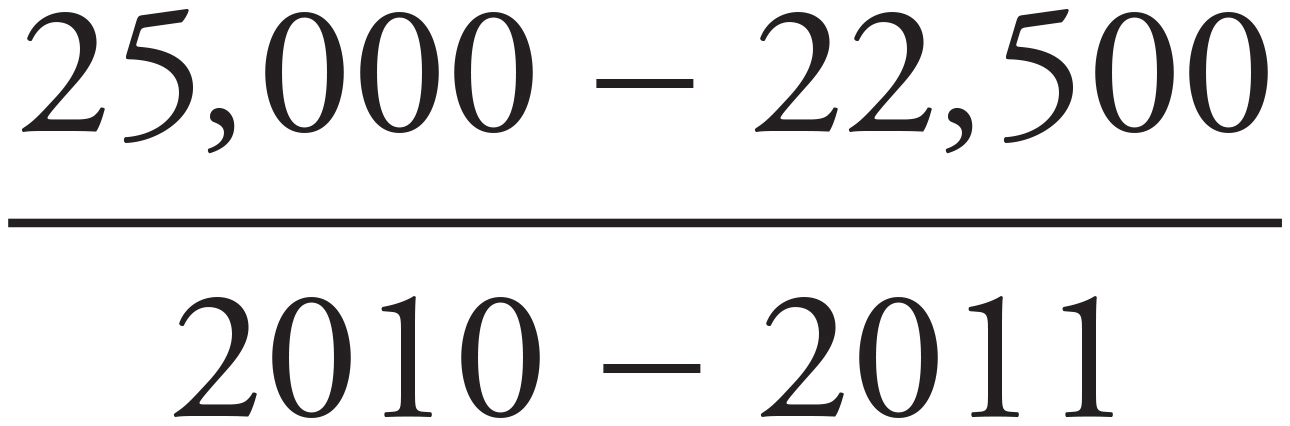 
. Simplify to get 
, or −2,500. Since the result is negative, it represents a decrease of 2,500. Therefore, the answer is (D).
8. C
The equation includes a −0.40c. A minus sign indicates some type of reduction. According to the question, the only deduction to the net proceeds is the cost of paying for cleaning supplies. It is logical to assume that the students pay 0.40 in cleaning supplies for each car that they wash. Therefore, the correct answer is (C).
12. C
Consider each answer and use Process of Elimination. Choice (A) is not supported by the graph because one employee had a linear decrease in energy, while the other employee’s energy increased and decreased in an exponential fashion; eliminate (A). Choice (B) is also not supported; one employee had low energy after lunch (and may be drowsy), but the other employee had the highest energy level immediately after lunch. Eliminate (B). Choice (C) fits the employee who started with high energy and decreased throughout the afternoon; keep (C). Choice (D) fits neither employee: one employee decreased throughout the afternoon, and the other employee increased and then rapidly decreased. Eliminate (D) and choose (C).
11. D
Whenever there are variables in the question and in the answer choices, think Plugging In. Plug in values that should work (those from 30–37) and values that shouldn’t work (those outside of the given range) and use Process of Elimination. If t = 37, the correct answer will provide a statement that is true. Plug 37 in for t in the answers and eliminate any answers that are not true. Choice (A) becomes |37 + 7| ≤ 37 or |44| ≤ 37. Since this statement is false, eliminate (A). Choice (B) becomes |37 − 3.5| ≤ 33.5 or |33.5| ≤ 33.5. Since this statement is true, keep (B). Choice (C) becomes |37 − 30| ≤ 7, or |7| ≤ 7. Since this statement is true, keep (C). Choice (D) becomes |37 − 33.5| ≤ 3.5, or |3.5| ≤ 3.5. Since this statement is true, keep (D). Next try a value that should not work, such as t = 29, in the remaining answer choices and eliminate any answers that provide a true statement. Choice (B) becomes |29 − 3.5| ≤ 33.5 or |25.5| ≤ 33.5. Since this statement is true, eliminate (B). Choice (C) becomes |29 − 30| ≤ 7 or |−1| ≤ 7. Since this statement is true eliminate (C). Therefore, the correct answer must be (D).
13. B
Whenever there are variables in the question, think Plugging In. Plug in 2, 3, and 4 as the consecutive integers. In this case, S = 2 + 3 + 4 = 9 and n = 3. The equation becomes 9 =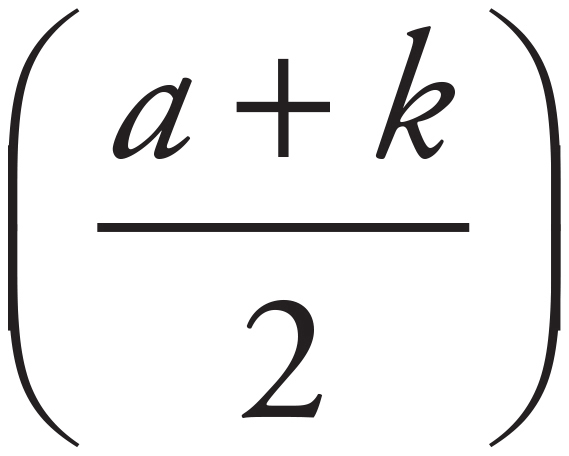 
(3). Divide both sides of the equation by 3 to get 3 = 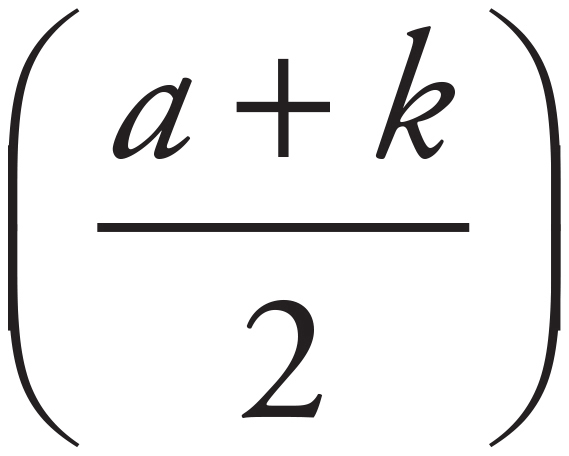. Multiply both sides by 2 to get a + k = 6. Next, see which answer choice equals 6. Choice (A) becomes 2 + 3 = 5, so eliminate (A). Choice (B) becomes 2 + 4 = 6. Keep (B), but check the remaining answers just in case. Choice (C) doesn’t work because there is only one middle integer, so eliminate (C). Choice (D) becomes 3 + 4 = 7. Eliminate (D). Therefore, the correct answer must be (B).
23. C
Use Process of Elimination to solve this question. Choices (A) and (B) are unlikely because 
≈ 0.004, which is a much smaller amount than anyone could deposit into an account or could be in the account. According to the problem, the annual interest rate is 5%. Because 5% = 0.05, the fraction likely has something to do with the interest. So keep (C). Eliminate (D) because is too small to refer to a number of months. The correct answer is (C).
CHAPTER 12
Drill 1
a. 36
b. 24
c. x = 10, y = 5
d. 30
e. 22
4. D
Because this is a square, the two sides are equal. Therefore, 2x + 1 = x + 3. Solve for x, and you get that x must be 2. Therefore, a side equals x + 3 or 2x + 1 = 5, so the area equals 25.
3. D
Here are four lines; a and b are parallel, d intersects a and b, and c does not intersect both parallel lines. In statement I, angles 1 and 5 do not have to be equal because a side of angle 1 is line c, which has nothing to do with the parallel lines. Thus, the angles in statement I do not have to be equal, and you can eliminate (A). The angles in statement II have to be equal because angles 2 and 7 are opposite angles (two angles made up of the same two lines) and opposite angles must be equal. Eliminate (C). The angles in statement III must be equal because angles 3 and 9 are made up of the same line (line d) and one of the parallel lines. In fact, 3, 6, 5, and 9 are all the same “small angle,” so eliminate (B). Therefore, statements II and III are true, and the correct answer is (D).
28. 60
Draw and label the diagonal of rectangle ABCD. Because you’ve made a right triangle, you can use the Pythagorean Theorem (a2 + b2 = c2) to determine the length of AB. One leg of the triangle is labeled 5, and the hypotenuse has a length of 13. Plug those values into the Pythagorean Theorem to get 52 + b2 = 132. Square everything that needs to be squared to get 25 + b2 = 169. Subtract 25 from both sides to get b2 = 144. Because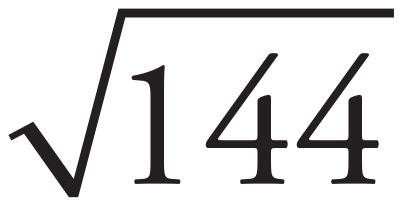 
= 12, AD has a length of 12. Plug these values into the area formula for a rectangle (A = lw). The area of the rectangle is equal to 5 × 12. Because 5 × 12 = 60, the area of the square is 60.
9. C
Because BC and AD are parallel, and CD is a transversal, ∠ADC and ∠BCD are supplementary interior angles. Therefore, their angle measures add up to 180°. Because ∠ADC has a degree measure of 95°, ∠BCD has a measure of 85°. Subtract 35 from 85 to see that ∠ACD has a measure of 50°. This matches (C).
Drill 2
a. 24
b. 10
c. 
, or 0.6
d. 20
e. 20
f. 
, or 
28. 7.5
SOHCAHTOA tells you that tangent is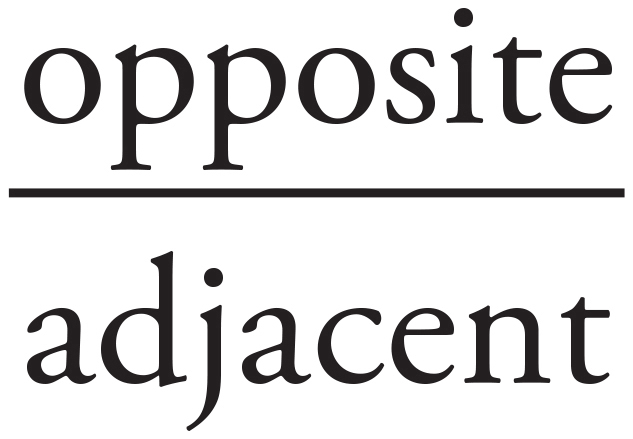 
. You can set up a proportion: 
. Cross-multiply: 14x = 105. Divide both sides by 14: x = 7.5.
14. 100
Because the triangle is isosceles, with AB = BC, you know that angles A and C must have the same measure. So angle A must also be 40°. Angles A and C have a combined measure of 80°, and you need a total of 180° in the triangle. Therefore, x must measure 100°.
8. C
The problem tells you that the triangle is isosceles, and you see there is a right angle present in the figure. This tells you that the base angles are 45° each. Since the length of side AB is 5, that means that the length of side BC is 5 as well. Using the relationships for a 45°-45°-90° right triangle, you can infer than the length of AC is 5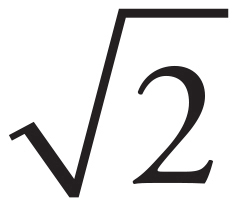. To find the perimeter, add all three sides together: 5 + 5 + 5 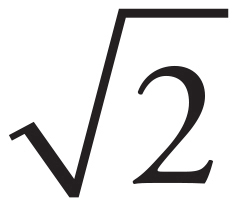= 10 + 5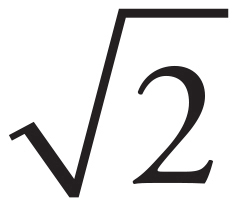. The correct choice is (C).
9. B
To find the answer, you need to know the total area. The formula for the area of a triangle is A = 
. To find the height, use a trigonometric ratio. Considering just the triangle on the right, you have a 30° angle. The adjacent side is 4, because it is half of the base. Because you have the adjacent side and need the opposite side, SOHCAHTOA tells you to use tan, which is 
. Therefore, tan 30° = 
. Multiplying both sides by 4 gives you h = 4 tan 30°, or approximately 2.3. You can also use the special 30°-60°-90° triangle proportions. If the side opposite the 30° is s, the side opposite the 60° angle is s. Make 4 = s and solve for s, and you also get 2.3 for the height. Since 2.3 m is the height, the area of the entire triangle is A =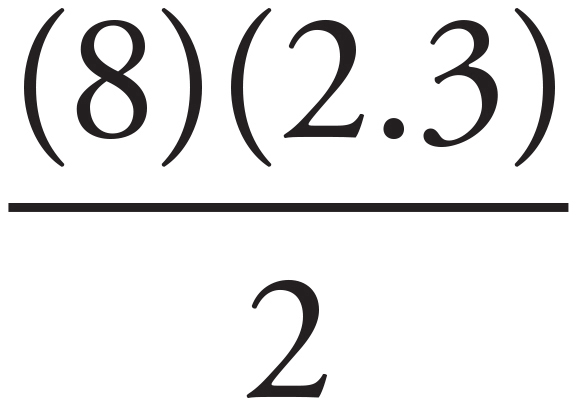 
, or approximately 9.2 m2. To cover 9.2 m2, the owner will need 
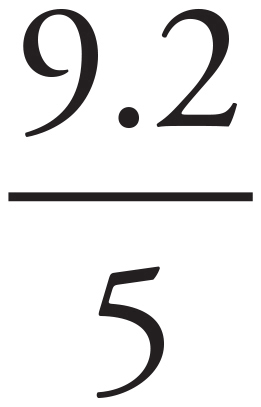buckets, which is 1.84. Since 1 bucket is not enough, round up to 2, which is (B).
10. D
Since these two triangles are right triangles and share the angle A, then all three angles must be congruent, and the triangles are therefore similar. You need to determine which sides correspond in order to set up a proportion. Since the only value given in the large triangle is the base, you need to determine the base of the smaller triangle in order to form your proportion. You may recognize the smaller triangle as a Pythagorean triple (5-12-13), but if you do not, you can use the Pythagorean Theorem to solve for the base, which is 12. Using this value, you can then set up a proportion: 
. Solving this for x will yield 10. Be careful though, the question did not ask for AD; it asked for BD. So you need to subtract 5 (the length of AB) from this to get BD = 5, which is (D).
13. C
If AB = BC, then ∠BCA = ∠BAC = 35°. Indicate that in the diagram and draw a line from point B to AC to create two right triangles:
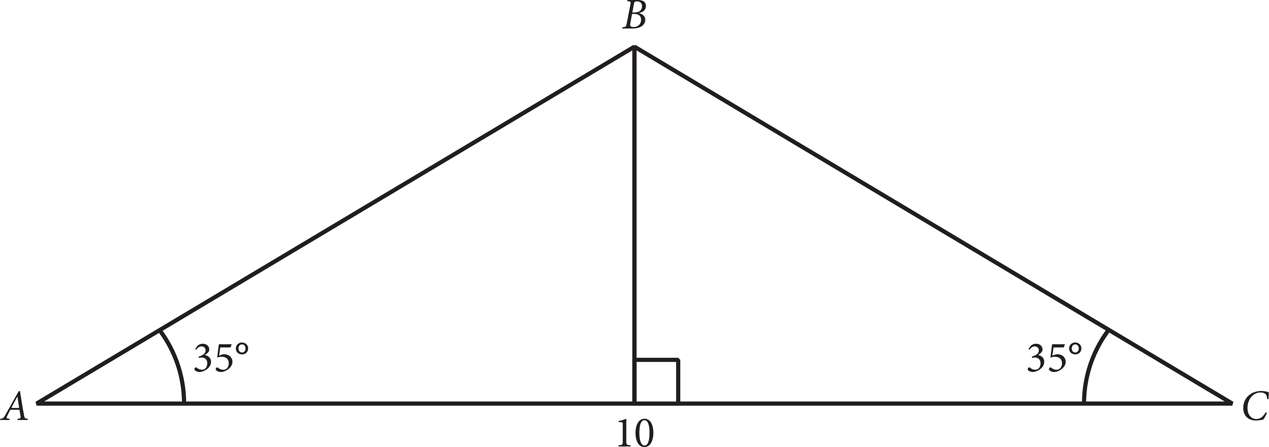
AB and BC are equal hypotenuses of the right triangles. You know the side adjacent to the 35° angle, so you want cosine: cos35° = 
. Solving this for AB, you get AB = 
. Multiply that by 2 and add that to 10 and you get 10 + 
for the perimeter, but that’s not an answer. However, (C) is 10+ 
. Remember that sinx = cos(90 − x), so sin 55° = cos 35°. Therefore, the answer is (C).
Drill 3
a. 16π
b. 8π
16. A
Angle AOB is 60 degrees, which is of 360 degrees. Since arc AB is 2π, it is of the total circumference. The circumference then is 6 × 2π, which comes to 12π. The diameter of the circle is 12, making the radius 6. The area of the circle then is 36π, (A).
18. C
Since there is no figure given, you should draw one according to the directions. The figure should look like the following:
Given that the area of the circle is 36π, the radius is 6. That means that the diameter is 12. The point where a tangent hits the circle makes a 90-degree angle, so angle OAC is 90 degrees. Now that you have a right triangle, you can use the Pythagorean Theorem to find that the length of BC is 13. Adding 5 + 12 + 13 gives you 30, (C).
12. B
The equation of a circle with its center at (h, k) is (x − h)2 + (y − k)2 = r2. To convert the given equation into this form, you must create two expressions that are perfect squares. Given x2 − 2x, you can create a perfect square by “completing the square.” Take half of 2, which is 1, and square it to get 1. Finally, add and subtract this number. This gives you x2 − 2x + 1 − 1. The expression x2 − 2x + 1 is a perfect square, giving you (x − 1)2 − 1. Do the same with y2 + 8y to get y2 + 8y + 16 − 16, which equals (y + 4)2 − 16. Now you have (x − 1)2 − 1 + (y + 4)2 − 16 + 8 = 0. Rearranging, you get (x − 1)2 + (y + 4)2 = 9. Because h = 1 and k = −4, you have a center of (1, −4), which is (B).
29. 5.25
Start by translating English to math. “Major arc PSR is 
the length of minor arc PQR” becomes PSR = PQR. Because PSR = 6π, you can substitute and then solve for PQR: 6π = PQR; 18π = 4PSR; 
π = PSR. Because major arc PSR and minor arc PQR make up the entire circumference of the circle, PRS + PQR is the circumference of the circle: 6π + π = 
π. The formula for circumference is 2πr, so you can solve for r: 2πr = π; 4r = 21; r =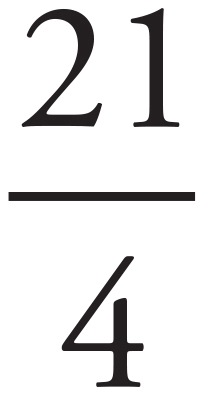 
, or 5.25.
Drill 4
3. B
There are variables in the answer choices, so plug in a number for a. How about 90, just to make the math easy? If a = 90, then the other angle inside the triangle must be equal to 60. Therefore, b must be equal to 120. What choice says 120, remembering that a = 90? Choice (B) does.
7. B
This is another great example of Plugging In. Make 3 the radius of Cone A and 4 the radius of Cone B. Set the height to 3. The volume of Cone A is therefore 9π, and the volume of Cone B is 16π. Divide both sides by π to get a ratio of 9:16. Choice (B) is correct.
5. A
Plug In! You are given a right triangle, so plug in for the sides of the right triangle. Make the triangle a Pythagorean triplet. Make the side opposite the angle with measure a° equal to 3, the side opposite the angle with measure b° equal to 4, and the hypotenuse equal to 5. SOHCAHTOA tells you that sine is 
, so sin a° = 
and x = . Cosine is 
, so cos b° = . Make x = in each answer choice, and look for what equals . Only (A) works.
22. A
Plug in for x, choosing 18 to make the math easier. Since A = πr2 and r = 18, the total area is 324π. Since C = 2πr, the total circumference is 36π. Minor arc PQ takes up 
or π of 36π, which is 
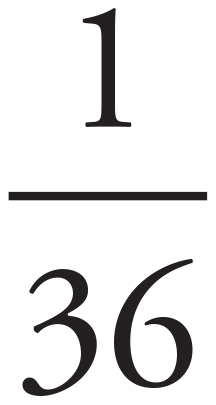. Sector POQ must therefore take up 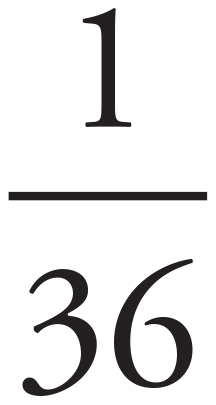of the area, which is 
324π = 9π. This is the target answer, so plug x = 18 into the answer choices to see which one equals 9π. Choice (A) becomes 
= 9π. This matches the target. Since all the other answers have the same numerator and different denominators, only (A) will work.
26. C
Start by drawing a rectangular box with three spheres in a row:
Next, plug in for the variable. Make r = 2. To find the volume between the box and the spheres, find the volume of the box and subtract the volume of the three spheres. If the radius of each sphere is 2, then the square faces on either end must have sides double the radius, or 4, The long dimension of the box will be 3 times 4, or 12. Therefore, the volume of the box is V = (4)(4)(12) = 192. To find the volume of one sphere, use the formula: V = π(2)3 = 
. Because there are three spheres, multiply this by three; the total volume of the three spheres is 32π. Therefore, the volume between the box and the spheres is 192 − 32π. This is your target; circle it. Make r = 2 in each answer and eliminate any choice that does not equal your target. The only choice that works is (C).
29. 160
According to the problem, w = l and 3w = h. Since you know that volume equals lwh, you can form an equation: ( w)(w)(3w) = 96. Now you know that 
w3 = 96. Solving this equation for w yields w = 4. From this, you can calculate that l = 2 and h = 12. The formula for surface area is Surface Area = 2lw + 2lh + 2hw. Plug in your values for l, w, and h into the equation to get surface area = 160.