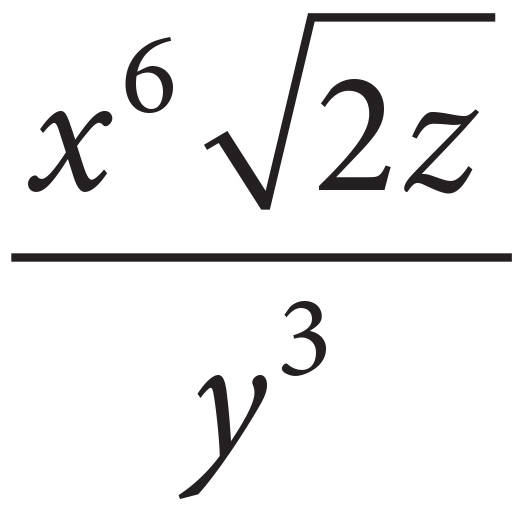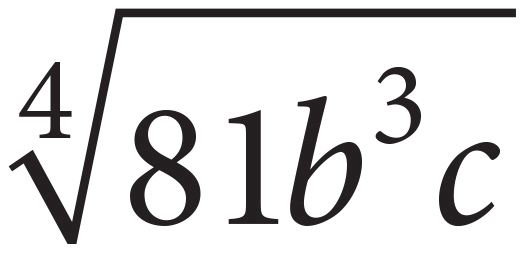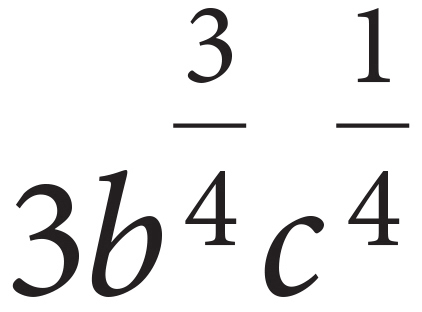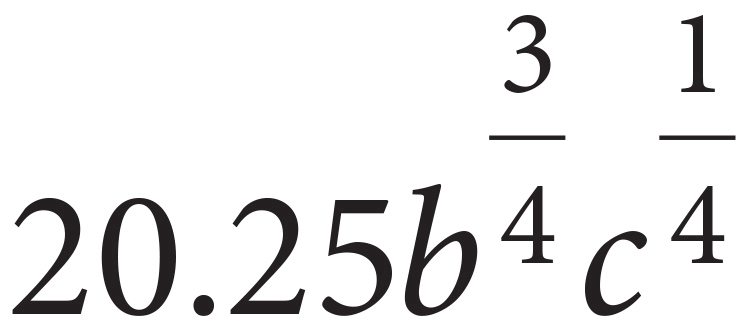Chapter 9

Math Basics

Although we’ll show you which mathematical concepts are most important to know for the PSAT, this book relies on your knowledge of basic math concepts. If you’re a little rusty, this chapter is for you. Read on for a review of the math basics you’ll need to know before you continue.

HOW TO CONQUER PSAT MATH

So what do you need to do? There are three important steps:

1. Know the basic content. Obviously you do need to know the basics of arithmetic, algebra, and geometry. We’ll cover what you need to know in this chapter.

2. Learn some PSAT-specific problem-solving skills. Since these basic concepts appear in ways you’re probably not used to from math class, you need to prepare yourself with a set of test-specific problem-solving skills designed to help you solve PSAT Math problems. We’ll cover the most important ones in the next chapter.

3. Have a sound overall testing strategy. This means knowing what to do with difficult questions or when calculator use is not allowed, and having a plan to pace yourself to get the maximum number of points in the time allotted. Be sure to read carefully the material in Chapter 3, to make sure you’re using the strategy that will get you the greatest number of points in the time you have.

(PERSONAL) ORDER OF DIFFICULTY

The Math sections on the PSAT are Sections 3 and 4. Section 3 contains 13 multiple-choice questions and 4 grid-in questions. Section 4 contains 27 multiple-choice questions and 4 grid-in questions. Within each question type, there is a loose order of difficulty, with most of the questions being of medium difficulty. (This means that the first few multiple choice and first few grid-in questions are likely to be rated as easy, and the last few multiple choice and last few grid-ins are typically considered the most difficult.) More important than any order of difficulty is your own Personal Order of Difficulty. Though the last questions of each type in a section are likely to be the hardest, use your own personal strengths and weaknesses to decide which questions to do and which to skip.

USING YOUR CALCULATOR

You are allowed to use a calculator on Section 4 of the PSAT, and you should definitely do so. You can use any graphing, scientific, or plain old four-function calculator, provided that it doesn’t have a keyboard.

There are a few simple rules to remember when dealing with your calculator:

1. Use the calculator you’re most comfortable with. You definitely don’t want to be trying to find the right button on test day. Ideally, you should be practicing with the same calculator you’ll use on test day.

2. Change your batteries the week before the test. If they run out during the test, there’s nothing you can do about it.

3. Be sure to hit the “clear” or “on/off” button after each calculation to reset the calculator after an operation. A common mistake to make when using your calculator is to forget to clear your last result.

4. Your calculator is very good at calculating, but watch out for mis-keying information. (If you type the wrong numbers in, you’ll get the wrong result.) Check each number on the display as you key it in.

5. For the most part, you’ll use your calculator for the basic operations of addition, subtraction, multiplication, and division; the ability to convert fractions to decimals and vice versa; and the ability to do square roots and exponents. Don’t forget, though, that it has handy buttons for things like sine, cosine, and i, should you encounter those on the test.

6. Then, there’s one really big, important rule whenever you think about using your calculator:

A calculator can’t think; it can only calculate.

What does this mean? It means that a calculator can’t think through a problem for you. You have to do the work of understanding and setting up the problem correctly to make sure you know what the right calculation will be to get the answer. Only then can you use the calculator, when it is allowed, to calculate the answer.

So use your paper and pencil to practice your problem-solving skills on all Math questions. You should always be sure to set up the problem in your test booklet—writing it down is still the best method—which will help you catch any errors you might make and allow you to pick up where you left off if you lose focus. Then, for questions in Section 4, move quickly to your calculator to chug your way through the arithmetic, and be careful to enter each number and operator correctly. Remember, using your calculator is already saving you time on these questions—don’t rush and lose the advantage that it gives you.

As you work through this book, look for calculator symbols next to questions on which calculator use would be allowed. If you don’t see the symbol, don’t use your calculator!

Drill 1

DEFINITIONS

One of the reasons that good math students often don’t get the credit they deserve on the PSAT is that they’ve forgotten one or more of these definitions—or they read too fast and skip over these “little” words. Be sure you know them cold and watch out for them!

Match the words with their definitions, and then come up with some examples. Answers can be found in Part III.

1. integers	a. numbers that a certain number can be divided by, leaving no remainder Examples:
2. positive numbers	b. integers that cannot be divided evenly by 2 Examples:
3. negative numbers	c. numbers that have no fractional or decimal parts Examples:
4. even numbers	d. numbers that are greater than zero Examples:
5. odd numbers	e. having a different value Examples:
6. factors	f. integers that can be divided by 2 evenly (with no remainder) Examples:
7. multiples	g. numbers that are less than zero Examples:
8. prime numbers	h. numbers that have exactly two distinct factors: themselves and 1 Examples:
9. distinct	i. numbers that can be divided by a certain number with no remainder Examples:
10. digit	j. a figure from 0 through 9 that is used as a placeholder Examples:
11. consecutive numbers	k. the result of addition Examples:
12. divisible	l. a whole number left over after division Examples:
13. remainder	m. the result of subtraction Examples:
14. sum	n. can be divided with no remainder Examples:
15. product	o. a number’s distance from zero; always a positive value Examples:
16. difference	p. numbers in a row Examples:
17. quotient	q. the result of division Examples:
18. absolute value	r. the result of multiplication Examples:

EXPONENTS AND SQUARE ROOTS

Exponents are just a shorthand for multiplication. Instead of writing 3 × 3 × 3 × 3, you can write 3⁴. Thus, you can handle exponents by expanding them out if necessary.

However, you can also multiply and divide exponents that have the same base using a shortcut called MADSPM. MADSPM also helps you remember how to deal with raising exponents to another power. Let’s see the breakdown:

• MA means when you see a MULTIPLICATION sign, ADD the exponents.

  So y² × y³ = y^{2 + 3} = y⁵.

• DS means when you see a DIVISION sign (or fraction), SUBTRACT the exponents. So = y⁵⁻² = y³.

• PM means when you see an exponent raised to a POWER, MULTIPLY the exponents. So (y²)³ = y^{2 × 3} = y⁶. (This is really easy to confuse with multiplication, so watch out!)

Be careful, because the rules of MADSPM don’t work for addition and subtraction. For example, 3² + 3⁵ does NOT equal 3⁷. (Crunch it on your calculator if you want to prove it.)

Warning

The rules for multiplying and dividing exponents do not apply to addition or subtraction:

2² + 2³ = 12

(2 × 2) + (2 × 2 × 2) = 12

It does not equal 2⁵ or 32.

Here are some additional rules to remember about exponents:

• Anything to the zero power equals 1: 3⁰ = 1. Mathematicians argue about whether 0⁰ is 1 or is undefined, but that won’t come up on the PSAT.

• Anything to the first power equals itself: 3¹ = 3.

• 1 to any power equals 1: 1³⁸⁷⁶ = 1.

• A negative exponent means to take the reciprocal of what would be the result as if the negative weren’t there: 2⁻² = .

• A fractional exponent has two parts (like any other fraction), the numerator, which is the power the base is raised to, and the denominator, which is the root of the base. For example, 8^2/3 = = 4.

Remember that in calculating the value of a root, you’re looking for what number multiplied by itself results in the number under the radical. In the above example, 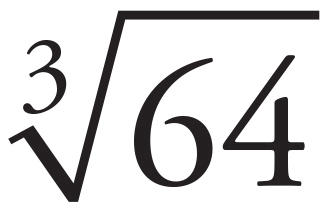= 4 because 4 × 4 × 4 = 64.

When you see the square root sign, that means to take the positive root only. So, 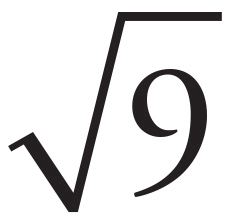= 3, but not –3.

Square roots work just like exponents: You can always multiply and divide roots, but you can add and subtract only with the same root.

Multiplication and Division:

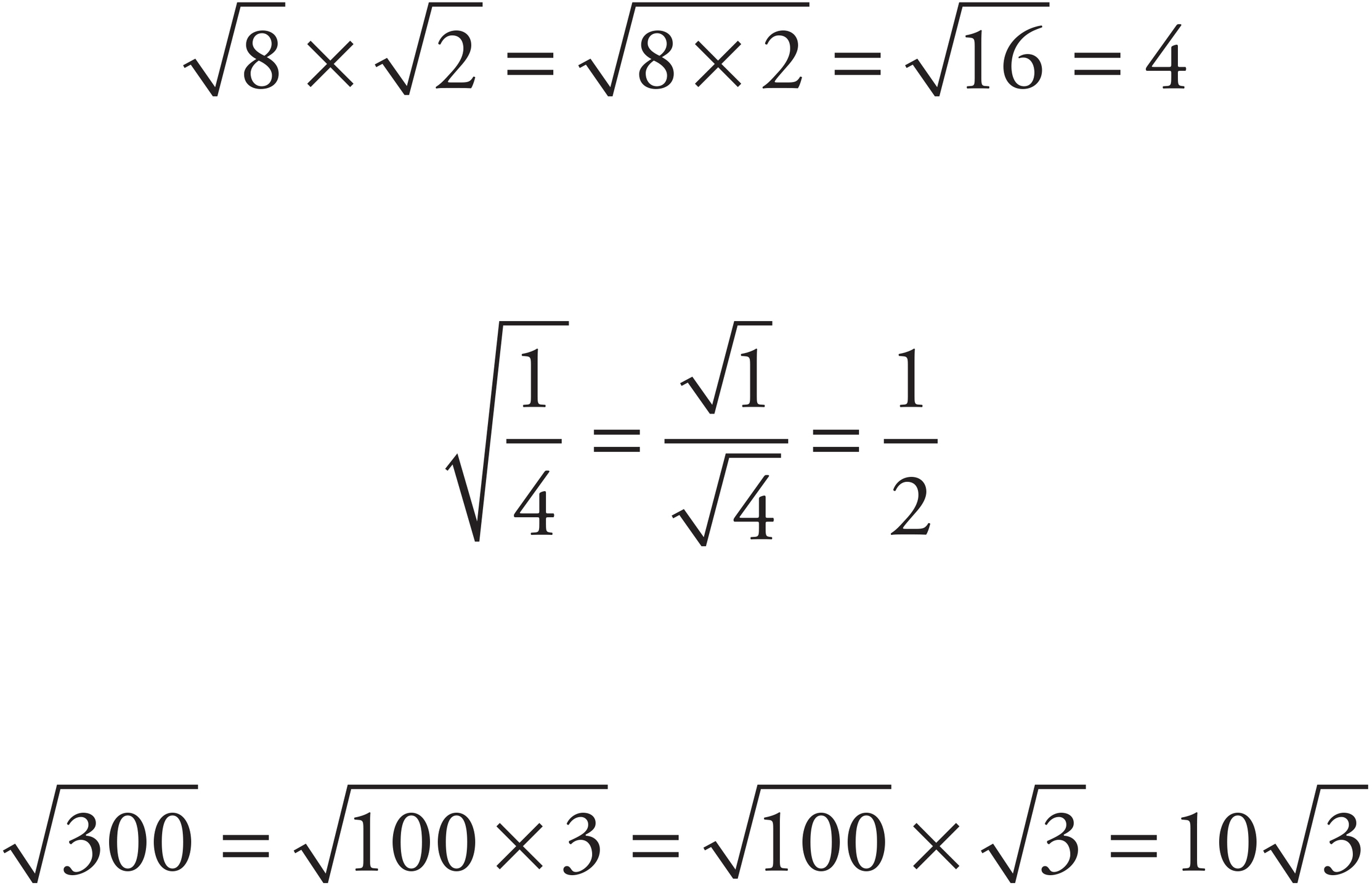
Addition and Subtraction:

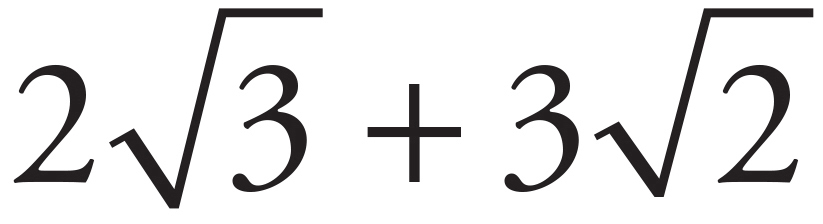 Cannot be added without a calculator since the terms do not have the same root.

Drill 2

Answers can be found in Part III.

a. 3³ × 3² =

b. =

c.(3³)² =

d. x⁶ × x² =

e. =

f. (x⁶)² =

g. =

h. =

i. =

j. =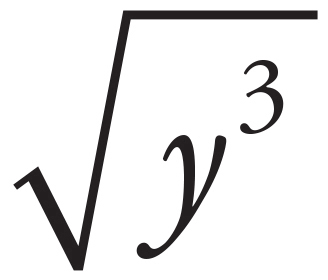

k. =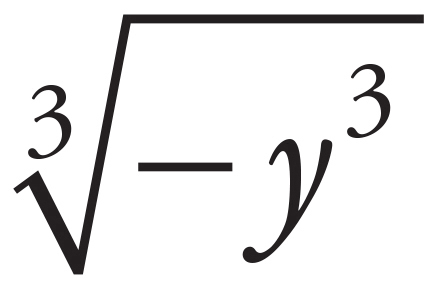

l. =

3. If 3⁴ = 9^x, what is the value of x ?

A) 2

B) 3

C) 4

D) 5

6. In the equation above, what is a possible value of m ?

A) 3

B) 4

C) 5

D) 6

5. If (3^x)³ = 3¹⁵, what is the value of x ?

A) 3

B) 5

C) 7

D) 9

8. If x^yx⁶ = x⁵⁴ and (x³)^z = x⁹, what is the value of y + z ?

A) 11

B) 12

C) 48

D) 51

7. If − 3 = 9, which of the following is a possible value of s ?

A)   12

B)   36

C)   81

D) 144

8. Which of the following is equivalent to the expression x⁶y⁻³z ?

A)

B)

C)

D)

9. Which of the following expressions is equivalent to ?

A)

B) 3b³c

C)

D) 20.25b³c

9. The function f(x) = k^0.3x, where k is a constant, can also be expressed as f(x) = for what value of B ?

A)   2.7

B)   9.3

C) 27

D) 30

10. If = 8x, which of the following could be the value of x ?

A) 2

B) 4

C) 6

D) 8

11. Which of the following expressions is equivalent to ?

A)

B)

C)

D) 3m⁴n⁻⁶

16. Which of the following values of b makes the equation above true?

A)   4

B)   6

C)   8

D) 12

23. Which of the following shows the expression in the form of A · (B)^y ?

A)

B)

C)

D)

EQUATIONS AND INEQUALITIES

An equation is a statement that contains an equals sign, such as 3x + 5 = 17.

To solve an equation, you must get the variable x alone on one side of the equals sign and everything else on the other side.

The first step is to put all of the variables on one side of the equation and all of the numbers on the other side, using addition and subtraction. As long as you perform the same operation on both sides of the equals sign, you aren’t changing the value of the variable.

Then you can divide both sides of the equation by the coefficient, which is the number in front of the variable. If that number is a fraction, you can multiply everything by its reciprocal.

For example:

Always remember the rule of equations:

Whatever you do to one side of the equation, you must also do to the other side.

The example above was fairly simple. The PSAT may test this idea with more complex equations and formulas, though. Just keep trying to isolate the variable in question by undoing the operations that have been done to it. Here’s an example.

14. Logging companies can use Doyle’s Log Rule to estimate the amount of usable lumber, in board feet B, that can be milled from logs. The rule is defined as B = , where d is the diameter inside the bark measured in inches at the small end of the log and L is the log length measured in feet. Which of the following gives the value of d, in terms of B and L ?

A)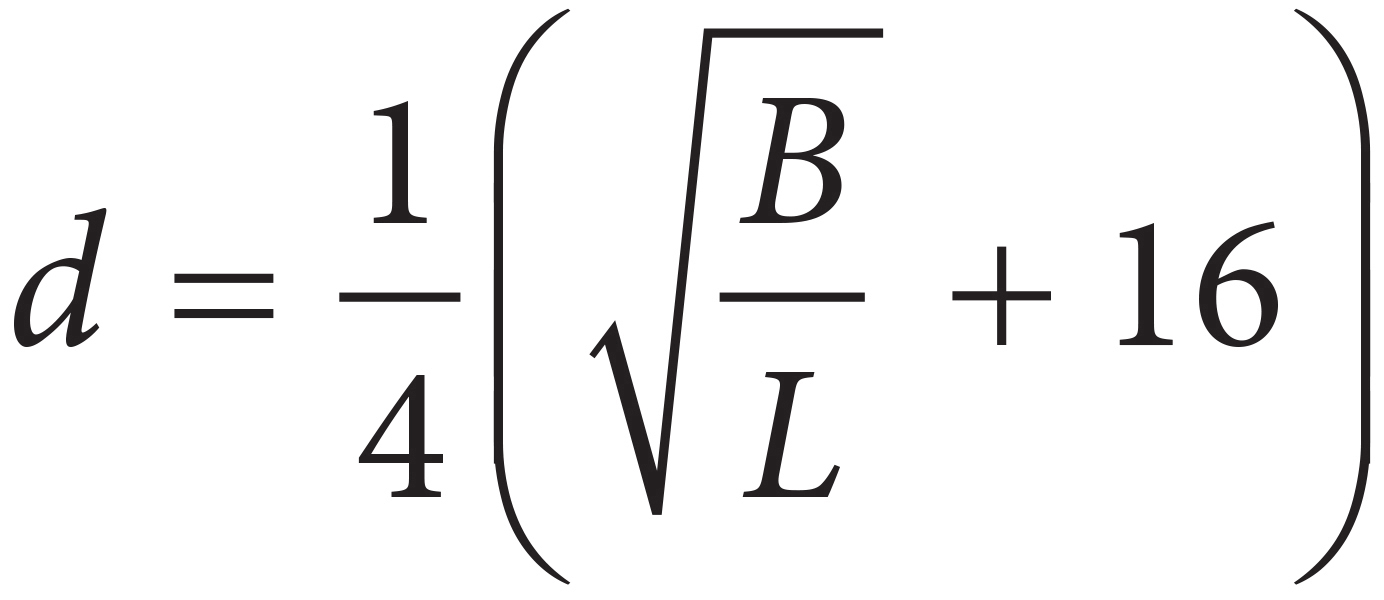

B)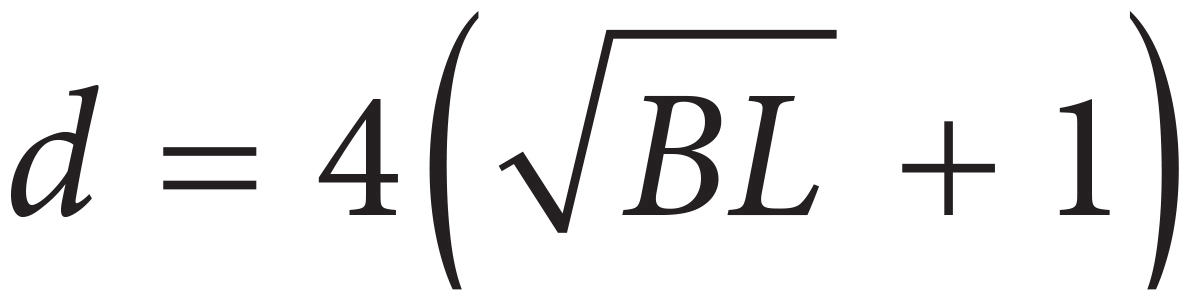

C)

D)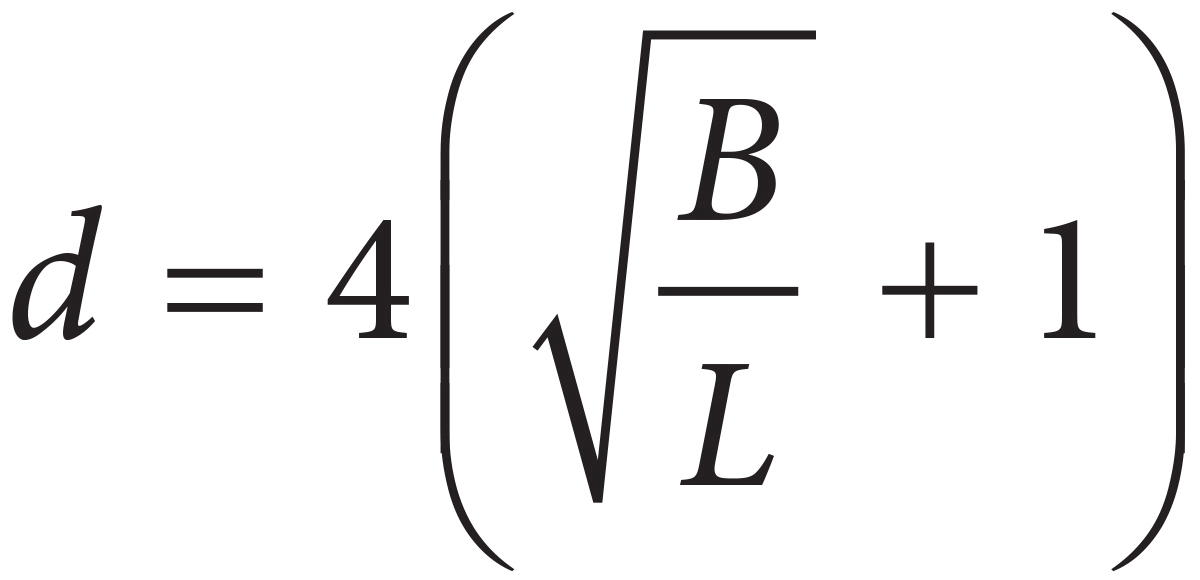

Here’s How to Crack It

Start with the L on the outside of the parentheses on the right. Divide both sides by L to get . Now undo the power of 2 outside the parentheses. Take the square root of both sides of the equation to get . Multiply both sides by 4 to get = d − 4. Add 4 to both sides to get + 4 = d. Factor out the 4 to get 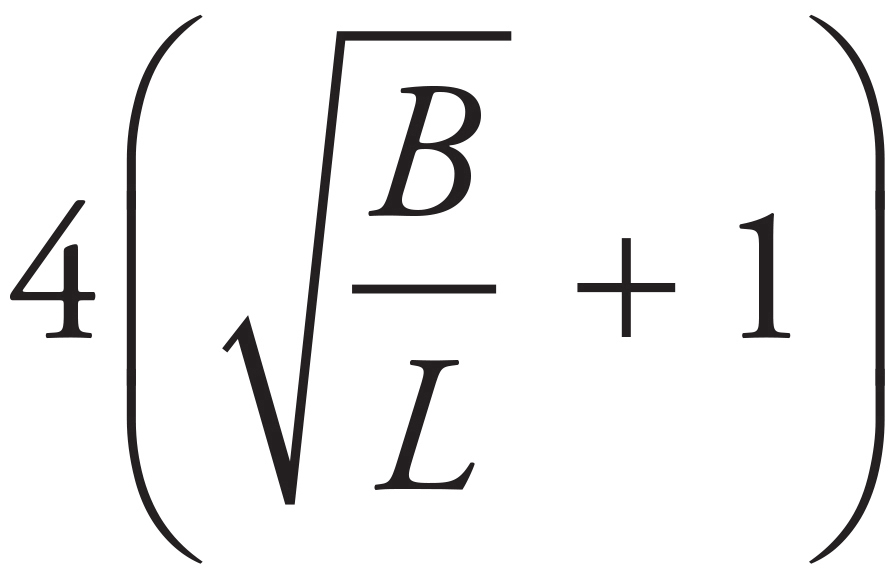= d. The correct answer is (D).

An inequality is any statement with one of these signs:

< (less than)

> (greater than)

≤ (less than or equal to)

≥ (greater than or equal to)

You can solve inequalities in the same way you solve equations, with one exception: whenever you multiply or divide an inequality by a negative value, you must change the direction of the sign: < becomes >, and ≤ becomes ≥.

For example:

In this case, we didn’t multiply or divide by a negative value, so the direction of the sign didn’t change. However, if we were to divide by a negative value, we would need to change the direction of the sign.

Now let’s look at how the PSAT may make things more complicated with a question about a range of values.

6. Which of the following is equivalent to −12 ≤ 3b + 3 ≤ 18 ?

A) −5 ≤ b ≤ 5

B) −5 ≤ b ≤ 6

C) −4 ≤ b ≤ 6

D)   3 ≤ b ≤ 5

Here’s How to Crack It

Like many problems on the PSAT, this question will be difficult if you try to do it all at once. Instead, break it down into Bite-Sized Pieces. Start with just part of the inequality, −12 ≤ 3b + 3. Remember that you can solve inequalities just like equations—provided that if you multiply or divide by a negative value, you swap the direction of the inequality sign. To solve this part of the inequality, though, you just need to subtract 3 from each side (giving you −15 ≤ 3b) and then divide each side by 3, which leaves you with −5 ≤ b. Now you can eliminate any choices that you know won’t work: (C) and (D) don’t have −5 in them. Now take the other part of the inequality: 3b + 3 ≤ 18. If you subtract 3 from each side and then divide by 3, you get b ≤ 5. Now you can cross off (B), and you’re left with (A).

SOLVING RATIONAL EQUATIONS

Since you are not always allowed to use your calculator on the PSAT, there will be some instances in which you will need to solve an equation algebraically. Even on the sections in which calculator use is permitted, you may find it faster and more effective to use your mathematical skills to efficiently answer a question. Another way ETS and the College Board may make your calculator less effective is by asking you to solve for an expression. A lot of the time, algebraic manipulation will be the means by which you can solve that problem.

Here is an example:

5. Which of the following is equivalent to ?

A)

B)

C)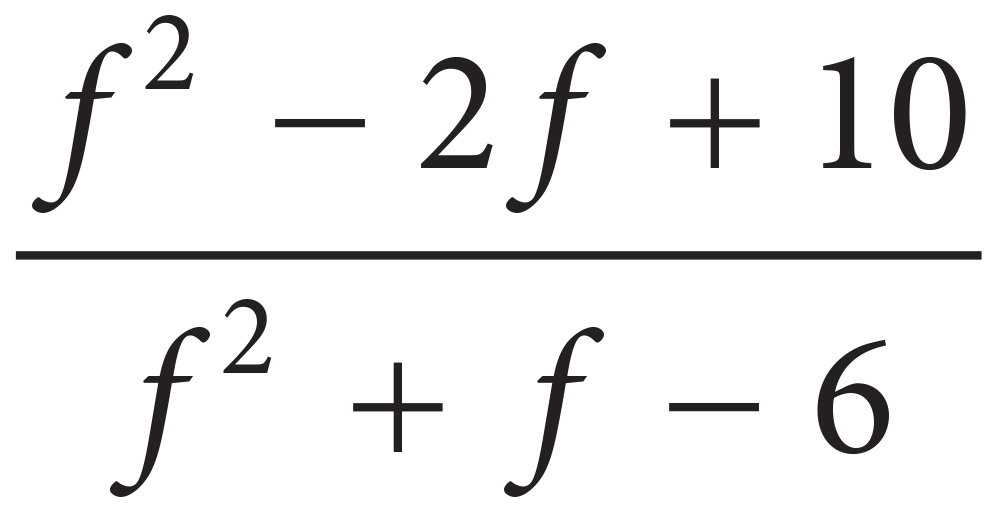

D)

Here’s How to Crack It

In order to be able to add these fractions, you need a common denominator. Multiply both the top and the bottom of the left fraction by (f + 3) and multiply both the top and bottom of the right fraction by (f − 2). The expression becomes − or . Now the numerators can be combined over the common denominator and you get = 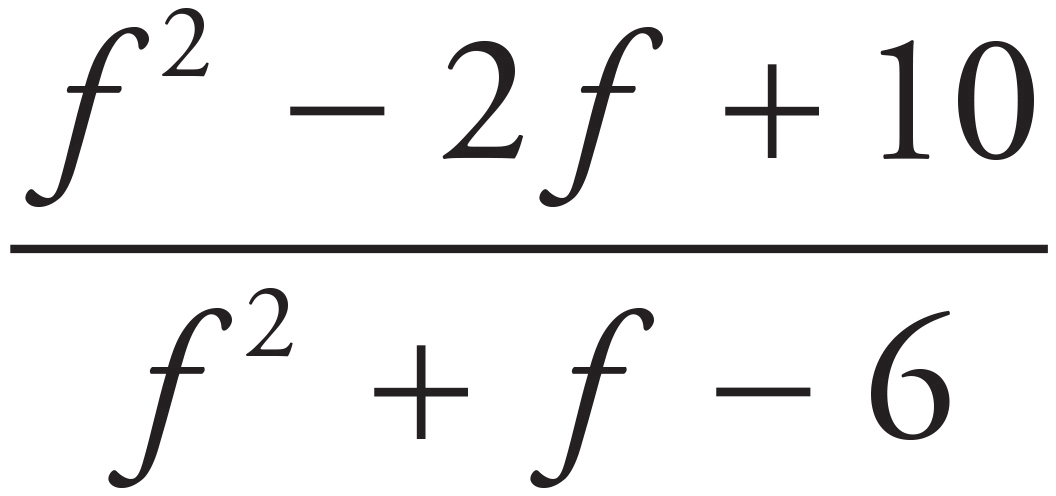, which is (C).

EXTRANEOUS SOLUTIONS

Sometimes solving a rational or radical expression makes funny things happen. Let’s look at an example.

Given the equation above, what is the value of z?

To add the fractions on the left side, you need a common denominator. Multiply the numerator and the denominator of the first fraction by (z − 2) and the numerator and denominator of the second fraction by (z + 2). Now the fractions can be added together.

The equation becomes

Since the denominators are equal, the numerators are equal. This gives you

(z − 2) + (z + 2) = 4

When you simplify the left side, you get 2z = 4, so z = 2. Sounds great, right? However, you need to plug this solution back into the original equation to make sure that it works. You get

Once simplified, two of the three denominators become zero. That is not allowed, so the solution you found isn’t really a solution at all. It is referred to as an “extraneous solution.” That term refers to any answer you get to an algebraic equation that results in a false statement when plugged back in to the original equation.

Here’s how it might look on the PSAT.

Extra Answers

Any time you are solving for a variable, make sure your solutions actually work. If they do not, they are “extraneous,” or extra.

3. Which of the following is a true statement about the equation above?

A) There are no solutions to the equation.

B) The solution is p = 2.

C) The solution is p = 3.

D) There are infinitely many solutions to the equation.

Here’s How to Crack It

When given two fraction sets equal to one another, you often have to cross-multiply to solve. In this case, though, the fractions have the same denominator. This tells you that their numerators are equal. Therefore, 3p = 6, so p = 2, right? But what if you put that value back into the denominators? They become 0, which can’t happen. Therefore, 2 is an extraneous solution and the answer is (A).

An answer like (D) would occur if literally any value for a variable would make the equation true, such as would be the case in x + 3 = x + 3.

ABSOLUTE VALUES

Absolute value is just a measure of the distance between a number and 0. Since distances are always positive, the absolute value of a number is also always positive. The absolute value of a number is written as |x|.

PSAT Smoke and Mirrors

When you’re asked to solve an equation involving an absolute value, it is very likely that the correct answer will be the negative result. Why? Because the test writers know that you are less likely to think about the negative result! Another way to avoid mistakes is to do all the math inside the absolute value symbols first, and then make the result positive.

When solving for the value of a variable inside the absolute value bars, it is important to remember that variable could be either positive or negative. For example, if |x| = 2, then x = 2 or x = −2 since both 2 and −2 are a distance of 2 from 0.

Here’s an example:

|x + 3| = 6

|y − 2| = 7

9. For the equations shown above, which of the following is a possible value of x − y ?

A) −14

B)   −4

C)   −2

D)   14

Here’s How to Crack It

To solve the first equation, set x + 3 = 6 and set x + 3 = −6. If x + 3 = −6, then the absolute value would still be 6. So, x can be either 3 or −9. Now, do the same thing to solve for y. Either y = 9 or y = −5.

To get the credited answer, you need to try the different combinations. One combination is x = −9 and y = −5. So, x − y = −9 − (−5) = −4, which is (B).

SIMULTANEOUS EQUATIONS

Simultaneous equations occur when you have two equations at the same time. Occasionally, all you have to do is stack the equations, and then add or subtract them, so try that first. Sometimes, it won’t get you exactly what you want, but it will get you close to it.

  x + 2y = 12

2x + y   = 9  

6. Given the system of equations above, what is the value of x + y ?

A)   3

B)   7

C)

D) 21

Here’s How to Crack It

This question involves simultaneous equations, so first try to stack and combine them. You’re being asked for x + y, so even getting the same number of x variables as y variables would be useful.

Let’s see what happens when you add the equations:

Now all you need to do is divide both sides of the equation by 3 to get the expression you’re being asked for, x + y, and you end up with the answer, 7. The correct answer is (B).

That was pretty simple, but simultaneous equations on the PSAT are rarely that straightforward. Let’s look at a really challenging one.

27. Two competing fast food restaurants sell both hamburgers and orders of French fries at the same prices. Burger Planet’s lunchtime sales can be modeled as 40h + 70f = $260.00, where h is the cost of a hamburger and f is the cost of an order of French fries. If Slider Heaven sells 80 hamburgers and 60 orders of French fries over the same period and outsells Burger Planet by $100, what is the total cost of three hamburgers and three orders of French fries at either establishment?

A)   $5.00

B)   $9.00

C) $11.00

D) $15.00

Here’s How to Crack It

The sales equation at Burger Planet is given in the question. Create an equation for Slider Heaven’s lunchtime sales so you can solve them. Slider Heaven’s sales can be modeled as 80h + 60f = 260 + 100 = 360. Adding these equations together or subtracting one from the other won’t give you the 3 burgers and 3 fries that you want. Instead, you need to create a common coefficient for one of the variables and then add or subtract the two equations from each other to get rid of that variable. In this case, multiply the Burger Planet equation by −2 to get −80h − 140f = −520. Place the two equations on top of each other and add:

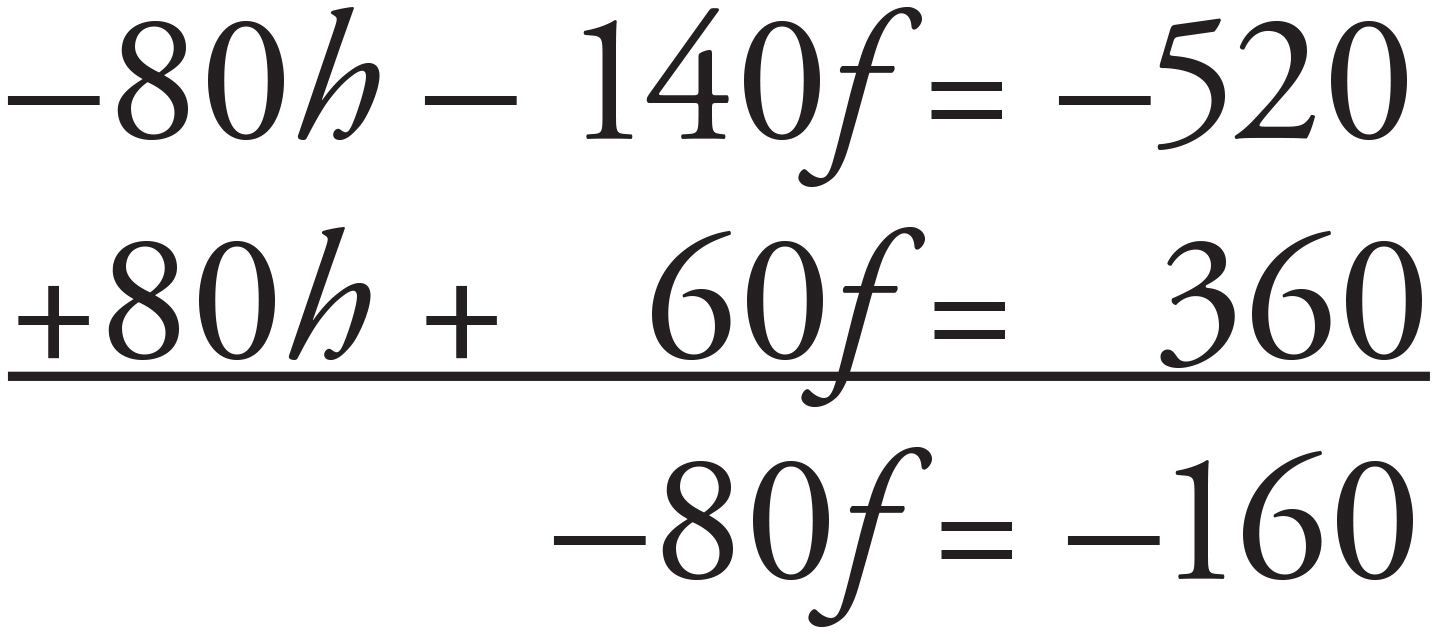
Divide both sides by −80 to get f = 2. Plug 2 into the Burger Planet equation to get 40h + 70(2) = 260. Solve for h to get 40h + 140 = 260, or 40h = 120, so h = 3. Therefore, the total cost of 3 hamburgers and 3 orders of French fries is 3(3) + 3(2) = 9 + 6 = 15. The correct answer is (D).

WRITING YOUR OWN EQUATIONS

For the most part, we’ve been looking at solving equations given to you in questions. That last question, though, required you to create one of your own. The PSAT Math sections are testing not only your math skills, but also, and possibly even more important to your score improvement, your reading skills. It is imperative that you read the questions carefully and translate the words in the problem into mathematical symbols.

ENGLISH	MATH EQUIVALENTS
is, are, were, did, does, costs	=
what (or any unknown value)	any variable (x, y, k, b)
more, sum	+
less, difference	−
of, times, product	× (multiply)
ratio, quotient, out of, per	÷ (divide)

Sometimes you’ll be asked to take a word problem and create equations or inequalities from that information. Usually they will not ask you to solve these equations/inequalities, so if you are able to locate and translate the information in the problem, you have a good shot at getting the correct answer. Always start with the most straightforward piece of information. What is the most straightforward piece of information? Well, that’s up to you to decide. Consider the following problem.

3. Elom joined a gym that charges a monthly fee of $35. A one-time enrollment fee of $40 is charged when he joins. Which of the following represents the total amount of fees that Elom has paid to his gym after m months, in dollars?

A) 35m + 40

B) 35 + 40m

C) 35m − 40

D) (35 + 40)m

Here’s How to Crack It

The question states that there is a monthly fee of $35 and that the variable m represents the number of months. Therefore, the correct answer should include 35m, so you can eliminate (B). The one-time enrollment fee of $40 has nothing to do with the number of months, so the 40 should be by itself. Eliminate (D), which multiplies the 40 by m. The fee should be added on, so the correct answer is (A).

Now let’s look at harder one. The following question has a lot more words and more than one inequality in each answer choice. This makes it even more important to translate one piece at a time and eliminate after each step.

5. Kai has two different after-school jobs, one at a bookstore and one at a grocery store. He can only work a total of 10 hours each week due to his heavy homework load. When he works at the bookstore, he earns $10 per hour, and when he works at the grocery store, he earns $13 per hour. He never earns less than $100 in a week, and he always works more hours at the bookstore because he can get free coffee from the café. Solving which of the following systems of inequalities yields the number of hours at the bookstore, b, and the number of hours at the grocery store, g, that Kai can work in one week?

A)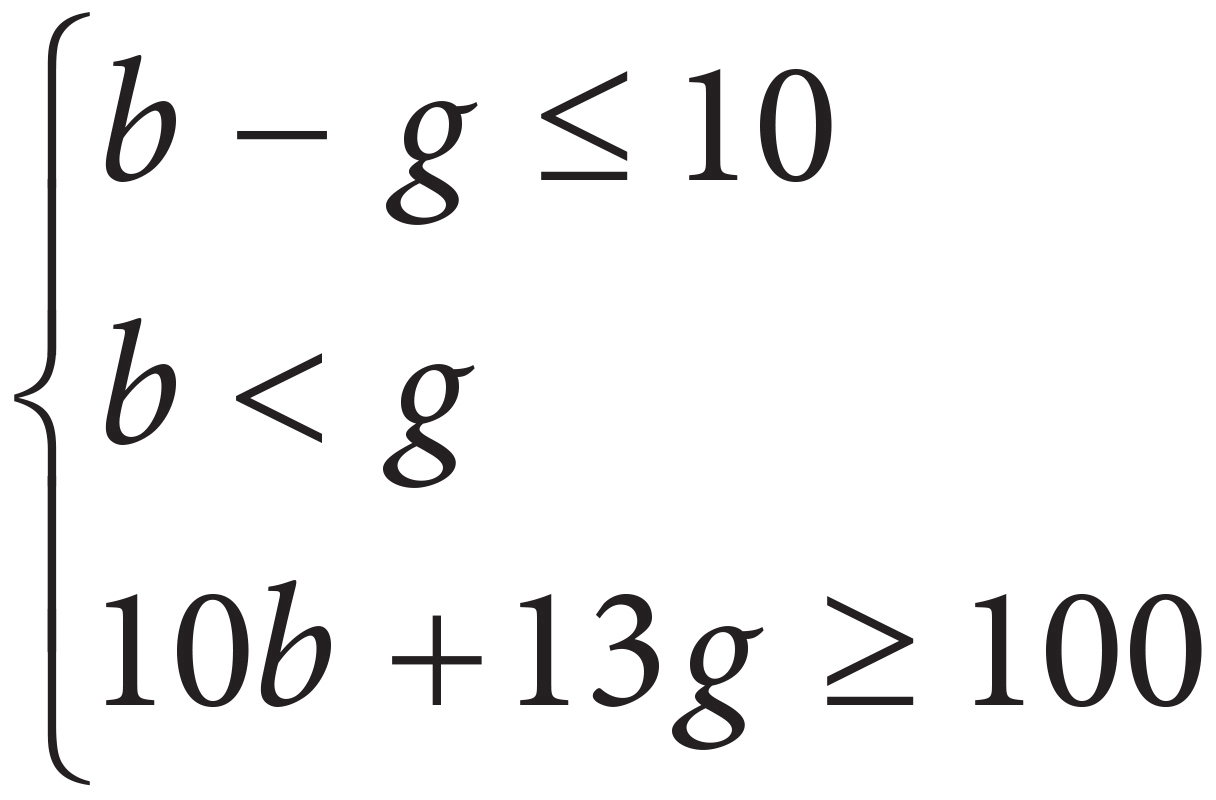

B)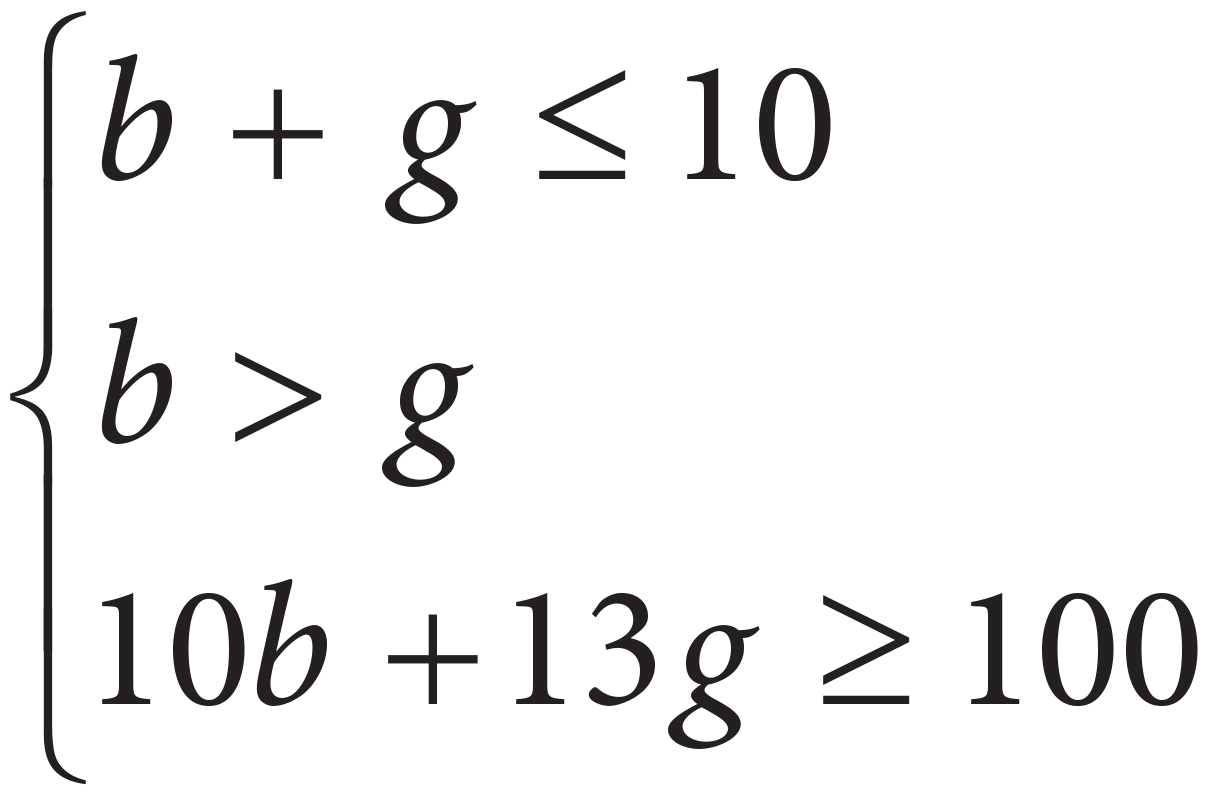

C)

D)

Here’s How to Crack It

Start with a straightforward piece of information to translate. If you start with the fact that Kai works more hours at the bookstore than at the grocery store, you can translate that into b > g. This would eliminate (A). If you start with the fact that Kai works no more than 10 hours each week, you can translate that into b + g ≤ 10. This would eliminate (D). Now, to decide between (B) and (C), compare the answers and see what the differences are. Choice (B) has a coefficient of 10 in front of the variable b. Check the question to see if 10 should be associated with b. Since b is the number of hours Kai works at the bookstore, and he earns $10 per hour there, the correct answer should have 10b, not 13b. Eliminate (C) and choose (B).

Drill 3

Answers can be found in Part III.

3. If a certain number is 3 more than 7 times itself, what is the number?

A) −3

B) −

C) −

D) −

2. If , then which of the following represents an equivalent equation for y, in terms of x ?

A)

B)

C)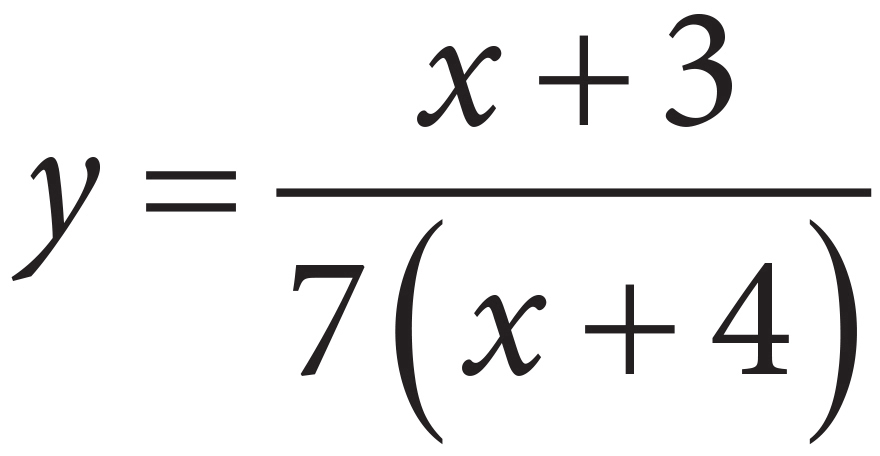

D)

5. Ann is writing a book that will include up to 98 recipes. She currently has 32 main dish recipes and 18 dessert recipes. If r represents the number of additional recipes that Ann could include in her book, which of the following inequalities represents all possible values of r ?

A) r − 50 ≥ 98

B) r − 50 ≤ 98

C) 98 − (32 + 18) − r ≤ 0

D) 98 − (32 + 18) − r ≥ 0

4. If , then which of the following is equal to bc ?

A)

B)

C)

D) 18ad

28. A fitness tracking watch collects data on how many miles a user walks per day. The data is collected from 12:00 A.M. each morning until 12:00 A.M. the following day, and resets each day at midnight. After one month of use, Debbie reviews her data in the fitness tracker. She discovers that her average daily miles walked are equal to one-hundredth of the square of the number of hours in one day. How many miles does Debbie walk in one day, on average, rounded to the nearest mile?

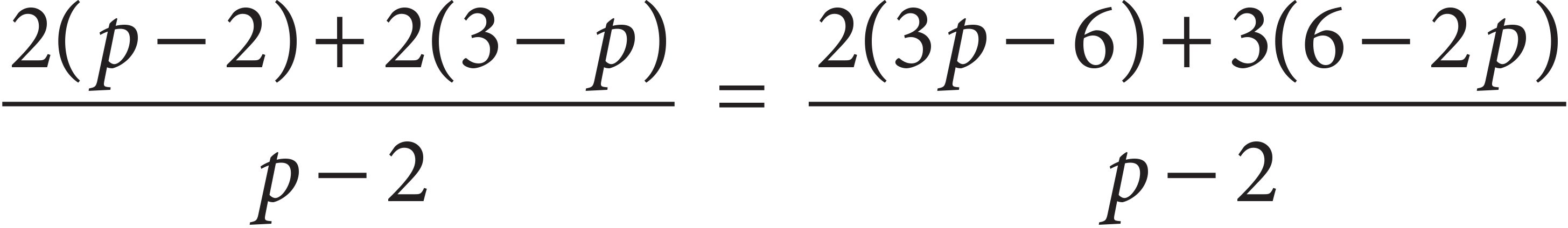
7. Which of the following is a true statement about the equation above?

A) There are no solutions to the equation.

B) The solution is p = 2.

C) The solution is p = 3.

D) There are infinitely many solutions to the equation.

8. A ski resort is renting skis for $30 and snowboards for $20 over a weekend. On Friday, 40 skis and snowboards were rented, and the resort collected $1,100 in rental fees. On Saturday, 55 skis and snowboards were rented and the resort collected $1,400 in rental fees. On Sunday, the resort rented 85 skis and snowboards and collected $2,100 rental fees. Solving which of the following system of equations yields the number of skis, s, and the number of snowboards, b, that were rented over the three-day weekend?

A) s + b = 50
30s + 20b = 180

B) s + b = 180
30s + 20b = 460

C) s + b = 180
30s + 20b = 4,600

D) s + b = 4,600
30s + 20b = 180

12. In the equation above, what is the value of m ?

A) −17

B) −12

C)     5

D)   10

−4(h + 5) = −3(2 − h) + 14

9. In the equation above, what is the value of h ?

A) −18

B)   −4

C)   

D) 18

23. A group of students sells different types of cookies at a bake sale to raise funds for a school trip. When the students sell two snickerdoodle cookies, s, and seven cinnamon cookies, c, they raise $14.00. When the students sell eight snickerdoodle cookies and three cinnamon cookies, they raise $17.50. Assuming the price per cookie does not change, which of the following equations represents a sale the students could make during the fundraiser?

A) 2s + 3c = $8.00

B) 4s + 6c = $16.25

C) 6s + 5c = $17.36

D) 8s + 7c = $24.50

10(3x + a) − a(4x + 2) = 2a(x + 4)

13. If the equation above has infinitely many solutions for x, what is the value of a ?

A) 5

B) 4

C) 3

D) 1

25. Laura has a recipe for cake that calls for both eggs and cups of flour. Laura can purchase five eggs and four cups of flour for $5.50 and nine eggs and eight cups of flour for $10.50. Based on these costs, what is the cost of the ten eggs that Laura will need for her recipe?

A)   $5.00

B)   $5.50

C)   $7.50

D) $10.50

THE COORDINATE PLANE

You will definitely see some questions in the coordinate plane, or xy-plane, on the PSAT. Let’s start by covering the basics here. You’ll see more advanced concepts in the Advanced Math Principles chapter. So let’s just review:

The x-axis is the horizontal axis, and the y-axis is the vertical axis. Points are given on the coordinate plane with the x-coordinate first. Positive x-values go to the right, and negative ones go to the left; positive y-values go up, and negative ones go down. So point A (3, 1) is 3 points to the right on the x-axis and 1 point up from the y-axis. Point B (2, −1) is 2 points to the right on the x-axis and 1 point down from the y-axis.

Slope is a measure of the steepness of a line on the coordinate plane. On most slope problems, you need to recognize only whether the slope is positive, negative, or zero. A line that goes up and to the right has positive slope; a line that goes down and to the right has negative slope, and a flat line has zero slope. In the figure below, ℓ₁ has positive slope, ℓ₂ has zero slope, and ℓ₃ has negative slope.

If you do need to calculate the slope, and the graph is drawn for you, here’s how: slope = . The slope of a line is equal to . To find the slope, take any two points on the line and count off the distance you need to get from one of these points to the other.

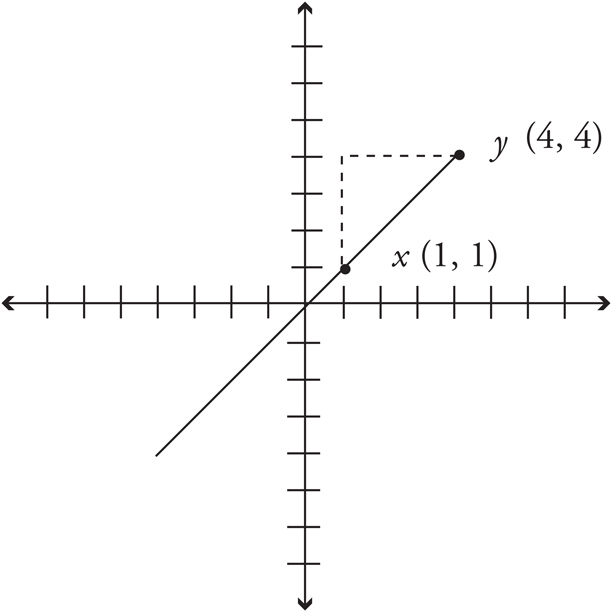
In the graph above, to get from point x to point y, we count up (rise) 3 units, and count over (run) 3 units. Therefore, the slope is = 1. Always remember to check whether the slope is positive or negative when you use = .

If you’re not given a figure and you can’t draw one easily using the points given, you can find the slope by plugging the coordinates you know into the slope formula. Just remember to plug the numbers into the formula carefully!

Knowing how to find the slope is useful for solving questions about perpendicular and parallel lines. Perpendicular lines have slopes that are negative reciprocals of one another. Parallel lines have the same slope and no solutions. You may also be given two equations that have infinitely many solutions.

Take a look at an example.

gx − hy = 78

4x + 3y = 13

20. In the system of equations above, g and h are constants. If the system has infinitely many solutions, what is the value of gh ?

A) −432

B)   −6

C)     6

D) 432

To Infinity…and Beyond!

When given two equations with infinitely many solutions, find a way to make them equal. The equations represent the same line.

Here’s How to Crack It

This question may have you scratching your head and moving on to the next question, but let’s explore what you can do to solve this before you decide it’s not worth your time. You may be surprised by how easy it is to solve a problem like this.

When they say that these equations have infinitely many solutions, what they are really saying is that these are the same equation, or that one equation is a multiple of the other equation. In other words, these two equations represent the same line. With that in mind, try to determine what needs to be done to make these equations equal. Since the right side of the equation is dealing with only a constant, first determine what you would need to do to make 13 equal to 78.

In this case, you need to multiply 13 by 6. Since we are working with equations, we need to do the same thing to both sides of the equation in order for the equation to remain equal.

6(4x + 3y) = 6 × 13

24x + 18y = 78      

Since both equations are now equal to 78, you can set them equal to one another, giving you this equation:

24x + 18y = gx − hy

You may know that when you have equations with the same variables on each side the coefficients on those variables must be equal, so you can deduce that g = 24 and h = −18. (Be cautious when you evaluate this equation. The test writers are being sneaky by using addition in one equation and subtraction in another.) Therefore, gh equals 24 × −18 = −432. Choice (A) is correct.

The equation of a line can take multiple forms. The most common of these is known as the slope-intercept form. If you know the slope and the y-intercept, you can create the equation of a given line. A slope-intercept equation takes the form y = mx + b, where m is the slope and b is the y-intercept.

Here’s an example.

5. If c is a constant less than 0, which of the following could be the graph of y = c(x + y) in the xy-plane?

A)

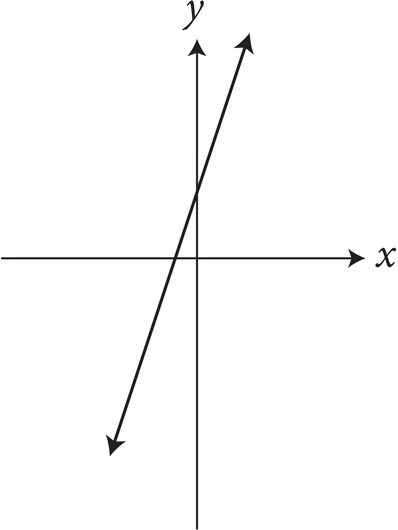
B)

C)

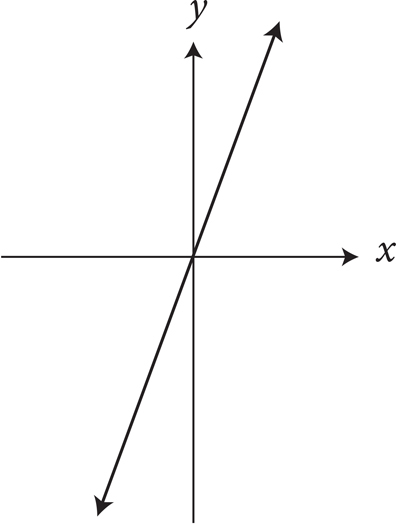
D)

Here’s How to Crack It

No points are labeled on the graphs in the answers, and the equation of the line has a mysterious c in it. If you knew the slope or y-intercept of the equation, you could use Process of Elimination. To see what is going on with this problem, make up a value for c that is less than 0. Let’s say that c = −2, in which case y = −2(x + y). Distribute the −2 to get y = −2x − 2y. Rewrite the equation so that it is in the slope-intercept form y = mx + b, to get 3y = −2x or y = −x. Therefore, the slope is − and the y-intercept is 0. In fact, no matter what value you picked for c, if c is a constant less than 0, the slope will be negative, and the y-intercept will be 0. Eliminate (A) and (C) since both of these lines have positive slopes. Eliminate answer (B) because the y-intercept is not 0. The correct answer is (D).

The distance formula looks quite complicated. The easiest way to solve the distance between two points is to connect them and form a triangle. Then use the Pythagorean Theorem. Many times, the triangle formed is one of the common Pythagorean triplets (3-4-5 or 5-12-13). We’ll talk more about the Pythagorean Theorem in the Additional Math Topics chapter.

The midpoint formula gives the midpoint of a line segment on the coordinate plane. For example, the line ST has points S (x₁, y₁) and T (x₂, y₂). To find the midpoint of this line segment, simply find the average of the x-coordinates and the y-coordinates. In our example, the midpoint would be .

To find the point of intersection of two lines, find a way to set them equal and solve for the variable. If the equations are already in y = mx + b form, set the mx + b part of the two equations equal and solve for x. If the question asks for the value of y, plug the value of x back into either equation to solve for y. It may also be possible to Plug In the Answers (see Chapter 10 for more on this) or graph the equations on your calculator. These skills will also help find the points of intersection between a line and a non-linear graph such as a parabola.

Sometimes, it’s a little trickier. Let’s look at a difficult question that combines several of the previous concepts.

24. Line 1 contains the points (2, 1) and (1, −2), and line 2 contains the points (−2, 9) and (10, −3). What is the y-coordinate of the point of intersection of lines 1 and 2 ?

A) −1

B)   3

C)   4

D)   7

Here’s How to Crack It

To solve this problem, first you need to find the equations of the two lines in order to set the equations equal to each other and find the value of x. Given two points on a line, you can find the slope using . Therefore, the slope of line 1 can be calculated as 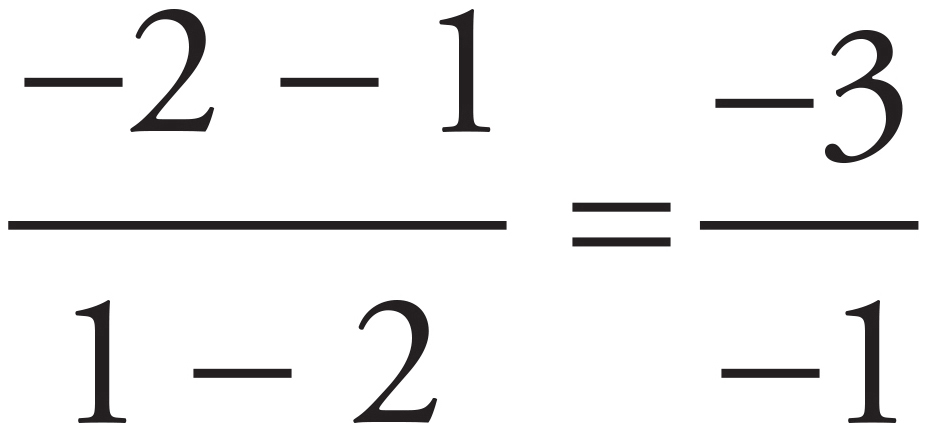= 3. Plug this and the coordinates of the easier point, (2, 1), into y = mx + b to find the value of b. The equation for line 1 becomes 1 = 3(2) + b. Solve for b to find that the value is −5, so line 1 is y = 3x − 5. The slope of line 2 can be calculated as = −1. Find the value of b: 9 = −1(−2) + b, so b = 7. The equation for line 2 is y = −x + 7. Set the two equations equal to each other to get 3x − 5 = −x + 7. Solve for x to get 4x − 5 = 7 or 4x = 12, so x = 3. Finally, plug x into one of the equations to solve for y. Plug x into the equation y = −x + 7, to get y = −3 + 7 = 4. Therefore, the correct answer is 4, which is (C).

Drill 4

Answers can be found in Part III.

a. How many units do you count up (rise) to get from point B to point A?

b. How many units must you count over (run) to get from point A to point B?

c. What is the slope of the line above?

(Remember, the line is going down to the right, so it must have a negative slope.)

d. What would be the slope of a line parallel to AB?

e. What would be the slope of a line perpendicular to AB?

f. What is the distance from point A to point B?

g. What is the midpoint of line segment AB?

2. If y = 6x + 3 and y = cx + 3 are the equations of perpendicular lines, then what is the value of c ?

A) −6

B) −

C)   

D)   6

6. Line l is shown in the graph above. If line m is parallel to line l, which of the following could be the equation of line m ?

A) y = −3x − 1

B) y = −x + 2

C) y = x − 3

D) y = 3x + 2

3. What is the y-intercept of the line with equation 2x + 3y = 12 ?

A) 4

B) 3

C) 2

D)

12. What is the x-intercept of the line in the graph above?

A) −1

B)   0

C)   1

D)   2

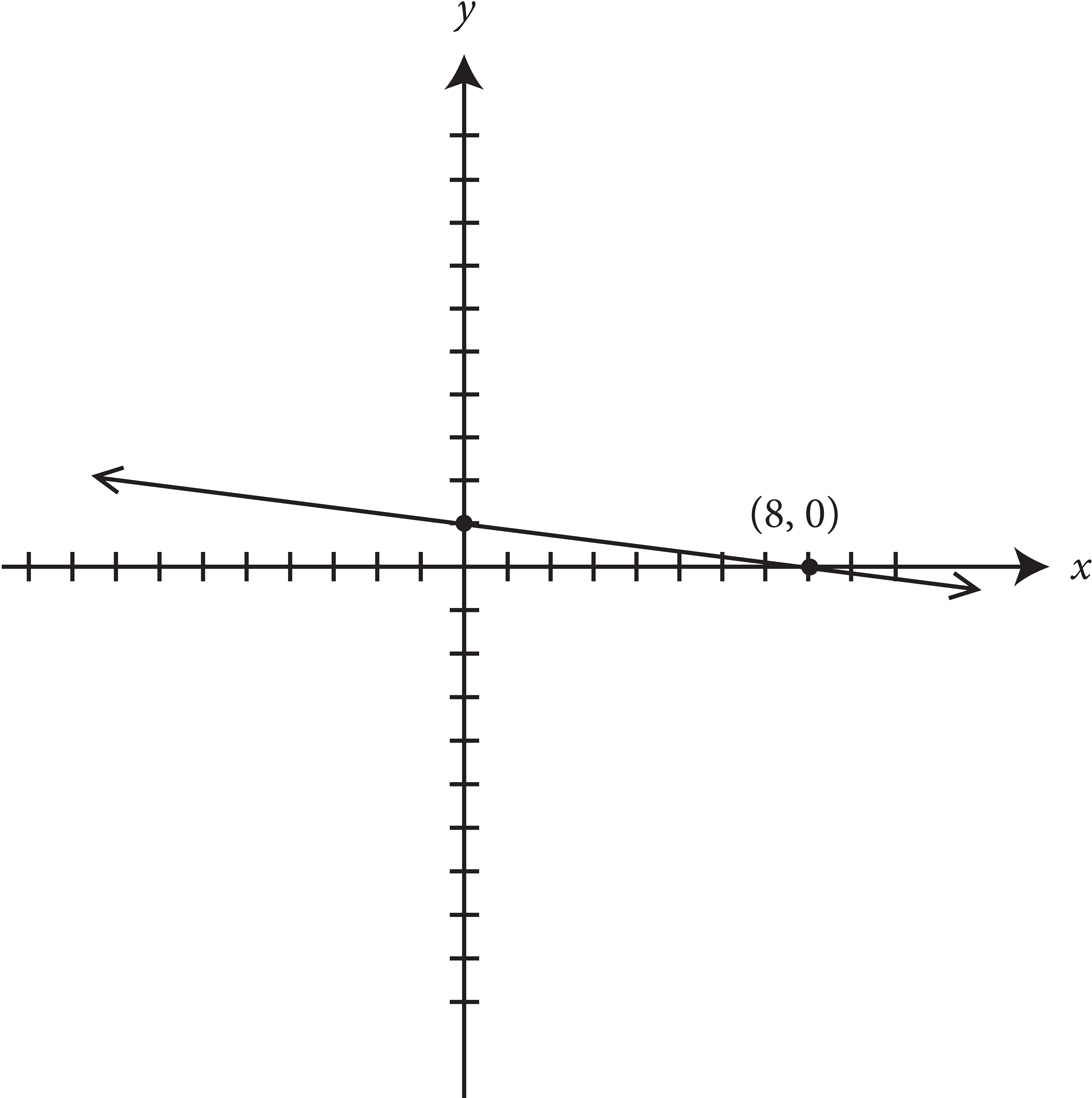
7. Which of the following could be the equation of the line in the graph above?

A) 2y − x = −8

B) 4y + x = −8

C) 8y − 3x = 8

D) 8y + x = 8

14. Which of the following is the slope of the line in the graph above?

A) −

B) −

C) −

D) −

15. The graph of a line is shown in the xy-plane above. It contains the points (3a, a) and , where a is a positive constant. Which of the following could be the equation of this line?

A) y = x − 2

B) y = x + 2

C) y = x − 2

D) y = x − 2

17. The equations above intersect at two points. What is the product of the y-coordinates of the two points of intersection?

CHARTS AND GRAPHS

Another basic math skill you will need for the PSAT is the ability to read charts and graphs. The PSAT now includes charts, graphs, and tables throughout the test (not just in the Math sections) to present data for students to analyze. The test writers believe this will better reflect what students learn in school and need to understand in the real world. The situations will typically include real-life applications, such as finance and business situations, social science issues, and science.

Since you’ll be seeing graphics throughout the test, let’s look at the types you may encounter and the skills you’ll need to be familiar with when you work with charts and graphs.

The Scatterplot

A scatterplot is a graph with distinct data points, each representing one piece of information. On the scatterplot below, each dot represents the number of televisions sold at a certain price point.

Here’s How to Read It

To find the cost of a television when 225 televisions are sold, start at 225 on the vertical axis and draw a horizontal line to the right until you hit a data point. Use the edge of your answer sheet as a straightedge if you have trouble drawing your own straight lines. Once you hit a point, draw a straight line down from it to the horizontal axis and read the number the line hits, which should be $1,500. To determine the number of televisions sold when they cost a certain amount, reverse the steps—start at the bottom, draw up until you hit a point, and then move left until you intersect the vertical axis.

A question may ask you to draw a “line of best fit” on a scatterplot diagram. This is the line that best represents the data. You can use the edge of your answer sheet as a ruler to help you draw a line that goes through most of the data.

The Line Graph

A line graph is similar to a scatterplot in that it shows different data points that relate the two variables. The difference with a line graph, though, is that the points have been connected to create a continuous line.

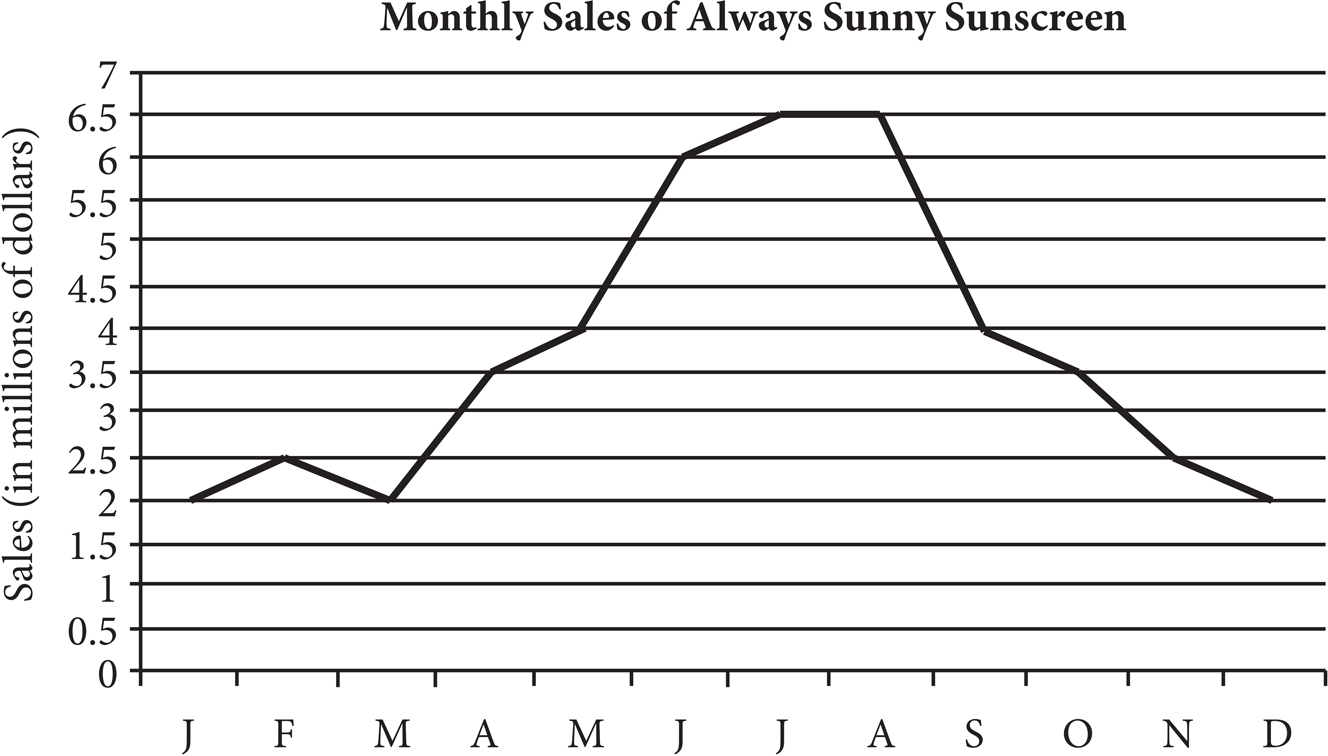
Here’s How to Read It

Reading a line graph is very similar to reading a scatterplot. Start at the axis that represents the data given, and draw a straight line up or to the right until you intersect the graph line. Then move left or down until you hit the other axis. For example, in February, indicated by an F on the horizontal axis, Always Sunny Sunscreen had 2.5 million in sales. Make sure to notice the units on each axis. If February sales were only $2.50, rather than $2.5 million, then this company wouldn’t be doing very well!

The Bar Graph (or Histogram)

Instead of showing a variety of different data points, a bar graph will show how many items belong to a particular category. If the variable at the bottom is given in ranges, instead of distinct items, the graph is called a histogram, but you read it the same way.

Here’s How to Read It

The height of each bar corresponds to a value on the vertical axis. In this case, the bar above Chile hits the line that intersects with 15 on the vertical axis, so there are 15 million people in Chile. Again, watch the units to make sure you know what the numbers on the axes represent. On this graph, horizontal lines are drawn at 5-unit intervals, making the graph easier to read. If these lines do not appear on a bar graph, use your answer sheet to determine the height of a given bar.

The Two-Way Table

A two-way table is another way to represent data without actually graphing it. Instead of having the variables represented on the vertical and horizontal axes, the data will be arranged in rows and columns. The top row will give the headings for each column, and the left-most column will give the headings for each row. The numbers in each box indicate the data for the category represented by the row and the column the box is in.

Here’s How to Read It

If you wanted to see the number of computers produced on Tuesday morning, you could start in the Morning Shift column and look down until you found the number in the row that says “Tuesday,” or you could start in the row for Tuesday and look to the right until you found the Morning Shift column. Either way, the result is 245. Some tables will give you totals in the bottom row and/or the right-most column, but sometimes you will need to find the totals yourself by adding up all the numbers in each row or in each column. More complicated tables will have more categories listed in rows and/or columns, or the tables may even contain extraneous information.

Figure Facts

Every time you encounter a figure or graphic on the PSAT, you should make sure you understand how to read it by checking the following things:

• What are the variables for each axis or the headings for the table?

• What units are used for each variable?

• Are there any key pieces of information (numbers, for example) in the legend of the chart that you should note?

• What type of relationship is shown by the data in the chart? For instance, if the chart includes curves that show an upward slope, then the graph shows a positive association, while curves that show a downward slope show a negative association.

• You can use the edge of your answer sheet as a ruler to help you make sure you are locating the correct data in the graph or to draw a line of best fit if necessary.

PROBABILITY

One topic that is often tested with two-way tables is probability. Probability refers to the chance that an event will happen, and it is given as a percent or a fractional value between 0 and 1, inclusive. A probability of 0 means that the event will never happen; a probability of 1 means that it is certain to happen.

For instance, if you have a die with faces numbered 1 to 6, what is the chance of rolling a 2? There is one face with the number 2 on it, out of 6 total faces. Therefore, the probability of rolling a 2 is .

What is the chance of rolling an even number on one roll of this die? There are 3 faces of the die with an even number (the sides numbered 2, 4, and 6) out of a total of 6 faces. Therefore, the probability of rolling an even number is , or .

Let’s look at how this concept will be tested on the PSAT.

18. A survey was conducted among a randomly chosen sample of full-time salaried workers about satisfaction in their current jobs. The table below shows a summary of the survey results.

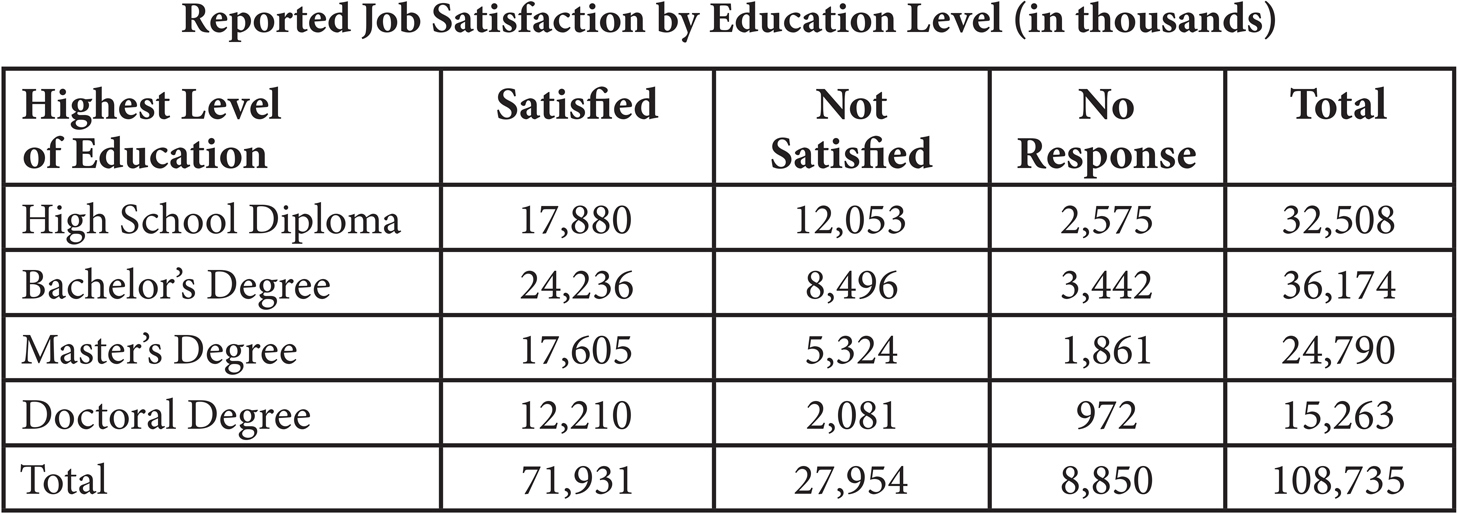
All persons who have earned a Master’s or Doctoral degree must have previously earned a Bachelor’s degree. What is the probability that a full-time salaried worker does NOT have a Bachelor’s degree?

A) 29.9%

B) 33.3%

C) 36.8%

D) 66.7%

Here’s How to Crack It

If everyone with a Master’s or Doctoral degree has a Bachelor’s degree, then the only people who do NOT have a Bachelor’s degree are those whose highest level of education is a High School Diploma. Find the probability of choosing someone with a High School Diploma out of the total: = 0.299 = 29.9%, which is (A).

GRIDS-INS: THE BASICS

You will see 8 questions on the PSAT that ask you to bubble in a numerical answer on a grid, rather than answer a multiple-choice question. These Grid-In questions are arranged in a loose order of difficulty, meaning they start easier and get progressively harder, and can be solved according to the methods outlined for the multiple-choice problems on the test. The last two grid-ins in Section 4 will be a paired set, but each question can be answered separately. Don’t worry that there are no answer choices—your approach is the same.

Keep Left

No matter how many digits in your answer, always start gridding in the leftmost column. That way, you’ll avoid omitting digits and losing points.

The only difficulty with grid-ins is getting used to the way in which you are asked to answer the question. For each question, you’ll have a grid like the following:

We recommend that you write the answer on top of the grid to help you bubble, but it’s important to know that the scoring machine reads only the bubbles. If you bubble incorrectly, the computer will consider the answer to be incorrect.

Here are the basic rules of gridding:

1. If your answer uses fewer than four boxes, you can grid it anywhere you like. To avoid confusion, we suggest that you start at the leftmost box. For example:

2. You can grid your answer as either a fraction or a decimal, if the fraction will fit.

You can grid an answer of .5 as either .5 or .

Relax

If your answer is a fraction and it fits in the grid (fraction bar included), don’t reduce it. Why bother? You won’t get an extra point for doing so. However, if your fraction doesn’t fit, reduce it or turn it into a decimal on your calculator.

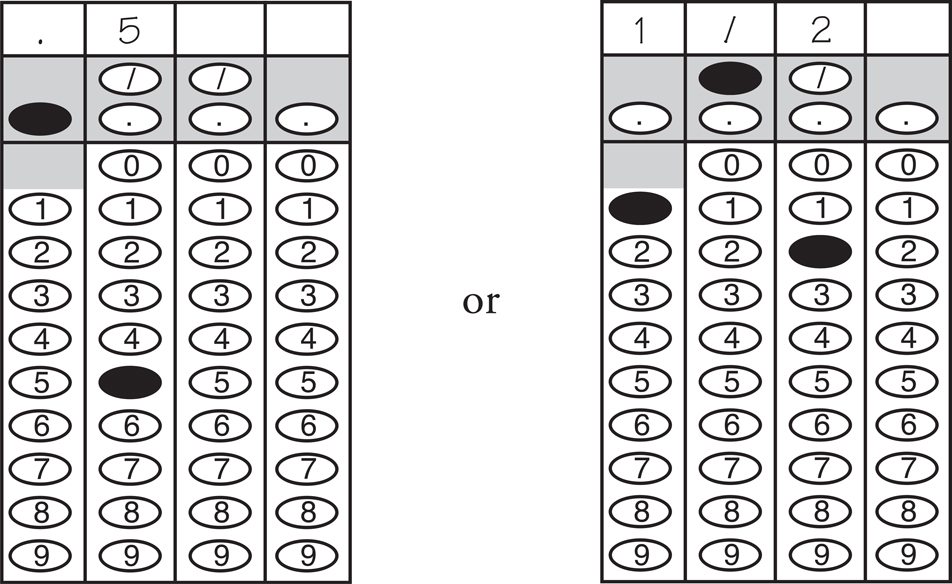
3. You do not need to reduce your fractions, if the fraction will fit.

If your answer is , you can grid it as , , or .5.

4. If you have a decimal that will not fit in the spaces provided, you must grid as many places as will fit.

If your answer is , you can grid it as , .666, or .667, but .66 is not acceptable.

You do not need to round your numbers, so we suggest that you don’t. There’s no reason to give yourself a chance to make a mistake if you don’t have to.

5. You cannot grid mixed numbers. Convert all mixed numbers to ordinary fractions.

If your answer is 2, you must convert it to or 2.5; otherwise the computer will read your 2 1/2 as 21/2.

Don’t Mix

Never grid in a mixed number. Change it into an improper fraction or decimal. To convert mixed fractions into improper fractions, all you have to do is multiply the denominator with the whole number in front of the fraction, then add that product to the numerator, and finally put that number over the denominator you started with.

6. You can’t grid π, square roots, variables, or negative numbers, so if you get an answer with one of those terms, you’ve made a mistake. Check your work.

Drill 5

Answers can be found in Part III.

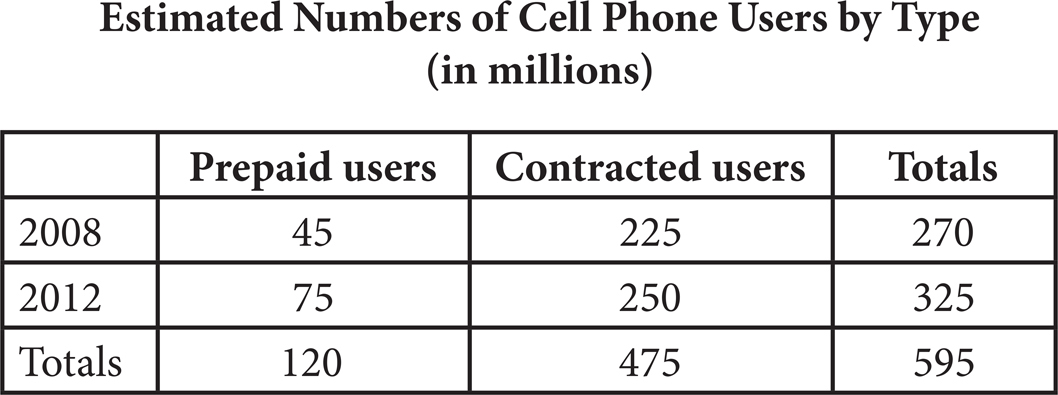
28. If a cell phone user is selected at random in 2008, what is the probability that user is a contracted user?

14. If 5x² = 125, what could be the value of 5x³ ?

z = 5 − 5[5z − 2(1 − z)]

15. In the equation above, what is the value of z ?

29. If 5 − = , what is the value of z ?

16. If 3a + 2b = 37 and 7a + 4b = 85, what is the value of b² + 6b − 10 ?

30. Linh travels from his home in Canada, where temperature is measured in degrees Celsius, to Houston, where temperature is measured in degrees Fahrenheit. The weather channel forecasts the high temperature in Houston for the next 2 days as 95 degrees and 86 degrees Fahrenheit, respectively. He wants to convert these temperatures from Fahrenheit to Celsius. To do so, he subtracts 32 from the degrees in Fahrenheit for each day and multiplies the difference by . How many degrees higher is the predicted temperature for the first day than the predicted temperature for the second day, in degrees Celsius?

31. Mathew and Moriah purchased a tandem bicycle for $540. If the amount Moriah paid was $30 less than twice the amount Mathew paid, how much, in dollars, did Moriah pay? (Disregard the dollar sign when gridding in your answer.)

17. Kimberly is an apiologist studying the sugar content of different sugar-water solutions to determine which is preferred by her hive of honeybees. After trying Solution 1, which has a sugar content of 25%, and Solution 2, which has a sugar content of 10%, she decides to make a new solution. She mixes 50 ounces of Solution 1 with some quantity of Solution 2 to make Solution 3, which has a sugar content of 15%. How many ounces of Solution 2 did Kimberly use to make Solution 3 ?

Summary

• The Math sections are arranged in a loose Order of Difficulty, which can make it easier to spot the less difficult problems. However, remember that the test writers’ idea of “easier” problems is not necessarily the same as your idea. Let your Personal Order of Difficulty be your guide.

• Write in your test booklet to set up problems, and then use your calculator (when allowed) to figure out solutions. And remember to type carefully—your calculator won’t check for mistakes.

• Review basic definitions again before the test to make sure you don’t get stuck on the “little words.”

• When you have to manipulate exponents, remember your MADSPM rules.

• To solve equations for a variable, isolate the variable. Make sure you perform the same operations on both sides of the equation.

• Inequalities can be worked just like equations, until you have to multiply or divide by a negative number. Then you need to flip the inequality sign.

• When solving radical and rational equations, be on the lookout for extraneous solutions. They are answers you get that don’t work when plugged back into the original equation.

• The absolute value of a number is the positive distance from zero, or practically, making the thing inside the | | sign positive. Everything inside the | | is equal to the positive and the negative value of the expression to which it is equal. Also remember that | | work like ( ); you need to complete all the operations inside the | | before you can make the value positive.

• To solve simultaneous equations, simply add or subtract the equations. If you don’t have the answer, look for multiples of your solutions. When the simultaneous equation question asks for a single variable and addition and subtraction don’t work, try to make something disappear. Multiply the equations by a constant to make the coefficient(s) of the variable(s) you want go to zero when the equations are added or subtracted.

• When writing a system of equations, start with the most straightforward piece of information.

• You can also use the equations in the answer choices to help you narrow down the possibilities for your equations. Eliminate any answers in which an equation doesn’t match your equation.

• Parallel lines have the same slope and no solutions. If two lines have the same slope and infinitely many solutions, they are actually the same line. Perpendicular lines have slopes that are negative reciprocals of one another.

• Rather than worrying about the distance formula, connect the two points and make the resulting line the hypotenuse of a right triangle. Then you can use the Pythagorean Theorem to find the distance.

• The coordinates of the midpoint of a line segment with endpoints (x₁, y₁) and (x₂, y₂) will be .

• When you encounter charts, carefully check the chart for information you should note, and remember that you can use your answer sheet as a ruler to help you locate information or to draw a line of best fit.

• Probability is a fractional value between 0 and 1 (inclusive), and it is equal to the number of outcomes the question is asking for divided by the total number of possible outcomes. It can also be expressed as a percent.

• When doing Grid-In questions, be sure to keep to the left, and don’t bother reducing fractions if they fit in the allotted spaces.