Topology and Abstract Algebra as Two Roads of Mathematical Comprehension
(1932)
We are not very pleased when we are forced to accept a mathematical truth by virtue of a complicated chain of formal conclusions and computations, which we traverse blindly, link by link, feeling our way by touch. We want first an overview of the aim and of the road; we want to understand the idea of the proof, the deeper context. A modern mathematical proof is not very different from a modern machine, or a modern test setup: the simple fundamental principles are hidden and almost invisible under a mass of technical details. When discussing Riemann in his lectures on the history of mathematics in the nineteenth century, Felix Klein said:
Undoubtedly, the capstone of every mathematical theory is a convincing proof of all of its assertions. Undoubtedly, mathematics inculpates itself when it foregoes convincing proofs. But the mystery of brilliant productivity will always be the posing of new questions, the anticipation of new theorems that make accessible valuable results and connections. Without the creation of new viewpoints, without the statement of new aims, mathematics would soon exhaust itself in the rigor of its logical proofs and begin to stagnate as its substance vanishes. Thus, in a sense, mathematics has been most advanced by those who distinguished themselves by intuition rather than by rigorous proofs.
The key element of Klein’s own method was an intuitive perception of inner connections and relations whose foundations are scattered. To some extent, he failed when it came to a concentrated and pointed logical effort. In his commemorative address for Dirichlet, Minkowski contrasted the minimum principle that Germans tend to name for Dirichlet (and that was actually applied most comprehensively by William Thomson) with the true Dirichlet principle: to conquer problems with a minimum of blind computation and a maximum of insightful thoughts. It was Dirichlet, said Minkowski, who ushered in the new era in the history of mathematics.1
What is the secret of such an understanding of mathematical matters, what does it consist in? Recently, there have been attempts in the philosophy of science to contrast understanding, the art of interpretation as the basis of the humanities, with scientific explanation, and the words intuition and understanding have been invested in this philosophy with a certain mystical halo, an intrinsic depth and immediacy. In mathematics, we prefer to look at things somewhat more soberly. I cannot enter into these matters here, and it strikes me as very difficult to give a precise analysis of the relevant mental acts. But at least I can single out, from the many characteristics of the process of understanding, one that is of decisive importance. One separates in a natural way the different aspects of a subject of mathematical investigation, makes each accessible through its own relatively narrow and easily surveyable group of assumptions, and returns to the complex whole by combining the appropriately specialized partial results. This last synthetic step is purely mechanical. The great art is in the first, analytic, step of appropriate separation and generalization. The mathematics of the last few decades has reveled in generalizations and formalizations. But to think that mathematics pursues generality for the sake of generality is to misunderstand the sound truth that a natural generalization simplifies by reducing the number of assumptions and by thus letting us understand certain aspects of a disarranged whole. Of course, it can happen that different directions of generalization enable us to understand different aspects of a particular concrete issue. Then it is subjective and dogmatic arbitrariness to speak of the true ground, the true source of an issue. Perhaps the only criterion of the naturalness of a severance and an associated generalization is their fruitfulness. If this process is systematized according to subject matter by a researcher with a measure of skill and “sensitive fingertips” who relies on all the analogies derived from his experience, then we arrive at axiomatics, which today is an instrument of concrete mathematical investigation rather than a method for the clarification and “deep-laying” of foundations.
In recent years mathematicians have had to focus on the general and on formalization to such an extent that, predictably, there have turned up many instances of cheap and easy generalizing for its own sake. Pólya has called it generalizing by dilution. It does not increase the essential mathematical substance. It is much like stretching a meal by thinning the soup. It is deterioration rather than improvement. The aged Klein said: “Mathematics looks to me like a store that sells weapons in peacetime. Its windows are replete with luxury items whose ingenious, artful and eye-catching execution delights the connoisseur. The true origin and purpose of these objects — the strike that defeats the enemy — have receded into the background and have been all but forgotten.” There is perhaps more than a grain of truth in this indictment, but, on the whole, our generation regards this evaluation of its efforts as unjust.
There are two modes of understanding that have proved, in our time, to be especially penetrating and fruitful. The two are topology and abstract algebra. A large part of mathematics bears the imprint of these two modes of thought. What this is attributable to can be made plausible at the outset by considering the central concept of real number. The system of real numbers is like a Janus head with two oppositely directed faces. In one respect it is the domain of the operations + and × and their inverses, in another it is a continuous manifold, and the two are continuously related. One is the algebraic and the other is the topological face of numbers. Since modern axiomatics is simpleminded and (unlike modern politics) dislikes such ambiguous mixtures of peace and war, it made a clean break between the two. The notion of size of number, expressed in the relations < and >, occupies a kind of intermediate relation between algebra and topology.
Investigations of continua are purely topological if they are restricted to just those properties and differences that are unchanged by arbitrary continuous deformations, by arbitrary continuous mappings. The mappings in question need only be faithful to the extent to which they do not collapse what is distinct. Thus it is a topological property of a surface to be closed like the surface of a sphere or open like the ordinary plane. A piece of the plane is said to be simply connected if, like the interior of a circle, it is partitioned by every crosscut. On the other hand, an annulus is doubly connected because there exists a crosscut that does not partition it but every subsequent crosscut does. Every closed curve on the surface of a sphere can be shrunk to a point by means of a continuous deformation, but this is not the case for a torus. Two closed curves in space can be intertwined or not. These are examples of topological properties or dispositions. They involve the primitive differences that underlie all finer differentiations of geometric figures. They are based on the single idea of continuous connection. References to a particular structure of a continuous manifold, such as a metric, are foreign to them. Other relevant concepts are limit, convergence of a sequence of points to a point, neighborhood, and continuous line.
After this preliminary sketch of topology I want to tell you briefly about the motives that have led to the development of abstract algebra. Then I will use a simple example to show how the same issue can be looked at from a topological and from an abstract-algebraic viewpoint.
All a pure algebraist can do with numbers is apply to them the four operations of addition, subtraction, multiplication, and division. If a system of numbers is a field, that is, if it is closed under these operations, then the algebraist has no means of going beyond it. The simplest field is the field of rationals. Another example is the field of numbers of the form 
rational. The well-known concept of irreducibility of polynomials is relative and depends on the field of coefficients of the polynomials, namely a polynomial f(x) with coefficients in a field K is said to be irreducible over K if it cannot be written as a product f1(x)·f2(x) of two non-constant polynomials with coefficients in K. The solution of linear equations and the determination of the greatest common divisor of two polynomials by means of the Euclidean algorithm are carried out within the field of the coefficients of the equations and of the polynomials respectively. The classical problem of algebra is the solution of an algebraic equation f(x) = 0 with coefficients in a field K, say the field of rationals. If we know a root θ of the equation, then we know the numbers obtained by applying to θ and to the (presumably known) numbers in K the four algebraic operations. The resulting numbers form a field K(θ) that contains K. In K(θ), θ plays a role of a determining number from which all other numbers in K(θ) are rationally derivable. But many — virtually all — numbers in K(θ) can play the same role as θ. It is therefore a breakthrough if we replace the study of the equation f(x) = 0 by the study of the field K(θ). By doing this we eliminate all manner of trivia and consider at the same time all equations that can be obtained from f(x) = 0 by means of Tschirnhausen transformations.2 The algebraic, and above all the arithmetical, theory of number fields is one of the sublime creations of mathematics. From the viewpoint of the richness and depth of its results it is the most perfect such creation.
There are fields in algebra whose elements are not numbers. The polynomials in one variable, or indeterminate, x, [with coefficients in a field], are closed under addition, subtraction, and multiplication but not under division. Such a system of magnitudes is called an integral domain. The idea that the argument x is a variable that traverses continuously its values is foreign to algebra; it is just an indeterminate, an empty symbol that binds the coefficients of the polynomial into a uniform expression that makes it easier to remember the rules for addition and multiplication. 0 is the polynomial all of whose coefficients are 0 (not the polynomial which takes on the value 0 for all values of the variable x). It can be shown that the product of two nonzero polynomials is ≠ 0. The algebraic viewpoint does not rule out the substitution for x of a number a taken from the field in which we operate. But we can also substitute for x a polynomial in one or more indeterminates y, z, . . . . Such substitution is a formal process which effects a faithful projection of the integral domain K [x] of polynomials in x onto K or onto the integral domain of polynomials K [y, z, . . .]; here “faithful” means subject to the preservation of the relations established by addition and multiplication. It is this formal operating with polynomials that we are required to teach students studying algebra in school. If we form quotients of polynomials, then we obtain a field of rational functions which must be treated in the same formal manner. This, then, is a field whose elements are functions rather than numbers. Similarly, the polynomials and rational functions in two or three variables, x, y or x, y, z with coefficients in K form an integral domain and field respectively.
Compare the following three integral domains: the integers, the polynomials in x with rational coefficients, and the polynomials in x and y with rational coefficients. The Euclidean algorithm holds in the first two of these domains, and so we have the theorem: If a, b are two relatively prime elements, then there are elements p, q in the appropriate domain such that
This implies that the two domains in question are unique factorization domains. The theorem (*) fails for polynomials in two variables. For example, x − y and x + y are relatively prime polynomials such that for every choice of polynomials p(x, y) and q(x, y) the constant term of the polynomial p(x, y)(x−y)+ q(x, y)(x + y) is 0 rather than 1. Nevertheless polynomials in two variables with coefficients in a field form a unique factorization domain. This example points to interesting similarities and differences.
There is yet another way of making fields in algebra. It involves neither numbers nor functions but congruences. Let p be a prime integer. Identify two integers if their difference is divisible by p, or, briefly, if they are congruent mod p. (To “see” what this means, wrap the real line around a circle of circumference p.) The result is a field with p elements. This representation is extremely useful in all of number theory. Consider, for example, the following theorem of Gauss that has numerous applications: If f(x) and g(x) are two polynomials with integer coefficients such that all coefficients of the product f(x) · g(x) are divisible by a prime p, then all coefficients of f(x) or all coefficients of g(x) are divisible by p. This is just the trivial theorem that the product of two polynomials can be 0 only if one of its factors is 0, applied to the field just described as the field of coefficients. This integral domain contains polynomials that are not 0 but vanish for all values of the argument; one such polynomial is xp − x. In fact, by Fermat’s theorem, we have
Cauchy uses a similar approach to construct the complex numbers. He regards the imaginary unit i as an indeterminate and studies polynomials in i over the reals modulo i2 + 1, that is he regards two polynomials as equal if their difference is divisible by i2 + 1. In this way, the actually unsolvable equation i2 + 1 = 0 is rendered, in some measure, solvable. Note that the polynomial i2 + 1 is prime over the reals. Kronecker generalized Cauchy’s construction as follows. Let K be a field and p(x) a polynomial prime over K. Viewed modulo p(x), the polynomials f(x) with coefficients in K form a field (and not just an integral domain). From an algebraic viewpoint, this process is fully equivalent to the one described previously and can be thought of as the process of extending K to K(θ) by adjoining to K a root of the equation p(θ) = 0. But it has the advantage that it takes place within pure algebra and gets around the demand for solving an equation that is actually unsolvable over K.
It is quite natural that these developments should have prompted a purely axiomatic buildup of algebra. A field is a system of objects, called numbers, closed under two operations, called addition and multiplication, that satisfy the usual axioms: both operations are associative and commutative, multiplication is distributive over addition, and both operations are uniquely invertible yielding subtraction and division respectively. If the axiom of invertibility of multiplication is left out, then the resulting system is called a ring. Now “field” no longer denotes, as before, a kind of sector of the continuum of real or complex numbers but a self-contained universe. One can apply the field operations to elements of the same field but not to elements of different fields. In this process we need not resort to artificial abstracting from the size relations < and >. These relations are irrelevant for algebra and the “numbers” of an abstract “number field” are not subject to such relations. In place of the uniform number continuum of analysis we now have the infinite multiplicity of structurally different fields. The previously described processes, namely adjunction of an indeterminate and identification of elements that are congruent with respect to a fixed prime element, are now seen as two modes of construction that lead from rings and fields to other rings and fields respectively.
The elementary axiomatic grounding of geometry also leads to this abstract number concept. Take the case of plane projective geometry. The incidence axioms alone lead to a “number field” that is naturally associated with it. Its elements, the “numbers,” are purely geometric entities, namely dilations. A point and a straight line are ratios of triples of “numbers” in that field, x1 : x2 : x3 and u1 : u2 : u3, respectively, such that incidence of the point x1 : x2 : x3 on the line u1 : u2 : u3 is represented by the equation
Conversely, if one uses these algebraic expressions to define the geometric terms, then every abstract field leads to an associated projective plane that satisfies the incidence axioms. It follows that a restriction involving the number field associated with the projective plane cannot be read off from the incidence axioms. Here the preexisting harmony between geometry and algebra comes to light in the most impressive manner. For the geometric number system to coincide with the continuum of ordinary real numbers, one must introduce axioms of order and continuity, very different in kind from the incidence axioms. We thus arrive at a reversal of the development that has dominated mathematics for centuries and seems to have arisen originally in India and to have been transmitted to the West by Arab scholars: Up till now, we have regarded the number concept as the logical antecedent of geometry, and have therefore approached every realm of magnitudes with a universal and systematically developed number concept independent of the applications involved. Now, however, we revert to the Greek viewpoint that every subject has an associated intrinsic number realm that must be derived from within it. We experience this reversal not only in geometry but also in the new quantum physics. According to quantum physics, the physical magnitudes associated with a particular physical setup (not the numerical values that they may take on depending on its different states) admit of an addition and a non-commutative multiplication, and thus give rise to a system of algebraic magnitudes intrinsic to it that cannot be viewed as a sector of the system of real numbers.3
And now, as promised, I will present a simple example that illustrates the mutual relation between the topological and abstract-algebraic modes of analysis. I consider the theory of algebraic functions of a single variable x. Let K(x) be the field of rational functions of x with arbitrary complex coefficients. Let f(z), more precisely f(z; x), be an nth degree polynomial in z with coefficients in K(x). We explained earlier when such a polynomial is said to be irreducible over K(x). This is a purely algebraic concept. Now construct the Riemann surface of the n-valued algebraic function z(x) determined by the equation f(z; x) = 0.4 Its n sheets extend over the x-plane. For easier transformation of the x-plane into the x-sphere by means of a stereographic projection we add to the x-plane a point at infinity. Like the sphere, our Riemann surface is now closed. The irreducibility of the polynomial f is reflected in a very simple topological property of the Riemann surface of z(x), namely its connectedness: if we shake a paper model of that surface it does not break into distinct pieces. Here you witness the coincidence of a purely algebraic and a purely topological concept. Each suggests generalization in a different direction. The algebraic concept of irreducibility depends only on the fact that the coefficients of the polynomial are in a field. In particular, K(x) can be replaced by the field of rational functions of x with coefficients in a preassigned field k which takes the place of the continuum of all complex numbers. On the other hand, from the viewpoint of topology it is irrelevant that the surface in question is a Riemann surface, that it is equipped with a conformal structure, and that it consists of a finite number of sheets that extend over the x-plane. Each of the two antagonists can accuse the other of admitting side issues and of neglecting essential features. Who is right? Questions such as these, involving not facts but ways of looking at facts, can lead to hatred and bloodshed when they touch human emotions. In mathematics, the consequences are not so serious. Nevertheless, the contrast between Riemann’s topological theory of algebraic functions and Weierstrass’s more algebraically directed school led to a split in the ranks of mathematicians that lasted for almost a generation.
Weierstrass himself wrote to his faithful pupil H. A. Schwarz: “The more I reflect on the principles of function theory — and I do this all the time — the stronger is my conviction that this theory must be established on the foundation of algebraic truths, and that it is therefore not the right way when, contrariwise, the ‘transcendent’ (to put it briefly) is invoked to establish simple and fundamental algebraic theorems — this is so no matter how attractive are, at a first glance, say, the considerations by means of which Riemann discovered so many of the most important properties of algebraic functions.” This strikes us now as one-sided; neither one of the two ways of understanding, the topological or the algebraic, can be acknowledged to have unconditional advantage over the other. And we cannot spare Weierstrass the reproach that he stopped midway. True, he explicitly constructed the functions as algebraic, but he also used as coefficients the algebraically unanalyzed, and in a sense unfathomable for algebraists, continuum of complex numbers. The dominant general theory in the direction followed by Weierstrass is the theory of an abstract number field and its extensions determined by means of algebraic equations. Then the theory of algebraic functions moves in the direction of a shared axiomatic basis with the theory of algebraic numbers. In fact, what suggested to Hilbert his approaches in the theory of number fields was the analogy [between the latter] and the state of things in the realm of algebraic functions discovered by Riemann by his topological methods. (Of course, when it came to proofs, the analogy was useless.)
Our example “irreducible-connected” is typical also in another respect. How visually simple and understandable is the topological criterion (shake the paper model and see if it falls apart) in comparison with the algebraic! The visual primality of the continuum (I think that in this respect it is superior to the 1 and the natural numbers) makes the topological method particularly suitable for both discovery and synopsis in mathematical areas, but is also the cause of difficulties when it comes to rigorous proofs. While it is close to the visual, it is also refractory to logical approaches. That is why Weierstrass, M. Noether and others preferred the laborious, but more solid-feeling, procedure of direct algebraic construction to Riemann’s transcendental-topological justification.5 Now, step by step, abstract algebra tidies up the clumsy computational apparatus. The generality of the assumptions and axiomatization force one to abandon the path of blind computation and to break the complex state of affairs into simple parts that can be handled by means of simple reasoning. Thus algebra turns out to be the El Dorado of axiomatics.
I must add a few words about the method of topology to prevent the picture from becoming altogether vague. If a continuum, say, a two-dimensional closed manifold, a surface, is to be the subject of mathematical investigation, then we must think of it as being subdivided into finitely many “elementary pieces” whose topological nature is that of a circular disk. These pieces are further fragmented by repeated subdivision in accordance with a fixed scheme, and thus a particular spot in the continuum is ever more precisely intercepted by an infinite sequence of nested fragments that arise in the course of successive subdivisions. In the one-dimensional case, the repeated “normal subdivision” of an elementary segment is its bipartition. In the two-dimensional case, each edge is first bipartitioned, then each piece of surface is divided into triangles by means of lines in the surface that lead from an arbitrary center to the (old and new) vertices. What proves that a piece is elementary is that it can be broken into arbitrarily small pieces by repetition of this division process. The scheme of the initial subdivision into elementary pieces — to be referred to briefly in what follows as the “skeleton” — is best described by labeling the surface pieces, edges, and vertices by means of symbols, and thus prescribing the mutual bounding relations of these elements. Following the successive subdivisions, the manifold may be said to be spanned by an increasingly dense net of coordinates which makes it possible to determine a particular point by means of an infinite sequence of symbols that play a role comparable to that of numbers. The reals appear here in the particular form of dyadic fractions, and serve to describe the subdivision of an open one-dimensional continuum. Other than that, we can say that each continuum has its own arithmetical scheme; the introduction of numerical coordinates by reference to the special division scheme of an open one-dimensional continuum violates the nature of things, and its sole justification is the practical one of the extraordinary convenience of the calculational manipulation of the continuum of numbers with its four operations. In the case of an actual continuum, the subdivisions can be realized only with a measure of imprecision; one must imagine that, as the process of subdivision progresses step by step, the boundaries set by the earlier subdivisions are ever more sharply fixed. Also, in the case of an actual continuum, the process of subdivision that runs virtually ad infinitum can reach only a certain definite stage. But in distinction to concrete realization, the localization in an actual continuum, the combinatorial scheme, the arithmetical nullform, is a priori determined ad infinitum; and mathematics deals with this combinatorial scheme alone. Since the continued subdivision of the initial topological skeleton progresses in accordance with a fixed scheme, it must be possible to read off all the topological properties of the nascent manifold from that skeleton. This means that, in principle, it must be possible to pursue topology as finite combinatorics. For topology, the ultimate elements, the atoms, are, in a sense, the elementary parts of the skeleton and not the points of the relevant continuous manifold. In particular, given two such skeletons, it must be possible to decide if they lead to concurrent manifolds. Put differently, it must be possible to decide if we can view them as subdivisions of one and the same manifold.
The algebraic counterpart of the transition from the algebraic equation f(z; x) = 0 to the Riemann surface is the transition from the latter equation to the field determined by the function z(x); this is so because the Riemann surface is uniquely occupied not only by the function z(x) but also by all algebraic functions in this field. What is characteristic for Riemann’s function theory is the converse problem: given a Riemann surface, construct its field of algebraic functions. The problem has always just one solution. Since every point 
of the Riemann surface lies over a definite point of the x-plane, the Riemann surface, as presently constituted, is embedded in the x-plane. The next step is to abstract from the embedding relation → x. As a result, the Riemann surface becomes, so to say, a free-floating surface equipped with a conformal structure and an angle measure. Note that in ordinary surface theory we must learn to distinguish between the surface as a continuous structure made up of elements of a specific kind, its points, and the embedding in 3-space that associates with each point of the surface, in a continuous manner, the point P in space at which is located. In the case of a Riemann surface, the only difference is that the Riemann surface and the embedding plane have the same dimension. To abstraction from the embedding there corresponds, on the algebraic side, the viewpoint of invariance under arbitrary birational transformations. To enter the realm of topology we must ignore the conformal structure associated with the free-floating Riemann surface. Continuing the comparison, we can say that the conformal structure of the Riemann surface is the equivalent of the metric structure of an ordinary surface, controlled by the first fundamental form, or of the affine and projective structures associated with surfaces in affine and projective differential geometry respectively.6 In the continuum of real numbers, it is the algebraic operations of + and · that reflect its structural aspect, and in a continuous group the law that associates with an ordered pair of elements their product plays an analogous role. These comments may have increased our appreciation of the relation of the methods. It is a question of rank, of what is viewed as primary. In topology we begin with the notion of continuous connection, and in the course of specialization we add, step by step, relevant structural features. In algebra this order is, in a sense, reversed. Algebra views the operations as the beginning of all mathematical thinking and admits continuity, or some algebraic surrogate of continuity, at the last step of specialization. The two methods follow opposite directions. Little wonder that they don’t get on well together. What is most easily accessible to one is often most deeply hidden to the other. In the last few years, in the theory of representation of continuous groups by means of linear substitutions, I have experienced most poignantly how difficult it is to serve these two masters at the same time. Such classical theories as that of algebraic functions can be made to fit both viewpoints. But viewed from these two viewpoints they present completely different sights.
After all these general remarks I want to use two simple examples that illustrate the different kinds of concept building in algebra and in topology. The classical example of the fruitfulness of the topological method is Riemann’s theory of algebraic functions and their integrals. Viewed as a topological surface, a Riemann surface has just one characteristic, namely its connectivity number or genus p. For the sphere p = 0 and for the torus p = 1. How sensible it is to place topology ahead of function theory follows from the decisive role of the topological number p in function theory on a Riemann surface. I quote a few dazzling theorems: The number of linearly independent everywhere regular differentials on the surface is p. The total order (that is, the difference between the number of zeros and the number of poles) of a differential on the surface is 2p − 2. If we prescribe more than p arbitrary points on the surface, then there exists just one single-valued function on it that may have simple poles at these points but is otherwise regular; if the number of prescribed poles is exactly p, then, if the points are in general position, this is no longer true. The precise answer to this question is given by the Riemann-Roch theorem in which the Riemann surface enters only through the number p. If we consider all functions on the surface that are everywhere regular except for a single place p at which they have a pole, then its possible orders are all numbers 1, 2, 3, . . . except for certain powers of p (the Weierstrass gap theorem). It is easy to give many more such examples. The genus p permeates the whole theory of functions on a Riemann surface. We encounter it at every step, and its role is direct, without complicated computations, understandable from its topological meaning (provided that we include, once and for all, the Thomson-Dirichlet principle as a fundamental function-theoretic principle).
The Cauchy integral theorem gives topology the first opportunity to enter function theory. The integral of an analytic function over a closed path is 0 only if the domain that contains the path and is also the domain of definition of the analytic function is simply connected. Let me use this example to show how one “topologizes” a function-theoretic state of affairs. If f(z) is analytic, then the integral ∫γ f(z)dz associates with every curve a number F(γ) such that
γ1 + γ2 stands for the curve such that the beginning of γ2 coincides with the end of γ1. The functional equation (†) marks the integral F(γ) as an additive path function. Also, each point has a neighborhood such that F(γ) = 0 for each closed path γ in that neighborhood. I will call a path function with these properties a topological integral, or briefly, an integral. In fact, all this concept assumes is that there is given a continuous manifold on which one can draw curves; it is the topological essence of the analytic notion of an integral. Integrals can be added and multiplied by numbers. The topological part of the Cauchy integral theorem states that on a simply connected manifold every integral is homologous to 0 (not only in the small but in the large), that is, F(γ) = 0 for every closed curve γ on the manifold. In this we can spot the definition of “simply connected.” The function-theoretic part states that the integral of an analytic function is a topological integral in our sense of the term. The definition of the order of connectivity [that we are about to state] fits in here quite readily. Integrals F1, F2, . . . , Fn on a closed surface are said to be linearly independent if they are not connected by a homology relation
with constant coefficients ci other than the trivial one, when all the ci vanish. The order of connectivity of a surface is the maximal number of linearly independent integrals. For a closed two-sided surface, the order of connectivity h is always an even number 2p, where p is the genus. From a homology between integrals we can go over to a homology between closed paths. The path homology
states that for every integral F we have the equality
If we go back to the topological skeleton that decomposes the surface into elementary pieces and replace the continuous point-chains of paths by the discrete chains constructed out of elementary pieces, then we obtain an expression for the order of connectivity h in terms of the numbers s, k, and e of pieces, edges, and vertices. The expression in question is the well-known Euler polyhedral formula h = k − (e + s) + 2. Conversely, if we start with the topological skeleton, then our reasoning yields the result that this combination h of the number of pieces, edges, and vertices is a topological invariant, namely it has the same value for “equivalent” skeletons which represent the same manifold in different subdivisions.
When it comes to application to function theory, it is possible, using the Thomson-Dirichlet principle, to “realize” the topological integrals as actual integrals of everywhere regular-analytic differentials on a Riemann surface. One can say that all of the constructive work is done on the topological side, and that the topological results are realized in a function-theoretic manner with the help of a universal transfer principle, namely the Dirichlet principle. This is, in a sense, analogous to analytic geometry, where all the constructive work is carried out in the realm of numbers, and then the results are geometrically “realized” with the help of the transfer principle lodged in the coordinate concept.
All this is seen more perfectly in uniformization theory, which plays a central role in all of function theory. But at this point, I prefer to point to another application which is probably close to many of you. I have in mind enumerative geometry, which deals with the determination of the number of points of intersection, singularities, and so on, of algebraic relational structures, which was made into a general, but very poorly justified, system by Schubert and Zeuthen. Here, in the hands of Lefschetz and van der Waerden, topology achieved a decisive success in that it led to definitions of multiplicity valid without exception, as well as to laws likewise valid without exception. Of two curves on a two-sided surface one can cross the other at a point of intersection from left to right or from right to left. These points of intersection must enter every setup with opposite weights +1 and −1. Then the total of the weights of the intersections (which can be positive or negative) is invariant under arbitrary continuous deformations of the curves; in fact, it remains unchanged if the curves are replaced by homologous curves. Hence it is possible to master this number through finite combinatorial means of topology and obtain transparent general formulas. Two algebraic curves are, actually, two closed Riemann surfaces embedded in a space of four real dimensions by means of an analytic mapping. But in algebraic geometry a point of intersection is counted with positive multiplicity, whereas in topology one takes into consideration the sense of the crossing. This being so, it is surprising that one can resolve the algebraic question by topological means. The explanation is that in the case of an analytic manifold, crossing always takes place with the same sense. If the two curves are represented in the x1, x2-plane in the vicinity of their point of intersection by the functions x1 = x1(s), x2 = x2(s) and 
, 
, then the sense ±1 with which the first curve intersects the second is given by the sign of the Jacobian
evaluated at the point of intersection. In the case of complex-algebraic “curves,” this criterion always yields the value +1. Indeed, let z1, z2 be complex coordinates in the plane and let s and t be the respective complex parameters on the two “curves.” The real and imaginary parts of z1 and z2 play the role of real coordinates in the plane. In their place, we can take z1, 
, z2, 
. But then the determinant whose sign determines the sense of the crossing is
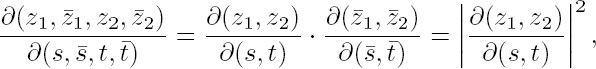
and thus invariably positive. Note that the Hurwitz theory of correspondence between algebraic curves can likewise be reduced to a purely topological core.
On the side of abstract algebra, I will emphasize just one fundamental concept, namely the concept of an ideal. If we use the algebraic method, then an algebraic manifold is given in 3-dimensional space with complex Cartesian coordinates x, y, z by means of a number of simultaneous equations
The fi are polynomials. In the case of a curve, it is not at all true that two equations suffice. Not only do the polynomials fi vanish at points of the manifold but also every polynomial f of the form
Such polynomials f form an “ideal” in the ring of polynomials. Dedekind defined an ideal in a given ring as a system of ring elements closed under addition and subtraction as well as under multiplication by ring elements. This concept is not too broad for our purposes. The reason is that, according to the Hilbert basis theorem, every ideal in the polynomial ring has a finite basis; there are finitely many polynomials f1, . . . , fn in the ideal such that every polynomial in the ideal can be written in the form (**). Hence the study of algebraic manifolds reduces to the study of ideals. On an algebraic surface there are points and algebraic curves. The latter are represented by ideals that are divisors of the ideal under consideration. The fundamental theorem of M. Noether deals with ideals whose manifold of zeros consists of finitely many points, and makes membership of a polynomial in such an ideal dependent on its behavior at these points. This theorem follows readily from the decomposition of an ideal into prime ideals. The investigations of E. Noether show that the concept of an ideal, first introduced by Dedekind in the theory of algebraic number fields, runs through all of algebra and arithmetic like Ariadne’s thread. Van der Waerden was able to justify the enumerative calculus by means of the algebraic resources of ideal theory.
If one operates in an arbitrary abstract number field rather than in the continuum of complex numbers, then the fundamental theorem of algebra, which asserts that every complex polynomial in one variable can be [uniquely] decomposed into linear factors, need not hold. Hence the general prescription in algebraic work: See if a proof makes use of the fundamental theorem or not. In every algebraic theory, there is a more elementary part that is independent of the fundamental theorem, and therefore valid in every field, and a more advanced part for which the fundamental theorem is indispensable. The latter part calls for the algebraic closure of the field. In most cases, the fundamental theorem marks a crucial split; its use should be avoided as long as possible. To establish theorems that hold in an arbitrary field it is often useful to embed the given field in a larger field. In particular, it is possible to embed any field in an algebraically closed field. A well-known example is the proof of the fact that a real polynomial can be decomposed over the reals into linear and quadratic factors. To prove this, we adjoin i to the reals and thus embed the latter in the algebraically closed field of complex numbers. This procedure has an analogue in topology which is used in the study and characterization of manifolds; in the case of a surface, this analogue consists in the use of its covering surfaces.
At the center of today’s interest is noncommutative algebra in which one does not insist on the commutativity of multiplication. Its rise is dictated by concrete needs of mathematics. Composition of operations is a kind of noncommutative operation. Here is a specific example. We consider the symmetry properties of functions f(x1, x2, . . . , xn) of a number of arguments. The latter can be subjected to an arbitrary permutation s. A symmetry property is expressed in one or more equations of the form
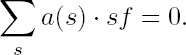
Here a(s) stands for the numerical coefficients associated with the permutation. These coefficients belong to a given field 
is a “symmetry operator.” These operators can be multiplied by numbers, added and multiplied, that is, applied in succession. The result of the latter operation depends on the order of the “factors.” Since all formal rules of computation hold for addition and multiplication of symmetry operators, they form a “noncommutative ring” (hypercomplex number system). The dominant role of the concept of an ideal persists in the noncommutative realm. In recent years, the study of groups and their representations by linear substitutions has been almost completely absorbed by the theory of noncommutative rings. Our example shows how the multiplicative group of n! permutations s is extended to the associated ring of magnitudes 
that admit, in addition to multiplication, addition and multiplication by numbers. Quantum physics has given noncommutative algebra a powerful boost.
Unfortunately, I cannot here produce an example of the art of building an abstract-algebraic theory. It consists in setting up the right general concepts, such as fields, ideals, and so on, in decomposing an assertion to be proved into steps (for example, and assertion “A implies B,” or A → B, may be decomposed into steps A → C, C → D, D → B), and in the appropriate generalization of these partial assertions in terms of general concepts. Once the main assertion has been subdivided in this way and the inessential elements have been set aside, the proofs of the individual steps do not, as a rule, present serious difficulties.
Whenever applicable, the topological method appears, thus far, to be more effective than the algebraic one. Abstract algebra has not yet produced successes comparable to the successes of the topological method in the hands of Riemann. Nor has anyone reached by an algebraic route the peak of uniformization scaled topologically by Klein, Poincaré, and Koebe. Here are questions to be answered in the future. But I do not want to conceal from you the growing feeling among mathematicians that the fruitfulness of the abstracting method is close to exhaustion. It is a fact that beautiful general concepts do not drop out of the sky. The truth is that, to begin with, there are definite concrete problems, with all their undivided complexity, and these must be conquered by individuals relying on brute force. Only then come the axiomatizers and conclude that instead of straining to break in the door and bloodying one’s hands, one should have first constructed a magic key of such and such shape and then the door would have opened quietly, as if by itself. But they can construct the key only because the successful breakthrough enables them to study the lock front and back, from the outside and from the inside. Before we can generalize, formalize and axiomatize there must be mathematical substance. I think that the mathematical substance on which we have practiced formalization in the last few decades is near exhaustion and I predict that the next generation will face in mathematics a tough time.7
Notes