By the mathematical way of thinking I mean first that form of reasoning through which mathematics penetrates into the sciences of the external world — physics, chemistry, biology, economics, etc., and even into our everyday thoughts about human affairs, and secondly that form of reasoning which the mathematician, left to himself, applies in his own field. By the mental process of thinking we try to ascertain truth; it is our mind’s effort to bring about its own enlightenment by evidence. Hence, just as truth itself and the experience of evidence, it is something fairly uniform and universal in character. Appealing to the light in our innermost self, it is neither reducible to a set of mechanically applicable rules, nor is it divided into watertight compartments like historic, philosophical, mathematical thinking, etc. We mathematicians are no Ku Klux Klan with a secret ritual of thinking. True, nearer the surface there are certain techniques and differences; for instance, the procedures of fact-finding in a courtroom and in a physical laboratory are conspicuously different. However, you should not expect me to describe the mathematical way of thinking much more clearly than one can describe, say, the democratic way of life.
A movement for the reform of the teaching of mathematics, which some decades ago made quite a stir in Germany under the leadership of the great mathematician Felix Klein, adopted the slogan “functional thinking.” The important thing which the average educated man should have learned in his mathematics classes, so the reformers claimed, is thinking in terms of variables and functions. A function describes how one variable y depends on another x; or more generally, it maps one variety, the range of a variable element x, upon another (or the same) variety. This idea of function or mapping is certainly one of the most fundamental concepts, which accompanies mathematics at every step in theory and application.
Our federal income tax law defines the tax y to be paid in terms of the income a; it does so in a clumsy enough way by pasting several linear functions together, each valid in another interval or bracket of income. An archeologist who, five thousand years from now, shall unearth some of our income tax returns together with relics of engineering works and mathematical books, will probably date them a couple of centuries earlier, certainly before Galileo and Vieta.1 Vieta was instrumental in introducing a consistent algebraic symbolism; Galileo discovered the quadratic law of falling bodies, according to which the drop s of a body falling in a vacuum is a quadratic function of the time t elapsed since its release:
g being a constant which has the same value for each body at a given place. By this formula Galileo converted a natural law inherent in the actual motion of bodies into an a priori constructed mathematical function, and that is what physics endeavors to accomplish for every phenomenon. The law is of much better design than our tax laws. It has been designed by Nature, who seems to lay her plans with a fine sense for mathematical simplicity and harmony. But then Nature is not, as our income and excess profits tax laws are, hemmed in by having to be comprehensible to our legislators and chambers of commerce.
Right from the beginning we encounter these characteristic features of the mathematical process: 1) variables, like t and s in the formula (1), whose possible values belong to a range, here the range of real numbers, which we can completely survey because it springs from our own free construction, 2) representation of these variables by symbols, and 3) functions or a priori constructed mappings of the range of one variable t upon the range of another s. Time is the independent variable kat’ exochen [par excellence].
In studying a function one should let the independent variable run over its full range. A conjecture about the mutual interdependence of quantities in nature, even before it is checked by experience, may be probed in thought by examining whether it carries through over the whole range of the independent variables. Sometimes certain simple limiting cases at once reveal that the conjecture is untenable. Leibnitz taught us by his principle of continuity to consider rest not as contradictorily opposed to motion, but as a limiting case of motion. Arguing by continuity he was able a priori to refute the laws of impact proposed by Descartes. Ernst Mach gives this prescription: “After having reached an opinion for a special case, one gradually modifies the circumstances of this case as far as possible, and in so doing tries to stick to the original opinion as closely as one can. There is no procedure which leads more safely and with greater mental economy to the simplest interpretation of all natural events.” Most of the variables with which we deal in the analysis of nature are continuous variables like time, but although the word seems to suggest it, the mathematical concept is not restricted to this case. The most important example of a discrete variable is given by the sequence of natural numbers or integers 1, 2, 3, . . . Thus the number of divisors of an arbitrary integer n is a function of n.
In Aristotle’s logic one passes from the individual to the general by exhibiting certain abstract features in a given object and discarding the remainder, so that two objects fall under the same concept or belong to the same genus if they have those features in common. This descriptive classification, e.g., the description of plants and animals in botany and zoology, is concerned with the actual existing objects. One might say that Aristotle thinks in terms of substance and accident, while the functional idea reigns over the formation of mathematical concepts.2 Take the notion of ellipse. Any ellipse in the x-y-plane is a set E of points (x, y) defined by a quadratic equation
whose coefficients a, b, c satisfy the conditions
The set E depends on the coefficients a, b, c; we have a function E(a, b, c) which gives rise to an individual ellipse by assigning definite values to the variable coefficients a, b, c. In passing from the individual ellipse to the general notion one does not discard any specific difference, one rather makes certain characteristics (here represented by the coefficients) variable over an a priori surveyable range (here described by the inequalities). The notion thus extends over all possible, rather than over all actually existing, specifications.3
From these preliminary remarks about functional thinking I now turn to a more systematic argument. Mathematics is notorious for the thin air of abstraction in which it moves. This bad reputation is only half deserved. Indeed, the first difficulty the man in the street encounters when he is taught to think mathematically is that he must learn to look things much more squarely in the face; his belief in words must be shattered; he must learn to think more concretely. Only then will he be able to carry out the second step, the step of abstraction where intuitive ideas are replaced by purely symbolic construction.
About a month ago I hiked around Longs Peak in the Rocky Mountain National Park with a boy of twelve, Pete. Looking up at Longs Peak he told me that they had corrected its elevation and that it is now 14,255 feet instead of 14,254 feet last year I stopped a moment asking myself what this could mean to the boy, and should I try to enlighten him by some Socratic questioning. But I spared Pete the torture, and the comment then withheld, will now be served to you. Elevation is elevation above sea level. But there is no sea under Longs Peak. Well, in idea one continues the actual sea level under the solid continents. But how does one construct this ideal closed surface, the geoid, which coincides with the surface of the oceans over part of the globe? If the surface of the ocean were strictly spherical, the answer would be clear. However, nothing of this sort is the case. At this point dynamics comes to our rescue. Dynamically the sea level is a surface of constant potential 
; more exactly 
denotes the gravitational potential of the earth, and hence the difference of at two points P, P′ is the work one must put into a small body of mass 1 to transfer it from P to P′. Thus it is most reasonable to define the geoid by the dynamical equation . If this constant value of fixes the elevation zero, it is only natural to define any fixed altitude by a corresponding constant value of , so that a peak P is called higher than P′ if one gains energy by flying from P to P′. The geometric concept of altitude is replaced by the dynamic concept of potential or energy. Even for Pete, the mountain climber, this aspect is perhaps the most important: the higher the peak the greater — ceteris paribus – the mechanical effort in climbing it By closer scrutiny one finds that in almost every respect the potential is the relevant factor. For instance the barometric measurement of altitude is based on the fact that in an atmosphere of given constant temperature the potential is proportional to the logarithm of the atmospheric pressure, whatever the nature of the gravitational field. Thus atmospheric pressure, generally speaking, indicates potential and not altitude. Nobody who has learned that the earth is round and the vertical direction is not an intrinsic geometric property of space but the direction of gravity should be surprised that he is forced to discard the geometric idea of altitude in favor of the dynamically more concrete idea of potential. Of course there is a relationship to geometry: In a region of space so small that one can consider the force of gravity as constant throughout this region, we have a fixed vertical direction, and potential differences are proportional to differences of altitude measured in that direction. Altitude, height, is a word which has a clear meaning when I ask how high the ceiling of this room is above its floor. The meaning gradually loses precision when we apply it to the relative altitudes of mountains in a wider and wider region. It dangles in the air when we extend it to the whole globe, unless we support it by the dynamical concept of potential. Potential is more concrete than altitude because it is generated by and dependent on the mass distribution of the earth.
Words are dangerous tools. Created for our everyday life they may have their good meanings under familiar limited circumstances, but Pete and the man in the street are inclined to extend them to wider spheres without bothering about whether they then still have a sure foothold in reality. We are witnesses of the disastrous effects of this witchcraft of words in the political sphere where all words have a much vaguer meaning and human passion so often drowns the voice of reason. The scientist must thrust through the fog of abstract words to reach the concrete rock of reality. It seems to me that the science of economics has a particularly hard job, and will still have to spend much effort, to live up to this principle. It is, or should be, common to all sciences, but physicists and mathematicians have been forced to apply it to the most fundamental concepts where the dogmatic resistance is strongest, and thus it has become their second nature. For instance, the first step in explaining relativity theory must always consist in shattering the dogmatic belief in the temporal terms past, present, future. You cannot apply mathematics as long as words still becloud reality.
I return to relativity as an illustration of this first important step preparatory to mathematical analysis, the step guided by the maxim, “Think concretely.” As the root of the words past, present, future, referring to time, we find something much more tangible than time, namely, the causal structure of the universe. Events are localized in space and time; an event of small extension takes place at a space-time or world point, a here-now. After restricting ourselves to events on a plane E we can depict the events by a graphic timetable in a three-dimensional diagram with a horizontal E plane and a vertical t axis on which time t is plotted. A world point is represented by a point in this picture, the motion of a small body by a world line, the propagation of light with its velocity c radiating from a light signal at the world point O by a vertical straight circular cone with vertex at O (light cone). The active future of a given world point O, here-now, contains all those events which can still be influenced by what happens at O, while its passive past consists of all those world points from which any influence, any message, can reach O. I here-now can no longer change anything that lies outside the active future; all events of which I here-now can have knowledge by direct observation or any records thereof necessarily lie in the passive past. We interpret the words past and future in this causal sense where they express something very real and important, the causal structure of the world.
The new discovery at the basis of the theory of relativity is the fact that no effect may travel faster than light. Hence while we formerly believed that active future and passive past bordered on each other along the cross-section of present, the horizontal plane t = const. going through O, Einstein taught us that the active future is bounded by the forward light cone and the passive past by its backward continuation.
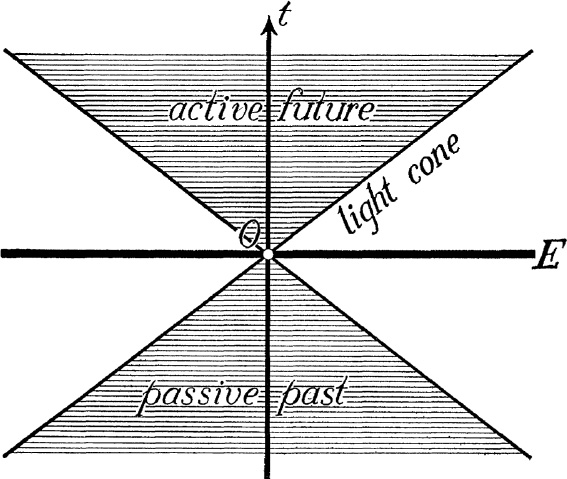
FIGURE 1
Active future and passive past are separated by the part of the world lying between these cones, and with this part I am here-now not at all causally connected. The essential positive content of relativity theory is this new insight into the causal structure of the universe. By discussing the various interpretations of such a simple question as whether two men, say Bill on earth and Bob on Sirius, are contemporaries, as to whether it means that Bill can send a message to Bob, or Bob a message to Bill, or even that Bill can communicate with Bob by sending a message and receiving an answer, etc., I often succeed soon in accustoming my listener to thinking in terms of causal rather than his wonted temporal structure. But when I tell him that the causal structure is not a stratification by horizontal layers t = const., but that active future and passive past are of cone-like shape with an interstice between, then some will discern dimly what I am driving at, but every honest listener will say: Now you draw a figure, you speak in pictures; how far does the simile go, and what is the naked truth to be conveyed by it? Our popular writers and news reporters, when they have to deal with physics, indulge in similes of all sorts; the trouble is that they leave the reader helpless in finding out how far these pungent analogies cover the real issue, and therefore more often lead him astray than enlighten him. In our case one has to admit that our diagram is no more than a picture, from which, however, the real thing emerges as soon as we replace the intuitive space in which our diagrams are drawn by its construction in terms of sheer symbols. Then the phrase that the world is a four-dimensional continuum changes from a figurative form of speech into a statement of what is literally true. At this second step the mathematician turns abstract, and here is the point where the layman’s understanding most frequently breaks off: the intuitive picture must be exchanged for a symbolic construction. “By its geometric and later by its purely symbolic construction,” says Andreas Speiser, “mathematics shook off the fetters of language, and one who knows the enormous work put into this process and its ever recurrent surprising successes cannot help feeling that mathematics today is more efficient in its sphere of the intellectual world, than the modern languages in their deplorable state or even music are on their respective fronts.” I shall spend most of my time today in an attempt to give you an idea of what this magic of symbolic construction is.4
To that end I must begin with the simplest, and in a certain sense most profound, example: the natural numbers or integers by which we count objects. The symbols we use here are strokes put one after another. The objects may disperse, “melt, thaw and resolve themselves into a dew,” but we keep this record of their number.5 What is more, we can by a constructive process decide for two numbers represented through such symbols which one is the larger, namely by checking one against the other, stroke by stroke. This process reveals differences not manifest in direct observation, which in most instances is incapable of distinguishing between even such low numbers as 21 and 22. We are so familiar with these miracles which the number symbols perform that we no longer wonder at them. But this is only the prelude to the mathematical step proper. We do not leave it to chance which numbers we shall meet by counting actual objects, but we generate the open sequence of all possible numbers which starts with 1 (or 0) and proceeds by adding to any number symbol n already reached one more stroke, whereby it changes into the following number n. As I have often said before, being is thus projected onto the background of the possible, or more precisely onto a manifold of possibilities which unfolds by iteration and is open into infinity. Whatever number n we are given, we always deem it possible to pass to the next n′. “Number goes on.” This intuition of the “ever one more,” of the open countable infinity, is basic for all mathematics.6 It gives birth to the simplest example of what I termed above an a priori surveyable range of variability. According to this process by which the integers are created, functions of an argument ranging over all integers n are to be defined by so-called complete induction, and statements holding for all n are to be proved in the same fashion. The principle of this inference by complete induction is as follows.7 In order to show that every number n has a certain property V it is sufficient to make sure of two things:
1. 0 has this property;
2. If n is any number which has the property V, then the next number n has the property V.
It is practically impossible, and would be useless, to write out in strokes the symbol of the number 1012, which the Europeans call a billion and we in this country, a thousand billions. Nevertheless we talk about spending more than 1012 cents for our defense program, and the astronomers are still ahead of the financiers. In July the New Yorker carried this cartoon: man and wife reading the newspaper over their breakfast and she looking up in puzzled despair: “Andrew, how much is seven hundred billion dollars?” A profound and serious question, lady! I wish to point out that only by passing through the infinite can we attribute any significance to such figures. 12 is an abbreviation of
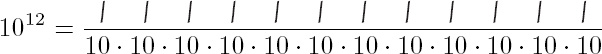
can not be understood without defining the function 10 · n for all n and this is done through the following definition by complete induction:
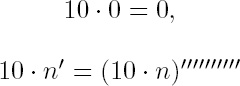
The dashes constitute the explicit symbol for 10, and, as previously, each dash indicates transition to the next number. Indian, in particular Buddhist, literature indulges in the possibilities of fixing stupendous numbers by the decimal system of numeration which the Indians invented, i.e., by a combination of sums, products and powers. I mention also Archimedes’s treatise “On the counting of sand,” and Professor Kasner’s Googolplex in his recent popular book on Mathematics and the Imagination.8
Our conception of space is, in a fashion similar to that of natural numbers, depending on a constructive grip on all possible places. Let us consider a metallic disk in a plane E. Places on the disk can be marked in concreto by scratching little crosses on the plate. But relatively to two axes of coordinates and a standard length scratched into the plate we can also put ideal marks in the plane outside the disk by giving the numerical values of their two coordinates. Each coordinate varies over the a priori constructed range of real numbers. In this way astronomy uses our solid earth as a base for plumbing the sidereal spaces. What a marvelous feat of imagination when the Greeks first constructed the shadows which earth and moon, illumined by the sun, cast in empty space and thus explained the eclipses of sun and moon! In analyzing a continuum, like space, we shall here proceed in a somewhat more general manner than by measurement of coordinates and adopt the topological viewpoint, so that two continua arising one from the other by continuous deformation are the same to us. Thus the following exposition is at the same time a brief introduction to an important branch of mathematics, topology.
The symbols for the localization of points on the one-dimensional continuum of a straight line are the real numbers. I prefer to consider a closed one-dimensional continuum, the circle. The most fundamental statement about a continuum is that it may be divided into parts. We catch all the points of a continuum by spanning a net of division over it, which we refine by repetition of a definite process of subdivision ad infinitum. Let S be any division of the circle into a number of arcs, say l arcs. From S we derive a new division S by the process of normal subdivision, which consists in breaking each arc into two. The number of arcs in S will then be 2l. Running around the circle in a definite sense (orientation) we may distinguish the two pieces, in the order in which we meet them, by the marks 0 and 1; more explicitly, if the arc is denoted by a symbol α then these two pieces are designated as α0 and α1. We start with the division S0 of the circle into two arcs + and −; either is topologically a cell, i.e., equivalent to a segment. We then iterate the process of normal subdivision and thus obtain 
seeing to it that the refinement of the division ultimately pulverizes the whole circle. If we had not renounced the use of metric properties we could decree that the normal sub-division takes place by cutting each arc into two equal halves. We introduce no such fixation; hence the actual performance of the process involves a wide measure of arbitrariness. However, the combinatorial scheme according to which the parts reached at any step border on each other, and according to which the division progresses, is unique and perfectly fixed. Mathematics cares for this symbolic scheme only. By our notation the parts occurring at the consecutive divisions are catalogued by symbols of this type
with + or − before the dot and all following places occupied by either 0 or 1. We see that we arrive at the familiar symbols of binary (not decimal) fractions. A point is caught by an infinite sequence of arcs of the consecutive divisions such that each arc arises from the preceding one by choosing one of the two pieces into which it breaks by the next normal subdivision, and the point is thus fixed by an infinite binary fraction. Let us try to do something similar for two-dimensional continua, e.g., for the surface of a sphere or a torus. The figures [2, 3] show how we may cast a very coarse net over either of them, the one consisting of two, the other of four meshes; the globe is divided into its upper and lower halves by the equator, the torus is welded together from four rectangular plates. The meshes are two-dimensional cells, or briefly, 2-cells which are topologically equivalent to a circular disk. The combinatorial description is facilitated by introducing also the vertices and edges of the division, which are 0- and 1-cells. We attach arbitrary symbols to them and state in symbols for each 2-cell which 1-cells bound it, and for each 1-cell by which 0-cells it is bounded. We then arrive at a topological scheme S. Here are our two examples:
FIGURE 2
FIGURE 3
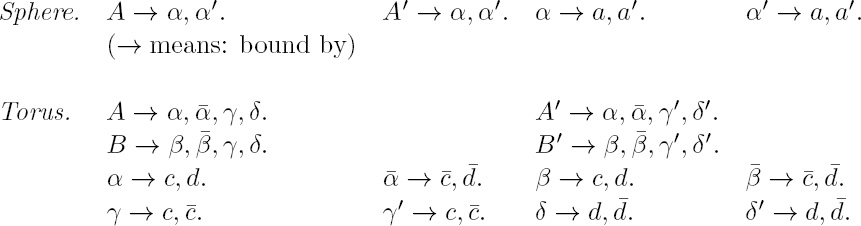
From this initial stage we proceed by iteration of a universal process of normal subdivision: On each 1-cell α = ab we choose a point which serves as a new vertex α and divides the 1-cell into two segments αa and αb; in each 2-cell A we choose a point A and cut the cell into triangles by joining the newly created vertex A with the old and new vertices on its bounding 1-cells by lines within the 2-cell. Just as in elementary geometry we denote the triangles and their sides by means of their vertices.
The figure [4] shows a pentagon before and after subdivision; the triangle Aβc is bounded by the 1-cells βc, Aβ, Ac, the 1-cell Ac for instance by the vertices c and A. We arrive at the following general purely symbolic description of the process by which the subdivided scheme S is derived from a given topological scheme S. Any symbol e2e1e0 made up by the symbols of a 2-cell e2, a 1-cell e1 and a 0-cell e0 in S such that e2 is bounded by e1 and e1 bounded by e0 represents a 2-cell 
of S′. This 2-cell 
in S is part of the 2-cell e2 in S. The symbols of cells in S which bound a given cell are derived from its symbol by dropping any one of its constituent letters. Through iteration of this symbolic process the initial scheme S0 gives rise to a sequence of derived schemes 
What we have done is nothing else than devise a systematic cataloguing of the parts created by consecutive subdivisions. A point of our continuum is caught by a sequence
which starts with a 2-cell e of S0 and in which the 2-cell e(n) of the scheme S(n) is followed by one of the 2-cells e(n+1) of S(n+1) into which e(n) breaks up by our subdivision. (To do full justice to the inseparability of parts in a continuum this description ought to be slightly altered. But for the present purposes our simplified description will do.) We are convinced that not only may each point be caught by such a sequence (Eudoxus), but that an arbitrarily constructed sequence of this sort always catches a point (Dedekind, Cantor). The fundamental concepts of limit, convergence, and continuity follow in the wake of this construction.
We now come to the decisive step of mathematical abstraction: we forget about what the symbols stand for. The mathematician is concerned with the catalogue alone; he is like the man in the catalogue room who does not care what books or pieces of an intuitively given manifold the symbols of his catalogue denote. He need not be idle; there are many operations which he may carry out with these symbols, without ever having to look at the things they stand for. Thus, replacing the points by their symbols (2) he turns the given manifold into a symbolic construct which we shall call the topological space {S0} because it is based on the scheme S0 alone.
FIGURE 4
The details are not important; what matters is that once the initial finite symbolic scheme S0 is given we are carried along by an absolutely rigid symbolic construction which leads from S0 to 
, from to 
, etc. The idea of iteration, first encountered with the natural numbers, again plays a decisive role. The realization of the symbolic scheme for a given manifold, say a sphere or a torus, as a scheme of consecutive divisions involves a wide margin of arbitrariness restricted only by the requirement that the pattern of the meshes ultimately becomes infinitely fine everywhere. About this point and the closely affiliated requirement that each 2-cell has the topological structure of a circular disk, I must remain a bit vague. However, the mathematician is not concerned with applying the scheme or catalogue to a given manifold, but only with the scheme itself, which contains no haziness whatsoever. And we shall presently see that even the physicist need not care greatly about that application. It was merely for heuristic purposes that we had to go the way from manifold through division to pure symbolism. In the same purely symbolic way we can evidently construct not only 1- and 2- but also 3, 4, 5, . . .-dimensional manifolds. An n-dimensional scheme S0 consists of symbols distinguished as 0, 1, 2, . . ., n-cells and associates with each i-cell ei (i = 1, 2, . . ., n) certain (i − 1)-cells of which one says that they bound ei. It is clear how the process of normal subdivision carries over. A certain such 4-dimensional scheme can be used for the localization of events, of all possible here-nows; physical quantities which vary in space and time are functions of a variable point ranging over the corresponding symbolically constructed 4-dimensional topological space. In this sense the world is a 4-dimensional continuum. The causal structure, of which we talked before, will have to be constructed within the medium of this 4-dimensional world, i.e., out of the symbolic material constituting our topological space. Incidentally the topological viewpoint has been adopted on purpose, because only thus our frame becomes wide enough to embrace both special and general relativity theory. The special theory envisages the causal structure as something geometrical, rigid, given once for all, while in the general theory it becomes flexible and dependent on matter in the same way as, for instance, the electromagnetic field.
In our analysis of nature we reduce the phenomena to simple elements each of which varies over a certain range of possibilities which we can survey a priori because we construct these possibilities a priori in a purely combinatorial fashion from some purely symbolic material. The manifold of space-time points is one, perhaps the most basic one, of these constructive elements of nature. We dissolve light into plane polarized monochromatic light beams with few variable characteristics like wavelength which varies over the symbolically constructed continuum of real numbers. Because of this a priori construction we speak of a quantitative analysis of nature; I believe the word quantitative, if one can give it a meaning at all, ought to be interpreted in this wide sense. The power of science, as witnessed by the development of modern technology, rests upon the combination of a priori symbolic construction with systematic experience in the form of planned and reproducible reactions and their measurements. As material for the a priori construction, Galileo and Newton used certain features of reality like space and time which they considered as objective, in opposition to the subjective sense qualities, which they discarded. Hence the important role which geometric figures played in their physics. You probably know Galileo’s words in the Saggiatore [Assayer] where he says that no one can read the great book of nature “unless he has mastered the code in which it is composed, that is, the mathematical figures and the necessary relations between them.”9 Later we have learned that none of these features of our immediate observation, not even space and time, have a right to survive in a pretended truly objective world, and thus have gradually and ultimately come to adopt a purely symbolic combinatorial construction.
While a set of objects determines its number unambiguously, we have observed that a scheme of division S0 with its consecutive derivatives 
can be established on a given manifold in many ways involving a wide margin of arbitrariness. But the question whether two schemes,
are fit to describe the same manifold is decidable in a purely mathematical way: it is necessary and sufficient that the two topological spaces {S0} and {T0} can be mapped one upon the other by a continuous one-to-one transformation – a condition which ultimately boils down to a certain relationship called isomorphism between the two schemes S0 and T0. (Incidentally the problem of establishing the criterion of isomorphism for two finite schemes in finite combinatorial form is one of the outstanding unsolved mathematical problems.) The connection between a given continuum and its symbolic scheme inevitably carries with it this notion of isomorphism; without it and without our understanding that isomorphic schemes are to be considered as not intrinsically different, no more than congruent figures in geometry, the mathematical concept of a topological space would be incomplete. Moreover it will be necessary to formulate precisely the conditions which every topological scheme is required to satisfy. For instance, one such condition demands that each 1-cell be bounded by exactly two 0-cells.
I can now say a little more clearly why the physicist is almost as disinterested as the mathematician in the particular way how a certain combinatorial scheme of consecutive divisions is applied to the continuum of here-nows which we called the world. Of course, somehow our theoretical constructions must be put in contact with the observable facts. The historic development of our theories proceeds by heuristic arguments over a long and devious road and in many steps from experience to construction. But systematic exposition should go the other way: first develop the theoretical scheme without attempting to define individually by appropriate measurements the symbols occurring in it as space-time coordinates, electromagnetic field strengths, etc., then describe, as it were in one breath, the contact of the whole system with observable facts. The simplest example I can find is the observed angle between two stars.10 The symbolic construct in the medium of the 4-dimensional world from which theory determines and predicts the value of this angle includes: (1) the world-lines of the two stars, (2) the causal structure of the universe, (3) the world position of the observer and the direction of his world line at the moment of observation. But a continuous deformation, a one-to-one continuous transformation of this whole picture, does not affect the value of the angle.Isomorphic pictures lead to the same results concerning observable facts. This is, in its most general form, the principle of relativity. The arbitrariness involved in our ascent from the given manifold to the construct is expressed by this principle for the opposite descending procedure, which the systematic exposition should follow.
So far we have endeavored to describe how a mathematical construct is distilled from the given raw material of reality. Let us now look upon these products of distillation with the eye of a pure mathematician. One of them is the sequence of natural numbers and the other the general notion of a topological space {S0} into which a topological scheme S0 develops by consecutive derivations 
In both cases iteration is the most decisive feature. Hence all our reasoning must be based on evidence concerning that completely transparent process which generates the natural numbers, rather than on any principles of formal logic like syllogism, etc. The business of the constructive mathematician is not to draw logical conclusions. Indeed his arguments and propositions are merely an accompaniment of his actions, his carrying out of constructions. For instance, we run over the sequence of integers 0, 1, 2, . . . by saying alternatingly even, odd, even, odd, etc., and in view of the possibility of this inductive construction which we can extend as far as we ever wish, we formulate the general arithmetical proposition: “Every integer is even or odd.” Besides the idea of iteration (or the sequence of integers) we make constant use of mappings or of the functional idea. For instance, just now we have defined a function π(n), called parity, with n ranging over all integers and π capable of the two values 0 (even) and 1 (odd), by this induction:
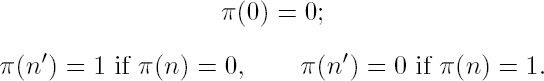
Structures such as the topological schemes are to be studied in the light of the idea of isomorphism. For instance, when it comes to introducing operators τ which carry any topological scheme S into a topological scheme τ(S) one should pay attention only to such operators or functions τ for which isomorphism of S and R entails isomorphism for τ(S) and τ(R).
Up to now I have emphasized the constructive character of mathematics. In our actual mathematics there vies with it the non-constructive axiomatic method. Euclid’s axioms of geometry are the classical prototype. Archimedes employs the method with great acumen and so do later Galileo and Huyghens in erecting the science of mechanics. One defines all concepts in terms of a few undefined basic concepts and deduces all propositions from a number of basic propositions, the axioms, concerning the basic concepts. In earlier times authors were inclined to claim a priori evidence for their axioms; however this is an epistemological aspect which does not interest the mathematician. Deduction takes place according to the principles of formal logic, in particular it follows the syllogistic scheme. Such a treatment more geometrico was for a long time considered the ideal of every science. Spinoza tried to apply it to ethics. For the mathematician the meaning of the words representing the basic concepts is irrelevant; any interpretation of them which fits, i. e., under which the axioms become true, will be good, and all the propositions of the discipline will hold for such an interpretation because they are all logical consequences of the axioms. Thus n-dimensional Euclidean geometry permits another interpretation where points are distributions of electric current in a given circuit consisting of n branches which connect at certain branch points. For instance, the problem of determining that distribution which results from given electromotoric forces inserted in the various branches of the net corresponds to the geometric construction of orthogonal projection of a point upon a linear subspace. From this standpoint mathematics treats of relations in a hypothetical-deductive manner without binding itself to any particular material interpretation. It is not concerned with the truth of axioms, but only with their consistency; indeed inconsistency would a priori preclude the possibility of our ever coming across a fitting interpretation. “Mathematics is the science which draws necessary conclusions,” says B. Peirce in 1870, a definition which was in vogue for decades after. To me it seems that it renders very scanty information about the real nature of mathematics, and you are at present watching my struggle to give a fuller characterization. Past writers on the philosophy of mathematics have so persistently discussed the axiomatic method that I don’t think it necessary for me to dwell on it at any greater length, although my exposition thereby becomes somewhat lopsided.
However I should like to point out that since the axiomatic attitude has ceased to be the pet subject of the methodologists its influence has spread from the roots to all branches of the mathematical tree. We have seen before that topology is to be based on a full enumeration of the axioms which a topological scheme has to satisfy. One of the simplest and most basic axiomatic concepts which penetrates all fields of mathematics is that of group. Algebra with its “fields,” “rings,” etc., is today from bottom to top permeated by the axiomatic spirit. Our portrait of mathematics would look a lot less hazy, if time permitted me to explain these mighty words which I have just uttered, group, field and ring. I shall not try it, as little as I have stated the axioms characteristic for a topological scheme. But such notions and their kin have brought it about that modern mathematical research often is a dexterous blending of the constructive and the axiomatic procedures. Perhaps one should be content to note their mutual interlocking. But temptation is great to adopt one of these two views as the genuine primordial way of mathematical thinking, to which the other merely plays a subservient role, and it is possible indeed to carry this standpoint through consistently whether one decides in favor of construction or axiom.
Let us consider the first alternative. Mathematics then consists primarily of construction. The occurring sets of axioms merely fix the range of variables entering into the construction. I shall explain this statement a little further by our examples of causal structure and topology. According to the special theory of relativity the causal structure is once for all fixed and can therefore be explicitly constructed. Nay, it is reasonable to construct it together with the topological medium itself, as for instance a circle together with its metric structure is obtained by carrying out the normal subdivision by cutting each arc into two equal halves. In the general theory of relativity, however, the causal structure is something flexible; it has only to satisfy certain axioms derived from experience which allow a considerable measure of free play. But the theory goes on by establishing laws of nature which connect the flexible causal structure with other flexible physical entities, distribution of masses, electromagnetic field, etc., and these laws in which the flexible things figure as variables are in their turn constructed by the theory in an explicit a priori way. Relativistic cosmology asks for the topological structure of the universe as a whole, whether it is open or closed, etc. Of course the topological structure can not be flexible as the causal structure is, but one must have a free outlook on all topological possibilities before one can decide by the testimony of experience which of them is realized by our actual world. To that end one turns to topology. There the topological scheme is bound only by certain axioms; but the topologist derives numerical characters from, or establishes universal connections between, arbitrary topological schemes, and again this is done by explicit construction into which the arbitrary schemes enter as variables. Wherever axioms occur, they ultimately serve to describe the range of variables in explicitly constructed functional relations.
So much about the first alternative. We turn to the opposite view, which subordinates construction to axioms and deduction, and holds that mathematics consists of systems of axioms freely agreed upon, and their necessary conclusions. In a completely axiomatized mathematics construction can come in only secondarily as construction of examples, thus forming the bridge between pure theory and its applications. Sometimes there is only one example because the axioms, at least up to arbitrary isomorphisms, determine their object uniquely; then the demand for translating the axiomatic set-up into an explicit construction becomes especially imperative. Much more significant is the remark that an axiomatic system, although it refrains from constructing the mathematical objects, constructs the mathematical propositions by combined and iterated application of logical rules. Indeed, drawing conclusions from given premises proceeds by certain logical rules which since Aristotle’s day one has tried to enumerate completely. Thus on the level of propositions, the axiomatic method is undiluted constructivism. David Hilbert has in our day pursued the axiomatic method to its bitter end where all mathematical propositions, including the axioms, are turned into formulas and the game of deduction proceeds from the axioms by rules which take no account of the meaning of the formulas. The mathematical game is played in silence, without words, like a game of chess. Only the rules have to be explained and communicated in words, and of course any arguing about the possibilities of the game, for instance about its consistency, goes on in the medium of words and appeals to evidence.
If carried so far, the issue between explicit construction and implicit definition by axioms ties up with the last foundations of mathematics. Evidence based on construction refuses to support the principles of Aristotelian logic when these are applied to existential and general propositions in infinite fields like the sequence of integers or a continuum of points. And if the logic of the infinite is taken into account, it seems impossible to axiomatize adequately even the most primitive process, the transition n → n′ from an integer to its follower n′. As K. Gödel has shown, there will always be constructively evident arithmetical propositions which cannot be deduced from the axioms however you formulate them, while at the same time the axioms, riding roughshod over the subtleties of the constructive infinite, go far beyond what is justifiable by evidence. We are not surprised that a concrete chunk of nature, taken in its isolated phenomenal existence, challenges our analysis by its inexhaustibility and incompleteness; it is for the sake of completeness, as we have seen, that physics projects what is given onto the background of the possible. However, it is surprising that a construct created by mind itself, the sequence of integers, the simplest and most diaphanous thing for the constructive mind, assumes a similar aspect of obscurity and deficiency when viewed from the axiomatic angle. But such is the fact; which casts an uncertain light upon the relationship of evidence and mathematics. In spite, or because, of our deepened critical insight we are today less sure than at any previous time of the ultimate foundations on which mathematics rests.
My purpose in this address has not been to show how the inventive mathematical intellect works in its manifold manifestations, in calculus, geometry, algebra, physics, etc., although that would have made a much more attractive picture. Rather, I have attempted to make visible the sources from which all these manifestations spring. I know that in an hour’s time I can have succeeded only to a slight degree. While in other fields brief allusions are met by ready understanding, this is unfortunately seldom the case with mathematical ideas. But I should have completely failed if you had not realized at least this much, that mathematics, in spite of its age, is not doomed to progressive sclerosis by its growing complexity, but is still intensely alive, drawing nourishment from its deep roots in mind and nature.
[An address delivered at the Bicentennial Celebration Conference of the University of Pennsylvania, 17 September 1940; the text here follows Weyl 1940; note that the text reprinted in WGA 3:710–718 is garbled.]
1 [François Viète (also known in his Latinized name Franciscus Vieta), 1540– 1603, was an important figure in the development of modern algebra, who introduced alphabetic symbolic notation for unknowns and coefficients as well as the general rules for manipulating them; see Klein 1968, 150–185, and Pesic 1997.]
2 [The English words customarily used to render Aristotle’s concepts are rather opaque; Weyl may here presume that the reader knows, from the meanings of the underlying Greek words, that “substance” (ousia) denotes the common essence (say of a biological genus), where “accident” (sumbebekos) denotes a quality of an individual member of that genus that does not specifically reflect its underlying essence. For example, some quality of a tree may reflect its particular “accidental” circumstances (like the local climate or water supply) rather than the essential qualities by which it can be distinguished from trees of other genera.]
3 Compare about this contrast Ernst Cassirer, Substanzbegriff und Funktionsbegriff, 1910 [Cassirer 1953], and my critical remark, Philosophie der Mathmetik und Naturwissenschaft, 1923, p. 111. [Weyl 2009b, 149–150, 216]
4 [Weyl gives further treatment of the philosophic aspect of symbols in his essay on “The Unity of Knowledge,” in Weyl 2009a, 194–203.]
5 [Shakespeare, Hamlet, I.ii.129–130.]
6 [Given the pervasive influence of Goethe on Weyl and his contemporaries, one wonders whether he intends an echo of Faust, Part I, line 1700: “Verweile doch, du bist so schön” (“Stay a while! You are so lovely”), in which Faust insists that he will never “grow stagnant nor be a slave” (line 1710). Weyl’s concept of number may thus be Faustian in character.]
7 [For the distinction between Weyl’s use of the terms “complete induction” and the contemporary meaning of this phrase, see above 31n6.]
8 [Weyl refers to Kasner and Newman 1940/2001, whose author, in conversations with children, devised the names “google” for 10100 and the less well-known term “googleplex” for 10google = 1010100.]
9 [Galileo 1957, 237–238.]
10 [This example dates back to Weyl’s 1927 writings; see Weyl 2009a, 30.]
