The reduction of mathematics to set-theory was the achievement of the epoch of Dedekind, Frege and Cantor, roughly between 1870 and 1895. As to the basic notion of set (to which that of function is essentially equivalent) there are two conflicting views: a set is considered either a collection of things (Cantor), or synonymous with a property (attribute, predicate) of things. In the latter case “x is a member of the set γ,” in formula x ∈ γ, means nothing but that x has the property γ. the property of being red or being odd is certainly prior to the set of all red bodies or of all odd numbers. On the other hand, if with regard to a bag of potatoes or a curve drawn by pencil on paper, the property of a potato to be in the bag or of a point to lie on the curve is introduced, then the set (or a more concrete structure representing the set) is prior to the property. Whatever the epistemological significance of this distinction, it leaves the mathematician cool, since for any property γ we may speak of the set γ of all elements which have the property, and with respect to a given set γ we may speak of the property to be a member of γ. When he adopts the term set in preference to property the mathematician indicates his intention to consider co-extensive properties as identical, two properties α and β being co-extensive if every element that has the property α has also the property β and vice versa (set = “Begriffsumfang[extension of concept],” Frege).1 Thus he will identify red and round in spite of their different “meanings” if every red body in the world happens to be round and vice versa.
The property π of “being prime” is represented by the propositional function P(x), read “x is prime,” with an argument x the range of significance of which is circumscribed by the concept “number.” (The natural numbers 1, 2, 3, · · · shall simply be called numbers; other numbers will be specified as rational, real, etc.) Indeed, understanding of the (false) proposition “6 is prime” requires that one understand what it means for any number x to be prime. Hence the proposition P(6) arises from the propositional function P(x) by the substitution x = 6. Besides properties we must consider binary, ternary, . . ., relations, represented by propositional functions of 2, 3, . . . arguments.
Although the mathematician need care little whether the language of properties or sets is used, he cannot afford to ignore another distinction sometimes confused with it: the distinction between what is considered as given and what he constructs from the given by the iterated combination of certain explicitly described constructive processes. For instance, in the axiomatic setup of elementary geometry one considers as given three categories of objects — points, lines (= straight lines) and planes, and a few relations between these objects (as “point lies on plane”). More complicated relations must be “defined,” i.e., logically constructed from these primitive relations. In that intuitive theory of natural numbers (arithmetic) which is truly basic for all mathematics, even the objects are not given but constructed from the first number 1 by iterating one process, addition of 1; while all arithmetical relations are logically constructed from the one basic relation thus established: y = x +1, “x is followed by y.” On the other hand, in a phenomenology of nature one would have to deal not only with categories of objects, as “bodies” or “events,” but also with whole categories of properties which are prior to all construction, e.g. with the continuum of color qualities.
Logical construction of propositional functions from other propositional functions consists in the combined iterated application of a few elementary operations. Among them are the primitive logical operators ∼ (not), ∩ (and), ∪ (or), and the two quantifiers (∃x), “there exists an x such that,” and (∀x), “for all x.” For instance, from two propositional functions S(x), T(x) we form
![]()
The quantifiers carry an argument x as index and “kill” that argument in the propositional function following the quantifier, just as the substitution of an individual number, say x = 6, does. The arithmetic operations + and × are primarily applied to numbers and from there carry over to functions, while the process of integration with respect to a variable x by its very nature refers to a function f(x). Just so, the logical operations ∼, ∩, ∪ deal primarily with propositions, while (∃x), (∀x) refer to propositional functions involving a variable x. The operator ∀ is primitive in the sense that the truth value (true or false) of a ∀ b depends only on the truth values of a and b. The same holds for ∼ and ∩. It is convenient to add the primitive operator of implication for which I use Hilbert’s symbol →: a → b is false if a is true and b false, but true for the three other combinations: a true, b true;a false, b true;a false, b false. Propositions without argument result when all variables have been eliminated by substitution of explicitly given individuals or by quantifiers. The construction of arithmetic propositions and propositional functions constitutes their “meanings.”
In introducing properties of numbers we presuppose that we know what we mean by “any number”; we shall say that the category of the elements to which the argument, in the propositional function under consideration refers must be given. We are assuming that this category is a closed realm of things existing in themselves, or, as we shall briefly say, is existential, when we ask with respect to a given property γ of its elements whether there exists an element of the property γ, with the expectation that, whatever the property γ, the question has a definite meaning and that there either exists such an element or every one of its elements has the opposite property ∼ γ. In number theory or in elementary geometry we assume the numbers or the points, lines, planes, to constitute existential categories in this sense. However, we envisage only single individual properties and relations, never anything like the category of “all possible properties of numbers.” This situation changes radically with the set-theoretic approach.
There we are forced to consider properties of numbers x as objects ξ of a new type to which the numbers stand in the relation x ∈ ξ. The proposition “6 is prime” is now looked upon as arising from the binary relation x ∈ ξ by substituting 6 for x, and the property π of being prime for the argument ξ. The “copula” ∈ corresponds to the word “is” in the spoken sentence “6 is prime.” Any propositional function P(x), like “x is prime,” gives rise to a corresponding property π = [x]P(x) (the property of being prime) such that P(x) is equivalent to x ∈ π. The operator [x] which effects transition from the propositional function to the corresponding property or set kills the argument x. For the sake of uniformity of notation we shall write henceforth ∈(x;ξ) instead of x ∈ ξ. In the same way a binary propositional function P(x, y) defines a relation π = [x, y]P(x, y) and ∈(xy;π) expresses the same as P(x, y), namely that x and y are in this relation π.
Let our further reflections be guided by two typical examples taken from Dedekind’s set-theoretic analysis of the two decisive steps in the building up of mathematics: his analysis of the sequence of numbers (in Was sind und was sollen die Zahlen 1887) and of the continuum of real numbers (in Stetigkeit und Irrrationalzahlen 1872).2 Our critical attention will be kept more alert by using Frege’s terminology of properties rather than that of sets.
I. A property α of numbers is said to be hereditary if for any number x that has the property α, the follower x + 1 also has it. Dedekind defines: A number b is less than a if there exists a hereditary property that a has but b has not.
Here it is not only supposed that we know what we mean by any property, but we refer to the totality of all possible properties. In applying the quantifiers to properties of numbers as well as to numbers, it is absolutely imperative to look upon properties as secondary objects related to our primary objects, the numbers, by the copula relation ∈. Heredity is even a property of properties. To be consistent we have to imagine objects of type 1 (the numbers), of type 2 (the properties of numbers), type 3, . . ., and the fundamental relation ∈(xn; xn + 1) connects a variable xn of type n with one xn + 1 of type n + 1. Let I(ξ) denote the proposition that ξ is hereditary. The definition of this propositional function whose Greek argument refers to the category “properties (or sets) of numbers” is as follows:
![]()
and Dedekind’s definition of x < y:
![]()
II. Dedekind, as Eudoxus had done more than 2000 years before him, characterizes a non-negative real number α by the set of all positive rational numbers (fractions) x > α. But for him any arbitrarily constructed (non-empty) set α of fractions (satisfying a certain condition, namely that along with any fraction b it contains every fraction > b) creates a corresponding real number α. The real number α is but a façon de parler for this set α. A set α consists of all fractions x satisfying a certain propositional function A(x);α = [x]A(x). Let I(ξ) be a propositional function whose argument ξ refers to properties of fractions. The (greatest) lower bound γ = [x]C(x) of a set of non-negative real numbers ξ can then be obtained as the join of all sets ξ for which I(ξ) holds:
In this way Dedekind proves that any set of non-negative real numbers has a lower bound. Again the quantifier (∃ξ) is applied to “all possible properties of fractions.”
But now let us pause to think what we have been doing. Properties of fractions are constructed by combined iterated application of a number of elementary logical operations O1, O2, · · · , Oh. Let us call any property α thus obtained a constructible property, or a property of level 1. We can then interpret (∃ξ) in the definition (1) as “There exists a constructible property ξ,” and this application of the quantifier is legitimate provided we admit its applicability to natural numbers. Indeed, the different manners in which one can form finite sequences with iteration out of h symbols O1, O2, · · · , Oh is not essentially more complicated than the possible finite sequences of one symbol 1. But the property γ = [x]C(x) defined by (1) is certainly not identical in its meaning with any of the properties of level 1 because it is defined in terms of the totality of all properties of level 1. It is therefore a property of higher level 2. Nevertheless it may be coextensive with a property of level 1, and this is exactly what Russell’s “axiom of reducibility” claims. But if the properties are constructed there is no room for an axiom here; it is a question which ought to be decided on the ground of the construction; and in our case that is a hopeless business. On the other hand, the edifice of our classical analysis collapses if we have to admit different levels of real numbers such that a real number is of level l + 1 when it is defined in terms of the totality of real numbers of level l. If we wish to save Dedekind’s proof we must abandon the constructive standpoint and assume that there is given, independently of all construction, an existential category “properties” or “second-type objects” (among which the constructible ones form but a small part) such that the following axiom holds, replacing the definition (1): For a given third-type object i there exists a second-type object γ such that
![]()
Here the arguments x and ξ refer to objects of first and second types, and ≡ means “coextensive.” That is a bold, an almost fantastic axiom; there is little justification for it in the real world in which we live, and none at all in the evidence on which our mind bases its constructions. With the assumption that properties constitute an existential category of given objects we return from Dedekind, who wanted to construct the real numbers out of the rational ones, to Eudoxus, for whom they were given by the points on a line; and instead of proving the existence of the lower bound on the ground of a definition of real numbers, we accept it as an axiom.
In reflecting on the source of the antinomies which had shown up at the fringe of Cantor’s general set-theory, Russell realized the necessity of distinguishing between the several levels.3 No doubt; by this fundamental insight, which he expressed somewhat loosely by his vicious circle principle: “No totality can contain members defined in terms of itself,” he cured the disease but, as shown by the Dedekind example, also imperiled the very life of the patient. Classical analysis, the mathematics of real variables as we know it and as it is applied in geometry and physics, has simply no use for a continuum of real numbers of different levels. With his axiom of reducibility Russell therefore abandoned the road of logical analysis and turned from the constructive to the existential-axiomatic standpoint,—a complete volte-face.4 After thus abolishing the several levels of properties, he still has the hierarchy of types: primary objects, their properties, properties of their properties, etc. And he finds that this alone will stop the known antinomies. But in the resulting system mathematics is no longer founded on logic, but on a sort of logician’s paradise, a universe endowed with an “ultimate furniture” of rather complex structure and governed by quite a number of sweeping axioms of closure. The motives are clear, but belief in this transcendental world taxes the strength of our faith hardly less than the doctrines of the early Fathers of the Church or of the scholastic philosophers of the Middle Ages.
Let us describe this structure in a little more detail. A few primary categories of elements are given; they are the ranges of significance for the lowest types of arguments. In a relation, each of the n (= 1 or 2 or 3 or · · ·) arguments x1, · · · , xn refers to a certain “type” k1, · · · , kn; the relation itself is of a type k* = {k1, · · · , kn}, determined by k1, · · · , kn, that stands higher than any of the constituents k1, · · · , kn. Draw a diagram representing k* by a dot and k1, · · · , kn by a row of dots below k* joined with it by straight lines, as you would depict a man k* and his descendants in a geneological tree. Descending from k* to its n constituents, and from them to their constituents, etc., one obtains a “topological tree” in which each end point is associated with one of the primary categories: this diagram describes the type k*. The fundamental relation is ∃(x1 · · · xn; x*) where x1, · · · , xn, refer to given types k1, · · · , kn and x* to k* = {k1, · · · , kn}. Existential categories of elements are supposed to be given, one for each possible type (including the lowest, the primary types). We mentioned at the beginning with what data axiomatic elementary geometry operates, or a phenomenology of nature may have to operate; our present “Russell universe” U is seen to be incomparably richer.
We give a few of the more obvious axioms on which its theory is to be erected. The universal normal form for propositional functions involving n variables x1, · · · , xn of given types k1, · · · , kn is ∈(x1 · · · xn;a*). Indeed, such a relation is itself an element a* of type k* = {k1, · · · , kn}. The relation of identity (x = y) between elements of type k is itself an element of type {k, k}; call it I = Ik. Similarly, let E = Ek1 · · · kn be the ∈ relation with its n + 1 arguments of types k1, · · · , kn, k* = {k1, · · · , kn}. The existence of these special elements must be stipulated explicitly:
Axiom 1. There is an element I = Ik of type {k, k} such that (xy;I) holds if and only if the elements x, y of type k are identical. There is an element E = Ek1 · · · kn of type K = {k1, · · · , kn, k*} such that ∈(x1 · · · xnx*;E) is coextensive with ∈(x1 · · · xn; x*), the variables x1, · · · , xn, and x* ranging over their respective categories k1, · · · , kn and k* = {k1, · · · , kn}.
The composite property “red or round” is no longer constructed from the descriptive properties “red,” “round,” but belongs with them to the category of properties given prior to all construction. Its existence must be guaranteed by one of the simpler axioms of closure.
Axiom 2. Given an element a* and an element b* of type k* = {k1, · · · , kn} there exists an element c* of the same type such that ∈(x1 · · · xn;c*) is coextensive with
![]()
(each xi varying over its category ki).
Substitution of a definite element b for a variable is taken care of by the
Axiom 3. Given an element a* of type k* = {k1, · · · , kn} and an element bn of type kn, there exists an element c of type k = {k1, · · · , kn−1;a) such that ∈(x1 · · · xn−1; a) is coextensive with ∈(x1 · · · xn−1bn;a*) (if x1, · · · , xn−1 vary over the categories k1, · · · kn−1).
Elimination of a variable xn, by the corresponding quantifier (∃xn) changes a relation a* of type k* into a relation a of type k:
Axiom 4. Given an element a* of type k* = {k1, · · · , kn}, there exists an element a of type k = {k1, · · · , kn−1} such that ∈(x1 · · · xn−1;a) is coextensive with (∃xn) ∈(x1 · · · xn−1xn;a*).
These are only a few typical axioms that indicate the direction. The reader must not look for them in the Principia Mathematica, which are conceived in a different style. But our system U embodies the same ideas in a form that seems to me both natural in itself and advantageous for a comparison with other systems W, Z presently to be discussed.
Our axioms serve as a basis for deduction in the same way as, for instance, the axioms of geometry; deduction takes place by that sort of logic on which one is used to rely in geometry or analysis, including the free use of “there exists” and “all” with reference to any fixed type in the hierarchy of types an dthe elements of the corresponding categories. While these categories, as well as the basic relation ∈, are considered as undefined, the logical terms like “not” ∼, “if then” →, “there is” (∃x), etc., have to be understood in their meaning and do not form part of the axiomatic system: the formalism of symbolic logic is merely used for the sake of conciseness.
If the Principia Mathematica set out to base mathematics on pure logic the result, as we now see, is quite different: an axiomatic world system has taken the place of logic. Its very structure, the hierarchy of types, cannot be described without resort to the intuitive concept of iteration. To develop, in Dedekind-Frege fashion, a theory of natural numbers from this system is therefore an enterprise of doubtful value.
Realizing the highly transcendental character of the axiomatic universe from which this system deduces mathematics, one wonders whether it is not possible to stick, in spite of everything, to the constructive standpoint, which seems so much more natural to the mathematician. We accept the hierarchy of types; but we assume only one category of primary objects, the numbers; and one basic binary relation between numbers, namely “x is followed by y.” All other relations of the various types are explicitly constructed, the quantifiers (∃x) and (∀x) being applied only to numbers and not to arguments of higher type. No axioms are postulated. What we can get in this way constitutes the ground level, or level 1. One could build over it a second level containing relations which are constructed by applying the quantifiers to the totality of relations of this or that type constructible on the first level, and proceed in the same manner from the second to a third level, etc. One would obtain a “ramified hierarchy” of types and levels. But in this way, as we have said before, nothing resembling our classical Calculus will result. The temptation to pass beyond the first level of construction must be resisted; instead, one should try to make the range of constructible relations as wide as possible by enlarging the stock of basic operations. It is a priori clear that iteration in some form must find a place among these irreducible principles of construction—contrary to the Dedekind-Frege program.
We begin again at the beginning. Let R(x, ξ) be a binary propositional function the two arguments x, ξ of which are of types k, κ respectively; for instance the relation “x is less than ξ” between numbers. We can then speak of the property of a number “to be less than ξ” (or of the set of all numbers less than ξ). This is obviously a property depending on ξ. In general terms we can form [x]R(x, ξ) = r*(ξ), which is an element of {k} depending on ξ such that R(x, ξ) is coextensive with ∈(x;r*(ξ)). If in addition to R(x, ξ) we have a propositional function S(x*) whose argument is of type k* = {k}, wecanform T(ξ) = S(r*(ξ)), or more explicitly,
![]()
This is the process of substitution generating T(ξ) from R(x, ξ) and S(x*).
Take now the particular situation that κ = {k}. Then argument and value of the function r*(ξ) = [x]R(x, ξ) are of the same type κ, and whenever that happens iteration becomes possible. Thus we define by complete induction a relation T(n, ξ) in which the argument n refers to the primary category of numbers, as follows:
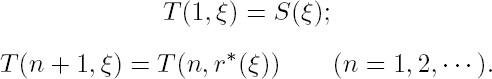
Adding the operation of substitution and iteration, as illustrated by these examples, to the other elementary logic operations, but without applying the quantifiers to anything else than numbers, the writer was able (in Das Kontinuum, 1918) to build up in a purely constructive way, and without axioms, a fair part of classical analysis, including for instance Cauchy’s criterion of convergence for infinite sequences of real numbers.5 In this system iteration plays the role which in set-theory was played by the uninhibited application of quantifiers. Our construction honestly draws the consequences of Russell’s logical insight into the tower of levels, which Dedekind had ignored inadvertently and Russell himself, afraid of its consequences, razed to the ground by his axiom of reducibility. Considering their common origin the axiomatic system U as outlined in section 4 and this constructive approach are remarkably different. But even here we have adhered to the belief that “there is” and “all” make sense when applied to natural numbers: in addition to logic we rely on this existential creed and the idea of iteration.
Essentially more radical and a further step toward pure constructivism is Brouwer’s intuitionistic mathematics.6 Brouwer made it clear, as I think beyond any doubt, that there is no evidence supporting the belief in the existential character of the totality of all natural numbers, and hence the principle of excluded middle in the form “Either there is a number of the given property γ, or all numbers have the property ∼ γ” is without foundation. The first part of the sentence is an abstract from some statement of fact in the form: The number thus and thus constructed has the property γ. The second part is one of hypothetic generality, asserting something only if · · · ; viz., if you are actually given a number, you may be sure that it has the property ∼ γ. The sequence of numbers which grows beyond any stage already reached by passing to the next number, is a manifold of possibilities open towards infinity; it remains forever in the status of creation, but is not a closed realm of things existing in themselves. That we blindly converted one into the other is the true source of our difficulties, including the antinomies—a source of more fundamental nature than Russell’s vicious circle principle indicated. Brouwer opened our eyes and made us see how far classical mathematics, nourished by a belief in the “absolute” that transcends all human possibilities of realization, goes beyond such statements as can claim real meaning and truth founded on evidence. According to his view and reading of history, classical logic was abstracted from the mathematics of finite sets and their subsets. (The word finite is here to be taken in the precise sense that the members of such a set are explicitly exhibited one by one.) Forgetful of this limited origin, one afterwards mistook that logic for something above and prior to all mathematics, and finally applied it, without justification, to the mathematics of infinite sets. This is the Fall and original sin of set-theory, for which it is justly punished by the antinomies. Not that such contradictions showed up is surprising, but that they showed up at such a late stage of the game!
Thanks to the notion of “Wahlfolge[choice sequence],” that is a sequence in statu nascendi in which one number after the other is freely chosen rather than determined by law, Brouwer’s treatment of real variables is in the closest harmony with the intuitive nature of the continuum; this is one of the most attractive features of his theory.7 But on the whole, Brouwer’s mathematics is less simple and much more limited in power than our familiar “existential” mathematics. It is for this reason that the vast majority of mathematicians hesitate to go along with his radical reform.
From this excursion to the left wing of the “constructionists” we return to the universe U with its hierarchy of types. Once one has committed oneself to the existential or axiomatic viewpoint, can one not go forth in the same direction and even erase all differences of types, taking only such precautions as are absolutely necessary to avoid the known contradictions? This is what Zermelo did in his Untersuchungen über die Grundlagen der Mengenlehre [Investigations on the Foundations of the Theory of Sets], 1908.8 His axioms deal with only one (existential) category of objects called elements or sets, and one basic relation x ∈ y, “x is member of y.” But he is forced to give up the principle that any well-defined property γ determines an element c such that x ∈ c whenever the element x has the property γ and vice versa. Properties are used by him merely to cut out subsets from a given set. Hence his axiom of selection: “Given a well-defined property γ and an element a, there is an element a′ such that x ∈ a if and only if x is member of a and has at the same time the property γ.” The notion of a well-defined property which enters into it is somewhat vague. But we know that we can make it precise by constructing properties by iterated combined application of some elementary constructive processes. Instead of saying that x has the property γ, let us say that x is a member of the class γ, x ∈ γ. We thus distinguish between elements or sets on the one hand, classes on the other, and formulate the axioms in terms of two undefined categories of objects, elements and classes. Since we postulate that two elements a, b are identical in case x ∈ a and x ∈ b are coextensive, and since each element a is associated with the class α of all elements x satisfying the condition x ∈ a, we are justified in identifying a with that class α. Then every element is a class and the axioms deal with one undefined fundamental relation x ∈ ξ, “the element x is member of the class ξ,” which has absorbed Zermelo’s relation x ∈ y between elements. The principles for the construction of properties are replaced by corresponding axioms for classes; e.g., given two classes α and β, there exists a class γ such that the statement (x ∈ α) ∪ (x ∈ β) about an arbitrary element x is coextensive with x ∈ y.
Since the axiom of selection can only generate smaller sets out of a given set, we need some vehicle that carries us in the opposite direction. Therefore two axioms are added guaranteeing the existence of the set of all subsets of a given set and the join of a given set of sets. It is essential that they be limited to sets = elements and do not apply to classes.
With the introduction of classes, which is due to Fraenkel, von Neumann, Bernays, and others, the axioms assume the same self-sustaining character as, for instance, the axioms of geometry; no longer do such general notions as “any well-defined property” penetrate into the axiomatic system from the outside. A complete table of axioms for this system, Z as we shall call it, is to be found on the first pages of Gödel’s monograph, Consistency of the Continuum Hypothesis.9 Even before the turn of the century Cantor himself had moved in the same direction by distinguishing “consistent classes” = sets and inconsistent classes.10 Not the hierarchy of types, but the non-admission among the decent “sets” of such classes as are too “big,” averts here the disaster of the familiar antinomies.
One might object to a system like Z on the ground that it does not rest on a real insight into the causes of the antinomies but patches up Cantor’s original conception by a minimum of concessions necessary to avoid the known contradictions. Indeed, we have no assurance of the consistency of Z, except from the empirical fact that so far no contradictions have resulted from it. But we are in no better position toward Russell’s universe U. And Z has its great advantages over U: it is of an essentially simpler structure and seems to be the most adequate basis for what is actually done in present-day mathematics. In particular, the “existential” Dedekind-Frege theory of numbers can be derived from it (Zermelo), and Gödel was able to show that Zermelo’s far-reaching axiom of choice in a very sharp form is consistent with the other axioms of Z.11
A new turn in the axiomatization of mathematics of paramount importance was inaugurated by Hilbert’s “Beweistheorie” [theory of proof] (since 1922).12 Hilbert sets out to prove (not the truth, but) the consistency of mathematics. He realizes that to that end mathematics and logic must first be completely formalized: all statements are to be replaced by formulas in which now also the logical operators ∼, ∩,(∃x) etc., appear as undefined symbols. Thus formalized logic is absorbed into formalized mathematics.13 The formulas have no meaning. A mathematical demonstration is a concrete sequence of formulas in which a formula is derived from the preceding ones according to certain rules comprehensible without recourse to any meaning of the formulas — just as in a game of chess each position is derived from the preceding one by a move obeying certain rules.Consistency, the fact that no such game of deduction may end with the formula ∼(1 = 1), must be proved by intuitive reasoning about the formulas which rests on evidence rather than on axioms, and respects throughout the limits of evidence as disclosed by Brouwer. But in this thinking about demonstrations, in following a hypothetic sequence of formulas leading up to the end formula ∼(1 = 1) our mind cannot help using that type of evidence in which the possibility of iteration is founded. In the axiomatization of mathematics Hilbert is forced to proceed with more restraint than Zermelo: if he is too liberal with his axioms he will lose all chance of ever proving their consistency; he is guided by an at least vaguely preconceived plan for such a proof. It is for this reason that he finds it advisable, for instance, to distinguish various levels of variables.
Hilbert’s formulas are concrete structures consisting of concrete symbols; the order in which the symbols follow one another in a formula, and also their identity in the same or different formulas, must be recognizable irrespective of little variations in their execution. Handling these symbols, we move on the same level of understanding as guides our daily life in our relationship to such tools as hammer or table or chair. Hilbert sees in it the most important prelogical foundation of mathematics, in fact of all science. But in addition his axioms of mathematics and the intuition of iteration of which the metamathematical nonaxiomatic reasoning about mathematics makes use are other extralogical ingredients of his system.
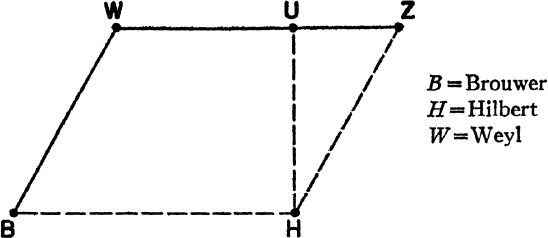
Our brief survey may be summarized in a little diagram in which the constructive tendency increases toward the left, the axiomatic toward the right, and also the relative “depth” of the foundations is indicated. Frege and after him Russell had hoped (1) to develop the theory of natural numbers on a sure basis without recourse to the intuitive idea of indefinite iteration, and (2) to make mathematics a part of logic. We have now seen that none of the systems discussed gives any hope of accomplishing (2), the subjugation of mathematics by logic. In U and Z elaborate systems of axioms form the basis, in W, B, and to a lesser degree also in U, the intuitive idea of iteration is indispensable. The extra-logical foundations of Hilbert’s theory have just been described. The only system which in a sense can claim to reach the goal (1) is Z. But even there the theory of numbers does not rest on logic alone, but on a highly transcendental system of axioms (the belief in whose consistency is supported by empirical facts, but not by reasons). Poincaré has proved right in his defense of mathematical induction as an indispensable and irreducible tool of mathematical reasoning.
It is likely that all mathematicians ultimately would have accepted Hilbert’s approach had he been able to carry it out successfully. The first steps were inspiring and promising. But then Gödel dealt it a terrific blow (1931), from which it has not yet recovered. Gödel enumerated the symbols, formulas, and sequences of formulas in Hilbert’s formalism in a certain way, and thus transformed the assertion of consistency into an arithmetic proposition. He could show that this proposition can neither be proved nor disproved within the formalism.14 This can mean only two things: either the reasoning by which a proof of consistency is given must contain some argument that has no formal counterpart within the system, i.e., we have not succeeded in completely formalizing the procedure of mathematical induction; or hope for a strictly “finitistic” proof of consistency must be given up altogether. When G. Gentzen finally succeeded in proving the consistency of arithmetic he trespassed those limits indeed by claiming as evident a type of reasoning that penetrates into Cantor’s “second class of ordinal numbers.”15
From this history one thing should be clear: we are less certain than ever about the ultimate foundations of (logic and) mathematics. Like everybody and everything in the world today, we have our “crisis.” We have had it for nearly fifty years. Outwardly it does not seem to hamper our daily work, and yet I for one confess that it has had a considerable practical influence on my mathematical life: it directed my interests to fields I considered relatively “safe,” and has been a constant drain on the enthusiasm and determination with which I pursued my research work. This experience is probably shared by other mathematicians who are not indifferent to what their scientific endeavors mean in the context of man’s whole caring and knowing, suffering and creative existence in the world.
[Published with the subtitle “a brief survey serving as a preface to a review of The Philosophy of Bertrand Russell” in Weyl 1946a;WGA 4:268–279. Weyl 1946b gives the text of his review of Schilpp 1951. In its original printed version, Weyl used the printed Greek symbol ![]() rather than its common present orthography as ∈, which we have used throughout the text here. Also, Weyl’s original references have been included as notes below.]
rather than its common present orthography as ∈, which we have used throughout the text here. Also, Weyl’s original references have been included as notes below.]
1 [See Burge 1984 for a discussion of this term in context.]
2 [Dedekind’s two fundamental writings, translated as “The Nature and Meaning of Numbers” and “Continuity and Irrational Numbers” are available in Dedekind 1963 and in Ewald 1996, 2:787–832, 765–778.]
3 “Mathematical Logic as Based on the Theory of Type,” Am. Jour. Math., v. 30, 1908, pp. 222–262. B. Russell and A. N. Whitehead, Principia Mathematica, 3 vols., Cambridge, 1910–13; 2nd ed. of vol. I, 1935.
4 I know very well that this is at odds with Russell’s own interpretation; he in the course of time became more and more inclined to visualize sets as “logical fictions.” “Though,” as Gödel adds, “perhaps the word fiction need not necessarily mean that these things do not exist, but only that we have no direct perceptions of them.” In the second edition of Volume I of the Principia Mathematica, an attempt is made to prove independently of the axiom of reducibility that at least all levels of natural numbers can be reduced to the five lowest. But as Gödel observes, the proof is far from being conclusive. [See] Gödel, “Russell’s Mathematical Logic,” in The Philosophy of Bertrand Russell, pp. 127, 145, 146 [Schilpp 1951].
5 But of course the theorem of the lower bound of an arbitrary set of nonnegative real numbers could not be upheld. [For a translation of Das Kontinuum, see Weyl 1994.]
6 Brouwer’s thesis “Over de grondslagen der wiskunde” appeared in 1907 [translated in Brouwer 1975]. For a list of his papers on the subject see A. Church’s “Bibliography of Symbolic Logic,” Jour. Symb. Logic, v. 1, 1936, pp. 121–218. [For helpful selections of his texts, see Ewald 1996, 2:1166–1207 and Mancosu 1998, 1–64, 286–295.]
7 [See Van Atten 2007.]
8 Annals of Mathematics Studies No. 3, Princeton, 1940;Math. Ann., v. 65, 1908, pp. 261–281. [See also Ewald 1996, 2:1208–1233.]
9 See also P. Bernays, Jour. Symb. Logic, v. 2, 1937, pp. 65–77 and the references given there. [Gödel 1986–2003, 2:33–101, reprints his monograph on the consistency of the continuum hypothesis.]
10 Cf. G. Cantor, Gesammelte Abhandlungen, ed. E. Zermelo, 1932, pp. 443– 451 (correspondence Cantor-Dedekind) [Cantor 1980].
11 [See Gödel 1986–2003, 2:33–101.]
12 Vol. 3 of Hilbert’s Collected Papers, 1937, and Hilbert-Bernays, Grundlagen der Mathematik, 2 vols. 1934 and 1939 [Hilbert and Bernays 1968–70].
13 In this regard the ground was well prepared for Hilbert by the Principia Mathematica. For the sake of comparison I mention one other completely formalized system, that of Quine. [See]Am. Math. Monthly, v. 44, 1937, pp. 70-80.
14 Monatsh. Math. Phys., v. 38, 1931, pp. 173–198 [Gödel 1986–2003, 1:144– 195].
15 Math. Ann., v. 112, 1936, pp. 493–565 [in Gentzen 1969].